パターン認識・
機械学習勉強会
第3回
@ワークスアプリケーションズ
中村晃一2014年2月27日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
モデル選択基準
前回に続いてモデル選択の話題を進めます.
前回は交差検証によって汎化性能を推定する方法を紹介しましたが, データが十分ある場合にはより複雑なモデルが選ばれやすいという傾向があります.
複雑さを考慮してモデルを評価する指標としては 赤池情報量基準 (Akaike information criterion, AIC) が有名で, 例えば以下のように定義されます(C.M.ビショップ「パターン認識と機械学習(上・下)」では等価ですが異なる定義がなされています).
赤池情報量基準
\[ \mathrm{AIC} = -2\ln L + 2M \] 但し, $L$ は最大尤度, $M$ はモデルのパラメータ数.
$\mathrm{AIC}$ が最小となるようにモデルを選択します.
回帰分析に最小二乗法を利用した場合は, 学習データ数を $n$, 残差平方和を $RSS$ として \[ \mathrm{AIC}\approx n\ln\left(\frac{RSS}{n}\right)+2M+\mathrm{const}.\] となります.(参考)
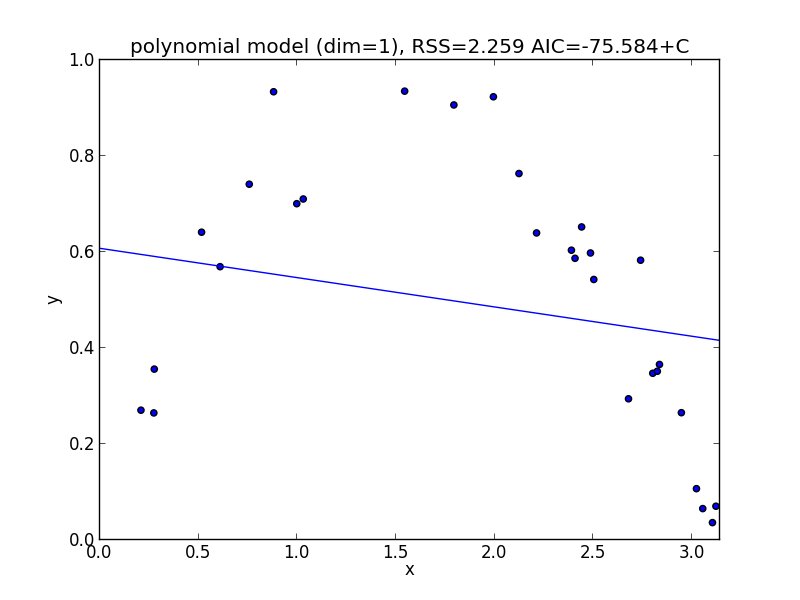
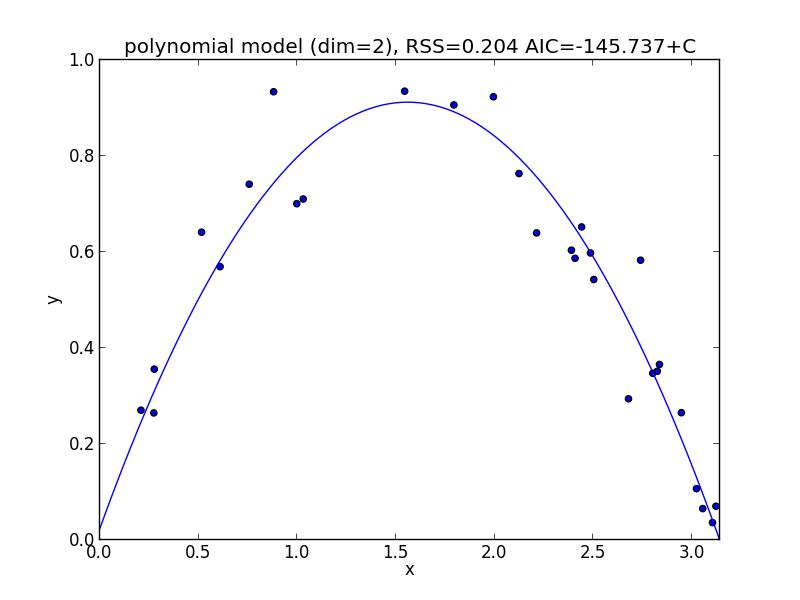
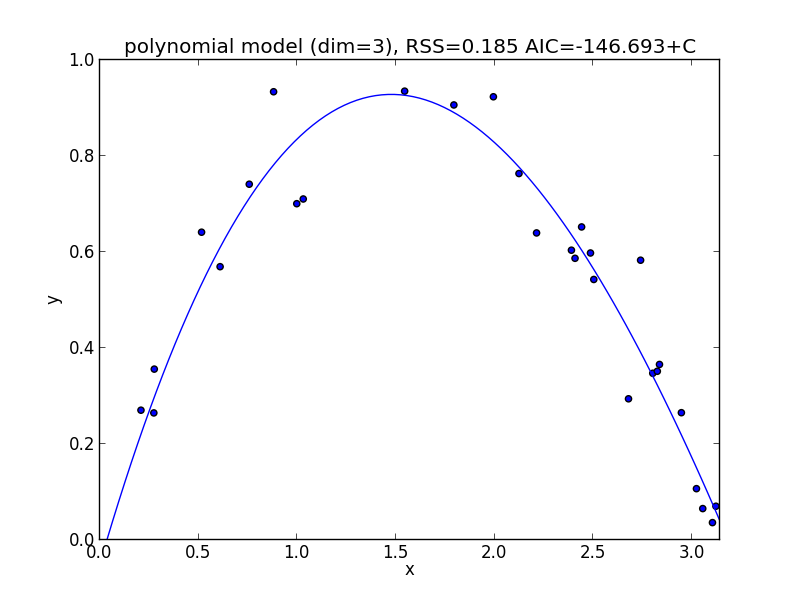
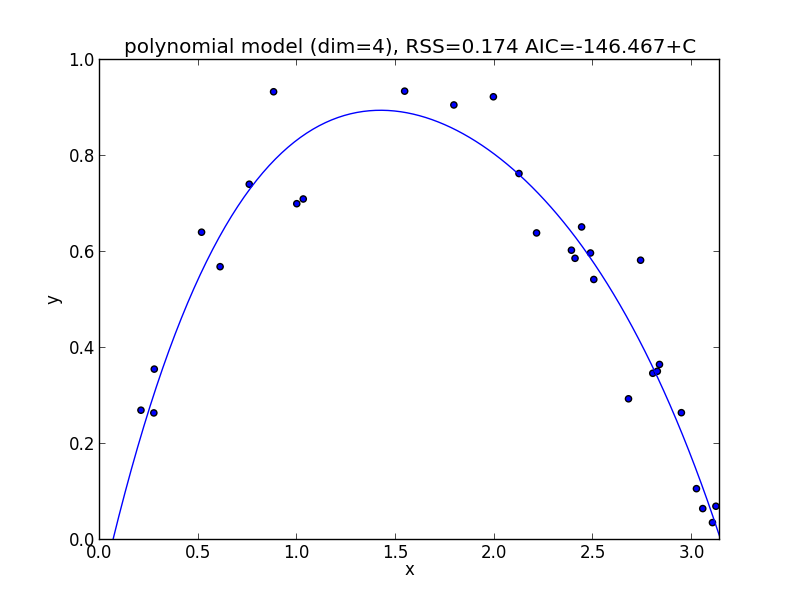
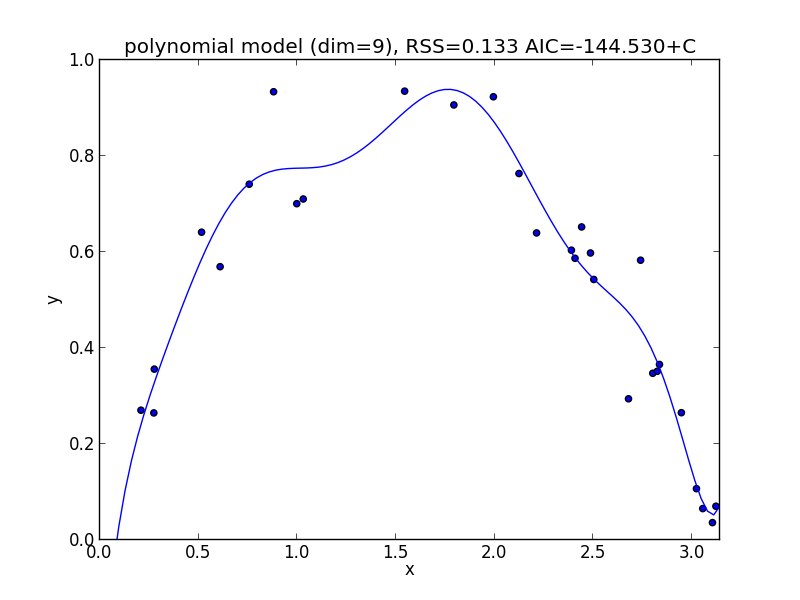
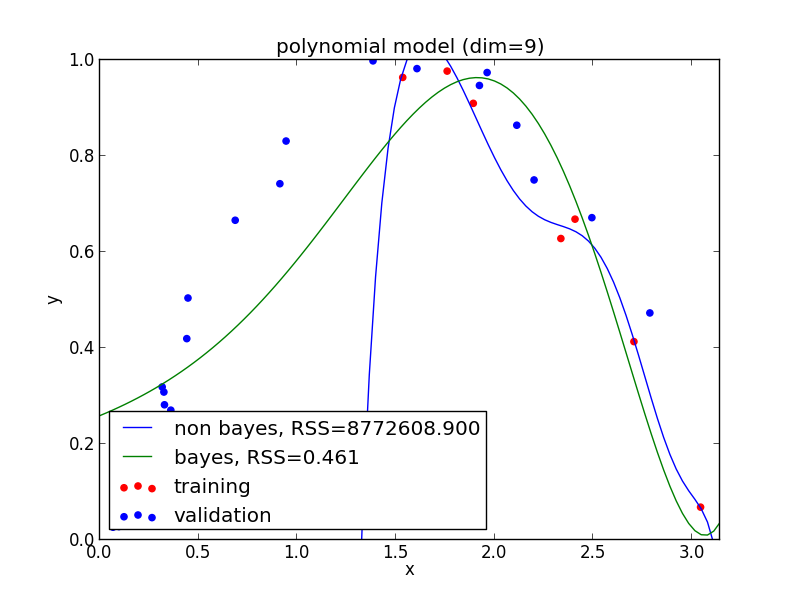
前回と同じフィッティングの問題で計算してみましょう.
1次式の場合
2次式の場合
3次式の場合
4次式の場合
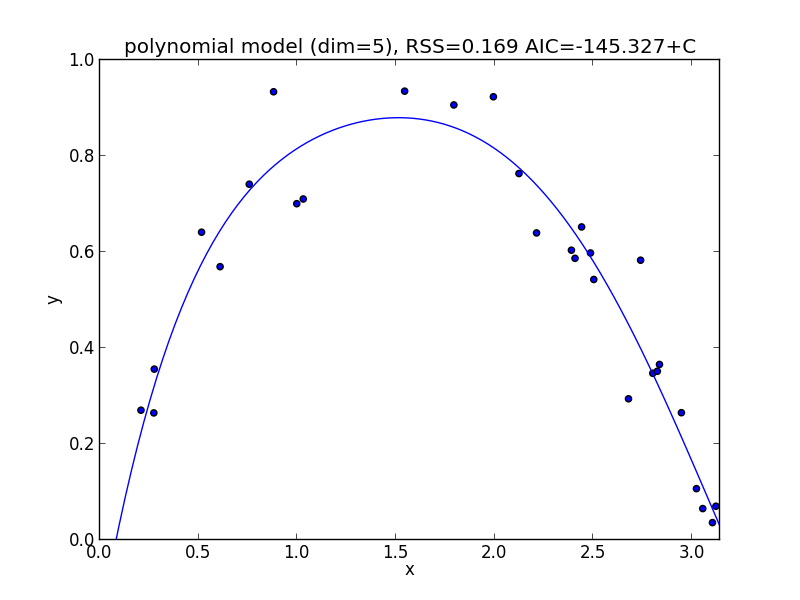
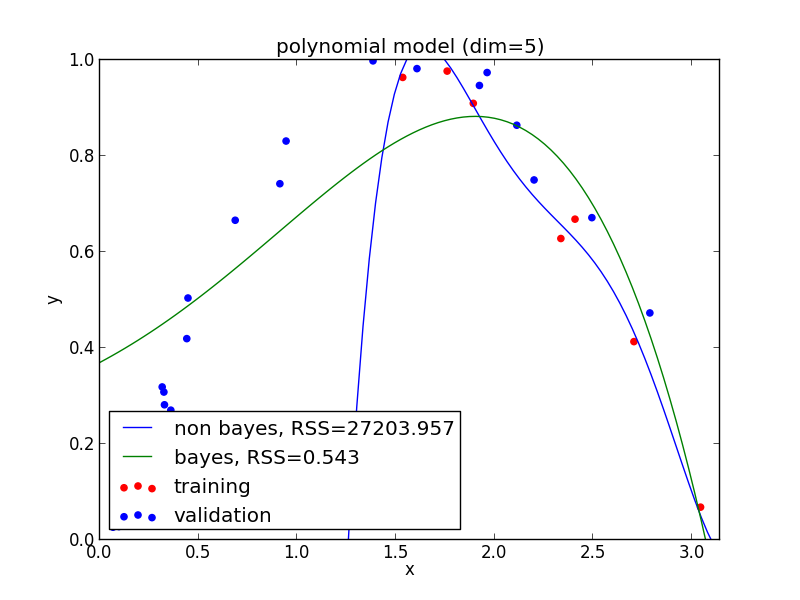
5次式の場合
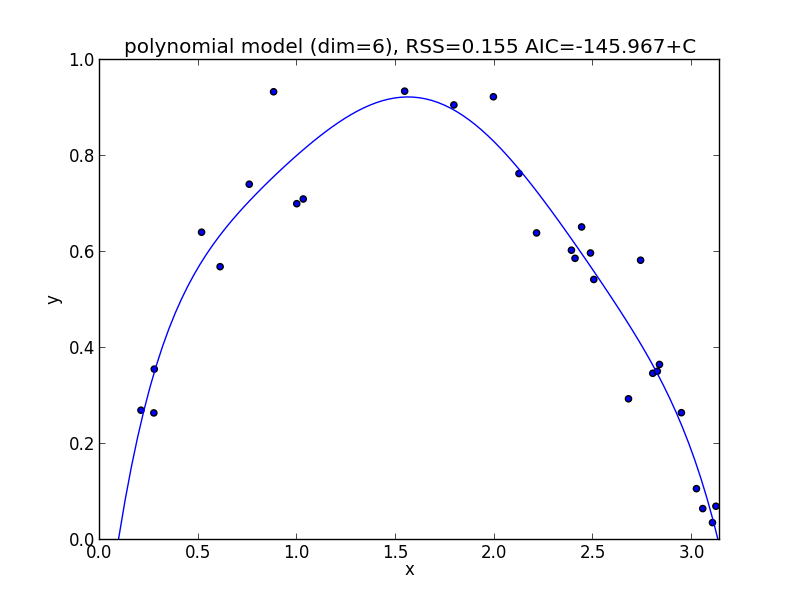
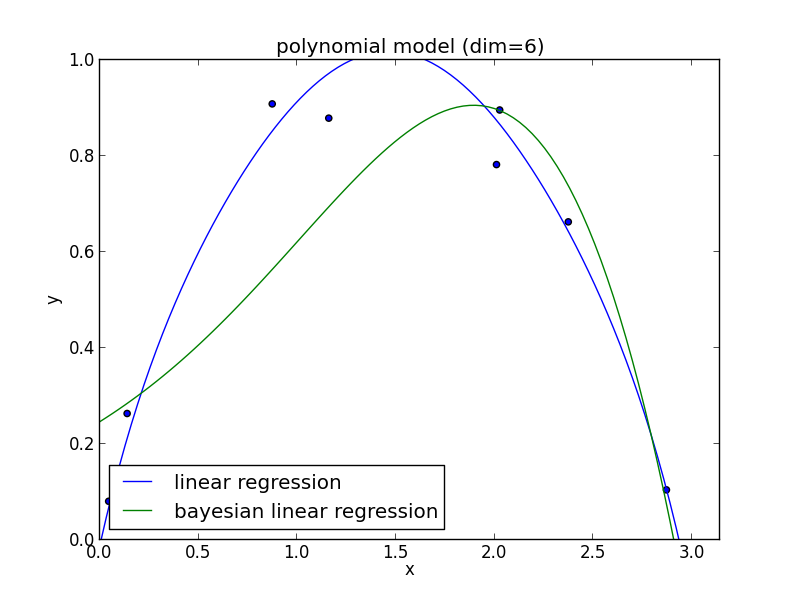
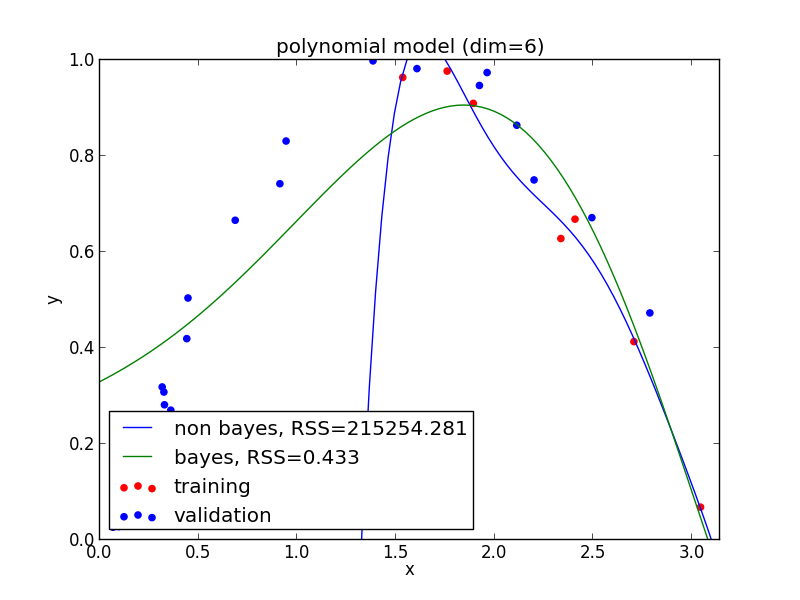
6次式の場合
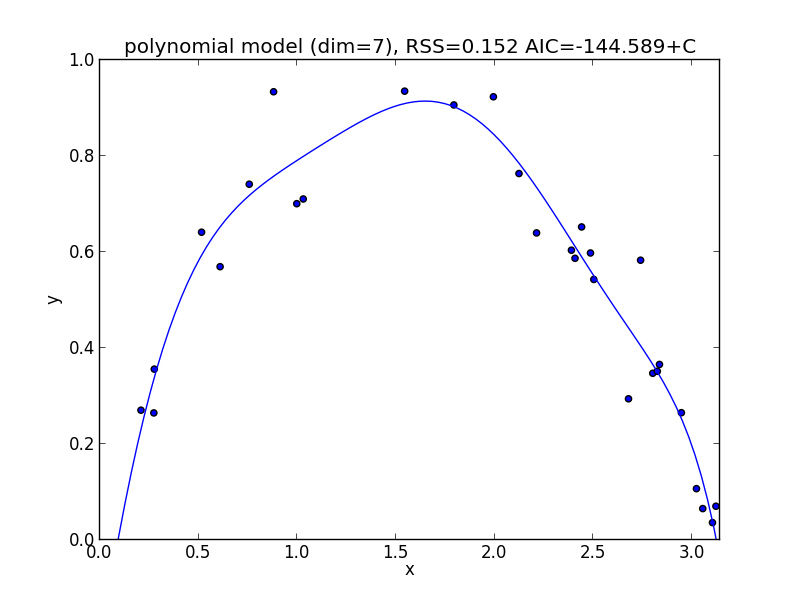
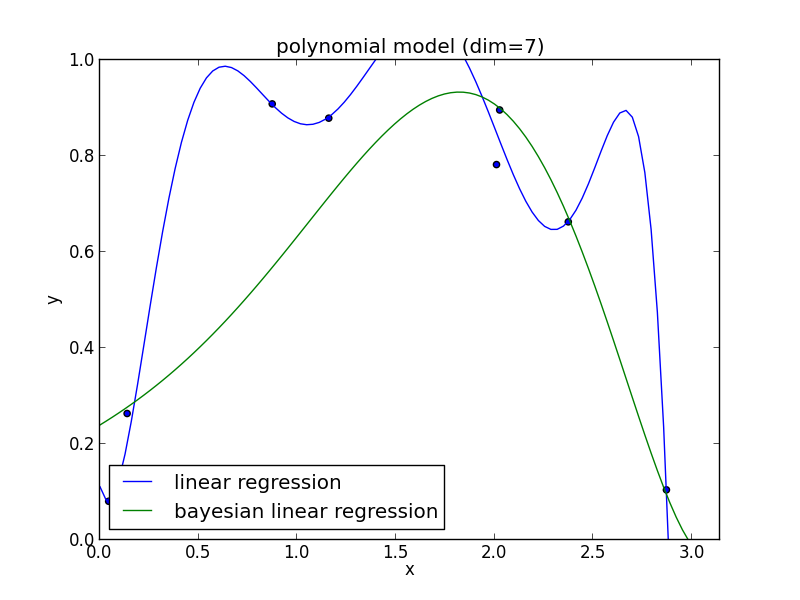
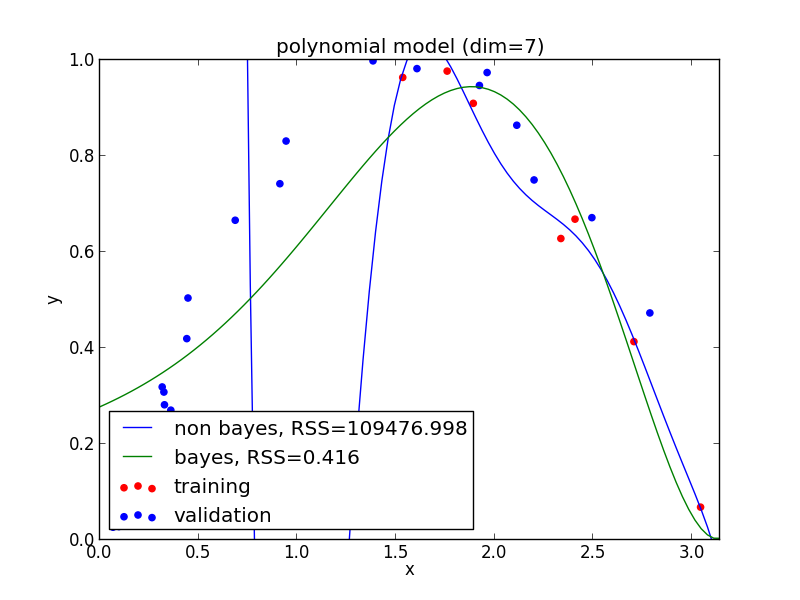
7次式の場合
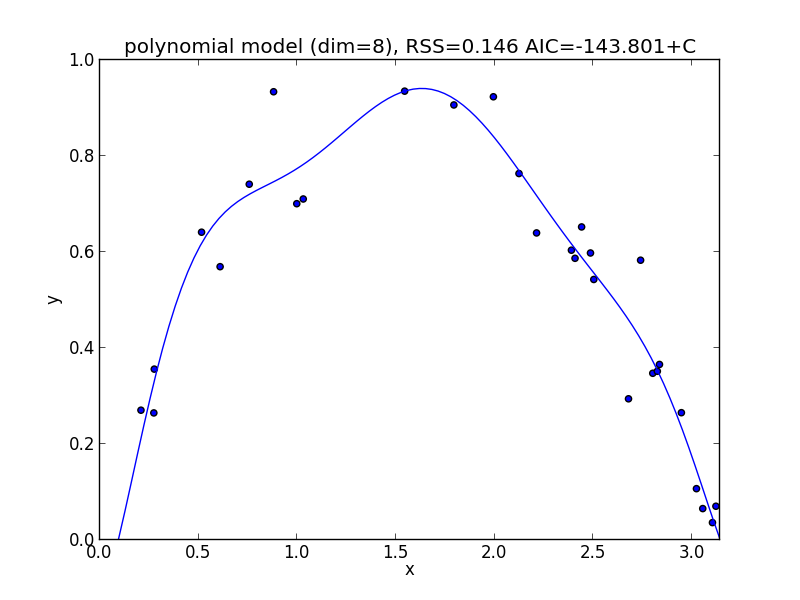
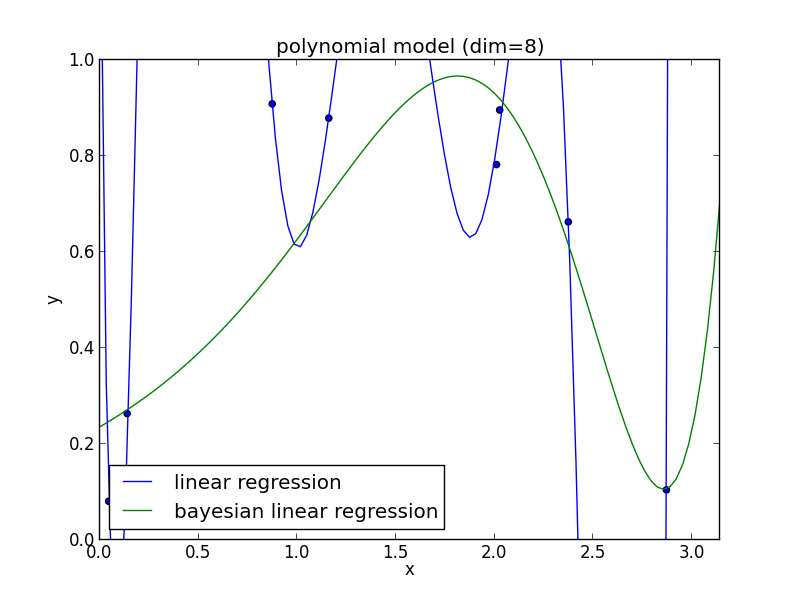
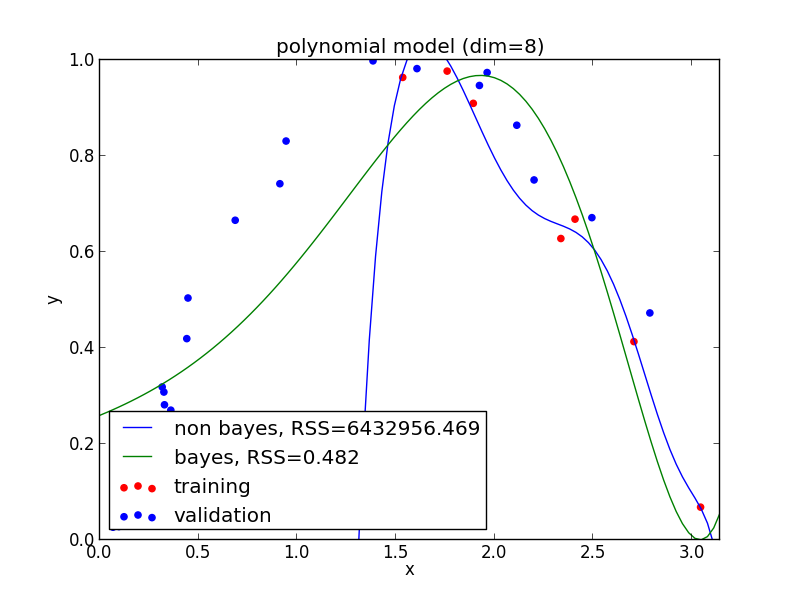
8次式の場合
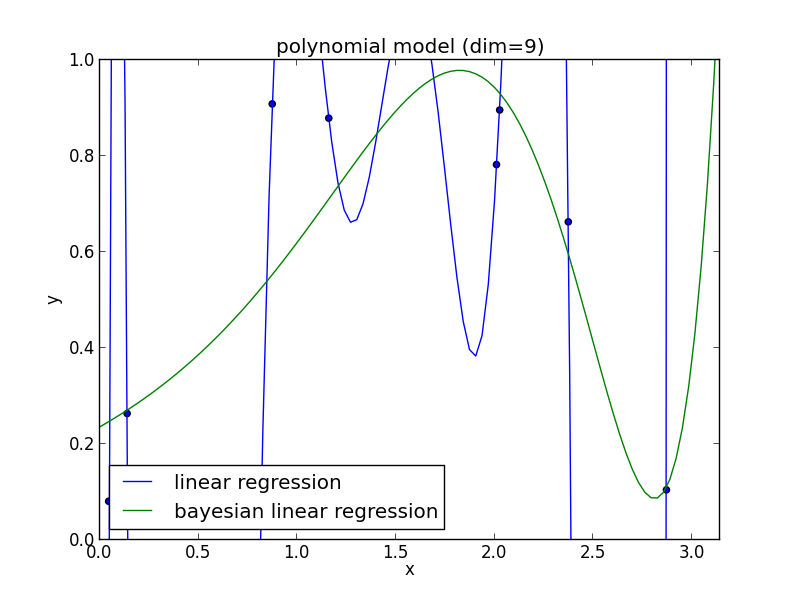
9次式の場合
今の例では $3$ 次のモデルでの$\mathrm{AIC}$ が最小となりました.
複雑なモデルにより大きなペナルティを課した ベイズ情報量基準 (Bayesian information criterion, BIC) というも物もあります.
ベイズ情報量基準
\[ \mathrm{BIC} = -2\ln L + M\ln n \] 但し, $L$ は最大尤度, $M$ はモデルのパラメータ数, $n$ は学習データの数.
他に, 最小記述長 (minimum description length, MDL)も有名ですが, $\mathrm{MDL}=\mathrm{BIC}/2$ なので, $\mathrm{BIC}$ と等価です.
モデル選択基準は非常に手軽に計算出来る反面, かなり粗い近似の元に導出されている量なのでニューラルネットワークなどの複雑な確率分布を用いる手法では誤った結果を導く事があります. 注意して利用してください.
ベイズ線形回帰
モデルのパラメータの分布も考慮にいれて回帰分析を行う事で, 過学習を回避する事が出来ます. ベイズ確率論に基づくモデル選択の問題に対する厳密なアプローチと言えます.
線形回帰
まずは 線形回帰 (linear regression) の復習をしましょう.
既知のベクトル値関数 $\Psi$ を用いて \[ f(\mathbf{x}, \mathbf{a}) = \mathbf{a}^T\Psi(\mathbf{x}) \] と表されるモデルを 一般化線形モデル (generalized linear model) と呼びます.
例えば, 多項式モデルは \[ \begin{aligned} &a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 \\ =&(a_n,a_{n-1},\ldots,a_1,a_0)\begin{pmatrix} x^n \\ x^{n-1} \\ \vdots \\ x \\ 1 \end{pmatrix} \end{aligned} \] と書けるので, 一般化線形モデルの1つです.
$\Psi(\mathbf{x})$ の成分はそのモデルの 基底 (basis) と呼ばれます. 多項式モデルの場合には $1,x,x^2,\ldots$ という基底をつかっています.
他に, よくつかうガウス基底とロジスティック・シグモイド基底を紹介します. 分野によってはフーリエ基底やウェーブレット基底なども利用されますが 省略します.
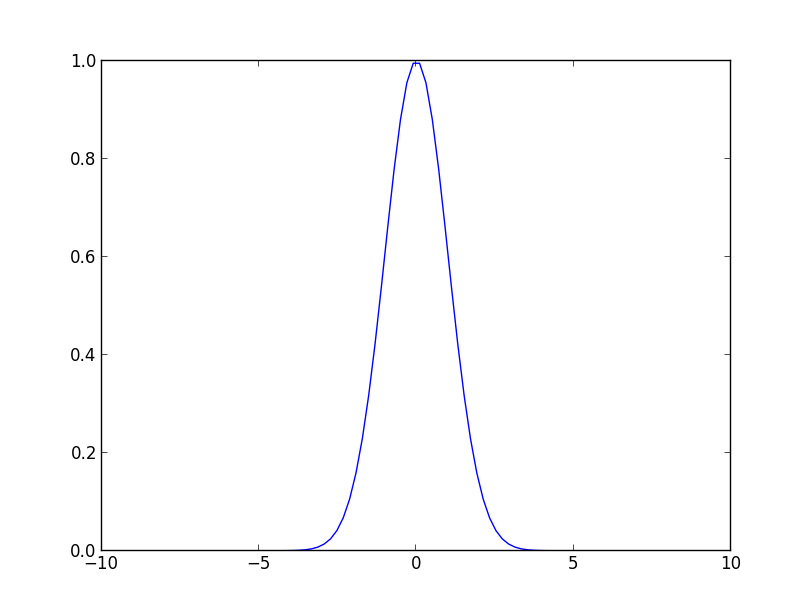
ガウス基底 (Gaussian basis) は \[ \psi_i(x) = \exp\left\{-\frac{(x-\mu_i)^2}{2\sigma^2}\right\} \] という形の基底です.正規分布に比例するもので, 局所的な分布を表現する為に利用できます.
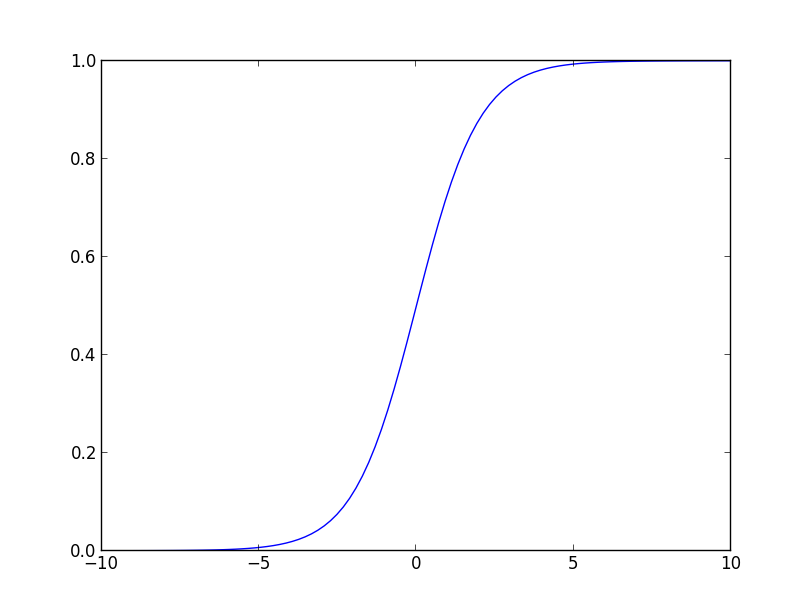
ロジスティック・シグモイド基底 (logictic sigmoid basis) は \[ \psi_i(x) = \frac{1}{1+\exp\left(-\frac{x-\mu_i}{\sigma}\right)} \] という形の基底です. 識別の問題では 0 か 1 の値をとる関数をよく考えますが, 不連続なので扱いが難しいです. この基底は0-1関数を微分可能なもので近似したものと考える事が出来ます.
最小二乗法
「観測誤差は正規分布に従う」という仮定に基づいてパラメータの最尤推定値を求める方法が 最小二乗法 (least squares method) です.
つまり, 個々の学習データ $(\mathbf{x}_i,y_i)$ を \[ y_i = f(\mathbf{x}_i,\mathbf{a}) + \varepsilon_i \] と表した時に, $\varepsilon_i\sim N(0, \sigma_i^2)$ であると仮定します.
学習データ $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\}$ が独立に生成されたと仮定すると, 尤度関数は \[ \begin{aligned} L(\mathbf{a}) &\propto \prod_{i} \exp\left\{-\frac{||y_i-f(\mathbf{x}_i,\mathbf{a})||^2}{2\sigma_i^2}\right\} \\ &= \exp\left\{-\frac{1}{2}\sum_i \frac{||y_i-f(\mathbf{x}_i,\mathbf{a})||^2}{\sigma_i^2}\right\} \end{aligned} \] となりますので,
$\mathbf{a}$ の最尤推定値は \[ \hat{\mathbf{a}}=\mathop{\rm arg~max}\limits_{\mathbf{a}}\sum_i \frac{||y_i-f(\mathbf{x}_i,\mathbf{a})||^2}{\sigma_i^2} \] となります.
特に $\sigma_i$ が全て等しいならば \[ \hat{\mathbf{a}}=\mathop{\rm arg~max}\limits_{\mathbf{a}}\sum_i ||y_i-f(\mathbf{x}_i,\mathbf{a})||^2 \] となり, 通常の最小二乗法の式が得られました.
一般化線形モデルの場合には \[ \sum_i ||y_i-\mathbf{a}^T\Psi(\mathbf{x}_i)||^2 \] を $\mathbf{a}$ で微分した物が $\mathbf{0}$ となる条件から, 最小二乗法の 正規方程式 (normal equation) \[ \mathbf{X}^T\mathbf{X}\mathbf{a}=\mathbf{X}^T\mathbf{y} \] が得られます. ただし, \[ \begin{aligned} \mathbf{X} &= (\Psi(\mathbf{x}_1),\Psi(\mathbf{x}_2),\ldots,\Psi(\mathbf{x}_m))^T \\ \mathbf{y} &= (y_1,y_2,\ldots,y_n)^T \end{aligned} \] です(参考).
最小二乗法の導出では, パラメータ $\mathbf{a}$ の分布が一切考慮されていない事がわかるとおもいます. つまり, $-\infty$ から $\infty$ まで全空間から残差平方和を最小化する $\mathbf{a}$ を単純に求めています.
これが過学習の生じる原因であると言えます.
ベイズ線形回帰
そこで, パラメータ $\mathbf{a}$ の事前分布 $\pi(\mathbf{a})$ を導入し, MAP推定を行いましょう.
ベイズの定理より, 事後分布 $\pi(\mathbf{a}|D)$ は事前分布と尤度関数の積に比例するので($\sigma_i=\sigma=\mathrm{const}.$ として) \[ \pi(\mathbf{a}|D)\propto \pi(\mathbf{a})\exp\left\{-\frac{1}{2\sigma^2}\sum_i ||y_i-\mathbf{a}^T\Psi(\mathbf{x}_i)||^2\right\} \] となります.
ここで, 事前分布 $\pi(\mathbf{a})$ も正規分布 $\mathcal{N}(\mathbf{a}_0,\mathbf{\Sigma}_0)$ であるとするならば, 事後分布 $\pi(\mathbf{a}|D)$ も正規分布 $\mathcal{N}(\mathbf{a},\mathbf{\Sigma})$ となります. ただし, \[ \begin{aligned} \mathbf{\Sigma}^{-1}&=\frac{1}{\sigma^2}\mathbf{X}^T\mathbf{X}+\mathbf{\Sigma}_0^{-1} \\ \mathbf{a} &= \mathbf{\Sigma}\left(\frac{1}{\sigma^2}\mathbf{X}^T\mathbf{y}+\mathbf{\Sigma}_0^{-1}\mathbf{a}_0\right) \end{aligned} \] となります. (参考)
数式が複雑で分かりにくいので特別な状況として, $\mathbf{\Sigma}_0 = \sigma_0^2I$ の場合を考えてみましょう.
前頁の式に代入して $\mathbf{\Sigma}$ を消去すると \[ \frac{1}{\sigma^2}\mathbf{X}^T\mathbf{X}\mathbf{a}+\frac{1}{\sigma_0^2}\mathbf{a} = \frac{1}{\sigma^2}\mathbf{X}^T\mathbf{y}+\frac{1}{\sigma_0^2}\mathbf{a}_0 \] となります.
$\alpha = \sigma^2/\sigma_0^2$ とおいて更に整理すると \[ \mathbf{X}^T(\mathbf{X}\mathbf{a}-\mathbf{y})+\alpha(\mathbf{a}-\mathbf{a}_0) \] となりますが, これから残差平方和に 正則化項 (regularization term) を追加した \[ \sum_i||\mathbf{y}-\mathbf{a}^T\Psi(\mathbf{x}_i)||^2 + \alpha||\mathbf{a}-\mathbf{a}_0||^2 \] の最小化を行っているのだという事が分かります.
つまり, $\mathbf{a}$ と $\mathbf{a}_0$ が離れすぎることに対してペナルティをあたえた最小二乗法であると言えます.
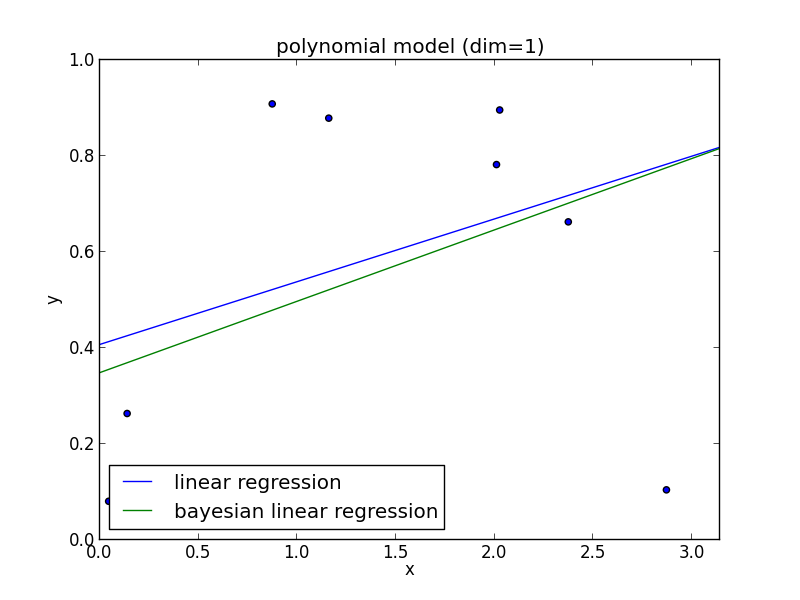
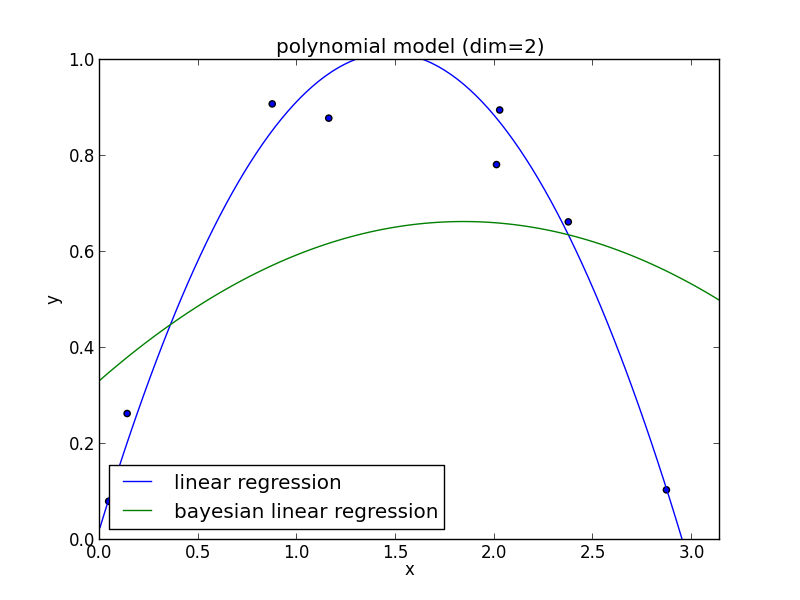
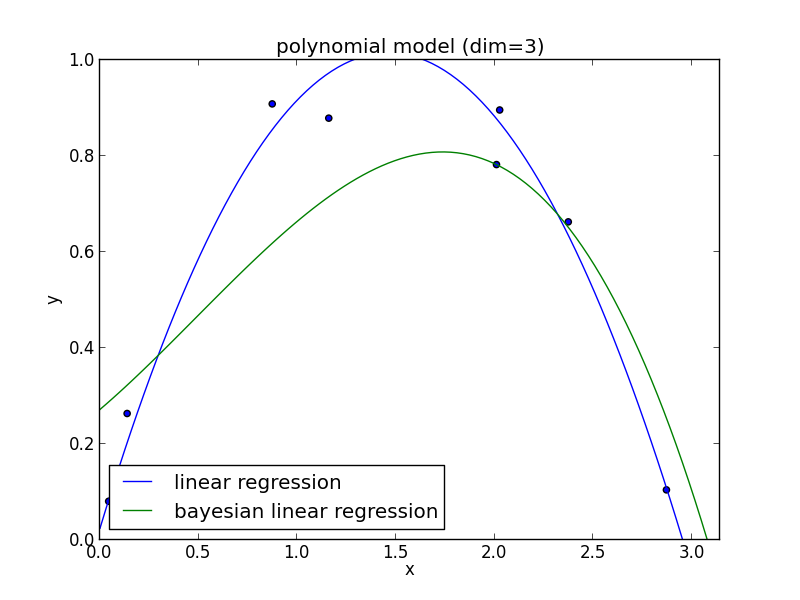
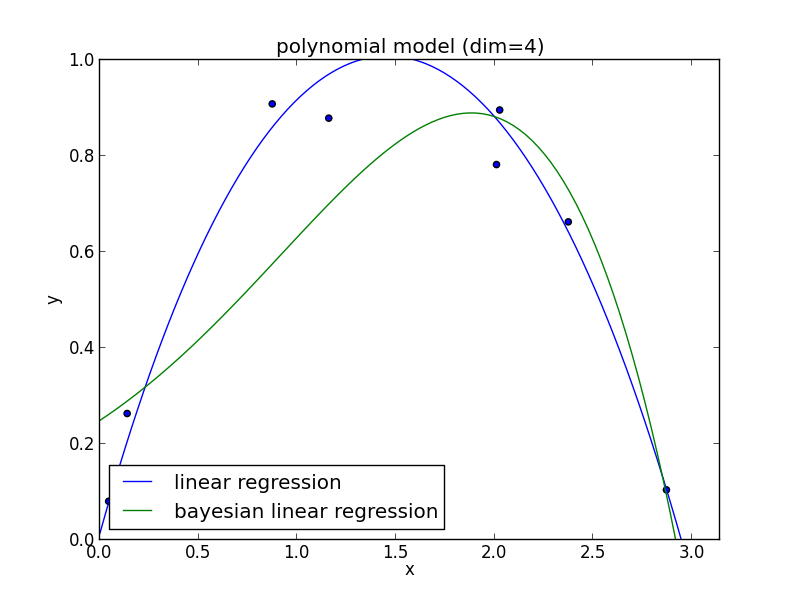
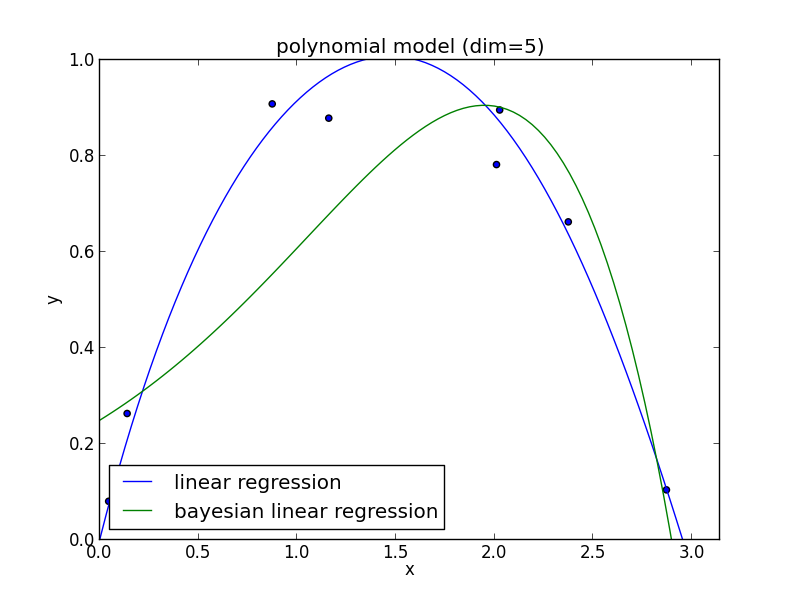
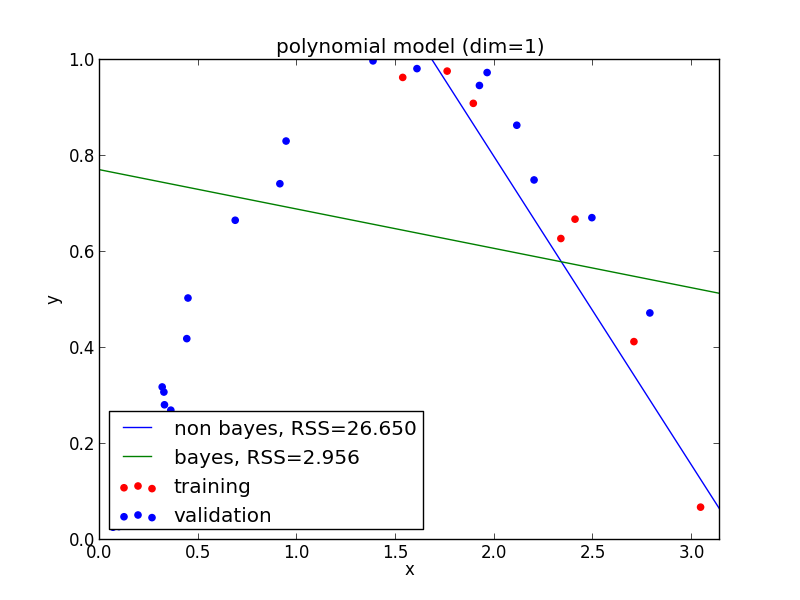
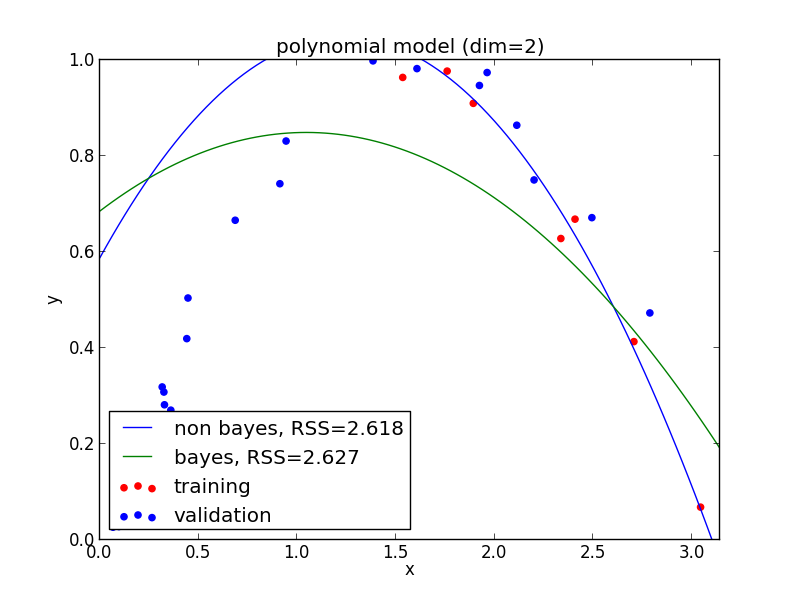
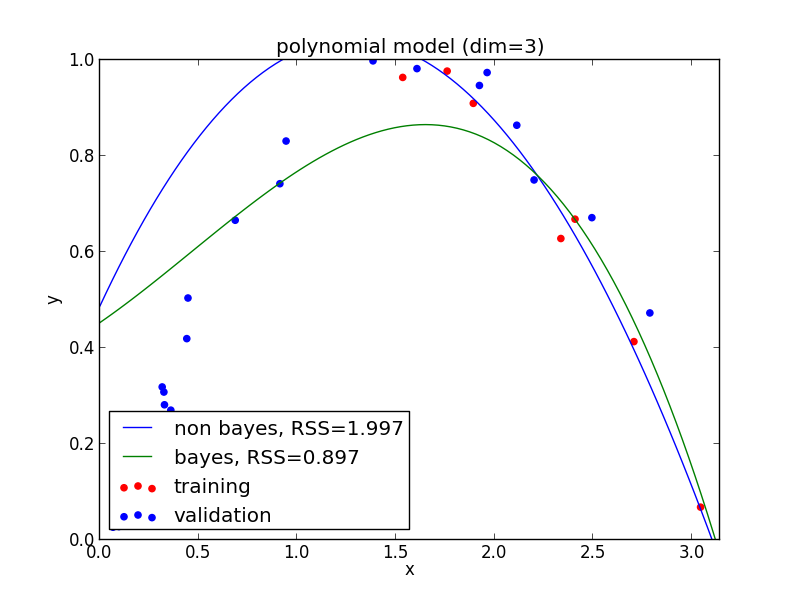
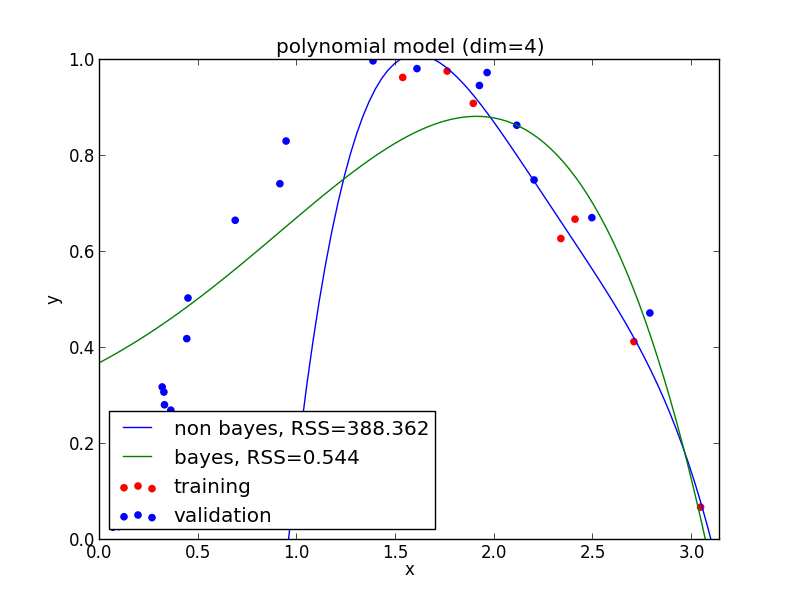
多項式フィッティングの問題をベイズ線形回帰で解いてみましょう. 多項式モデルでは, 高次の項ほど変動が大きいので$\mathbf{\Sigma}_0=\sigma_0^2I$ という仮定は妥当ではありません. 高次の係数ほど $0$ に近いであろうと想定して, 以下のような事前分布を使ってみます. \[ \small{\begin{aligned} \mathbf{a}_0 &= (0, 0, \ldots, 0)^T \\ \mathbf{\Sigma}_0 &= \begin{pmatrix} \sigma_n^2 & 0 & \cdots & 0 \\ 0 & \sigma_{n-1}^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & \sigma_0^2 \end{pmatrix}, \quad (\sigma_0 > \sigma_1 > \cdots > \sigma_{n-1} > \sigma_n) \end{aligned}} \]
1次式の場合
2次式の場合
3次式の場合
4次式の場合
5次式の場合
6次式の場合
7次式の場合
8次式の場合
9次式の場合
高次の多項式でも過学習を避ける事ができている事がわかります. 次頁以降にはホールド・アウト検証の結果も載せておきます.
現実の問題で現れる分布は単純なモデルでは表せない事が多く複雑なモデルの使用は避けられません. ベイズ回帰ではそのような問題を適切に解くことが出来ます.
1次式の場合
2次式の場合
3次式の場合
4次式の場合
5次式の場合
6次式の場合
7次式の場合
8次式の場合
9次式の場合
さて, 今回誤差の分布が正規分布であるとかパラメータの事前分布が正規分布であるなどの仮定をおきましたが, 計算が簡単だからという事が大きいです.
単純な問題ばかりではつまらないので, ベイズ線形回帰の応用に進む前にMCMC法という計算機を利用した確率計算の手法を紹介します.
マルコフ連鎖モンテカルロ法
確率の計算では非常に高次元の重積分が必要になります.
例えば, $f(\mathbf{x})$ の分布 $\pi(\mathbf{x})$ における期待値は積分 \[ E[f(\mathbf{x})] = \int f(\mathbf{x})\pi(\mathbf{x})\mathrm{d}\mathbf{x} \] となります.
また, 同時分布 $\pi(\mathbf{x}, \mathbf{y})$ から $\mathbf{x}$ の分布を求める(周辺化を行う)為には \[ \pi(\mathbf{x}) = \int \pi(\mathbf{x},\mathbf{y})\mathrm{d}\mathbf{y} \] という積分が必要です.
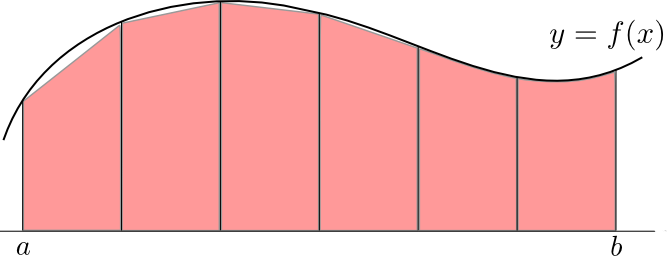
低次の積分ならば積分区間を $N$ 分割して近似する数値積分法を利用する事が出来ますが(参考), この方法では, $d$ 次元の重積分を行うのに $O(N^d)$ の計算量が必要になります.
モンテカルロ法とは
モンテカルロ法 (Monte Carlo method) とは乱数を用いて行う数値計算法の総称です.
高次の重積分を効率的に計算する為に必要です.
モンテカルロ法は大数の強法則を基本原理とします.
大数の強法則
平均が $\mathbf{\mu}$ で分散が有限の同一の分布に独立に従う確率変数 $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n$ があるとき, ($E[|\mathbf{x}_i|]<\infty$ ならば)その標本平均 \[ \overline{\mathbf{x}}_n = \frac{1}{n}\sum_{i=1}^n\mathbf{x}_i \] について \[ p\left(\lim_{n\rightarrow\infty}\overline{\mathbf{x}}_n=\mu\right) = 1 \] が成り立つ.
この法則に基づいて, 期待値 $E[f(\mathbf{x})]$ の近似値を以下のように求める事が出来ます.
- $\pi(\mathbf{x})$ に独立に従うサンプル $\mathbf{x}_1,\ldots,\mathbf{x}_n$ を多数生成する.
- $E[f(\mathbf{x})]$ の近似値を \[ E[f(\mathbf{x})]\approx \frac{1}{n}\left\{f(\mathbf{x}_1)+f(\mathbf{x}_2)+\cdots+f(\mathbf{x}_n)\right\} \] によって求める.
簡単な例として, 標準正規分布 $N(0, 1)$ の分散 (もちろんこれは $1$ に等しい) をモンテカルロ法で計算してみましょう.
平均が $\mu$ の時の分散は \[ V[x] = E[(x-\mu)^2] \] である事を使います.
これは以下の様なコードで簡単に実行出来ます. 試しに $1000$ サンプルで一度実行してみた結果は \[ 0.947868542873 \] となりました. もちろん, 実行の度に数値は変わります.
# -*- coding: utf-8 -*-
from numpy import *
N = 1000
# N(0,1) に従う乱数を N 個生成
x = random.randn(N)
print average((x-0)**2)
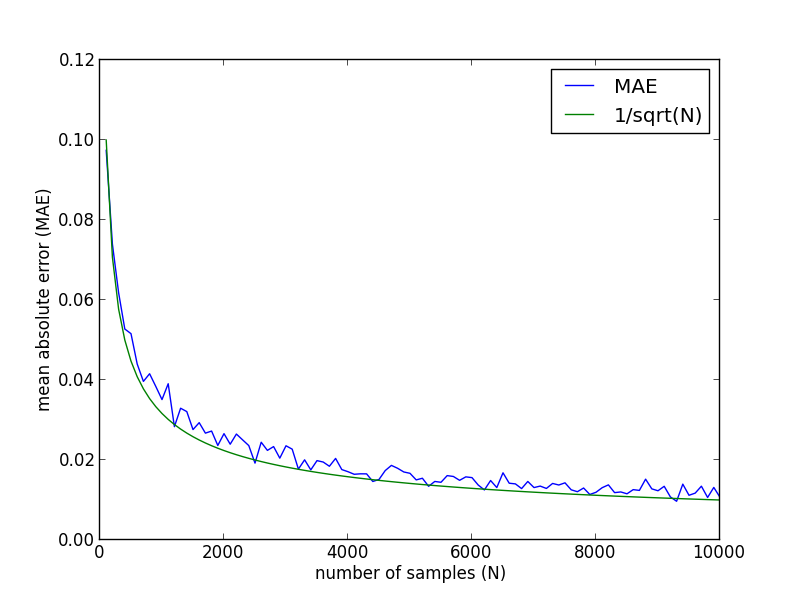
今の例において, サンプル数 $N$ に対する絶対誤差の平均は以下の様になります. 一般に, モンテカルロ法では $1/\sqrt{N}$ のオーダーで誤差が減少していきます.
ここで \[ E[f(\mathbf{x})] = \int f(\mathbf{x})\pi(\mathbf{x})\mathrm{d}\mathbf{x} \] ですから, 重積分の計算を期待値の計算に帰着してランダムサンプリングを利用する事が出来ます.
まずは, 簡単な例で数式を用いずに説明しましょう.
正方形領域 $[-1,1]\times[-1,1]$ 上の一様乱数 $(x,y)$ を生成したとき, これが単位円の中に入る確率は面積比と等しく $\pi/4$ です.
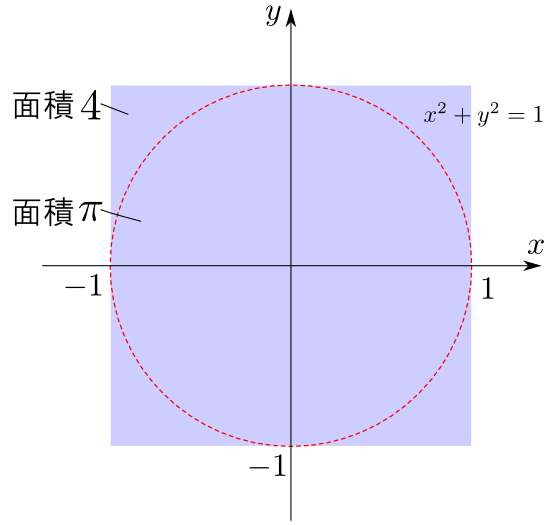
よって,ランダムサンプリングによって円の中に入る点の数の比率を計算すれば, $\pi$ の近似値を求める事が出来ます.
例えば1万サンプルで計算してみると $3.1276$ などの数値が得られます.
# -*- coding: utf-8 -*-
from numpy import *
N = 10000
# [-1,1] x [-1,1] 上の一様乱数を N 点生成
x = random.uniform(-1, 1, N)
y = random.uniform(-1, 1, N)
# 円内に入った点の比率から円周率を計算
print 4.0*count_nonzero(x**2 + y**2 <= 1)/N
今の例で行ったのは \[ f(x,y) = \left\{\begin{array}{cc} 1 & (x^2+y^2 \leq 1) \\ 0 & (x^2+y^2 \geq 1) \end{array}\right. \] に対する \[ \pi = \int_{-1}^1 \int_{-1}^1 f(x,y)\mathrm{d}x\mathrm{d}y \] という(広義)重積分の近似計算です.
ここで $[-1,1]\times[-1,1]$ 上の一様分布の密度関数は $u(x,y) = 1/4$ なので, \[ \pi = 4\int_{-1}^1 \int_{-1}^1 f(x,y)u(x,y)\mathrm{d}x\mathrm{d}y \] と表す事が出来ますから \[ \pi = 4E_u[f(x,y)] \] という期待値計算に帰着出来るというわけです($E_u$ は分布 $u$ 上での期待値という意味).
重点的サンプリング
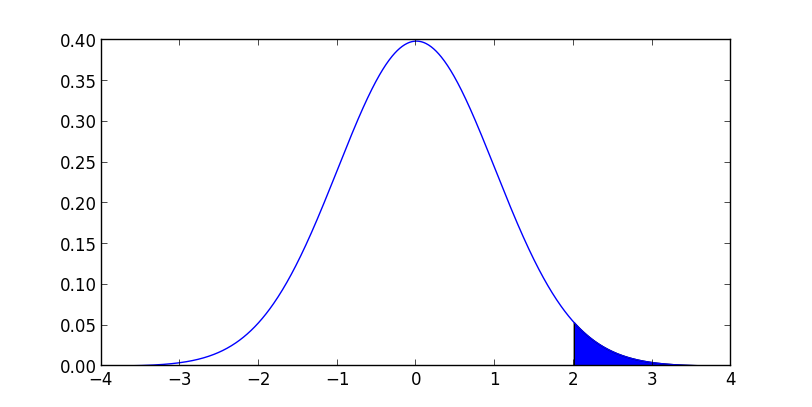
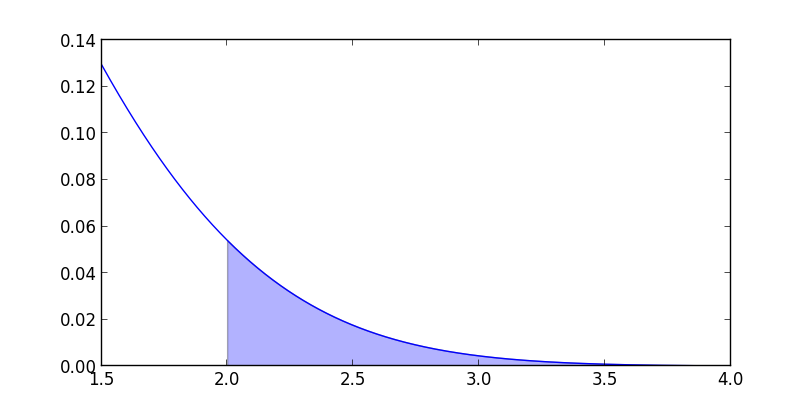
続いて, 標準正規分布 $N(0,1)$ における確率 $p(x \geq 2)$ を考えましょう. これは $N(0,1)$ の密度関数を $\pi(x)$ とすれば \[ p(x \geq 2) = \int_2^\infty \pi(x)\mathrm{d}x \] となります.
これを $N(0,1)$ からのサンプリングによって求めた場合 $x < 2$ の領域からのサンプリングは無駄になるので, 必要なサンプル数が大きくなってしまいます.
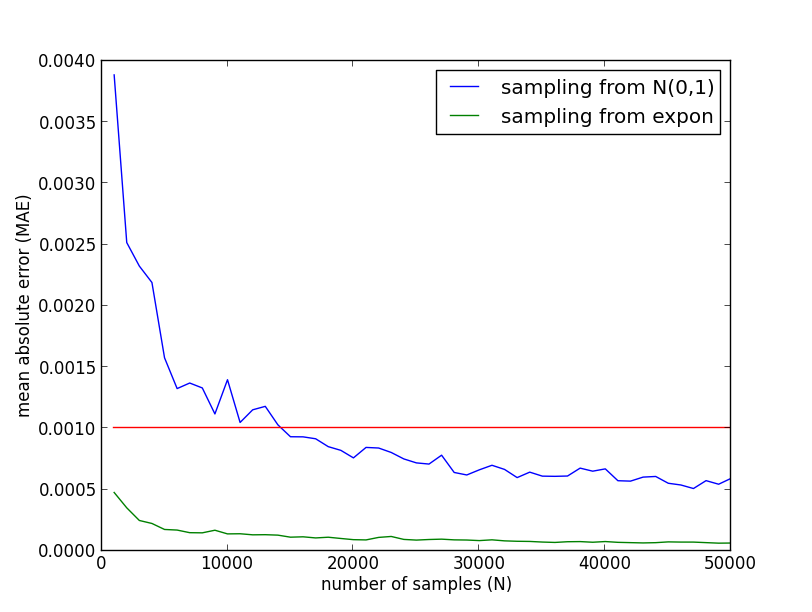
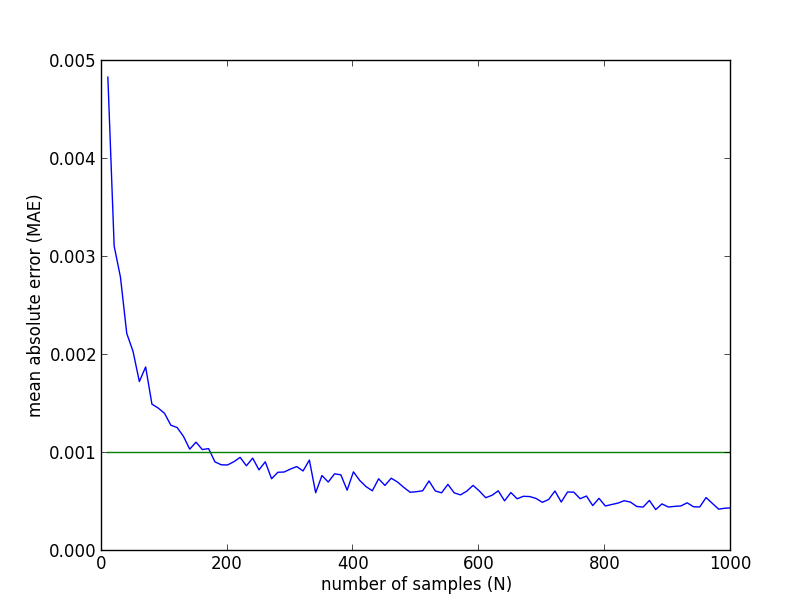
実際の実験結果は以下のようになりました. 例えば平均絶対誤差を $0.001$ 未満にする為には, 15000サンプルほどは必要になるということが分かります.
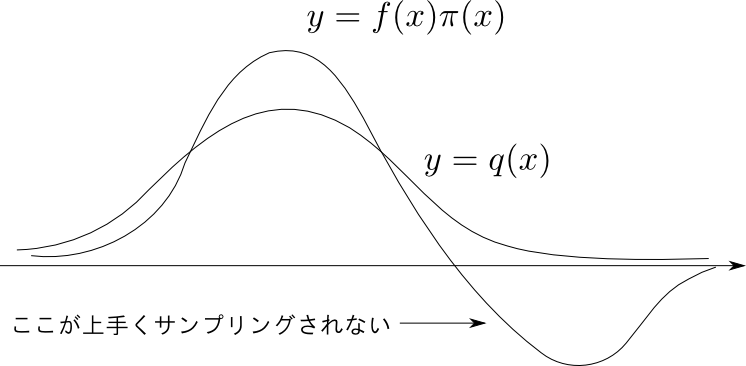
精度を上げる為には以下の部分だけを重点的にサンプリング出来れば良いです.
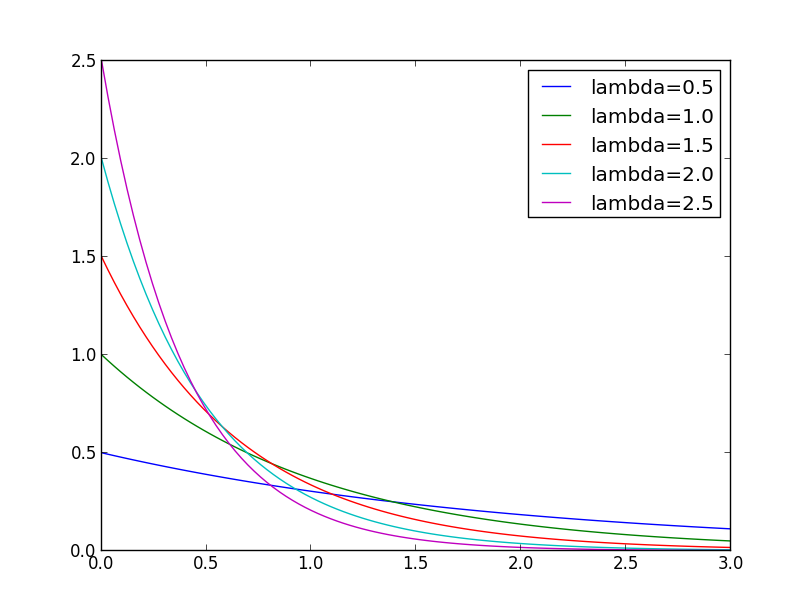
指数分布は $x\geq 0$ という形の領域に分布するので都合がよいです. これを $2$ だけ平行移動して使いましょう.
$\pi(\mathbf{x})$ に関するサンプリングを $q(\mathbf{x})$ に関するサンプリングに取り替えるには等式 \[ \int f(\mathbf{x})\pi(\mathbf{x})\mathrm{d}\mathbf{x} = \int f(\mathbf{x})\frac{\pi(\mathbf{x})}{q(\mathbf{x})}q(\mathbf{x})\mathrm{d}\mathbf{x} \] が使えます. つまり \[ E_\pi[f(\mathbf{x})] = E_q\left[f(\mathbf{x})\frac{\pi(\mathbf{x})}{q(\mathbf{x})}\right] \] です. これを 重点的サンプリング (importance sampling) と呼びます.
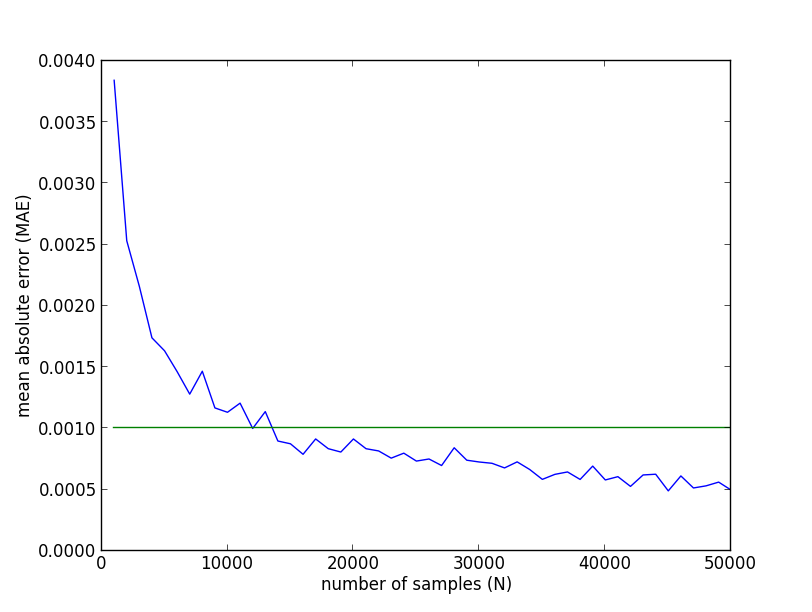
以下が先ほどの実験との比較ですが, 圧倒的に精度が良い事が分かります.
重点的サンプリングの方を詳しく見ると, 200サンプルほどで平均誤差 $0.001$ 未満を達成しているようです.
$q(\mathbf{x})$ の選び方ですが, これは $f(\mathbf{x})\pi(\mathbf{x})$ の値の大小とある程度一致しているものを選びます.
棄却サンプリング
$\pi(\mathbf{x})$ から直接サンプリングを行うのが難しいという場合もあります. そこでやはりサンプリングが可能な他の分布 $q(\mathbf{x})$ の利用を考えます.
重点的サンプリングをこの目的に利用する事も可能ですが, 他に 棄却サンプリング (rejection sampling) という方法があります.
以下が棄却サンプリングの手順です.
- $M$ を $\pi(\mathbf{x}) \leq Mq(\mathbf{x})$ を満たす定数とする.
- $q(\mathbf{x})$ からサンプル $\mathbf{a}$ をとる.
- $\pi(\mathbf{a})/Mq(\mathbf{a})$ の確率で $\mathbf{x}=\mathbf{a}$ を採択する. 採択できなかったら2に戻る.
まず \[ p(\mathbf{x}\text{を採択}|\mathbf{x}) = \frac{\pi(\mathbf{x})}{Mq(\mathbf{x})} \] であるので \[ \begin{aligned} p(\text{採択}) &= \int p(\mathbf{x}\text{を採択}|\mathbf{x})q(\mathbf{x})\mathrm{d}\mathbf{x}\\ &= \frac{1}{M}\int\pi(\mathbf{x})\mathrm{d}\mathbf{x}\\ &= \frac{1}{M} \end{aligned} \] となります.
よって採択された $\mathbf{x}$ の分布は \[ \begin{aligned} \pi(\mathbf{x}|\text{採択}) &= \frac{p(\text{採択}|\mathbf{x})q(\mathbf{x})}{p(\text{採択})} \\ &= \frac{\pi(\mathbf{x})}{M}\div\frac{1}{M} \\ &= \pi(\mathbf{x}) \end{aligned} \] となるので, $\pi(\mathbf{x})$ からのサンプリングが実現します.
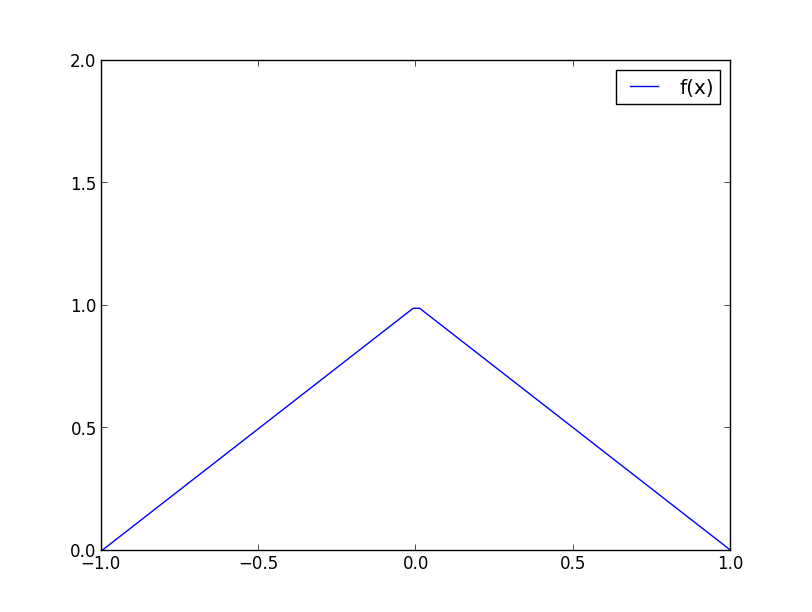
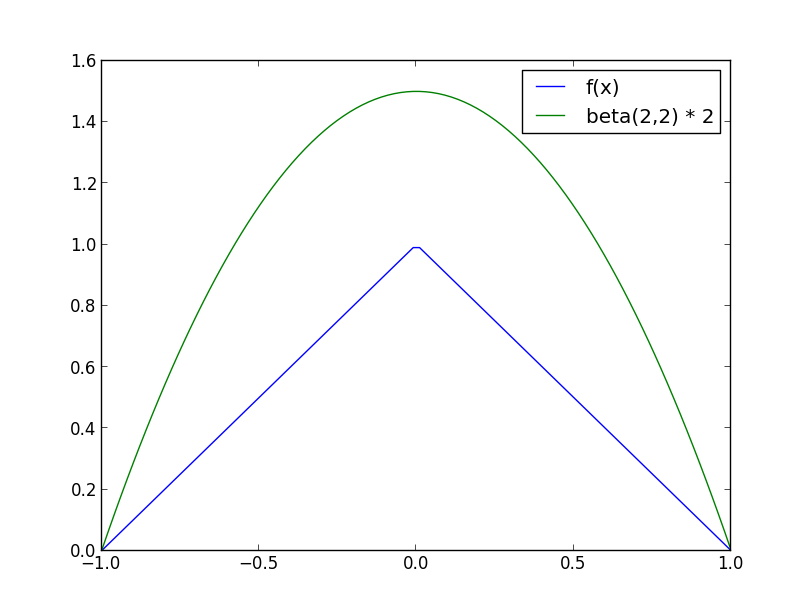
例えば, 人工的に作った以下の分布 (密度関数:$f(x)=1-|x|, (|x|\leq 1)$) からサンプリングしたいとします.
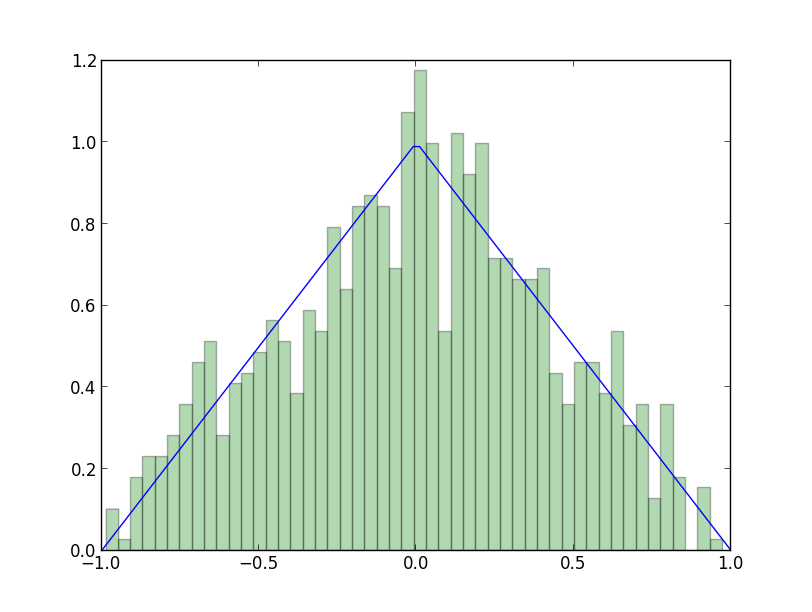
$a \leq x \leq b$ という形の領域なのでベータ分布を使えます. $Be(2, 2)$ を使い, $M=2$ としてみましょう.
棄却法で1000サンプル生成する実験を行った所以下のようになりました. 採択率は $1/M$ なので, 実際には約 $M$ 倍のサンプルが生成されます(以下の実験では $1995$ サンプル).
以上重点的サンプリングと棄却サンプリングを紹介しましたが, いずれも分布 $q(\mathbf{x})$ の選択が重要です.
- 重点的サンプリングでは出来るだけ $f(\mathbf{x})\pi(\mathbf{x})$ の値が大きいところからサンプリングしたい.
- 棄却法では $M$ を出来るだけ $1$ に近づけたい.
しかし, 現実の分布は非常に複雑なので適切な $q(\mathbf{x})$ を選ぶ事は困難です.
また, 高次元空間特有の問題もあります.
再び例として $\pi$ の計算の問題を考えましょう.

半径 $1$ の球と, 一辺 $1$ の立方体の体積は以下のようになります. \[ \begin{array}{|c||c|c|}\hline \text{次元} & \text{球の体積} & \text{立方体の体積} \\ \hline\hline 2\text{次元} & 3.14 & 4 \\ 3\text{次元} & 4.19 & 8 \\ 4\text{次元} & 4.93 & 16 \\ 5\text{次元} & 5.26 & 32 \\ 6\text{次元} & 5.17 & 64 \\ \hline \end{array} \]
半径 $1$ の $n$次元球の体積は $\sqrt{\pi^n}/\Gamma(n/2+1)$.
高次元の空間では $(\text{球の体積})/(\text{立方体の体積})$ がほとんど $0$ になってしまうので, サンプルのほとんどが捨てられてしまう事になります.
一辺の長さが $1$ の $n$ 次元立方体の,厚みが $\varepsilon/2 > 0$ の表面部分の体積が占める割合は \[\frac{\text{(表面部分の体積)}}{\text{(全体の体積)}} \approx \frac{1-(1-\varepsilon)^d}{1} \xrightarrow{d\rightarrow\infty} 1 \] となります.
つまり, 高次元の空間の体積はそのほとんどが表面部分に集中してしまう ので一様なサンプリングでは必要なサンプル数が指数的に増加してしまいます. 次元の呪い と呼ばれる問題の1つです.
マルコフ連鎖
時間 $t$ と共に変化する確率変数 $\mathbf{x}^{(t)}$ を 確率過程 (stochastic process) と呼びます.
確率過程のうち, 時刻 $t+1$ の様子が時刻 $t$ の状態のみから決まるもの. つまり, \[ \pi(\mathbf{x}^{(t+1)}|\mathbf{x}^{(0)}, \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(t)}) = \pi(\mathbf{x}^{(t+1)} | \mathbf{x}^{(t)}) \] を満たすものを マルコフ連鎖 (Markov chain) と呼びます.
簡単な例として, 以下のような3状態を持つマルコフ過程を考えてみましょう.
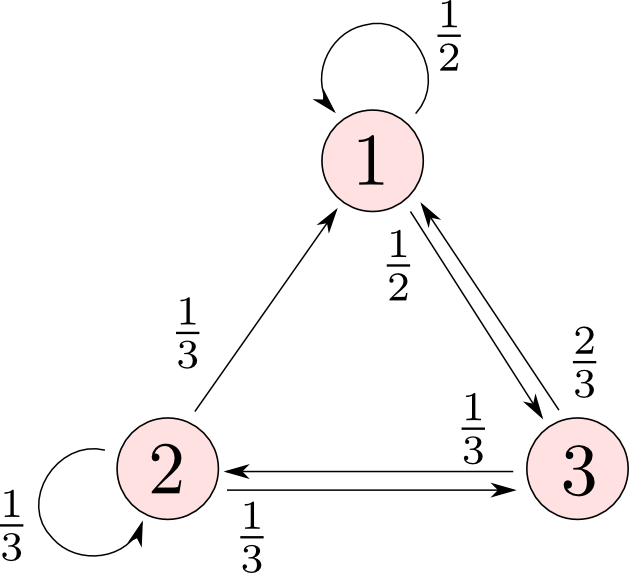
時刻 $t$ に状態 $i$ に存在する確率を $p^{(t)}_i$ とすれば, これは以下のように行列を用いて書くことが出来ます.
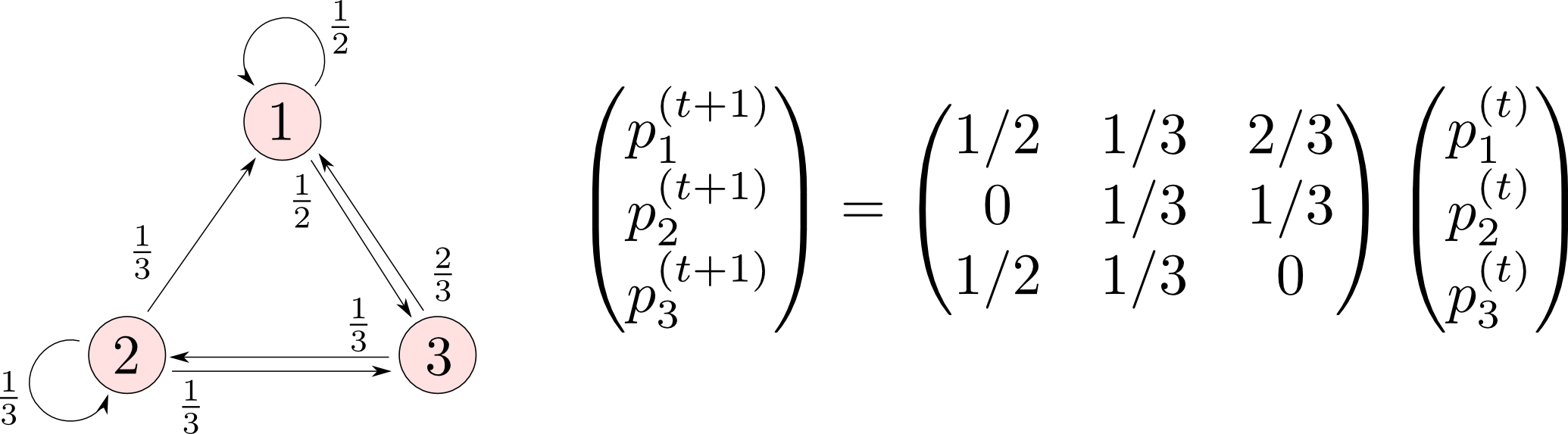
では, $\mathbf{p}^{(0)} = (1, 0, 0)^T$ として確率の変化を見てみましょう.
t=0 : [ 1. 0. 0.]
t=1 : [ 0.5 0. 0.5]
t=2 : [ 0.58333333 0.16666667 0.25 ]
t=3 : [ 0.51388889 0.13888889 0.34722222]
t=4 : [ 0.53472222 0.16203704 0.30324074]
t=5 : [ 0.52353395 0.15509259 0.32137346]
t=6 : [ 0.52771348 0.15882202 0.31346451]
t=7 : [ 0.52577375 0.15742884 0.31679741]
t=8 : [ 0.52656143 0.15807542 0.31536315]
t=9 : [ 0.52621462 0.15781286 0.31597252]
t=10 : [ 0.52635994 0.15792846 0.3157116 ]
t=11 : [ 0.52629719 0.15788002 0.31582279]
t=12 : [ 0.5263238 0.15790094 0.31577527]
t=13 : [ 0.52631239 0.15789207 0.31579554]
t=14 : [ 0.52631725 0.15789587 0.31578688]
t=15 : [ 0.52631517 0.15789425 0.31579058]
t=16 : [ 0.52631605 0.15789494 0.315789 ]
t=17 : [ 0.52631568 0.15789465 0.31578968]
t=18 : [ 0.52631584 0.15789477 0.31578939]
t=19 : [ 0.52631577 0.15789472 0.31578951]
実は初期状態が $1,2,3$ のどれであっても, 十分に時間が経過すると \[ \lim_{t\rightarrow\infty}\mathbf{p}^{(t)} = \frac{1}{19}(10, 3, 6)^T \] という確率分布に収束します.
つまり, このマルコフ過程を $10:3:6$ の比率で $1,2,3$ を出力する乱数発生器とみなす事が出来ます.
実験としてマルコフ連鎖の最初の $10$ ステップを捨てて, 続く $1000$ ステップをサンプリングした所, 状態 $1,2,3$ の出現頻度は \[ 0.552 \quad:\quad 0.144 \quad:\quad 0.304 \] となりました. (prog3-7.py)
確率過程なので各状態間には依存関係がありますが, 巨視的には $10:3:6$ という分布に従ってサンプリングする事が出来た事になります.
一般に, 離散状態のマルコフ過程は 推移確率行列 (transition probability matrix) $\mathbf{P}$ によって \[ \mathbf{p}^{(t+1)}=\mathbf{P}\mathbf{p}^{(t)} \] と表す事ができます.
この連鎖が適切な条件(エルゴード性 (ergodicity))を満たす時, $t\rightarrow\infty$ において $\mathbf{p}^{(t)}$ は \[ \mathbf{p} = \mathbf{P}\mathbf{p} \] を満たす分布 $\mathbf{p}$ に収束します. これをマルコフ連鎖の 不変分布 (invariant distribution) と呼びます.
マルコフ連鎖モンテカルロ法
マルコフ連鎖モンテカルロ法 (Markov chain Monte Carlo methods, MCMC法) とは, サンプリングを行いたい分布 $\pi(\mathbf{x})$ が不変分布になるようなマルコフ連鎖を生成する事によって, $\pi(\mathbf{x})$ からのランダムサンプリングを実現する手法です.
MCMC法では現在の状態を考慮して
- 確率密度の高い所にいるなら出来るだけそこに留まる
- 確率密度の低い所にいるなら, 高い方を目指して移動する
というように移動をくりかえします. これによって重点的サンプリングを実現する事ができます.
MCMC法にはいくつかの手法が存在しますが, 今回は メトロポリス・ヘイスティングス法 (Metropolis-Hastings, MH法) を紹介します.
詳細釣り合い条件
連続的な分布では, $\mathbf{x}$ にいる時に $\mathbf{x}'$ へ移動する確率密度 $k(\mathbf{x}'|\mathbf{x})$ を 推移核 (transition kernel) と呼びます.
この時, 詳細釣り合い条件 (detailed balance condition) と呼ばれる以下の条件が成立するならば, このマルコフ連鎖の不変分布が $\pi(\mathbf{x})$ となる事が分かっています.
時刻 $t$ における分布が $\pi(\mathbf{x}^{(t)})$ である時, 次の時刻の分布は \[ \pi'(\mathbf{x}^{(t+1)})=\int k(\mathbf{x}^{(t+1)}|\mathbf{x}^{(t)})\pi(\mathbf{x}^{(t)})\mathrm{d}\mathbf{x}^{(t)} \] となりますが, 詳細釣り合い条件が成立しているならば \[ \begin{aligned} \pi'(\mathbf{x}^{(t+1)})&=\int k(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})\pi(\mathbf{x}^{(t+1)})\mathrm{d}\mathbf{x}^{(t)} \\ &=\pi(\mathbf{x}^{(t+1)})\int k(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})\mathrm{d}\mathbf{x}^{(t)} \\ &=\pi(\mathbf{x}^{(t+1)}) \end{aligned} \] となります. つまり, 時刻 $t+1$ における分布もやはり $\pi$ であるということになります.
今, 目標とする分布 $\pi(\mathbf{x})$ はわかっていて, 推移核 $k(\mathbf{x}'|\mathbf{x})$ はわからないという状況です.
そこで, サンプリングが可能な 提案分布 (proposal distribution) $q(\mathbf{x}'|\mathbf{x})$ を用意します.
提案分布が詳細釣り合い条件を満たさないなら \[ q(\mathbf{x}'|\mathbf{x})\pi(\mathbf{x}) > q(\mathbf{x}|\mathbf{x}')\pi(\mathbf{x}') \] であると仮定できます.
$q(\mathbf{x}'|\mathbf{x})$ に従って $\mathbf{x}$ から $\mathbf{x'}$ へ推移するのですが, 棄却サンプリングを行えばこの確率を下げる事が出来ます. これによって左辺を小さくし, 両辺が等しくなるように調節します.
採択する確率 $a$ は \[ aq(\mathbf{x}'|\mathbf{x})\pi(\mathbf{x}) = q(\mathbf{x}|\mathbf{x}')\pi(\mathbf{x}') \] を満たせば良いですから \[ a = \frac{q(\mathbf{x}|\mathbf{x}')\pi(\mathbf{x}')}{q(\mathbf{x}'|\mathbf{x})\pi(\mathbf{x})} \] となります. 但し先ほどの仮定が満たされない場合には $a=1$ とします.
まとめましょう.
メトロポリス・ヘイスティングス法
- 目標分布を $\pi(\mathbf{x})$, 提案分布を $q(\mathbf{x}'|\mathbf{x})$ とする.
- 提案分布 $q(\mathbf{x}^{(t+1)}|\mathbf{x}^{(t)})$ に従って, $\mathbf{x}^{(t+1)}$ を生成する.
- 次の採択確率に従ってこれを採択する. \[ a = \mathrm{min}\left\{\frac{q(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})\pi(\mathbf{x}^{(t+1)})}{q(\mathbf{x}^{(t+1)}|\mathbf{x}^{(t)})\pi(\mathbf{x}^{(t)})}, 1 \right\} \]
マルコフ連鎖の最初の方は初期状態への依存性が高いので捨てる. これを バーンイン(burn-in) と呼ぶ.
ランダム・ウォーク
ランダム・ウォーク (random walk) とは$\mathbf{x}^{(t)}$ から $\mathbf{x}^{(t+1)}$ への推移が \[ \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} + \mathbf{z} \] と記述されるような確率過程です. $\mathbf{z}$ は正規分布や $t$ 分布など対称的な分布からとります.
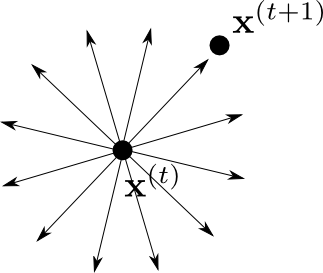
ランダム・ウォークでは $\mathbf{x}$ から $\mathbf{x'}$ へ行く確率と, $\mathbf{x}'$ から $\mathbf{x}$ へ行く確率が等しいので, $q(\mathbf{x}'|\mathbf{x})=q(\mathbf{x}|\mathbf{x}')$ となり, 採択確率は \[ a = \mathrm{min}\left\{\frac{\pi(\mathbf{x}')}{\pi(\mathbf{x})}, 1 \right\} \] となります.
$\pi(\mathbf{x}')/\pi(\mathbf{x})$ がより大きい方向に進みやすいので, 密度の高い部分が重点的にサンプリングされるというわけです.
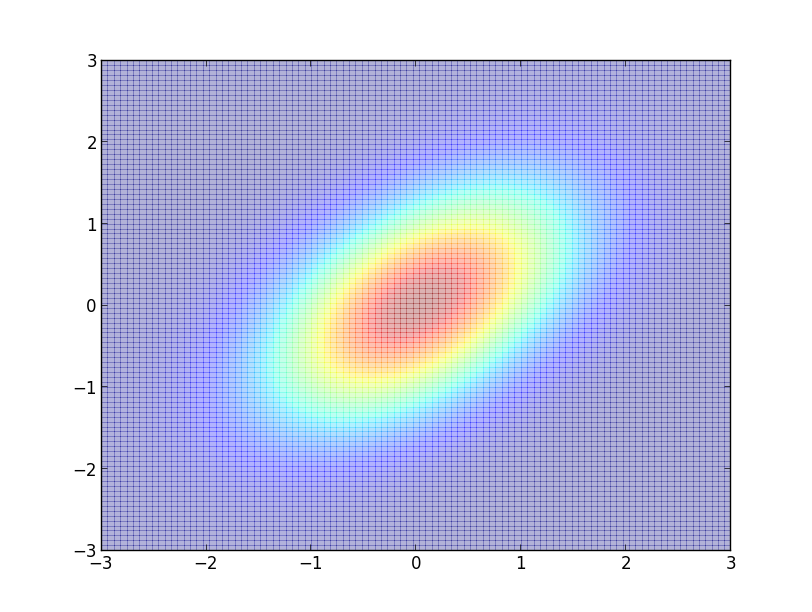
では例として, 二次元正規分布 \[ \small{ \mathcal{N}\left(\mathbf{0}, \begin{pmatrix} 1 & 1/2 \\ 1/2 & 1 \end{pmatrix} \right)} \] からサンプリングしてみましょう.

ランダム・ウォークに用いる $\mathbf{z}$ は二次元正規分布 \[ \mathcal{N}(\mathbf{0}, \sigma^2I) \] からとることにします.
開始点はわざとずらして $\mathbf{x}^{(0)} = (2,-2)^T$ としてみます.
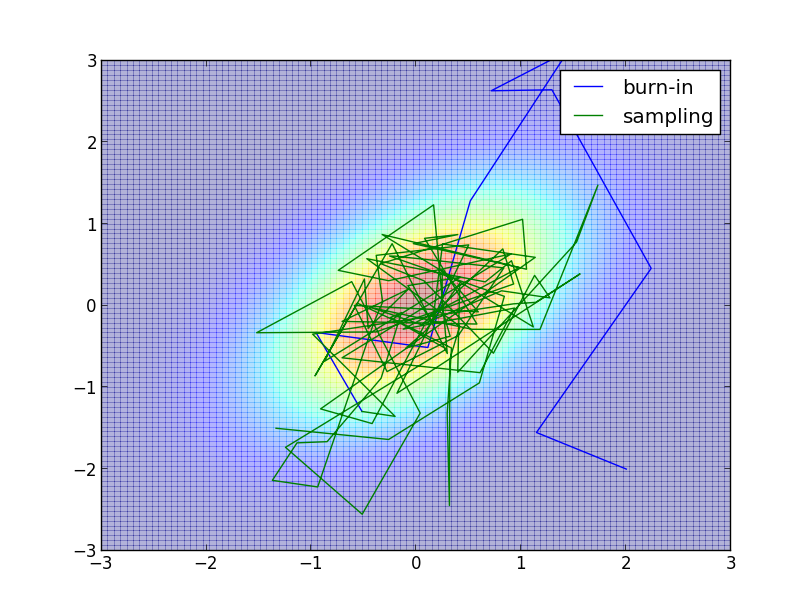
以下は $\sigma=1$, バーンイン期間 $10$ ステップ、 サンプル数 $100$ での例です. 図の見やすさの為に値を小さくしていますが, 実際にはバーンイン期間・サンプル数共にもっと多く取る必要があります.
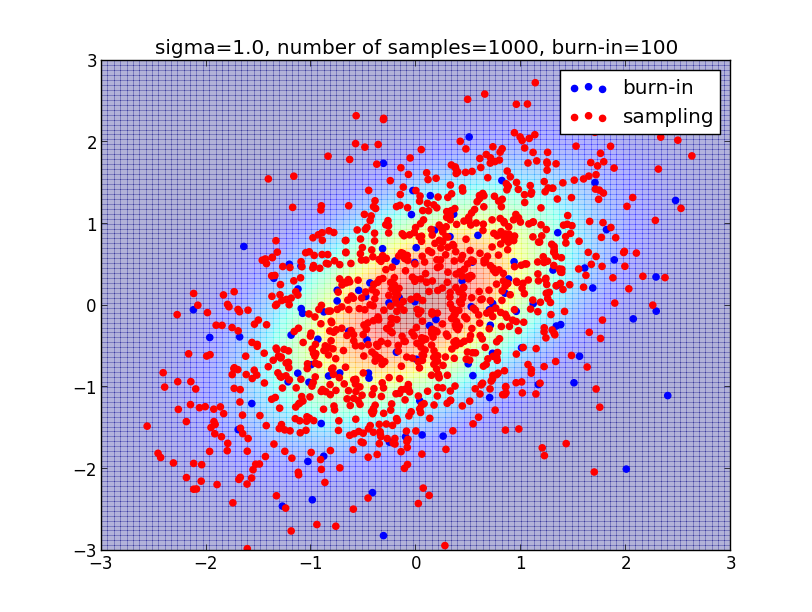
$\sigma=1$, バーンイン期間 $100$、 サンプル数 $1000$ だと以下のようになります. 母分布の密度をよく反映したサンプリングができている事がわかると思います.
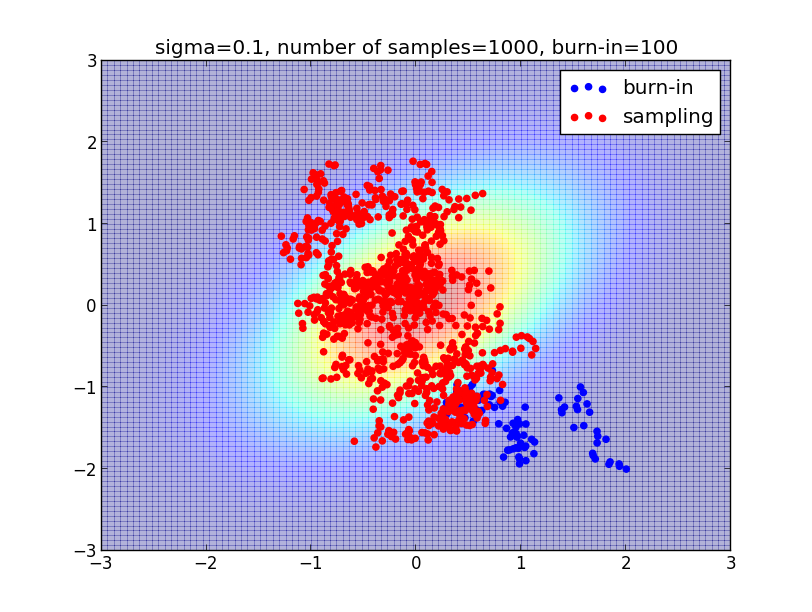
ランダム・ウォークのパラメータ $\sigma$ は一歩で進む距離を調節するものです. $\sigma$ をあまり小さくし過ぎるとサンプリングに偏りが出てしまいます.
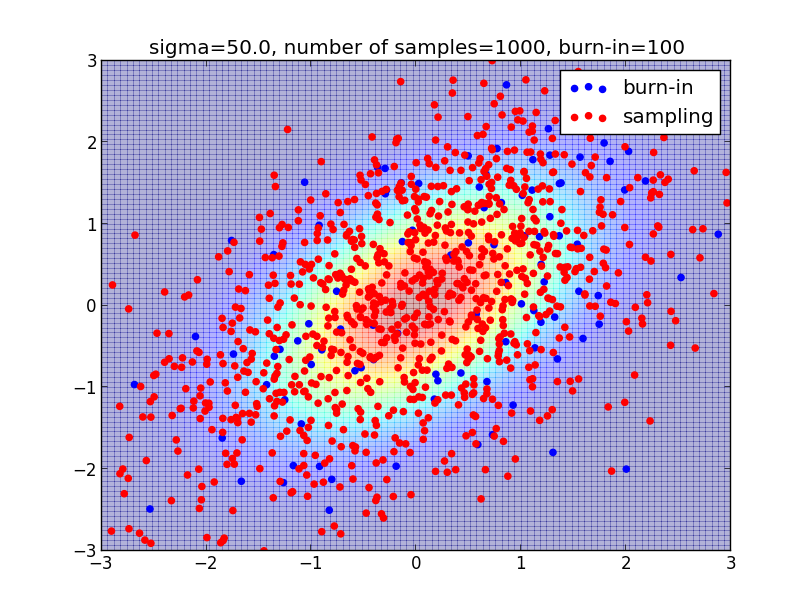
かと言って $\sigma$ を大きくしすぎると無駄なサンプリングが増えます. $\sigma$ の値を決める一般的な方法はありません. 取り組む問題毎に検討が必要です.
第3回はここで終わります
MCMC法は必須技術ですので良く復習してください. より詳しい話題は実際の問題に適用しながら説明していこうと思います.
次回は MCMC法 を利用したパラメータ推定など応用を見ていこうと思います.