パターン認識・
機械学習勉強会
第1回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

自己紹介

• 中村晃一
• 東京大学 大学院 情報理工学系研究科
  コンピュータ科学専攻 後期博士課程 2年
• プログラム最適化・言語処理系の実装技術・人間と言語の関係等に興味があります.
• twitter: @9_ties

はじめに

この会について

• パターン認識・機械学習の基礎を勉強します.
• 基本的な微積分・線形代数・確率統計の知識を前提とします.
• 資料中のサンプルコードは主にPythonで書きます.ライブラリはNumPy, SciPy, Matplotlibを利用します.

数式の記法について

• 列ベクトル・行列はボールド体の小文字・大文字で表します. \[\text{列ベクトル}: \mathbf{a},\quad\text{行列}: \mathbf{A} \]
• 行ベクトルは列ベクトルの転置によって表します. \[\text{行ベクトル}: \mathbf{a}^T \]
• 成分は対応する非ボールド体の文字に添字を付けて表します. \[\text{$\mathbf{a}$ の第 $i$ 成分}: a_i,\quad\text{行列の$(i,j)$成分}: A_{ij}\] 添字は $0$-originの場合も $1$-originの場合もあります.
• 零ベクトルは $\mathbf{0}$, 零行列は $\mathbf{O}$, 単位行列は $\mathbf{I}$ と表します.

第1回の内容

パターン認識・機械学習とは一体どのような技術であるのか, イントロダクションを行います.

パターン認識とは

パターン認識 (Pattern recognition) とは広い意味では人間が行っているような認知を機械に行わせる事を指します.

パターン認識の技術は身近な所で利用されています.

• 画像: デジカメの顔認識, 郵便の自動仕分け, 画像検索, $\ldots$
• 音声: スマートフォンの音声入力, コールセンターの自動応答, $\ldots$
• 文章: メールフィルタリング, テキスト検索, テキスト分類, $\ldots$
• モーション: タッチパネル, ゲーム機のインタフェース, $\ldots$

最も基本的なパターン認識の形は, データをそれが表す物の属すクラスに分類する事です.

例: 画像データの分類

→ 「風車」

今後は「パターン認識」と言ったらこの種類の処理を指すことにします.

数学的に言えば, 入力データのドメイン $O$ とクラスの集合 $C=\{c_1,c_2,\ldots\}$ に対して各データにクラスを割り当てる関数 \[ f: O \rightarrow C \] で出来るだけ誤りの無い物を構築する事が目標となります.

「出来るだけ誤りの無い」という事の意味については後で説明します.

一般に入力データのドメインは非常に高次元の空間になります.

例えば, $240 \times 320$pxで RGBの3チャンネルからなる画像は \[ 3\times 240\times 320 = 230400\text{個} \] の数値からなります.

つまり, このサイズの画像は約23万次元の空間内に分布するということになります.

従って, 識別精度を出来るだけ損なわずに入力データの次元を削る という事が重要になります.

また,次元削減にも限度がありますので 高次元のデータを効率的に処理する 為の数学的な工夫・アルゴリズム的な工夫も重要になります.

パターン認識の流れ

パターン認識は大きく3つのフェーズからなります.

1. 前処理
2. 特徴抽出
3. 識別

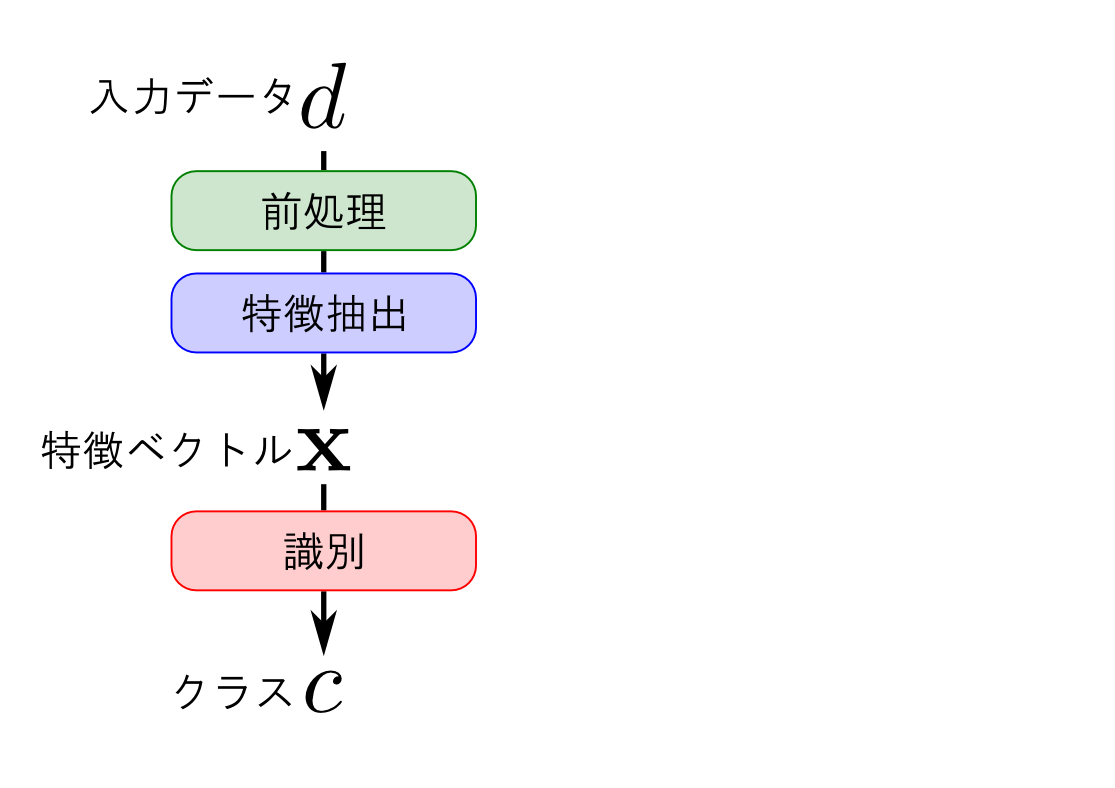
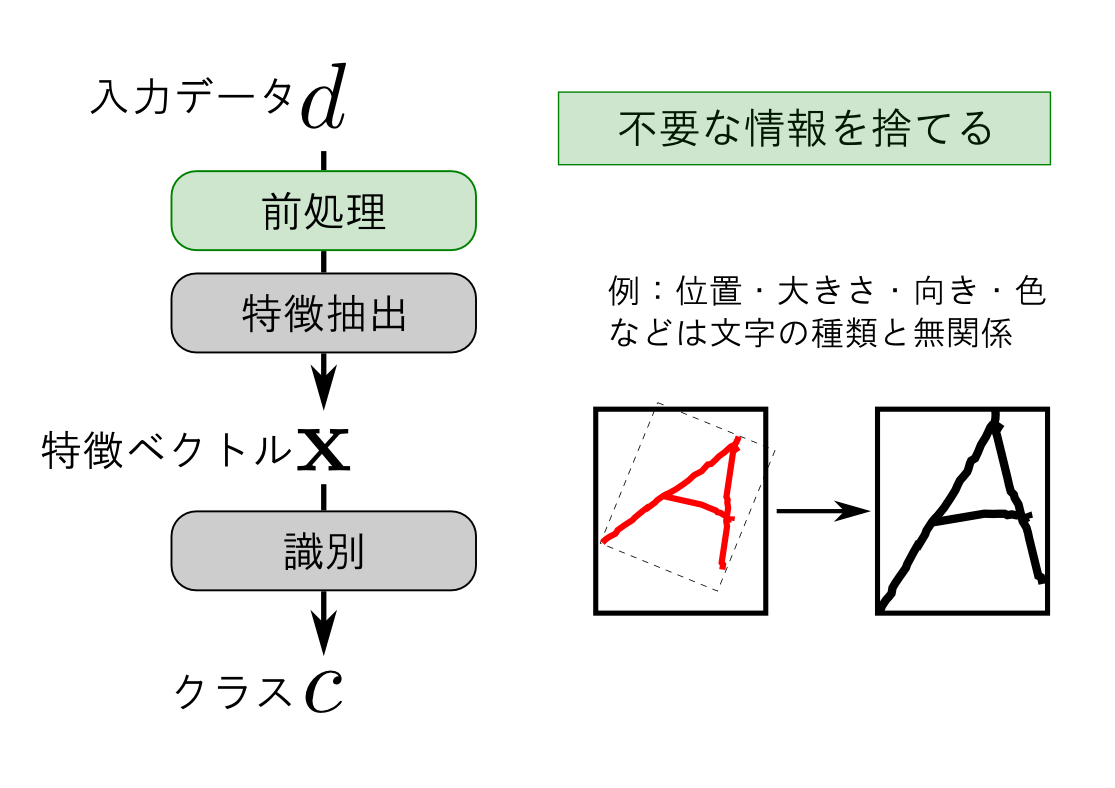
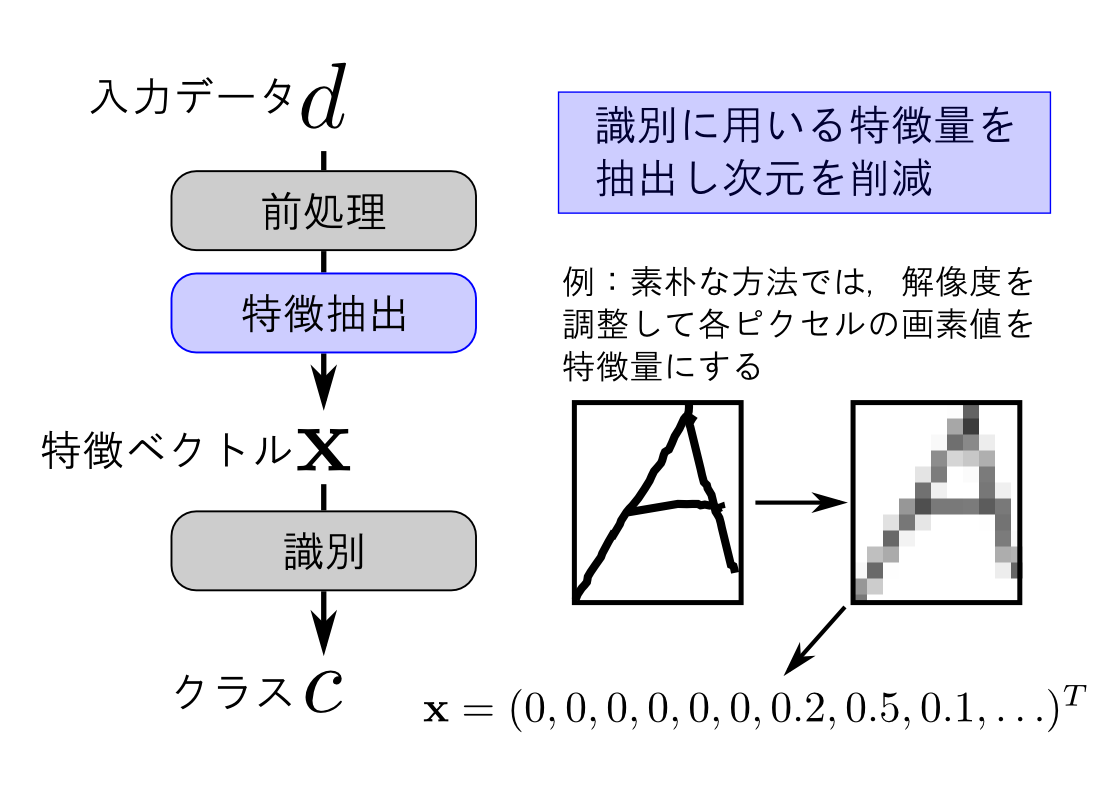
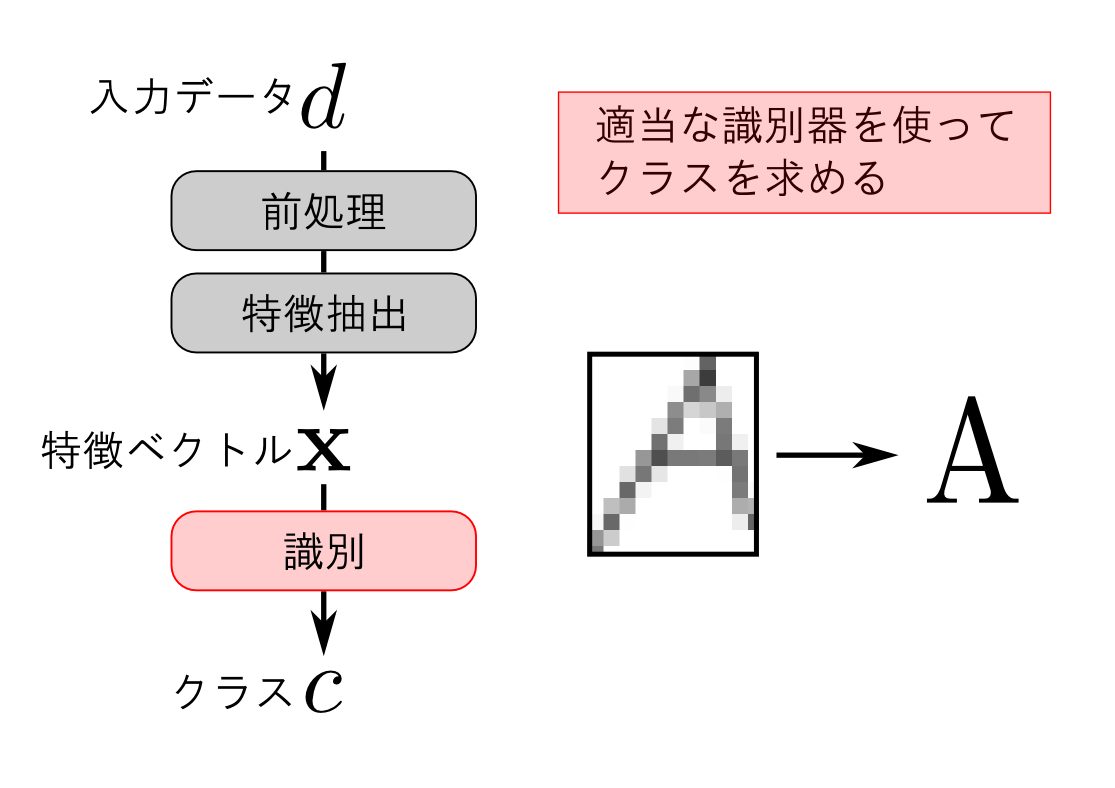
パターン認識の精度に最も影響するのが特徴抽出だと思います. データの形式・データの表す物が持つ特徴を良く観察してこれを設計する必要があります.

例えば「文字は主に線で構成される」という事に注目すると各ピクセルを特徴量とするのは あまり賢くなさそうです.

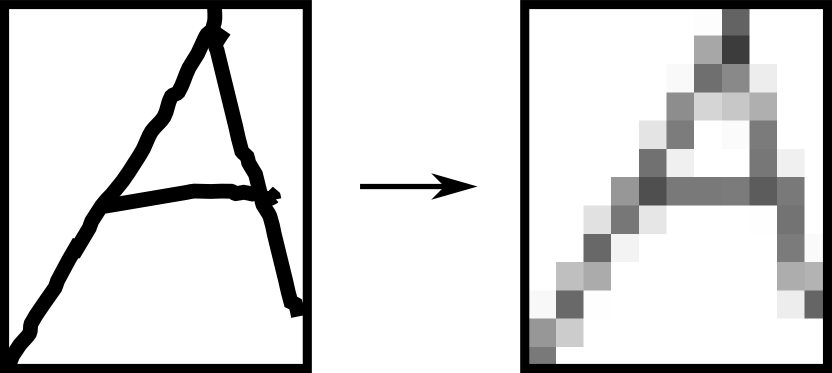
代わりに,単純なセグメントからなるマスクを複数用意して, マスクされた部分の一致度を特徴量とする方法が考えられます.

代わりに,単純なセグメントからなるマスクを複数用意して, マスクされた部分の一致度を特徴量とする方法が考えられます.

代わりに,単純なセグメントからなるマスクを複数用意して, マスクされた部分の一致度を特徴量とする方法が考えられます.

代わりに,単純なセグメントからなるマスクを複数用意して, マスクされた部分の一致度を特徴量とする方法が考えられます.

この様に特徴抽出は非常に難しくまた面白い部分なのですが, 各分野に固有の話題ばかりですので この勉強会では特徴抽出の一般論と特に有名な手法だけを紹介します.

一方で, 「識別」は完全に数学の問題となります. そこでまずは識別器の理論について進めていきます.

パターン識別の手法

今回はパターン識別の代表的な手法をざっと紹介します. 数学的な話・アルゴリズム的な話は来週以降詳しくやっていきます.

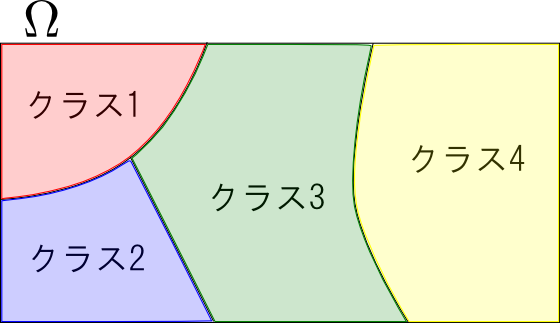
特徴ベクトル (feature vector) のなす空間を 特徴空間 (feature space) と呼びます. これを $\Omega$ と表しましょう.

識別器とは $\Omega$ の各点に $C=\{c_1,c_2,\ldots,\}$ のいずれかを割り当てる関数 $\varphi: \Omega \rightarrow C$ の事です.

識別器 $\varphi: \Omega\rightarrow C$ を定めると言うことは, 特徴空間 $\Omega$ を幾つかの領域に分割しラベルを振る という事に他なりません.

各領域をどのように表現するか？どのように分割を行うか？$\mathbf{x}$ が属する領域をどうやって求めるか？という事を考える事になります.

特徴空間の分割が既知の法則に従って出来るのならばそれで良いのですが, 法則が分からない場合には 学習データ (learning examples) から識別器を構築します.

学習データはいくつかの特徴ベクトルとそのクラスの組 $D=\{(\mathbf{x}_1,y_1),\ldots,(\mathbf{x}_n,y_n)\}$ からなります.

prog1-1.py

テンプレートマッチング

各クラスを１つの 代表ベクトル (representative vector) で表現し, 代表ベクトルと入力 $\mathbf{x}$ の距離によって $\mathbf{x}$ が属すクラスを決定する手法を テンプレートマッチング (template matching) と呼びます.

最も単純な距離の測り方は ユークリッド距離(euclidean distance) を利用する事です.

つまり入力 $\mathbf{x}$ と代表ベクトル $\mathbf{\mu}_c$ の距離を \[ ||\mathbf{x}-\mathbf{\mu}_c||^2=(\mathbf{x}-\mathbf{\mu}_c)^T(\mathbf{x}-\mathbf{\mu}_c) \] で求めます.

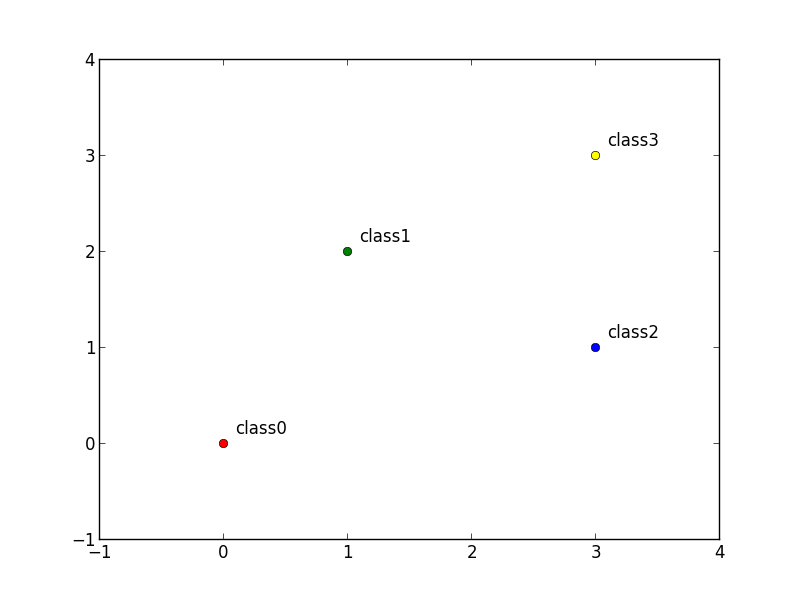
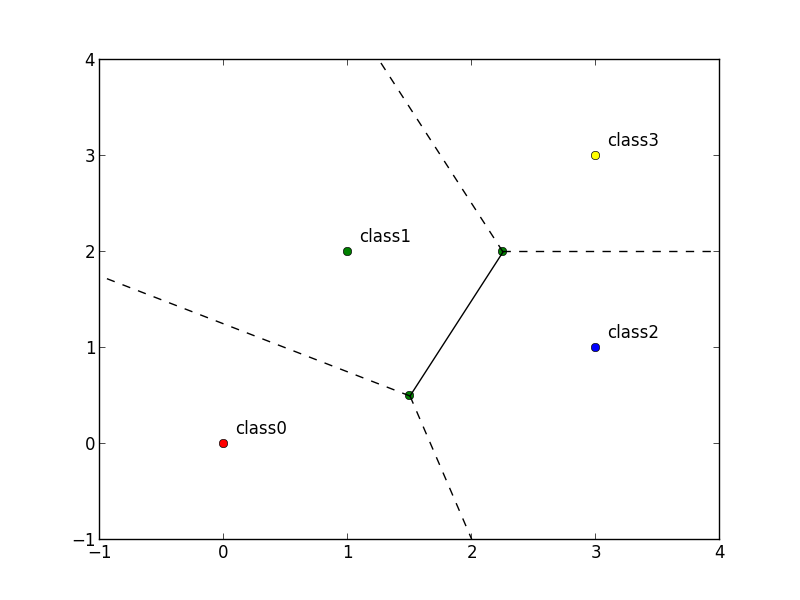
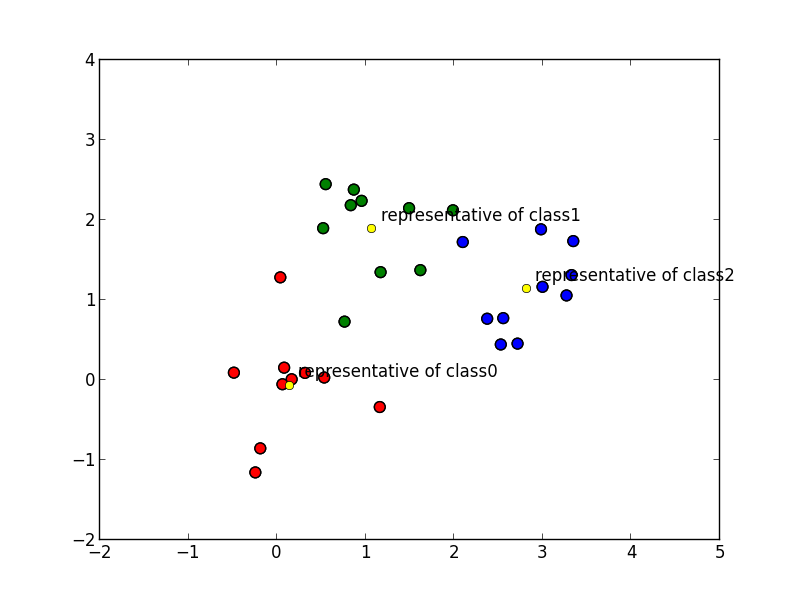
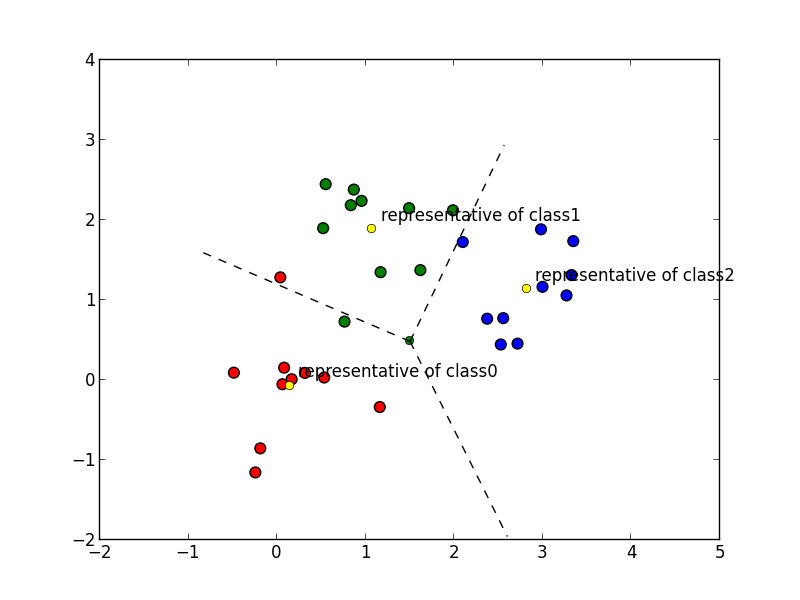
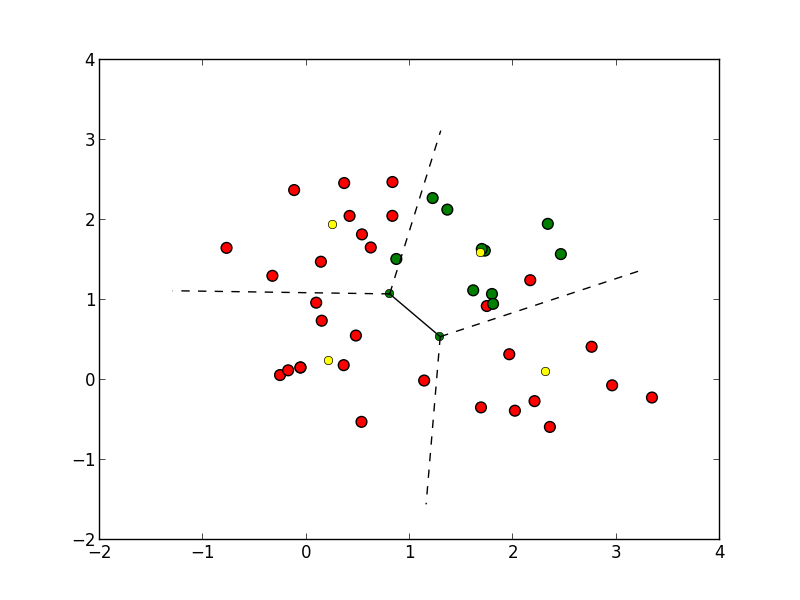
代表ベクトルが以下の様になっているならば, 特徴空間は以下の様に分割(ボロノイ分割 (Voronoi tessellation))されます.

prog1-2.py

代表ベクトルが以下の様になっているならば, 特徴空間は以下の様に分割(ボロノイ分割 (Voronoi tessellation))されます.

prog1-2.py

学習データ $D$ をもとにした代表ベクトルの決定方法には複数の方法がありますが, 単純な方法は 同じクラスに属する特徴ベクトルの重心 を代表ベクトルとする方法です.

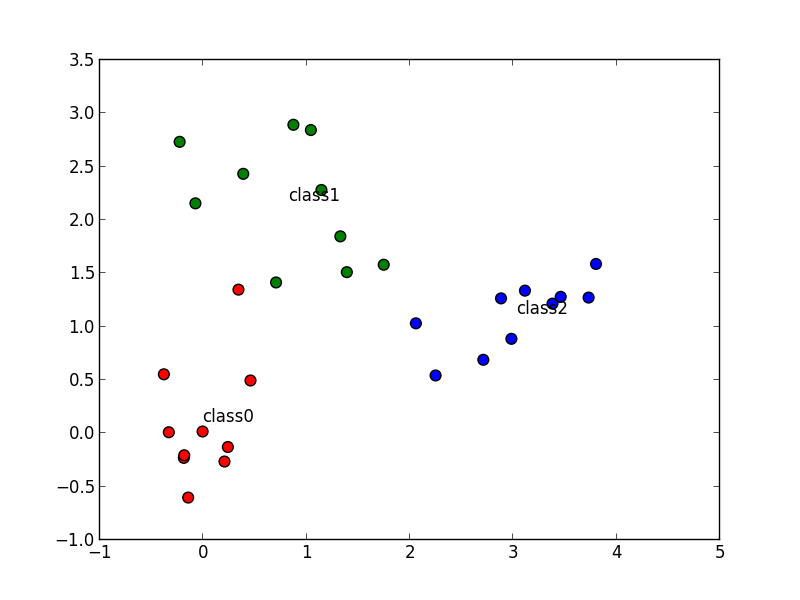
以下の学習データに対して

prog1-3.py

以下が代表ベクトルで

prog1-3.py

次のように分割されます.

prog1-3.py

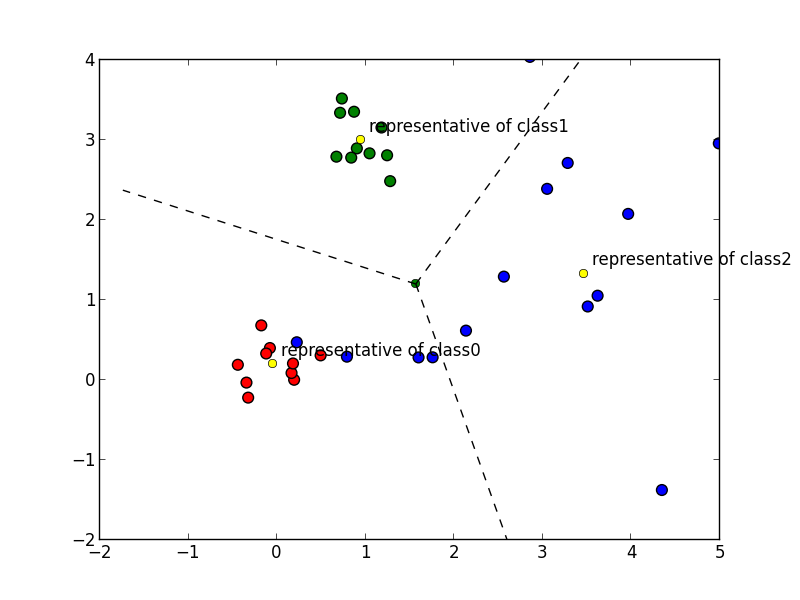
クラスによって分散が異なる場合 にユークリッド距離を使うと, 以下の図のように分散の大きいクラスでの識別精度が低下してしまいます.

prog1-4.py

これは, クラス $c$ の分布の分散共分散行列を $\mathbf{\Sigma}_c$ として $\mathbf{x}$ と代表ベクトル $\mathbf{\mu}_c$ の距離を \[ (\mathbf{x}-\mathbf{\mu}_c)^T\mathbf{\Sigma}_c^{-1}(\mathbf{x}-\mathbf{\mu}_c) \] で測る事によって調整する事が出来ます. これを マハラノビス距離 (Maharanobis distance)と呼びます. $\mathbf{\Sigma}_c$ は一般には分からないので標本分散(これは母分散の最尤推定量)などを代わり使います.

数学的な根拠は後の回に説明する予定です.

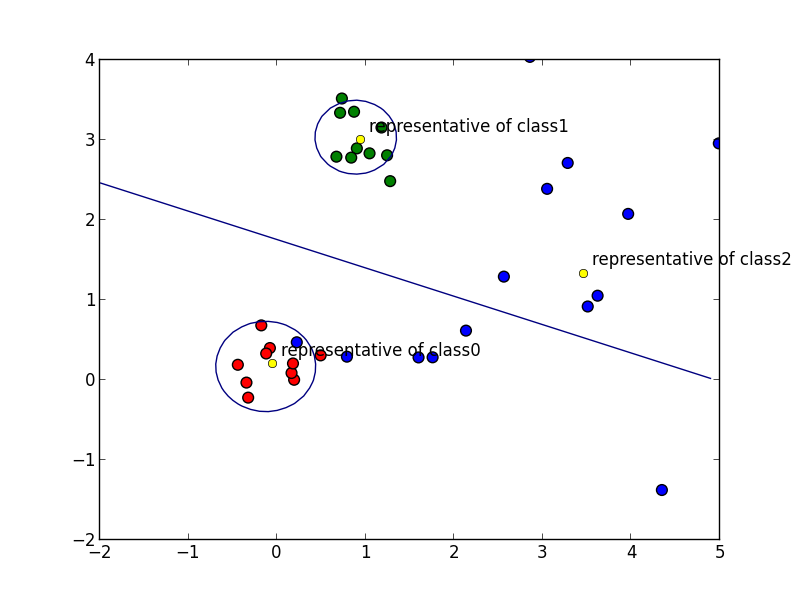
先ほどの例をマハラノビス距離で識別すると以下のようになります. 各曲線はクラス間の識別面であり, これらは二次曲線となっています.

prog1-4.py

代表ベクトルを複数持たせる事によってより複雑な分布を表現するという方法(マルチテンプレート法)もあります. 代表ベクトルの決め方は難しいですが, クラスタリングなどの手法を併用します.

prog1-5.py

$k$近傍法

入力 $\mathbf{x}$ に対して学習データを近い順番に $k$ 個選び, 多数決によって $\mathbf{x}$ が属すクラスを決定する手法を $k$近傍法 ($k$-nearest-neighbours classification rule, $k$-NN法) と呼びます.

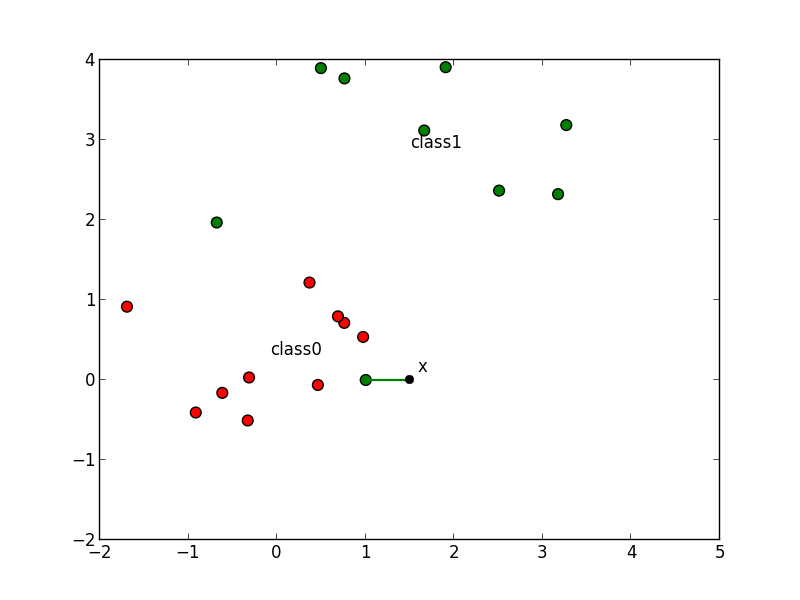
例えば以下の $\mathbf{x}$ は $5$-NN法 ではクラス $0$ に分類されます.

prog1-6.py

$k$-NN法は単純な方法で複雑な識別面を表現する事ができ学習データが十分にある場合には非常に良い識別精度を発揮します.

一方 $k$ が小さすぎると以下の例 ($k=1$)のように学習データのノイズを拾ってしまいます. $k$ の決定については後の回にやります.

prog1-7.py

$k$近傍法では学習データ集合 $D$ が大きいほど計算量が大きくなります. また, $D$ 全体を保存しておかなければいけません.

学習データが密に分布している場合は kdツリー などの空間分割アルゴリズムが効果的です.

疎に分布している場合には近似的な最近傍探索アルゴリズムが利用されます. 詳しくは後の回に紹介します.

識別関数

クラス毎に 識別関数 (dicriminant function) \[ f_c: \Omega \rightarrow \mathbb{R} \] を定め, この値が最小(もしくは最大)となる $c$ を $\mathbf{x}$ のクラスとする方法を考える事が出来ます.

ユークリッド距離によるテンプレートマッチング法は \[ f_c(\mathbf{x}) = ||\mathbf{x}-\mathbf{\mu}_c||^2 \] という識別関数, マハラノビス距離によるテンプレートマッチング法は \[ f_c(\mathbf{x}) = (\mathbf{x}-\mathbf{\mu}_c)^T\mathbf{\Sigma}_c^{-1}(\mathbf{x}-\mathbf{\mu}_c) \] という識別関数によって表す事が出来ます.

従ってテンプレートマッチングは識別関数による識別法の１つです.

問題は識別関数 $f_c(\mathbf{x})$ をどのように決定するのかということです.

1つの方法は, テンプレートマッチング法の様に幾何学的な考察を行う事です. 後の回に紹介しますが, 他には部分空間法などの手法があります.

２つ目の方法は $f_c(\mathbf{x})$ を パラメトリックモデル (parametric model) $f_c(\mathbf{x},\mathbf{a})$ として 表現し, パラメータ $\mathbf{a}$ に関する最適化問題に帰着する事です.

パラメトリックモデルというのはいくつかの未知パラメータによって決定されるモデルの事です.

例えば, 線形識別関数 (linear discriminant function)と呼ばれるモデルは \[\begin{aligned} f_c(\mathbf{x}) &= \mathbf{a}_c^T\mathbf{x}+b_c \\ &= a_{c1}x_1 + a_{c2}x_2 + \cdots + a_{cm}x_m + b_c \end{aligned} \] と表されます.

クラス $c_1,c_2$ の間の識別面は \[ \small{\begin{aligned} &f_{c_1}(\mathbf{x})=f_{c_2}(\mathbf{x})\\ \Leftrightarrow &(a_{c_11}-a_{c_21})x_1+\cdots+(a_{c_1m}-a_{c_2m})x_m+(b_{c_1}-b_{c_2}) = 0 \end{aligned}} \] より平面となるので, 線形識別関数を使うと特徴空間は平面で区切られて行くことになります.

実はユークリッド距離によるテンプレートマッチングは線形識別関数による識別と等価です.

であり, $||\mathbf{x}||^2$ は $c$ によらないですから $||\mathbf{x}-\mathbf{\mu}_c||^2$ が最小となるのは 線形識別関数 \[ f_c(\mathbf{x})=\mathbf{\mu}_c^T\mathbf{x}-\frac{1}{2}||\mathbf{\mu}_c||^2 \] が最大となる時です.

既知のベクトル値関数 $\Psi: \Omega \rightarrow \mathbb{R}^m$ によって \[ \begin{aligned} f_c(\mathbf{x}) &= \mathbf{a}_c^T\Psi(\mathbf{x}) \\ &= a_{c1}\psi_1(\mathbf{x}) + a_{c2}\psi_2(\mathbf{x}) + \cdots + a_{cm}\psi_m(\mathbf{x}) \end{aligned} \] と表されるモデルは 一般化線形識別関数 (generalized linear discriminant function) と呼ばれます.

つまり, 特徴ベクトルを $\Psi$ で変換してから線形識別関数で識別するというモデルです.

例えば, 入力が一次元の時 \[ \psi_i(x) = x^i \qquad (0\leq i \leq m) \] とおけば一般化線形識別関数は \[ f_c(x) = a_0 + a_1x + a_2x^2 + \cdots + a_mx^m \] となります. これは $k$ 次の 多項式モデル (polynomial model) に他なりません.

さて, パラメータを最適化する為の評価基準は様々考える事が出来ますが今回は 平均二乗誤差最小化 (least mean squared error) による手法を紹介します.

まず, クラスが全部で $k$ 個あるとしてそれをそれらを $c_1,c_2,\ldots,c_k$ とします. 識別関数を束にした関数 \[ \mathbf{f}(\mathbf{x}) = (f_{c_1}(\mathbf{x}),f_{c_2}(\mathbf{x}),\ldots,f_{c_k}(\mathbf{x}))^T \] と各 $c_i$ に対して $i$ 番目だけが $1$ のベクトル \[ \mathbf{p}_{c_i} = (0,0,\ldots,0,1,0,\ldots,0,0)^T \] を定めます.

学習データ $D=\{(\mathbf{x}_1,y_1),\ldots,(\mathbf{x}_n,y_n)\}$ に対して \[ \frac{1}{n}\sum_{i=1}^n || \mathbf{f}(\mathbf{x}_i) - \mathbf{p}_{y_i}||^2 \] を平均二乗誤差と呼びます. これが最小化となるように各 $\mathbf{a}_c$ を決定します.

つまり $\mathbf{f}(\mathbf{x}_i)$ と $\mathbf{p}_{y_i}$ が出来るだけ近づく様に最適化を行います.

\[ f_c(\mathbf{x}) = \mathbf{a}_c^T\Psi(\mathbf{x}) \] を代入すると \[ \begin{aligned} \mathbf{f}(\mathbf{x}) &= (\mathbf{a}_{c_1}^T\Psi(\mathbf{x}), \mathbf{a}_{c_2}^T\Psi(\mathbf{x}),\ldots,\mathbf{a}_{c_k}^T\Psi(\mathbf{x}))^T \\ &= (\mathbf{a}_{c_1},\mathbf{a}_{c_2},\dots,\mathbf{a}_{c_k})^T\Psi(\mathbf{x}) \end{aligned} \] となるので, $\mathbf{A} = (\mathbf{a}_{c_1},\mathbf{a}_{c_2},\ldots,\mathbf{a}_{c_k})$ と置けば \[ \mathbf{f}(\mathbf{x})=\mathbf{A}^T\Psi(\mathbf{x}) \] となります.

従って \[ \begin{aligned} \sum_{i=1}^n||\mathbf{f}(\mathbf{x}_i)-\mathbf{p}_{y_i}||^2 &= \sum_{i=1}^n||\mathbf{A}^T\Psi(\mathbf{x}_i)-\mathbf{p}_{y_i}||^2 \\ &= \sum_{i=1}^n (\Psi(\mathbf{x}_i)^T\mathbf{A}-\mathbf{p}_{y_i}^T)(\mathbf{A}^T\Psi(\mathbf{x}_i)-\mathbf{p}_{y_i}) \\ &= \sum_{i=1}^n \left\{ \Psi(\mathbf{x}_i)^T\mathbf{A}\mathbf{A}^T\Psi(\mathbf{x}_i)-2\Psi(\mathbf{x}_i)^T\mathbf{A}\mathbf{p}_{y_i}+||\mathbf{p}_{y_i}||^2 \right\} \end{aligned} \] となるので, これを $g(\mathbf{A})$ とおいて $\mathbf{A}$ で微分(資料末尾に補足説明)すると \[ \frac{\partial g(\mathbf{A})}{\partial \mathbf{A}} = 2\sum_{i=1}^n\left\{\Psi(\mathbf{x}_i)\Psi(\mathbf{x}_i)^T\mathbf{A}-\Psi(\mathbf{x}_i)\mathbf{p}_{y_i}^T\right\} \] となります.

これは \[ \begin{aligned} \mathbf{X} &= (\Psi(\mathbf{x}_1),\Psi(\mathbf{x}_2),\ldots,\Psi(\mathbf{x}_n))^T \\ \mathbf{P} &= (\mathbf{p}_{y_1},\mathbf{p}_{y_2},\ldots,\mathbf{p}_{y_n})^T \\ \end{aligned} \] と置けば \[ \frac{\partial g(\mathbf{A})}{\partial \mathbf{A}} = 2(\mathbf{X}^T\mathbf{X}\mathbf{A}-\mathbf{X}^T\mathbf{P}) \] と表されるので,

平均二乗誤差が最小となるのは \[ \frac{\partial g(\mathbf{A})}{\partial \mathbf{A}}=O\Leftrightarrow \mathbf{X}^T\mathbf{X}\mathbf{A}=\mathbf{X}^T\mathbf{P} \] が成立する時となります.

特に $\mathbf{X}^T\mathbf{X}$ が正則ならば \[ \color{red}{ \mathbf{A} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{P} } \] が求めるパラメータです.

一般に $\mathbf{X}^T\mathbf{X}$ が正則でないならば $\mathbf{X}$ の擬似逆行列 $\mathbf{X}^+$ によって \[ \color{red}{ \mathbf{A} = \mathbf{X}^+\mathbf{P} } \] となります.

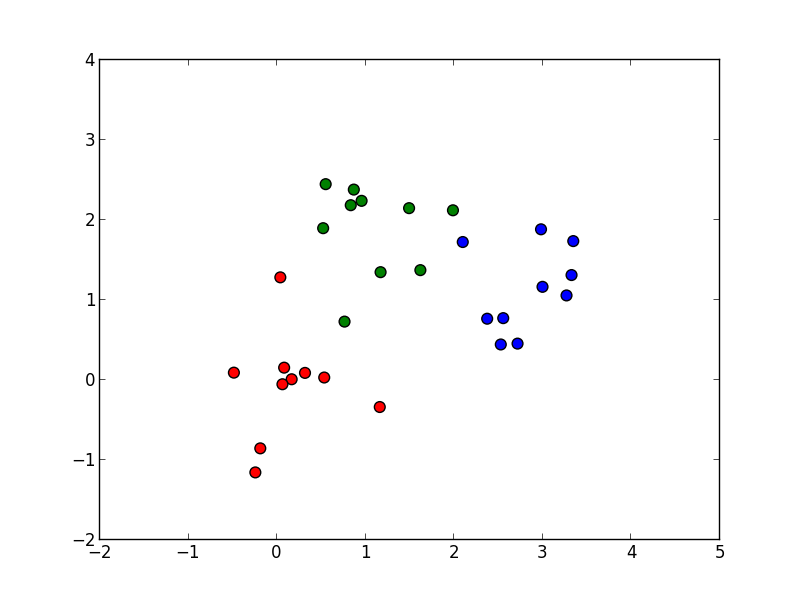
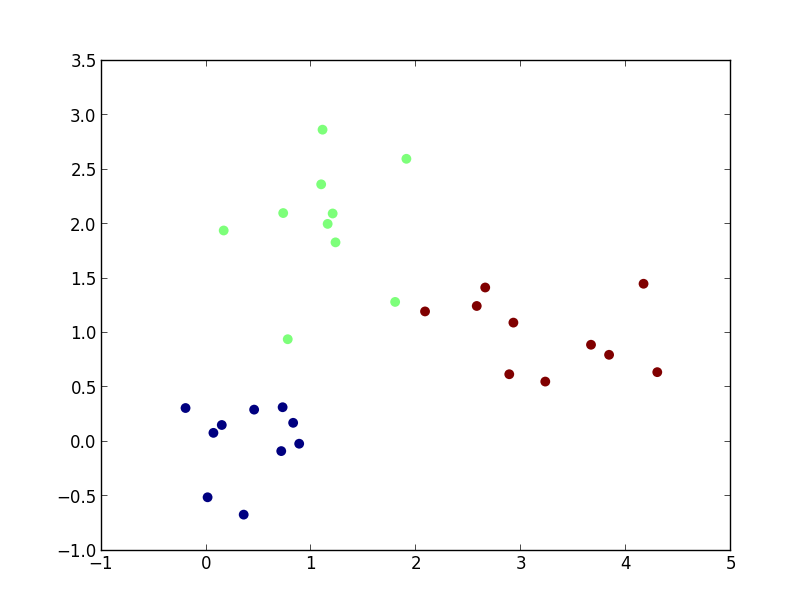
平均二乗誤差最小化による一般化線形識別関数の構築を行ってみましょう. まずは以下のデータをサンプルとして使います.

prog1-8-1.py

コードは以下のようになります.

# -*- coding: utf-8 -*-
import sys
from numpy import *
from scipy import linalg
from matplotlib.pyplot import *

data = loadtxt(sys.argv[1], delimiter="\t")

xs = data[0:2,:].T   # 学習データ [[x0,y0], [x1,y1], ...]
cs = int_(data[2,:]) # 正解クラス [c0, c1, ...]

# 学習データの数
N = len(xs)

# クラスの数
K = max(cs)+1

#### 特徴ベクトルの変換関数 ####
def phi(x):
    return [x[0], x[1], 1]
    #return [x[0]**2, x[1]**2, x[0]*x[1], x[0], x[1], 1]

#### パラメータの最適化 ####
# phi(特徴ベクトル)を行に並べた行列
X = array([ phi(xs[i]) for i in range(N) ])

# 正解クラス番号の成分だけ1にしたベクトルpを
# 行に並べた行列
P = zeros([N, K])
for i in range(N):
    P[i, cs[i]] = 1

# X^TXA = X^TP を満たす A が求めるパラメータ
A = linalg.solve(X.T.dot(X), X.T.dot(P))

# 擬似逆行列を使う場合
# A = linalg.pinv(X).dot(P)

# 最小二乗法を実行してくれる関数もあります
# A,residues,rank,s=linalg.lstsq(X, P)

#### 識別器の構築 ####
def distance(x, i):
    t = zeros(K)
    t[i] = 1
    return linalg.norm(x-t)

# (x, y) と (0,...,0,1,0,...,0) の距離が最小のクラスに分類
def classify(x, y):
    p = A.T.dot(phi([x, y]))
    return argmin([distance(p, i) for i in range(K)])

#### どんな感じで空間が分割されたか見てみましょう ####
# 表示領域の設定
xmin = min(xs[:,0]); xmax = max(xs[:,0])
ymin = min(xs[:,1]); ymax = max(xs[:,1])
xmin -= (xmax-xmin)/20
xmax += (xmax-xmin)/20
ymin -= (ymax-ymin)/20
ymax += (ymax-ymin)/20
xlim(xmin, xmax)
ylim(ymin, ymax)

X, Y = meshgrid(linspace(xmin, xmax, 100), linspace(ymin, ymax, 100))
Z = vectorize(classify)(X, Y)
pcolor(X, Y, Z, alpha=0.1)
scatter(xs[:,0], xs[:,1], c=cs, s = 50, linewidth=0)
show()

線形識別関数 \[ f_c(\mathbf{x}) = a_{c0}x_0 + a_{c1}x_1 + a_{c2} \] での識別を行ってみましょう. これは \[ \Psi(\mathbf{x}) = (x_0, x_1, 1)^T \] とおいた場合の一般化線形識別関数ですから, 前頁のコードにおいて

def phi(x):
    return [x[0], x[1], 1]

結果は以下のようになります.

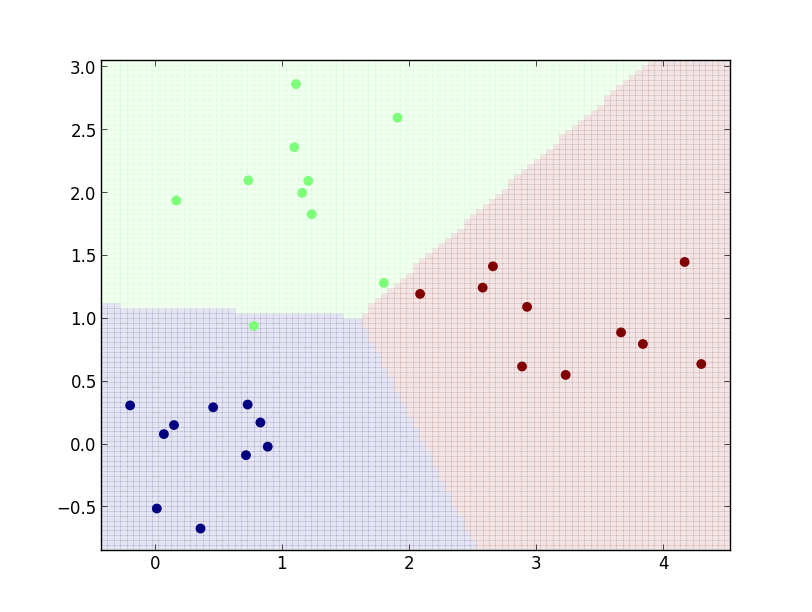
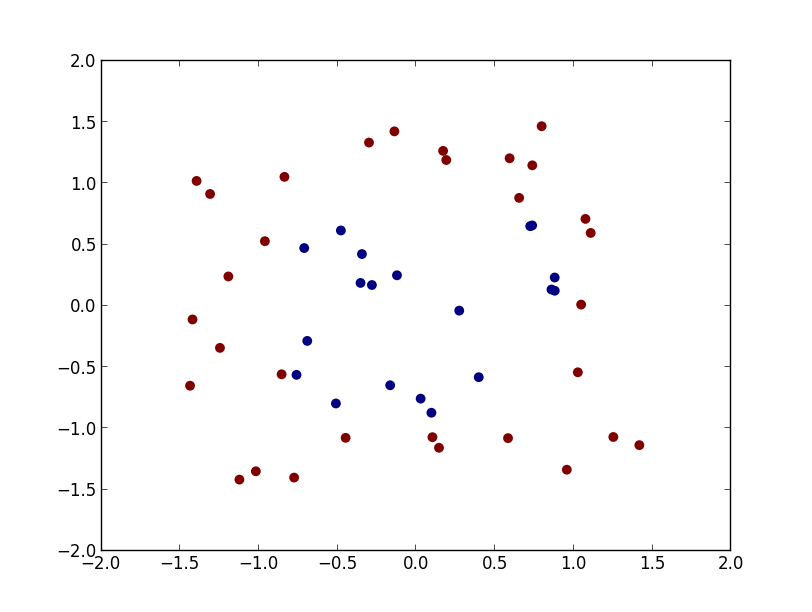
続いて以下のような学習データでやってみましょう.

prog1-8-3.py

今度は変数について2次の識別関数 \[ f_c(\mathbf{x}) = a_{c0}x_0^2 + a_{c1}x_1^2 + a_{c2}x_0x_1 + a_{c3}x_0 + a_{c4}x_1 + a_{c5} \] を使ってみましょう. これは \[ \Phi(\mathbf{x})=(x_0^2,x_1^2,x_0x_1,x_0, x_1,1)^T \] とおいた場合なので, 先ほどのコードを

def phi(x):
    return [x[0]**2, x[1]**2, x[0]*x[1], x[0], x[1], 1]

と修正して実行します.

結果は以下のようになります.

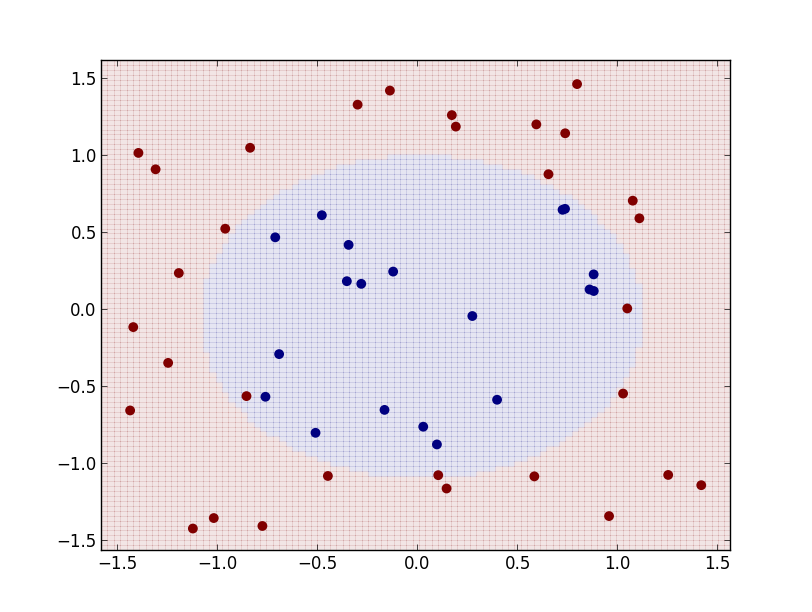
この様に一般化線形識別関数という統一的なモデルで様々な識別面を表す事ができます. また, 数学的な取り扱いも容易である事から様々な手法の基礎として用いられる事が多いです.

識別器を組み合わせる

単純な識別器を複数組み合わせる事によって精度を向上させる事が出来ると期待出来ます.

例えば線形識別関数は平面で領域を分割する事しか出来ませんが, それを複数組み合わせれば 例えば楕円領域を表す事が出来ます.

決定木

複数の識別器を使って段階的に識別を行っていく方法を決定木 (decision tree)による識別と言います.

最初は大まかに分類していきながら徐々に細かい特徴を見ていきます.

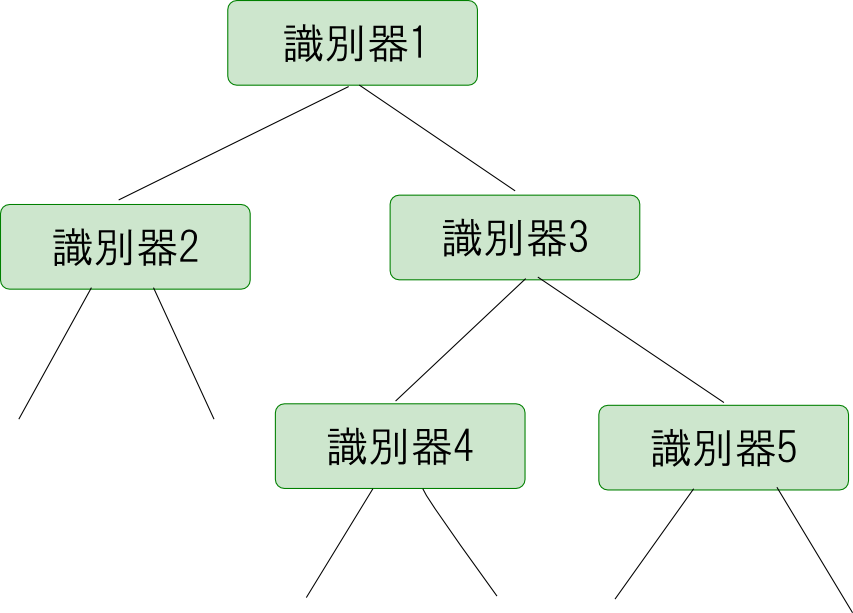
決定木を自動的に構築する問題も非常に難しいです. ルートから再帰的に入力の分割を行っていくのですが, どの識別器を使うのか？ 構築を終了出来る条件は何か？という事を考える必要があります.

ニューラルネットワーク

神経細胞を模したような単純な識別器をネットワーク状に結合して出来上がる識別器を ニューラルネットワーク (neural network)と呼びます.

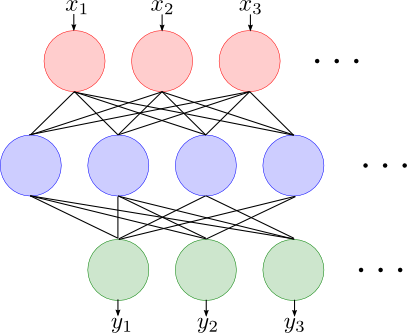
ニューラルネットワークの素子は以下の図の様な構造をしています. 各入力線に重み $w_1,w_2,\ldots,w_m$ としきい値 $\theta$ が定められており \[ x_1w_1 + x_2w_2 + \cdots + x_mw_m > \theta \] であるならば $1$ を,そうでなければ $0$ を出力します.

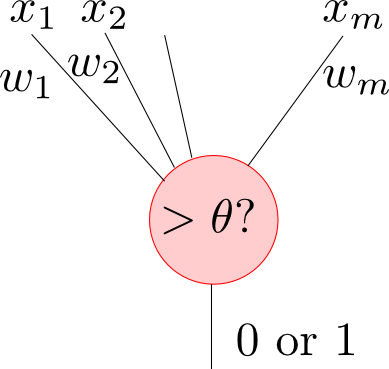
\[ x_1w_1 + x_2w_2 + \cdots + x_mw_m = \theta \] は平面なので素子１つは入力の空間を平面で切るという非常に単純なものです. これをネットワーク状に結合する事によって全体として非常に複雑な識別面を形成する事が出来ます.

ニューラルネットワークも重み$\mathbf{w}$ としきい値 $\mathbf{\theta}$ というパラメータを持つパラメトリックモデルと考える事が出来ます.

パラメータの学習には バックプロパゲーション (backpropagation) という手法が有名です. これも後の回に扱いたいと思います.

集団学習

識別器を組み合わせる方法として, 単純な識別器の結果の多数決を取るという方法も考えられます. これは集団学習(ensemble learning)という方法です.

同じ学習データで同じ学習をしたら同じ識別器が出来上がってしまうので, 使用する学習データのサブセットや学習方法を変えながら個々の識別器を構築します.

有名な バギング (bagging)とブースティング (boosting)について後の回に紹介したいと思います.

第１回はここで終わります

パターン認識という技術がどのようなものであるか理解していただけたと思います. 次回はベイズ統計の復習をした後, 識別器の評価であるとか事前知識の利用といった基礎的な話題を進めていきます.

補足: ベクトル・行列でのスカラー関数の微分

スカラー関数 $f(\mathbf{x})$ に対してそのベクトル $\mathbf{x}$ での微分係数を \[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} = \left( \frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots,\frac{\partial f(\mathbf{x})}{\partial x_n}\right)^T \] と定めます. つまりこれは勾配 \[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}}=\mathrm{grad} f(\mathbf{x}) \] に他ならないので, 極値をとる点では \[ \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}}=\mathbf{0} \] となります.

定数 $c$ に対しては当然 \[ \frac{\partial c}{\partial \mathbf{x}} = \mathbf{0} \] となります.

定数ベクトルとの内積 $\mathbf{a}^T\mathbf{x}=\mathbf{x}^T\mathbf{a}$ に対しては成分計算をしてみると \[ \frac{\partial}{\partial\mathbf{x}}\mathbf{a}^T\mathbf{x} = \frac{\partial}{\partial\mathbf{x}}\mathbf{x}^T\mathbf{a}=\mathbf{a} \] である事が判ります.

二次形式 \[ \mathbf{x}^T\mathbf{A}\mathbf{x} = \sum_{i,j} a_{ij}x_ix_j \] については \[ \begin{aligned} \frac{\partial}{\partial x_k} \mathbf{x}^T\mathbf{A}\mathbf{x} &= \sum_{i,j} a_{ij}\frac{\partial}{\partial x_k} x_ix_j=\sum_{i,j}a_{ij}(x_j\delta_i^k+x_i\delta_j^k) \\ &= \sum_j a_{kj}x_j + \sum_i a_{ik}x_i \end{aligned} \] なので \[ \frac{\partial}{\partial \mathbf{x}} = (\mathbf{A}+\mathbf{A}^T)\mathbf{x} \] となります($\delta_{ij}$ はクロネッカーのデルタ).

特に $||\mathbf{A}\mathbf{x}||^2$ については \[ ||\mathbf{A}\mathbf{x}||^2 = \mathbf{x}^T\mathbf{A}^T\mathbf{A}\mathbf{x} \] なので \[ \frac{\partial}{\partial\mathbf{x}}||\mathbf{A}\mathbf{x}||^2 = (\mathbf{A}^T\mathbf{A}+(\mathbf{A}^T\mathbf{A})^T)\mathbf{x} = 2\mathbf{A}^T\mathbf{A}\mathbf{x} \] となります.

よって例えば, \[ || \mathbf{A}\mathbf{x}-\mathbf{b}||^2 = ||\mathbf{A}\mathbf{x}||^2-2\mathbf{x}^T\mathbf{A}^T\mathbf{b}+||\mathbf{b}||^2 \] を最小にする $\mathbf{x}$ は \[ \frac{\partial}{\partial\mathbf{x}}||\mathbf{A}\mathbf{x}-\mathbf{b}||^2 = 2(\mathbf{A}^T\mathbf{A}\mathbf{x}-\mathbf{A}^T\mathbf{b}) \] より \[ \mathbf{A}^T\mathbf{A}\mathbf{x}=\mathbf{A}^T\mathbf{b} \] の解となります. これは最小二乗法による回帰分析などでよく出てくる方程式です.

同様に行列変数 $\mathbf{X}=(\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_m)$ を引数に取るスカラー関数 $f(\mathbf{X})$ に対して, 行列 $\mathbf{X}$ での微分係数を \[ \frac{\partial f(\mathbf{X})}{\partial \mathbf{X}} = \left( \frac{\partial f(\mathbf{X})}{\partial\mathbf{x}_1}, \frac{\partial f(\mathbf{X})}{\partial\mathbf{x}_2},\ldots, \frac{\partial f(\mathbf{X})}{\partial\mathbf{x}_m}, \right) \] $f(X)$ が極値を取るならば, 全ての方向の勾配が $\mathbf{0}$ になるので \[ \frac{\partial f(\mathbf{X})}{\partial \mathbf{X}} = \mathbf{O} \] となります.

ベクトルの場合と同様に公式を導くと, 定数 $c$ については \[ \frac{\partial}{\partial\mathbf{X}}c = \mathbf{O} \] です.

$\mathbf{a}^T\mathbf{X}\mathbf{b}$ に対しては \[ \mathbf{a}^T\mathbf{X}\mathbf{b}=\sum_{i,j}a_iX_{ij}b_j \] なので \[ \frac{\partial}{\partial X_{kl}}\mathbf{a}^T\mathbf{X}\mathbf{b}=\sum_{i,j}a_i\delta_i^k\delta_j^lb_j = a_kb_l \] ですから \[ \frac{\partial}{\partial \mathbf{X}}\mathbf{a}^T\mathbf{X}\mathbf{b} = \mathbf{a}\mathbf{b}^T \] です.

$\mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{b}$ については \[ \mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{b} = \sum_{i,j,k}a_iX_{ik}X_{jk}b_j \] なので \[ \begin{aligned} \frac{\partial}{\partial X_{pq}} &= \sum_{i,j,k}a_i(\delta_i^p\delta_k^qX_{jk}+\delta_k^p\delta_j^qX_{ik})b_j \\ &= \sum_j a_pX_{jq}b_j + \sum_ia_iX_{ip}b_q \\ \end{aligned} \] となります. よって \[ \frac{\partial}{\partial \mathbf{X}}\mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{b} = (\mathbf{a}\mathbf{b}^T+\mathbf{b}\mathbf{a}^T)X \] となります. $\mathbf{a}^T\mathbf{X}^T\mathbf{X}\mathbf{b}$ などについても同様に計算を行います.