プログラマの為の
数学勉強会
第17回
(於)ワークスアプリケーションズ中村晃一
2014年1月23日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
回帰分析(続き)
重回帰分析
独立変数が \(m\) 個のモデルでの回帰分析を重回帰分析と呼びます.

最小二乗法による重回帰分析は一変数(単回帰分析)の場合とほとんど同じです. 観測値 \(Y\) と理論値 \(f(X_1,X_2,\ldots,X_m)\) の誤差 \(Y-f(X_1,X_2,\ldots,X_m)\) が正規分布に従うと仮定して, 最尤推定法で \(f(X_1,X_2,\ldots,X_n)\) を決定します.
最小二乗法(重回帰分析)
観測値の誤差分布の分散が一定であると仮定出来る場合, データ列 \((\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\) に対して残差平方和 \[ \sum_{i=1}^n\left\{ y_i-f(\mathbf{x}_i) \right\}^2 \] を最小とする \(f\) としてモデルを決定する.
最小二乗法:線型回帰
モデル \(y=f(\mathbf{x})\) が既知の関数 \(g_1(\mathbf{x}),g_2(\mathbf{x}),\ldots,g_m(\mathbf{x})\) とパラメータ \(a_1,a_2,\ldots,a_m\) によって \[ f(\mathbf{x}) = a_1g_1(\mathbf{x})+a_2g_2(\mathbf{x})+\cdots+a_mg_m(\mathbf{x}) \] と表される場合, \[ \begin{aligned} G &= (g_j(\mathbf{x}_i))_{1\leq i\leq n, 1\leq j\leq m} \\ \mathbf{a}&=(a_1,a_2,\ldots,a_m)^T \\ \mathbf{y}&=(y_1,y_2,\ldots,y_n)^T \end{aligned} \] とおけば 正規方程式 \[ \color{yellow}{ G^TG\mathbf{a}=G^T\mathbf{y} } \] の解が最小二乗法による \(a_1,a_2,\ldots,a_m\) の推定値を与える.例えば, 従属変数 \(Z\) を \(X,Y\) で説明するモデルが \[ z = ax+by + c \] という形の場合は, 観測データ \((x_1,y_1,z_1),(x_2,y_2,z_2),\ldots,(x_n,y_n,z_n) \) に対して \[ G = \begin{pmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots \\ x_n & y_n & 1 \end{pmatrix}, \mathbf{a} = (a,b,c)^T, \mathbf{z} = (z_1,z_2,\ldots,z_n)^T \] とおいて, \[ G^TG\mathbf{a}=G^T\mathbf{z} \] を解きます.
\[ z = ax^2+bxy+cy^2+dx+ey+f \] という形ならば, \[ \begin{aligned} G &= \begin{pmatrix} x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_n^2 & x_ny_n & y_n^2 & x_n & y_n & 1 \\ \end{pmatrix}\\ \mathbf{a} &= (a,b,c,d,e,f)^T\\ \mathbf{z} &= (z_1,z_2,\ldots,z_n)^T \end{aligned} \] とおいて, \[ G^TG\mathbf{a}=G^T\mathbf{z} \] を解きます.
例題
以下のデータ(ex17-1.dat)に対して \(z=ax+by+c\) というモデルを最小二乗法によって当てはめて下さい.
#x y z
9.83 -5.50 635.99
-9.97 -13.53 163.78
-3.91 -1.23 86.94
-3.94 6.07 245.35
-13.67 1.94 1132.88
-14.04 2.79 1239.55
4.81 -5.43 214.01
7.65 15.57 67.94
5.50 7.26 -1.48
-3.34 1.34 104.18
以下がコーディング例です.
import numpy as np
from scipy import linalg as LA
data = np.loadtxt("ex17-1.dat", comments="#", delimiter="\t")
x = data[:,0]
y = data[:,1]
z = data[:,2]
N = len(x)
G = np.array([x, y, np.ones(N)]).T
print LA.solve(G.T.dot(G), G.T.dot(z))
実行結果は \[ a= -30.0, b = 3.65, c = 322\] とまりました. つまり, \[ z = -30.0x + 3.65y+ 322 \] という方程式を得る事が出来ました.

練習問題
例題と同一のデータ(ex17-1.dat)に対して \(z=ax^2+bxy+cy^2+dx+ey+f\) というモデルを当てはめて下さい.
結果は \[ z = 4.86x^2 -4.25xy + 1.25y^2-7.56x+2.68y-6.87 \] となります.
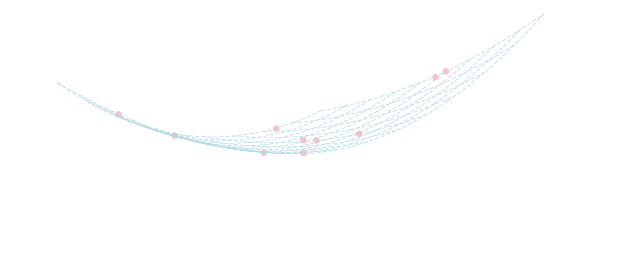
独立変数の選び方
変数 \(Y\) を説明する変数 \(X_1,X_2,\ldots,X_n\) は無相関である事が仮定されます. そうでなければ 多重共線性 という性質が生じて以下の様な問題が発生します.
- 回帰方程式の係数が期待されるものとは異なる
- 正規方程式が解を持たない, もしくは大きな誤差が発生する
変数はむやみに増やせば良いものではないという事に注意してください.
例えば, 以下のデータに対して\(z = ax+by+c\)というモデルを当てはめてみましょう. \[ \begin{array}{|c|cccccccccc|}\hline x&30&36&47&48&50&52&55&55&55&60\\ \hline y&16&29&54&55&33&56&48&57&62&72\\ \hline z&48&69&108&114&67&124&91&106&116&132\\ \hline \end{array} \]
表を見ると, \(x\) が増加すると \(z\) も増加する傾向にある事がわかります.
しかし, 重回帰の結果は \[ z = \color{yellow}{-0.8}x + 2.0y + 43.0 \] となり, \(x\) の係数が負になってしまいます.
\(x,y\) の相関係数は約 \(\color{yellow}{0.9}\) となりますので, \(x,y\) には強い正の相関が存在します. これがこの直感に反する結果の原因です.
質的なデータの利用
説明変数として「男か女か?」の様な数量ではない質的なデータを利用したい場合があります. この様な場合には以下のようなダミー変数を用意して, 先ほどと同様に重回帰を行います. \[ X = \left\{\begin{array}{cc} 1 & (\text{男の場合}) \\ 0 & (\text{女の場合}) \end{array}\right. \]
3つ以上のカテゴリを持つデータの場合は注意が必要です. \(n\) 個のカテゴリ \(C_1,C_2,\ldots,C_n\) を持つデータに対して \[ X = \left\{\begin{array}{cc} 1 & (\text{$C_1$ の場合}) \\ 2 & (\text{$C_2$ の場合}) \\ \vdots & \vdots \\ n & (\text{$C_n$ の場合}) \end{array}\right. \] の様に1つの変数を割り当てるのはよくある誤りです.
このような場合は \(n-1\)個のダミー変数 \(X_1,X_2,\ldots,X_{n-1}\) を用意して \[ X_i = \left\{\begin{array}{cc} 1 & (\text{$C_i$ の場合}) \\ 0 & (\text{それ以外}) \end{array}\right. \] とします. \(X_1=X_2=\ldots=X_{n-1}=0\) の場合にカテゴリ \(C_n\) のデータであるという事になります.
\(n\) が大きいと独立変数の数が増えるので, 解析に必要な標本数も増加します. また多重共線性の問題が生じる可能性も高まる事に注意が必要です.
例題
以下のデータに対して重回帰分析を行いましょう. \[ \begin{array}{|cccccccccccc|} \hline A& A& A& A& B& B& B& B& C& C& C& C \\ \hline S& S& T& T& S& S& T& T& S& S& T& T \\ \hline 65& 80& 33& 36& 108& 117& 45& 62& 142& 150& 82& 89 \\ \hline \end{array} \]
1行目をダミー変数 \(X_A,X_B\), 2行目をダミー変数 \(X_S\) に置き換えれば以下の様になります. \[ \begin{array}{|c|cccccccccccc|} \hline X_A & 1& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0 \\ \hline X_B & 0& 0& 0& 0& 1& 1& 1& 1& 0& 0& 0& 0 \\ \hline X_S & 1& 1& 0& 0& 1& 1& 0& 0& 1& 1& 0& 0 \\ \hline Y & 65& 80& 33& 36& 108& 117& 45& 62& 142& 150& 82& 89 \\ \hline \end{array} \] これに重回帰分析を行えば回帰方程式 \[ y = -62.25x_A -32.75 x_B + 52.5 x_S + 89.5 \] を得る事が出来ます.
モデルの良さの評価
回帰分析の結果を評価する為には決定係数や赤池情報量基準などの指標が利用されます. また, 検定の手法を応用してより細かく回帰方程式を調べていく事が出来ます.
決定係数
決定係数
観測値を\(y_1,y_2,\ldots,y_n\), 回帰方程式の基づく理論値を\(f_1,f_2,\ldots,f_n\) とする. また,\(y_i\) の平均を\(\overline{y}\) とする. 以下の量を決定係数と呼ぶ. \[ R^2 = 1 - \frac{\sum_{i=1}^n (y_i-f_i)^2}{\sum_{i=1}^n (y_i-\overline{y})^2} \]
\(y_i-f_i\) が観測値と理論値の誤差なので, \(R^2\) が \(1\) に近いほど当てはまりが良い と考える事が出来ます.
例題
以下の2つのデータセットに対して \(y=x\) という回帰方程式を当てはめた場合の決定係数を計算してみましょう.
データセット1 \[ \begin{array}{|c|cccccccccc|} \hline X&17.6&10.7&7.3&15.5&4.9&11.1&10.0&12.7&4.1&18.4 \\ \hline Y&14.4&10.0&8.0&14.9&4.5&8.4&8.4&11.8&2.8&19.8 \\ \hline \end{array} \]
データセット2 \[ \begin{array}{|c|cccccccccc|} \hline X&5.6&15.7&13.5&2.1&15.2&9.0&18.0&8.8&11.2&12.9\\ \hline Y&20.6&7.7&17.8&-5.0&18.6&11.8&19.3&5.6&10.0&8.0\\ \hline \end{array} \]
データセット1に対しては\(R^2 = 0.89\) となります.
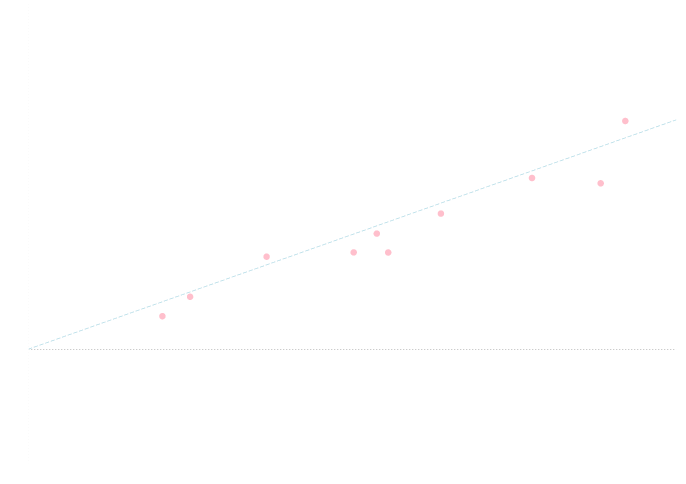
データセット2に対しては\(R^2 = 0.27\) となります.

決定係数 \(R^2\) には回帰方程式の項の数が増えるほどより良くなる傾向があります. そこで, 項の数が異なるモデル同士を比較する場合には自由度調整済みの決定係数を利用します.
自由度調整済みの決定係数
観測値を\(y_1,y_2,\ldots,y_n\), 回帰方程式の基づく理論値を\(f_1,f_2,\ldots,f_n\) とする. \(y_i\) の平均を\(\overline{y}\) とする. また, 回帰方程式が \[ y= a_1g_1(\mathbf{x}) + a_2g_2(\mathbf{x}) + \cdots + a_mg_m(\mathbf{x})+c\quad (\text{$c$ は定数}) \] という線型回帰方程式であるとする. この時 以下の量を自由度調整済みの決定係数と呼ぶ. \[ R^2 = 1 - \frac{\sum_{i=1}^n (y_i-f_i)^2/(n-m-1)}{\sum_{i=1}^n (y_i-\overline{y})^2/(n-1)} \]
例題
以下のデータセットに対して \(y=ax+b,y=ax^2+bx+c\) という2つの回帰方程式を当てはめた場合の決定係数を比較してみましょう. \[ \begin{array}{|c|cccccccccc|} \hline X & -1.2&1.9&-3.4&-0.4&2.9&2.9&3.5&-0.6&2.0&3.7 \\ \hline Y & 4.6& -0.6&22.3&-0.0&-0.0&5.0&3.1&5.3&1.9&8.4 \\ \hline \end{array} \]
モデル \(y=ax+b\) で回帰分析を行うと \[ y =-1.6x + 6.8 \] となり, 決定係数は\(m=1\)の場合の計算を行って\(R^2 = 0.32\) となります.

モデル \(y=ax^2+bx+c\) で回帰分析を行うと \[ y = 1.1x^2 -2.5x + 0.9 \] となり, 決定係数は \(m=2\) の場合の計算を行って \(R^2 = 0.90\) となります.

練習問題
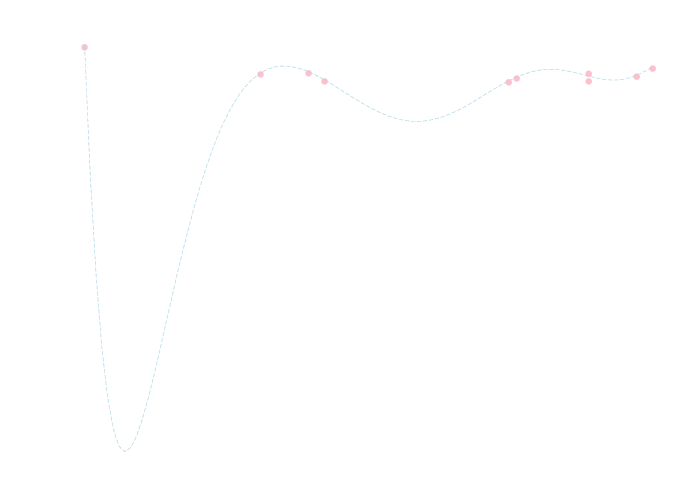
例題のデータセットに対して, 9次方程式を当てはめた場合の決定係数を求めて下さい.
回帰方程式は \[\small{ y=-0.01x^9+0.05x^8+0.11x^7-0.39x^6-1.0x^5-2.7x^4+16x^3+7.8x^2-32x-11 } \] となります. 決定係数は自由度調整をしないと \(R^2 = 0.97\) となり2次のモデルより良いという結果になります. しかし, 下のグラフを見れば分かるようにデータのノイズまで忠実に再現してしまっており決して良いモデルとはいえません.
一方で, 自由度調整を行うと \(R^2 = 0.72\) となり 2次のモデルの方が良いと判断する事が出来ます.
赤池情報量基準
赤池情報量基準
\[ \mathrm{AIC} = -2\ln L + 2k \] \(L\) は尤度の最大値, \(k\) は自由変数の数.
モデルとデータがよく一致するほど尤度 \(L\) が大きくなるので \(\mathrm{AIC}\) は小さくなります. \(2k\) はモデルが複雑になることに対するペナルティであり, \(\mathrm{AIC}\) が小さいほど良い値であると言えます.
最小二乗法では, 誤差 \(Y-f(X_1,X_2,\ldots,X_n)\) が正規分布 \(N(0,\sigma^2)\) に従うと仮定しているので, データ列\((\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\) に対して 尤度は \[ L = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(y_i-f(\mathbf{x}_i))^2}{2\sigma^2}\right\} \] となります. 従って \[ \begin{aligned} \ln L &= -\frac{n}{2}\ln(2\pi\sigma^2)-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-f(\mathbf{x}_i))^2\\ &= -\frac{n}{2}\ln(2\pi\sigma^2)-\frac{RSS}{2\sigma^2} \end{aligned} \] となります.但し, \(RSS=\sum(y_i-f(\mathbf{x}_i))^2\) です.
ここで\(\sigma^2\)の値はわからないので, (母集団が正規分布の場合の母分散の最尤推定量である)標本分散によって \[ \sigma^2 = \frac{1}{n}\sum_{i=1}^n(y_i-f(\mathbf{x}_i))^2 = \frac{RSS}{n} \] とおくと \[ \ln L = -\frac{n}{2}\ln\left(\frac{2\pi}{n}RSS\right)-\frac{n}{2} \] となるので \[ \mathrm{AIC}=-2\ln L+2k = n\ln\left(\frac{RSS}{n}\right)+2k+n(\ln 2\pi+1) \] となります. 最後の項はモデルの選び方によらない定数なので\(\mathrm{AIC}\)の大小には関係ありません. 従って, 最小二乗法を使う場合には, \[ \color{yellow}{ n\ln\left(\frac{RSS}{n}\right)+2k } \] が小さいほど良いモデルであると言えます.
先ほどの例題のデータについて \[ y=a_kx^k+a_{k-1}x^{k-1}+\cdots+a_1k+a_0 \] というモデルで \(\mathrm{AIC}\) を計算すると以下の様になります.
\[ \begin{array}{|c|c|c|c|c|}\hline k & 1 & 2 & 3 & 4 & \cdots \\ \hline \mathrm{AIC} & 63.5 & 45.3 & 47.2 & 48.9 & \cdots \\ \hline \end{array} \]従って最も良いモデルは2次のものだと判断出来ます.

\(\mathrm{AIC}\)の計算には以下のコードを利用しました.
# -*- coding: utf-8 -*-
import numpy as np
from scipy import linalg as LA
from math import log, pi
data = np.loadtxt("ex17-5.dat", comments="#", delimiter="\t")
x = data[:,0]
y = data[:,1]
N = len(x)
k = 4 # パラメータの数x^kの項まで使う
# 回帰分析
G = np.array([x**i for i in range(k+1)]).T
a = LA.solve(G.T.dot(G), G.T.dot(y))
# AICの計算(最後の項もつけておいた)
f = G.dot(a)
AIC = N*log(np.sum((y-f)**2)/N) + 2*k + N*(log(2*pi)+1)
print AIC
回帰分析と検定
回帰方程式 \[ y=a_0+a_1x_1+a_2x_2+\cdots+a_mx_m \] の各係数について詳しく調べる為には検定の手法を利用します.
全く同一の独立変数の実現値 \(\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n\) を用いて回帰分析を行っても, その都度誤差が生じて \(\mathbf{y}\) 及び \(\mathbf{a}=(a_1,a_2,\ldots,a_m)^T\) の推定値も変化します. つまり, 実際には \(\mathbf{a}\)の推定値は確率変数であると考える事が出来ます.
データセット \((\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\) に対して \[ \mathbf{y}=G\mathbf{a}+\mathbf{\varepsilon} \] が成立しているとします. ここで \(G\) は既に説明したものであり, \(\mathbf{\varepsilon}\) は誤差項です. ここで幾つかの仮定をおきます.
- \(\mathbf{\varepsilon},\mathbf{y}\)は確率変数であって, \(\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n\)は確率変数ではない.
- 誤差は平均が\(0\)で分散が同一の正規分布に従い, 無相関である. つまり, \[ \begin{aligned} E[\varepsilon] &= \mathbf{0}\\ E[\varepsilon_i\varepsilon_i]&=\sigma^2\\ E[\varepsilon_i\varepsilon_j]&=0\quad (i\neq j) \end{aligned} \]
\(\mathbf{a}\) の推定値は \[ \hat{\mathbf{a}} = (G^TG)^{-1}G^T\mathbf{y} \] だったので, \[ \begin{aligned} E[\hat{\mathbf{a}}] &= (G^TG)^{-1}G^TE[\mathbf{y}]\\ &= (G^TG)^{-1}G^TE[G\mathbf{a}+\mathbf{\varepsilon}]\\ &=(G^TG)^{-1}G^TGE[\mathbf{a}]+\mathbf{0}\\ &=\mathbf{a} \end{aligned} \] が成り立ちます(これから\(\hat{\mathbf{a}}\) が不偏推定量である事もわかります.).
また\(\hat{\mathbf{a}}\)の分散共分散行列は \[ \begin{aligned} V[\hat{\mathbf{a}}]&=E[(\hat{\mathbf{a}}-\mathbf{a})(\hat{\mathbf{a}}-\mathbf{a})^T] \\ &=E[(G^TG)^{-1}G^T\mathbf{\varepsilon}\mathbf{\varepsilon}^TG(G^TG)^{-1}] \\ &=(G^TG)^{-1}G^TE[\mathbf{\varepsilon}\mathbf{\varepsilon}^T]G(G^TG)^{-1} \\ &=\sigma^2(G^TG)^{-1}G^TG(G^TG)^{-1} \\ &= \sigma^2(G^TG)^{-1} \end{aligned} \]
以上の結果と正規分布の再生性から以下の事が言えます.
回帰方程式の係数の分布
重回帰分析による回帰方程式の係数の推定量 \(\hat{\mathbf{a}}\) は多変量正規分布 \(N(\mathbf{a},\sigma^2 (G^TG)^{-1})\) に従う.
この事が分かってしまえば, 既に学習した推定や検定の手法を利用する事が出来ます.
例題
以下のデータセットに対して \(z=ax+by+c\) というモデルで回帰分析を行った場合のパラメータ\(\mathbf{a}=(a,b,c)^T\)について調べてみましょう.
\[ \begin{array}{|c|cccccccccc|} \hline x & 5.4& 6.2& 4.3& 1.2& 6.2& 4.0& 4.0& 3.9& 6.4& 6.6 \\ \hline y & 4.7& 0.2& 0.5& 5.1& 3.6& 7.3& 10.0& 5.5& 9.6& 8.9 \\ \hline z & 11.8& 0.3& 2.8& 8.2& 10.9& 19.3& 15.8& 17.9& 21.7& 18.1 \\ \hline \end{array} \]\[ \sigma^2(G^TG)^{-1} = \sigma^2\begin{pmatrix} 0.04 & -0.0004 & -0.2 \\ -0.0004& 0.009 & -0.05 \\ -0.2 & -0.05 & 1 \end{pmatrix} \] となるので, 回帰分析で得られる推定値 \(\hat{\mathbf{a}}=(\hat{a},\hat{b},\hat{c})^T\) は真の値 \(\mathbf{a}=(a,b,c)^T\) が平均で上の行列が分散共分散行列である多変量正規分布に従います.
ここで \(a=0\) であるか否かといった事を検定してみましょう. \(a=0\) ならば \(z = by+c\) となるので 変数 \(x\) と \(z\) には全く関係ないという事になります. \[ \begin{aligned} H_0 &: a=0 \\ H_1 &: a\neq 0 \end{aligned} \]
前頁の結果より \(a\) の推定値 \(\hat{a}\) は \(H_0\) の元で \(N(0, 0.04\sigma^2)\) に従います. ここで \(\sigma^2\) の値は分からないのでその推定量として \[ S^2=\frac{\sum\{z_i-(\hat{a}x_i+\hat{b}y_i+\hat{c})\}^2}{n-2-1} \] を使うと(分母の\(-2\)は独立変数が\(2\)つある事より), \[ t = \frac{\hat{a}}{\sqrt{0.04S^2}} \] は自由度 \(n-2-1\) の\(t\) 分布に従います.
\(\hat{b},\hat{c}\) についても全く同様に計算すると \[ \begin{array}{|c|ccc|} \hline \text{係数} & \hat{a} & \hat{b} & \hat{c} \\ \hline \text{推定値} & 0.42 & 1.8 & 0.45 \\ \hline t & 0.59 & 5.5 & 0.11 \\ \hline \end{array} \] 有意水準を\(\alpha=0.05\) とすると自由度\(n-2-1=7\)の\(t\)分布の両側\(\alpha\)点は \(t_\alpha = 2.26\) となるので, これよりも外れている \(\hat{b}\) については帰無仮説を棄却する事が出来ます. つまり有意に \(b\neq 0\) と言えます. 一方, \(a\neq 0\) という事は言えないので \(x\) には \(z\) を説明する変数として意味があるとは言えません.
以下が \(t\)検定の為に利用したコードです.
# -*- coding: utf-8 -*-
import numpy as np
from scipy import linalg as LA
from scipy import stats
from math import log,sqrt,pi
data = np.loadtxt("ex17-6.dat", comments="#", delimiter="\t")
x = data[:,0]
y = data[:,1]
z = data[:,2]
N = len(x)
# 回帰分析
G = np.array([x, y, np.ones(N)]).T
m = 2 # 変数の数
a = LA.solve(G.T.dot(G), G.T.dot(z))
## a について t検定
S2 = np.sum( (z-G.dot(a))**2 )/(N-m-1)
t = a/np.sqrt(np.diag(LA.inv(G.T.dot(G)))*S2)
print "a_hat = ", a
print "t = ", t
# 両側α点 (α=0.05)
print "t_alpha = %.3f" % stats.t.ppf(0.975, N-m-1)
同様にして, \[ \begin{aligned} H_0&:\text{定数項以外の係数は全て0} \\ H_1&:\text{定数項以外の少なくとも1つの項の係数は0ではない} \end{aligned} \] という検定を行う事も出来ます. 回帰分析の結果に意味があると言える為には \(H_0\) が棄却される必要があります. 詳しくは省略しますが, この場合は \(F\) 分布を利用した検定を利用します.
以上で行った様な計算は統計解析ツールで簡単に出来ます(が, 理解を深める為に一度実装してみることをおすすめします). 以下は \(R\) という言語での回帰分析と検定の例です.
> data <- read.csv("ex17-6.dat", sep="\t", header=F)
> data
V1 V2 V3
1 5.4 4.7 11.8
2 6.2 0.2 0.3
3 4.3 0.5 2.8
4 1.2 5.1 8.2
5 6.2 3.6 10.9
6 4.0 7.3 19.3
7 4.0 10.0 15.8
8 3.9 5.5 17.9
9 6.4 9.6 21.7
10 6.6 8.9 18.1
> fm <- lm(V3 ~ V1 + V2, data) # 回帰分析
> summary(fm)
Call:
lm(formula = V3 ~ V1 + V2, data = data)
Residuals:
Min 1Q Median 3Q Max
-4.7719 -2.0030 0.0345 1.1379 5.6762
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4506 4.0054 0.113 0.913584
V1 0.4156 0.7037 0.591 0.573370
V2 1.8459 0.3390 5.445 0.000961 *** <- 係数やt値. Pr(>|t|)が有意水準αより小さいほど重要な変数.
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.544 on 7 degrees of freedom
Multiple R-squared: 0.8115, Adjusted R-squared: 0.7576 <- 自由度調整済み決定係数(Adjusted R-squared)
F-statistic: 15.07 on 2 and 7 DF, p-value: 0.002909 <- この回帰分析に意味があったか(F検定)? p-valueが有意水準αより小さいならばOK.
今回はここで終わります。
次回はベイズ統計学の初歩的な内容を取り上げます. 各種アルゴリズムの実装は難しいので既存のツールを使うかもしれません. 上手く行くと統計学編は来週で終了となります.