機械学習に基づく
自然言語処理勉強会
第2回
@ナビプラス
中村晃一2014年11月27日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.
文書の分類問題
分類問題とは?
機械学習における 分類問題 (classification problem) とは,特徴ベクトルの空間内の各点 $\mathbf{x}$ に対して (何らかの観点で)適切なラベル $\mathbb{K}=\{1,2,\ldots,K\}$ を割り当てるタスクを指します.
自然言語処理においてはメールの分類,ニュース記事の分類,販売商品の分類など様々な応用が考えられます.
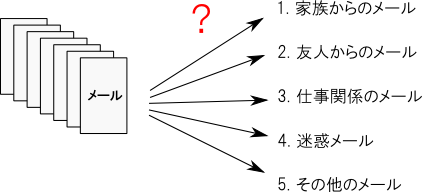
今回は 教師付き学習 (supervised learning) という学習法に基づく手法を紹介します.
分類問題における教師付き学習とは,学習データ $\mathbf{X}=\{(\mathbf{x}_1,t_1),\ldots,(\mathbf{x}_N,t_N)\}$ から分類器を学習するものです. ここで $\mathbf{x}_i$ は学習用サンプルで, $t_i$ はその正解ラベルです.
全特徴ベクトルの空間を $\Omega$ と書くことにします. 例えば,頻度ベクトル表現なら $\Omega=\mathbb{N}^W\quad(W:\text{単語数})$,Tf-Idf表現なら $\Omega=\mathbb{R}^W\quad(W:\text{単語数})$ などです.
多くの場合 $\Omega$ には何らかの距離(通常はユークリッド距離)か,何らかの類似度を入れて考えます.
分類問題とは(何らかの観点で最適な)写像 \[ f: \mathbb{R}^W \rightarrow \mathbb{K} \] を構築せよ、という問題です.
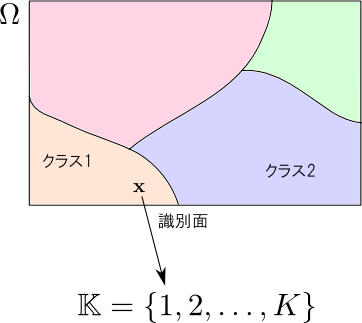
この関数を 識別関数 (classification function) などと呼びます. 識別関数で分けられた $\mathbb{R}^W$ の$K$個の互いに素な部分集合 $\mathbf{C}_k = f^{-1}(k)$ それぞれを クラス (class) と呼びます.
識別関数が与えられると,$\Omega$ が $K$ 個の部分集合に区切られる事になります. この各クラスの境界を 識別面 (classification plane) と呼びます. 分類問題は,(何らかの観点で最適な)識別面を構築する問題として解釈する事も出来ます.
識別関数(≒識別面)を直に考えるアプローチの他に,特徴ベクトル $\mathbf{x}$ がクラス $k$ に所属する確率 \[ p(k|\mathbf{x}) \] を一旦考えるというアプローチも応用が広く重要です.
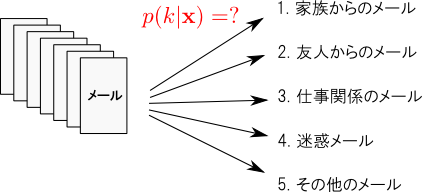
ベイズの定理 (Bayes's theorem) より \[ p(k|\mathbf{x}) = \frac{p(\mathbf{x}|k)p(k)}{p(\mathbf{x})} \propto p(\mathbf{x}|k)p(k) \] なので「クラス $k$ におけるデータの分布 $p(\mathbf{x}|k)$」をモデル化すれば, $p(k|\mathbf{x})$ も計算する事が出来ます. これを 確率的生成モデル (probabilistic generative model) と呼びます.
一方, \[ p(k|\mathbf{x}) = \text{何らかの数式} \] という形で,所属確率 $p(k|\mathbf{x})$ を直接モデル化する方法もあります.
これは 確率的識別モデル (probabilisitc classification model) と呼ばれます.
所属確率 $p(k|\mathbf{x})$ から識別関数をどうやって作れば良いのかは自明な問題ではないですが, 単純に分類の正解率を最大化したいならば「所属確率が最大のクラスに割り当てる」とすれば良いです. つまり \[ f(\mathbf{x}) =\mathop{\rm arg~max}\limits_{k}p(k|\mathbf{x}) \] とします. これを 事後確率最大化(maximum a posteriori, MAP) 推定と言います.
分類の良し悪しを単純な正解率と考えられない状況では工夫が必要です. 通常は分類結果に基いて何らかのアクション(メールを特定フォルダに入れるなど)が行われますので, その効果まで総合的に考える必要が生じます.
詳しくは省略しますが, 統計的決定理論 (statistical decision theory) について調べて下さい.
以下,代表的な識別器を幾つか紹介していきます.
まず,確率論的なモデルの例として
- 生成モデル:単純ベイズモデル
- 識別モデル:対数線形モデル
非確率論的なモデルの例として
- サポートベクターマシン
- k近傍法
を紹介します.
単純ベイズ分類
単純ベイズ分類
単純ベイズ分類器(naive bayes classifier) とは確率的生成モデルとして 単純ベイズモデル (naive bayes model) を利用した分類器の事です.
単純ベイズモデルとは, 各クラスにおいて,特徴量が全て独立である と仮定したモデルです.
例えば,ある文書に「政治」という単語が出現したならば,それを知る前と比べて「国際」という単語の出現確率は(ベイズ的な意味では)増加すると思います. このように、文書における単語の出現は一般には独立ではないと考えられます.
これを「各単語は全く無関係に発生する」と仮定してしまうのが単純ベイズモデルです.
文書 $d$ の二値ベクトル表現を $\mathbf{d}=(w_1,w_2,\ldots,w_D)$ とします.
計算したいものは,クラス $k$ において $\mathbf{d}$ が生成する確率 \[ p(w_1,w_2,\ldots,w_D|k) \] ですが,$w_1,w_2,\ldots,w_D$ は全て独立であると考えるので \[ p(w_1,w_2,\ldots,w_D|k) = p(w_1|k)p(w_2|k)\cdots p(w_D|k) = \prod_{i=1}^Dp(w_i|k) \] となります.
ここでは,二値ベクトル表現を用いましたが, この場合 $w_i=0,1$ のいずれかなので $p(w_i|k)$ はベルヌーイ分布となります. 従って,以上のモデルは 単純ベイズベルヌーイモデル (naive bayes bernoulli model) と呼ばれます.
二値ベクトルの代わりに頻度(回数)ベクトル表現を用いた場合には, 多項モデル (multinomial model) と呼ばれます. 多項モデルでは文書の長さも確率変数となります. 各単語の出現回数は文書長に影響を受ける為です.
その他のBOWモデルについても単純ベイズの仮定を導入する事が可能です. その場合に \[ p(w_i|k) \] は正規分布やベータ分布など特徴量の性質に応じてモデル化する事になります.
単純ベイズとはあくまで変数の独立性関係に関するモデルであって,各変数毎の具体的な分布と組み合わせて使用する事になります.
20newsgroupsデータセットで実験してみます. このデータセットでは各文書毎のトピックが教師データとして与えられているのでそれを学習させてみます.
前処理としてポーターのステマーを施します. 約1万文書のうち9割の文書を学習し,残りの1割の文書に対する正解率を調べます.
ベルヌーイモデル、多項モデルそれぞれを実験結果は以下です. コードは prog2-1.py です.
| モデル | 正解率 | 訓練時間 | 予測時間 |
|---|---|---|---|
| 単純ベイズ(ベルヌーイ) | 78.4% | 0.185秒 | 0.081秒 |
| 単純ベイズ(多項) | 89.3% | 0.180秒 | 0.017秒 |
対数線形モデル
対数線形モデル
対数線形モデル (loglinear model) は代表的な確率的識別モデルの1つで,文書 $\mathbf{d}$ がクラス $k$ に所属する確率を \[ p(k|\mathbf{d}) \propto \exp(\mathbf{w}_k^T \mathbf{d}) \] とモデル化します.
ロジスティックモデル (logistic model) や 最大エントロピーモデル (maximum entropy model) と呼ばれるものと同じです(「対数線形」はこれらよりもっと広い範囲のモデルを指します).
より一般には,素性関数 $\phi$ というものを導入した \[ p(k|\mathbf{d}) \propto \exp(\mathbf{w}^T\phi(\mathbf{d},k)) \] とします.
素性関数とは文書と正解ラベルから特徴ベクトルへ変換する関数で,これを導入する事によって様々な問題を同一のモデルで表現したり,モデルの複雑性を抑えたりといった事が出来ます.
以降は,前頁の立式を元に進めます.
確率的生成モデルの場合は各 $p(w_i|k)$ を学習してから,間接的に $p(k|\mathbf{d})$ を構築しました. こちらの場合は同時確率 $p(\mathbf{d},k)$ が計算出来るので,識別問題以外にも様々な応用の可能性があります.
一方,対数線形モデルでは直接 $p(k|\mathbf{d})$ を学習させるので一般に識別性能は向上します. その反面,確率モデルとしての応用可能性は若干下がります.
対数線形モデルでは,学習データ $\{(\mathbf{d}_1,t_1),(\mathbf{d}_2,t_2),\ldots,(\mathbf{d}_N,t_N)\}$ に対して,事後確率の対数尤度 \[ \sum_{i=1}^N \log p(t_i|\mathbf{d}_i) \] が最大となるようにパラメータ $\mathbf{w}_k$の学習を行います.
これは解析的に解くことが出来ない為,数値的解法が利用されます. (詳しくは パターン認識機械学習勉強会第5回 )
自然言語処理の場合には,特徴ベクトル空間がスカスカ(データスパースネス問題)なので過学習が起きやすくなってしまいますから,極端な $\mathbf{w}_k$ が学習されないように正則化項を追加したものを最大化するという事も多いです. 例えば \[ \sum_{i=1}^N \log p(t_i|\mathbf{d}_i) - \alpha \sum_{k=1}^K ||\mathbf{w}_k||^2 \] などです.
以下が,先ほどと同じデータセットに対する実験結果です. やはり精度が向上しています. コードは prog2-2.py です.
| モデル | 正解率 | 訓練時間 | 予測時間 |
|---|---|---|---|
| 単純ベイズ(ベルヌーイ) | 78.4% | 0.185秒 | 0.081秒 |
| 単純ベイズ(多項) | 89.3% | 0.180秒 | 0.017秒 |
| 対数線形 | 90.0% | 32.155秒 | 0.016秒 |
サポートベクターマシン
サポートベクトルマシン (support vector machine, SVM) とは確率的モデルに基づかない分類器で,最大マージン分類という考え方を用いています. 非常に高い識別性能を持ちます.
最大マージン分類器
2クラス場合を考えます. 今, 学習データ $\{(\mathbf{d}_1,t_1),(\mathbf{d}_2,t_2),\ldots,(\mathbf{d}_n,t_n)\}\quad(t_i=\pm 1)$ に対して,適当な変換 $\Psi$ を施した結果,平面で分離できるようになっているとします.

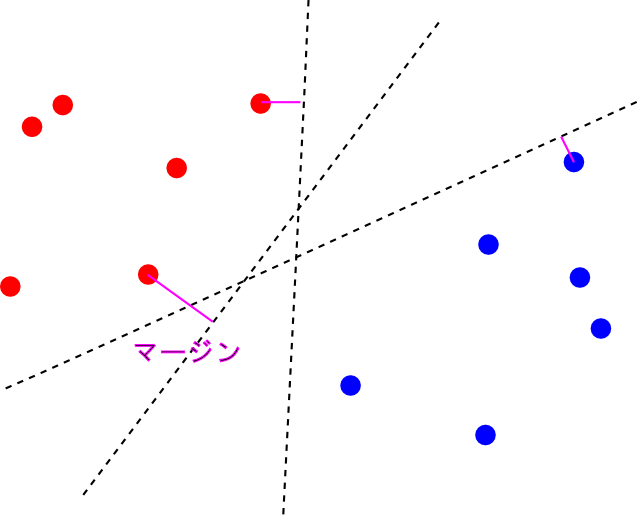
この時, 2つのクラスを分離する識別面は唯一に定まりません.
そこで, 最も近い $\Psi(\mathbf{x}_i)$ までの距離(マージン)が最大となるような識別面を選ぶ事にします. これを 最大マージン分類器(maximum margin classifier)と呼びます.
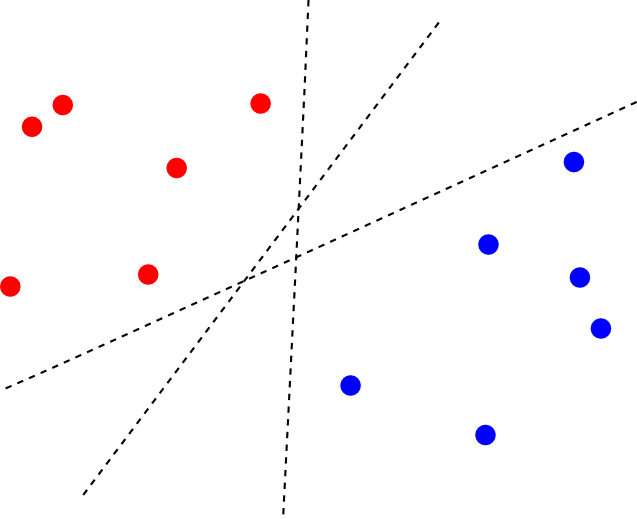
この時, 2つのクラスを分離する識別面は唯一に定まりません.
そこで, 最も近い $\Psi(\mathbf{x}_i)$ までの距離(マージン)が最大となるような識別面を選ぶ事にします. これを最大マージン分類器(maximum margin classifier)と呼びます.
このアイデアによって,未知のデータに対する高い性能(汎化性能)を実現しています.
訓練文書数を $N$,特徴ベクトルの次元を $D$ とすると, SVMを訓練する為には $\mathcal{O}(N^2)$ 程度の計算時間が必要となります.
計算時間が $D$ に依存しないという事に注目しましょう. SVMでは非常に高い次元の特徴ベクトルや無限次元の特徴ベクトルを使う事が出来ます.
一方で,訓練文書数が増えると劇的に計算時間が増加してしまい,数万文書ほどが限界です. 精度が下がりますが 確率的勾配降下法 (stochastic gradient method) などの近似解法を利用する事で大規模なデータセットにも利用出来ます.
詳しくは パターン認識・機械学習勉強会第12回 をご覧下さい.
先ほどのデータセットに対する実験結果です. SVM(SGD) は確率的勾配降下法を使った場合です. コードは prog2-3.py です.
| モデル | 正解率 | 訓練時間 | 予測時間 |
|---|---|---|---|
| 単純ベイズ(ベルヌーイ) | 78.4% | 0.185秒 | 0.081秒 |
| 単純ベイズ(多項) | 89.3% | 0.180秒 | 0.017秒 |
| 対数線形 | 90.0% | 32.155秒 | 0.016秒 |
| SVM | 88.9% | 6.501秒 | 0.012秒 |
| SVM(SGD) | 85.6% | 0.380秒 | 0.011秒 |
k近傍法
$k$近傍法
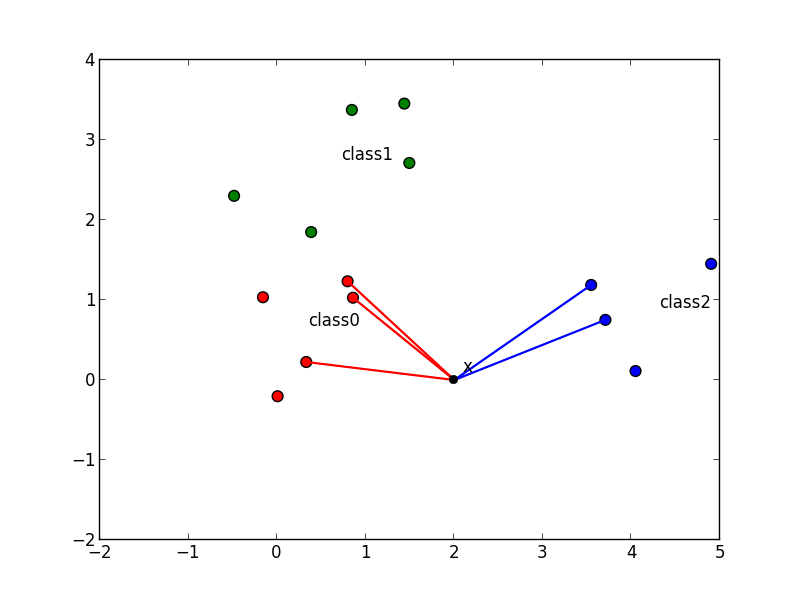
入力 $\mathbf{x}$ に対して学習データを近い順番に $k$ 個選び, 多数決によって $\mathbf{x}$ が属すクラスを決定する手法を $k$近傍法 ($k$-nearest-neighbours classification rule, $k$-NN法) と呼びます.
例えば以下の $\mathbf{x}$ は $5$-NN法 ではクラス $0$ に分類されます.
$k$-NN法がこれまでに紹介したものと全く異なるのは,単純ベイズにおける $p(w_i|k)$ や対数線形モデルにおける $\mathbf{w}_k$ などのパラメータが存在しないという事です.
こういったモデルは ノンパラメトリックモデル (non-parametric model) と呼ばれます.
$k$-NN法は単純な方法で複雑な識別面を表現する事ができ学習データが十分にある場合には非常に良い識別精度を発揮します.
一方 $k$ が小さすぎると以下の例 ($k=1$)のように学習データのノイズを拾ってしまいます.
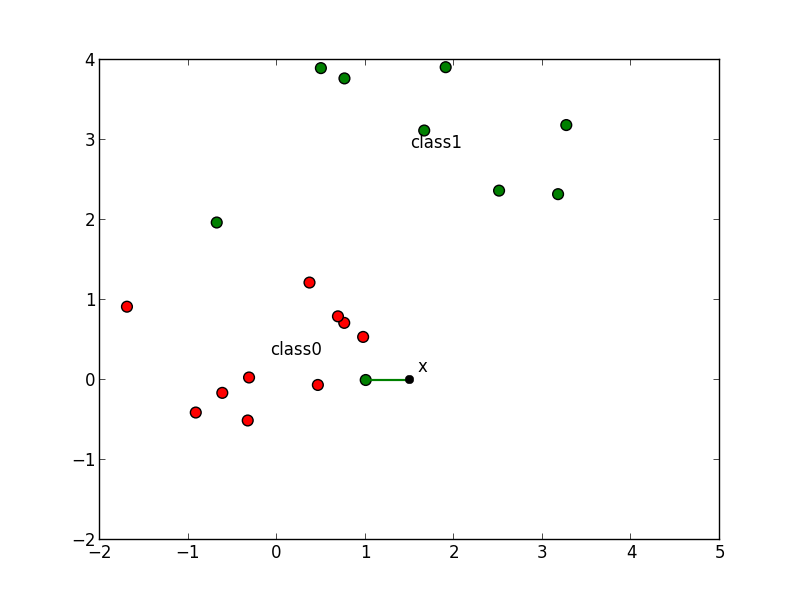
また,$k$近傍法では学習データ集合 $D$ 全体を保存しておかなければいけないという問題もあります.
また $D$ のサイズが,予測の計算量にも影響するという事にも注意しなければいけません.
実験結果です. 但し,単純な頻度ベクトルでは精度が出ないので $k$ 近傍法のみTf-Idfを使っています. また $k=5$ とし,ユークリッド距離を利用しています. コードは prog2-3.py です.
訓練時間がほぼ無い代わりに,予測時間が長くなるという特徴が判ると思います.
| モデル | 正解率 | 訓練時間 | 予測時間 |
|---|---|---|---|
| 単純ベイズ(ベルヌーイ) | 78.4% | 0.185秒 | 0.081秒 |
| 単純ベイズ(多項) | 89.3% | 0.180秒 | 0.017秒 |
| 対数線形 | 90.0% | 32.155秒 | 0.016秒 |
| SVM | 88.9% | 6.501秒 | 0.012秒 |
| SVM(SGD) | 85.6% | 0.380秒 | 0.011秒 |
| K-NN | 80.7% | 0.030秒 | 1.481秒 |
第2回はここで終わります
次回は「文書のクラスタリング問題」を紹介します.