パターン認識・
機械学習勉強会
第12回
@ワークスアプリケーションズ
中村晃一2014年5月22日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
サポートベクターマシン
本日からテキスト第7章スパースカーネルマシンに進みます.
サポートベクターマシン (support vector machine, SVM) とは, マージン最大化という方針に基づいて汎化性能を高めた識別器であり, 非常に優れた性能を発揮する事が出来ます.
最大マージン分類器
2クラスの識別問題を考えます. 今, 学習データ $\{(\mathbf{x}_1,t_1),(\mathbf{x}_2,t_2),\ldots,(\mathbf{x}_n,t_n)\}\quad(t_i=\pm 1)$ が適当な特徴ベクトル $\Psi(\mathbf{x}_1),\Psi(\mathbf{x}_2),\ldots,\Psi(\mathbf{x}_n)$ に関して線形分離可能であると仮定します.
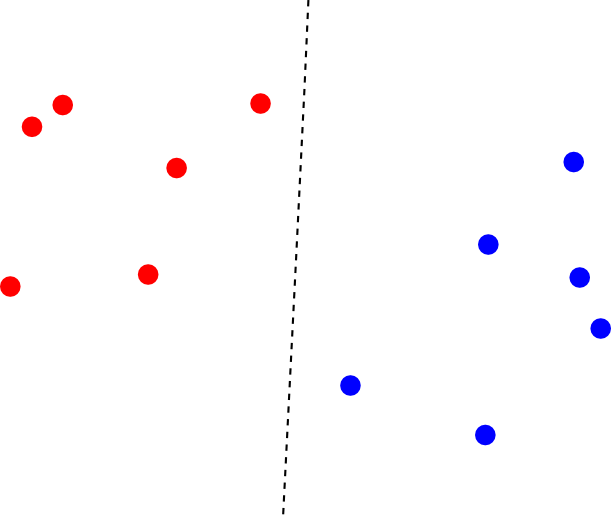
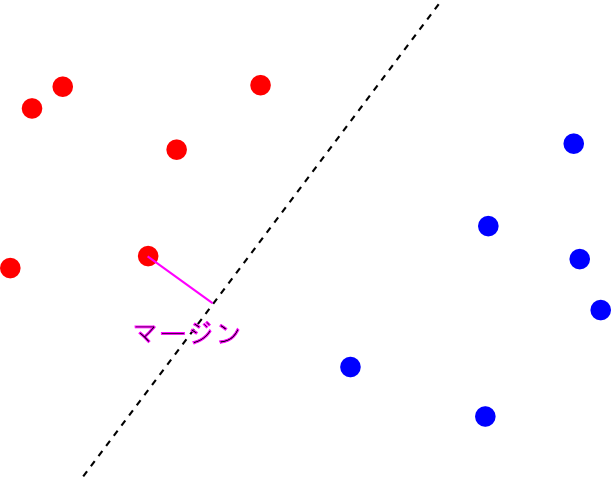
この時, 2つのクラスを分離する識別面は唯一に定まりません.
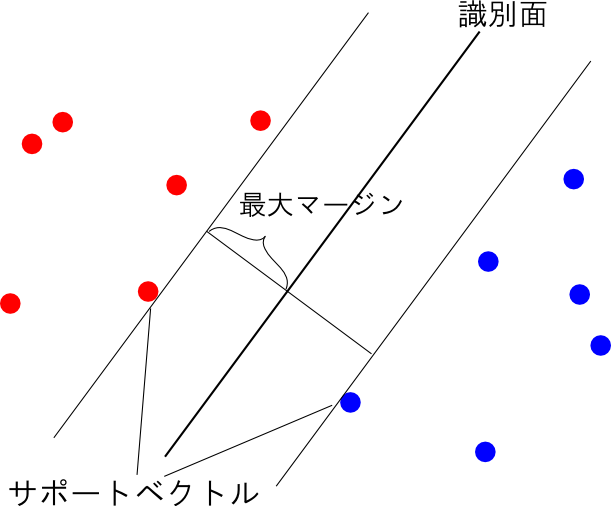
そこで, 最も近い $\Psi(\mathbf{x}_i)$ までの距離(マージン)が最大となるような識別面を選ぶ事にします. これを 最大マージン分類器(maximum margin classifier)と呼びます.
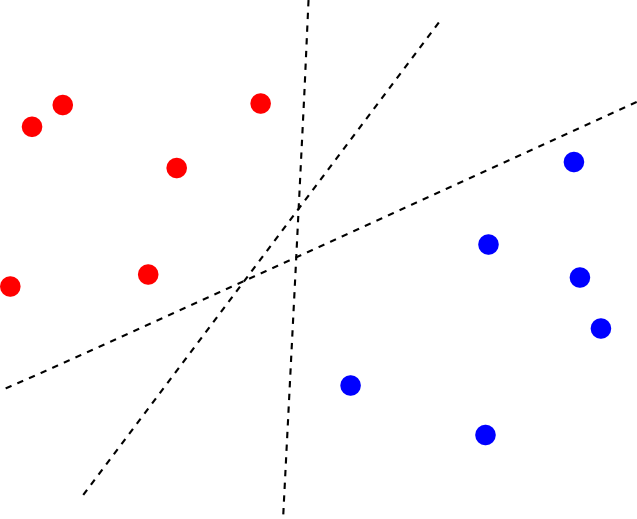
この時, 2つのクラスを分離する識別面は唯一に定まりません.
そこで, 最も近い $\Psi(\mathbf{x}_i)$ までの距離(マージン)が最大となるような識別面を選ぶ事にします. これを最大マージン分類器(maximum margin classifier)と呼びます.
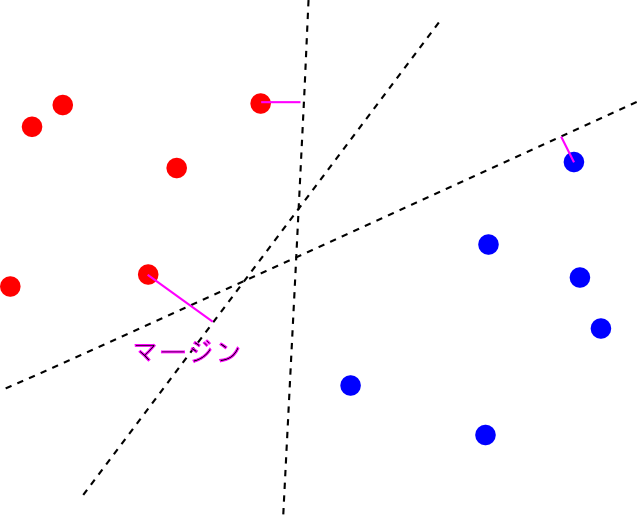
マージンが最大になる時, 識別面からちょうどマージンの分だけ離れた面上に必ず1つ以上の特徴ベクトルが乗ります. これを(広い意味での) サポートベクトル (support vector) と呼びます.
以上の考え方に基き, 数式化していきましょう. まず, 線形識別関数を定数項を別にして \[ f(\mathbf{x})=\mathbf{w}^T\Psi(\mathbf{x})+\theta \] とおきます.
学習データが線形分離可能である事は $f(\mathbf{x}_i)$ と $t_i$ が同符号であること, つまり \[ t_if(\mathbf{x}_i) > 0\qquad (i=1,2,\ldots, n) \] が成り立つ事です.
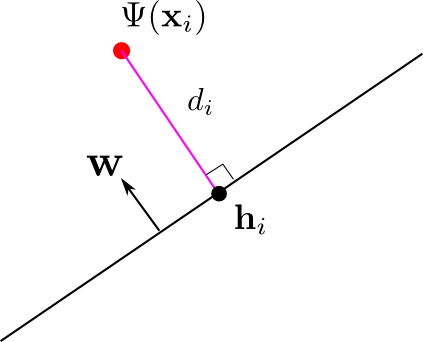
点 $\Psi(\mathbf{x}_i)$ から識別面に下ろした垂線の足を $\mathbf{h}_i$, 符号付き距離を $d_i$ とおくと, $\mathbf{w}$ が識別面の法ベクトルである事から \[ \mathbf{h}_i = \Psi(\mathbf{x}_i)-d_i\frac{\mathbf{w}}{||\mathbf{w}||},\quad \mathbf{w}^T\mathbf{h}_i + \theta = 0 \] となるので, これを解けば \[ |d_i| = \frac{|\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta|}{||\mathbf{w}||} = \frac{|f(\mathbf{x}_i)|}{||\mathbf{w}||} \] となります.
さらに, $t_i = \pm 1$ と $t_if(\mathbf{x}_i)> 0$ より \[ |f(\mathbf{x}_i)|=t_if(\mathbf{x}_i) \] が成り立つので \[ |d_i| = \frac{t_if(\mathbf{x}_i)}{||\mathbf{w}||} \] と書くことが出来ます.
従って, 最大マージンを与える識別面は \[ \mathop{\rm arg~max}\limits_{\mathbf{w},\theta}\mathop{\rm min}\limits_{i}\frac{t_if(\mathbf{x}_i)}{||\mathbf{w}||} = \mathop{\rm arg~max}\limits_{\mathbf{w},\theta}\frac{1}{||\mathbf{w}||}\mathop{\rm min}\limits_{i}t_if(\mathbf{x}_i) \] を求める事によって得られます.
ここで $(\mathbf{w},\theta)\mapsto (k\mathbf{w},k\theta)$ と実数倍しても \[ \frac{t_if(\mathbf{x}_i)}{||\mathbf{w}||}=\frac{t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)}{||\mathbf{w}||} \] が不変である事に注意すれば, \[ \mathop{\rm min}\limits_{i} t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) = 1\] となるように $(\mathbf{w},\theta)$ を選ぶ事が出来ます.
すると, 解くべき問題は \[ \mathop{\rm arg~max}\limits_{\mathbf{w},\theta}\frac{1}{||\mathbf{w}||} = \mathop{\rm arg~min}\limits_{\mathbf{w},\theta}\frac{1}{2}||\mathbf{w}||^2 \] となります.
さらに, \[ \mathop{\rm min}\limits_{i} t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) = 1\] という条件は \[ t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) \geq 1\qquad(i=1,\ldots,n) \] と同値です. 何故ならば等号が成立するベクトル(サポートベクトル)が必ず存在する為です.
以上より最大マージン分類器の最適化問題が以下の様に定式化されます.
最大マージン分類器の最適化
\[ t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) \geq 1\qquad(i=1,\ldots,n) \] という条件下で \[ \frac{1}{2}||\mathbf{w}||^2 \] が最小となるような $\mathbf{w},\theta$ を求める.次に,この問題を双対問題(dual problem)に変換しましょう.
双対定理の(特別な場合)
以下の2つの問題の解はもし存在するならば一致する.
【主問題】
条件 $g_i(\mathbf{x})\leq 0\quad (i=1,\ldots,n)$ の下で $f(\mathbf{x})$ を最小とする $\mathbf{x}$.
【双対問題】
条件 $\mu_i \geq 0\quad (i=1,\ldots,n)$ の下で
\[ \mathop{\rm min}\limits_{\mathbf{x}}\left\{f(\mathbf{x})+\sum_i\mu_ig_i(\mathbf{x})\right\} \]
を最大とする $\mathbf{x}$ (及び $\boldsymbol{\mu}$).
今回の場合は, $t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) \geq 1$ も$||\mathbf{w}||^2/2$も凸である(凸最適化問題である)ので, \[ L(\mathbf{w}, \theta, \boldsymbol{\mu})=\frac{1}{2}||\mathbf{w}||^2-\sum_i\mu_i\{t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)-1\} \] が $\mathbf{w}, \theta$ に関して最小となるのは \[ \frac{\partial L}{\partial \mathbf{w}}=\mathbf{0},\quad\frac{\partial L}{\partial \theta}=0 \] の時です. これを用いて $\mathbf{w},\theta$ を消去すれば双対問題を得る事が出来ます.
最大マージン分類器の最適化問題の双対版
条件 \[ \mu_i \geq 0\quad(i=1,\ldots,n),\quad \sum_i \mu_i t_i = 0 \] の下で \[ \tilde{L}(\boldsymbol{\mu}) = -\frac{1}{2}\sum_{i,j}\mu_i\mu_jt_it_jk(\mathbf{x}_i,\mathbf{x}_j)+\sum_i\mu_i \] を最大化する. 但し, $k(\mathbf{x}_i,\mathbf{x}_j)=\Psi(\mathbf{x}_i)^T\Psi(\mathbf{x}_j)$.
【前頁の導出】
$\mathbf{p} = (\mu_1t_1,\ldots,\mu_nt_n)^T$, $\mathbf{X}$ を計画行列, $\mathbf{K}=\mathbf{X}\mathbf{X}^T$ とすると
\[ \begin{aligned}
\frac{\partial L}{\partial \mathbf{w}} &= \mathbf{w}-\sum_{i=1}^n \mu_it_i\Psi(\mathbf{x}_i) = \mathbf{w}-\mathbf{X}^T\mathbf{p} \\
\frac{\partial L}{\partial \theta} &= -\sum_{i=1}^n \mu_it_i = 0
\end{aligned} \]
より,
\[ \begin{aligned}
&||\mathbf{w}||^2 = \mathbf{p}^T\mathbf{X}\mathbf{X}^T\mathbf{p}=\mathbf{p}^T\mathbf{K}\mathbf{p} \\
&\sum_i\mu_i\{t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)-1\} = \mathbf{p}^T\mathbf{X}\mathbf{w}-\sum_i\mu_i = \mathbf{p}^T\mathbf{K}\mathbf{p}-\sum_i\mu_i
\end{aligned} \]
従って
\[ L = \sum_i\mu_i - \frac{1}{2}\mathbf{p}^T\mathbf{K}\mathbf{p} = \sum_i\mu_i - \frac{1}{2}\sum_{i,j}\mu_i\mu_jt_it_jk(\mathbf{x}_i,\mathbf{x}_j) \]
最適解を与える $\mathbf{w},\theta,\boldsymbol{\mu}$ では, 以下の カルーシュ・キューン・タッカー条件 (Karush-Kuhn-Tucker condition, KKTcondition) と呼ばれる条件が成立します. \[ \begin{aligned} &\mu_i \geq 0\\ &t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta) \geq 1\\ &\mu_i\{t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)-1\} = 0 \end{aligned} \] これから $\mu_i > 0$ ならば $\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta = t_i$ が成立する事が分かります.
この $\mu_i > 0$ を満たす $\Psi(\mathbf{x}_i)$ を サポートベクトル(support vector)と呼びます.
元の識別関数をパラメータ $\boldsymbol{\mu}$ を用いて書き直すと \[ f(\mathbf{x}) = \sum_i \mu_it_ik(\mathbf{x}_i,\mathbf{x})+\theta \] となります.
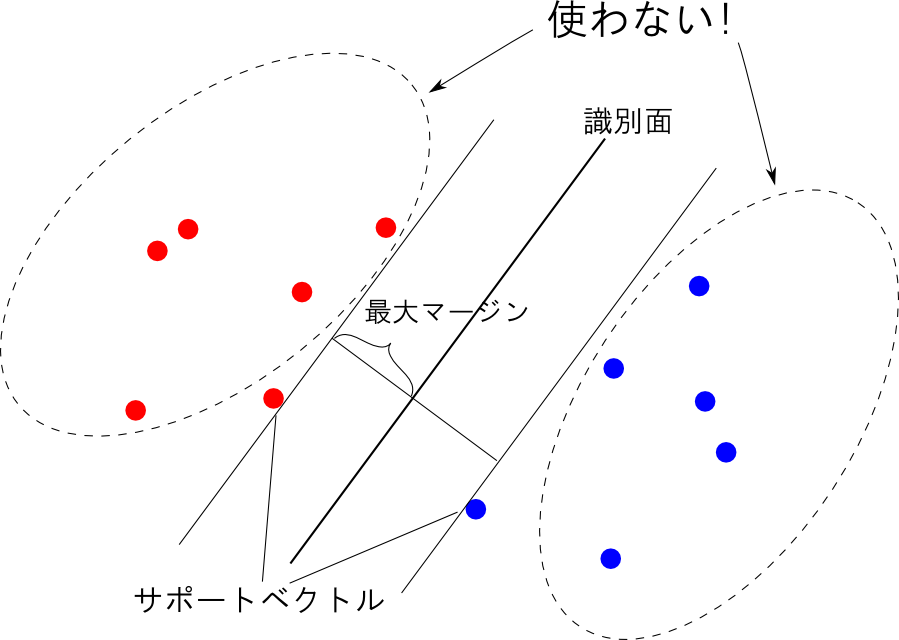
ここで, サポートベクトル以外では $\mu_i = 0$ となる 事に注目しましょう. 従って, サポートベクトルのインデックスの集合を $\mathcal{S}$ とおくと, 上の式は \[ f(\mathbf{x}) = \sum_{i\in\mathcal{S}} \mu_it_ik(\mathbf{x}_i,\mathbf{x})+\theta \] と書き直す事が出来ます.
識別関数の構成にサポートベクトルしか使わないというのがこのモデルの最大の特徴です.
但し, $\theta$ は任意のサポートベクトルが \[ t_i(\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)= 1 \quad (i\in\mathcal{S})\] を満たすことより求めます.
テキストによれば演算誤差を考慮して \[\begin{aligned} \theta &= \frac{1}{|\mathcal{S}|}\sum_{i\in\mathcal{S}}\left\{t_i-\mathbf{w}^T\Psi(\mathbf{x}_i)\right\} \\ &= \frac{1}{|\mathcal{S}|}\sum_{i\in\mathcal{S}}\left\{t_i-\sum_{j\in\mathcal{S}}\mu_jt_jk(\mathbf{x}_i,\mathbf{x}_j)\right\} \\ \end{aligned} \] とすると良いだろうという事です.
続いてサポートベクターマシンの学習について説明します. 以下を解きたいわけですが, 勾配法等では計算量が大きくなってしまいます. そこで Sequential minimal optimization (SMO法) という物を紹介します.
最大マージン分類器の最適化問題の双対版
条件 \[ \mu_i \geq 0\quad(i=1,\ldots,n),\quad \sum_i \mu_i t_i = 0 \] の下で \[ \tilde{L}(\boldsymbol{\mu}) = -\frac{1}{2}\sum_{i,j}\mu_i\mu_jt_it_jk(\mathbf{x}_i,\mathbf{x}_j)+\sum_i\mu_i \] を最大化する. 但し, $k(\mathbf{x}_i,\mathbf{x}_j)=\Psi(\mathbf{x}_i)^T\Psi(\mathbf{x}_j)$.
SMO法は反復法であり, 適当な初期値 $\boldsymbol{\mu}^{(0)}$ から出発して, 更新 $\boldsymbol{\mu}^{(k)} \rightarrow \boldsymbol{\mu}^{(k+1)}$ を繰り返します. この際, 一度には2つの成分しか動かさないというのがポイントです.
今, $\mu_p$ と $\mu_q$ だけ動かすとします. この時, 制約条件より \[ t_p\mu_p + t_q\mu_q = c = \mathrm{const.} \] が成立している必要があります. 特に \[ \frac{\partial \mu_q}{\partial \mu_p} = -\frac{t_p}{t_q} =-t_pt_q\] となります.
以下, $K_{ij} = k(\mathrm{x}_i,\mathrm{x}_j)$ とおきます. $\tilde{L}$ を $\mu_p$ の関数とみなして微分すると \[ \begin{aligned} &\frac{\partial}{\partial \mu_p}\tilde{L} \\ =&-\frac{1}{2}\left\{\sum_{ij}\frac{\partial \mu_i}{\partial \mu_p}\mu_jt_it_jK_{ij}+\sum_{ij}\mu_i\frac{\partial \mu_j}{\partial \mu_p}t_it_jK_{ij}\right\}+\sum_i\frac{\partial \mu_i}{\partial\mu_p}\\ =&-\frac{1}{2}\left\{\sum_j\mu_jt_pt_jK_{pj}-\sum_j\mu_jt_pt_jK_{qj}+\sum_{i}\mu_it_it_pK_{ip}-\sum_{i}\mu_it_it_pK_{iq}\right\}+1-t_pt_q\\ =&-\left\{\sum_i\mu_it_pt_iK_{pi}-\sum_i\mu_it_pt_iK_{qi}\right\}+1-t_pt_q \end{aligned} \] となります.
従って, $\mu_p\mapsto \mu_p+\Delta_p, \mu_q\mapsto\mu_q-t_pt_q\Delta_p $ と更新するならば \[ (K_{pp}-2K_{pq}+K_{qq})\Delta_p = 1-t_pt_q + \sum_i\mu_it_pt_iK_{qi}-\sum_i\mu_it_pt_iK_{pi} \] つまり, \[\begin{aligned} \Delta_p &= \frac{1-t_pt_q + t_p(\sum_i\mu_it_iK_{qi}-\sum_i\mu_it_iK_{pi})}{K_{pp}-2K_{pq}+K_{qq}} \\ &=\frac{1-t_pt_q+t_p\{f(\mathbf{x}_q)-f(\mathbf{x}_p)\}}{K_{pp}-2K_{pq}+K_{qq}} \end{aligned}\] となります.
この時, $t_p\mu_p+t_q\mu_q=c, \mu_p\geq 0, \mu_q \geq 0$ が成立していなければならないので, 以下を満たすように $\Delta_p$ のクリッピングを行う必要があります.
- $t_p=t_q$ のときは \[ 0 \leq \mu_p + \Delta_p \leq c/t_p \]
- $t_p=-t_q$ のときは \[ \mathrm{max}\{0,c/t_p\}\leq \mu_p+\Delta_p\]
次に, 動かす $\mu_p,\mu_q$ の選択基準ですが SMO法の発見者であるJohn C. Plattの論文に従うならば以下の様になります.
- KKT条件を破る $\mu_p$ を1つめに選ぶ.
- 続いて$|f(\mathbf{x}_q)-f(\mathbf{x}_p)|$ が最大となる $\mu_q$ を次に選ぶ.
これを繰り返して, $\tilde{L}$ が収束するまで反復を繰り返せば学習完了です.
- Platt, John C. "Fast training of support vector machines using sequential minimal optimization." (1999): 185-208.
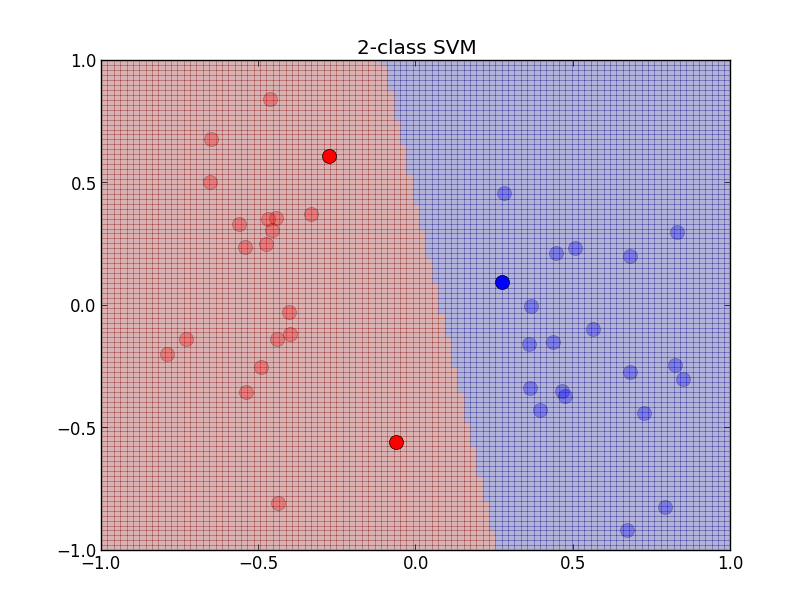
実装例です. 線形カーネルを用いており, 色の濃い点がサポートベクトルです.
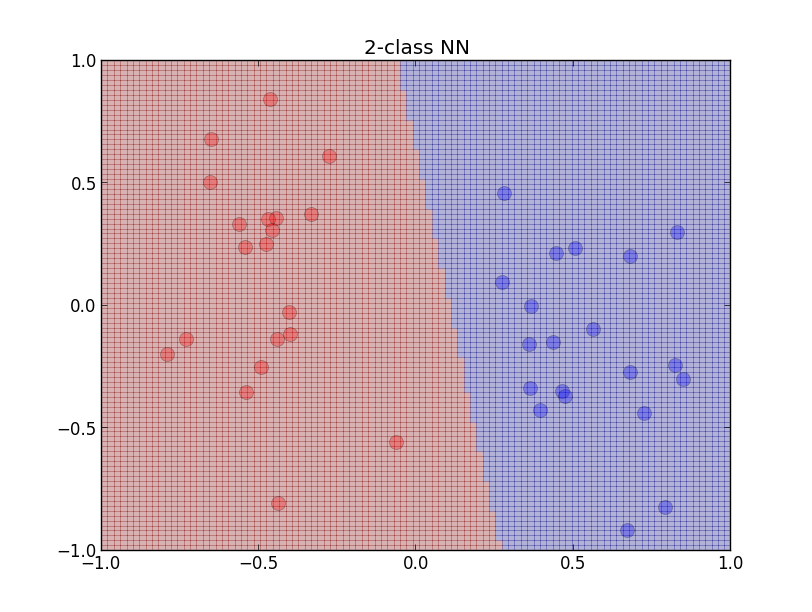
以下はニューラルネットワークを用いた場合です. 若干青いグループに識別面が寄っています.
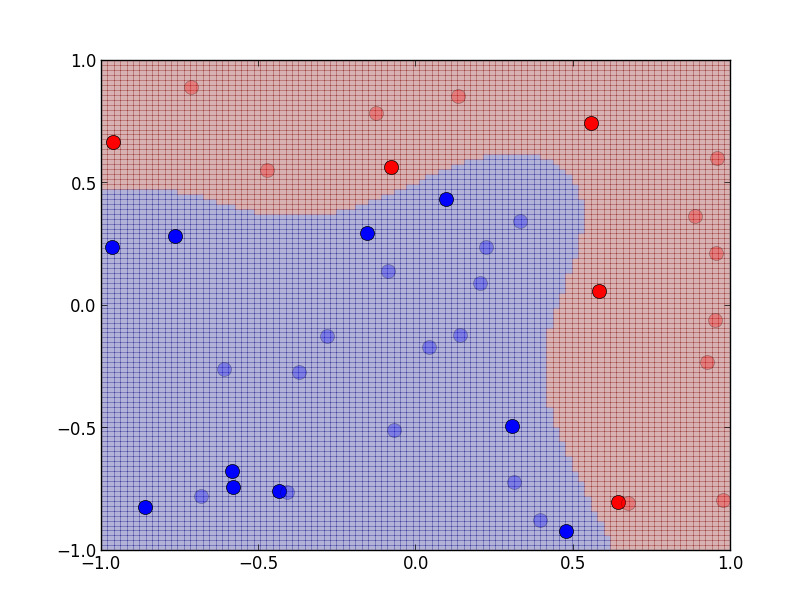
分散パラメータが$\sigma=0.8$のガウスカーネルを用いた例です.
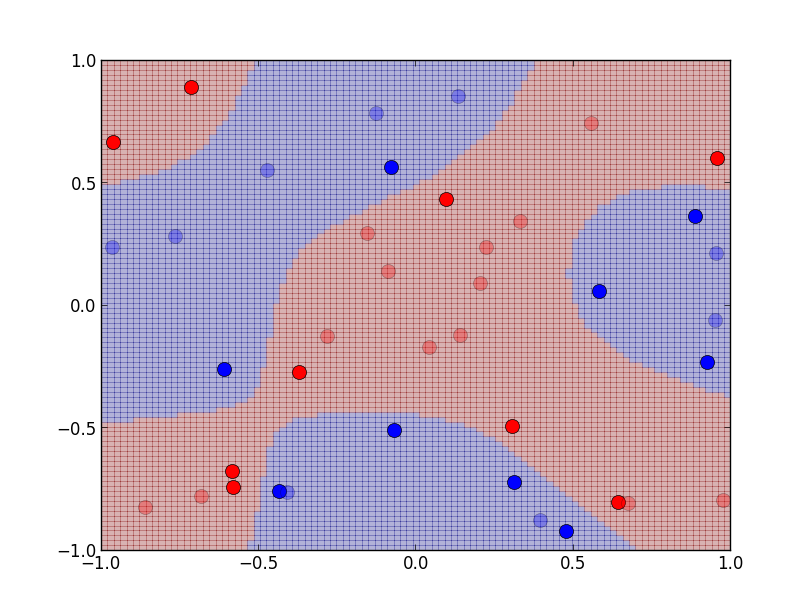
もっと複雑な分布の例です. こちらでは$\sigma=0.4$にしています.
ソフトマージン
先ほどまでは, 学習データの線形分離が可能という条件を前提としていました.
しかし, 実際には上手く分離出来るとは限りません. 識別誤差の発生を許容するサポートベクターマシンを ソフトマージンSVM と呼びます. 一方, これまでやったものはハードマージンSVMと呼ばれます.
そこで, 各学習データ $(\mathbf{x}_i,t_i)$ に対して スラック変数 (slack variable) $\xi_i\geq 0$ を導入して \[ t_if(\mathbf{x}_i) \geq 1 \] の代わりに \[ t_if(\mathbf{x}_i) \geq 1 - \xi_i \] という条件を考えます.
下図の様に, $0 < \xi_i < 1$ の場合は最大マージンよりも内側に入ってきますが, それでも正しく識別されます. $\xi_i > 1$ になってしまうと, そのデータは誤って識別されます.
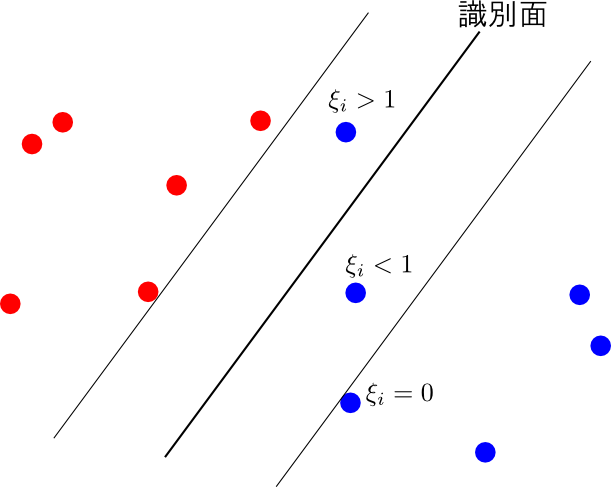
従って $\xi_i$ は出来るだけ小さい方が望ましいので, 先ほどの $||\mathbf{w}||^2/2$ に代わって \[ \frac{1}{2}||\mathbf{w}||^2 + C\sum_i \xi_i \] を最小化する事を考えます.
つまり, まとめると以下のようになります.
ソフトマージンSVMの最適化
\[ \begin{aligned} &t_i(\mathbf{w}^T\Psi(\mathbf{x}_i))\geq 1-\xi_i \\ &\xi_i \geq 0 \end{aligned} \] という条件下で \[ \frac{1}{2}||\mathbf{w}||^2 + C\sum_i \xi_i \] が最小となるような $\mathbf{w}$, $\boldsymbol{\xi}$ を求める.
これを先ほどと同様に双対問題に変換します. 細かい計算はここでは省略します.
ソフトマージンSVMの最適化問題の双対版
\[ 0 \leq \mu_i \leq C, \quad \sum_i\mu_i t_i = 0 \] という条件下で \[ \tilde{L}(\boldsymbol{\mu}) = -\frac{1}{2}\sum_{i,j}\mu_i\mu_jt_it_jk(\mathbf{x}_i,\mathbf{x}_j)+\sum_i\mu_i \] が最小となるような $\boldsymbol{\mu}$ を求める.
ハードマージンSVMの場合と異なる点は \[ 0 \leq \mu_i \] が \[ 0 \leq \mu_i \leq C \] に変わった所です. 従って, クリッピングのルールが以下のように修正されます.
- 【$t_p=t_q$ の時】 \[ \mathrm{max}\{0,c/t_p-C\}\leq \mu_p + \Delta_p \leq \mathrm{min}\{C,c/t_p\} \]
- 【$t_p=-t_q$ の時】 \[ \mathrm{max}\{0,c/t_p\}\leq \mu_p + \Delta_p \leq \mathrm{min}\{C,C+c/t_p\} \]
定数項$\theta$の計算は先ほどと同様に \[ \theta = \frac{1}{|\mathcal{M}|}\sum_{i\in\mathcal{M}}\left\{t_i-\sum_{j\in\mathcal{M}}\mu_jt_jk(\mathbf{x}_i,\mathbf{x}_j)\right\} \] で行います. 但し, $\mathcal{M}$ は $0 < \mu_i < C$ を満たす $i$ の集合です.
更に, KKT条件は以下のようになります.
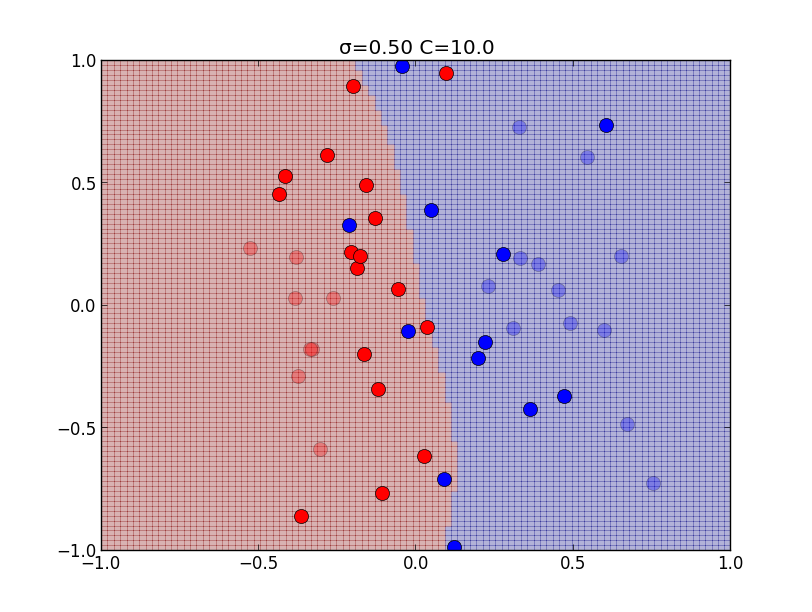
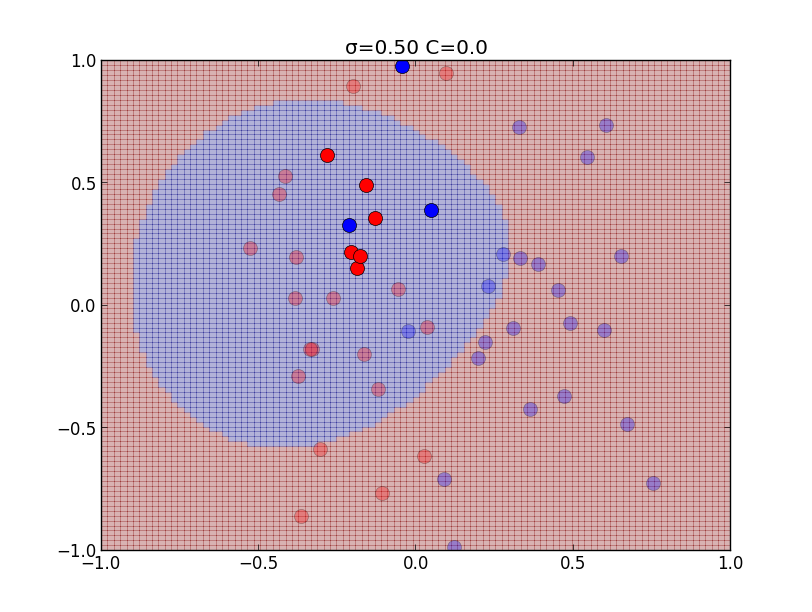
\[ \begin{aligned} &0 \leq \mu_i \leq C,\quad \xi_i \geq 0\\ &t_if(\mathbf{x}_i)-1+\xi_i \geq 0 \\ &\mu_i\{t_if(\mathbf{x}_i)-1+\xi_i\} = 0 \\ &\xi_i(C-\mu_i) = 0 \end{aligned} \] $0\leq \mu_i < C$ の時は最後の等式より $\xi_i = 0$ となるので, ハードマージンの場合と同値になり, $\mu_i = C$ の場合には \[ t_if(\mathbf{x}_i)-1+\xi_i = 0,\quad \xi_i \geq 0 \] より \[ t_if(\mathbf{x}_i)\leq 1 \] となります.以下はカーネルの分散パラメータ $\sigma$と, ソフトマージンのパラメータ $C$ を色々変えて学習を行ったものです.
以下はカーネルの分散パラメータ $\sigma$と, ソフトマージンのパラメータ $C$ を色々変えて学習を行ったものです.
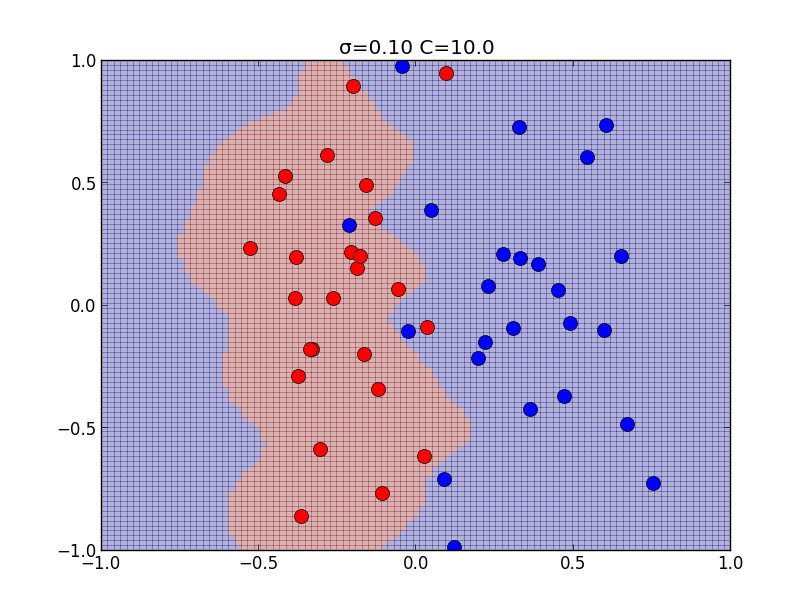
以下はカーネルの分散パラメータ $\sigma$と, ソフトマージンのパラメータ $C$ を色々変えて学習を行ったものです.
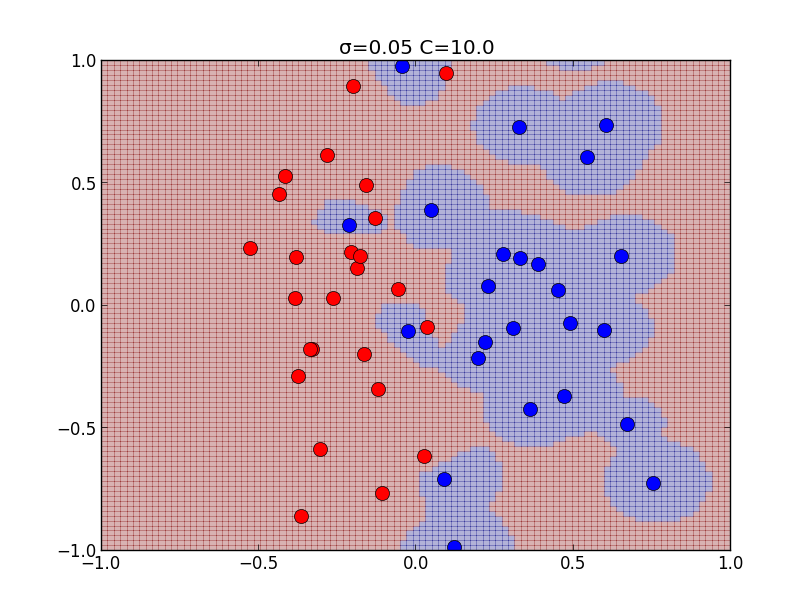
以下はカーネルの分散パラメータ $\sigma$と, ソフトマージンのパラメータ $C$ を色々変えて学習を行ったものです.
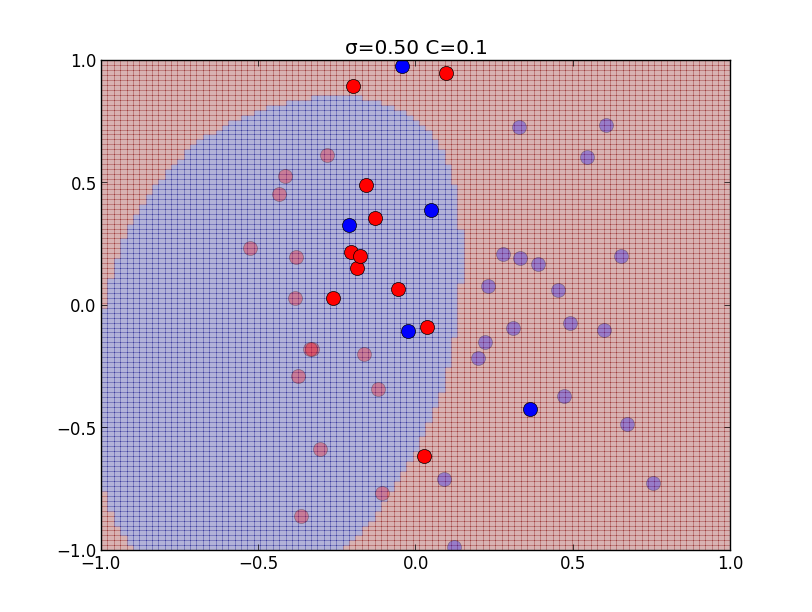
以下はカーネルの分散パラメータ $\sigma$と, ソフトマージンのパラメータ $C$ を色々変えて学習を行ったものです.
第12回はここで終わります
次回はSVMを用いた多クラス識別等の話題を紹介し, 第7章を終了します.