パターン認識・機械学習勉強会第5回 @ ワークスアプリケーションズ

パターン認識・
機械学習勉強会
第5回

@ワークスアプリケーションズ

中村晃一
2014年3月13日

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

線形識別モデル:ロジスティック回帰

前回に引き続き線形識別モデル(PRML第4章)を進めていきます.

前回は

線形識別関数の最適化に最小二乗法を用いるのは不適切である.
そこで, 目標ベクトル $\mathbf{t}$ の確率的生成モデルを考えると,
2クラスの場合, ロジスティック・シグモイド関数 $\sigma$ でモデル化出来る事がわかった.

という話をしました.

続いてこのモデルに基づく回帰分析の手法の解説をします.

少し難しめですが, 非線形回帰は初登場の話題なので頑張りましょう.

2クラスロジスティック回帰

まず２クラスの場合に, ロジスティックモデル \[ p(C_1|\mathbf{x})=\sigma(\mathbf{w}^T\Psi(\mathbf{x})) \] のパラメータ $\mathbf{w}$ を最尤法で決定する問題を考えます.

以下, 簡単の為 $\boldsymbol{\phi} = \Psi(\mathbf{x})$ と書きます.

まず, \[ p(C_1|\boldsymbol{\phi})=\sigma(\mathbf{w}^T\boldsymbol{\phi}) \] の時, \[ p(C_2|\boldsymbol{\phi})=1-p(C_1|\boldsymbol{\phi}) \] となります.

学習データの一組 $(\boldsymbol{\phi}, t)\,(t\in\{0,1\})$ を, $\mathbf{x}$ がクラス $C_1$ の時に $t=1$ となるように定めれば, 尤度は \[ L(\mathbf{w}|\boldsymbol{\phi},t) = \left\{\begin{array}{cc} \sigma(\mathbf{w}^T\boldsymbol{\phi}) & (t = 1\text{のとき}) \\ 1-\sigma(\mathbf{w}^T\boldsymbol{\phi}) & (t = 0\text{のとき}) \end{array}\right.\] となりますが, これは \[ L(\mathbf{w}|\boldsymbol{\phi},t) = \sigma(\mathbf{w}^T\boldsymbol{\phi})^t\left\{1-\sigma(\mathbf{w}^T\boldsymbol{\phi})\right\}^{1-t} \] と書くことが出来ます.

よって, 学習データ $D=\{(\boldsymbol{\phi}_1,t_1),(\boldsymbol{\phi}_2,t_2),\ldots,(\boldsymbol{\phi}_n,t_n)\}$ に対する対数尤度は \[ L(\mathbf{w}|D) = \prod_{i}\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)^{t_i}\left\{1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)\right\}^{1-t_i} \] より \[ \ln L(\mathbf{w}|D) = \sum_i\left[t_i\ln\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)+(1-t_i)\ln\left\{1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)\right\}\right] \] となります. これを最大にする $\mathbf{w}$ を求める事が目標です. しかし, これは非線形な関数 $\sigma$ を含むので最小二乗法のように簡単には解けません.

まず $\ln L$ の微分係数を調べておきましょう. 順番にやってみると \[ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}\sigma(x) &= \frac{\mathrm{d}}{\mathrm{d}x}\frac{1}{1+\exp(-x)} \\ &= \frac{\exp(-x)}{(1+\exp(-x))^2} \\ &= \frac{1}{1+\exp(-x)}\left\{1-\frac{1}{1+\exp(-x)}\right\} \\ &= \sigma(x)(1-\sigma(x)) \end{aligned} \] なので

\[ \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln \sigma(\mathbf{w}^T\boldsymbol{\phi}) &= \frac{1}{\sigma(\mathbf{w}^T\boldsymbol{\phi})}\frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\sigma(\mathbf{w}^T\boldsymbol{\phi}) \\ &= \frac{1}{\sigma(\mathbf{w}^T\boldsymbol{\phi})}\sigma(\mathbf{w}^T\boldsymbol{\phi})\left\{1-\sigma(\mathbf{w}^T\boldsymbol{\phi})\right\}\frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\mathbf{w}^T\boldsymbol{\phi} \\ &= \{1-\sigma(\mathbf{w}^T\boldsymbol{\phi})\}\boldsymbol{\phi} \end{aligned} \] となります. 同様に \[ \frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln \{1-\sigma(\mathbf{w}^T\boldsymbol{\phi})\} = -\sigma(\mathbf{w}^T\boldsymbol{\phi})\boldsymbol{\phi} \] となります.

よって \[ \begin{aligned} &\frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln L(\mathbf{w}|D) \\ =&\sum_i\left[t_i(1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i))\boldsymbol{\phi}_i+(1-t_i)(0-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i))\boldsymbol{\phi}_i\right] \end{aligned} \] となりますが, これをよく見ると \[ \frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln L(\mathbf{w}|D) = \sum_i (t_i-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i))\boldsymbol{\phi}_i \] と書けます.

さらに, \[ \begin{aligned} \mathbf{t}&=(t_1,t_2,\ldots,t_n)^T\\ \mathbf{y}&=(\sigma(\mathbf{w}^T\boldsymbol{\phi}_1),\sigma(\mathbf{w}^T\boldsymbol{\phi}_2),\ldots,\sigma(\mathbf{w}^T\boldsymbol{\phi}_n))^T\\ \mathbf{X}&=(\boldsymbol{\phi}_1,\boldsymbol{\phi}_2,\ldots,\boldsymbol{\phi}_n)^T \end{aligned} \] と置けば, \[ \frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln L(\mathbf{w}|D) = \mathbf{X}^T(\mathbf{t}-\mathbf{y}) \] となります. これが対数尤度の勾配 $\nabla\ln L$ です.

\[ \frac{\mathrm{d}}{\mathrm{d}\mathbf{w}}\ln L(\mathbf{w}|D) = \sum_i (t_i-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i))\boldsymbol{\phi}_i \] を再び $\mathbf{w}$ で微分すれば ヘッセ行列 (Hessian matrix) \[ \mathbf{H}=-\sum_i\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)(1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i))\boldsymbol{\phi}_i\boldsymbol{\phi}_i^T \] が得られます.

整理すれば以下の様になります. \[ \begin{aligned} \mathbf{H}&=-\mathbf{X}^T\mathbf{R}\mathbf{X}\\ \mathbf{R}&=\begin{pmatrix} \sigma(\mathbf{w}^T\boldsymbol{\phi}_1)(1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_1)) & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma(\mathbf{w}^T\boldsymbol{\phi}_n)(1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_n)) \end{pmatrix} \end{aligned} \]

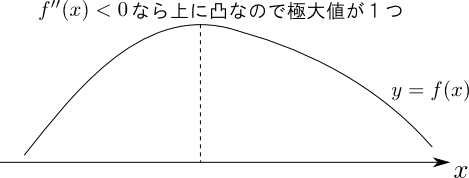
前頁の $\mathbf{H}$ は $\mathbf{R}$ の対角成分が全て正であることに注意すると, \[ \text{任意の $\mathbf{x}$ に対して $\mathbf{x}^T\mathbf{H}\mathbf{x} < 0$} \] が成り立つので, 負定値 (negative definite) である事が分かります. これは「$\ln L$ は極大値を唯一つ持ち,極小値は持たない」という事を示します

高校数学で学んだ $f''(x) < 0$ ならばグラフは上に凸という事の一般化です.

まとめましょう.

ロジスティックモデルにおける対数尤度 $\ln L$

$\ln L$ は唯一つの極大値を持ち極小値は持たない.

勾配: $\nabla \ln L = \mathbf{X}^T(\mathbf{t}-\mathbf{y})$
ヘッセ行列: $\mathbf{H} = -\mathbf{X}^T\mathbf{R}\mathbf{X}$

ここで \[ \begin{aligned} \mathbf{t}&=(t_1,t_2,\ldots,t_n)^T\\ \mathbf{y}&=(\sigma(\mathbf{w}^T\boldsymbol{\phi}_1),\sigma(\mathbf{w}^T\boldsymbol{\phi}_2),\ldots,\sigma(\mathbf{w}^T\boldsymbol{\phi}_n))^T\\ \mathbf{X}&=(\boldsymbol{\phi}_1,\boldsymbol{\phi}_2,\ldots,\boldsymbol{\phi}_n)^T \end{aligned} \] $\mathbf{R}$ は対角行列で \[ R_{ii} = \sigma(\mathbf{w}^T\boldsymbol{\phi}_i)(1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)) \]

さて, $\ln L$ の最大化を行うために本日は基本的な３つの手法の紹介を行います.

ニュートン・ラフソン法
最急降下法
確率的勾配降下法

ニュートン・ラフソン法

$\ln L$ は凸関数なので $\ln L$ を最大にする $\mathbf{w}$ を求める事を, $\nabla \ln L = \mathbf{0}$ を満たす $\mathbf{w}$ を求める問題に帰着して解くことが出来ます.

非線形方程式の反復解法では ニュートン・ラフソン法 (Newton-Raphson method) が有名です.

ニュートン・ラフソン法では, 適当な初期値 $\mathbf{w}_0$ を定め, \[ \mathbf{w}_{k+1} = \mathbf{w}_k - \mathbf{H}_k^{-1}\nabla \ln L_k \] によって反復を行い $\mathbf{w}$ を収束させます.

この単純なニュートン・ラフソン法では必ずしも極小値に収束するとは限らず極大値に収束したり発散してしまう場合があります。そこで準ニュートン法というものが登場しますが、これは後の回に説明します。

一変数方程式 $f'(x)=0$ にニュートン・ラフソン法(参考) を適用すると \[ x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)} \] という反復公式が得られますが, これを多変数に拡張したものです. 二次収束します.

先ほどの式を代入すると \[ \mathbf{w}_{k+1} = \mathbf{w}_k + (\mathbf{X}^T\mathbf{R}_k\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{t}-\mathbf{y}_k) \] となります. 行列 $\mathbf{R}$ は $\mathbf{w}$ を含むので反復の度に計算が必要である事に注意しましょう.

$\mathbf{R}$ は重み付け行列と呼ばれるので, 上記のアルゴリズムは 反復再重み付け最小二乗法 (iterative reweighted least squares method, IRLS) と呼ばれます.

IRLS法による2クラスロジスティック回帰

適当な初期値 $\mathbf{w}_0$ から始め \[ \mathbf{w}_{k+1} = \mathbf{w}_k + (\mathbf{X}^T\mathbf{R}_k\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{t}-\mathbf{y}_k) \] で反復を行って $\mathbf{w}$ を求める.

ここで \[ \begin{aligned} \mathbf{t}&=(t_1,t_2,\ldots,t_n)^T\\ \mathbf{y}_k&=(\sigma(\mathbf{w}_k^T\boldsymbol{\phi}_1),\sigma(\mathbf{w}_k^T\boldsymbol{\phi}_2),\ldots,\sigma(\mathbf{w}_k^T\boldsymbol{\phi}_n))^T\\ \mathbf{X}&=(\boldsymbol{\phi}_1,\boldsymbol{\phi}_2,\ldots,\boldsymbol{\phi}_n)^T \end{aligned} \] $\mathbf{R}$ は対角行列で \[ R_{ii} = \sigma(\mathbf{w}_k^T\boldsymbol{\phi}_i)(1-\sigma(\mathbf{w}_k^T\boldsymbol{\phi}_i)) \]

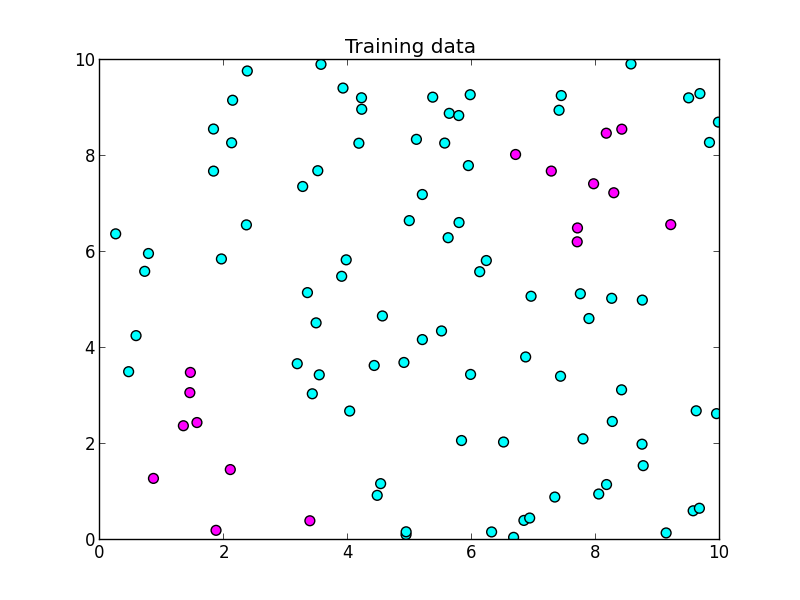
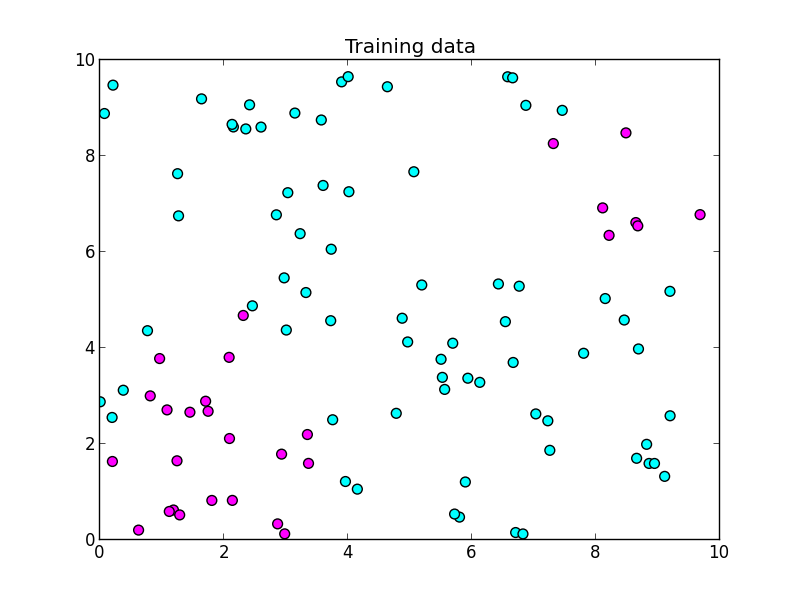
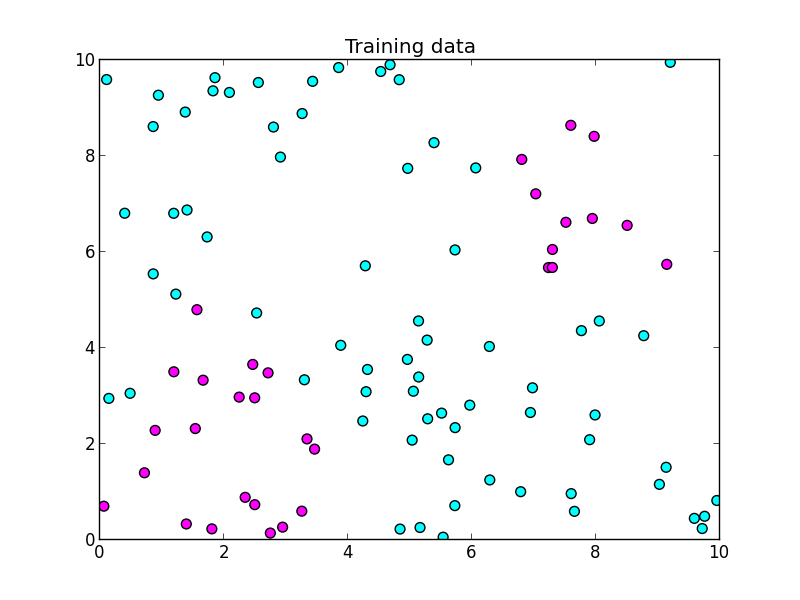
細かい話の前に, 簡単な実装例をお見せします.以下を学習データとします.

prog5-1.py

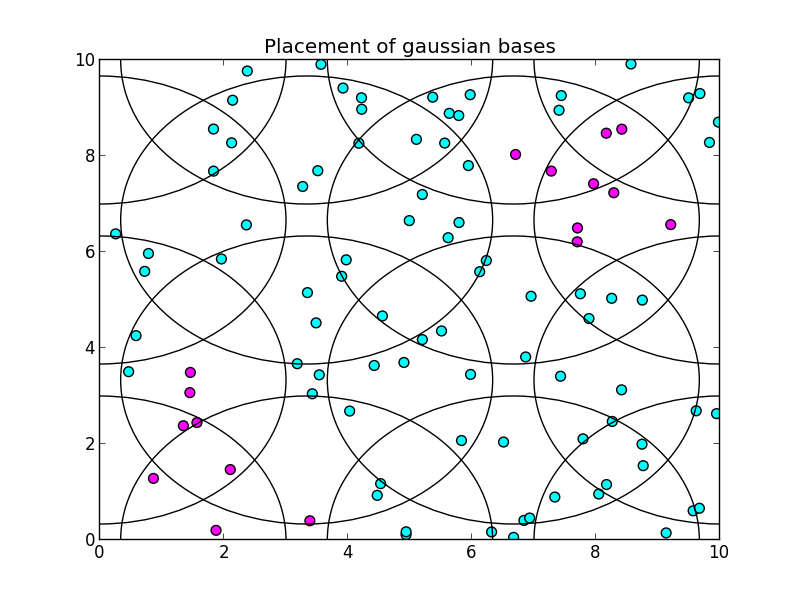
ガウス基底を以下のように配置して使う事にしました. 各円の半径は基底の標準偏差パラメータの値です.

prog5-1.py

初期状態では $\mathbf{w}=\mathbf{0}$ としました.

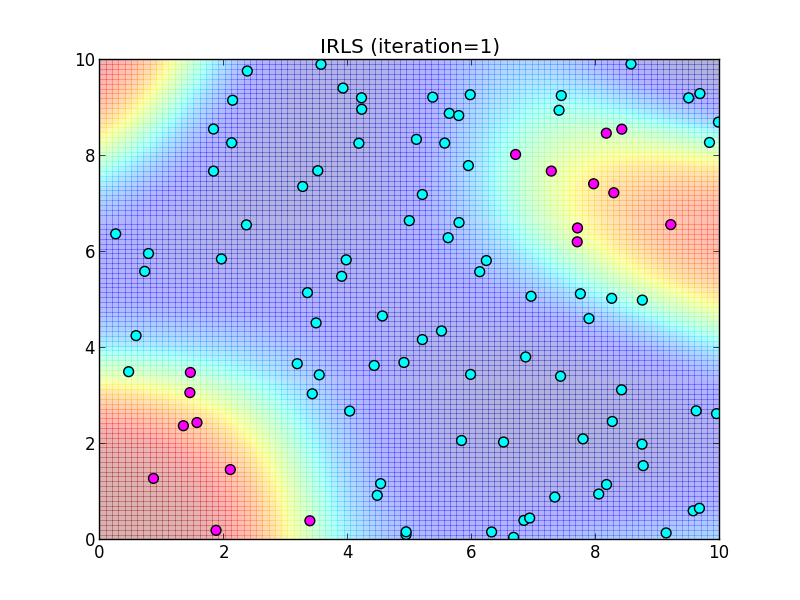
反復1回目.

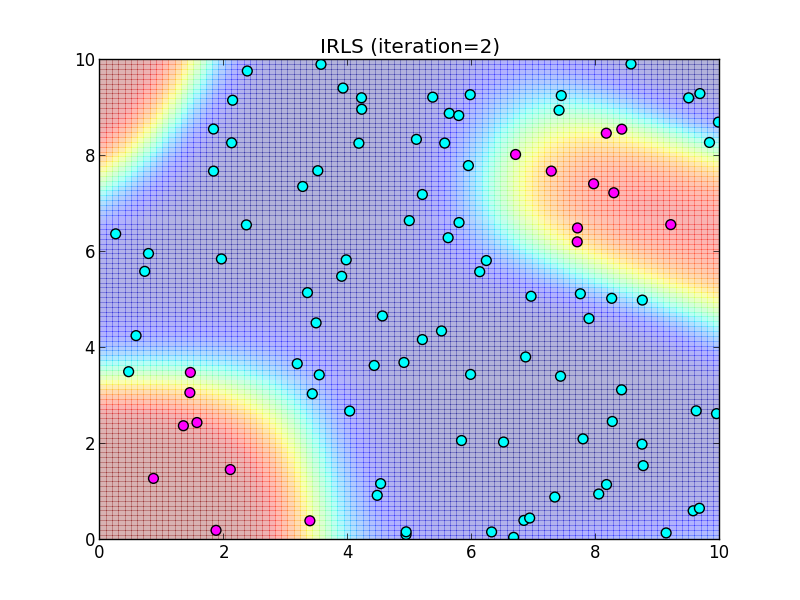
反復2回目.

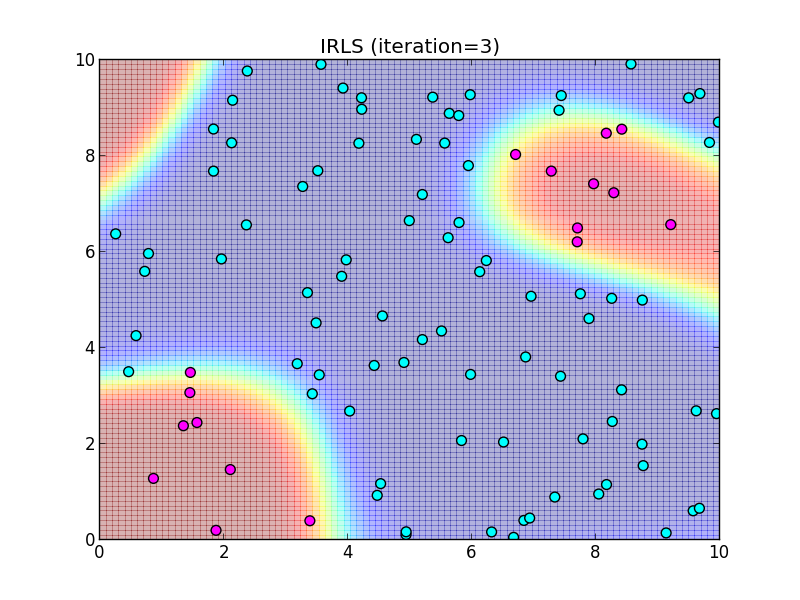
反復3回目.

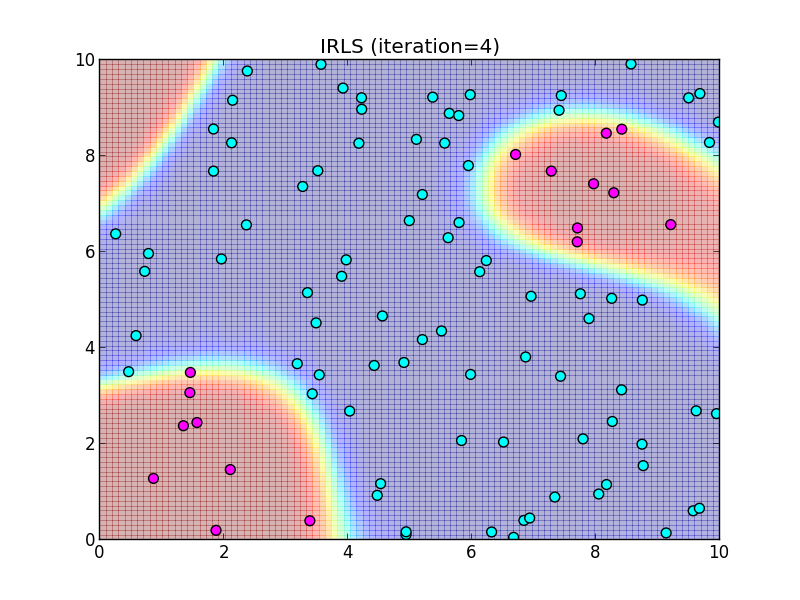
反復4回目.

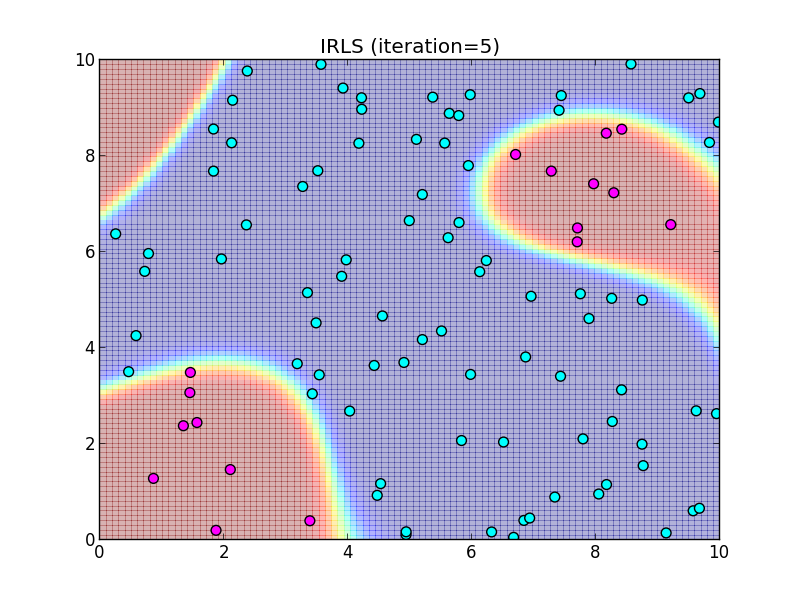
反復5回目.

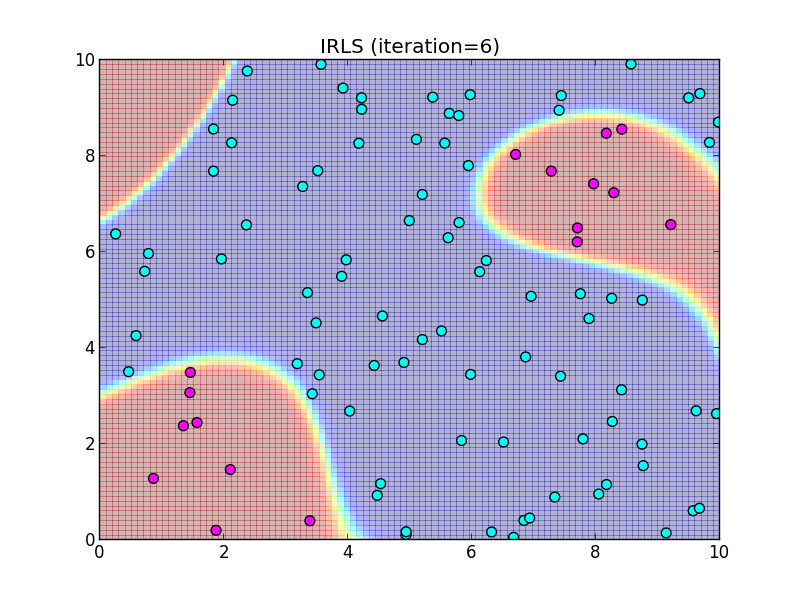
反復6回目.

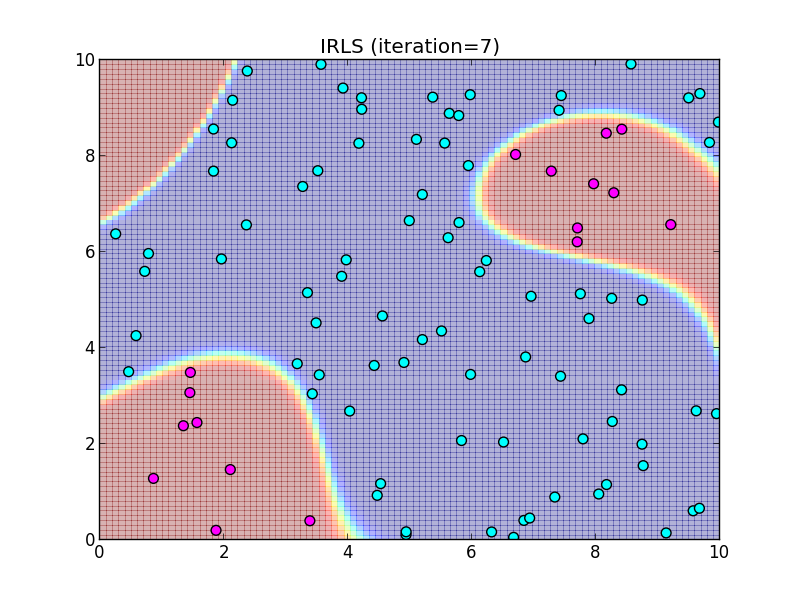
反復7回目.

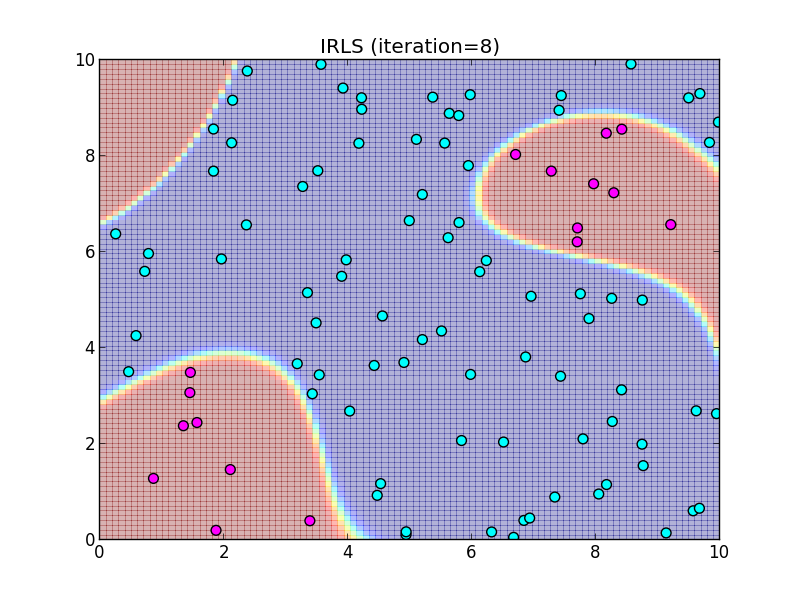
反復8回目.

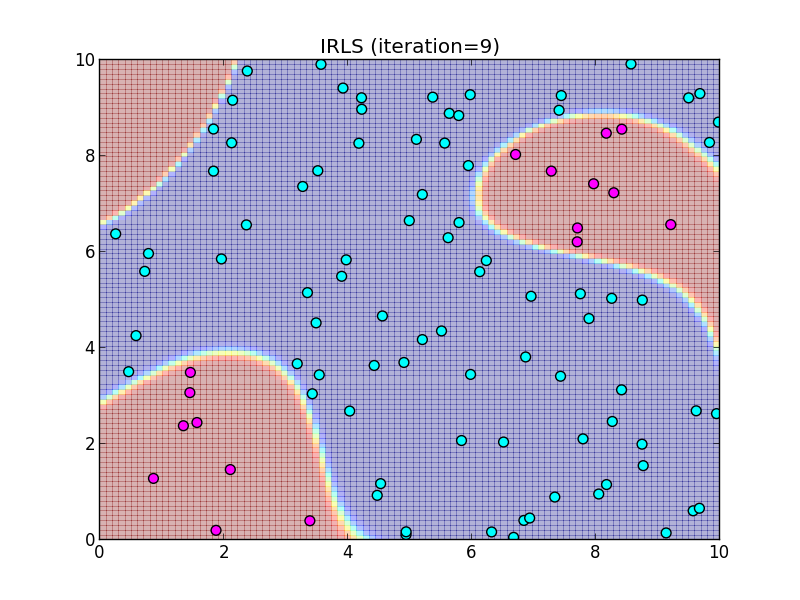
反復9回目.

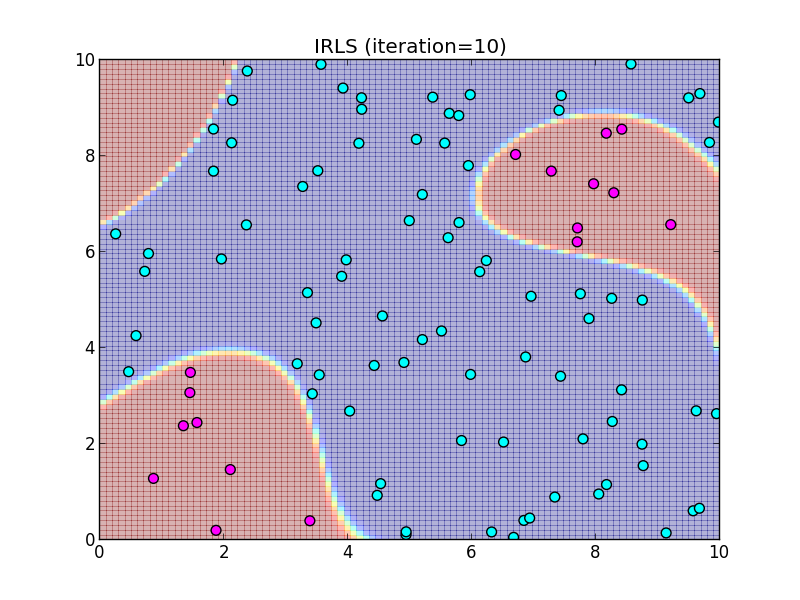
反復10回目.

この様に, IRLS は収束が非常に速いという事が特徴です.

一方で, 次頁以降で説明するような事柄に注意が必要です.

計算上の注意

シグモイド関数 \[ \sigma(a) = \frac{1}{1+\exp(-a)} \] は指数関数 $\exp$ を含む為, 簡単にオーバーフロー・アンダーフロー・情報落ちを起こします.

倍精度の場合, オーバーフロー・アンダーフローを防ぐ為には, 引数は大体 $[-709, 745]$ の範囲内になければいけません.

>>> from math import exp
>>> exp(709)
8.218407461554972e+307
>>> exp(710)
Traceback (most recent call last):
  File "", line 1, in 
OverflowError: math range error
>>> exp(-745)
5e-324
>>> exp(-746)
0.0

また, $[-36, 36]$ あたりを外れると完全に情報が落ちます.

>>> from math import exp
>>> (1 + exp(36)) - exp(36)
1.0
>>> (1 + exp(37)) - exp(37)
0.0
>>> (1 + exp(-36)) - 1
2.220446049250313e-16
>>> (1 + exp(-37)) - 1
0.0

オーバーフローやアンダーフローは例えば \[ \sigma(a) = \frac{1}{2}(1+\tanh (a/2)) \] などの等式を用いると回避する事が出来ますが, それでも情報落ちは起きてしまいます.

アンダーフローや情報落ちが起きると, 本来 $0 < \sigma(a) < 1$ であるシグモイド関数の値が $0$ や $1$ になってしまいます. このとき, $(\mathbf{X}^T\mathbf{R}\mathbf{X})^{-1}$ が特異行列になってしまうので, アルゴリズムを実行する事ができなくなります.

誤差が出やすい事を理解し, 行列の条件数を追跡するなど大きな誤差が生じた場合に検出出来るようにする工夫が必要です.

停止条件について

IRLSの反復を停止する一般的な方法もありません.

通常のニュートン・ラフソン法では $\mathbf{w}_n$ と $\mathbf{w}_{n+1}$ の相対誤差 \[ \frac{||\mathbf{w}_n-\mathbf{w}_{n+1}||}{||\mathbf{w}_n||} \] がある値以下である事を停止条件としますが, IRLSではその前に $(\mathbf{X}^T\mathbf{R}\mathbf{X})^{-1}$ が特異行列になってしまったりします.

現実には以下の様な複数の終了条件を組合せてアルゴリズムを実行する事になると思います.

相対誤差 $||\mathbf{w}_n-\mathbf{w}_{n+1}||/||\mathbf{w}_n||$ がある値以下の時に停止.
残差平方和 $\sum_i||t_i-\sigma(\mathbf{w}_n^T\boldsymbol{\phi}_i)||^2$ がある値以下の時に停止.
$(\mathbf{X}^T\mathbf{R}\mathbf{X})^{-1}$ が特異行列に近づいてしまったら停止.
反復回数上限に達したら停止.

勾配法

IRLSよりも一般に収束が遅いですが使いやすい手法に 勾配法 (gradient method) があります.

勾配法とは,勾配 $\nabla f(\mathbf{x})$ を参考にして局面を下っていくもしくは登っていく手法です. 移動先をどのように決定するかによって幾つかの手法があります.

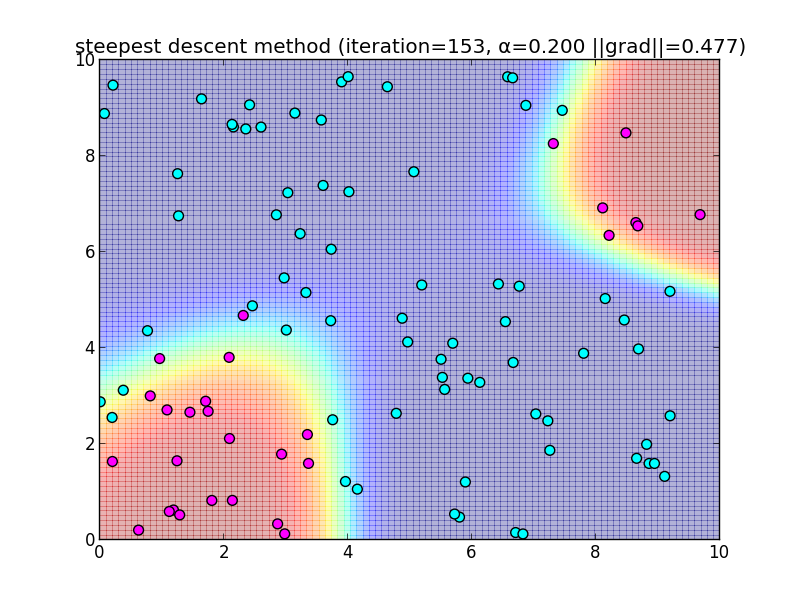
最急降下法

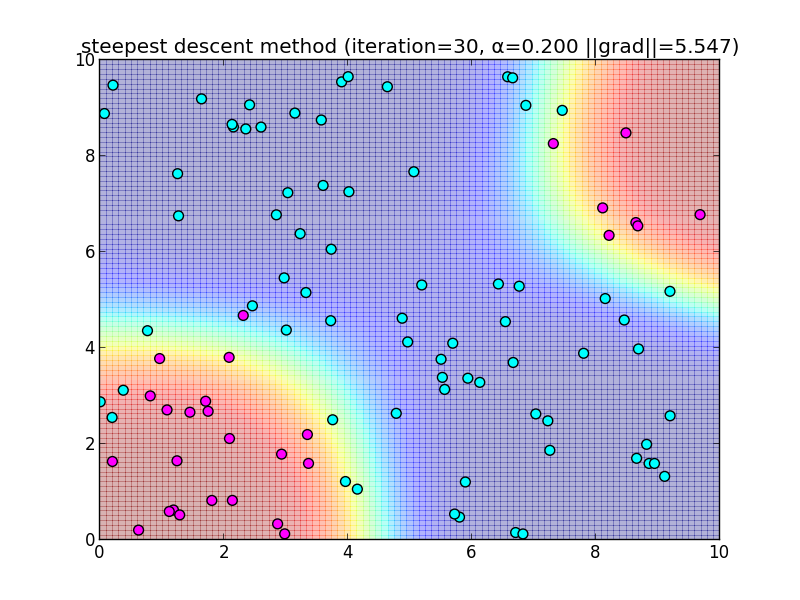
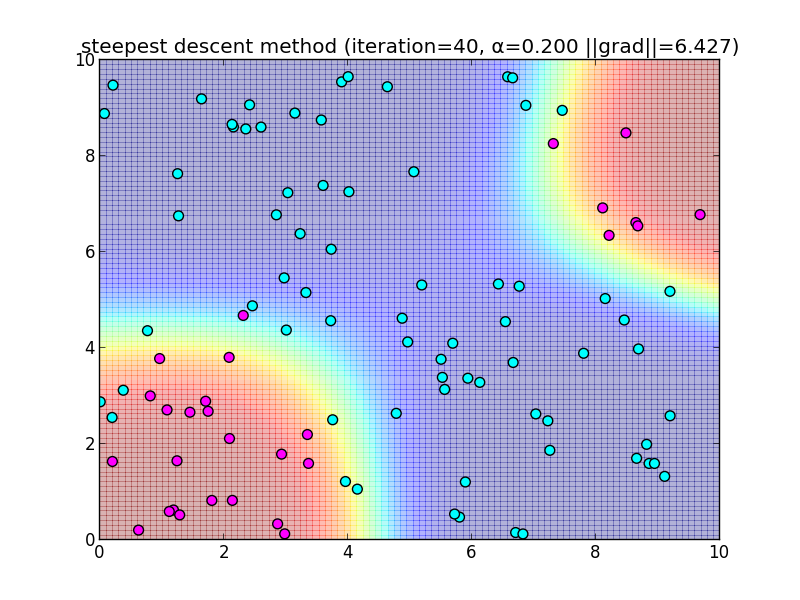
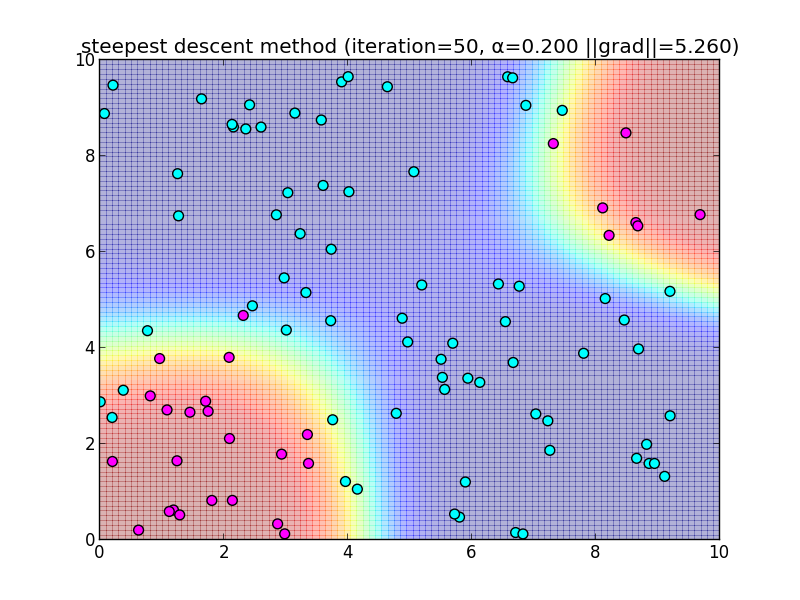
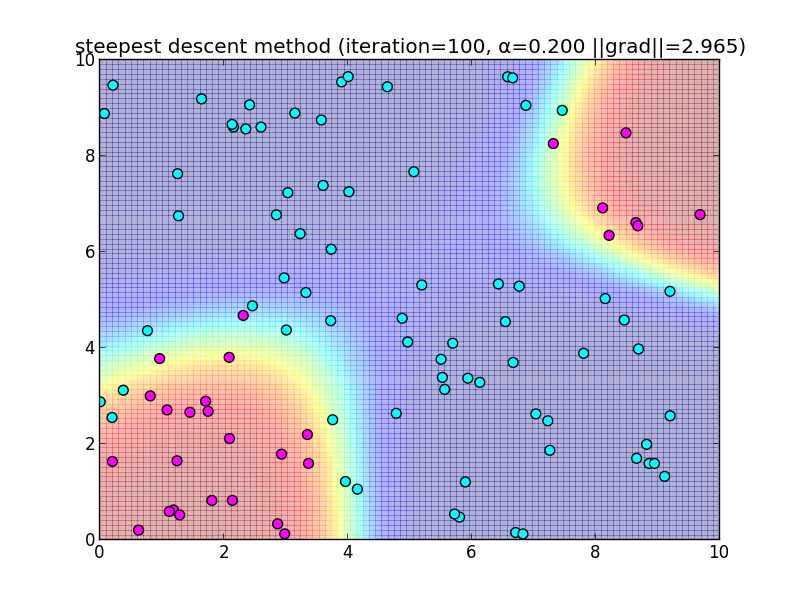
勾配 $\nabla \ln L = \mathbf{X}^T(\mathbf{t}-\mathbf{y})$ は, 点$\mathbf{w}$における $\ln L$ の増加率の最も急な方向を向いています. その反対方向に向かって進んでいけば極小値にたどり着くことができます. これを 最急降下法 (steepest descent method) と呼びます. (今回は最大値を求めたいので勾配の方向に進みます.)

具体的には,適当なパラメータ $\alpha$ を用意して \[ \begin{aligned} \mathbf{w}_{k+1} &= \mathbf{w}_k + \alpha\nabla \ln L \\ &= \mathbf{w}_k + \alpha\mathbf{X}^T(\mathbf{t}-\mathbf{y}) \end{aligned} \] によって進んでいきます. 最大値では勾配が $\mathbf{0}$ になるので, 適当なノルムを用いて $||\nabla \ln L||<\varepsilon$ という条件で終了します.

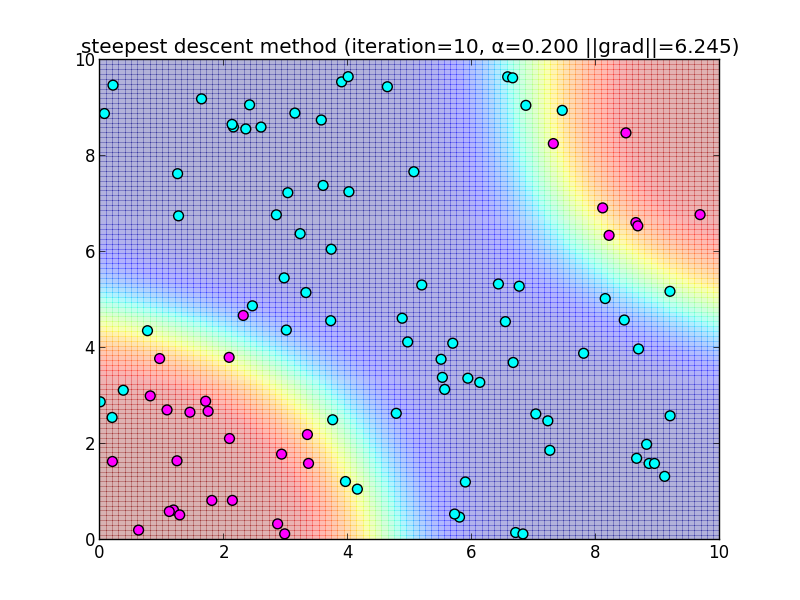
先ほどと同様のデータに適用してみます.

反復10回目の様子.

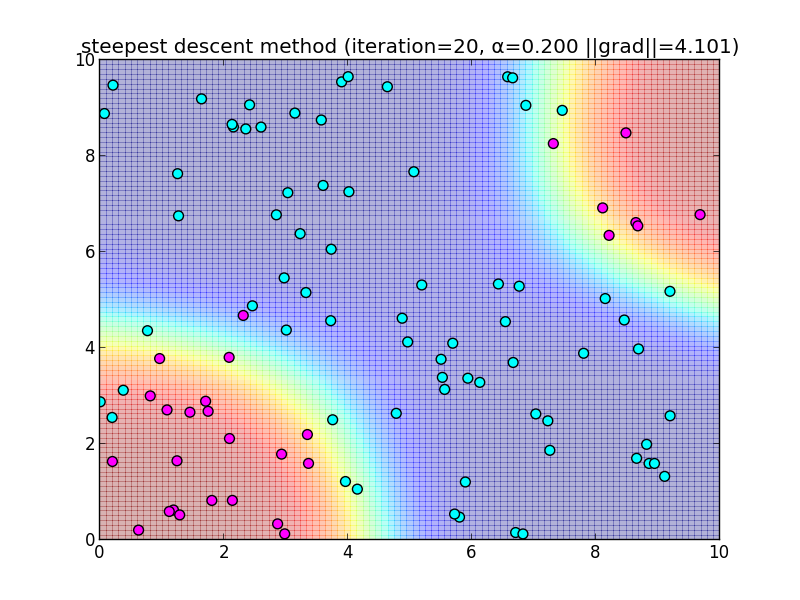
反復20回目の様子.

反復30回目の様子.

反復40回目の様子.

反復50回目の様子.

反復100回目の様子.

153回目で反復停止.

簡単なアルゴリズムである反面、IRLSに比べると収束が大分遅いという事が分かると思います. 今回は $\alpha = 0.2$ と固定して使いましたが, これをを動的に変更するなどのバリエーションもあります.

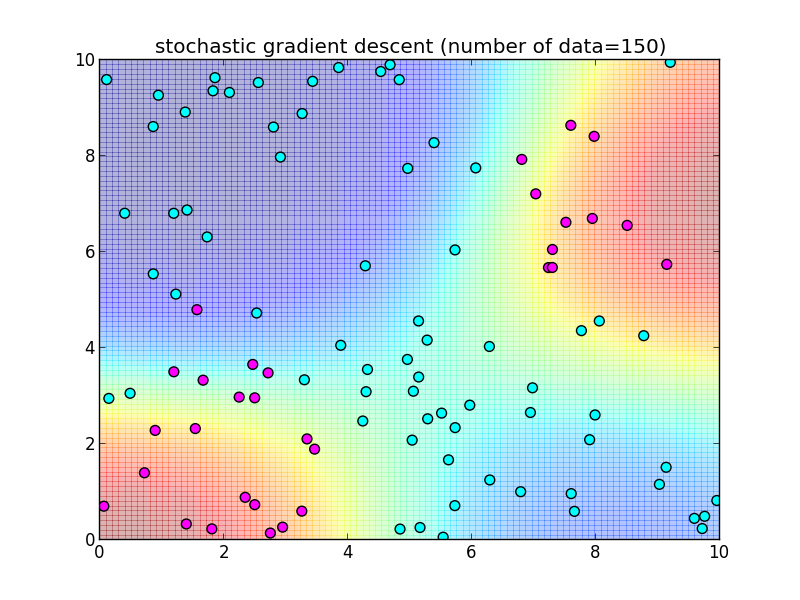
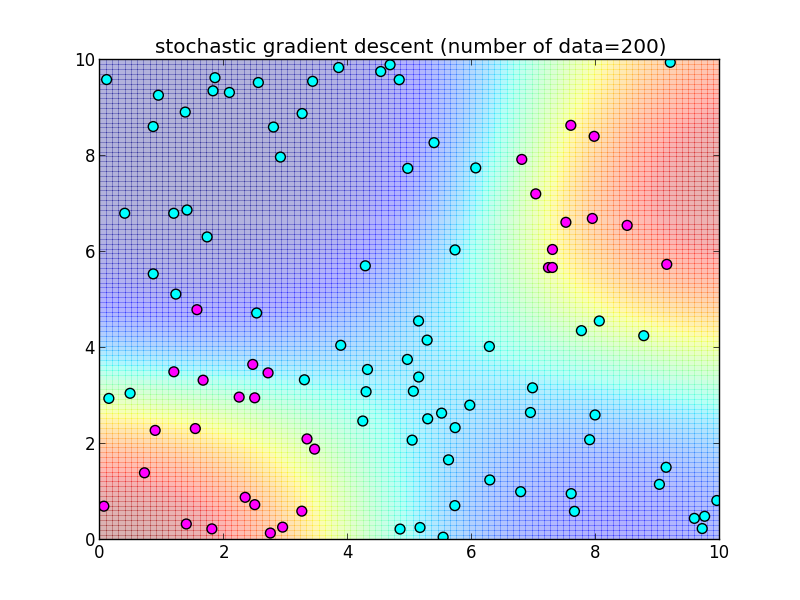
確率的勾配降下法

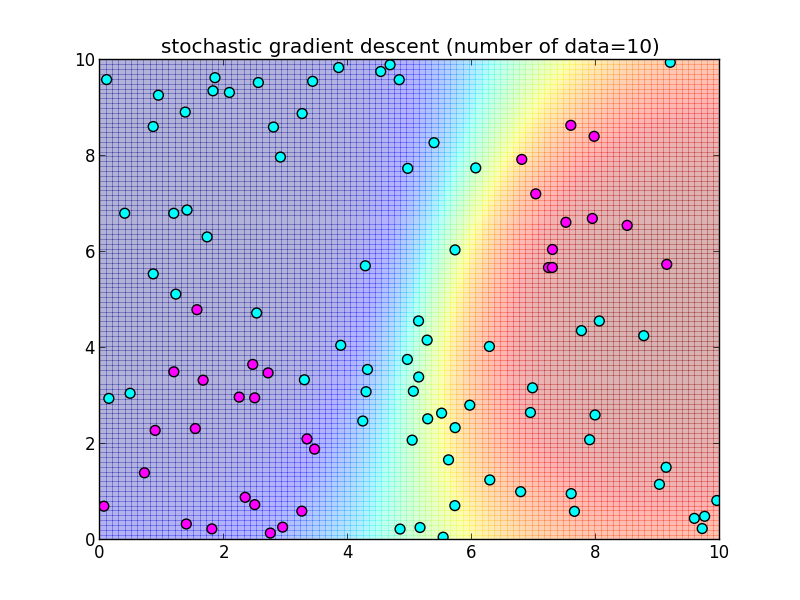
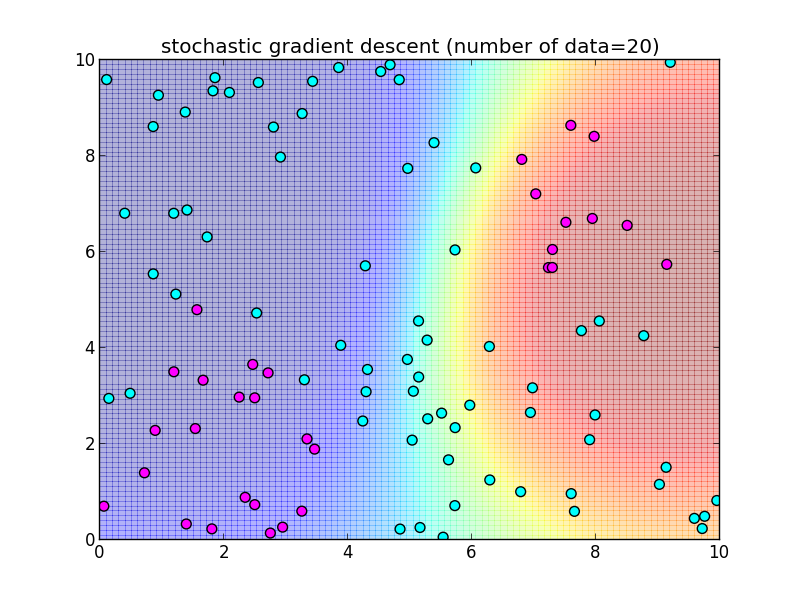
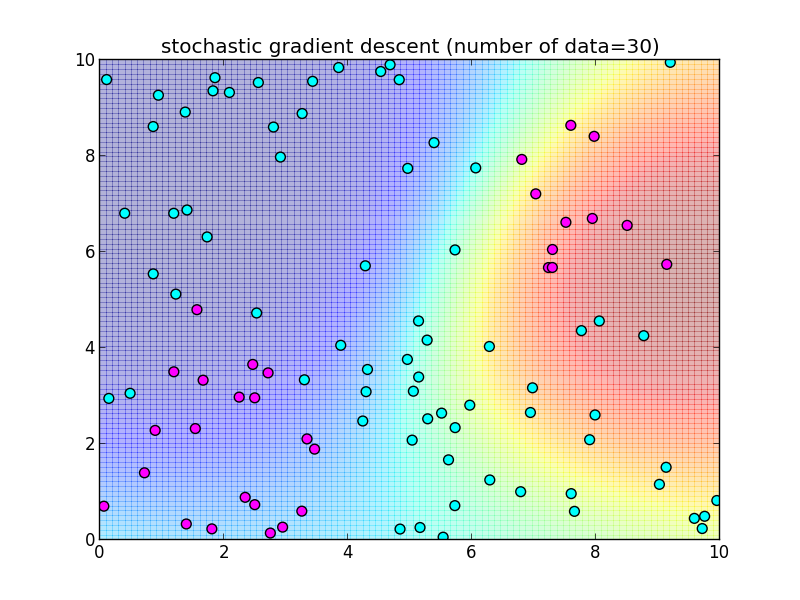
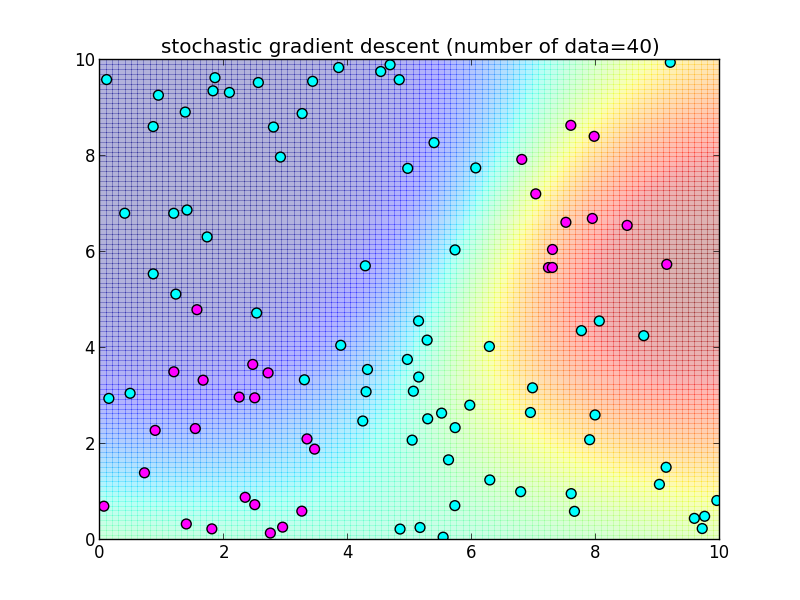
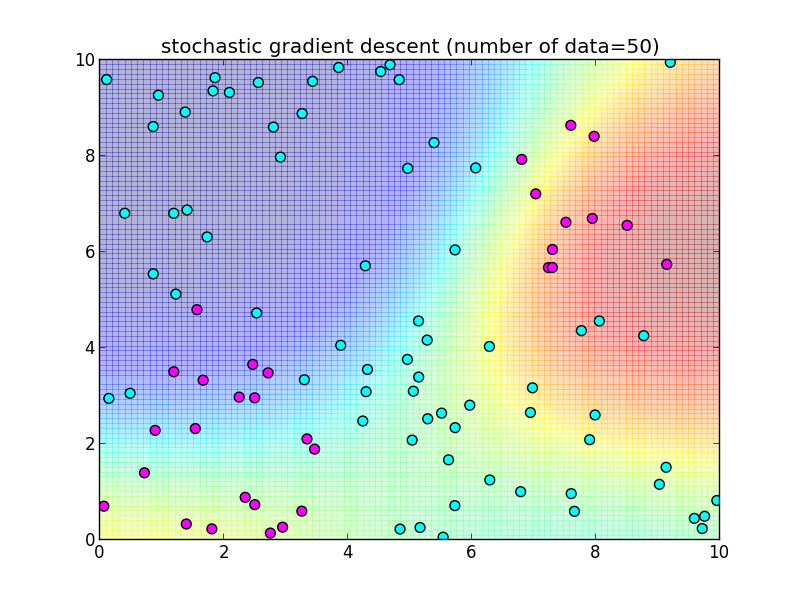
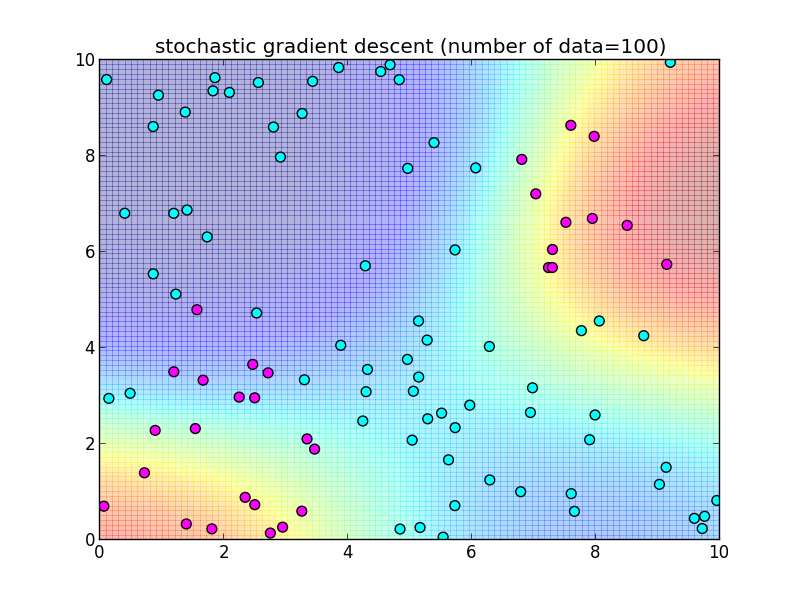
再急降下法では学習データを全て使って $\nabla \ln L$ を計算しました. 学習データを 1つずつ順番に使うように変更した物を 確率的勾配降下法 (stochastic gradient descent) と呼びます.

学習データを先頭から順番に処理出来るオンラインアルゴリズムになっています.

つまり, \[ \mathbf{w}_{k+1} = \mathbf{w}_k + \eta_k (t_{k+1}-\sigma(\mathbf{w}_k^T\boldsymbol{\phi}_{k+1}))\boldsymbol{\phi}_{k+1} \] によって更新を行います. $\eta_k$ は学習率を調整するパラメータで, 徐々に小さくしていきます.

先ほどと同様のデータに適用してみます.今回は $n$ 個のデータセット全体を2週する形で, トータル $2n$ 回の反復を行ってみました.

反復10回目の様子.

反復20回目の様子.

反復30回目の様子.

反復40回目の様子.

反復50回目の様子.

反復100回目の様子.

反復150回目の様子.

反復200回目の様子.

多クラスロジスティック回帰

クラス数 $K$ が $3$ 以上の場合を考えます. \[ p(C_i|\mathbf{x}) = \frac{\pi(\mathbf{x}|C_i)p(C_i)}{\pi(\mathbf{x})} = \frac{\pi(\mathbf{x}|C_i)p(C_i)}{\sum_jg \pi(\mathbf{x}|C_j)p(C_j)} \] において, \[ a_i = \ln\pi(\mathbf{x}|C_i)p(C_i) \] と置けば, \[ p(C_i|\mathbf{x}) = \frac{\exp(a_i)}{\sum_j\exp(a_j)} \] となります. この関数は ソフトマックス (softmax function) と呼ばれます.

ソフトマックス関数と呼ばれるのは, 全ての $j\neq i$ に対して $a_i \gg a_j$ の時には \[ \exp(a_j-a_i) \approx 0 \] となるので \[ p(C_i|\mathbf{x}) \approx 1 \] となり, そうでなければ \[ p(C_i|\mathbf{x}) \approx 0 \] となるからです.

多クラスの場合も同様に \[ a_i = \mathbf{w}_i^T\boldsymbol{\phi} \] とモデル化します.

学習データの一組 $(\boldsymbol{\phi}, \mathbf{t})$ は 1-of-K符号化によって定めます.

学習データ $D=\{(\boldsymbol{\phi}_1,\mathbf{t}_1),\ldots,(\boldsymbol{\phi}_n,\mathbf{t}_n)\}$ に対する尤度関数は \[ L(\mathbf{w}_1,\ldots,\mathbf{w}_K|D) = \prod_{i=1}^n\prod_{k=1}^K p(C_k|\boldsymbol{\phi}_i)^{t_{ik}} \] となるので対数尤度は \[ \ln L(\mathbf{w}_1,\ldots,\mathbf{w}_K|D) = \sum_{i=1}^n\sum_{k=1}^K t_{ik}\ln p(C_k|\boldsymbol{\phi}_i) \]

これを $\mathbf{w}_j$ で微分すると, 先ほどと同様にして \[ \frac{\partial}{\partial\mathbf{w}_j}\ln L = \sum_{i=1}^n(t_{ik}-p(C_j|\boldsymbol{\phi}_i))\boldsymbol{\phi}_i \] となるので, これを $\mathbf{w}_1,\mathbf{w}_2,\ldots,\mathbf{w}_K$ について縦に並べたものが対数尤度の勾配となります. \[ \begin{pmatrix} \frac{\partial}{\partial\mathbf{w}_1}\ln L \\ \vdots \\ \frac{\partial}{\partial\mathbf{w}_K}\ln L \\ \end{pmatrix} \]

さらにもう一度 $\mathbf{w}_k$ で微分すると \[ \begin{aligned} &\mathbf{H}_{jk} = \frac{\partial^2}{\partial\mathbf{w}_k\partial\mathbf{w}_j}\ln L = -\sum_{i=1}^np(C_k|\boldsymbol{\phi}_i)(\delta_{jk}-p(C_j|\boldsymbol{\phi}_i))\boldsymbol{\phi}_i\boldsymbol{\phi}_i^T \\ &\qquad\qquad\text{($\delta_{jk}$はディラックの $\delta$ 関数)} \end{aligned} \] となるので, これを並べたブロック行列 \[ \mathbf{H} = \begin{pmatrix} \mathbf{H}_{11} & \mathbf{H}_{12} & \cdots & \mathbf{H}_{1K} \\ \mathbf{H}_{21} & \mathbf{H}_{22} & \cdots & \mathbf{H}_{2K} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{H}_{K1} & \mathbf{H}_{K2} & \cdots & \mathbf{H}_{KK} \end{pmatrix} \] がヘッセ行列となります.

多クラスの場合のサンプルコードはまだ作っていないので, 後で更新します.

第5回はここで終わります

資料の作成が追いつかなかったのでここで一旦終了します. 次回はベイジアンロジスティック回帰に進みます. テキストではラプラス近似を利用した手法を紹介していますが, この勉強会ではMCMCを利用して解いてみます.