パターン認識・
機械学習勉強会
第8回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

ニューラルネットワーク

前回に続きニューラルネットワークの解説を行います. 5.3節以降技術的な話題が多くなりますが、特に重要なものに絞ります.

実装の検証

誤差逆伝播法はニューラルネットワークに対する何らかの誤差関数 $E(\mathbf{x},\mathbf{w})$ の, 重み $w_{ji}$ に関する微分係数 \[ \frac{\partial E}{\partial w_{ji}} \] を計算するものでした.

一方, 数値微分法 (numerical differentiation) によってこれを近似的に計算する事も出来ます. 2つの結果を比較する事によって実装の検証を行います.

例えば, 中心差分法 (central difference) では, 微小量 $\varepsilon > 0$ に対して \[ \frac{\partial E}{\partial w_{ji}} = \frac{E(w_{ji} + \varepsilon)-E(w_{ji} - \varepsilon)}{2\varepsilon} + O(\varepsilon^2) \] となります(参考).

各微分係数の計算に2回の順伝播が必要なので, 計算量は重みの数 $W$ に対して $\mathcal{O}(W^2)$ となります.

前回実装したものを中心差分の結果と比較した所以下のようになりました。実装は誤っていないようです。 (prog8-1.py)

誤差逆伝播で求めた微分係数
[  3.40753294  27.62924471   4.04890811 -14.67453553  -5.83120129
  32.10422817  40.14607951  40.10717238  24.84976142  58.85584348]
中心差分 (eps=0.010000) で求めた微分係数
[  3.40736966  27.62873587   4.04890491 -14.67486427  -5.83108375
  32.10315101  40.14607951  40.10717238  24.84976142  58.85584348]

ヤコビ行列

ニューラルネットワーク $\mathbf{y}=f(\mathbf{x},\mathbf{w})$ に対して, \[ J_{ij} = \frac{\partial y_i}{\partial x_j} \] という微分係数, は入力の変動に対する, 出力の変動を表します.

$J_{ij}$ を $(i,j)$ 成分にもつ行列は ヤコビ行列 (Jacobian matrix) と呼ばれます.

ヤコビ行列が必要となる典型的な場面は 不変性 (invariance) の評価です.

例えば文字認識の問題を考えましょう. 文字画像(入力)に平行移動・回転・拡大などの変換を行ってもそのクラス(出力)は不変です.

出力 $y_k$ は, 入力 $x_i$ に $x_i$ と直接接続する素子の入力 $a_j$ を介してのみ依存するので \[ J_{ki} = \frac{\partial y_k}{\partial x_i} = \sum_j \frac{\partial a_j}{\partial x_i}\frac{\partial y_k}{\partial a_j} = \sum_j w_{ji}\frac{\partial y_k}{\partial a_j} \] となります.

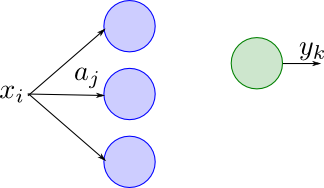
誤差逆伝播法によって $\delta_{ji} = \partial y_j/\partial a_i$ を計算することは出来るので, 以下の手順でヤコビ行列を計算出来ます.

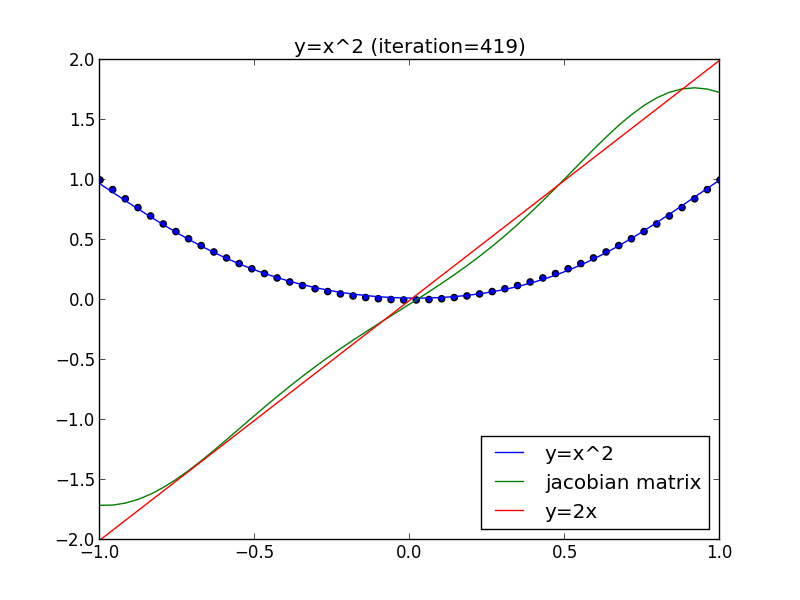
$y=x^2$ を学習させた例で試してみましょう. \[ \frac{\mathrm{d} y}{\mathrm{d} x} = 2x \] となるはずです.

prog7-1.py

以下のようなネットワークでしたので, 出力層については \[ \frac{\partial y}{\partial a} = 1 \] で計算します.

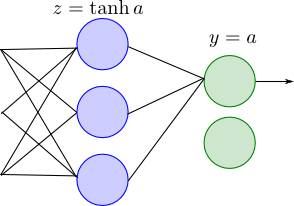
以下が計算結果のプロットです. 確かに $y=2x$ になっている事が分かります. 定義域の境界では関数が不連続であるので誤差が大きくなります.

prog8-2.py

第8回はここで終わります

資料作成が間に合わず中途半端になってしまって大変申し訳ありませんでした。次回、ニューラルネットワークを終了します。