プログラマの為の
数学勉強会
第3回
(於)ワークスアプリケーションズ中村晃一
2013年9月26日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPythonで記述しています。
微分法の応用
準備
最初に,本日の議論に必要となる連続性,微分可能性,極値,ロルの定理について説明します。
連続性
\[ \lim_{x\rightarrow a}f(x) = f(a) \] が成立する時,\(f(x)\)は\(x=a\)で連続であるという。
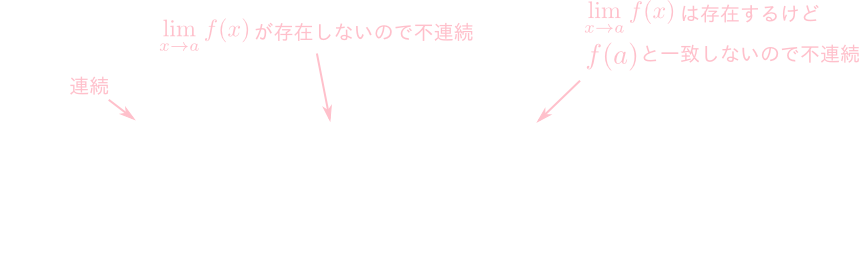
微分可能性
\[ f'(a) = \lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h} \] が収束する時,\(f(x)\)は\(x=a\)で微分可能であるという。
同様に,\(n\)階微分係数\(f^{(n)}(a)\)が存在する時\(x=a\)で\(n\)回微分可能であるという。
直感的には,微分可能性は曲線が滑らかであるという事だと解釈できます。また証明は省略しますが,\(f(x)\)が\(x=a\)で微分可能ならばその点で連続である事を示す事が出来ます。
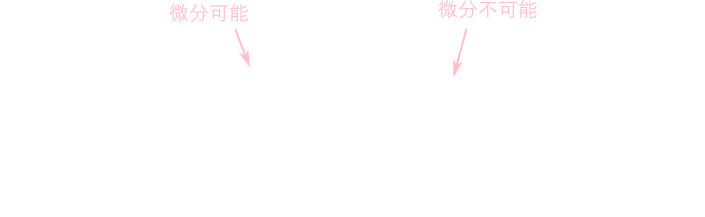
極大値・極小値
局所的に見れば最大・最小となる値を極値と言います。
「最も良い~を求める」という形の問題の多くは何らかの最大値・最小値問題に帰着します。極値はその候補になるため重要です。
極値
\(f(x\))を連続な関数,\(a\)を定数とする。適当な\(\varepsilon > 0\)が存在して \(f(a)\)が区間(\(a-\varepsilon, a+\varepsilon\))の最大値となるならば, \(f(a)\)を極大値,最小値となるならば極小値といい,これらを併せて極値という。
つまり,\(f(a)\)が極大値である事は絶対値の十分小さい\(h\)に対して常に \[ f(a+h) \leq f(a) \] が成り立つ事だと言えます。極小値も同様です。この形の論法をよく使います。
\(f(a)\)が極大値であるとき,\(f'(a)\)がどうなるか考えます。
今言ったように,十分小さい\(h\)に対して常に\(f(a+h)-f(a) \leq 0\) が成り立ちます。従って \[ \begin{array}{c} h<0\text{ならば}\frac{f(a+h)-f(a)}{h}\geq 0\\ h>0\text{ならば}\frac{f(a+h)-f(a)}{h}\leq 0 \end{array}\cdots(1) \] となります。
ところで\(f'(a)\)が存在するならば \[ f'(a) = \lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h} \] だったので,(1)より\(f'(a) = 0\)でなければいけません(もちろん厳密には\(\varepsilon-\delta\)論法で示します)。
以上の議論は\(f(a)\)が極小値の時も同様です。
極値と導関数の関係
\(f(x)\)が\(x=a\)で微分可能のとき, \[ f(a)\text{が極値ならば}f'(a) = 0\] が成立する。
直感的には\(y=f(x)\)が滑らかなグラフならば,山の頂点・谷の底で接線が水平になるという事です。
今の定理は\(f'(a)=0\)の時\(f(a)\)が極大値なのか極小値なのかそもそも極値なのか何も言っていないので注意してください。さらに詳しく調べる為にはより高階の微分係数を考える必要があるので,その為の定理を得た後に再び考察します。
ロルの定理
\(f(x)\)が区間\([a,b]\)で連続,区間\((a,b)\)で微分可能で \[ f(a)=f(b) = 0\] ならばある\(a < c < b\)が存在して \[ f'(c) = 0 \] を満たす。
【証明】
\(f(x)\)が閉区間\([a,b]\)で連続なので,この区間内に必ず最大値と最小値を持つ(最大値・最小値の定理)。
特に\(f(a)=f(b)=0\)なので最大値・最小値の少なくとも一方は開区間\((a,b)\)に存在する。
開区間\((a,b)\)内の最大値または最小値は極値でもあるので,これを\(f(c)\)とすると\(f(x)\)は開区間\((a,b)\)で微分可能であるから \[ f'(c) = 0 \] となる。□
テイラーの定理
テイラーの定理という,微分法の応用を考える上で非常に重要な定理を紹介します。
この定理は様々な場面で利用するのですが,ここでは数値計算を意識して「近似と誤差の評価」という観点から出発したいと思います。
多項式近似
計算機は非常に単純な計算しか行えないので,様々な関数\(f(x)\)を和・積のみで計算出来る\(n\)次多項式で
の様に近似する一般的な方法があると大変嬉しいです。
例えば,\(x = 0\)の近くでは \[ \cos x \approx 1 - \frac{x^2}{2} \] という二次式での近似が出来ます。こういった式を得る一般的な方法,誤差を評価する方法を考えたいのです。
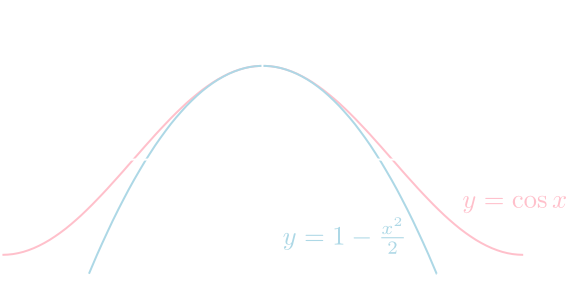
>>> from math import cos
>>> for i in range(10):
... x = i*0.1
... print "cos({0})={1:.5f}, 1-({0})^2/2={2:.5f}"\
... .format(x, cos(x), 1-x*x/2)
...
cos(0.0)=1.00000, 1-(0.0)^2/2=1.00000
cos(0.1)=0.99500, 1-(0.1)^2/2=0.99500
cos(0.2)=0.98007, 1-(0.2)^2/2=0.98000
cos(0.3)=0.95534, 1-(0.3)^2/2=0.95500
cos(0.4)=0.92106, 1-(0.4)^2/2=0.92000
cos(0.5)=0.87758, 1-(0.5)^2/2=0.87500
cos(0.6)=0.82534, 1-(0.6)^2/2=0.82000
cos(0.7)=0.76484, 1-(0.7)^2/2=0.75500
cos(0.8)=0.69671, 1-(0.8)^2/2=0.68000
cos(0.9)=0.62161, 1-(0.9)^2/2=0.59500
\(x = 0\)以外を中心とした場合も考えたいので,\(x = a\)を中心として \[ \color{yellow}{f(x)\approx \alpha_0 + \alpha_1(x-a)+\alpha_2(x-a)^2+\cdots+\alpha_n(x-a)^n}\cdots(1)\] という近似を考えます。\(f(x)\)は\(x=a\)で\(n\)回微分可能であるとします。
まず,\(x = a\)で(1)の両辺が一致するように\( \alpha_0 = f(a) \)と定めます。
次に(1)の両辺を微分すると \[ f'(x) \ \text{と}\ \alpha_1 + 2\alpha_2(x-a)+\cdots+n\alpha_n(x-a)^{n-1}\] となるので,\(x=a\)での微分係数も一致するように\( \alpha_1 = f'(a) \)と定めます。
もう一度微分すると \[ f''(x)\ \text{と}\ 2\alpha_2 + 6\alpha_3(x-a)+\cdots+n(n-1)\alpha_n(x-a)^{n-2}\] となるので,\(x=a\)での二階微分係数も一致するように\( \alpha_2 = \frac{f''(a)}{2}\)と定めます。
このように\(x = a\)での各微分係数が一致するように係数を決めていった多項式が良い\(n\)次近似多項式となるのではないかと予想できます。
但し,ここまでは誤差がどの程度出るか判らないので使い物になりません。
誤差の項も他の項と同じく「\((x-a)^{n+1}\)の~倍」という形をしていると便利でしょう。そこで \[ \begin{aligned} f(x) = & f(a) +f'(a)(x-a) + \frac{f''(a)}{2}(x-a)^2 + \\ &\cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \color{yellow}{r\times(x-a)^{n+1}} \cdots (2) \end{aligned} \] が成立するように\(r\)を定めます。
ここで,天下り的ですが\(x\)を固定して \[ \begin{aligned} F(h) = &f(h)+f'(h)(x-h)+\frac{f''(h)}{2}(x-h)^2 + \\ &\cdots + \frac{f^{(n)}(h)}{n!}(x-h)^n + r(x-h)^{n+1}-f(x) \end{aligned} \] という\(h\)の関数を考えます。複雑な関数に見えますが(2)より \[ \color{yellow}{F(a) = F(x) = 0} \] が成り立ちます。
従ってロルの定理より,\(x \neq a\)かつ「\(F\)が\(a,x\)を含む区間で\(F(h)\)が連続・微分可能\(\cdots (3)\)」ならば,ある\(a < c < x\text{または}x < c < a\)が存在して \[ \color{yellow}{F'(c) = 0} \] が成立します。
\(F(h)\)の定義より,(3)は「\(f\)が\(a,x\)を含む区間で\(n+1\)回微分可能かつ,\(n+1\)階導関数が連続」と言い換えられます。
最後に
より
となるので, \[ F'(c) = 0\ \Leftrightarrow\ \color{yellow}{r = \frac{f^{(n+1)}(c)}{(n+1)!}} \] が得られます。
テイラーの定理
\(a\neq x\)の時,\(f\)が\(a,x\)を含む区間で\(n+1\)回微分可能で\(f^{(n+1)}\)が連続ならば,ある\(c\)が\(a\)と\(x\)の間(\(a < c < x\ \text{または}\ x < c < a\))に存在して \[ \begin{aligned} f(x) = &f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\\ &\cdots +\frac{f^{(n)}(a)}{n!}(x-a)^n + \frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1} \end{aligned}\] が成立する。
右辺の剰余項\(\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\)を\(0\)と置いた物を,\(f(x)\)の\(a\)の周りでの\(n\)次近似式という。
テイラーの定理において\(n=0\)と置いた物は平均値の定理と呼ばれます。
例
\(\cos x\)の\(x=0\)の周りでの2次近似式と剰余項を求めて下さい。\(f(x)=\cos x\)とおくと\(f'(x)=-\sin x,\ f''(x)=-\cos x\)なので\(f(0)=1,\ f'(0)=0,\ f''(0)=-1\)。また\(f'''(x)=\sin x\)であるからテイラーの定理より \[ \begin{aligned} \cos x&= 1 + 0\times x + \frac{-1}{2}x^2 + \frac{\sin c}{3!}x^3 \\ &= 1-\frac{x^2}{2}+\frac{\sin c}{6}x^3 \end{aligned} \] を満たす\(c\)が\(0, x\)の間に存在します。
つまり,\(0\)の周りで \[ \cos x \approx 1-\frac{x^2}{2},\quad\text{剰余項:}\frac{\sin c}{6}x^3 \ \text{($c$は$0$と$x$の間に存在)} \]
例続き
今の二次近似の誤差が\(10^{-4}\)未満に収まる\(x\)の範囲を調べて下さい。\(|\sin c| \leq |c| < |x|\)が成立するので\( \left|\frac{\sin c}{6}x^3\right| < \frac{|x|^4}{6} \)と剰余項を評価できます。よって \[ \frac{|x|^4}{6} < 10^{-4}\ \Leftrightarrow\ |x| < 6^{\frac{1}{4}} 10^{-1} = 0.15\cdots \] の範囲であれば十分です。
>>> from math import cos
>>> for i in range(6):
... x = i*0.05
... print "cos({0:.2f})={1:.5f}, 1-({0:.2f})^2/2={2:.5f}, err={3:.5e}"\
... .format(x, cos(x), 1-x*x/2, cos(x)-(1-x*x/2))
...
cos(0.00)=1.00000, 1-(0.00)^2/2=1.00000, err=0.00000e+00
cos(0.05)=0.99875, 1-(0.05)^2/2=0.99875, err=2.60395e-07
cos(0.10)=0.99500, 1-(0.10)^2/2=0.99500, err=4.16528e-06
cos(0.15)=0.98877, 1-(0.15)^2/2=0.98875, err=2.10779e-05
cos(0.20)=0.98007, 1-(0.20)^2/2=0.98000, err=6.65778e-05
cos(0.25)=0.96891, 1-(0.25)^2/2=0.96875, err=1.62422e-04
【練習問題】 \( \exp x \)の\(x=0\)の周りでの\(n\)次近似式を求めて,\(e=\exp 1\)の近似値を求めて下さい。
【解答】 \(f(x)=\exp x\)は何度微分しても\(\exp x\)なので\(f^{(k)}(0)=\exp 0= 1\)。従って\(0\)の周りで \[ \exp x = 1 + x + \frac{x^2}{2}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}+\frac{\exp c}{(n+1)!}x^{n+1} \] と展開出来るので \[ \color{yellow}{e \approx 1 + 1 + \frac{1}{2} + \frac{1}{3!} + \cdots + \frac{1}{n!}},\quad\text{剰余:}\frac{e^c}{(n+1)!} \quad (0 < c < 1)\] となります。
>>> t = 1 # n!の値
>>> e = 1
>>> for k in range(1,10):
... t *= k # k! = k*(k-1)!
... e += 1.0/t
... print "{0}: {1:.15f}".format(k, e)
...
1: 2.000000000000000
2: 2.500000000000000
3: 2.666666666666667
4: 2.708333333333333
5: 2.716666666666666
6: 2.718055555555555
7: 2.718253968253968
8: 2.718278769841270
9: 2.718281525573192
テイラー展開
\(f(x)\)が無限回微分可能であるとする。ある\(r > 0\)に対して\(-r < x-a < r\)の時 \[ \lim_{n\rightarrow \infty}\frac{f^{(n)}(c)}{n!}(x-a)^n = 0\quad\text{($c$は$a$と$x$の間)} \qquad\cdots(1)\] となるならば,この範囲内で \[ f(x) = f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots \] が成立する。これを\(a\)の周りでのテイラー級数といい,これを得る事をテイラー展開という。 (1)が成立するような\(r\)の最大値を収束半径という。
\(0\)の周りでのテイラー級数は特にマクローリン級数と呼ばれます。
主要なマクローリン展開の公式
\(x\)は実数であるとします。
\[ \begin{aligned} \exp x &= \sum_{k=0}^{\infty}\frac{x^k}{k!} = 1 + x + \frac{x^2}{2!} +\frac{x^3}{3!}+\cdots &\text{(収束範囲:全実数)}\\ \ln (1+x) &= \sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}x^k = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots &\text{(収束範囲:$-1 < x < 1$)}\\ (1+x)^{\alpha} &= \sum_{k=0}^{\infty}\binom{\alpha}{k}x^k = 1+ \alpha x + \frac{\alpha(\alpha-1)}{2!}x^2 +\cdots &\text{(収束範囲:$-1 < x < 1$)} \\ \frac{1}{1-x} &= \sum_{k=0}^{\infty}x^k = 1 + x + x^2 + x^3 + \cdots &\text{(収束範囲:$-1 < x < 1$)} \\ \sin x &= \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1} = x - \frac{x^3}{3!} + \frac{x^5}{5!} -\cdots &\text{(収束範囲:全実数)} \\ \cos x &= \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k)!}x^{2k} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots &\text{(収束範囲:全実数)} \end{aligned} \]
\(\sin x\)のテイラー展開の様子
\(\exp x\)のテイラー展開の様子
\(\ln x\)のテイラー展開の様子(収束範囲の様子をよく観察しましょう)
ランダウの\(\mathcal{O}\)記法
\(0\)の周りで\(f(x)\approx g(x)\)と近似したとき,\(x\)が\(0\)に十分近いときの誤差を\(|x|^n\)の適当な定数倍で抑えられるということを \[ f(x) = g(x) + \mathcal{O}(x^n) \] と表します。例えば \[ \cos x = 1 - \frac{x^2}{2} + \mathcal{O}(x^4) \] などと書きます。
関数の変化と微分係数
テイラーの定理を応用する\(f(x)\)の変化の様子と微分係数の関係について様々な事を示す事が出来ます。ここでは増減,凹凸,極大・極小の判定という3つの話題を紹介します。
増減
\(x=a\)を含む区間で\(f(x)\)が微分可能,\(f'(x)\)が連続であるとします。テイラーの定理より\(x\)が\(a\)に十分近いとき \[ f(x) = f(a) + f'(c)(x-a) \] と表せます。
ここで\(f'(a) > 0\)ならば\(x\)と\(a\)が十分近いとき\(f'(c) > 0\)となるので, \[ \begin{aligned} x > a\ \text{ならば}\ f(x) > f(a) \\ x < a\ \text{ならば}\ f(x) < f(a) \end{aligned} \] となります。つまり\(f'(a) > 0\)ならば\(x=a\)の近辺で\(f(x)\)は単調に増加する事が判ります。\(f'(a) < 0\)の場合も同様です。
増減と微分係数
\(x=a\)で\(f(x)\)が微分可能,\(f'(x)\)が連続のとき \[ \begin{aligned} f'(a) > 0\ \text{ならば}\ f(x)\text{は$x=a$の近辺で単調増加} \\ f'(a) < 0\ \text{ならば}\ f(x)\text{は$x=a$の近辺で単調減少} \end{aligned} \]
\(f'(a)\)は接線の傾きなので直感的にも理解出来ると思います。
凹凸
\(x=a\)を含む区間で\(f(x)\)が2回微分可能,\(f''\)が連続であるとします。テイラーの定理より\(x\)が\(a\)に十分近いとき \[ f(x) = f(a) + f'(a)(x-a) + \frac{f''(c)}{2}(x-a)^2 \] と表せます。 従って,\(f''(a) > 0\)ならば\(x\)と\(a\)が十分に近いとき\(f''(c) > 0\)となるので \[ f(x) > f(a) + f'(a)(x-a) \] が成立します。
これは\(x=a\)の近辺で\(y=f(x)\)のグラフが接線\(y=f(a)+f'(a)(x-a)\)よりも上にある事を意味します。
凹凸と微分係数
\(x=a\)で\(f(x)\)が2回微分可能,\(f''(x)\)が連続のとき \[ \begin{aligned} f''(a) > 0\ \text{ならば}\ y=f(x)\text{は$x=a$の近辺で下に凸} \\ f''(a) < 0\ \text{ならば}\ y=f(x)\text{は$x=a$の近辺で上に凸} \end{aligned} \]
極大・極小
\(f(x)\)は\(x=a\)を含む区間で2回微分可能で,\(f(a)\)が極値であるとすると \(x\)が\(a\)に十分近い時,ある\(c\)が\(a\)と\(x\)の間に存在して \[ \begin{aligned} &f(x) = f(a) + f'(a)(x-a) + \frac{f''(c)}{2}(x-a)^2\\ \Leftrightarrow &f(x)-f(a) = \frac{f''(c)}{2}(x-a)^2\qquad(\because f'(a)=0) \end{aligned} \] と表せます。
従って\(f''\)が連続で,\(f''(a) < 0\)だとすると\(x\)が\(a\)に十分近い時 \[ f(x)-f(a) < 0 \ \Leftrightarrow\ f(x) < f(a) \] となるので\(f(a)\)が極大値である事が判ります。極小値についても同様です。
極値の判定
\(f(x)\)を\(x=a\)で2回微分可能で,\(f''\)が連続であるとする。この時 \[ \begin{aligned} &f'(a) = 0,\ f''(a) < 0\ \text{ならば}\ f(a)\text{は極大値}\\ &f'(a) = 0,\ f''(a) > 0\ \text{ならば}\ f(a)\text{は極小値}\\ \end{aligned} \] である。
差分法
関数を変化を考える上で微分係数が重要な役割を果たす事が分かったと思います。
ところで,多くの場合\(f(x)\)の表式は既知ではありませんので, 観測などで得られた離散的な\(x\)における\(f(x)\)の値から微分係数を近似的に調べる必要があります。
前進差分・後進差分
\(f(x+\Delta x)\)を\(x\)の周りでテイラー展開すると \[ f(x+\Delta x) = f(x) + f'(x)\Delta x + \mathcal{O}(\Delta x^2) \] となるので \[ f'(x) = \frac{f(x+\Delta x)-f(x)}{\Delta x} + \mathcal{O}(\Delta x) \] と近似出来ます。これを前進差分と言います。
同様に\(f(x-\Delta x)\)を\(x\)の周りでテイラー展開すると \[ f(x-\Delta x) = f(x) - f'(x)\Delta x + \mathcal{O}(\Delta x^2) \] となるので \[ f'(x) = \frac{f(x)-f(x-\Delta x)}{\Delta x} + \mathcal{O}(\Delta x) \] と近似できます。これを後進差分と言います。
前進差分・後進差分
\[ \begin{aligned} f'(x) &\approx \frac{f(x+\Delta x)-f(x)}{\Delta x} \\ f'(x) &\approx \frac{f(x)-f(x-\Delta x)}{\Delta x} \\ \end{aligned} \] どちらも誤差は(\(f(x)\)が十分滑らかならば)\(\mathcal{O}(\Delta x)\)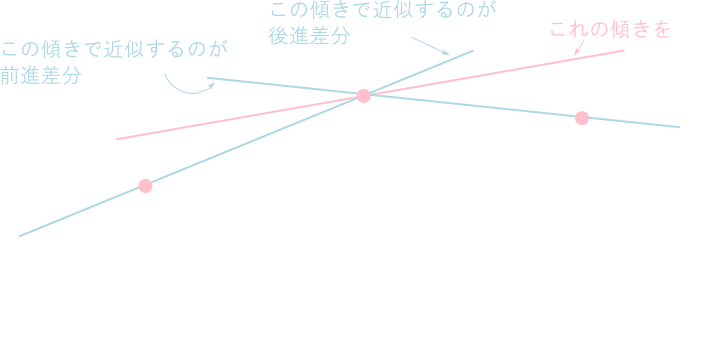
中心差分
\(f(x+\Delta x)\)と\(f(x-\Delta x)\)を\(x\)の周りでテイラー展開すると \[ \begin{aligned} f(x+\Delta x) &= f(x) + f'(x)\Delta x + \frac{f''(x)}{2}\Delta x^2 + \mathcal{O}(\Delta x^3) \\ f(x-\Delta x) &= f(x) - f'(x)\Delta x + \frac{f''(x)}{2}\Delta x^2 + \mathcal{O}(\Delta x^3) \end{aligned} \] となるので2式を引けば \[ f(x+\Delta x)-f(x-\Delta x) = 2f'(x)\Delta x + \mathcal{O}(\Delta x^3) \] すなわち \[ f'(x) = \frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x} + \mathcal{O}(\Delta x^2) \] となります。これを中心差分と言います。
中心差分
\[ f'(x) \approx \frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x} \] 誤差は\(\mathcal{O}(\Delta x^2)\)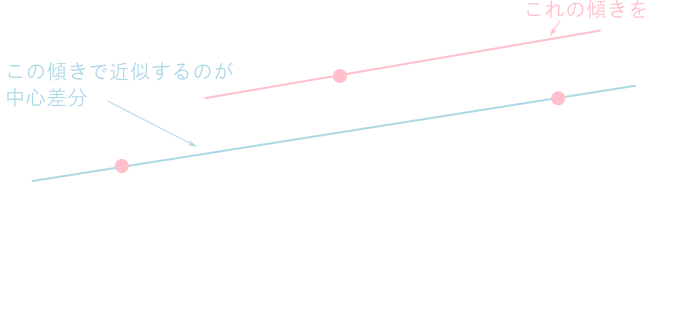
例
\(\exp x\)の\(x=0\)での微分係数(真の値は\(1\))を前進差分・後進差分・中心差分で求めて下さい。>>> from math import exp
>>> for e in range(1,6):
... dx = 10**(-e)
... print "{0:.0e} {1:.15f} {2:.15f} {3:.15f}"\
... .format(dx, (exp(0+dx)-exp(0))/dx, (exp(0)-exp(0-dx))/dx, (exp(0+dx)-exp(0-dx))/(2*dx))
...
1e-01 1.051709180756477 0.951625819640405 1.001667500198441
1e-02 1.005016708416795 0.995016625083189 1.000016666749992
1e-03 1.000500166708385 0.999500166624978 1.000000166666681
1e-04 1.000050001667141 0.999950001666638 1.000000001666890
1e-05 1.000005000006965 0.999995000017240 1.000000000012102
二階差分
\(f(x+\Delta x)\)と\(f(x-\Delta x)\)を\(x\)の周りでテイラー展開すると \[ \begin{aligned} f(x+\Delta x) &= f(x) + f'(x)\Delta x + \frac{f''(x)}{2}\Delta x^2 + \frac{f'''(x)}{6}\Delta x^3 + \mathcal{O}(\Delta x^4) \\ f(x-\Delta x) &= f(x) - f'(x)\Delta x + \frac{f''(x)}{2}\Delta x^2 - \frac{f'''(x)}{6}\Delta x^3 + \mathcal{O}(\Delta x^4) \end{aligned} \] となるので2式を足せば \[ f(x+\Delta x)+f(x-\Delta x) = 2f(x) + f''(x)\Delta x^2 + \mathcal{O}(\Delta x^4) \] すなわち \[ f''(x) = \frac{f(x+\Delta x) - 2f(x) + f(x-\Delta x)}{\Delta x^2} + \mathcal{O}(\Delta x^2) \] となります。これを二階差分と言います。
二階差分
\[ f''(x) \approx \frac{f(x+\Delta x) - 2f(x) + f(x-\Delta x)}{\Delta x^2} \] 誤差は\(\mathcal{O}(\Delta x^2)\)差分法によって求めた微分係数の近似値を利用して,方程式の解や微分方程式の解を数値的に求める事が出来ます。これは次回やります。
多変数関数の微分法
方向微分係数
例として二変数関数\(z = f(x,y)\)について考えます。このグラフは何らかの曲面となります。 一変数関数の場合の微分係数は各点の傾きを表していましたが,多変数関数の場合は下図のように方向によって傾きが変わるという事を考慮しなければいけません。
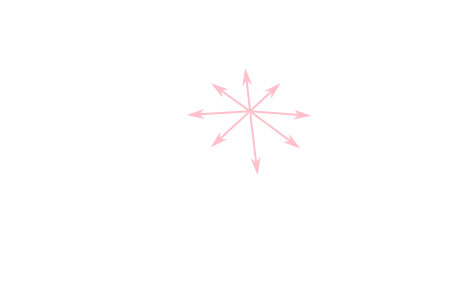
\(xy\)平面上の点\(\mathbf{x} = (a,b)\)からベクトル\(\mathbf{u}=(\alpha,\beta)\)の方向に適当に進んだ点の座標は \[ \mathbf{x} + h\mathbf{u} = (a + h\alpha, b + h\beta) \] と表せます。これを用いて \[ \frac{\partial f}{\partial \mathbf{u}}(a,b) = \lim_{h\rightarrow 0}\frac{f(a+h\alpha, b+h\beta) - f(a,b)}{h} \] と定義される量を\(\mathbf{u}\)に沿った方向微分係数と言います。
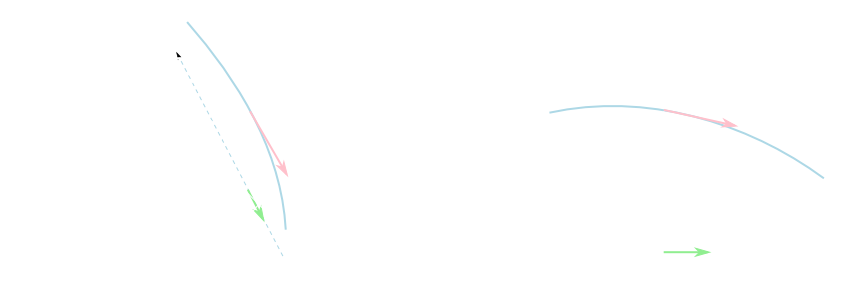
方向微分係数
\[ \frac{\partial f}{\partial \mathbf{u}}(a,b) = \lim_{h\rightarrow 0}\frac{f(a+h\alpha, b+h\beta) - f(a,b)}{h} \] を二変数関数\(f(x,y)\)の点\((a,b)\)におけるベクトル\(\mathbf{u}\)に沿った方向微分係数という。\(||\mathbf{u}||=\sqrt{\alpha^2+\beta^2}=1\)のとき,これは\(\mathbf{u}\)の方向の曲面の傾きを表す。
一般に,\(n\)変数関数\(f(x_1,\cdots,x_n)\)に対して点\(\mathbf{a} = (a_1,\cdots,a_n)\)におけるベクトル\(\mathbf{u} = (u_1,\cdots,u_n)\)に沿った方向微分係数を \[ \begin{aligned} \frac{\partial f}{\partial \mathbf{u}}(\mathbf{a}) &= \lim_{h\rightarrow 0}\frac{f(\mathbf{a}+h\mathbf{u})-f(\mathbf{a})}{h}\\ &=\lim_{h\rightarrow 0}\frac{f(a_1+hu_1,\cdots,a_n+hu_n)-f(a_1,\cdots,a_n)}{h} \end{aligned} \] によって定義する。
例
\(f(x,y)=x^2+y^2\)の点\((1,1)\)における各方向の傾きを求めて下さい。ベクトル\(\mathbf{u}=(\alpha,\beta)\)に沿った方向微分係数は \[ \frac{\partial f}{\partial \mathbf{u}}(1,1)=\lim_{h\rightarrow 0}\frac{(1+h\alpha)^2+(1+h\beta)^2 - (1^2+1^2)}{h} = 2\alpha+2\beta \] となります。特に\(\mathbf{u}=(\cos\theta,\sin\theta)\)とおけば\(||\mathbf{u}||=1\)なので,その方向の傾きは \[ 2\cos\theta + 2\sin\theta = 2\sqrt{2}\sin\left(\theta + \frac{\pi}{4}\right) \] となります。これから例えば\(\mathbf{u}=(\pm\frac{1}{\sqrt{2}},\pm\frac{1}{\sqrt{2}})\)の方向の傾きが最も急で,その傾きは\(\pm2\sqrt{2}\)であるといった事が判ります。
偏微分係数
二変数関数\(f(x,y)\)の\(y\)を固定して\(x\)のみを変数とみなした時の微分係数を\(x\)に関する偏微分係数と言います。 つまり,点\((a,b)\)における\(x\)に関する偏微分係数は \[ \frac{\partial f}{\partial x}(a,b) = \lim_{h\rightarrow 0}\frac{f(a+h, b)-f(a, b)}{h} \] と定義されます。これは\(\mathbf{u}=(1,0)\)に沿った方向微分係数だと考える事もできます。
\(y\)に関する偏微分係数も同様です。
偏微分係数・偏導関数
\[ \frac{\partial f}{\partial x}(a,b) = \lim_{h\rightarrow 0}\frac{f(a+h, b) - f(a,b)}{h} \] を二変数関数\(f(x,y)\)の点\((a,b)\)における\(x\)に関する偏微分係数という。
一般に,\(n\)変数関数\(f(x_1,\cdots,x_n)\)に対して点\(\mathbf{a} = (a_1,\cdots,a_n)\)における\(x_k\)に関する偏微分係数は \[ \frac{\partial f}{\partial x_k}(\mathbf{a})=\lim_{h\rightarrow 0}\frac{f(a_1,\cdots,a_k+h,\cdots,a_n)-f(a_1,\cdots,a_n)}{h} \] によって定義され, \[ \left.\frac{\partial f}{\partial x_k}\right|_{\mathbf{x}=\mathbf{a}},\ \frac{\partial f}{\partial x_k}(\mathbf{a}),\ f_{x_k}(\mathbf{a}) \] などと表記する。
また,点\(\mathbf{x}=\mathbf{a}\)を動かしたものは関数となり,これを偏導関数という。
高階偏導関数
二変数関数\(f(x,y)\)を\(x\)で偏微分して偏導関数 \[ \frac{\partial f}{\partial x} =f_x\] を得た後に,これをさらに\(y\)で偏微分すれば高階の偏導関数 \[ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2 f}{\partial y\partial x} = f_{xy}\] を得る事が出来ます。このようにして高階の偏導関数を定義する事が出来ます。
ここで,微分する変数の順序が異なる \[ \frac{\partial^2 f}{\partial y\partial x} = f_{xy}\ \text{と}\ \frac{\partial^2 f}{\partial x\partial y} = f_{yx}\] は同一なのか?という疑問が生じると思います。
一般にこれらは異なるのですが,\(f_{xy}\)が連続ならば一致するという事を示す事が出来ます。証明は省略します。
関数\(f\)が十分滑らかならば偏導関数は微分する変数の順序に依らないという事を覚えておいて下さい。そして非常に特殊な場合を除き,この仮定は成立しますので,今後は十分滑らかな関数を想定します。偏微分係数と方向微分係数
二変数関数に関して \[ \begin{aligned} \frac{\partial f}{\partial \mathbf{u}}(a,b) &= \lim_{h\rightarrow 0}\frac{f(a+h\alpha, b+h\beta) - f(a,b)}{h} \\ &= \tiny{\lim_{h\rightarrow 0}\left\{\frac{f(a+h\alpha, b+h\beta)-f(a, b+h\beta)}{h\alpha}\alpha + \frac{f(a,b+h\beta)-f(a,b)}{h\beta}\beta\right\}}\\ &= f_x(a,b)\alpha + f_y(a,b)\beta \end{aligned} \] であるので,偏微分係数があれば方向微分係数を求める事が出来ます。
偏微分係数・偏導関数
関数\(f(\mathbf{x})=f(x_1,\cdots,x_n)\)の点\(\mathbf{a}=(a_1,\cdots,a_n)\)におけるベクトル\(\mathbf{u}=(u_1,\cdots,u_n)\)の方向の方向微分係数は \[ \frac{\partial f}{\partial\mathbf{u}}(\mathbf{a}) = f_{x_1}(\mathbf{a})u_1+\cdots + f_{x_n}(\mathbf{a})u_n \] となる。
また,\(||\mathbf{u}||=1\)の時の偏微分係数の大きさ \[ \left|\frac{\partial f}{\partial\mathbf{u}}(\mathbf{a})\right| \] はベクトル\((f_{x_1}(\mathbf{a}),\cdots,f_{x_n}(\mathbf{a}))\)とベクトル\(\mathbf{u}\)が平行のとき最大値 \[ \sqrt{f_{x_1}(\mathbf{a})^2 + \cdots + f_{x_n}(\mathbf{a})^2}\] を取る。
後半の事実はコーシー・シュワルツの不等式により示されます。
【練習問題】
先ほどの\(f(x,y) = x^2 + y^2\)の例を今の定理を利用して解いて下さい。
各偏導関数は\((f_x, f_y) = (2x, 2y)\)となるので,ベクトル\(\mathbf{u}=(\alpha,\beta)\)に沿った方向微分係数は \[ f_x\alpha + f_y\beta = 2\alpha x + 2\beta y \] となります。特に,点\((1,1)\)における微分係数は \[ 2\alpha + 2\beta \] となります。また \[ (f_x(1,1), f_y(1,1)) = (2, 2) \] なので,これと平行な方向の傾きが最大となりその大きさは \[ ||(f_x(1,1), f_y(1,1))|| = \sqrt{2^2+2^2} = 2\sqrt{2} \] となります。
勾配
ベクトル\((f_{x_1}(\mathbf{a}),\cdots,f_{x_n}(\mathbf{a}))\)は非常に重要なベクトルで\(\mathbf{x}=\mathbf{a}\)における勾配と呼ばれ, \[ \mathrm{grad} f(\mathbf{a}) = (f_{x_1}(\mathbf{a}),\cdots,f_{x_n}(\mathbf{a})) \] と表されます。\(\mathrm{grad} f(\mathbf{a})\)は\(\mathbf{x}=\mathbf{a}\)において最も急な方向(増加率最大な方向)を向いており,その長さが傾きの大きさになっています。
応用:勾配法
曲面\(y=f(x_1,\cdots,x_n)\)の最も傾斜の急な方へ下っていくと\(f\)の最小値に辿りつけそうな気がします。つまり今説明した事実より,適当な定数\(\lambda\)を取って \[ \mathbf{x_{k+1}} = \mathbf{x_k} - \lambda \mathrm{grad} f(\mathbf{x_k}) \] の様に位置を更新して行けば最小値を得る事が出来そうです。
これは勾配法(最急降下法)と呼ばれる重要な探索アルゴリズムです。実際には単純なやり方にはいろいろ問題もありますが,基本となるアイデアは理解出来るでしょう。線型代数の回には共役勾配法という同種の解法を紹介します。

例
\(f(x,y)=x^2-4xy+5y^2-2y+2\)の最小値を最急降下法で調べてみます。厳密には\((x,y)=(2,1)\)の時最小値\(1\)を取ります。\[ \mathrm{grad}f = (2x-4y, -4x+10y-2) \] なので \[ (x_{k+1}, y_{k+1}) = (x_k - \lambda(2x_k-4y_k), y_k-\lambda (-4x_k+10y_k-2)) \] と更新していきます。
以下の計算例の様に,工夫しないと収束が遅いです。また\(\lambda\)をちょっと大きくしただけで\(\infty\)に発散してしまいます。よりよい方法は後々やっていきます。
>>>> x = 0
>>> y = 0
>>> l = 0.1
>>> for i in range(100):
... if (i%10 == 0):
... print "step:{0} (x,y)=({1:.5f},{2:.5f}) f(x,y)={3:.5f}"\
... .format(i,x,y,x*x-4*x*y+5*y*y-2*y+2)
... newx = x - l * (2*x-4*y)
... newy = y - l * (-4*x+10*y-2)
... x = newx
... y = newy
...
step:0 (x,y)=(0.00000,0.00000) f(x,y)=2.00000
step:10 (x,y)=(0.54667,0.39801) f(x,y)=1.42457
step:20 (x,y)=(0.97501,0.57543) f(x,y)=1.21118
step:30 (x,y)=(1.27710,0.70057) f(x,y)=1.10504
step:40 (x,y)=(1.49016,0.78882) f(x,y)=1.05225
step:50 (x,y)=(1.64042,0.85106) f(x,y)=1.02599
step:60 (x,y)=(1.74640,0.89496) f(x,y)=1.01293
step:70 (x,y)=(1.82114,0.92592) f(x,y)=1.00643
step:80 (x,y)=(1.87386,0.94775) f(x,y)=1.00320
step:90 (x,y)=(1.91104,0.96315) f(x,y)=1.00159
応用:エッジの検出
簡単にコードが書ける偏微分の応用例として画像のエッジ検出の話題を紹介します。画像は各点\((x,y)\)に色を表す数値が割り当てられているので二変数関数だと思う事が出来ます。勾配を調べれば色が変化が大きく変化している箇所が判るのでエッジが検出できます。検出精度を上げる為にはさらに高階の微分係数を利用する事になります。
このようにデータを解析する際にその特徴がよく分かるように事前に変換を行う事がよくあります。連続的なデータが対象の場合には偏微分法の知識を利用して特徴を調べる事になります。
簡単なコーディングの例です。各ピクセルの値を勾配の大きさに単純に置き換えるだけの例です。 高階微分係数を利用する実装の例も是非調べて見て下さい。
import math
from PIL import Image
im = Image.open("image.jpg") # グレイスケールの画像を渡して下さい
new = Image.new(im.mode, im.size, None)
ipix = im.load()
opix = new.load()
im.show()
for x in xrange(1, im.size[0]-1):
for y in xrange(1, im.size[1]-1):
dx = (ipix[x+1, y] - ipix[x-1, y])/2 # x方向の偏微分係数(中心差分で近似)
dy = (ipix[x, y+1] - ipix[x, y-1])/2 # y方向の偏微分係数(中心差分で近似)
opix[x, y] = math.sqrt(dx**2 + dy**2) # 勾配の大きさ
new.show()

今回はここで終わります。
次回は全微分,多変数関数のテイラー展開などのやり残した定理を確認した後, 線型反復法やニュートン法などの非線形方程式の数値解法, 微分方程式の解析的解法とオイラー法やルンゲクッタ法などの常微分方程式の数値解法の紹介をします。