プログラマの為の
数学勉強会
第4回
(於)ワークスアプリケーションズ中村晃一
2013年10月3日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPythonで記述しています。
多変数関数の微分法(続き)
一変数関数で学んだ事を多変数関数版に拡張していきます。
以降登場する関数は必要なだけ微分可能で導関数が連続であるとし,いちいち断らない事にします。
全微分
前回の話より,一変数関数\(y = f(x)\)において,\(x\)を\(\Delta x\)増加させたときの\(y\)の増加量\(\Delta y = f(x+\Delta x)-f(x)\)は,\(|\Delta x|\)が十分小さいならば \[ \color{yellow}{\Delta y} = f(x+\Delta x)-f(x) = \color{yellow}{f'(x)\Delta x + \mathcal{O}(\Delta x^2)} \] と評価する事が出来ます。
これは適当な定数\(M > 0\)が存在して,\(|\Delta x|\)が十分小さい時に \[ |\Delta y - f'(x)\Delta x| < M\Delta x^2 \] が成立するという意味です。
同様に,二変数関数\(z = f(x,y)\)で \[ \Delta z = f(x+\Delta x, y+\Delta y) - f(x, y) \] を考えます。まず\(x\)について \[ f(x+\Delta x, y+\Delta y) = f(x, y + \Delta y) + \frac{\partial f}{\partial x}(x, y+\Delta y)\Delta x + \mathcal{O}(\Delta x^2) \] と展開する事ができます。
ここで偏導関数は連続であると仮定しているので, \[ \frac{\partial f}{\partial x}(x, y+\Delta y) = \frac{\partial f}{\partial x}(x, y) + \varepsilon \] と表すと,\(\Delta y\rightarrow 0\)のとき\(\varepsilon \rightarrow 0\)となります。
さらに\(f(x, y + \Delta y)\)を\(y\)について展開すると \[ f(x, y + \Delta y) = f(x, y) + \frac{\partial f}{\partial y}(x, y)\Delta y + \mathcal{O}(\Delta y^2) \] となります。
まとめると, \[ \small{f(x+\Delta x, y+\Delta y) = f(x, y) + \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y + \varepsilon \Delta x + \mathcal{O}(\Delta x^2) + \mathcal{O}(\Delta y^2)}\] と書けるので,\(\Delta x^2 \leq \Delta x^2 + \Delta y^2\)などの関係を使って剰余項を見やすく書けば \[ \Delta z = \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y + \mathcal{O}(\Delta x^2 + \Delta y^2) \] と表す事が出来ます。
多変数関数\(f\)の増分\(\Delta f\)をこのように,独立変数の増分\(\Delta x, \Delta y\)を用いて表せる事を\(f\)は全微分可能であると言い, \[ \mathrm{d} z = \frac{\partial f}{\partial x}\mathrm{d} x + \frac{\partial f}{\partial y}\mathrm{d} y \] と書き表します。
全微分
多変数関数\(f(x_1,\cdots,x_n)\)が各変数に関して一回微分可能であるとする。 絶対値の十分小さい\(\Delta x_1,\cdots, \Delta x_n\)に対して \(\Delta f = f(x_1+\Delta x_1, \cdots, x_n + \Delta x_n) - f(x_1,\cdots,x_n) \)を \[ \Delta f = \frac{\partial f}{\partial x_1}\Delta x_1 + \cdots + \frac{\partial f}{\partial x_n}\Delta x_n + \mathcal{O}(\Delta x_1^2 + \cdots + \Delta x_n^2) \] と表す事ができるとき,\(f\)は全微分可能であると言い,この事を \[ \mathrm{d} f = \frac{\partial f}{\partial x_1}\mathrm{d} x_1 + \cdots + \frac{\partial f}{\partial x_n}\mathrm{d} x_n \] と表す。
\(\mathrm{grad}f = \left(\frac{\partial f}{\partial x_1},\cdots,\frac{\partial f}{\partial x_n}\right)\)は曲面の勾配を表していたので直感的にも理解出来ると思います。
例
\( f(x,y) = x\sin y \)という関数の全微分を求めましょう。\(f(x,y)\)は全ての点で無限回微分可能なので全微分出来る事は明らかで \[ \mathrm{d} f = \frac{\partial f}{\partial x}\mathrm{d} x + \frac{\partial f}{\partial y}\mathrm{d} y = (\sin y)\mathrm{d}x + (x\cos y)\mathrm{d} y \] となります。

合成微分法
多変数関数\( f(x_1, \cdots, x_n) \)が全微分可能ならば \[ \Delta f = \frac{\partial f}{\partial x_1}\Delta x_1 + \cdots + \frac{\partial f}{\partial x_n}\Delta x_n + \mathcal{O}(\Delta x_1^2 + \cdots + \Delta x_n^2) \] と表されるので,\(x_1,\cdots,x_n\)がさらに\(t\)の関数ならば \[ \frac{\Delta f}{\Delta t} = \frac{\partial f}{\partial x_1}\frac{\Delta x_1}{\Delta t} + \cdots + \frac{\partial f}{\partial x_n}\frac{\Delta x_n}{\Delta t} + \frac{1}{\Delta t}\mathcal{O}(\Delta x_1^2 + \cdots + \Delta x_n^2) \] となります。\(x_1,\cdots,x_n\)が\(t\)に関して微分可能ならばこの右辺は\(\Delta t\rightarrow 0\)のとき収束するので \[ \color{yellow}{\frac{\mathrm{d}f}{\mathrm{d}t} = \frac{\partial f}{\partial x_1}\frac{\mathrm{d}x_1}{\mathrm{d}t} + \cdots + \frac{\partial f}{\partial x_n}\frac{\mathrm{d}x_n}{\mathrm{d}t}} \] となります。剰余項については \[ \lim_{\Delta t\rightarrow 0}\frac{\Delta x_i^2}{\Delta t} = \lim_{\Delta t\rightarrow 0}\frac{\Delta x_i}{\Delta t}\Delta x_i = \frac{\mathrm{d}x_i}{\mathrm{d} t}\times 0 = 0 \] となる事を利用しています。
合成微分法
多変数関数\( f(x_1, \cdots, x_n) \)に関して\(x_1,\cdots,x_n\)が\(t\)の関数ならば \[ \frac{\mathrm{d}f}{\mathrm{d}t} = \frac{\partial f}{\partial x_1}\frac{\mathrm{d}x_1}{\mathrm{d}t} + \cdots + \frac{\partial f}{\partial x_n}\frac{\mathrm{d}x_n}{\mathrm{d}t} \] となる。
同様に\(x_1,\cdots,x_n\)が\(u_1,\cdots,u_m\)の多変数関数ならば \[ \begin{aligned} \frac{\partial f}{\partial u_1} &= \frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial u_1} + \cdots + \frac{\partial f}{\partial x_n}\frac{\partial x_n}{\partial u_1} \\ &\vdots \\ \frac{\partial f}{\partial u_m} &= \frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial u_m} + \cdots + \frac{\partial f}{\partial x_n}\frac{\partial x_n}{\partial u_m} \\ \end{aligned} \] となる。
例
\(x = \cos \theta, y = \sin \theta\)のときの\(z = x^2+xy+y^2\)の\(\theta\)に対する変化率を求めます。合成微分の公式より \[ \begin{aligned} \frac{\mathrm{d}z}{\mathrm{d}\theta} &= \frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}\theta} + \frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}\theta} = (2x+y)(-\sin\theta) + (x+2y)\cos\theta \\ &= -(2\cos\theta + \sin\theta)\sin\theta + (\cos\theta + 2\sin\theta)\cos \theta = \cos 2\theta \end{aligned} \] となります。
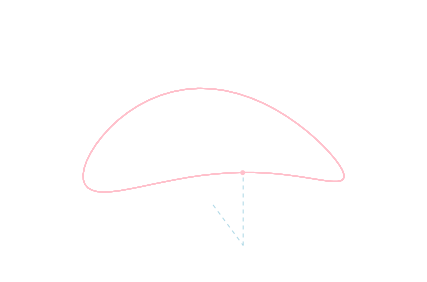
多変数関数のテイラーの定理
前回,関数の変化の様子と微分係数を結びつけるテイラーの定理が重要である事を学びました。これを多変数関数に拡張します。
テイラーの定理
\(a\neq x\)の時,\(f\)が\(a,x\)を含む区間で\(n+1\)回微分可能で\(f^{(n+1)}\)が連続ならば,ある\(c\)が\(a\)と\(x\)の間(\(a < c < x\ \text{または}\ x < c < a\))に存在して \[ \begin{aligned} f(x) = &f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\\ &\cdots +\frac{f^{(n)}(a)}{n!}(x-a)^n + \frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1} \end{aligned}\] が成立する。
二変数関数\(f(x,y)\)の\(\mathbf{a}=(a,b)\)の周りでの展開を考えます。必要なだけ微分可能・連続であるとします。
ポイントはベクトル\(\mathbf{u}=(\alpha,\beta)\)を固定して,\(h\)に関する一変数関数 \[ f(\mathbf{a}+h\mathbf{u})=f(a+\alpha h, b+\beta h) \] のマクローリン展開を考える事です。
合成微分法より \[ \frac{\mathrm{d}}{\mathrm{d}h}f(a+\alpha h, b+\beta h) = \frac{\partial f}{\partial x}\alpha + \frac{\partial f}{\partial y}\beta = \left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)f(a+\alpha h, b+\beta h)\] となります。もう一度微分すると \[ \frac{\mathrm{d}^2}{\mathrm{d}h^2}f(a+\alpha h, b+\beta h) = \left(\alpha^2\frac{\partial^2}{\partial x^2}+2\alpha\beta\frac{\partial^2}{\partial x\partial y}+\beta^2\frac{\partial^2}{\partial y^2}\right)f(a+\alpha h, b+\beta h) \] となり繰り返せば \[ \frac{\mathrm{d}^n}{\mathrm{d}h^n}f(a+\alpha h, b+\beta h) = \left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)^nf(a+\alpha h, b+\beta h)\] と書き表す事が出来ます。
従って,マクローリン展開を行うとある\(c\)が\(0\)と\(h\)の間に存在して \[ \begin{aligned} &f(a+\alpha h, b +\beta h) = f(a,b) + \left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)f(a,b)h \\ &\qquad+ \frac{1}{2!}\left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)^2f(a,b)h^2 + \cdots + \frac{1}{n!}\left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)^nf(a,b)h^n \\ &\qquad+ \frac{1}{(n+1)!}\left(\alpha\frac{\partial}{\partial x}+\beta\frac{\partial}{\partial y}\right)^{n+1}f(a+c\alpha,b+c\beta)h^{n+1} \\ \end{aligned} \] と表せ,\(a+\alpha h = x,\ b+\beta h = y\)と置き直せば \[ \scriptsize{\begin{aligned} f(x, y) &= f(a,b) + \left((x-a)\frac{\partial}{\partial x}+(y-b)\frac{\partial}{\partial y}\right)f(a,b) + \frac{1}{2!}\left((x-a)\frac{\partial}{\partial x}+(y-b)\frac{\partial}{\partial y}\right)^2f(a,b)\\ &\qquad + \cdots + \frac{1}{n!}\left((x-a)\frac{\partial}{\partial x}+(y-b)\frac{\partial}{\partial y}\right)^nf(a,b) \\ &\qquad + \frac{1}{(n+1)!}\left((x-a)\frac{\partial}{\partial x}+(y-b)\frac{\partial}{\partial y}\right)^{n+1}f(c_x,c_y) \\ \end{aligned}} \] となります。但し\(c_x\)は\(a,x\)の間,\(c_y\)は\(b,y\)の間に存在します。
二変数以上の関数も同様で,一般には以下のようになります。
多変数関数版テイラーの定理
\[ \small{\begin{aligned} f(x_1,\cdots,x_m) &= \sum_{k=0}^n\frac{1}{k!}\left((x_1-a_1)\frac{\partial}{\partial x_1} + \cdots + (x_m-a_m)\frac{\partial}{\partial x_m}\right)^kf(a_1,\cdots,a_m) \\ &+ \frac{1}{(n+1)!}\left((x_1-a_1)\frac{\partial}{\partial x_1} + \cdots + (x_m-a_m)\frac{\partial}{\partial x_m}\right)^{n+1}f(c_1,\cdots,c_m) \end{aligned}} \] 但し\(c_i\)は\(a_i\)と\(x_i\)の間に存在する。
例
\( f(x,y) = \sin(x+y) \)の点\(\left(\frac{\pi}{4},\frac{\pi}{4}\right)\)の周りでの2次の近似式を求めてみます。\[ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = \cos(x+y),\ \frac{\partial^2 f}{\partial x^2} = \frac{\partial^2 f}{\partial y^2} = \frac{\partial^2 f}{\partial x\partial y} = -\sin(x+y) \] なので,公式を用いれば \[ f(x,y) \approx 1 - \frac{1}{2}(x-\frac{\pi}{4})^2 - (x-\frac{\pi}{4})(y-\frac{\pi}{4}) - \frac{1}{2}(y-\frac{\pi}{4})^2 \] を得ます。
多変数関数の極値
多変数関数\(f(x_1,\cdots,x_n)\)においても局所的に見た時の最大値・最小値を極値と言います。つまり,十分\(|h_1|,\cdots,|h_n|\)が小さい時に \[ f(a_1+h_1,\cdots,a_n+h_n) \leq f(a_1,\cdots,a_n) \] が常に成り立つならば\(f(a_1,\cdots,a_n)\)を極大値と呼びます。極小値も同様です。
すると,一変数関数のときの議論と全く同様にして \[ \frac{\partial f}{\partial x_1}(a_1,\cdots,a_n) = \cdots = \frac{\partial f}{\partial x_n}(a_1,\cdots,a_n) = 0 \] である事が必要となります。
極値と偏微分係数の関係
\( f(a_1,\cdots,a_n) \)が極値ならば \[ \frac{\partial f}{\partial x_1}(a_1,\cdots,a_n)=\cdots = \frac{\partial f}{\partial x_n}(a_1,\cdots,a_n)=\cdots = 0 \] である。これは\(f(\mathbf{a})\)が極値ならば\(\mathrm{grad}f(\mathbf{a}) = \mathbf{0}\)ということなので,直感的には極値を取る点において曲面が水平になる事だと言えます。

一変数関数では\(f''(a)\)の正負によって\(f(a)\)が極大値・極小値のいずれであるかを調べる事が出来ましたが,多変数関数で同様の判定を行う為には線型代数の知識(行列式と二次形式)が必要となります。そこでこの話題は後に回します。
例:最小二乗法
データ列\((x_1,y_1),\cdots,(x_n,y_n)\)に対して,\(y=ax+b\)という直線モデルを当てはめる事を考えます。そこで残差平方和 \[ E = \sum_i (ax_i+b - y_i)^2 \] が極値を取る為の\(a,b\)を求めてみます。
\[ \frac{\partial E}{\partial a} = \frac{\partial E}{\partial b} = 0 \] であれば良いので,計算すると \[ \begin{aligned} \frac{\partial E}{\partial a} &= \sum_i 2x_i(ax_i+b-y_i) = 2(\sum_i x_i^2)a + 2(\sum_i x_i)b - 2\sum_i x_iy_i = 0\\ \frac{\partial E}{\partial b} &= \sum_i 2(ax_i+b-y_i) = 2(\sum_i x_i)a + 2nb - 2\sum_iy_i = 0 \end{aligned} \] という方程式を得ます。これを解くと \[ \color{yellow}{a = \frac{n\sum_i x_iy_i-\sum_i x_i\sum_i y_i}{n(\sum_i x_i^2)-(\sum_i x_i)^2},\ b = \frac{(\sum_i x_i^2)\sum_i y_i - \sum_i x_i\sum_i x_iy_i}{n(\sum_i x_i^2)-(\sum_i x_i)^2}} \] となります。これが実際に極値を与える事,さらにそれが最小値である事に関しては後の回に扱います。
例続き
データ列\((x_1,y_1),\cdots,(x_n,y_n)\)に対して,直線モデル\(y=ax+b\)を当てはめた時の\(a,b\)を最小二乗法で求めるプログラムを書いて下さい。
先ほどの公式に従って計算するだけです。
import csv
reader = csv.reader(open("data.csv", "rb"), delimiter=",")
sumx = 0 # sum x
sumy = 0 # sum y
sumx2 = 0 # sum x^2
sumxy = 0 # sum xy
n = 0 # number of the data
for x,y in reader:
x = float(x)
y = float(y)
sumx += x
sumy += y
sumx2 += x*x
sumxy += x*y
n += 1
a = (n*sumxy-sumx*sumy)/(n*sumx2-sumx*sumx)
b = (sumx2*sumy-sumx*sumxy)/(n*sumx2-sumx*sumx)
print "y={0:.5f}x + {1:.5f}".format(a, b)
適当に生成したサンプルデータdata1.csvに先ほどにプログラムを使用した例が以下の様になります。
直線モデルは簡単でしたが,例えば多項式モデル \[y=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x_1+a_0\] での当てはめを行いたい場合はどうなるでしょうか?
この場合も同様に計算すると\(k = 0,1,\cdots,n\)に対して \[ (\sum_i x_i^kx_i^n)a_n + \cdots + (\sum_i x_i^k)a_0 = \sum_i x_i^ky_i \] という\(n+1\)元連立一次方程式を解く問題に帰着します。この計算にも線型代数が必要になりますので後に紹介します。
また,最小二乗法の背景知識や結果の評価などは統計の回にやります。
方程式の数値解法
方程式の数値解法
方程式\( x^2 = 2 \)を\(x = \pm \sqrt{2}\)と厳密に解くことに対して,\(x \approx 1.41421356\)のような数値を近似的に求める事を方程式を数値的に解くと言います。
微分法を応用して,方程式 \[ f(x) = 0\] や \[ f(x_1,\cdots,x_n) = 0\] を数値的に解く手法をいくつか紹介します。
線型反復法
最初に \[ \color{yellow}{f(x)=x} \] という形の方程式を考えます。
真の解\(\alpha\)を中心にテイラーの定理を用いると,ある\(c\)が\(x,\alpha\)の間に存在して \[ f(x) - f(\alpha) = f'(c)(x-\alpha) \] と表されます。ここで\(f(\alpha) = \alpha\)だから \[ |f(x)-\alpha| = |f'(c)||x-\alpha| \] となります。
ここで\(f'(c) < 1\)を満たすならば \[ |f(x)-\alpha| < |x-\alpha| \] となるので\(f(x)\)は\(x\)より真の解\(\alpha\)に近づくという事になります。
線型反復法
方程式\( f(x) = x \)の解の一つを\(\alpha\)とする。
\(x=\alpha\)を含む適当な区間で常に\( |f'(x)| \leq r < 1 \)となるような定数\(r\)が存在するならば,この区間内に初期値\(x_0\)を取ると数列 \[ x_{n+1} = f(x_n) \] は\(\alpha\)に収束する。
これは\(y=f(x)\)と\(y=x\)の交点を求める事に相当します。下図の様に交点付近での\(f'(x)\)の値が\(\alpha\)に近づくか否かに影響します。
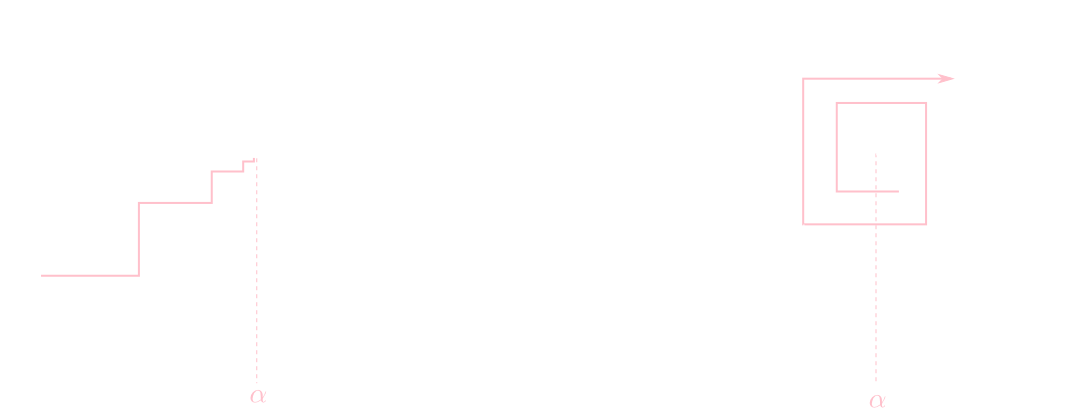
例
\(\sqrt{x} = x\)に線型反復法を使用する事を考えてみます。\( \sqrt{x}=x \)の解は0と1ですが,\((\sqrt{x})'=\frac{1}{2\sqrt{x}}\)なので \[ \left|\frac{1}{2\sqrt{x}}\right| < 1\ \Leftrightarrow\ x > \frac{1}{4} \cdots(1)\] の成立が必要です。\(x=1\)は(1)の範囲にあるので,この範囲内に\(x_0\)を取れば\(1\)に収束します。しかし\(x=0\)は(1)を満たさないので,線型反復法で求める事は出来ません。
>>> from math import sqrt
>>> x = 1.5
>>> x = sqrt(x); x
1.224744871391589
>>> x = sqrt(x); x
1.1066819197003215
>>> x = sqrt(x); x
1.0519895055086441
>>> x = sqrt(x); x
1.0256653964664324
>>> x = sqrt(x); x
1.012751399143162
>>> x = sqrt(x); x
1.0063555033601008
>>> x = sqrt(x); x
1.0031727186083665
>>> x = sqrt(x); x
1.001585103028378
>>> x = sqrt(x); x
1.0007922376939071
>>> x = sqrt(x); x
1.0003960404229453
>>> x = sqrt(x); x
1.000198000609352
>>> x = sqrt(x); x
1.0000989954046309
>>> x = sqrt(x); x
1.0000494964773647
>>> x = sqrt(x); x
1.0000247479324522
>>> x = sqrt(x); x
1.0000123738896696
>>> x = sqrt(x); x
1.0000061869256958
>>> x = sqrt(x); x
1.000003093458063
>>> x = sqrt(x); x
1.0000015467278354
>>> x = sqrt(x); x
1.0000007733636187
>>> x = sqrt(x); x
1.0000003866817346
>>> x = sqrt(x); x
1.0000001933408487
線型反復法の収束の速さ
第\(n\)ステップでの誤差を \[ |x_n - \alpha| = \varepsilon_n \] と置くと\(\alpha\)と\(x_n\)が近いとき \[ \frac{\varepsilon_{n+1}}{\varepsilon_n} = \left|\frac{f(x_n)-f(\alpha)}{x_n-\alpha}\right| \approx |f'(\alpha)| \] となります。つまり,線型反復法の第\(n\)ステップ目での誤差は \[ \varepsilon_n \approx \varepsilon_0|f'(\alpha)|^n \] 程度となります。つまり\(|f'(\alpha)|\)が小さいほど速く収束し, 約\(- 1/\log_{10}|f'(\alpha)|\)ステップで精度が一桁良くなるという事が判ります。
例
\( \cos x = x \)の解を線型反復法で求めましょう。\(y=\cos x\)と\(y=x\)のグラフを書いてみると\(x = 0.7\)の近くに解がありそうです。この近辺で\(|(\cos x)'| = |\sin x|\)を1未満の定数で押さえられるのも明らかです。
以下が計算例です。\( \log_{10}|(\cos x)'|_{x=0.7} = \log_{10}|\sin 0.7| \approx -0.2 \)なので,約5ステップで一桁精度が改善しているはずです。
>>> from math import cos
>>> x = 0.7 # x(n)
>>> xm1 = 0 # x(n-1)
>>> for i in range(1, 60):
... if abs(x-xm1)<1e-10:
... break
... x, xm1 = cos(x), x
... print "step:{0} x={1}".format(i, x)
...
step:1 x=0.764842187284
step:2 x=0.721491639598
step:3 x=0.750821328839
step:4 x=0.731128772573
step:5 x=0.744421183627
step:6 x=0.735480200406
step:7 x=0.74150865166
step:8 x=0.73745045315
step:9 x=0.740185285397
step:10 x=0.738343610351
step:11 x=0.739584428695
step:12 x=0.738748709662
step:13 x=0.739311710338
step:14 x=0.73893248917
step:15 x=0.73918794747
step:16 x=0.73901587239
step:17 x=0.739131786367
step:18 x=0.739053706287
step:19 x=0.739106302407
step:20 x=0.739070873227
step:21 x=0.73909473884
step:22 x=0.739078662717
step:23 x=0.739089491805
step:24 x=0.73908219721
step:25 x=0.739087110941
step:26 x=0.739083800994
step:27 x=0.739086030615
step:28 x=0.739084528716
step:29 x=0.739085540413
step:30 x=0.739084858922
step:31 x=0.739085317983
step:32 x=0.739085008754
step:33 x=0.739085217054
step:34 x=0.73908507674
step:35 x=0.739085171257
step:36 x=0.73908510759
step:37 x=0.739085150477
step:38 x=0.739085121587
step:39 x=0.739085141048
step:40 x=0.739085127939
step:41 x=0.739085136769
step:42 x=0.739085130821
step:43 x=0.739085134828
step:44 x=0.739085132129
step:45 x=0.739085133947
step:46 x=0.739085132722
step:47 x=0.739085133547
step:48 x=0.739085132991
step:49 x=0.739085133366
step:50 x=0.739085133114
step:51 x=0.739085133284
step:52 x=0.739085133169
step:53 x=0.739085133246
【練習問題】
\(\sqrt{2}\)の値を線型反復法を利用して求めて下さい。
【解答】
方程式\( x^2-2=0 \)を解くことにします。\(f(x)=x\)という形で,\(x=\sqrt{2}\)の近辺で\(|f'(x)|\leq r < 1 \)と押さえなければいけない事に注意して下さい。例えば
\[ k(x^2-2) + x = x\]
という形を考えると\(f'(x) = 2kx + 1\)なので,\(k = -\frac{1}{3}\)などと取れば十分です。
他にも\(x = \frac{x}{2}+\frac{1}{x}\)といった変形などいろいろ試してみてください。
>>> x = 1.5
>>> xm1 = 0
>>> for i in range(1, 10):
... if abs(x-xm1)<1e-10:
... break
... x, xm1 = -(x*x-2)/3+x, x
... print "step:{0} x={1}".format(i, x)
...
step:1 x=1.41666666667
step:2 x=1.41435185185
step:3 x=1.41422146491
step:4 x=1.41421401431
step:5 x=1.41421358822
step:6 x=1.41421356385
step:7 x=1.41421356246
step:8 x=1.41421356238
加速法
収束速度を改善する手法を加速法と呼びます。様々な手法が存在しますがここではエイトケンの\(\Delta^2\)法を紹介します。
線型反復法の2ステップ分を\(x=\alpha\)の周りの一次近似で表すと \[ \begin{aligned} x_{i+1}-\alpha &\approx f'(\alpha)(x_i-\alpha) \\ x_{i+2}-\alpha &\approx f'(\alpha)(x_{i+1}-\alpha) \\ \end{aligned} \] となります。これらから\(f'(\alpha)\)を消去して\(\alpha\)について解くと \[ \alpha \approx \color{yellow}{x_i-\frac{(x_{i+1}-x_i)^2}{x_{i+2}-2x_{i+1}+x_i}} \] と\(\alpha\)の近似値に一気に近づける事が出来ます。線型反復法の3\(n\)ステップ目にこの近似式を用いれば,収束を加速する事が出来ます。
例
\( \cos x = x \)の解をエイトケンの\(\Delta^2\)法で求めましょう。>>> from math import cos
>>> x = 0.7 # x(n)
>>> xm1 = 0; xm2 = 0 # x(n-1) and x(n-2)
>>> for i in range(1, 30):
... if abs(x-xm1)<1e-10:
... break
... if i%3 == 0:
... x, xm1, xm2 = xm2 - (xm1-xm2)*(xm1-xm2)/(x-2*xm1+xm2), x, xm1
... else:
... x, xm1, xm2 = cos(x), x, xm1
... print "step:{0} x={1}".format(i, x)
...
step:1 x=0.764842187284
step:2 x=0.721491639598
step:3 x=0.738861290021
step:4 x=0.739235898166
step:5 x=0.738983567731
step:6 x=0.739085125763
step:7 x=0.739085138235
step:8 x=0.739085129834
step:9 x=0.739085133215
step:10 x=0.739085133215
ニュートン法
次は\(\color{yellow}{f(x)=0}\)の解\(\alpha\)を求める問題を考えます。ここで \[ g(x) = x - \frac{f(x)}{f'(x)} \] と置くと\(g(\alpha) = \alpha\),また \[ g'(x) = 1 - \frac{\{f'(x)\}^2-f(x)f''(x)}{\{f'(x)\}^2} = \frac{f(x)f''(x)}{\{f'(x)\}^2} \] なので\(\color{yellow}{g'(\alpha)=0}\)となります。
線型反復法の収束速度は\(|g'(\alpha)|\)が小さいほど速いので,ニュートン法は非常に速く収束する事が期待できます。また,\(g'\)が連続ならば必ず\(x=\alpha\)の近辺で\(|g'(x)|\leq r < 1\)と押さえる事が出来ます。
ニュートン法
方程式\(f(x)=0\)の解を\(\alpha\)とする。
\(x=\alpha\)を含む適当な区間で\(f'(x)\neq 0\),\(f(x),f'(x),f''(x)\)が連続ならば,この区間内に初期値\(x_0\)を取れば数列 \[ x_{n+1} = x_{n} - \frac{f(x_n)}{f'(x_{n})} \] が\(\alpha\)に収束する。
図示的には,下図の様に\(x=x_{i}\)の点で引いた接線と\(x\)軸の交点の値を\(x_{i+1}\)とする更新式になっています。
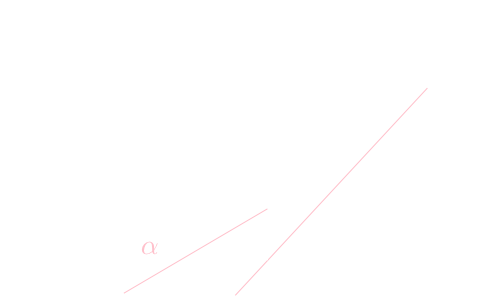
例
\( \cos x = x \)の解をニュートン法で求めましょう。\(f(x)=x-\cos x\)とおけば\(f'(x)=1+\sin x\)なので \[ x_{n+1}=x_n-\frac{x_n-\cos x_n}{1+\sin x_n}\] という更新式を使います。
>>> from math import sin, cos
>>> x = 0.7 # x(n)
>>> xm1 = 0 # x(n-1)
>>> for i in range(1, 60):
... if abs(x-xm1)<1e-10:
... break
... x, xm1 = x - (x-cos(x))/(1+sin(x)), x
... print "step:{0} x={1}".format(i, x)
...
step:1 x=0.739436497848
step:2 x=0.739085160465
step:3 x=0.739085133215
step:4 x=0.739085133215
ニュートン法の収束の速さ
\[ g(x) = x - \frac{f(x)}{f'(x)} \] と置くと\(g(\alpha) = \alpha, g'(\alpha) = 0\)だったので \(g(x)\)を\(x=\alpha\)の周りで展開すると,ある\(c\)が存在して \[ g(x) = \alpha + \frac{g''(c)}{2}(x-\alpha)^2 \] つまり \[ |g(x)-\alpha| = \left|\frac{g''(c)}{2}\right||x-\alpha|^2 \] と表せます。従って,数列\(x_{n+1}=g(x_n)\)の\(\alpha\)からの誤差は\(|x_n-\alpha|^2\)にほぼ比例して減少していきます。
このような収束の仕方を二次収束と言います。
次は多変数の方程式へと進みたい所ですが,線型代数の知識がやはり必要となります。ニュートン法の問題点なども含め、より実戦的な話題は線型代数の回に再び取り上げます。
今回はここで終わります。
今回は時間が足りず微分方程式の数値解法を扱う事ができませんでした。 次回は常微分方程式・偏微分方程式の数値解法と積分法・重積分法・数値積分法を扱います。