パターン認識・
機械学習勉強会
第13回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

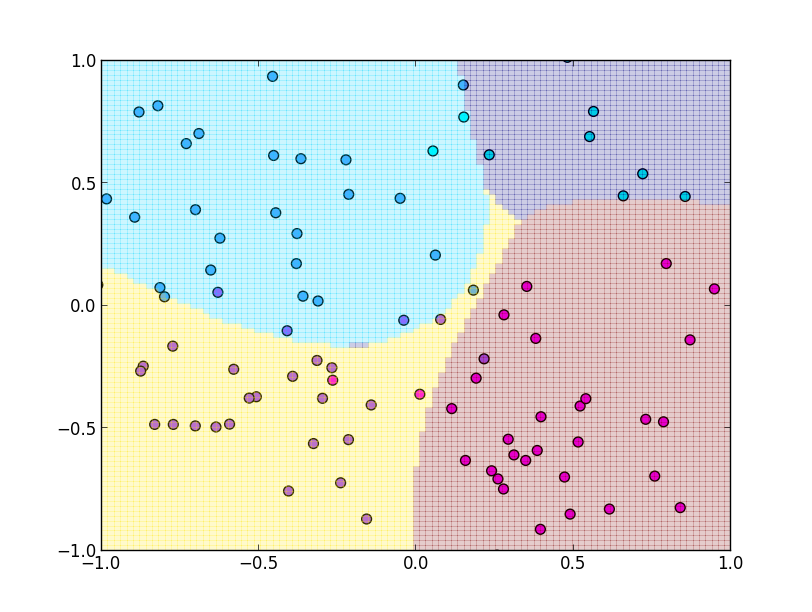
多クラスSVM

SVMは2クラス識別の為の分類器ですが, これを複数組み合わせるなどの方法によって$K$ クラス $(K > 2)$の識別に利用する事が出来ます. 簡単に説明します.

one-versus-the-rest法

one-versus-the-rest法では, データ$\mathbf{x}$ がクラス $k$ かそれ以外であるかを識別するSVM $f_k(\mathbf{x})$ を $K$ クラスそれぞれについて構築し, \[ f(\mathbf{x}) = \mathop{\rm arg~max}\limits_{k}f_k(\mathbf{x}) \] によって $\mathbf{x}$ のクラスを決定します.

実装例です. ガウスカーネルを利用しています.

prog13-1.py

今説明したone-versus-the-rest法にはいくつか問題点があります. 例えば, 1対他という形で学習を行うのでデータ数に大きく差が出てしまうという問題です.

テキストには1対1のSVMを $K(K-1)/2$ 個組み合わせる方法など他のアプローチも紹介されています. ここでは詳しくはやりません.

SVM回帰

続いて, 回帰分析の為のSVMを紹介します.

通常は観測値 $t_i$ とモデルによる予測値 $y_i$ の誤差の平方 \[ |y_i-t_i|^2 \] を用いて最小二乗法などの立式を用いますが, 今回は $\epsilon$-insensitive誤差関数 \[ E_{\epsilon}(y_i-t_i)=\left\{\begin{array}{cl} 0 & (|y_i-t_i|<\epsilon\text{の時}) \\ |y_i-t_i|-\epsilon & (\text{それ以外}) \end{array}\right.\] を用います. $\epsilon$ 以下の誤差を $0$ に丸める事によってスパース性を実現する事が目標です.

この誤差関数の様子を図示すると下のようになります.

$\epsilon$-insensitive誤差関数を用いて, 学習データに対する正則化項付きの誤差関数を \[ E(\mathbf{w}) = C\sum_{i=1}^n E_{\epsilon}(y_i-t_i)+\frac{1}{2}||\mathbf{w}||^2 \] と表します. $C > 0$は通常正則化項に付ける係数$\lambda$ の逆数です. これを最小化する様な $\mathbf{w}$ を求める事が目標になります.

続いて, 各データポイントについて2つのスラック変数 $\xi_i$ と $\hat{\xi_i}$ を導入して, \[ \begin{aligned} \xi_i &= \mathop{\rm max}\{t_i-y_i-\epsilon, 0\} \\ \hat{\xi_i} &= \mathop{\rm max}\{-t_i+y_i-\epsilon, 0\} \\ \end{aligned} \] とおきます.

$t_i \geq y_i+\epsilon$ の時は \[ \xi_i = t_i-y_i-\epsilon, \quad \hat{\xi_i} = 0 \] $t_i \leq y_i-\epsilon$ の時は \[ \xi_i = 0,\quad \hat{\xi_i} = -(t_i-y_i)-\epsilon \] $y_i-\epsilon \leq t_i \leq y_i+\epsilon$ の時は \[ \xi_i = 0, \hat{\xi_i} = 0\] となります.

つまり, 距離$\epsilon$より上に外れた時の誤差が $\xi_i$ であり, 下に外れた時の誤差が $\hat{\xi_i}$ となります.

また, \[ E_{\epsilon}(y_i-t_i) = \xi_i + \hat{\xi_i} \] となります.

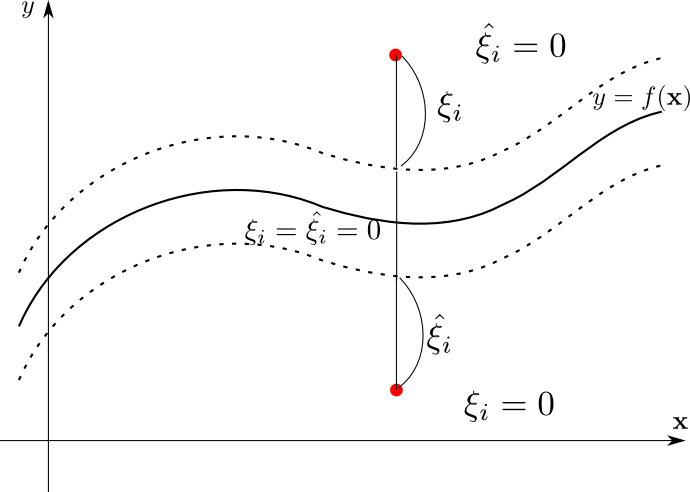
従って, 先ほどの問題は以下のように書きなおす事が出来ます.

前回と同様に, これを双対問題に書き直します. 不等式制約が4つあるのでそれぞれについて変数 $\mu_i,\hat{\mu_i},a_i,\hat{a_i}\geq 0$ を導入して \[ \begin{aligned} \tilde{L}&=C\sum_i(\xi_i+\hat{\xi_i})+\frac{1}{2}||\mathbf{w}||^2-\sum_i\mu_i\xi_i-\sum_i\hat{\mu_i}\hat{\xi_i}\\ &-\sum_ia_i(\xi_i-t_i+y_i+\epsilon)-\sum_i\hat{a_i}(\hat{\xi_i}+t_i-y_i+\epsilon) \end{aligned}\] とおき, これを $\mathbf{w},\theta,\xi_i,\hat{\xi_i}$ に関して最小化した後に $\mu_i,\hat{\mu_i},a_i,\hat{a_i}$ について最大化します.

実際に計算すると, 以下の双対問題を得ます(次頁).

【導出の方針】
$y_i = \mathbf{w}^T\Psi(\mathbf{x}_i) + \theta$ より $\partial y_i/\partial\mathbf{w}=\Psi(\mathbf{x}_i), \partial y_i/\partial\theta = 1$ なので \[ \begin{aligned} \frac{\partial \tilde{L}}{\partial\mathbf{w}}&= \mathbf{w}-\sum_i(a_i-\hat{a_i})\Psi(\mathbf{x}_i) \\ \frac{\partial \tilde{L}}{\partial\theta} &= - \sum_i(a_i-\hat{a_i})\\ \frac{\partial \tilde{L}}{\partial\xi_i} &= C-\mu_i-a_i \\ \frac{\partial \tilde{L}}{\partial\hat{\xi_i}} &= C-\hat{\mu_i}-\hat{a_i} \\ \end{aligned} \] よって,$\tilde{L}$ が $\mathbf{w},\theta$ に関して最小となる点では \[ \mathbf{w} = \sum_i(a_i-\hat{a_i})\Psi(\mathbf{x}_i),\quad \sum_i(a_i-\hat{a_i})=0,\quad a_i+\mu_i=\hat{a_i}+\hat{\mu_i}=C \] が成り立つ. これを $\tilde{L}$ に代入する.

回帰方程式は \[ y = \mathbf{w}^T\Psi(\mathbf{x}) + \theta \] に $\mathbf{w} = \sum_i(a_i-\hat{a_i})\Psi(\mathbf{x}_i)$ を代入して \[ y = \sum_i (a_i-\hat{a_i})k(\mathbf{x}_i,\mathbf{x}) + \theta \] となります.

従って, 回帰方程式の構築には $a_i-\hat{a_i}\neq 0$ であるサポートベクター $\Psi(\mathbf{x}_i)$ のみがあれば良いという事になります.

KKT条件は先ほどの不等式制約に以下を加えたものです. \[ \begin{aligned} &a_i(\xi_i - t_i+y_i+\epsilon) = 0\\ &\hat{a_i}(\hat{\xi_i} + t_i-y_i+\epsilon) = 0\\ &\mu_i\xi=(C-a_i)\xi_i = 0 \\ &\hat{\mu_i}\hat{\xi_i}=(C-\hat{a_i})\hat{\xi_i} = 0 \end{aligned} \]

$y_i-\epsilon < t_i < y_i + \epsilon$ の場合には $\xi_i+t_i-y_i+\epsilon,\hat{\xi_i}-t_i+y_i+\epsilon > 0$ となるので, $a_i=\hat{a_i} = 0$ となります. つまり, $y=f(\mathbf{x})$ から距離 $\epsilon$ 以内の点はサポートベクターではないことが分かります.

$\theta$ の計算ですが, $0 < a_i < C$ ならば $\xi_i = 0$ となるため \[ - t_i + y_i + \epsilon = -t_i + (\mathbf{w}^T\Psi(\mathbf{x}_i)+\theta)+\epsilon = 0 \] つまり \[ \theta = t_i -\epsilon - \mathbf{w}^T\Psi(\mathbf{x}_i) = t_i-\epsilon - \sum_j (a_j-\hat{a_j})k(\mathbf{x}_i,\mathbf{x}_j) \] となります.

同様に $0 < \hat{a_i} < C$ ならば \[ \theta = t_i + \epsilon - \sum_j(a_j-\hat{a_j})k(\mathbf{x}_i,\mathbf{x}_j) \] となります. 前回同様 これら $\theta$ の平均値を取って $\theta$ を求めます.

SMO法で学習を行わせてみます. まず数式を簡単にする為に \[ u_i = a_i + \hat{a_i},\quad v_i = a_i-\hat{a_i} \] とおくと, 以下の問題に帰着されます.

$v_i$ を固定して $u_i$ のみを動かせば, $u_i \geq |v_i|$ である事より, 条件 $-C \leq v_i \leq C$ 及び $\sum_i v_i = 0$ の下で \[ \tilde{L}(\mathbf{v})= -\frac{1}{2}\sum_{i,j}v_iv_j K_{ij} - \epsilon\sum_i |v_i| + \sum_i v_it_i \] を最大化すれば良いです.

これは絶対値関数を含みますが $v_i\neq 0$ では $\mathrm{d}|x|/\mathrm{d}x=\mathrm{sgn}(x)$ となります.

$v_p, v_q$ を動かす事にすると $v_p + v_q = \mathrm{const.}$ であるので \[ \frac{\partial \tilde{L}}{\partial v_p} = -\sum_i(K_{pi}-K_{qi})v_i-\epsilon(\mathrm{sgn}(v_p)-\mathrm{sgn}(v_q))+t_p-t_q \] となります. 従って $v_p \rightarrow v_p+\Delta_p, v_q \rightarrow v_q - \Delta_p$ と動かして $0$ と置くことによって \[ \Delta_p = \frac{\sum_i(K_{qi}-K_{pi})v_i+t_p-t_q-\epsilon(\mathrm{sgn}(v_p+\Delta_p)-\mathrm{sgn}(v_q-\Delta_p))}{K_{pp}-2K_{pq}+K_{qq}} \] となります.

これは両辺に $\Delta_p$ を含みますが $\mathrm{sgn}(v_p+\Delta_p)-\mathrm{sgn}(v_p-\Delta_p)$ は $\Delta_p$ について単調増加するので $\Delta_p$ は唯一つしか存在しません. $\mathrm{sgn}(v_p+\Delta_p)-\mathrm{sgn}(v_p-\Delta_p)=0,\pm 2$ の3パターンしかないので1つずつチェックすればOKです.

その後前頁の条件に従ってクリッピングを行って更新を行います. $v_p,v_q$ の選び方は前回と同様でKKT条件を満たさない $p$ を選んだ後, $|\sum_i(K_{qi}-K_{pi})v_i|=|f(\mathbf{x}_q)-f(\mathbf{x}_p)|$ が最大となる $q$ を選びます.

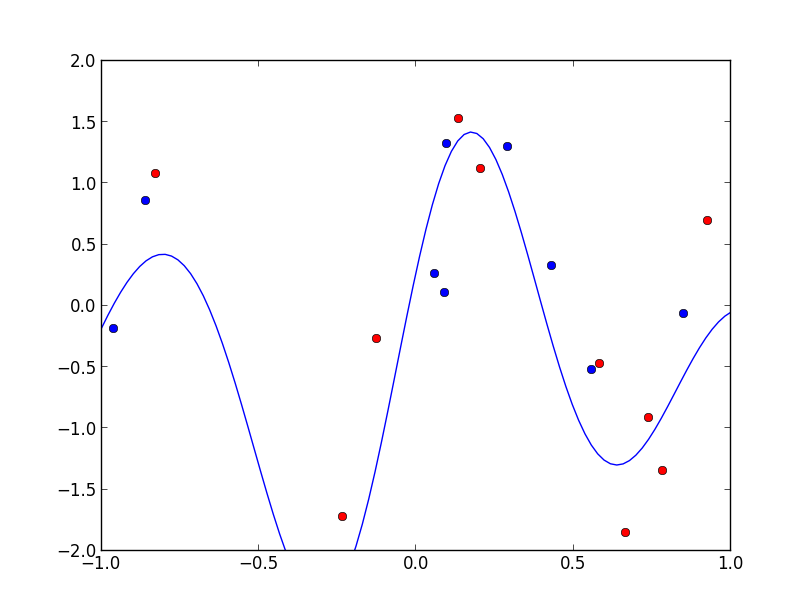
実装例です. ガウスカーネルを用いており, 赤い点のみが回帰方程式の構築に使われています. この例では学習データ数20 に対して, 11点で回帰方程式を表す事が出来ています.

prog13-3.py

関連ベクターマシン

ベイズ的なカーネル法を用いて構成されるSVMと同様のスパースカーネルマシンを 関連ベクターマシン (relevance vector machine) と呼びます.

SVMと異なり確率論に基づいているので, 事後分布の計算が可能であるなどの好ましい性質を持ちます. また, 性能面でもよりスパースな方程式を出力する事ができます.

回帰問題で説明します. 入力データ $\mathbf{x}$ に対する 観測データ $t$ が分布 \[ p(t|\mathbf{x},\mathbf{w},\beta) = \mathcal{N}(t|f(\mathbf{x}),\beta^{-1}) \] に従って得られるとします. $\beta$ は観測誤差の分散の逆数であり, $\mathbf{w}$ は回帰方程式のパラメータです.

回帰方程式はSVMと同様に \[ f(\mathbf{x})=\sum_{i=1}^n w_ik(\mathbf{x}_i,\mathbf{x})+\theta \] という形を考えます. $w_i=0$ となる項が出来るだけ多くなるように学習を行う事が目標となります.

以下, 記述を簡単にする為 \[ f(\mathbf{x})=\mathbf{w}^T\Psi(\mathbf{x}) \] と書きます. \[ \begin{aligned} &\mathbf{w}=(w_1,w_2,\ldots,w_n,\theta) \\ &\psi_i(\mathbf{x})=k(\mathbf{x}_i,\mathbf{x})\quad (i=1,\ldots,n)\\ &\psi_{n+1}(\mathbf{x})=1 \end{aligned} \] です.

学習データ $\{(\mathbf{x}_1,t_1),\ldots,(\mathbf{x}_n,t_n)\}$ に対する尤度関数は \[ L(\mathbf{w}) = p(\mathbf{t}|\mathbf{D},\mathbf{w},\beta) = \prod_{i=1}^n p(t_i|\mathbf{x}_i,\mathbf{w},\beta) \] となります. 但し $\mathbf{t}=(t_1,\ldots,t_n)^T,\mathbf{D}=(\mathbf{x}_1,\ldots,\mathbf{x}_n)^T$ です.

$\mathbf{w}$ の事前分布はこれまでと同様に平均が $0$ の正規分布を利用する事にします. 但し, $w_i$ 毎に異なる精度パラメータを用います. \[ p(\mathbf{w}|\boldsymbol{\alpha})=\prod_{i=1}^n\mathcal{N}(w_i|0,\alpha_i^{-1}) \] 但し, $\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_m)^T$ です.

$\alpha_i$ が非常に大きい値となるならば, $w_i = 0$ とみなす事が出来ます.

さて第11回の公式を用いれば $\mathbf{w}$ の事後分布は \[ p(\mathbf{w}|\mathbf{t},\mathbf{D},\boldsymbol{\alpha},\beta)\propto L(\mathbf{w})p(\mathbf{w}|\boldsymbol{\alpha})=\mathcal{N}(\mathbf{w}|\mathbf{m},\mathbf{\Sigma}) \] \[ \begin{aligned} \mathbf{m} &= \beta \mathbf{\Sigma}\mathbf{X}^T\mathbf{t}\\ \mathbf{\Sigma} &= (\mathbf{A}+\beta\mathbf{X}^T\mathbf{X})^{-1} \end{aligned} \] となります. 但し $\mathbf{X}$ は計画行列で, $\mathbf{A}$ は $\alpha_1,\ldots,\alpha_m$ を対角に持つ対角行列です.

先ほどの特徴ベクトルのおき方より, \[ \mathbf{X} = \begin{pmatrix} k(\mathbf{x}_1,\mathbf{x}_1) & k(\mathbf{x}_1,\mathbf{x}_2) & \cdots & k(\mathbf{x}_1,\mathbf{x}_n) & 1 \\ k(\mathbf{x}_2,\mathbf{x}_1) & k(\mathbf{x}_2,\mathbf{x}_2) & \cdots & k(\mathbf{x}_2,\mathbf{x}_n) & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \\ k(\mathbf{x}_n,\mathbf{x}_1) & k(\mathbf{x}_n,\mathbf{x}_2) & \cdots & k(\mathbf{x}_n,\mathbf{x}_n) & 1 \\ \end{pmatrix} \] という形になります.

さて, $\mathbf{w}$ の事後分布に対するMAP推定を行ってこれを学習したいのですが,超パラメータ $\boldsymbol{\alpha},\beta$ の値が不明であるということをどうにかしないといけません.

そこで エビデンス近似 (evidence approximation) や EM法 という手法を利用する事が出来ます. EM法は後の回にやるのでエビデンス近似の説明をします.

エビデンス近似の考え方はそんなに難しくなく, $\mathbf{w}$ に関してのみ周辺化を行った尤度 \[ p(\mathbf{t}|\mathbf{D},\boldsymbol{\alpha},\beta) = \int p(\mathbf{t}|\mathbf{D},\mathbf{w},\beta)p(\mathbf{w}|\boldsymbol{\alpha})\mathrm{d}\mathbf{w} \] を最大化とする $\boldsymbol{\alpha},\beta$ を最適な超パラメータの近似値として利用します.

この積分もやはり第11回にやった公式を用いれば \[ p(\mathbf{t}|\mathbf{D},\boldsymbol{\alpha},\beta) = \mathcal{N}(\mathbf{t}|\mathbf{0},\mathbf{C}) \] 但し, \[ \mathbf{C} = \beta^{-1}\mathbf{I} + \mathbf{X}\mathbf{A}^{-1}\mathbf{X}^T \] となり, 対数を取ると \[ \ln p(\mathbf{t}|\mathbf{D},\boldsymbol{\alpha},\beta) = -\frac{1}{2}\mathbf{t}^T\mathbf{C}\mathbf{t}-\frac{1}{2}\ln|\mathbf{C}|+\mathrm{const.} \] となりますので, これを準ニュートン法などで最大化する事になります. この計算はガウス過程の所でやったものと同様です.

ここでは結果だけ示すと, 以下のようになります.

学習された超パラメータを $\boldsymbol{\alpha}^*, \beta^*$ とすると, あらたな入力 $\mathbf{x}$ に対する観測値 $t$ の分布は \[ \begin{aligned} p(t|x,\mathbf{D},\mathbf{t},\boldsymbol{\alpha}^*,\beta^*) &= \int p(t|\mathbf{x},\mathbf{w},\beta^*)p(\mathbf{w}|\mathbf{D},\mathbf{t},\boldsymbol{\alpha}^*,\beta^*)\mathrm{d}\mathbf{w}\\ &= \mathcal{N}(t|\mathbf{m}^T\Psi(\mathbf{x}), \sigma^2(\mathbf{x})) \end{aligned} \] となります. 但し $\sigma^2(\mathbf{x}) = (\beta^*)^{-1}+\Psi(\mathbf{x})^T\Sigma\Psi(\mathbf{x})$ です.

つまり, $\mathbf{w} = \mathbf{m}$ とすれば良い事になります.

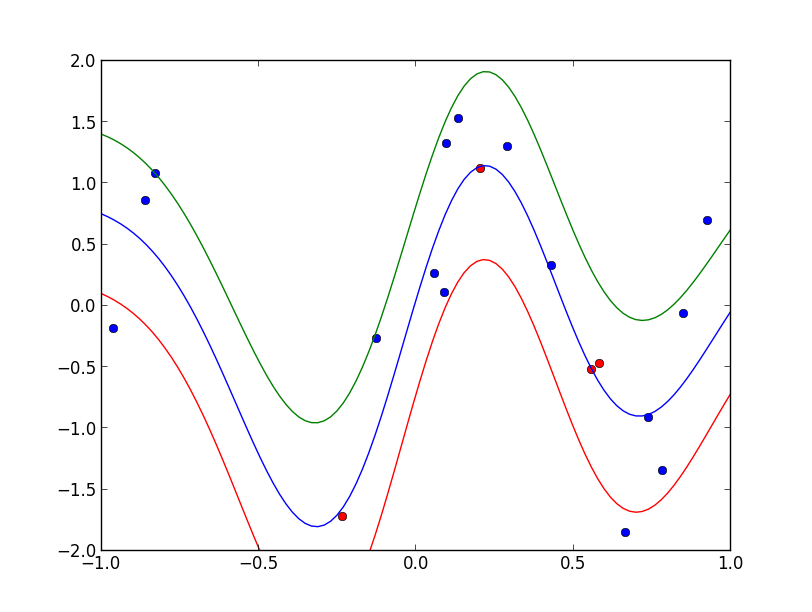
実装例です. ガウスカーネルを用いており, 赤い点のみが回帰方程式の構築に使われています. 上下の曲線は標準偏差を表しています. この例では学習データ数20 に対して, 5点だけで回帰方程式を表す事が出来ています.

prog13-2.py

第13回はここで終わります

次回から第8章グラフィカルモデルに入り, ベイジアンネットワークなどの話をします.