パターン認識・
機械学習勉強会
第11回
@ワークスアプリケーションズ
中村晃一2014年5月15日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
カーネル法:ガウス過程
前回は, 誤差関数の式変形により双対表現 \[ E(\mathbf{a}) = \mathbf{a}^T\mathbf{K}^2\mathbf{a} - 2\mathbf{a}^T\mathbf{K}\mathbf{y} + \mathbf{y}^T\mathbf{y}+\lambda \mathbf{a}^T\mathbf{K}\mathbf{a} \] を得る事によって機械的にカーネル法を導きました.
しかし, ベイズ的な考察によっても自然とカーネル関数が出てきます.
例として線形回帰モデル \[ y = \mathbf{w}^T\Psi(\mathbf{x}) \] を考えます.
これをベイズ的に扱うので, $\mathbf{w}$ の事前分布を設定します. まず \[ \mathbf{w} \sim \mathcal{N}(\mathbf{0}, \alpha^{-1}\mathbf{I}) \] である場合を考えます.$\alpha$は分散の逆数で,精度パラメータと呼びます.
ここで, 入力データ $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n$ を与えると, 理論値 $y_1,y_2,\ldots,y_n$ が得られますが, $\mathbf{w}$ が確率変数である事より $y_i$ も確率変数となります.
そこで $\mathbf{y}=(y_1,y_2,\ldots,y_n)^T$ すなわち, \[ \mathbf{y} = \mathbf{X}\mathbf{w} \quad (\text{$\mathbf{X}$は計画行列})\] が従う確率分布について考えます.
各 $w_i$ が正規分布に従い互いに独立なので, その線形和で書ける $y_j$ もやはり正規分布に従います(正規分布の再生性). 従って平均と分散だけ判れば, $\mathbf{y}$ の分布が決定します.
実際に計算してみると \[ \mathbb{E}[\mathbf{y}] = \mathbb{E}[\mathbf{X}\mathbf{w}] = \mathbf{X}\mathbb{E}[\mathbf{w}] = \mathbf{0} \] よって \[ \mathrm{cov}[\mathbf{y}] = \mathbb{E}[\mathbf{y}\mathbf{y}^T] = \mathbf{X}\mathbb{E}[\mathbf{w}\mathbf{w}^T]\mathbf{X}^T = \frac{1}{\alpha}\mathbf{X}\mathbf{X}^T = \mathbf{K} \] となります. つまり, $\mathbf{y}$ の事前分布が \[ \mathbf{y} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{K}\right) \] となる事が分かりました.
ただし, $\mathbf{K}$ はカーネル関数 \[ K_{ij} = k(\mathbf{x}_i,\mathbf{x}_j)=\frac{1}{\alpha}\Psi(\mathbf{x}_i)^T\Psi(\mathbf{x}_j) \] で定まるグラム行列です. この時, \[ k(\mathbf{x},\mathbf{x}') = \mathbb{E}[y(\mathbf{x})y(\mathbf{x}')] \] であるので, カーネル関数 $k(\mathbf{x},\mathbf{x}')$ を共分散関数として解釈する事が出来ます.
このモデルのポイントはカーネル関数によって $\mathbf{y}$ の事前分布が完全に決定されるという事です.
これまでは $y$ と $\mathbf{x}$ の関係を $y = f(\mathbf{x},\mathbf{w})$ とモデル化し $\mathbf{w}$ に事前分布を定めるという方法でベイズ的な分析を行ってきました。
しかし, 今の例と同様にパラメータ $\mathbf{w}$ を導入すること無く, $\mathbf{y}=(y_1,y_2,\ldots,y_n)^T$ の事前分布を直接 \[ p(\mathbf{y}) = \mathcal{N}(\mathbf{y}|\mathbf{0},\mathbf{K}) \] によって定めるという新しいアプローチを考える事が出来ます.
ここでは, どのような学習データ $y_1,\ldots,y_n$ に対しても常に \[ p(\mathbf{y}) = \mathcal{N}(\mathbf{y}|\mathbf{0},\mathbf{K}) \] が成り立つと仮定していますが, この様なモデルをガウス過程と呼びます.
ガウス過程・ガウスランダム場
どのような $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n$ を選んでも $\mathbf{y}=(y_1,y_2,\ldots,y_n)^T$ の従う分布が正規分布となるならば, このモデル $y=y(\mathbf{x})$ を ガウスランダム場(Gaussian random field) と呼びます. 特に独立変数が1つである場合にこれを ガウス過程 (Gaussian process) と呼びますが, 今後は両方ともガウス過程と呼ぶことにします.
ガウスランダム場は平均値関数 $\mu(\mathbf{x})=\mathbb{E}[y(\mathbf{x})]$ と共分散関数 $k(\mathbf{x},\mathbf{x}') = \mathbb{E}[y(\mathbf{x})y(\mathbf{x}')]$ によって定まります.
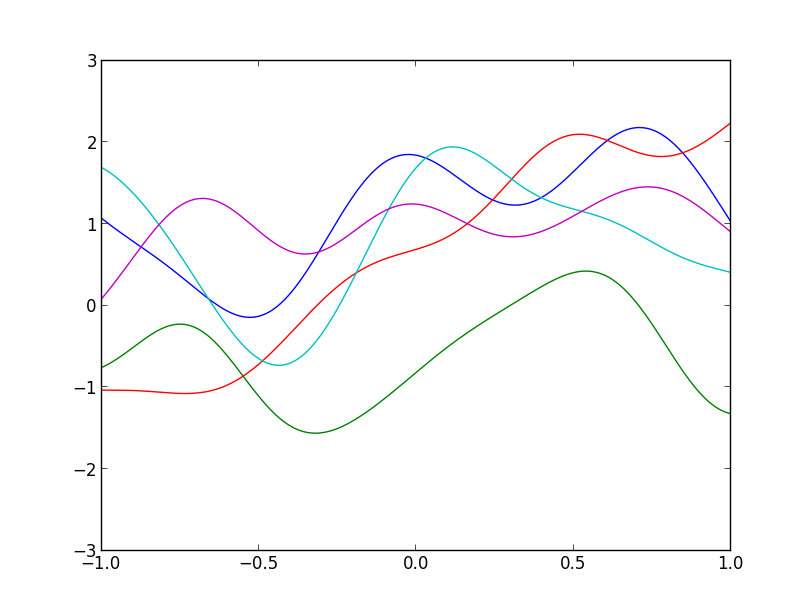
以下は $\mu(x) = 0$ 及びガウスカーネル \[ k(x, x') = \exp(-|x-x'|^2/2\sigma^2) \] で定まるガウス過程からのサンプル例です.($\sigma=0.3$)
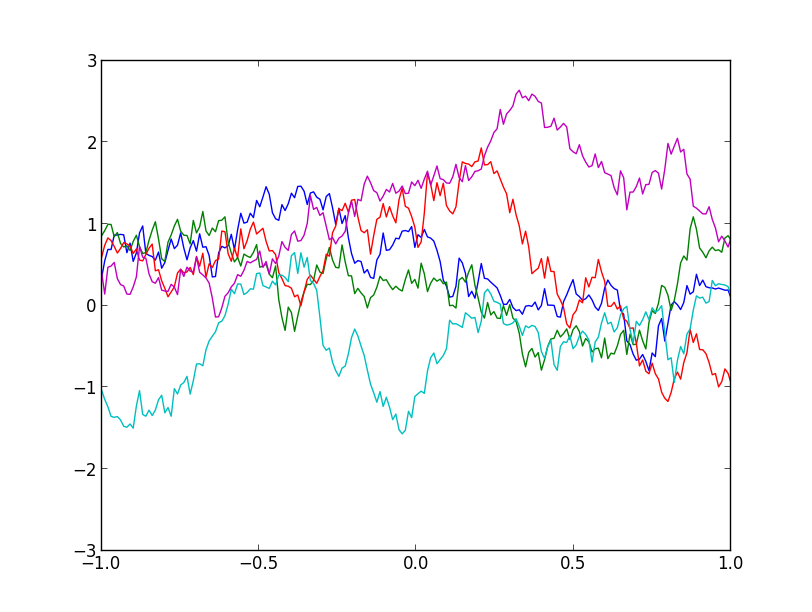
以下は $\mu(x) = 0$ 及び指数カーネル \[ k(x, x') = \exp(-\theta|x-x'|) \] で定まるガウス過程からのサンプル例です.($\theta=1$)
ガウス過程回帰
今, 観測データの組 $(\mathbf{x}_i, t_i)$ が \[ t_i = y_i + \varepsilon_i \] と表されるとします. $\varepsilon_i$ はノイズを表す確率変数です.
$\varepsilon_i$ が正規分布に従うと仮定し, \[ p(t_i | y_i) = N(t_i|y_i, \beta^{-1}) \] とおきます. $\beta$ は精度パラメータです.
個々のノイズ $\varepsilon_1, \ldots, \varepsilon_n$ が独立に同一の分布から生じるならば, $i=1,\ldots,n$ についてまとめて \[ p(\mathbf{t}|\mathbf{y}) = \mathcal{N}(\mathbf{t}|\mathbf{y},\beta^{-1}\mathbf{I}) \] と書くことが出来ます.
さらに, $\mathbf{y}$ をガウス過程としてモデル化し \[ p(\mathbf{y}) = \mathcal{N}(\mathbf{0},\mathbf{K}) \] とします.
すると, 観測値の分布は \[ \begin{aligned} p(\mathbf{t}) &= \int p(\mathbf{t}|\mathbf{y})p(\mathbf{y})\mathrm{d}\mathbf{y} \\ &= \mathcal{N}(\mathbf{t}|\mathbf{0},\mathbf{C})\quad (\mathbf{C} = \mathbf{K}+\beta^{-1}\mathbf{I}) \end{aligned} \] となります(次頁の公式).
正規分布の周辺化の公式
\[ \begin{aligned} p(\mathbf{x})&=\mathcal{N}(\mathbf{x}|\boldsymbol{\mu},\mathbf{\Lambda}^{-1}) \\ p(\mathbf{y}|\mathbf{x}) &=\mathcal{N}(\mathbf{y}|\mathbf{A}\mathbf{x}+\mathbf{b},\mathbf{L}^{-1}) \end{aligned} \] ならば \[ p(\mathbf{y}) = \mathcal{N}(\mathbf{y}|\mathbf{A}\boldsymbol{\mu}+\mathbf{b},\mathbf{L}^{-1}+\mathbf{A}\boldsymbol{\Lambda}^{-1}\mathbf{A}^T) \]さて, 今やりたい事は学習データ $\{(\mathbf{x}_1,t_1),\ldots,(\mathbf{x}_n,t_n)\}$ が与えられている時に, 新しい $\mathbf{x}_{n+1}$ に対する $t_{n+1}$ を予測する事です. つまり, $\mathbf{t}=(t_1,\ldots,t_n)^T$ が与えられた時の, $t_{n+1}$ の分布 \[ p(t_{n+1}|\mathbf{t}) \] を求めれば良いです.
まず, 先ほどの全く同様にして \[ p(\mathbf{t},t_{n+1}) = \mathcal{N}(\mathbf{t},t_{n+1}|\mathbf{0},\mathbf{C}') \] となります. 但し \[ \begin{aligned} \mathbf{C}' &= \begin{pmatrix} \mathbf{C}& \mathbf{k} \\ \mathbf{k}^T & c \end{pmatrix} \\ \mathbf{k} &= (k(\mathbf{x}_1, \mathbf{x}_{n+1}),\ldots,k(\mathbf{x}_n,\mathbf{x}_{n+1}))^T\\ c &= k(\mathbf{x}_{n+1},\mathbf{x}_{n+1})+\beta^{-1} \end{aligned} \] です.
すると, 求める $t_{n+1}$ の分布は \[ p(t_{n+1}|\mathbf{t})=\mathcal{N}(t_{n+1}|\mu, \sigma^2) \] となります. 但し \[ \begin{aligned} \mu &= \mathbf{t}^T\mathbf{C}^{-1}\mathbf{k}\\ \sigma^2 &= c - \mathbf{k}^T\mathbf{C}^{-1}\mathbf{k} \end{aligned} \] です(次頁で解説).
従って, $\mathbf{a}=\mathbf{C}^{-1}\mathbf{t}$ と置けば \[ y = \sum_{i=1}^n a_ik(\mathbf{x}_i,\mathbf{x}) \] となります. これを ガウス過程回帰 (Gaussian process regression) といいます.
【前頁の結果の説明】
\[ \begin{aligned}
\mathbf{C}'^{-1} = \begin{pmatrix}\mathbf{C}&\mathbf{k}\\\mathbf{k}^T&c\end{pmatrix}^{-1} = \begin{pmatrix} \cdots & -\alpha \mathbf{C}^{-1}\mathbf{k} \\ -\alpha(\mathbf{C}^{-1}\mathbf{k})^T & \alpha\end{pmatrix}\\
\qquad (\alpha = (c-\mathbf{k}^T\mathbf{C}^{-1}\mathbf{k})^{-1})
\end{aligned} \]
と書けるので, $(\mathbf{t},t_{n+1})\mathbf{C}'^{-1}(\mathbf{t},t_{n+1})^T$ を $t_{n+1}$ について整理すれば
\[ \alpha(t_{n+1}^2 -\mathbf{t}^T\mathbf{C}^{-1}\mathbf{k}t_{n+1})+\cdots = \alpha||t_{n+1}-\mathbf{t}^T\mathbf{C}^{-1}\mathbf{k}||^2+\cdots \]
となる為.
まとめると以下のようになります.
ガウス過程回帰
学習データ $\{(\mathbf{x}_1,t_1),\ldots,(\mathbf{x}_n,t_n)\}$ に対して, $\mathbf{t} = (t_1,\ldots,t_n)^T$ とおく. また, 正定値カーネル $k(\mathbf{x},\mathbf{x}')$ で定まるグラム行列 $\mathbf{K}$ と精度パラメータ $\beta > 0$ に対して \[ \mathbf{a} = (\mathbf{K} + \beta^{-1}\mathbf{I})^{-1}\mathbf{t} \] とおく.
この時, 回帰方程式は \[ y = \sum_{i=1}^n a_ik(\mathbf{x}_i,\mathbf{x}) \] となる.
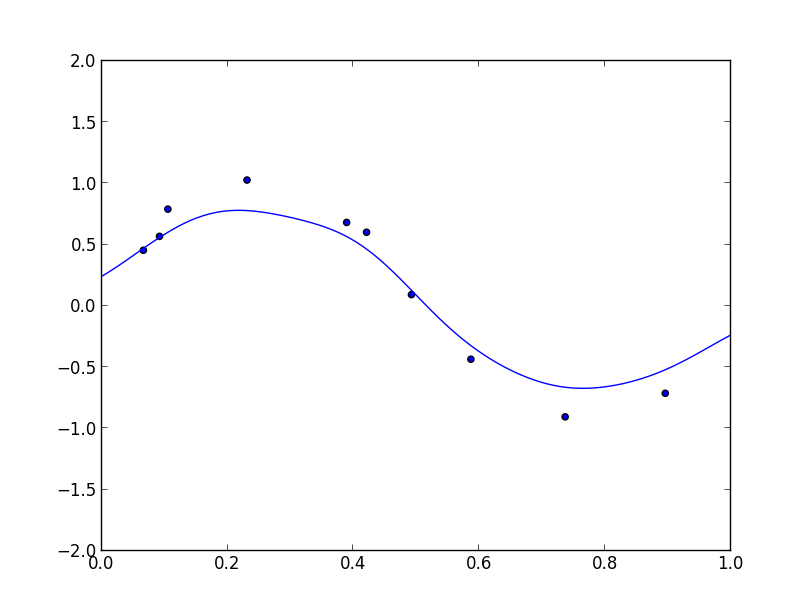
以下がガウス過程回帰の実験例です. ($\sigma=0.1$のガウスカーネル, 精度パラメータ$\beta=2$)
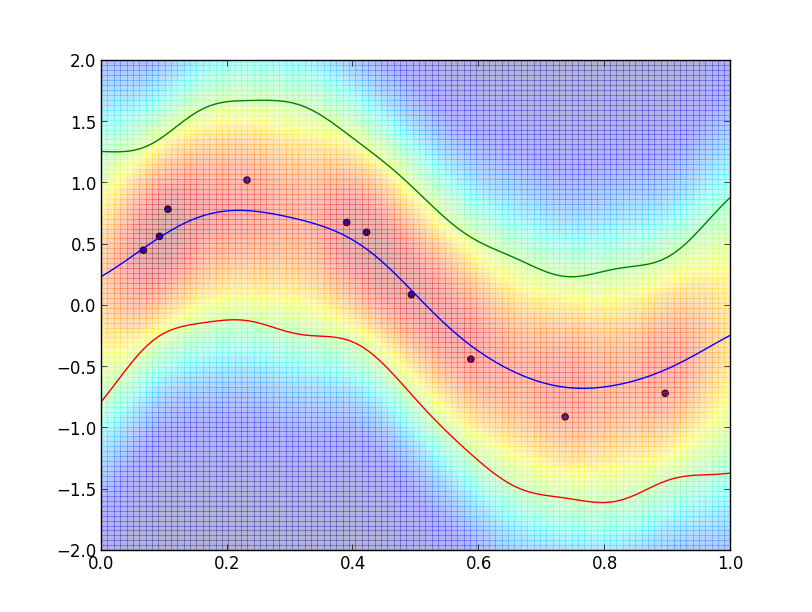
この時の $p(t|\mathbf{t})$ は以下の様になっています.
ガウス過程回帰で用いられるカーネル
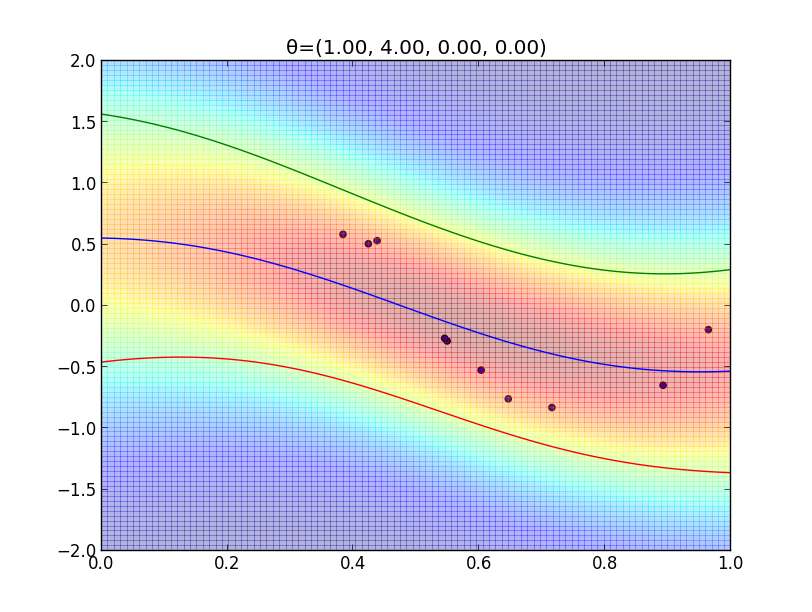
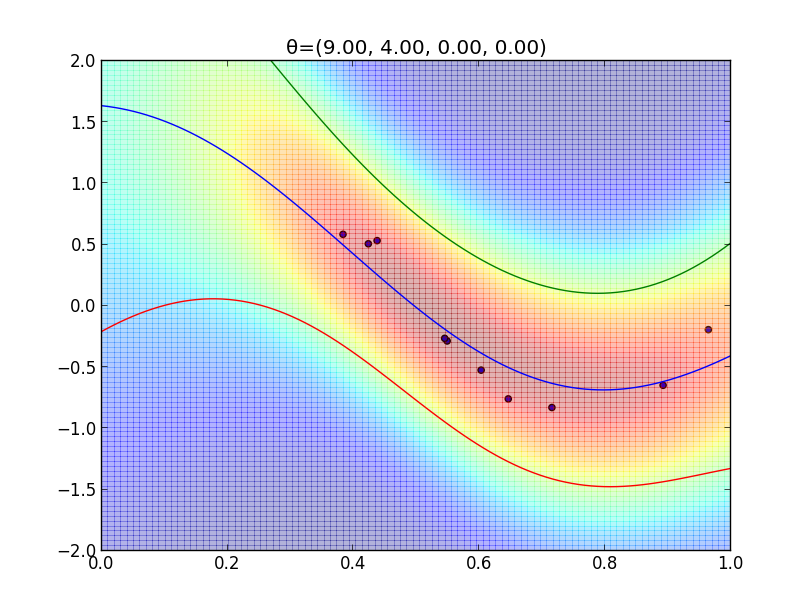
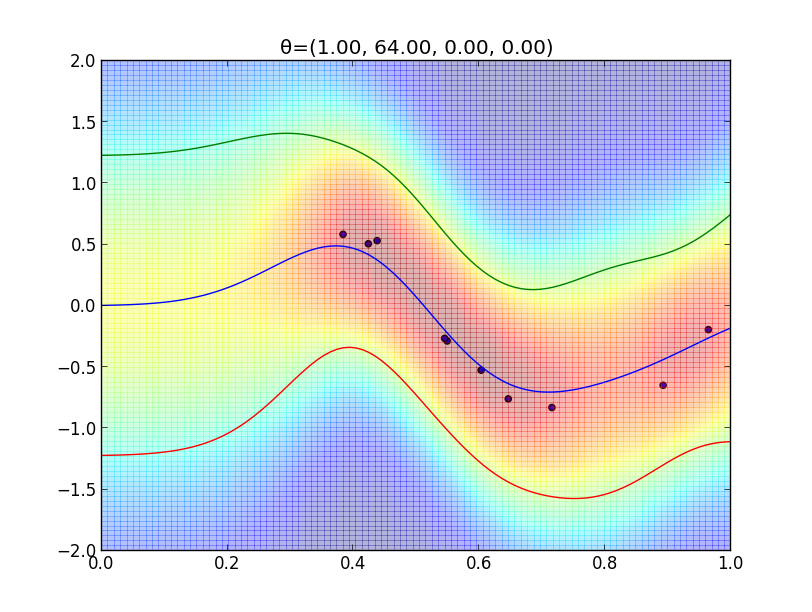
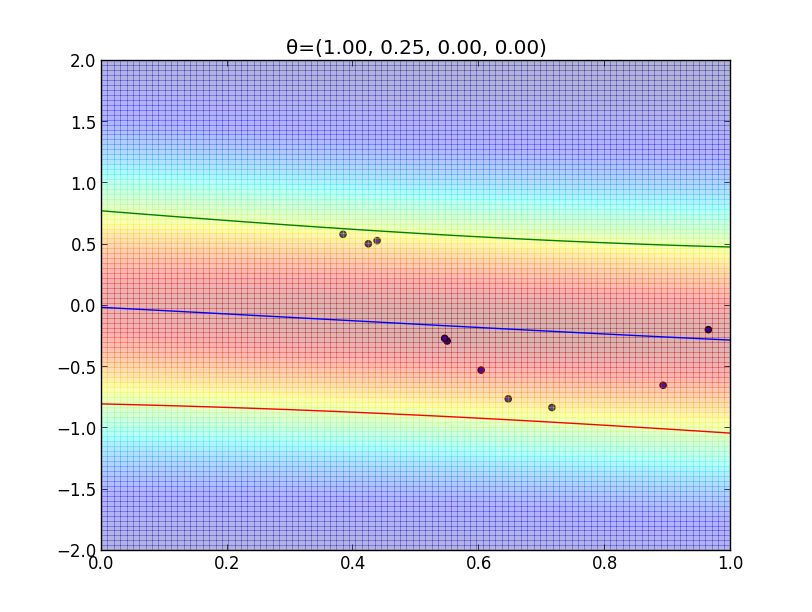
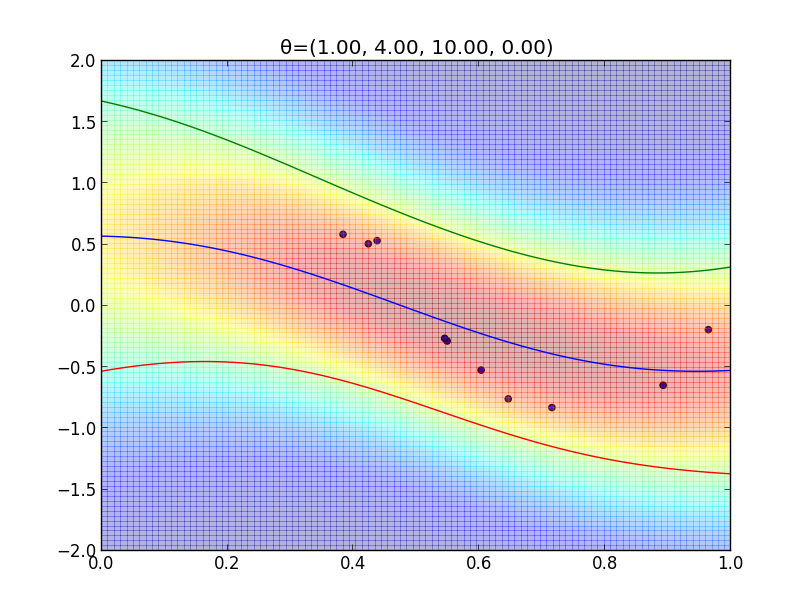
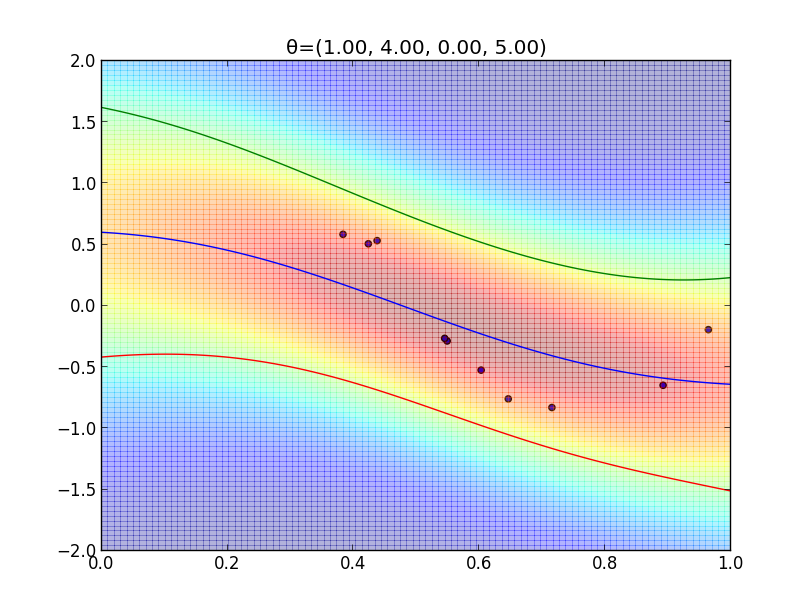
今の例ではガウスカーネルを用いましたが, 一般には \[ k(\mathbf{x},\mathbf{x}')=\theta_0\exp\left(-\frac{\theta_1}{2}||\mathbf{x}-\mathbf{x}'||^2\right) + \theta_2 + \theta_3\mathbf{x}^T\mathbf{x}' \] という形のカーネルが良く利用されます.
$\boldsymbol{\theta}=(\theta_1,\theta_2,\theta_3,\theta_4)$ を色々変えた時のフィッティングの様子を見てみましょう.
超パラメータの学習
今の例における $\boldsymbol{\theta}=(\theta_0,\theta_1,\theta_2,\theta_3)$ は事前分布の設定に関わるパラメータであり, このようなパラメータを超パラメータ (hyper parameter)と呼びます.
続いて超パラメータを学習する事を考えます. 最尤法を使うならば \[ L(\boldsymbol{\theta}|\mathbf{t})=p(\mathbf{t}|\boldsymbol{\theta}) \] を最大化すれば良いです.
先ほど確認した様に \[ \begin{aligned} p(\mathbf{t}|\boldsymbol{\theta}) &= \mathcal{N}(\mathbf{t}|\mathbf{0},\mathbf{C})\qquad \small{(\mathbf{C} = \mathbf{K}+\beta^{-1}\mathbf{I})}\\ &= \frac{1}{(\sqrt{2\pi})^n\sqrt{|\mathbf{C}|}}\exp\left\{-\frac{1}{2}\mathbf{t}^T\mathbf{C}^{-1}\mathbf{t}\right\} \end{aligned} \] であるので, 対数尤度は \[ \ln L(\boldsymbol{\theta}|\mathbf{t}) = -\frac{1}{2}\ln |\mathbf{C}|-\frac{1}{2}\mathbf{t}^T\mathbf{C}^{-1}\mathbf{t}-\frac{n}{2}\ln(2\pi) \] となります.
これを最大化したいので勾配を計算します. 結果は以下のようになります. \[ \frac{\partial}{\partial \theta_i}\ln L(\boldsymbol{\theta}|\mathbf{t}) = -\frac{1}{2}\mathrm{Tr}\left(\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta_i}\right)+\frac{1}{2}\mathbf{t}^T\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta_i}\mathbf{C}^{-1}\mathbf{t} \] となります(次頁で解説).
【前頁解説】
\[ \mathbf{C}\mathbf{C}^{-1}=\mathbf{I} \]
の両辺を $\theta_i$ で微分すると
\[ \frac{\partial \mathbf{C}}{\partial\theta_i}\mathbf{C}^{-1}+\mathbf{C}\frac{\partial\mathbf{C}^{-1}}{\partial\theta_i} = \mathbf{O} \]
となるので
\[ \frac{\partial\mathbf{C}^{-1}}{\partial\theta_i}=-\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta_i}\mathbf{C}^{-1} \]
また, $\mathbf{C}$ の固有値・固有ベクトルを $(\lambda_i,\mathbf{u}_i)\quad (i=1,\ldots,n)$ とする. $\{\mathbf{u}_i\}$は正規直交基底をなすようにとる. $\mathbf{C}$は対称行列だから \[ \mathbf{C} = \sum_i\lambda_i\mathbf{u}_i\mathbf{u}_i^T \] と表す事が出来, \[ \frac{\partial \mathbf{C}}{\partial\theta} = \sum_i\frac{\partial\lambda_i}{\partial\theta}\mathbf{u}_i\mathbf{u}_i^T+\sum_i2\lambda_i\mathbf{u}_i\frac{\partial\mathbf{u}_i^T}{\partial\theta} \] となる.
これと \[ \mathbf{C}^{-1} = \sum_i\frac{1}{\lambda_i}\mathbf{u}_i\mathbf{u}_i^T \] を掛けて, $\mathbf{u}_i^T\mathbf{u}_j = \delta_{ij}$ を用いると \[ \mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta} = \sum_i\frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial\theta}\mathbf{u}_i\mathbf{u}_i^T+\sum_i2\mathbf{u}_i\frac{\partial\mathbf{u}_i^T}{\partial\theta} \] となる. よって $\mathrm{Tr}(\mathbf{a}\mathbf{b}^T)=\mathbf{a}^T\mathbf{b}$ を用いて \[ \mathrm{Tr}\left(\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta}\right) = \sum_i\frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial\theta}\mathbf{u}_i^T\mathbf{u}_i+\sum_i2\mathbf{u}_i^T\frac{\partial\mathbf{u}_i}{\partial\theta} \] となり, $||\mathbf{u}_i||^2=1$ とこの両辺を微分して得られる \[ 2u_i^T\frac{\partial u_i}{\partial\theta} = 0 \] を代入すれば \[ \mathrm{Tr}\left(\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta}\right) = \sum_i\frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial\theta} \] となる.
ここで $|\mathbf{C}|=\prod_i\lambda_i$ であるから \[ \begin{aligned} \frac{\partial}{\partial\theta}\ln|\mathbf{C}|&=\frac{\partial}{\partial\theta}\sum_i\ln\lambda_i\\ &= \sum_i\frac{1}{\lambda_i}\frac{\partial\lambda_i}{\partial\theta} \end{aligned} \] となる.
よって \[ \frac{\partial}{\partial\theta}\ln|\mathbf{C}| = \mathrm{Tr}\left(\mathbf{C}^{-1}\frac{\partial\mathbf{C}}{\partial\theta}\right) \] となる.
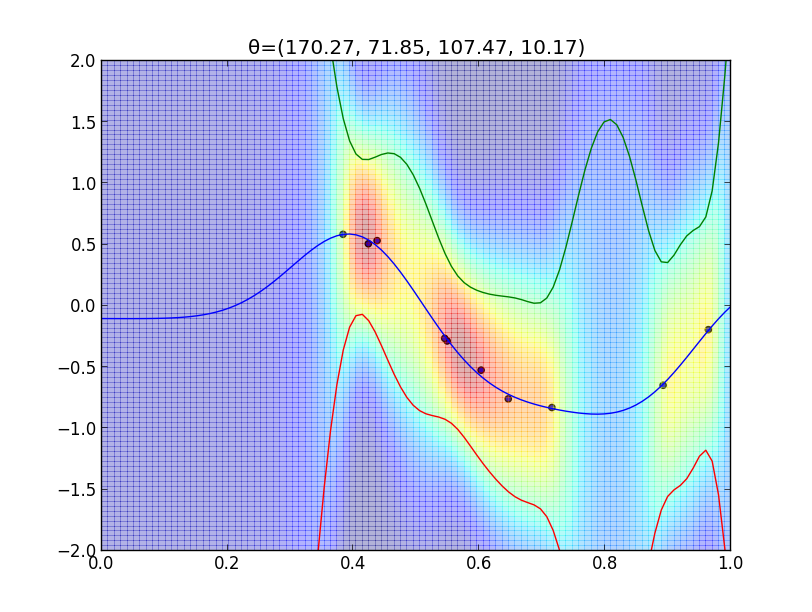
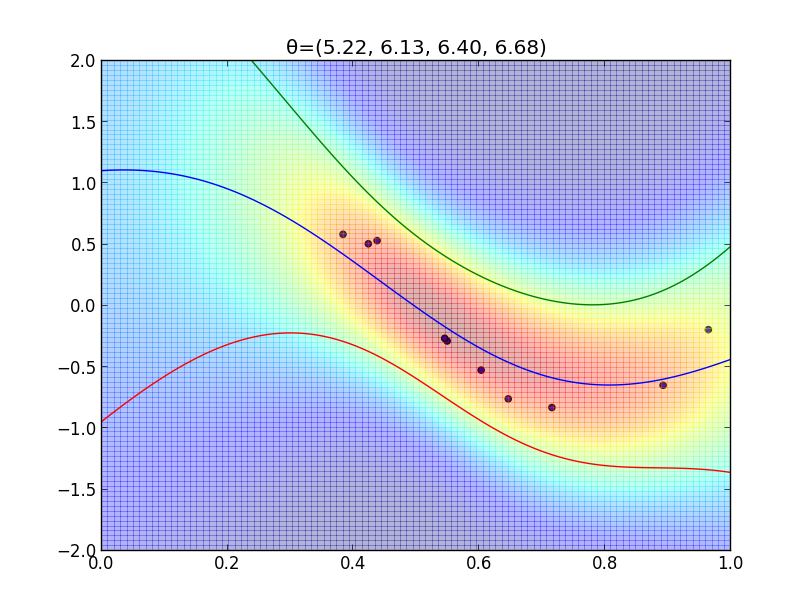
以下は先ほどのカーネル \[ k(\mathbf{x},\mathbf{x}')=\theta_0\exp\left(-\frac{\theta_1}{2}||\mathbf{x}-\mathbf{x}'||^2\right) + \theta_2 + \theta_3\mathbf{x}^T\mathbf{x}' \] に対する学習結果です.
最尤法ではなくMAP推定でもやってみます. 事後分布の密度の対数は \[ \ln p(\boldsymbol{\theta}|\mathbf{t})= \ln L(\boldsymbol{\theta}|\mathbf{t}) + \ln p(\boldsymbol{\theta}) + \mathrm{const.}\] なので, $\theta_i$ は互いに独立だとすれば \[ \ln p(\boldsymbol{\theta}|\mathbf{t})= \ln L(\boldsymbol{\theta}|\mathbf{t}) + \sum_{i=0}^3\ln p(\theta_i) + \mathrm{const.}\] となります.
$\boldsymbol{\theta}$ の事前分布ですが, $\theta_i \geq 0$ でなければならないので正規分布は使えません.
そこで, ガンマ分布 \[ p(\theta_i) \approx \theta_i^{k_i-1}\exp(-\theta_i/s_i) \qquad (\theta_i \geq 0)\] を使ってみます. $k_i$は形状母数, $s_i$ は尺度母数です. すると \[\ln p(\theta_i) = -\frac{\theta_i}{s_i} + (k_i-1)\ln\theta_i + \mathrm{const.} \] なので \[\frac{\partial}{\partial\theta_i} \ln p(\boldsymbol{\theta}|\mathbf{t})= \frac{\partial}{\partial\theta_i}\ln L(\boldsymbol{\theta}|\mathbf{t}) - \frac{1}{s_i} + \frac{k_i-1}{\theta_i}\] となります.
MAP推定による超パラメータの学習結果は以下のようになります. $(k_i = 2, s_i = 2)$
ガウス過程に基づく識別問題
続いてガウス過程モデルに基づく識別問題を考えます.
2クラスの場合は, これまでと同様にロジスティックモデル \[ y=\sigma(a(\mathbf{x})) \] を用います. $\sigma$ はシグモイド関数です.
ここで, 活性化関数 $a(\mathbf{x})$ をガウス過程によってモデル化する事を考えます.
先ほどと同様に学習データ $\{(\mathbf{x}_1,t_1),\ldots,(\mathbf{x}_n,t_n)\}$ が与えられた時に, 新たな $\mathbf{x}_{n+1}$ に対する $t_{n+1}$ の分布 \[ p(t_{n+1}|\mathbf{t}) \] を考えます. この時, 仮定より $\mathbf{a}=(a(\mathbf{x}_1),\ldots,a(\mathbf{x}_n))$ 及び $a_{n+1}=a(\mathbf{x}_{n+1})$ に対して \[ \begin{aligned} p(\mathbf{a}) &= \mathcal{N}(\mathbf{a}|\mathbf{0},\mathbf{C}) \\ p(\mathbf{a},a_{n+1}) &= \mathcal{N}(\mathbf{a},a_{n+1}|\mathbf{0},\mathbf{C}') \end{aligned} \] と置くことが出来ます.
さらに, 先ほどと同様に \[ \mathbf{C} = \mathbf{K} + \nu\mathbf{I} \qquad (\nu > 0)\] とおきます.
回帰の例では誤差の分散の逆数 $\beta$ によって $\mathbf{C} = \mathbf{K} + \beta^{-1}\mathbf{I}$ となりましたが, 上で登場した $\nu$ はそれと異なるので注意が必要です. 何故ならば, 識別問題における学習データは離散的なので誤差が存在しないからです.
$\nu$ は $\mathbf{C}$ の正定値性の為に導入される人工的なパラメータです.
さて, 求める $t_{n+1}$ の分布は \[ p(t_{n+1}|\mathbf{t}) = \int p(t_{n+1}|a_{n+1})p(a_{n+1}|\mathbf{t})\mathrm{d}a_{n+1} \] により定まりますが, これをどうやって計算するのかが問題となります. 面倒なのは$p(a_{n+1}|\mathbf{t})$ の部分です.
ここではテキストに沿って, ラプラス近似 (Laplace approximation) を用いる方法を紹介します.
まず, ベイズの定理を2度用いて \[ \begin{aligned} p(a_{n+1}|\mathbf{t})&=\int p(a_{n+1},\mathbf{a}|\mathbf{t})\mathrm{d}\mathbf{a} \\ &= \frac{1}{p(\mathbf{t})}\int p(\mathbf{t}|a_{n+1},\mathbf{a})p(a_{n+1},\mathbf{a})\mathrm{d}\mathbf{a}\\ &= \frac{1}{p(\mathbf{t})}\int p(\mathbf{t}|\mathbf{a})p(a_{n+1}|\mathbf{a})p(\mathbf{a})\mathrm{d}\mathbf{a}\\ &= \int p(\mathbf{a}|\mathbf{t})p(a_{n+1}|\mathbf{a})\mathrm{d}\mathbf{a}\\ \end{aligned} \] と変形します.
続いて, 回帰の時と同様にガウス過程の仮定を利用して \[ p(a_{n+1}|\mathbf{a}) = \mathcal{N}(a_{n+1}|\mathbf{a}^T\mathbf{C}^{-1}\mathbf{k}, c-\mathbf{k}^T\mathbf{C}^{-1}\mathbf{k}) \] を得ます.
また, \[ p(\mathbf{t}|\mathbf{a}) =\prod_{i=1}^n \sigma(a_i)^{t_i}(1-\sigma(a_i))^{1-t_i} \] です.
ここでラプラス近似を使います. ラプラス近似とは $f(\mathbf{x})$ の対数を一旦取って, $\nabla \ln f(\mathbf{x})$ が $\mathbf{0}$ になる点 $\mathbf{x}_0$ の周りで2次テイラー展開を行う事によって $f(\mathbf{x})$ を近似するものです.
実際にやってみると, $\mathbf{x}_0$ で1階微分の項が消える事から \[ \ln f(\mathbf{x})\approx \ln f(\mathbf{x}_0) - \frac{1}{2} (\mathbf{x}-\mathbf{x}_0)^T\mathbf{A}(\mathbf{x}-\mathbf{x}_0) \] となります. 但し $\mathbf{A} = -\nabla\nabla \ln f(\mathbf{x})|_{\mathbf{x}=\mathbf{x}_0}$ です.
すると, \[ f(\mathbf{x}) \approx f(\mathbf{x}_0) \exp\left\{-\frac{1}{2}(\mathbf{x}-\mathbf{x}_0)^T\mathbf{A}(\mathbf{x}-\mathbf{x}_0) \right\} \] となります. これがラプラス近似の公式です. 正規表現の密度関数と同じ形である事に注意しましょう.
いま, \[ p(\mathbf{a}|\mathbf{t})\approx p(\mathbf{t}|\mathbf{a})p(\mathbf{a}) \] を計算する為に, 右辺のラプラス近似を行います.
まず, 対数を取ります. \[ \begin{aligned} \Psi(\mathbf{a}) &= \ln p(\mathbf{t}|\mathbf{a}) + \ln p(\mathbf{a}) \\ &= -\frac{1}{2}\ln|\mathbf{C}| - \frac{1}{2}\mathbf{a}^T\mathbf{C}^{-1}\mathbf{a} - \frac{n}{2}\ln(2\pi) \\ & + \sum_{i=1}^n\left\{t_i\ln\sigma(a_i) + (1-t_i)\ln(1-\sigma(a_i))\right\} \end{aligned} \] 続いて, 2階微分係数まで計算します.
まず, \[ \nabla \Psi(\mathbf{a}) = -\mathbf{C}^{-1}\mathbf{a} + \mathbf{t} - \boldsymbol{\sigma} \] となります. 但し $\boldsymbol{\sigma}=(\sigma(a_1),\ldots,\sigma(a_n))^T$ です.
【$\mathbf{t}-\boldsymbol{\sigma}$の導出】
\[ \frac{\partial}{\partial a_i}\sigma(a_i) = \sigma(a_i)(1-\sigma(a_i)) \]
なので
\[ \frac{\partial}{\partial a_i}\ln\sigma(a_i) = 1-\sigma(a_i) \]
同様に
\[ \frac{\partial}{\partial a_i}\ln(1-\sigma(a_i)) = -\sigma(a_i) \]
従って
\[
\frac{\partial}{\partial a_i}\sum_{i=1}^n\left\{t_i\ln\sigma(a_i) + (1-t_i)\ln(1-\sigma(a_i))\right\}
=t_i(1-\sigma(a_i))-(1-t_i)\sigma(a_i)
=t_i - \sigma(a_i)
\]
続いて \[ \nabla\nabla \Psi(\mathbf{a}) = -\mathbf{W} - \mathbf{C}^{-1} \] となります. 但し $\mathbf{W}$ は対角行列であり, $W_{ii} = \sigma(a_i)(1-\sigma(a_i))$ です.
さて, $\nabla \Psi(\mathbf{a}) = \mathbf{0}$ となる点を見つけなければいけませんが, \[ \nabla \Psi(\mathbf{a}) = -\mathbf{C}^{-1}\mathbf{a} + \mathbf{t} - \boldsymbol{\sigma} \] を解析的に $\mathbf{a}$ について解くことは出来ません.
そこで, ニュートン・ラフソン法(第5回)を利用することが出来ます. 更新式は \[ \begin{aligned} \mathbf{a}^{(k+1)} &= \mathbf{a}^{(k)} - (\nabla\nabla \Psi(\mathbf{a}))^{-1}\nabla \Psi(\mathbf{a})\\ &= \mathbf{a}^{(k)} + (\mathbf{W}+\mathbf{C}^{-1})^{-1}(-\mathbf{C}^{-1}\mathbf{a}^{(k)} + \mathbf{t} - \boldsymbol{\sigma})\\ &= \mathbf{C}(\mathbf{W}\mathbf{C}+\mathbf{I})^{-1}(\mathbf{W}\mathbf{a}^{(k)} + \mathbf{t} - \boldsymbol{\sigma})\\ \end{aligned} \] となります. この極限値を \[ \mathbf{a}_0 = \lim_{k\rightarrow\infty}\mathbf{a}^{(k)} \] とおきます.
すると, ラプラス近似の公式より $C$ を定数として \[ p(\mathbf{a}|\mathbf{t})\approx C\exp\left\{-\frac{1}{2}(\mathbf{a}-\mathbf{a}_0)^T(\mathbf{W}+\mathbf{C}^{-1})(\mathbf{a}-\mathbf{a}_0)\right\} \] となります. よって, 右辺は正規分布の密度関数の形をしていますから \[ p(\mathbf{a}|\mathbf{t}) \approx \mathcal{N}(\mathbf{a}|\mathbf{a}_0, (\mathbf{W}+\mathbf{C}^{-1})^{-1}) \] となります.
以上より \[ \begin{aligned} p(\mathbf{a}|\mathbf{t}) &= \mathcal{N}(\mathbf{a}|\mathbf{a}_0, (\mathbf{W}+\mathbf{C}^{-1})^{-1}) \\ p(a_{n+1}|\mathbf{a}) &= \mathcal{N}(a_{n+1}|\mathbf{a}^T\mathbf{C}^{-1}\mathbf{k}, c-\mathbf{k}^T\mathbf{C}^{-1}\mathbf{k}) \end{aligned} \] なので, \[ p(a_{n+1}|\mathbf{t}) = \mathcal{N}(\mathbf{k}^T(\mathbf{t}-\boldsymbol{\sigma}), c-\mathbf{k}^T(\mathbf{W}^{-1}+\mathbf{C})^{-1}\mathbf{k}) \] となります.
【導出】
平均 $\mu$ は $\mathbf{C}^{-1}\mathbf{a}_0 = \mathbf{t}-\boldsymbol{\sigma}$ を用いて
\[ \mu = \mathbf{k}^T\mathbf{C}^{-1}\mathbf{a}_0 = \mathbf{k}^T(\mathbf{t}-\boldsymbol{\sigma}) \]
分散 $\sigma^2$ は公式 $(A+B)^{-1}=A^{-1}-A^{-1}(B^{-1}+A^{-1})^{-1}A^{-1}$ を用いて
\[\begin{aligned}
\sigma^2 &= c-\mathbf{k}^T\mathbf{C}^{-1}\mathbf{k}+\mathbf{k}^T\mathbf{C}^{-1}(\mathbf{W}+\mathbf{C}^{-1})^{-1}\mathbf{C}^{-1}\mathbf{k} \\
&= c-\mathbf{k}^T(\mathbf{W}^{-1}+\mathbf{C})^{-1}\mathbf{k}
\end{aligned}\]
最初の式を思い出すと \[ p(t_{n+1}|\mathbf{t}) = \int p(t_{n+1}|a_{n+1})p(a_{n+1}|\mathbf{t})\mathrm{d}a_{n+1} \] だったので, \[ p(t_{n+1}=1|\mathbf{t})=\int \sigma(a_{n+1})\mathcal{N}(\mu,\sigma^2)\mathrm{d}a_{n+1} \] となります. 但し $\mu,\sigma^2$は前頁の値です.
この計算には \[ \int \sigma(a)\mathcal{N}(a|\mu,\sigma^2)\mathrm{d}a \approx \sigma\left(\frac{\mu}{\sqrt{1+\pi\sigma^2/8}} \right) \] という近似を利用できます(次頁).
【前頁の近似の導出】
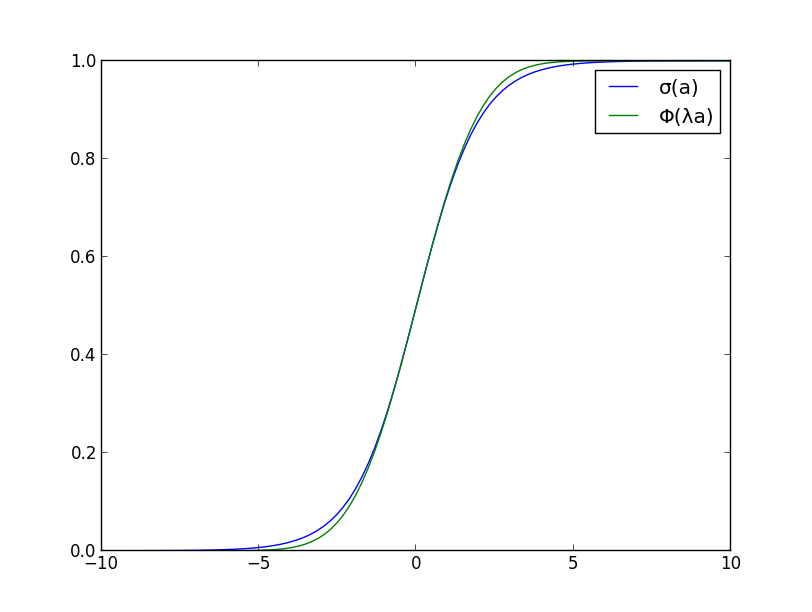
まず,シグモイド関数を標準正規分布の累積関数
\[ \Phi(a)=\int_{-\infty}^a\mathcal{N}(x|0,1)\mathrm{d}x \]
を用いて近似する. この時
\[ \sigma'(0) = \sigma(0)(1-\sigma(0))=\frac{1}{4},\qquad \Phi'(0) = \frac{1}{\sqrt{2\pi}} \]
であるので, $a=0$ における勾配が一致するようにすると
\[ \sigma(a) \approx \Phi(\lambda a)\qquad (\lambda=\sqrt{\pi/8}) \]
となる.
すると, \[\begin{aligned} \int \sigma(a)\mathcal{N}(a|\mu,\sigma^2)\mathrm{d}a &\approx \int\Phi(\lambda a)\mathcal{N}(a|\mu,\sigma^2)\mathrm{d}a \\ &= \int_{-\infty}^\infty\int_{-\infty}^{\lambda a}\mathcal{N}(t|0,1)\mathcal{N}(a|\mu,\sigma^2)\mathrm{d}t\mathrm{d}a\\ \end{aligned} \] となる. ここで $(u,v) = (a, -\lambda a + t)$ と置換すれば \[\begin{aligned} &\int_{-\infty}^\infty\int_{-\infty}^{\lambda a}\mathcal{N}(t|0,1)\mathcal{N}(a|\mu,\sigma^2)\mathrm{d}t\mathrm{d}a\\ =& \int_{-\infty}^\infty\int_{-\infty}^0\mathcal{N}(\lambda u+v|0,1)\mathcal{N}(u|\mu,\sigma^2)\mathrm{d}v\mathrm{d}u \\ =& \frac{1}{2\pi\sigma}\int_{-\infty}^0\int_{-\infty}^\infty \exp\left\{-\frac{(\lambda u + v)^2}{2}-\frac{(u-\mu)^2}{2\sigma^2}\right\}\mathrm{d}u\mathrm{d}v \\ =&\frac{1}{2\pi\sigma}\int_{-\infty}^0\int_{-\infty}^\infty \exp\left\{-\frac{\lambda^2+\sigma^{-2}}{2}\left(u-\frac{\mu\sigma^{-2}-\lambda v}{\lambda^2+\sigma^{-2}}\right)^2\right\}\exp\left\{-\frac{(v+\lambda\mu)^2}{2(\lambda^2\sigma^2+1)}\right\}\mathrm{d}u\mathrm{d}v \end{aligned} \]
\[\begin{aligned} =&\frac{1}{\sqrt{2\pi(\lambda^2\sigma^2+1)}}\int_{-\infty}^0\exp\left\{-\frac{(v+\lambda\mu)^2}{2(\lambda^2\sigma^2+1)}\right\}\mathrm{d}v \\ \end{aligned} \] となるので $t = (v+\lambda\mu)/\sqrt{\lambda^2\sigma^2+1}$ と置換すれば \[\begin{aligned} =&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\lambda\mu/\sqrt{\lambda^2\sigma^2+1}}\exp(-t^2/2)\mathrm{d} t\\ =&\Phi\left(\frac{\lambda\mu}{\sqrt{\lambda^2\sigma^2+1}}\right) \\ \end{aligned} \] となり, 最後に再び $ \sigma(a) \approx \Phi(\lambda a)$ を用いれば \[\begin{aligned} =&\sigma\left(\frac{\mu}{\sqrt{1+\lambda^2\sigma^2}}\right) =\sigma\left(\frac{\mu}{\sqrt{1+\pi\sigma^2/8}}\right) \end{aligned} \] となる. ■
以上をまとめると以下のようになります.
ガウス過程を用いた識別
\[ y = p(t_{n+1}|\mathbf{t}) = \sigma\left(\frac{\mu}{\sqrt{1+\pi\sigma^2/8}}\right) \] 但し \[ \mu = \mathbf{k}^T(\mathbf{t}-\boldsymbol{\sigma}),\quad \sigma^2 = c-\mathbf{k}^T(\mathbf{W}^{-1}+\mathbf{C})^{-1}\mathbf{k} \] \[ \mathbf{C}=\mathbf{K}+\nu\mathbf{I},\quad k_i = k(\mathbf{x}_i,\mathbf{x}),\quad c = k(\mathbf{x},\mathbf{x})+\nu \] \[ W_{ii} = \sigma(a_i)(1-\sigma(a_i)), W_{ij}=0\quad(i\neq j) \] であり, $\boldsymbol{\sigma}$ 及び $\mathbf{W}$ は \[ \mathbf{a}^{(k+1)} = \mathbf{C}(\mathbf{I}+\mathbf{W}\mathbf{C})^{-1}(\mathbf{t}-\boldsymbol{\sigma}+\mathbf{W}\mathbf{a}^{(k)}) \] の極限値 $\mathbf{a}_0$ における値を用いる.
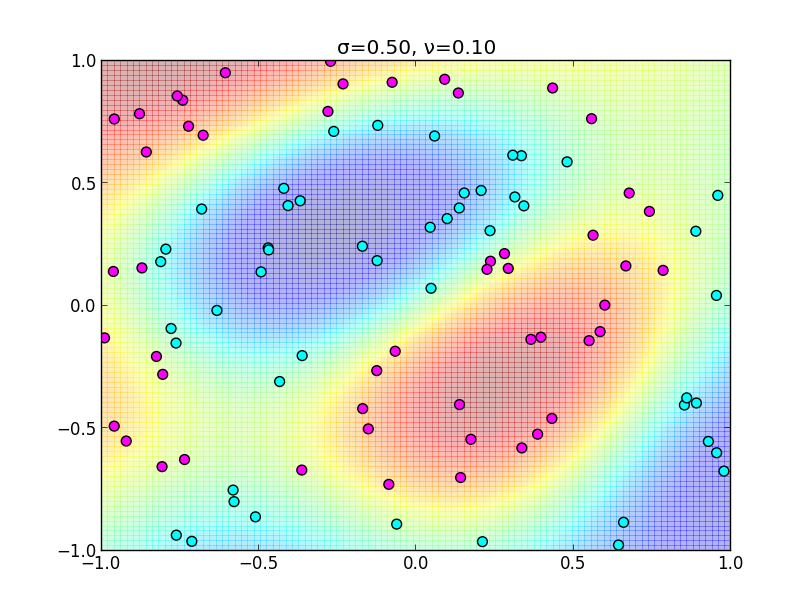
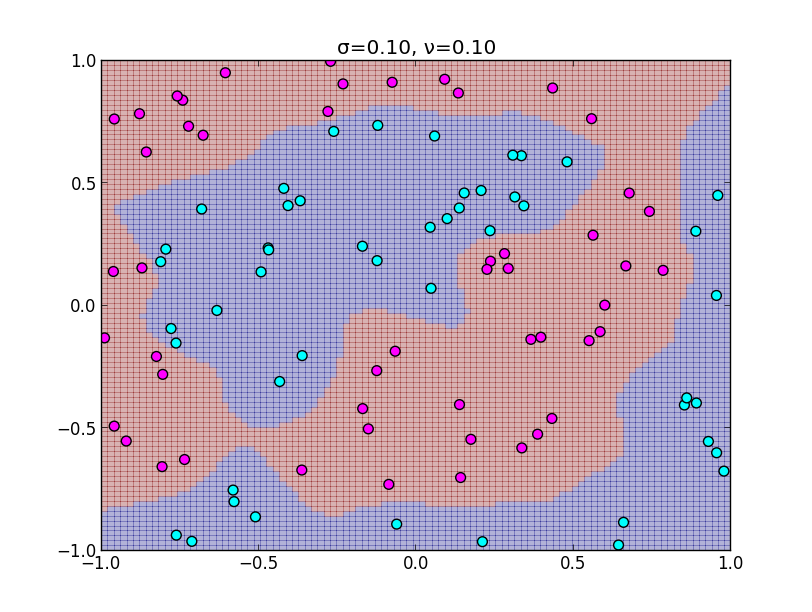
以下が実装例です. ガウスカーネル $k(\mathbf{x},\mathbf{x}')=\exp(-||\mathbf{x}-\mathbf{x}'||^2/2\sigma^2)$ を用いています.
以下が実装例です. ガウスカーネル $k(\mathbf{x},\mathbf{x}')=\exp(-||\mathbf{x}-\mathbf{x}'||^2/2\sigma^2)$ を用いています.
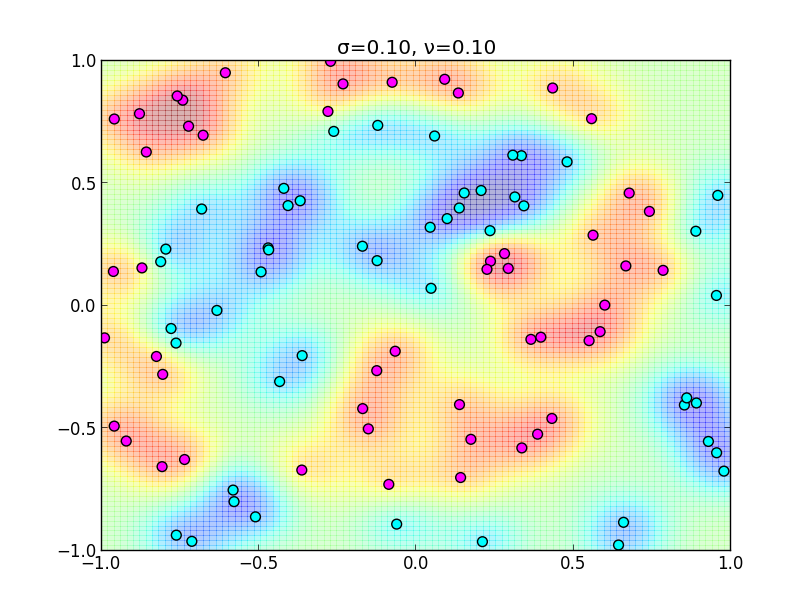
ガウスカーネルの $\sigma$ を小さくしすぎると下の様になってしまいます. $\sigma$ が小さいならば $\mathbf{x}$ と $\mathbf{x}'$ かなり近づかないと, 共分散 $k(\mathbf{x},\mathbf{x}')$ が大きくならない為です.
ガウスカーネルの $\sigma$ を小さくしすぎると下の様になってしまいます. $\sigma$ が小さいならば $\mathbf{x}$ と $\mathbf{x}'$ かなり近づかないと, 共分散 $k(\mathbf{x},\mathbf{x}')$ が大きくならない為です.
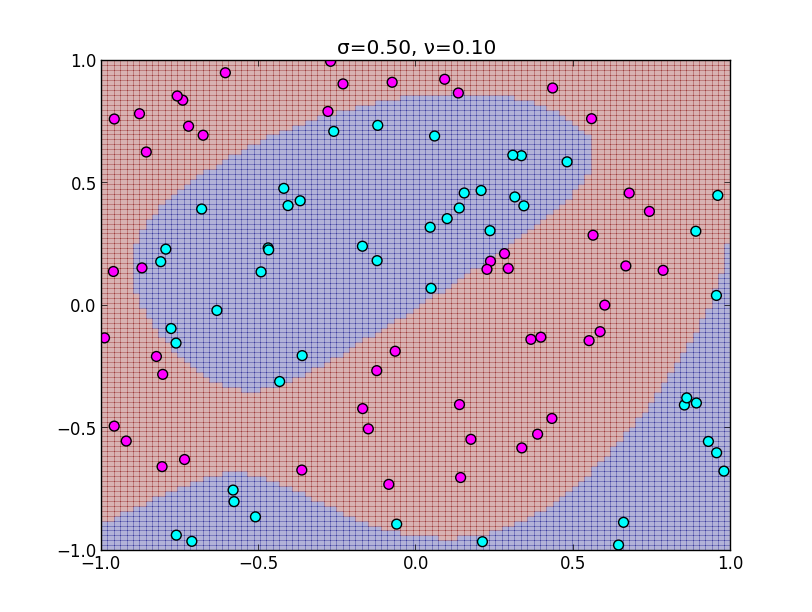
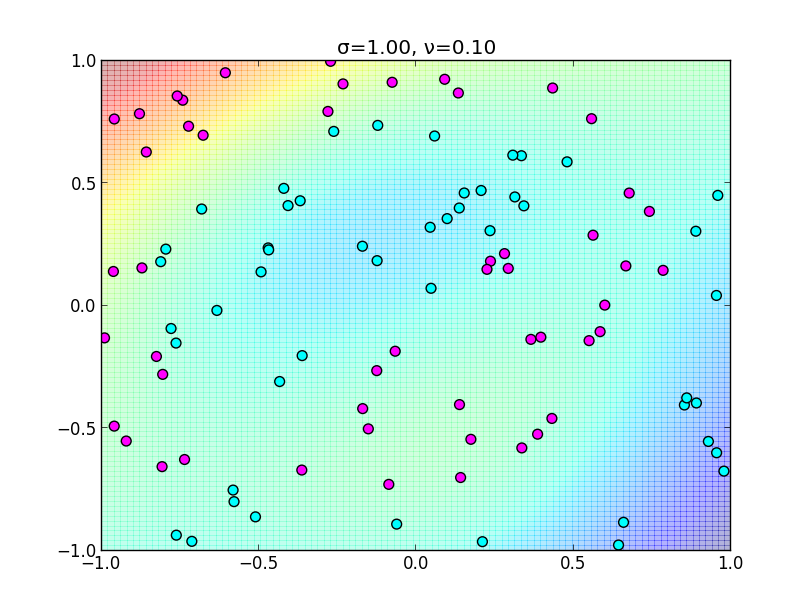
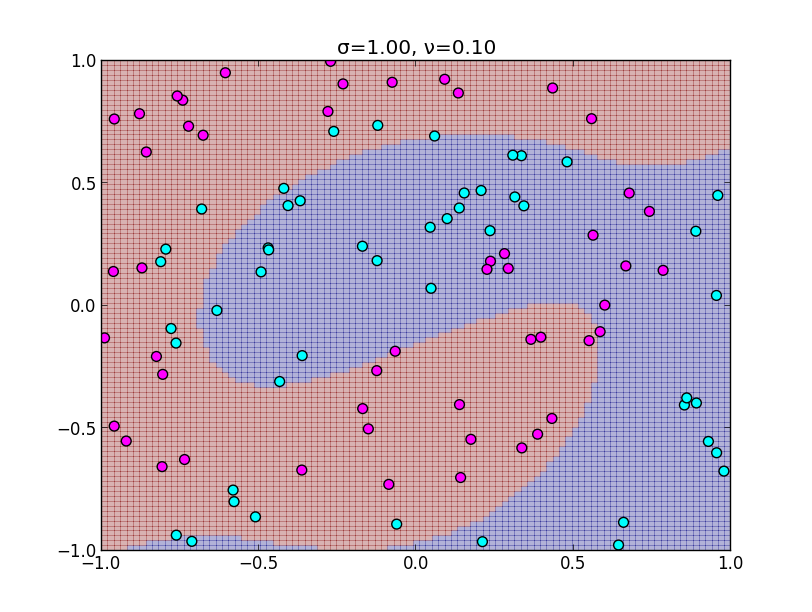
同様に $\sigma$ を大きくしすぎると以下のようになります.
同様に $\sigma$ を大きくしすぎると以下のようになります.
ニューラルネットワークとの関係
Neal[1996]によると, 隠れ層の数が $M$ 個のベイジアンニューラルネットワークの多くにおいて \[ M\rightarrow\infty \] の極限を考えると, ネットワークの出力がガウス過程となります. つまり隠れ層が無限個のニューラルネットワークと見なす事が出来ます.
但し極限を取ることによって失われてしまう情報がある($M\rightarrow\infty$ では全ての出力 $y_i$が独立になる等)為, 一概にガウス過程モデルの方が優れていると言えるわけではありません.
第11回はここで終わります
次回は第7章スパースカーネルマシンに進みます. サポートベクタマシンの話題が主です.