パターン認識・
機械学習勉強会
第9回
@ワークスアプリケーションズ
中村晃一2014年4月24日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
ニューラルネットワーク
前回は資料作成が間に合わず大変申し訳ありませんでした。 本日もニューラルネットワークの解説を行います。
テキスト4章後半の非常に発展的な題材は, 後の回の手法の方が実装が優しいので後に回すことにし, 直線探索やBFGS法などに重点を置くことします.準ニュートン法
前回は最急降下法を実装しましたが、収束はあまり速くありません. ニュートン・ラフソン法を用いれば反復回数を大きく減らす事が出来ますが、その収束性は保証されておらず(これは勾配法も同じ)、さらに収束したからと言ってそれが極小値であるとは限りません.
そこで, 準ニュートン法 (quasi-Newton method) という手法が登場します。
ニュートン・ラフソン法を復習すると, 適当な初期値 $\mathbf{w}_0$ を定め, \[ \mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} - \left(\mathbf{H}^{(k)}\right)^{-1}\nabla \mathbf{E}^{(k)} \] によって反復を行う方法でした. $\nabla \mathbf{E}^{(k)}$ はステップ $k$ での誤差関数の勾配, $\mathbf{H}^{(k)}$ はステップ $k$ での誤差関数のヘッセ行列です.
ここでは主に2つの事が問題になります. 1つは前頁で述べた収束性の問題です.もう一つはヘッセ行列の逆行列を計算するコストが非常に大きいということです.
準ニュートン法では,ヘッセ行列を他の正定値対称行列で近似し,さらに逆行列を直接計算しなくても良いような工夫を行います.
ヘッセ行列の近似
テキスト 5.4 節にはヘッセ行列 $\left(\mathbf{H}^{(k)}\right)^{-1}$ の各種近似計算法が紹介されていますが, ここでは 外積による近似 (outer product approximation) を紹介します.
出力が1つの場合を考えると, 誤差関数が残差平方和の半分 \[ E = \frac{1}{2}\sum_{n=1}^N (y_n-t_n)^2 \] の場合 \[ \nabla E = \sum_{n=1}^N (y_n-t_n)\nabla y_n \] なので \[ \mathbf{H} = \nabla\nabla E = \sum_{n=1}^N \nabla y_n (\nabla y_n)^T + \sum_{n=1}^N (y_n-t_n)\nabla\nabla y_n \] となります.
ここで, $E$ の最小値の付近では $\nabla y_n \approx \mathbf{0}$ になっているので $\nabla \nabla y_n \approx \mathbf{O}$ ですから \[ \mathbf{H} \approx \sum_{n=1}^N\nabla y_n (\nabla y_n)^T \] と近似出来ます. これを外積による近似と言います.
今, \[ \mathbf{H}_N = \sum_{n=1}^N\mathbf{b}_n\mathbf{b}_n^T \qquad (\mathbf{b}_n = \nabla y_n)\] とおきます.
これをデータ1つずつについて漸進的に計算出来るように \[ \mathbf{H}_{L+1} = \mathbf{H}_L + \mathbf{b}_{L+1}\mathbf{b}_{L+1}^T \] という形に直します.
ここで, Woodburyの公式(の特別な場合である) \[ (\mathbf{H}+\mathbf{b}\mathbf{b}^T)^{-1} = \mathbf{H}^{-1} - \frac{\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\mathbf{H}^{-1}}{1+\mathbf{b}^T\mathbf{H}^{-1}\mathbf{b}} \] が成立するので(次頁), \[ \mathbf{H}_{L+1}^{-1} = \mathbf{H}_L^{-1}-\frac{\mathbf{H}_L^{-1}\mathbf{b}_{L+1}\mathbf{b}_{L+1}^T\mathbf{H}_L^{-1}}{1+\mathbf{b}^T_{L+1}\mathbf{H}_L^{-1}\mathbf{b}_{L+1}} \] となります.
但し, $\mathbf{H}_0$ は小さい $\alpha$ に対して $\mathbf{H}_0 \approx \alpha I$ と近似します.
【前頁の等式の証明】
まず
\[ \mathbf{H}^{-1}(\mathbf{H}+\mathbf{b}\mathbf{b}^T) = I + \mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T \qquad\cdots(1)\]
また,
\[ \begin{aligned}
\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\mathbf{H}^{-1}(\mathbf{H}+\mathbf{b}\mathbf{b}^T) &=
\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T+\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\\
&= \mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T+(\mathbf{b}^T\mathbf{H}^{-1}\mathbf{b})\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\\
& \qquad\qquad \text{($\because\, \mathbf{b}^T\mathbf{H}^{-1}\mathbf{b}$はスカラー)} \\
&= (1+\mathbf{b}^T\mathbf{H}^{-1}\mathbf{b})\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T
\end{aligned} \]
より
\[ \frac{\mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T\mathbf{H}^{-1}}{1+\mathbf{b}^T\mathbf{H}^{-1}\mathbf{b}}(\mathbf{H}+\mathbf{b}\mathbf{b}^T) = \mathbf{H}^{-1}\mathbf{b}\mathbf{b}^T \qquad\cdots(2)\]
$(1)$から$(2)$を引いて終了.
準ニュートン法の計算量
$\mathbf{A},\mathbf{B}$ が $n\times n$ 行列, $\mathbf{x},\mathbf{y}$ が $n$次元ベクトルの時のこれら積の計算量は以下のようになります.
- $\mathbf{A}\mathbf{B}$ は $\mathcal{O}(n^3)$ 時間
- $\mathbf{A}\mathbf{x}, \mathbf{x}^T\mathbf{A}$ は $\mathcal{O}(n^2)$ 時間
- $\mathbf{x}\mathbf{x}^T$ は $\mathbf{O}(n^2)$ 時間
従って, 準ニュートン法の1ステップの更新は \[ \mathbf{H}_{L+1}^{-1} = \mathbf{H}_L^{-1}-\frac{((\mathbf{H}_L^{-1}\mathbf{b}_{L+1})\mathbf{b}_{L+1}^T)\mathbf{H}_L^{-1}}{1+(\mathbf{b}^T_{L+1}\mathbf{H}_L^{-1})\mathbf{b}_{L+1}} \] という順序で積を計算すると $\mathcal{O}(W^2)$ となります.
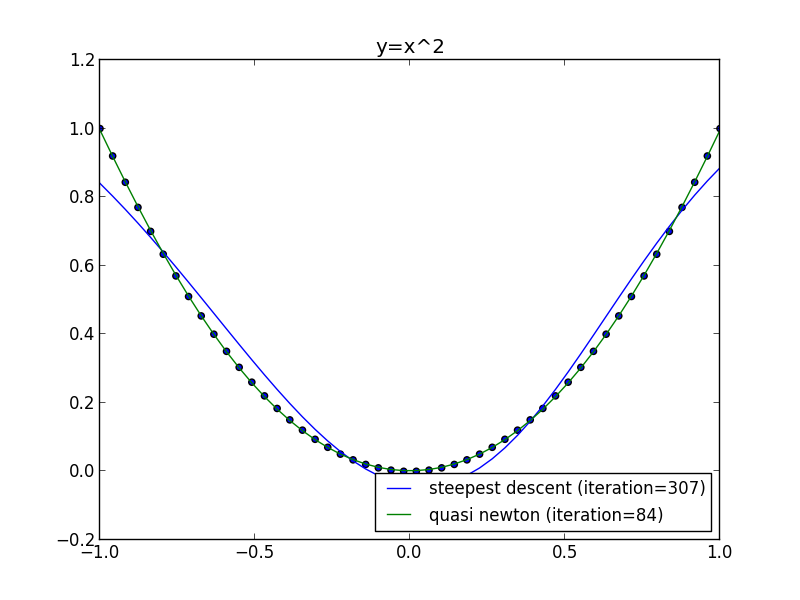
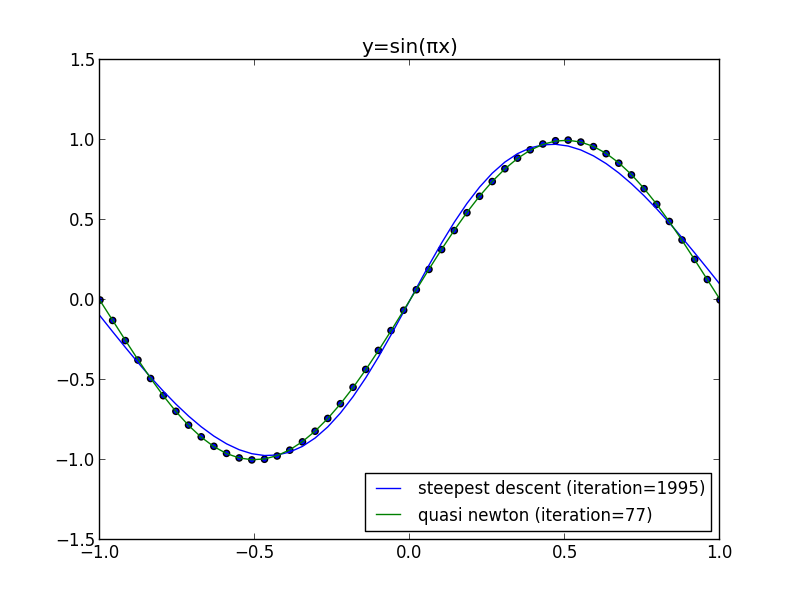
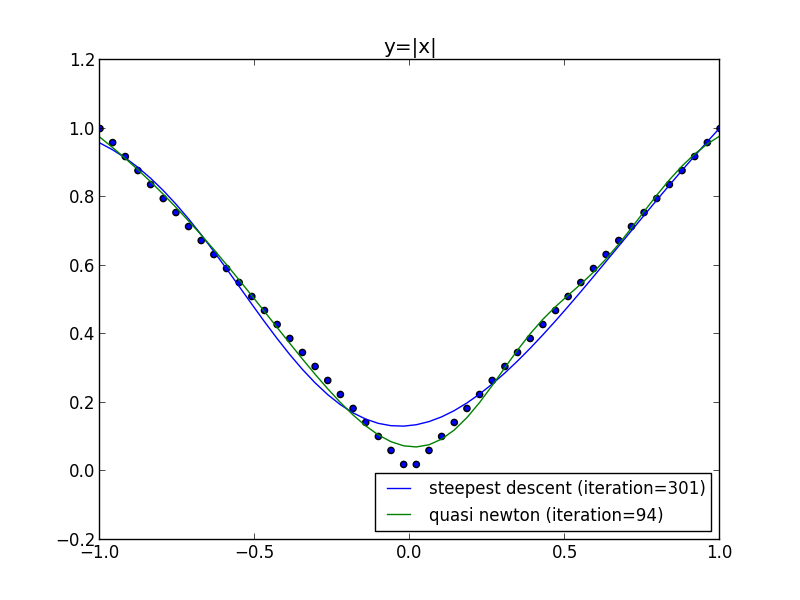
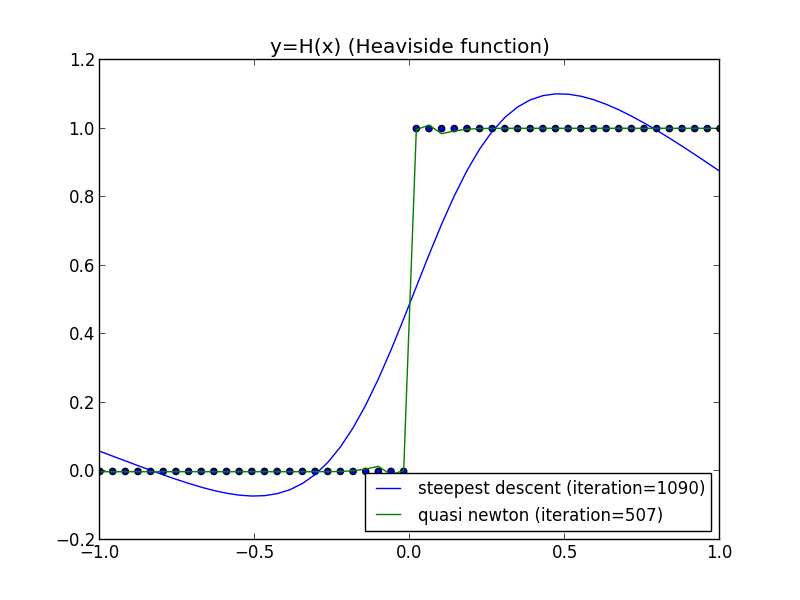
前回の問題に適用してみます.
以下の例は上手くいかない場合もあります. 後で説明します.
直線探索の利用
今紹介した手法では, ヘッセ行列・その逆行列の計算量を削減する事は出来ましたが,収束性の問題が解決していません. そこで 線形探索 (line search)という手法を用いて,収束性が保証されるようにステップサイズを調整するという方法が取られます.
詳細は省きますが, Armijoの条件 (Armijoの条件) と Wolfeの条件 (Wolfe condition) と呼ばれるものを満たせば大域的収束性が保証される事が分かっています.
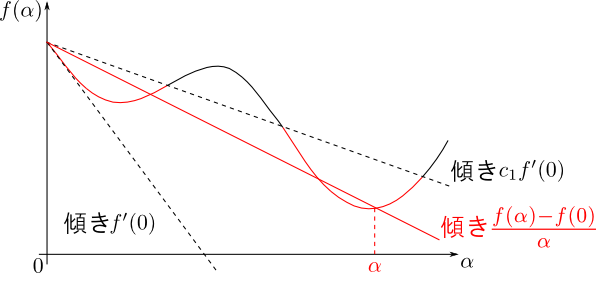
$f(\alpha) = E(\mathbf{w}+\alpha\mathbf{p})$ とおきます.
まず, $0 < c_1 < 1$ を満たす小さな $c_1$に対して \[ \frac{f(\alpha)-f(0)}{\alpha} \leq c_1 f'(0) \] が成立する必要があります. これは $\alpha$ の上限を定め, Armijoの条件と呼ばれます.
続いて $0 < c_1 < c_2 < 1$ を満たす比較的大きい $c_2$ に対して \[ f'(\alpha) \geq c_2f'(0) \] を満たす必要があります. これは $\alpha$ の下限を定め, Wolfeの条件と呼ばれます. こちらも整理すると \[ \mathbf{p}^T\nabla E(\mathbf{w}+\alpha\mathbf{p}) \geq c_2\mathbf{p}^T\nabla E(\mathbf{w}) \] となります.
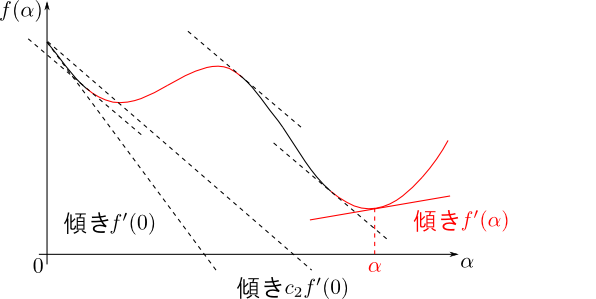
まとめると以下の様になります.
Armijo,Wolfeの条件によるステップサイズの決定
- $\alpha > 0$ を適当に決める.
- Armijoの条件を満たさないなら $\alpha$ は大きすぎるのでより小さくし最初に戻る. \[ E(\mathbf{w}+\alpha\mathbf{p})\leq E(\mathbf{w})+c_1\alpha\mathbf{p}^T\nabla E(\mathbf{w}) \]
- Wolfeの条件を満たさないなら $\alpha$ は小さすぎるのでより大きくし最初に戻る. \[ \mathbf{p}^T\nabla E(\mathbf{w}+\alpha\mathbf{p}) \geq c_2\mathbf{p}^T\nabla E(\mathbf{w}) \]
BFGS公式
先ほどのWoodburyの公式は解りやすいのですが, 各$\mathbf{w}_k$に対してヘッセ行列の逆行列の近似計算を一から行うのでまだ効率が悪いです.
$\mathbf{w}_k$ の時点で得られたヘッセ行列を元に次の時点でのヘッセ行列を近似計算すればもっと効率が良く, BFGS公式(Broyden-Fletcher-Goldfarb-Shanno公式) という手法が有名です.
二次のテイラー展開を元に導出するのですが, 複数の段階を経るので面倒です. (参考: サンディエゴ大の講義ノート)
BFGS公式
$\mathbf{w}_k$ に対する $f(\mathbf{w}_k)$ のヘッセ行列 $\mathbf{H}_k$ の逆行列 $\mathbf{B}_k$ を求める.- $\mathbf{w}_0, \mathbf{B}_0$ を定める.
- $\mathbf{w}_{k+1} = \mathbf{w}_k - \alpha\mathbf{B}_k\nabla f(\mathbf{w}_k)$ とする. $\alpha$ は直線探索で求める.
- $\mathbf{s}_k = \mathbf{w}_{k+1}-\mathbf{w}_k,\,\mathbf{y}_k = \nabla f(\mathbf{w}_{k+1})-\nabla f(\mathbf{w}_k)$ とし, \[ \begin{aligned} \mathbf{B}_{k+1} &= \mathbf{B}_k + \frac{\mathbf{s}_k^T\mathbf{y}_k+\mathbf{y}_k^T\mathbf{B}_k\mathbf{y}_k}{(\mathbf{s}_k^T\mathbf{y}_k)^2}\mathbf{s}_k\mathbf{s}_k^T\\ &-\frac{1}{\mathbf{s}_k^T\mathbf{y}_k}\left(\mathbf{B}_k\mathbf{y}_k\mathbf{s}_k^T + (\mathbf{B}_k\mathbf{y}_k\mathbf{s}_k^T)^T \right) \end{aligned} \] によって更新し,1に戻る.
ロジスティック回帰
続いて識別の問題にニューラルネットワークを利用する事を考えましょう.
2クラス識別のモデルはロジスティックシグモイド関数 $\sigma$ によって \[ y = \sigma(a(\mathbf{x},\mathbf{w})) \] と表す事が出来るので, 出力層の活性化関数を $ y = \sigma(a)$ とします. 隠れ層は前と同じく $z = \tanh a$ としましょう.
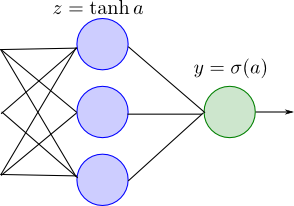
第5・6回に解説した様に, この場合最小化するものは \[ E = - \sum_{n=1}^N\left\{t_n\ln y_n + (1-t_n)\ln(1-y_n)\right\} \] です.
これらから誤差逆伝播法で使う出力層での誤差を計算すると \[ \begin{aligned} \frac{\partial y_n}{\partial a} &= y_n(1-y_n) \\ \frac{\partial E_n}{\partial a} &= y_n - t_n \end{aligned} \] となります.
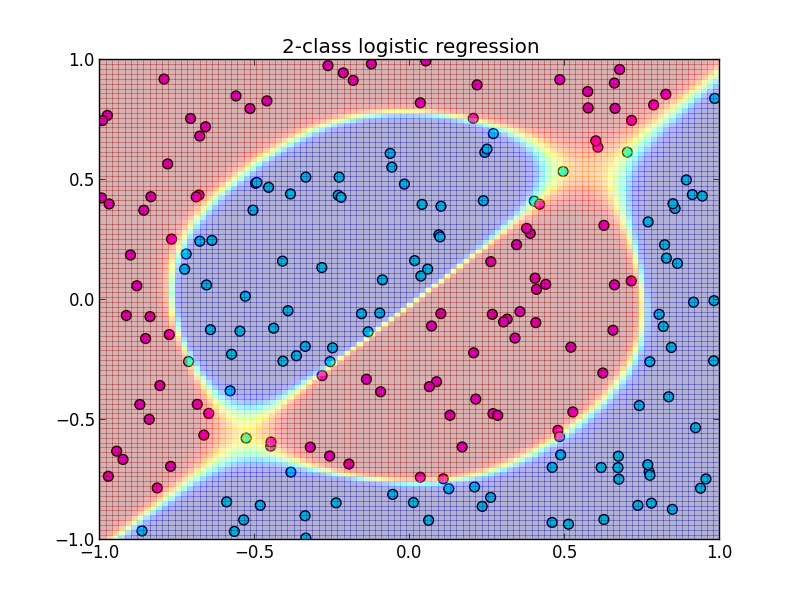
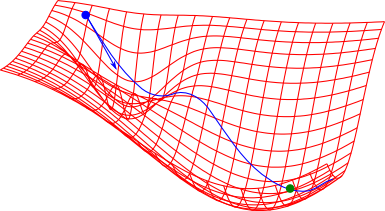
以下はWoodburyの公式での実装例です. 隠れ層の素子数は $4$ です.
多クラス $(K > 2)$ の場合は, ソフトマックス関数を用いてクラス $k$ に関する出力が \[ y_k(\mathbf{x},\mathbf{w})= p(C_k|\mathbf{x},\mathbf{w})=\frac{\exp(a_k(\mathbf{x},\mathbf{w}))}{\sum_i \exp(a_i(\mathbf{x},\mathbf{w}))} \] とモデル化されるのでした.
最小化するものは \[ E = -\sum_{n=1}^N\sum_{k=1}^Kt_{nk}\ln y_k \] です.
出力層での誤差を計算すると, $n$ 番目のデータに対して \[ \begin{aligned} \frac{\partial y_k}{\partial a_i} &= y_k(t_i-y_i) \\ \frac{\partial E_n}{\partial a_i} &= y_i-t_i \end{aligned} \] となりますので, これを使って誤差逆伝播を行います.
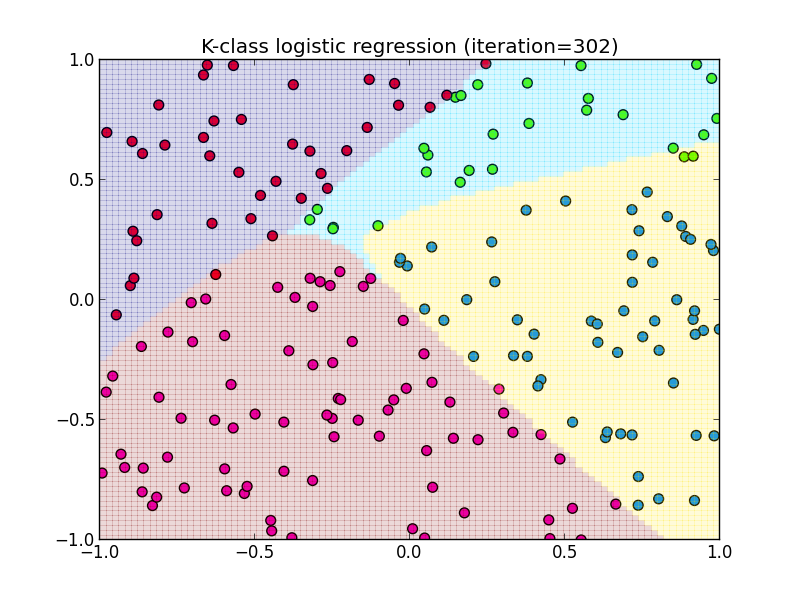
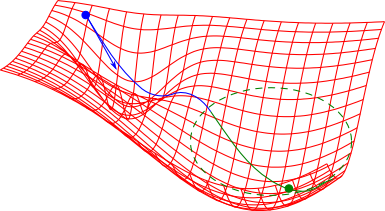
以下はBFGSの公式での実装例です. 隠れ層の素子数は $4$ です.
正則化
ニューラルネットワークによって表されるモデルの複雑さは隠れ層の素子の数 $M$ によって決まります. 既に説明したように, $M$ の大小によって汎化性能が変わります.
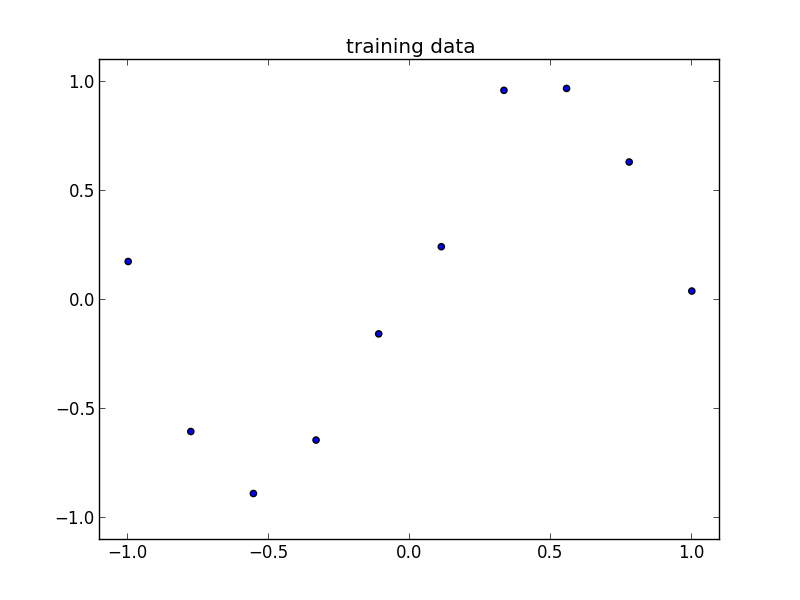
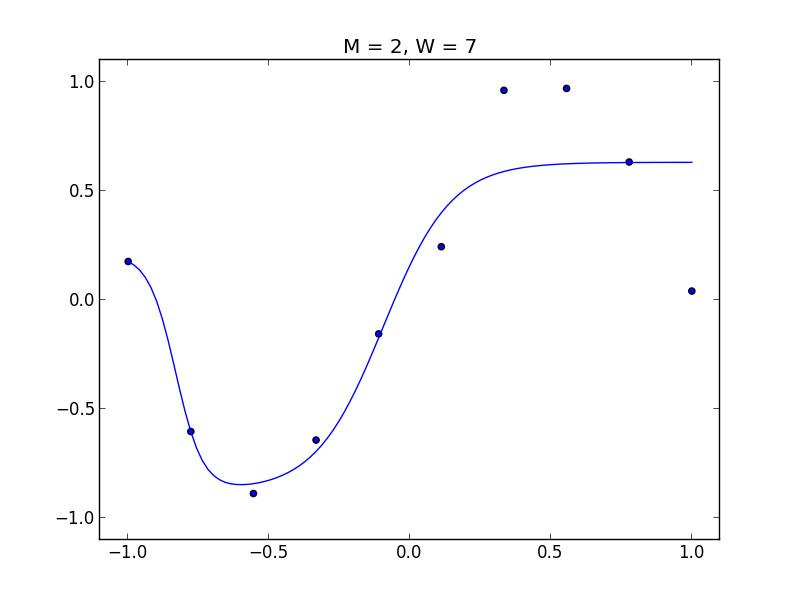
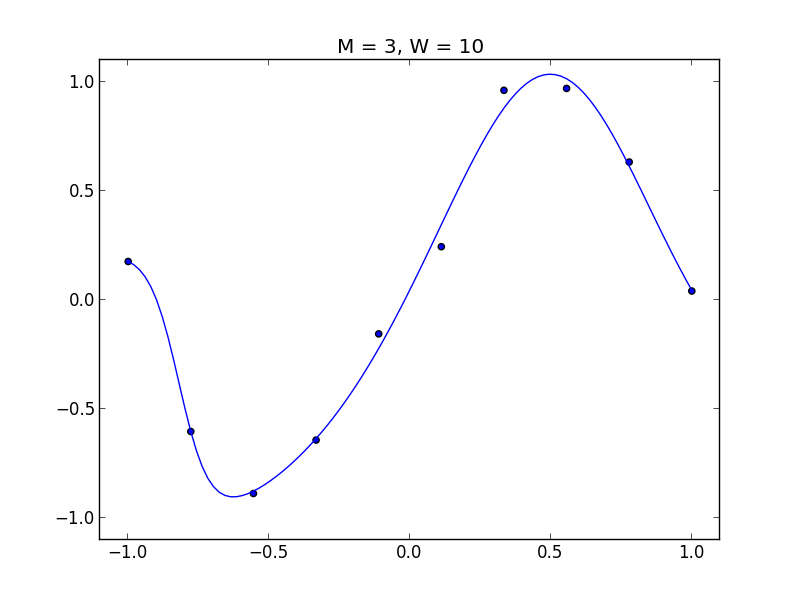
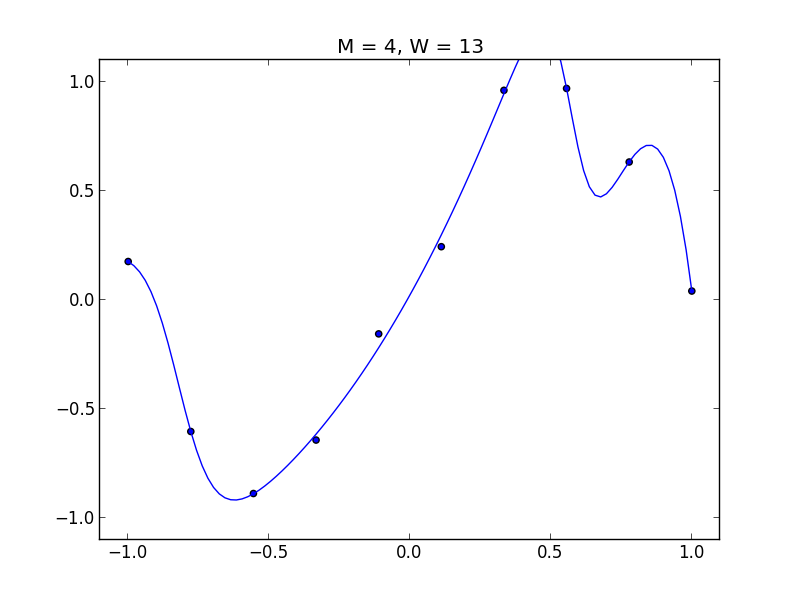
以下のデータで見てみましょう.
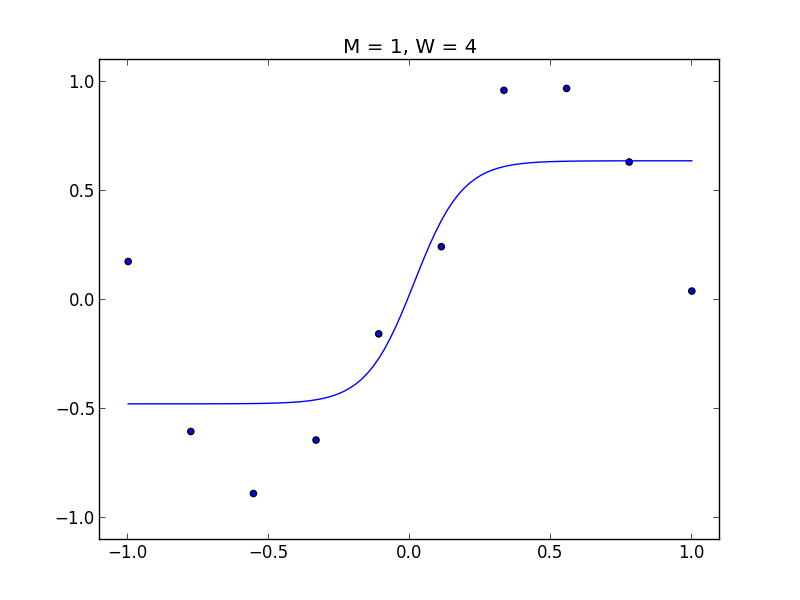
$M = 1$
$M = 2$
$M = 3$
$M = 4$, 過学習が見られます.
単純な対策は既に説明したように, 誤差関数に正則化項 (regularization term) \[ \widetilde{E}(\mathbf{w}) = E(\mathbf{w}) + \frac{\lambda}{2}||\mathbf{w}||^2 \] を付与する事です.
この時 \[ \nabla \widetilde{E}(\mathbf{w}) = \nabla E(\mathbf{w}) + \lambda\mathbf{w} \] となります.
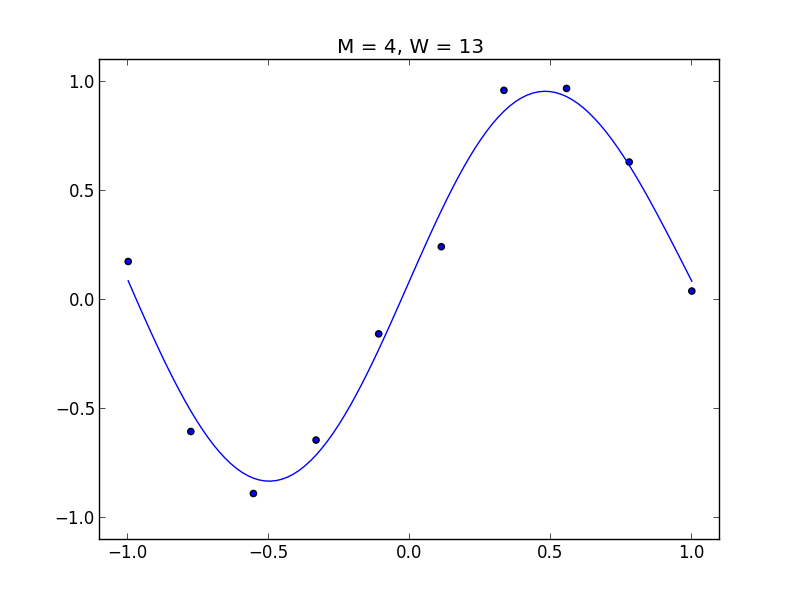
以下は$M=4$において$\lambda=10^{-3}$の正規化項を付与した例です.
第9回はここで終わります
次回からテキスト第5章のカーネル法に進みたいと思います.