パターン認識・
機械学習勉強会
第7回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

ニューラルネットワーク

本日はPRML第5章に進みます.

第1回に紹介したように, ニューラルネットワークとは例えば下図のような素子を複数接続して出来る識別器です.

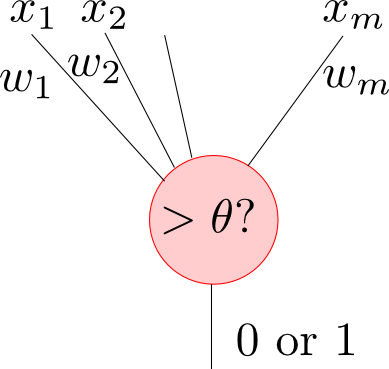
一般化すると, 入力が $m$ 次元である素子は

• 重みパラメータ (weight parameter) : $w_0,w_1,w_2,\ldots,w_m$
• 活性化関数 (activation function) : $h$

から構成され \[ f(x_1,x_2,\ldots,x_m) = h(w_1x_1+w_2x_2+\cdots+w_mx_m+w_0) \] という関数を表します.

例えば $h$ を ヘヴィサイド関数 (Heaviside function) \[ h(a) = \left\{\begin{array}{cc} 0 & (a < 0) \\ 1 & (a > 0) \end{array}\right. \] とし, $w_0 = -\theta$ とおけば最初に紹介した素子となります.

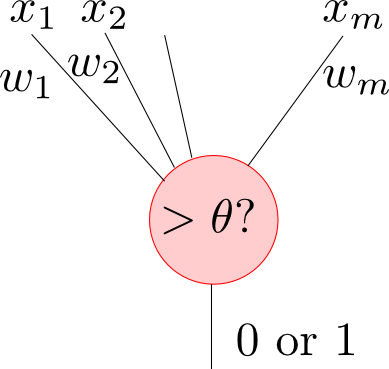
この素子を一つだけ用いた識別器は 単純パーセプトロン (simple perceptron) と呼ばれます.

興味のある方はテキストを参照して下さい. 今回は, より一般的な多層のニューラルネットワークに絞って解説を行います.

ヘヴィサイド関数は不連続なので数学的な取り扱いが面倒です.

そこで活性化関数としてはロジスティックシグモイド関数 \[ h(a) = \frac{1}{1+\exp(-a)} \] や \[ h(a) = \tanh a \] やソフトマックス関数などが使われる事が多いです. 詳しくは後で説明します.

さて, このような素子を多段に接続すると一体何が起こるのでしょうか.

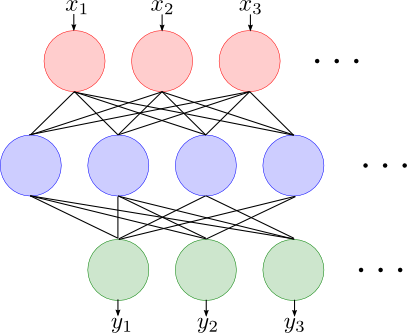
ダミー変数 $x_0 = 1$ を使う事にすると, $m$入力の 素子一つは \[ y = h\left(\sum_{i=0}^m w_ix_i\right) \] と書けます.

前回までに説明した線形識別モデルは \[ y=f\left(\sum_i w_i\phi_i(\mathbf{x})\right) \] という形で表せるので, ニューラルネットワークの素子一つだけの場合に対応する事が分かります.

2層の場合を考えます.

1層目に $m$ 個の素子を用意した場合, 入力が $D$ 次元ならば \[ y = h_2\left(\sum_{i=0}^{m} w^{(2)}_ih_1\left(\sum_{j=0}^{D}w^{(1)}_{ij} x_j\right)\right) \] となります. ただし $w^{(1)}_{ij}$ は1層目の $i$ 番目の素子の入力 $j$ の重み, $w^{(2)}_i$ は2層目の素子の入力 $i$ の重み, $h_1,h_2$ はそれぞれの層の活性化関数です.

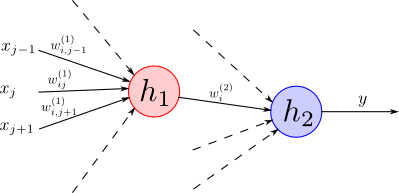
線形識別モデル \[ y=f\left(\sum_i w_i\phi_i(\mathbf{x})\right) \] と2層のニューラルネットワーク \[ y = h_2\left(\sum_{i=0}^{m} w^{(2)}_ih_1\left(\sum_{j=0}^{D}w^{(1)}_{ij} x_j\right)\right) \] を見比べると, 基底 $\phi_i(\mathbf{x})$ が $\displaystyle h_1\left(\sum_{j=0}^{D}w^{(1)}_{ij} x_j\right)$ に置き換わっています.

つまり,

• 線形識別モデルでは基底関数があらかじめ固定されている.

のに対して,

• 多層ニューラルネットワークでは基底関数自体も学習の対象である.

という一般化が行われています.

以上の考察から素子の数や活性化関数についてより良く理解出来ます.

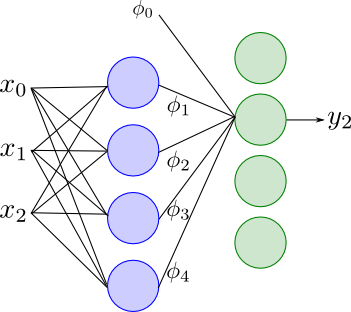
例えば, 2層のネットワークにおいて第1層の活性化関数は基底の形状を定めます. 青い素子が4つなので基底は4つです.

第2層の活性化関数は線形識別モデルにおける $f$ に相当します. 従って識別の問題ではロジスティックシグモイド関数などを使う事になります.

誤差逆伝播法

続いて, ネットワークの訓練方法について説明します.

これまでと同様に, 最小二乗法や最尤法やMAP推定法などを利用します. とりあえずここでは何らかの関数 $E(\mathbf{w})$ の最小化をしたいとしましょう.

$E(\mathbf{w})$ は非線形な関数となりますので, 勾配 $\nabla E(\mathbf{w})$ やヘッセ行列 $\mathbf{H}(\mathbf{w})=\nabla\nabla E(\mathbf{w})$ を是非使いたいですが, ニューラルネットワークは複雑なのでこの計算が面倒です.

誤差逆伝播法 もしくは バックプロパゲーション (backpropagation) とはニューラルネットワークの偏微分係数を効率的に計算する為の手法です.

基本的なアイデアは合成微分則の利用です.

例えば \[ F(x) = f(g(h(x))) \] の導関数は, 具体的な関数形を求めなくてもその導関数を計算する事が出来ます.

つまり, \[ \frac{\mathrm{d} F(x)}{\mathrm{d} x} = \frac{\mathrm{d}f(z)}{\mathrm{d}z}\frac{\mathrm{d}z}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm{d}x}\quad (z = g(y), y=h(x)) \] という形にして, $f,g,h$ それぞれに関する微分係数の計算に帰着する事が出来ます.

$E(\mathrm{w})$ が個々の学習データ毎の誤差の和 \[ E(\mathbf{w}) = \sum_{n=1}^N E_n(\mathbf{w}) \] に分解出来るとして, $\nabla E_n(\mathbf{w})$ について考えます.

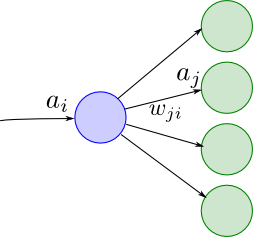
素子 $i$ から素子 $j$ への接続の重みを $w_{ji}$ として, 全ての $i,j$ の組合せに対して \[ \frac{\partial E_n}{\partial w_{ji}} \] を計算する事が目標です.

素子 $i$ の出力を $z_i$, 素子 $j$ への入力和を $a_j$ とします.

$E_n$ は $a_j$ を介してのみ $w_{ji}$ に依存する事に注意すれば \[ \frac{\partial E_n}{\partial w_{ji}} = \frac{\partial E_n}{\partial a_j}\frac{\partial a_j}{\partial w_{ji}} \] となります.

今後 $\delta_j = \partial E_n/\partial a_j$ と書くことにします. また, $a_j = \sum_i w_{ji} a_i$ なので $\partial a_j/\partial w_{ji} = z_i$ ですから \[ \frac{\partial E_n}{\partial w_{ji}} = \delta_j z_i \] となります.

ある入力 $\mathbf{x}$ に対して各 $z_i$ は簡単に計算する事が出来ますから, 各 $\delta_j$ を計算する事が出来れば十分です.

ここで $\delta_i$ について考えると, $E_n$ は素子 $i$ の出力を受け取る素子 $j$ の入力 $a_j$ を介して $a_i$ に依存するので合成微分則より \[ \delta_i = \frac{\partial E_n}{\partial a_i} = \sum_j \frac{\partial E_n}{\partial a_j}\frac{\partial a_j}{\partial a_i} = \sum_j\delta_j\frac{\partial a_j}{\partial a_i}\] となります.

さらに, 素子 $i$ の活性化関数を $h_i$ とすると \[ a_j = \sum_i w_{ji} h_i(a_i) \] であったので, \[ \frac{\partial a_j}{\partial a_i} = w_{ji} h_i'(a_i) \] となります.

以上をまとめると, 誤差 $\delta_i$ の逆伝播公式 \[ \delta_i = h_i'(a_i) \sum_j w_{ji}\delta_j \] が得られます.

ネットワークの出力部における $\delta$ の値は直接計算する事が出来るので, そこから逆にネットワークを辿りながら各 $\delta$ を計算する事になります.

まとめましょう.

逆伝播法の計算量は重みパラメータの数 $W$ が十分大きい場合には $\mathcal{O}(W)$ となります.

各 $w_{ji}$ に対する $W$個の偏導関数を一回の誤差伝播で求めてしまう事が出来る大変効率の良いアルゴリズムとなっています.

例

以下のような2層のネットワークを考えます. 入力は $D$ 次元, 第1層(隠れ層)の素子は $M$ 個で活性化関数は $\tanh$, 第2層(出力層)の素子は $K$ 個で活性化関数は恒等関数とします.

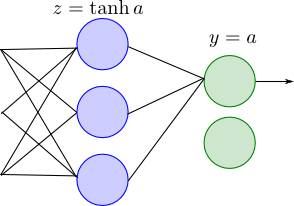
誤差関数には残差平方和の半分 \[ E_n = \frac{1}{2}\sum_{k=1}^K(y_k-t_k)^2 \] を使う事にします.

すると, 出力ユニット $k$ に対する誤差は \[ \delta_k = \frac{1}{2}\frac{\partial }{\partial a_k} \sum_{k=1}^K(y_k-t_k)^2 = y_k-t_k \qquad(\because y_k=a_k)\] となります. これは出力の誤差に他なりません. これが$\delta_i$ を「誤差」と呼ぶ理由です.

隠れユニット $j$ に対する誤差は \[ (\tanh x)' = 1-\tanh^2 x \] である事に注意すると \[ \delta_j = (1-\tanh^2 a_j)\sum_{k=1}^K w_{jk}\delta_k \] となります.

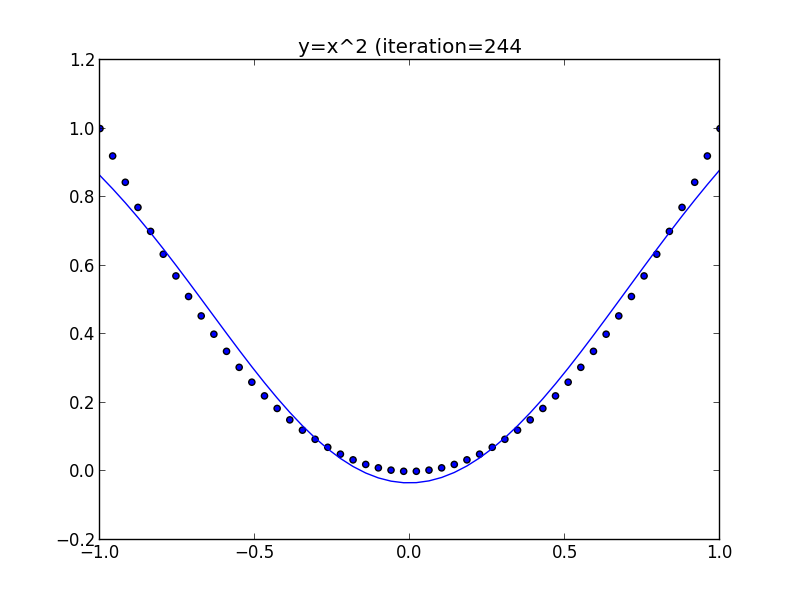
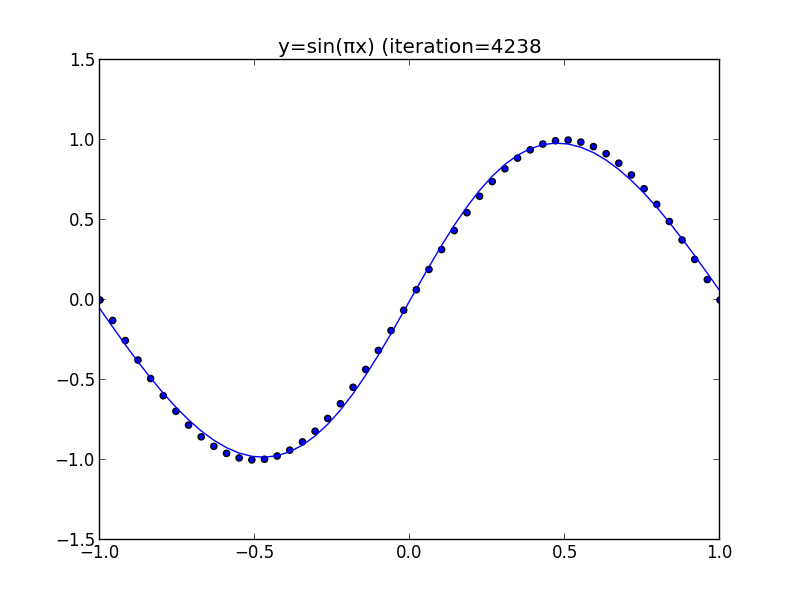
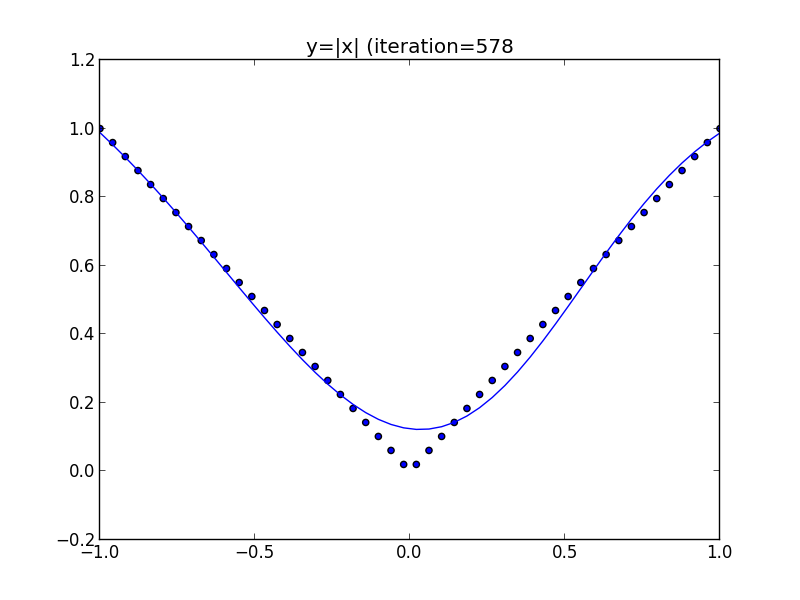
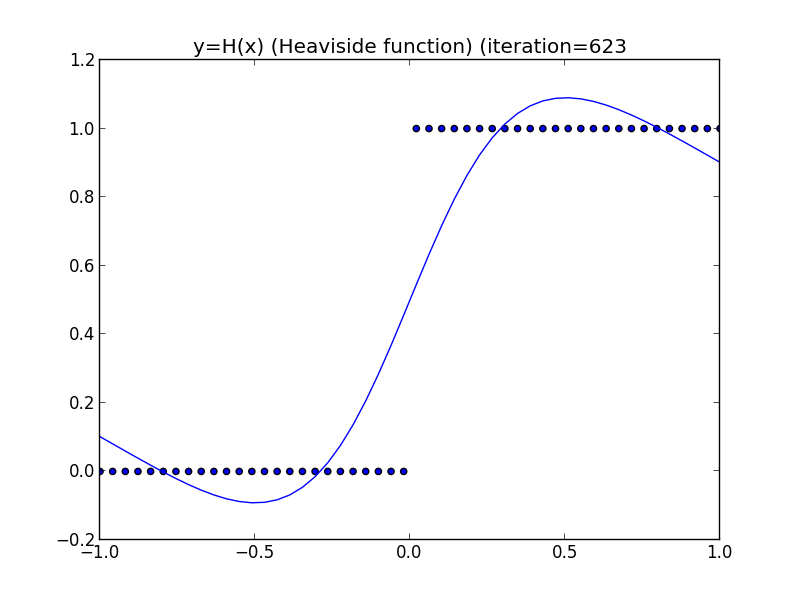
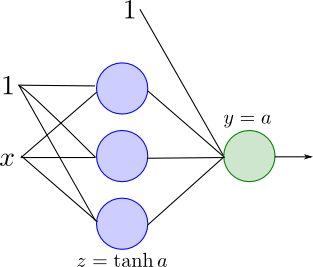
今のモデルを用いてテキスト5.1節の図5.3を再現してみたいと思います.

この例では隠れ層は3素子, 出力層は1素子です. ダミー変数も考慮して最適化するパラメータは10個となります.

学習は再急降下法を利用して行いました. 復習すると再急降下法では適当なパラメータ $\alpha$ を定め \[ \begin{aligned} \mathbf{w}^{(t+1)}&=\mathbf{w}^{(t)} - \alpha\nabla E(\mathbf{w})\\ &=\mathbf{w}^{(t)} - \alpha\sum_{n=1}^N\nabla E_n(\mathbf{w})\\ \end{aligned} \] による反復を行います.

今は $E(\mathbf{w})$ を最小化したいので, 符号はマイナスです.

各点が学習データ(50点), 曲線がニューラルネットワークの出力です.

prog7-1.py

隠れ層の素子が十分にあるならばニューラルネットワークは任意の(厳密には定義域が有界で閉である)関数を任意の精度で近似出来るという事が分かっています.

再急降下法は性能が低いので,ヘヴィサイド関数では良い精度を達成出来ていませんが, 来週さらに良い方法を紹介します.

第7回はここで終わります

次回はニューラルネットワークの訓練に関する技術的な話題をいくつか紹介します. その後,パターン識別への応用やベイズ的な手法の紹介をします.