パターン認識・
機械学習勉強会
第6回
@ワークスアプリケーションズ
中村晃一2014年3月27日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
線形識別モデル:ベイズロジスティック回帰
前回・前々回に引き続き線形識別モデル(PRML第4章)を進めていきます.
今回はロジスティック回帰のベイズ的な取り扱いについて紹介します.
パラメータ $\mathbf{w}$ の事前分布を $\pi(\mathbf{w})$ とすれば ベイズの定理より 事後分布は \[ \pi(\mathbf{w}|D) \propto L(\mathbf{w}|D)\pi(\mathbf{w}) \] となります.
前回, ロジスティック回帰の計算において「正則化項を付与する場合もあるか?」という質問がありましたが, \[ \pi(\mathbf{w}) = \mathcal{N}(\mathbf{0}, \sigma^2\mathbf{I}) \] であるならば, \[ \ln\pi(\mathbf{w}|D)=\ln L(\mathbf{w}|D) - \color{red}{\frac{1}{2\sigma^2}||\mathbf{w}||^2} + \mathrm{const}. \] となるので, ベイズロジスティックモデルの特別な場合として正則化項が現れます.
さて, \[ \pi(\mathbf{w}|D) \propto L(\mathbf{w}|D)\pi(\mathbf{w}) \] における事後分布 $\pi(\mathbf{w}|D)$ は一般に複雑な形の関数になり解析的に調べる事が難しいですが, MCMC法を使うと $\pi(\mathbf{w}|D)$ から直接サンプリングを行う事が出来ます.
ランダム・ウォークによるMH法を利用する事にすると, 推移 $\mathbf{w} \rightarrow \mathbf{w}'$ の採択確率が \[ \min\left\{\frac{\pi(\mathbf{w}'|D)}{\pi(\mathbf{w}|D)}, 1\right\} \] となるのでした.
定数倍はキャンセルされるのでこれは \[ \min\left\{\frac{L(\mathbf{w}'|D)\pi(\mathbf{w}')}{L(\mathbf{w}|D)\pi(\mathbf{w})}, 1\right\} \] と等しいです.
アンダーフローを回避する為に一旦 \[ \ln L(\mathbf{w}'|D) + \ln\pi(\mathbf{w}') - \ln L(\mathbf{w}|D) - \ln\pi(\mathbf{w}) \] を求める事にします.
前回説明したように2クラスの場合には \[ \ln L(\mathbf{w}|D) = \sum_i\left[t_i\ln\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)+(1-t_i)\ln\left\{1-\sigma(\mathbf{w}^T\boldsymbol{\phi}_i)\right\}\right] \] です.
また例えば, 事前分布が \[ \pi(\mathbf{w}) = \mathcal{N}(\mathbf{w}_0,\mathbf{\Sigma}) \] の時には \[ \ln \pi(\mathbf{w}) = -\frac{1}{2}(\mathbf{w}-\mathbf{w}_0)^T\mathbf{\Sigma}^{-1}(\mathbf{w}-\mathbf{w}_0)+\mathrm{const}. \] となりますので, これで計算しましょう.
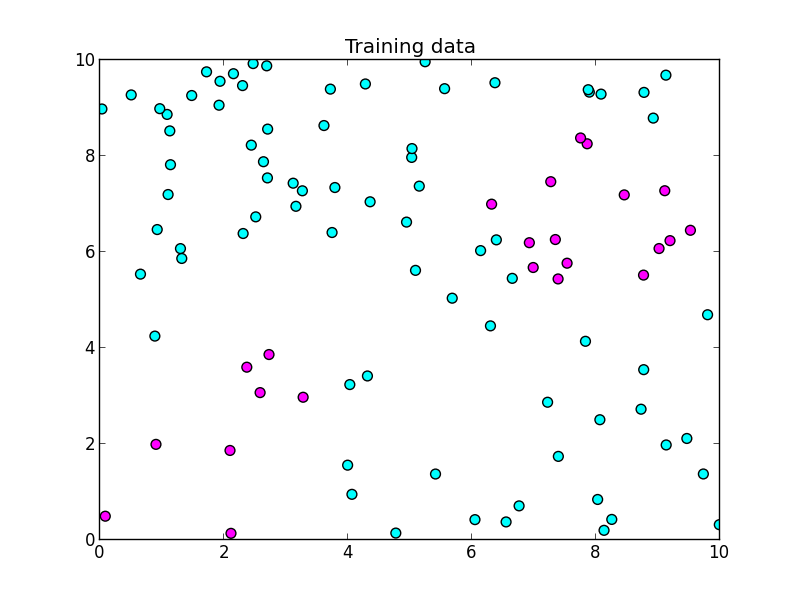
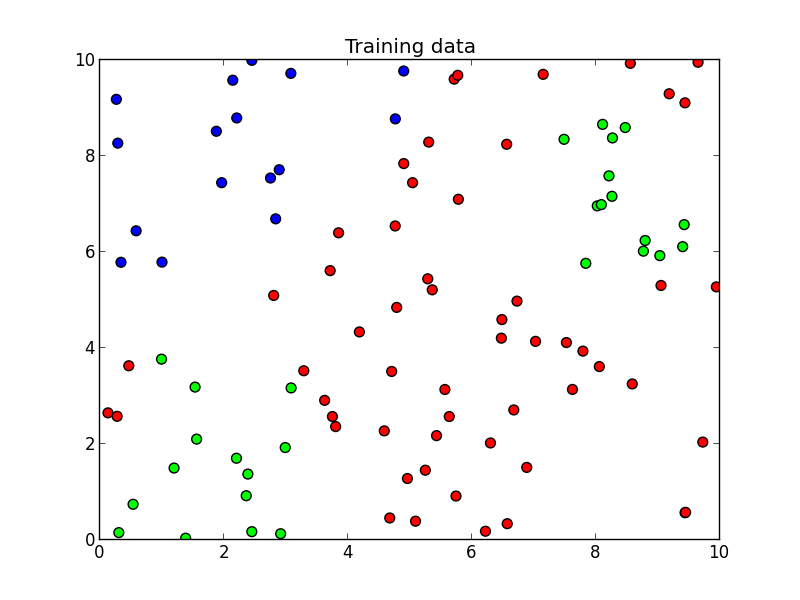
前回と同じく以下を学習データとします. 基底も前回と同じく $4\times 4$ 個のガウス基底を配置します.
パラメータは以下のようにしました.
- マルコフ連鎖の初期状態: $\mathbf{w}^{(0)} = \mathbf{0}$
- ランダム・ウォークの標準偏差パラメータ: $1$
- バーンイン期間: $1000$
- 事前分布の平均: $\mathbf{w}_0 = \mathbf{0}$
- 事前分布の分散: $\mathbf{\Sigma} = 100\mathbf{I}$
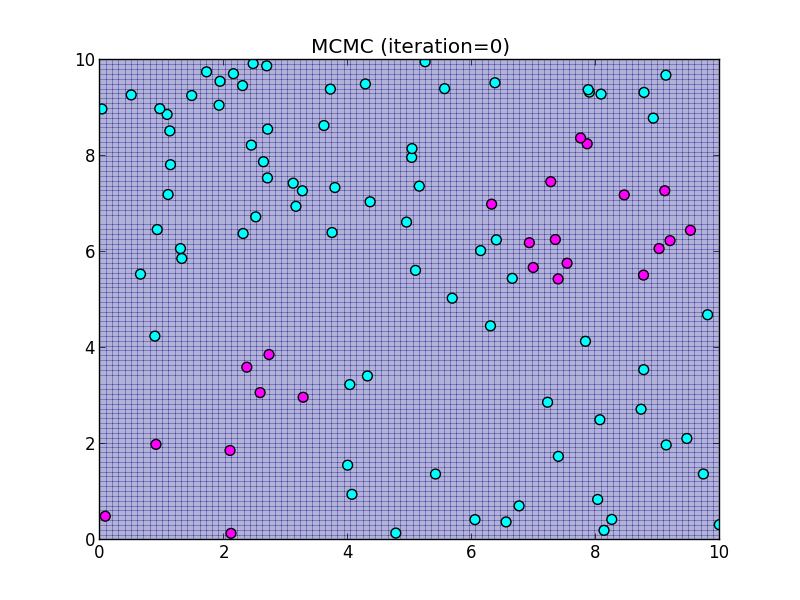
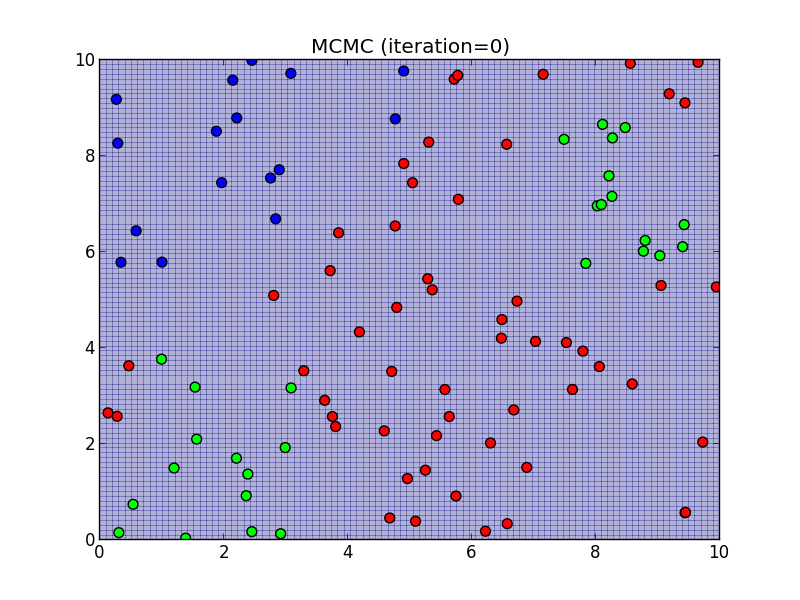
初期状態.
初期状態.
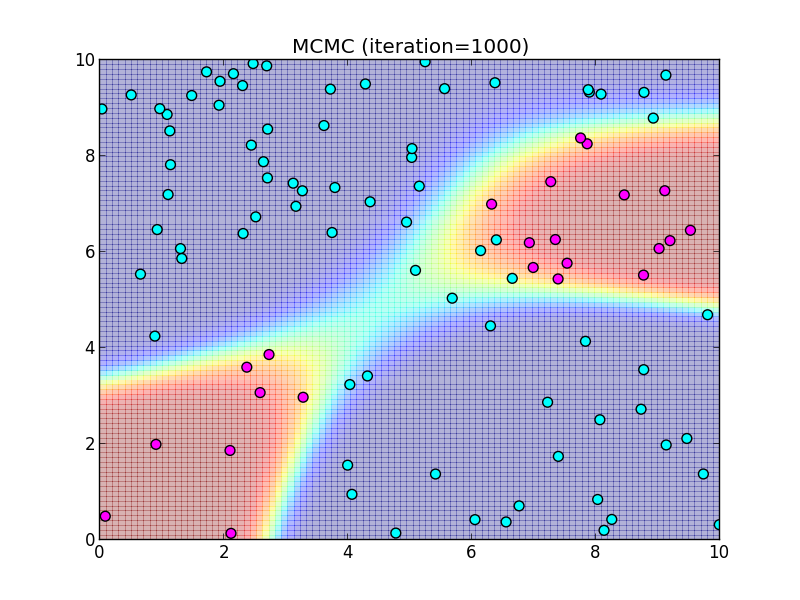
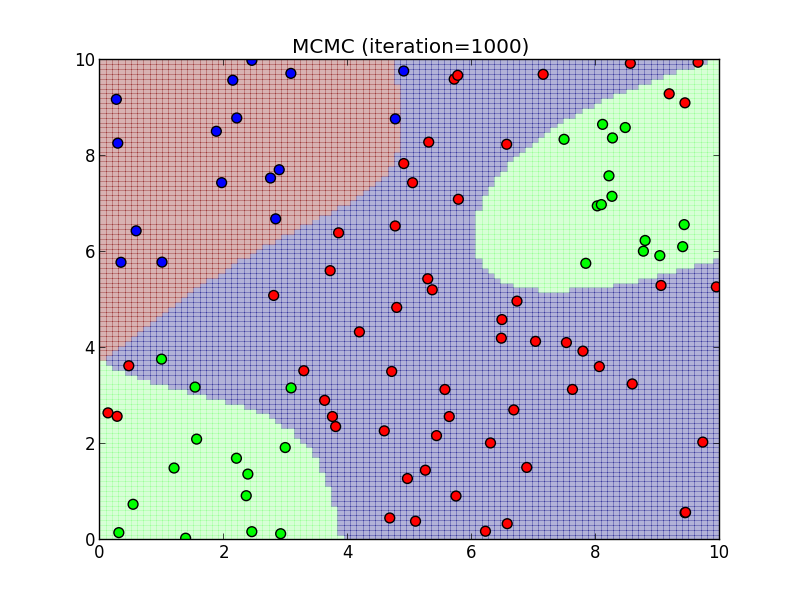
(バーンイン後)1000ステップ.
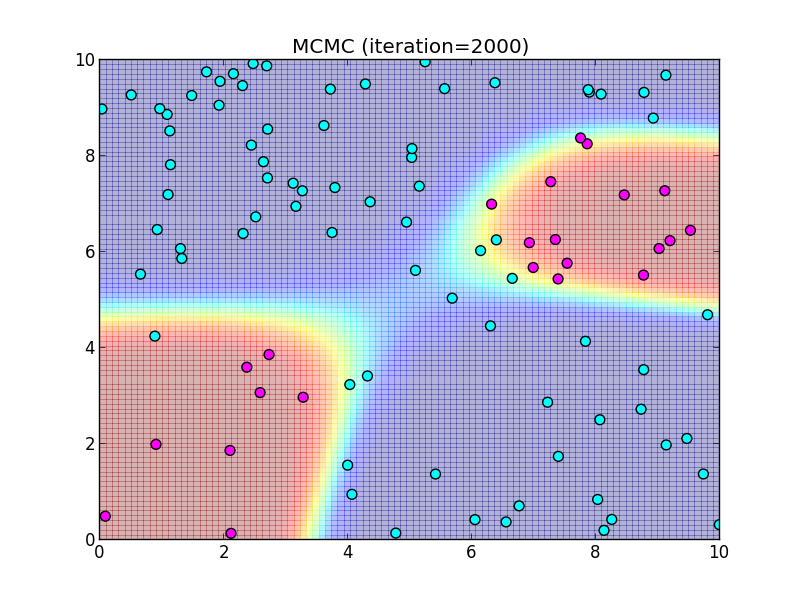
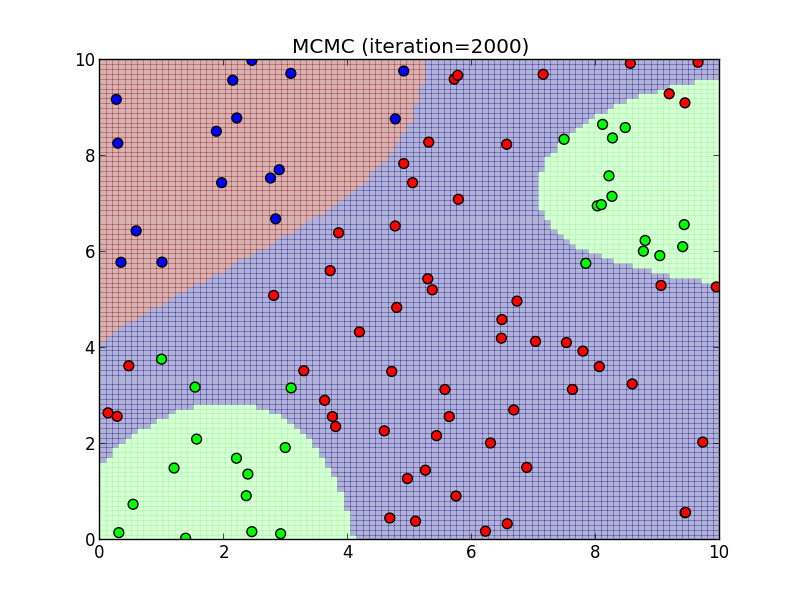
2000ステップ.
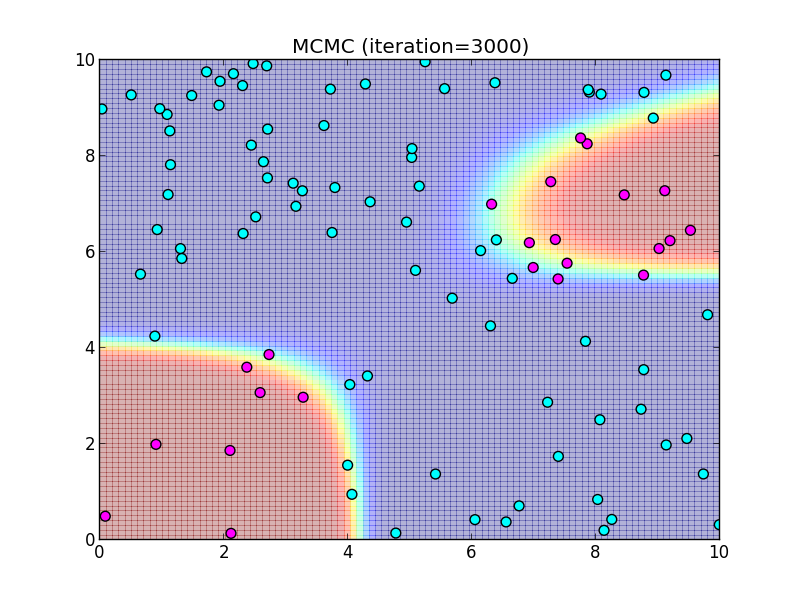
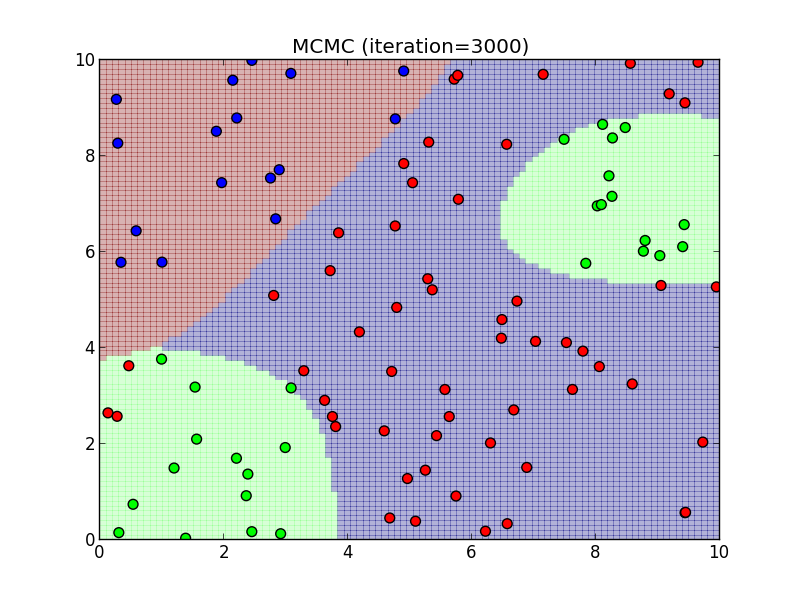
3000ステップ.
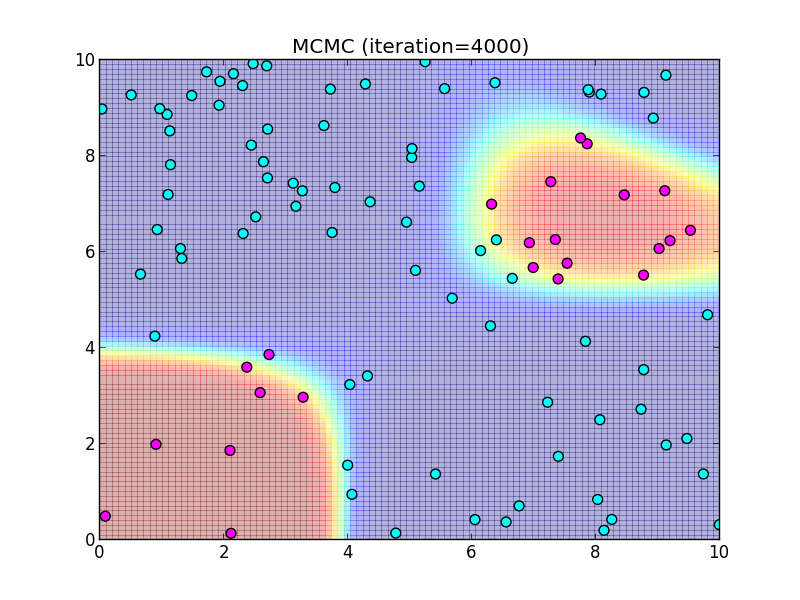
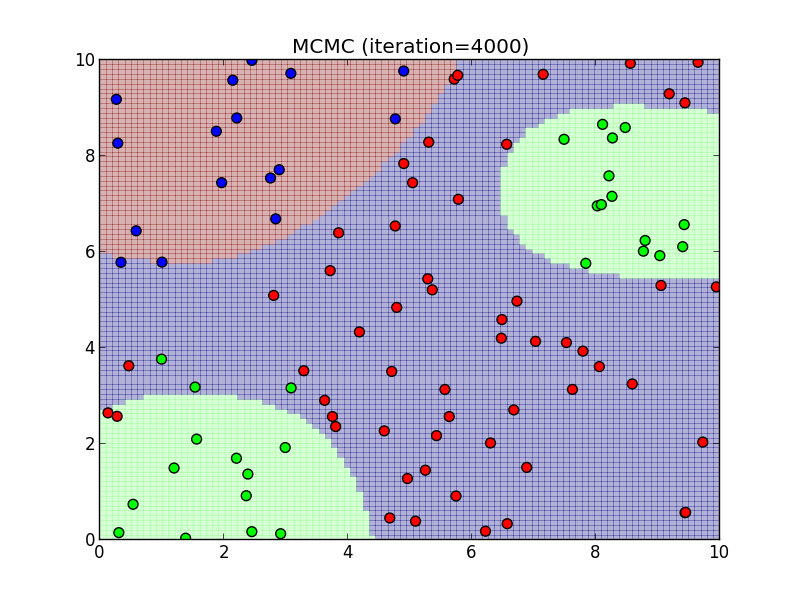
4000ステップ.
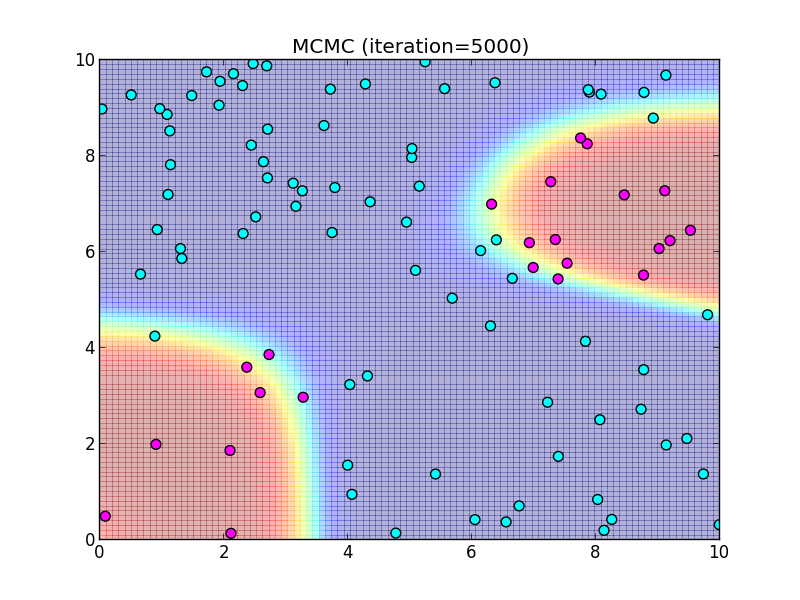
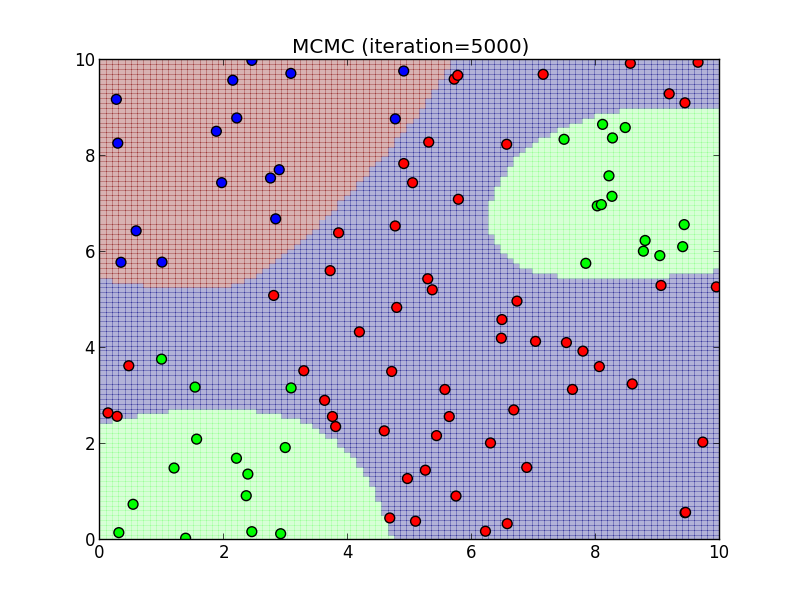
5000ステップ.
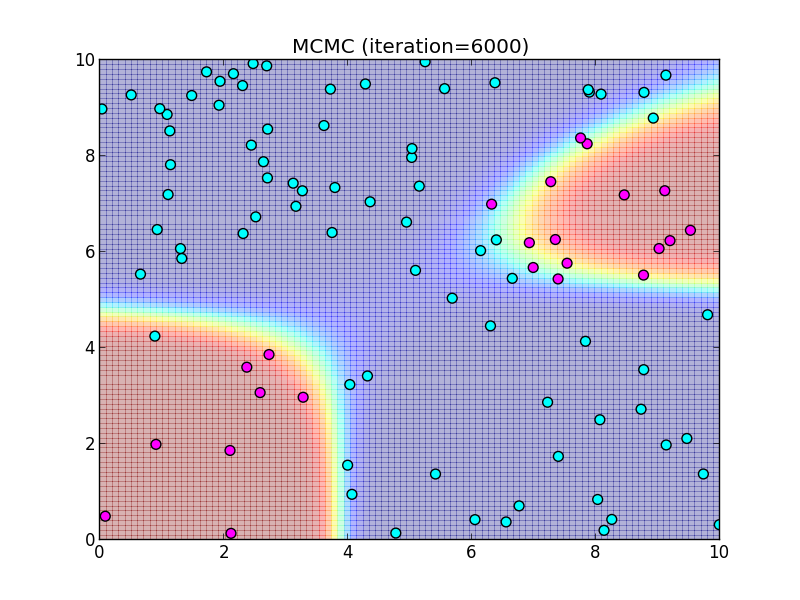
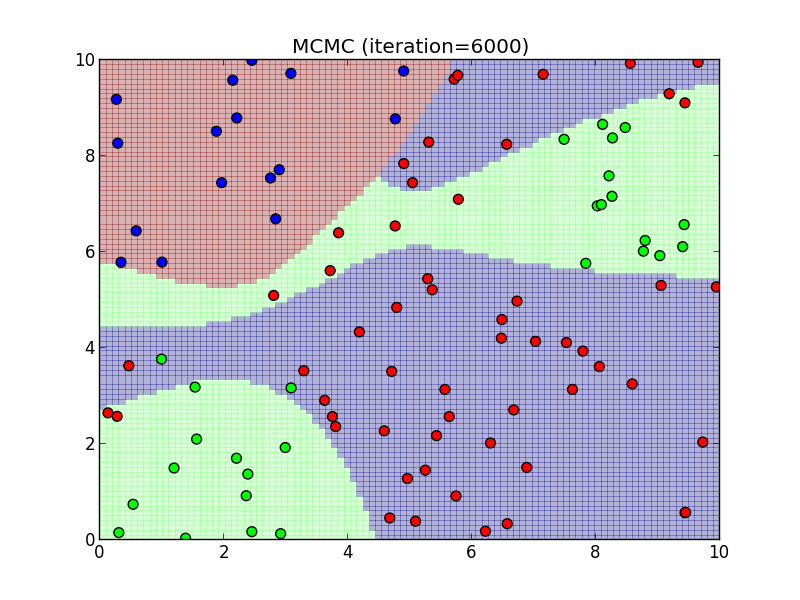
6000ステップ.
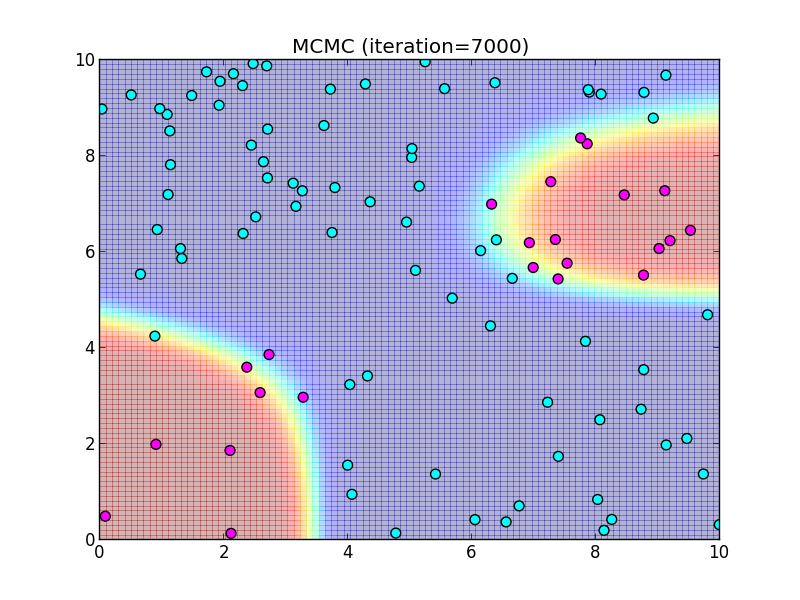
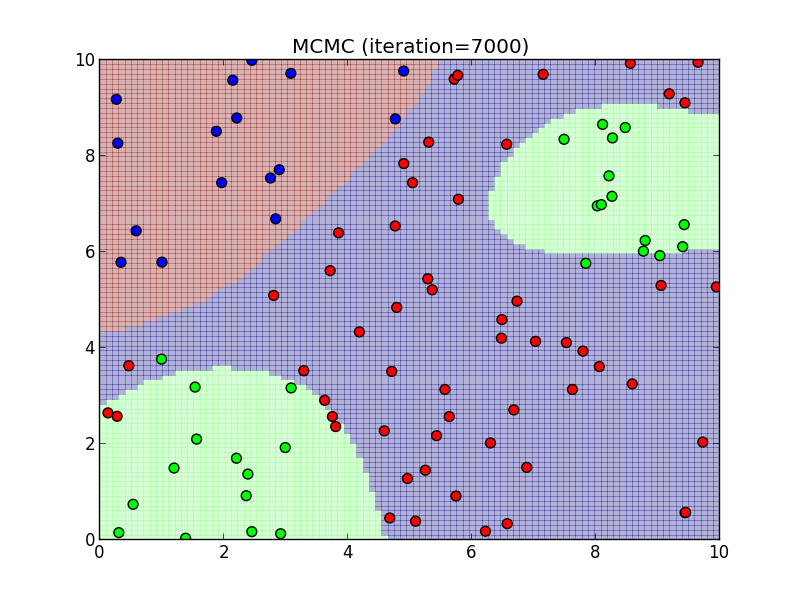
7000ステップ.
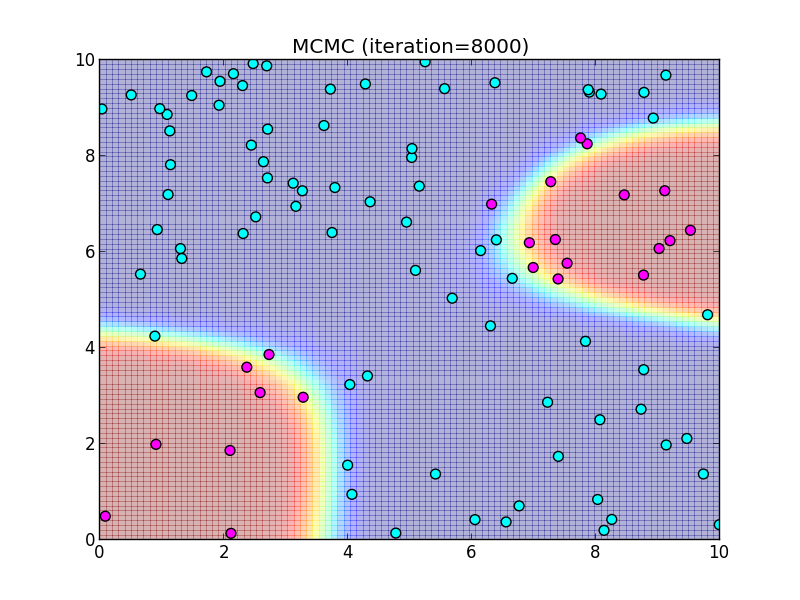
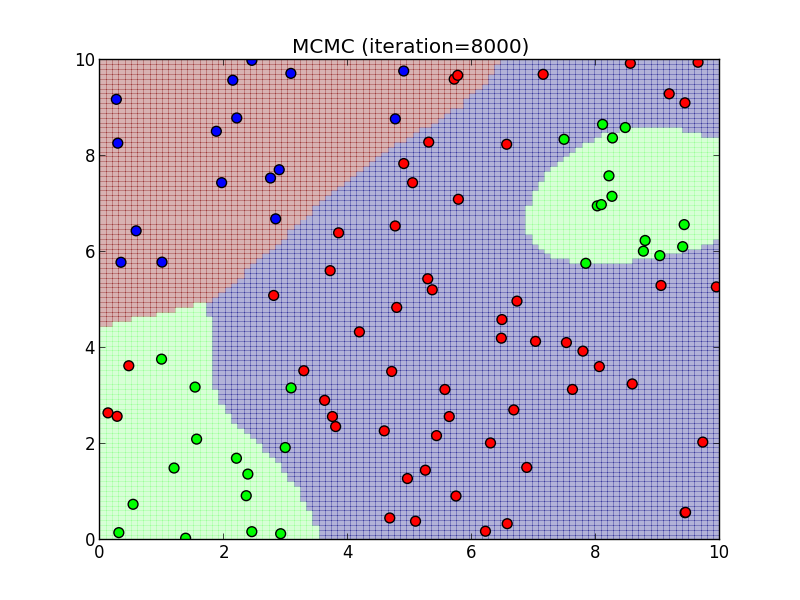
8000ステップ.
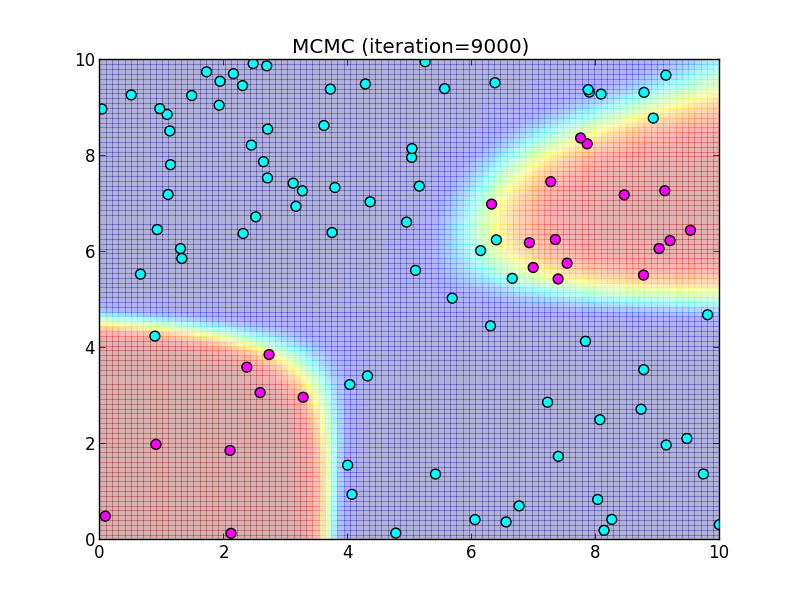
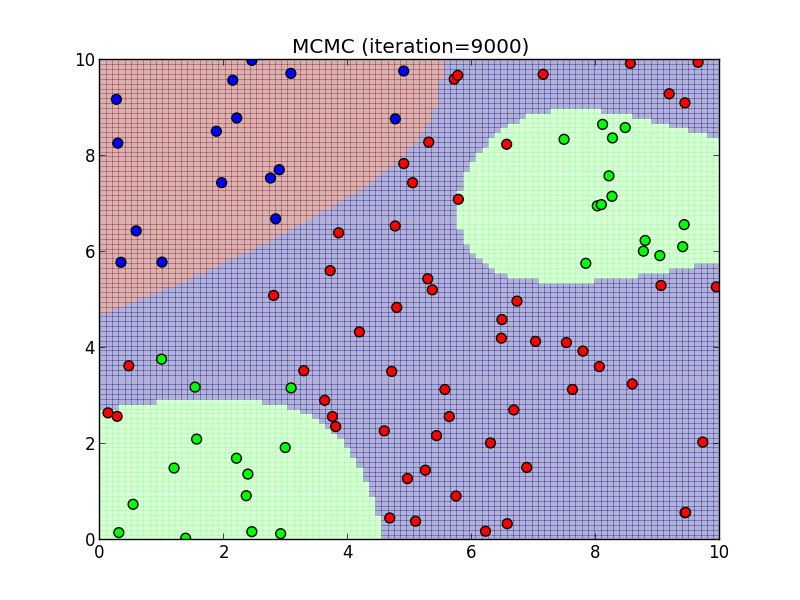
9000ステップ.
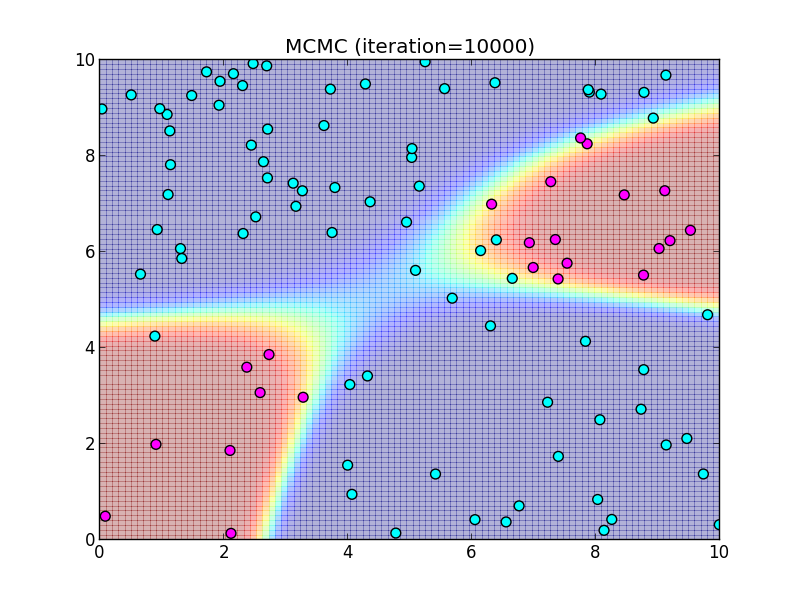
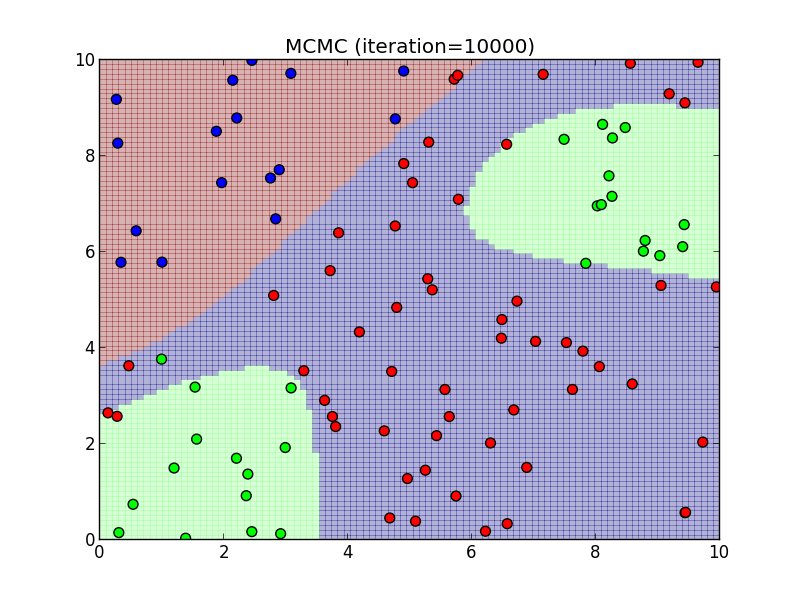
10000ステップ.
多クラスの場合も試してみましょう. 前回説明したように, 多クラスの場合の対数尤度は \[ \ln L(\mathbf{w}_1,\ldots,\mathbf{w}_K|D) = \sum_{i=1}^n\sum_{k=1}^K t_{ik}\ln p(C_k|\boldsymbol{\phi}_i) \] となります. ここで $p(C_k|\boldsymbol{\phi}_i)$ はソフトマックス関数 \[ p(C_k|\boldsymbol{\phi}_i) = \frac{\exp(\mathbf{w}_k^T\boldsymbol{\phi}_i)}{\sum_j \exp(\mathbf{w}_j^T\boldsymbol{\phi}_i)} \] です.
計算上の注意ですが, ソフトマックス関数の対数は \[ \ln p(C_k|\boldsymbol{\phi}_i) = \mathbf{w}_k^T\boldsymbol{\phi}_i - \ln \sum_j \exp(\mathbf{w}_j^T\boldsymbol{\phi}_i) \] となるので, 右辺第2項の部分にはより数値的に安定な $\mathrm{logsumexp}$ 関数を利用する事が出来ます. \[ \ln p(C_k|\boldsymbol{\phi}_i) = \mathbf{w}_k^T\boldsymbol{\phi} - \mathrm{logsumexp}_j(\mathbf{w}_j^T\boldsymbol{\phi}_i) \]
また $\sum_{k=1}^Kt_{ik}=1$ である事に注意すれば \[ \sum_{k=1}^Kt_{ik}\ln p(C_k|\boldsymbol{\phi}_i) = \sum_{k=1}^Kt_{ik}\mathbf{w}_k^T\boldsymbol{\phi}_i - \mathrm{logsumexp}_j(\mathbf{w}_j^T\boldsymbol{\phi}_i) \] というシンプルな形に変形出来ます.
以下を学習データとします. 3クラスのケースです.
パラメータは以下のようにしました.
- マルコフ連鎖の初期状態: $\mathbf{w}^{(0)} = \mathbf{0}$
- ランダム・ウォークの標準偏差パラメータ: $0.5$
- バーンイン期間: $1000$
- 事前分布の平均: $\mathbf{w}_{k,0} = \mathbf{0}$
- 事前分布の分散: $\mathbf{\Sigma}_k = 100\mathbf{I}$
初期状態.
初期状態.
(バーンイン後)1000ステップ.
2000ステップ.
3000ステップ.
4000ステップ.
5000ステップ.
6000ステップ.
7000ステップ.
8000ステップ.
9000ステップ.
10000ステップ.
今回はランダムウォークに基づくMH法を利用してある程度上手く行きましたが, ランダムウォークの一歩の大きさをどの程度にするかなど自明でない問題があります. 一歩を大きく取り過ぎるとなかなか収束せず, 小さく取り過ぎると偏ったサンプリングになってしまいます.
PRMLの11.4節ではより良い手法として スライスサンプリング (Slice sampling) という手法が紹介されています. こちらも参照してください.
線形識別モデル:フィッシャーの線形判別
ロジスティックモデルはデータの確率的生成モデルに基づくかなり厳密な方法であると言えますが, それ以外の考え方も面白いので是非知っておきましょう.
特徴ベクトルの次元が $D$ 次元であるならば \[ \mathbf{w}^T\boldsymbol{\phi} \] は $D$ 次元空間から1次元空間への射影であると考える事が出来ます.
2クラスの判別は, この射影がある閾値 $\theta$ を超えるか否かで判別しているという事に他なりません.

この時, 2つのクラスが出来るだけ分離されるように $\mathbf{w}$ を調整する事が目標となります.
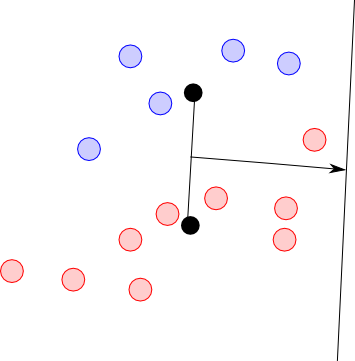
一つの考え方として2つのクラスの重心が十分に離れるように射影するという方法が考えられます.
クラス $C_i$ に属す学習データの数を $N_i$ とすると, 各クラスの重心は \[ \boldsymbol{\mu}_1 = \frac{1}{N_1}\sum_{\boldsymbol{\phi}_i \in C_1}\boldsymbol{\phi}_i, \boldsymbol{\mu}_2 = \frac{1}{N_2}\sum_{\boldsymbol{\phi}_i \in C_2}\boldsymbol{\phi}_i \] となりますので, この場合 \[ |\mathbf{w}\boldsymbol{\mu}_1 - \mathbf{w}\boldsymbol{\mu}_2|^2 \] を最大化する事となります.
しかし, この方法は単純すぎて上手く行きません.
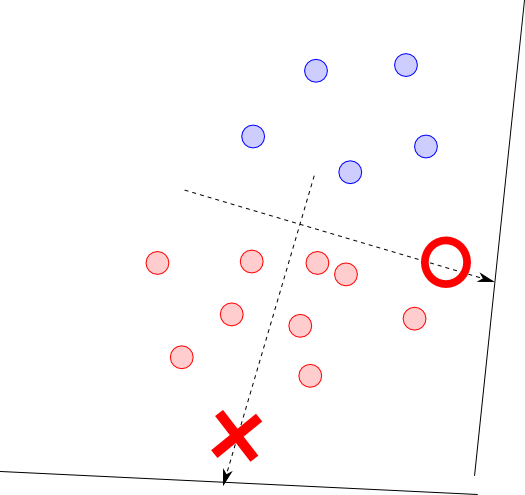
射影軸上での重心が離れていても, 下図のようにデータの分散が大きいならば上手く分離されないという事が起こります.
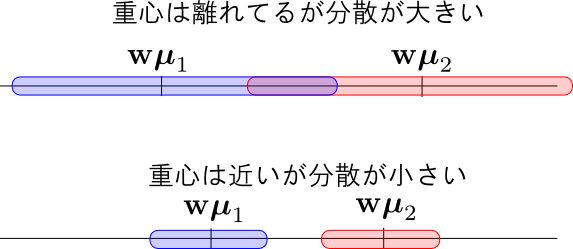
そこで, 以下の量を最大化する事を考えます. これは, 重心が出来るだけ離れ, 分散が出来るだけ小さい時に最大になります. これを フィッシャーの判別基準 (Fisher's criterion) と呼びます.
\[ J(\mathbf{w}) = \frac{|\mu_1-\mu_2|^2}{\sigma_1^2 + \sigma_2^2} \] \[ \mu_i = \frac{1}{N_i}\sum_{\boldsymbol{\phi} \in C_i}\boldsymbol{\phi},\quad \sigma_i^2 = \sum_{\boldsymbol{\phi}\in C_i}|\mathbf{w}^T\boldsymbol{\phi}-\mu_i|^2 \]ベクトル・行列を用いて書き直せば \[ J(\mathbf{w}) = \frac{\mathbf{w}^T\mathbf{S}_B\mathbf{w}}{\mathbf{w}^T\mathbf{S}_W\mathbf{w}} \] \[ \begin{aligned} \mathbf{S}_B &= (\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)^T \\ \mathbf{S}_W &= \sum_{\boldsymbol{\phi}\in C_1}(\boldsymbol{\phi}-\boldsymbol{\mu}_1)(\boldsymbol{\phi}-\boldsymbol{\mu}_1)^T + \sum_{\boldsymbol{\phi}\in C_2}(\boldsymbol{\phi}-\boldsymbol{\mu}_2)(\boldsymbol{\phi}-\boldsymbol{\mu}_2)^T \end{aligned} \] となります. $\mathbf{S}_B$ を クラス間共分散 (between-class covariance), $\mathbf{S}_W$ を クラス内共分散 (within-class covariance) と呼びます.
$J(\mathbf{w})$ の勾配を求めてみると, 分数関数の微分公式によって \[ \nabla J(\mathbf{w}) = \frac{2(\mathbf{w}^T\mathbf{S}_W\mathbf{w})\mathbf{S}_B\mathbf{w}-2(\mathbf{w}^T\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w}}{(\mathbf{w}^T\mathbf{S}_W\mathbf{w})^2} \] となりますので, \[ (\mathbf{w}^T\mathbf{S}_W\mathbf{w})\mathbf{S}_B\mathbf{w}=(\mathbf{w}^T\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w} \] を解けば良いという事になります.
これは固有値問題に帰着して解くことが出来ます(勉強会当日は数値解法が必要と言ってしまいました.すみません.).
実は $\mathbf{S}_W^{-1}\mathbf{S}_B$ の最大固有値に対応する固有ベクトルが求める $\mathbf{w}$ となります.
詳しくは省略しますが,$\mathbf{S}_W^{-1}\mathbf{S}_B$ の固有ベクトルと固有値の組 $\mathbf{a},\lambda$ に対して \[ (\mathbf{a}^T\mathbf{S}_W\mathbf{a})\mathbf{S}_B\mathbf{a}=\frac{1}{\lambda}(\mathbf{a}^T\mathbf{S}_B\mathbf{a})\mathbf{S}_W\lambda\mathbf{a} = (\mathbf{a}^T\mathbf{S}_B\mathbf{a})\mathbf{S}_W\mathbf{a} \] と \[ \frac{\mathbf{a}^T\mathbf{S}_B\mathbf{a}}{\mathbf{a}^T\mathbf{S}_W\mathbf{a}} = \lambda\] が成立する事から理解出来るかと思います.
しかし, 今は$\mathbf{w}$ の方向だけわかれば良いのでもっと簡単な方法があります.
\[ \mathbf{S}_B\mathbf{w}=(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)^T\mathbf{w} \propto \boldsymbol{\mu}_1-\boldsymbol{\mu}_2\] より \[ \begin{aligned} &(\mathbf{w}^T\mathbf{S}_W\mathbf{w})\mathbf{S}_B\mathbf{w}=(\mathbf{w}^T\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w} \\ \Leftrightarrow& \mathbf{S}_W\mathbf{w} \propto \boldsymbol{\mu}_1-\boldsymbol{\mu}_2 \\ \Leftrightarrow& \mathbf{w} \propto\mathbf{S}_W^{-1}(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)\\ \end{aligned} \] と書くことが出来ます. これを フィッシャーの線形判別 (Fisher's linear discriminant) と呼びます.
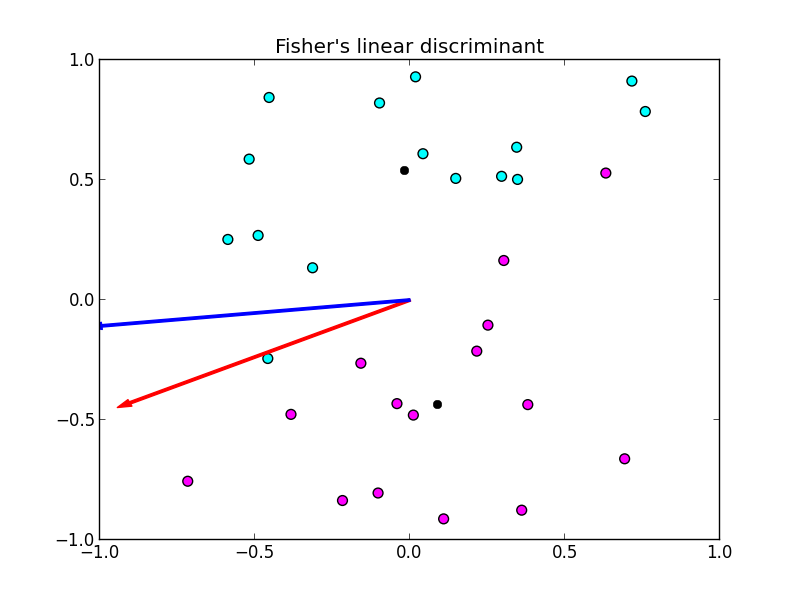
簡単な計算例は以下の様になります. 青い矢印が重心の分離のみを考えた射影方向, 赤い矢印がフィッシャーの線形判別による射影方向です.
ここで, フィッシャーの線形判別は実際には判別を行っているのではなくて射影の方向のみを与えている事に注意して下さい. 射影した後に改めて何らかの識別を行う必要があります.
フィッシャーの線形判別は識別の手法ではなく, 適切な射影方向を求め次元を削減する方法( 次元圧縮 (dimension compression)) の一つと見なす事が出来ます.
一般化して $D$ 次元のデータを $D'$ 次元に削減する問題を考えましょう. またクラスの数も増やします.
多次元・多クラスへの一般化
$K > 2$ クラスの場合に, 特徴空間の次元 $D$ を $D'$ 次元に削減する事を考えます. これを $D'\times D$ 行列 $\mathbf{W}$ によって \[ \mathbf{y} = \mathbf{W}\boldsymbol{\phi} \] で行う事にします.
$\boldsymbol{\mu}_k$ をクラス $C_k$ の重心とすると, クラス内共分散 $\mathbf{S}_W$ は \[ \mathbf{S}_W = \sum_{k=1}^K\sum_{\boldsymbol{\phi}\in C_k}(\boldsymbol{\phi}-\boldsymbol{\mu}_k)(\boldsymbol{\phi}-\boldsymbol{\mu}_k)^T \] と一般化する事が出来ます.
クラス間共分散は $\boldsymbol{\mu}$ を全特徴ベクトルの平均として \[ \mathbf{S}_B = \sum_{k=1}^KN_k(\boldsymbol{\mu}_k-\boldsymbol{\mu})(\boldsymbol{\mu}_k-\boldsymbol{\mu})^T \] と一般化する事が出来ます. 詳しくは PRMLの4.1.6節を参照して下さい. ここで $N_k$ は $C_k$ に属す標本の数です.
この $\mathbf{S}_W,\mathbf{S}_B$ を用いてフィッシャーの判別基準を一般化したものは \[ J(\mathbf{W}) = \mathrm{Tr}\{(\mathbf{W}^T\mathbf{S}_W\mathbf{W})^{-1}(\mathbf{W}^T\mathbf{S}_B\mathbf{W})\} \] と書くことが出来ます. これを最大化する為にはやはり固有値計算を行います.
$\mathbf{S}_W^{-1}\mathbf{S}_B$ の固有ベクトルを固有値の大きい方から順番に $D'$ 個取り列に並べたものが求める $\mathbf{W}$ です.
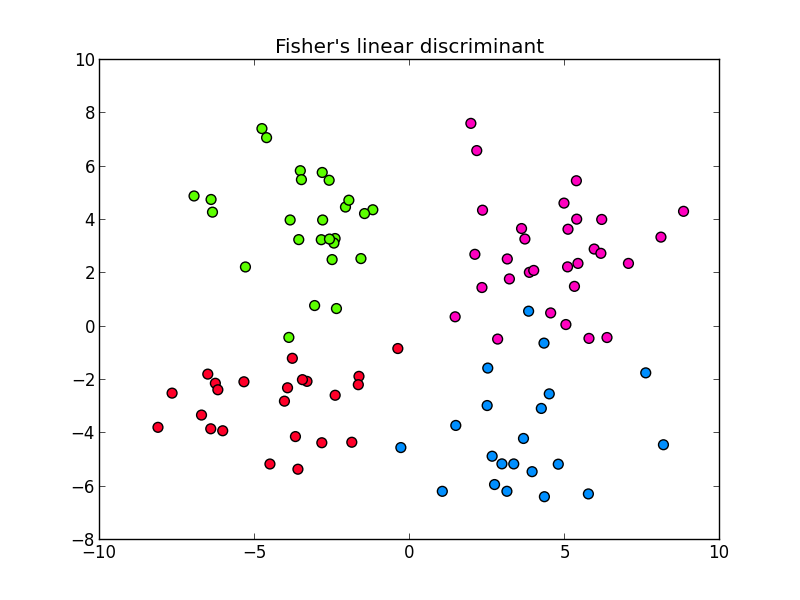
以下は5次元の4クラスからなるデータ(prog6-5.dat)を2次元平面に射影した例です.(ファイル中の最後の列の値はクラスの番号.) この例では次元を減らしても各クラスを上手く分離する事が出来ました.
第6回はここで終わります
次回からPRML第5章のニューラルネットワークに進みます. 第4章のパーセプトロンはニューラルネットワークの一種なので5章でまとめて説明する事にします.