パターン認識・
機械学習勉強会
第23回

@ナビプラス

謝辞

会場・設備の提供をしていただきました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.

本日がこの勉強会シリーズの最終回となります.

本日はテキストの最後の章「モデルの結合」をやります. これまでに紹介しました学習器を複数組み合わせる事によってより複雑なデータに対する識別や回帰を行う方法を紹介します.

集団学習

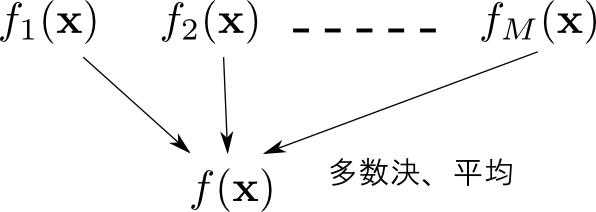
学習データ $\mathbf{X}$ を元に複数のモデル $f_1(\mathbf{x}),\ldots,f_M(\mathbf{x})$ を学習させ，それらの合議(多数決や平均)によって最終的な結果を求めるというアプローチを 集団学習(ensemble learning) と呼びます. 各 $f_1,\ldots,f_M$ の事を 弱学習器(weak learner) と呼びます.

用いる弱学習器の種類，弱学習器の学習方法，合議の方法などによって幾つかの手法が存在します．

バギング

バギング(bagging) は非常に単純な集団学習アルゴリズムです.

バギングでは，学習データセット $\mathbf{X}$ から $M$ 個のデータセット $\mathbf{X}_1,\ldots,\mathbf{X}_M$ を ブートストラップ (bootstrap) という方法で作ります.

そしてそれぞれ適当なモデルで学習させて $M$ 個の弱学習器 $f_1(\mathbf{x}),\ldots,f_M(\mathbf{x})$ を作り識別の場合には多数決，回帰の場合にはそれらの平均を最終的な結果とします.

同じデータセット $\mathbf{X}$ を学習させてしまったら、全ての弱学習器が全く同じものになってしまいます．ブートストラップとは元の学習データ $\mathbf{X}$ から異なる $M$ 個のデータセット $\mathbf{X}_1,\ldots,\mathbf{X}_M$ を作る方法の１つです.

方法は簡単で，$m = 1,2,\ldots,M$ について $\mathbf{X}$ から重複を許して何個か($|\mathbf{X}|$個など)サンプリングしたものを $X_m$ とします.

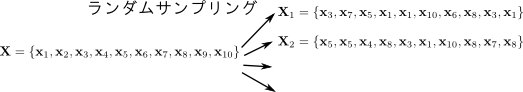
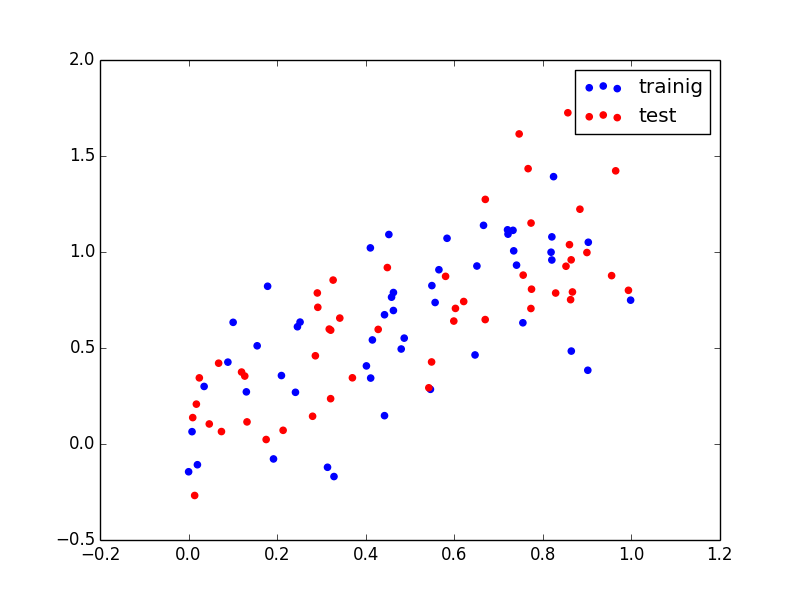
以下のようなデータセットに対する回帰問題を用いてバギングの効果を見てみます. 青い点が訓練用，赤い点が検証用です.

弱学習器には単純な線形モデル $y=ax+b+\varepsilon$ を用いました.

prog23-2.py

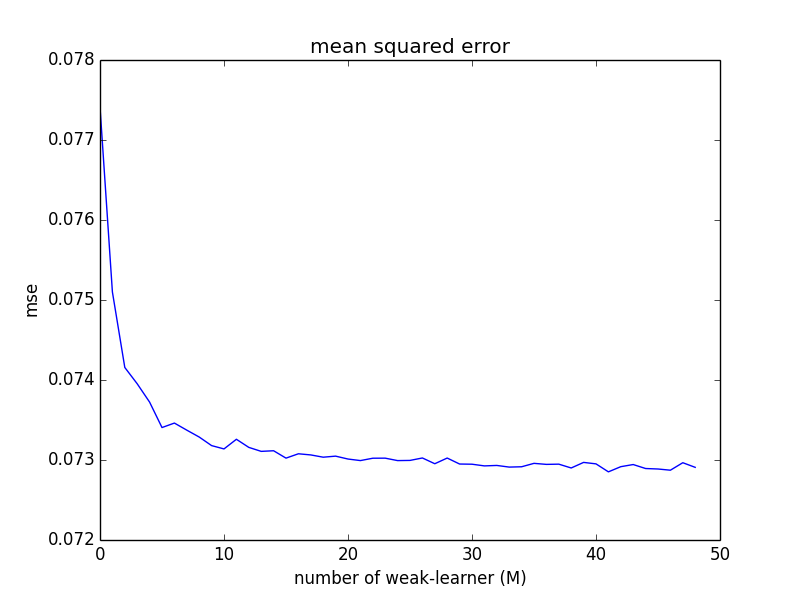
弱学習器の数 $M$ を変えながら，検証用セットに対する二乗誤差平均の期待値の推定値をプロットすると以下のようになります. 学習器の数を増やすと(平均的に)性能が向上していく事が分かります.

prog23-2.py

単純に平均を取っただけで何故精度が上がるのかを考えます．

真の回帰方程式を $y=f(\mathbf{x})$ とします. $m$ 番目に学習されたモデルを \[ f_m(\mathbf{x}) = f(\mathbf{x}) + \varepsilon_m(\mathbf{x}) \] と表すと二乗誤差の期待値は \[ \mathbb{E}[\{f_m(\mathbf{x}) - f(\mathbf{x})\}^2] = \mathbb{E}[\varepsilon_m(\mathbf{x})^2] \] となります.

すると，$M$ 個の弱学習器全体での二乗誤差の期待値の平均は \[ E_{\mathrm{AV}} = \frac{1}{M}\sum_{m=1}^M\mathbb{E}[\varepsilon_m(\mathbf{x})^2] \] です.

バギングによるモデルは \[ \hat{f}(\mathbf{x}) = \frac{1}{M}\sum_{m=1}^M f_m(\mathbf{x}) \] なので，これと真のモデルの二乗誤差の期待値は以下のようになります. \[\begin{aligned} E_{\mathrm{COM}} &= \mathbb{E}\left[\left\{\hat{f}(\mathbf{x})-f(\mathbf{x})\right\}^2\right] \\ &=\mathbb{E}\left[\left\{\frac{1}{M}\sum_{m=1}^M\{f(\mathbf{x})+\varepsilon_m(\mathbf{x})\}-f(\mathbf{x})\right\}^2\right] \\ &= \mathbb{E}\left[\left\{\frac{1}{M}\sum_{m=1}^M\varepsilon_m(\mathbf{x})\right\}^2\right] \\ &= \frac{1}{M^2}\mathbb{E}\left[\left\{\sum_{m=1}^M\varepsilon_m(\mathbf{x})\right\}^2\right] \\ \end{aligned} \]

ここでコーシー・シュワルツの不等式から \[ \left\{\sum_{m=1}^M\varepsilon_m(\mathbf{x})\right\}^2 \leq M\sum_{m=1}^M\varepsilon_m(\mathbf{x})^2 \] が成り立つ事を使えば \[ \color{red}{ E_{\mathrm{COM}} \leq E_{\mathrm{AV}} } \] となります. つまり，平均を取って出来るモデルは個々の弱学習器の平均的な性能よりも優れているという事が分かります.

性能向上の目安ですが \[ \mathbb{E}[\varepsilon_m(\mathbf{x})] = 0,\quad \mathrm{Cov}[\varepsilon_i(\mathbf{x}),\varepsilon_j(\mathbf{x})] = 0 \quad (i\neq j) \] ならば \[ E_{\mathrm{COM}} = \frac{1}{M^2}\mathbb{E}\left[\left\{\sum_{m=1}^M\varepsilon_m(\mathbf{x})\right\}^2\right] = \frac{1}{M^2}\sum_{m=1}^M\mathbb{E}\left[\varepsilon_m(\mathbf{x})^2\right] \] が成り立つので， \[ E_{\mathrm{COM}} = \frac{1}{M}E_{\mathrm{AV}} \] となります. 実際には $\mathrm{Cov}[\varepsilon_i(\mathbf{x}),\varepsilon_j(\mathbf{x})] = 0$ という事はまずないので，ここまで良い精度にはなりません.

ブースティング

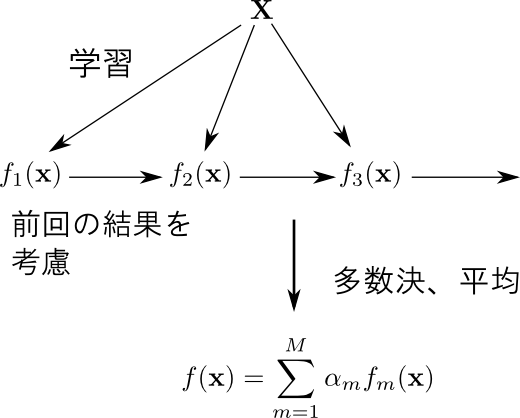
ブースティング (boosting) と呼ばれる手法は，$M$ 個の弱学習器を順番に学習し，前の弱学習器の学習結果を次の弱学習器の学習で利用する事で積極的に性能をあげようとするものです. AdaBoost (Adaptive Boosting) というアルゴリズムが有名です.

バギングと異なり個々の学習器は対等ではないので，重み付きでの多数決・平均値を取ります.

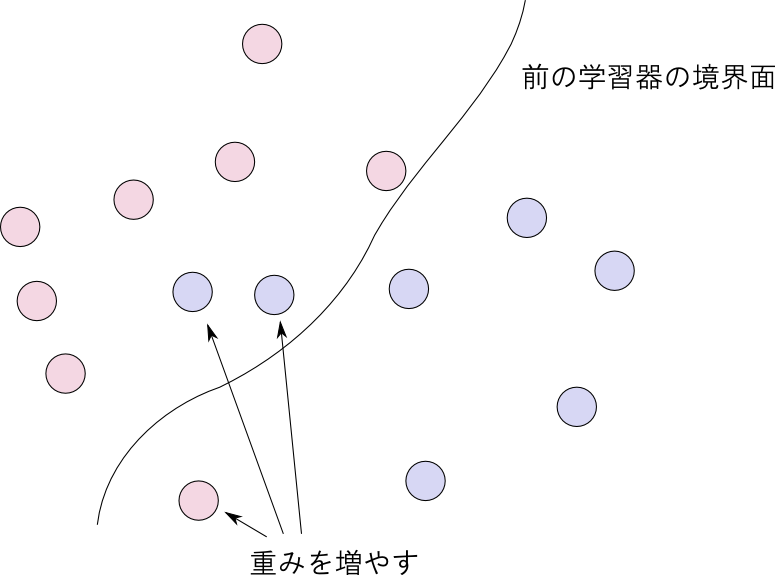
AdaBoostでは， 重み付き誤差関数(weighted error function) を用いて学習セットに色を付けます.

つまり, モデル $\hat{f}$ の誤差を各データ $(\mathbf{x}_n,t_n)$ 毎に重み $w_n$ を付与した \[ \sum_{n=1}^N w_n E(\hat{f}(\mathbf{x}_n), t_n) \] で計算します.

識別の場合は単純損失関数などを用います. この場合 $E(y,t) = (\text{正解なら $0$, そうでなければ $1$})$ とします.

$f_m$ が識別に失敗したデータには大きな重みを付与して次の $f_{m+1}$ ではそれらをより良く識別しようというのがAdaBoostの考え方です.

AdaBoostは 指数損失関数 (exponential error function) \[ E(y,t) = \exp(-ty) \] を用いた経験損失 \[ J = \sum_{n=1}^N\exp\left\{-t_nf_m(\mathbf{x}_n)\right\} \] を反復法を用いて最小化するアルゴリズムであると解釈する事が出来ます。

ここで $f_m(\mathbf{x})$ のモデルとして弱学習器 $g_\ell(\mathbf{x})$ の線形結合 \[ f_m(\mathbf{x}) = \frac{1}{2}\sum_{\ell=1}^m \alpha_\ell g_\ell(\mathbf{x}) \] で表される物を考えます. $1/2$ は計算を簡単にする為のものです.

弱学習器 $g_\ell(\mathbf{x})$ は $\{-1, 1\}$ のいずれかを返す二値の識別器とします. 従って $\mathrm{sign}(f_m(\mathbf{x}))$ は $g_\ell$ の結果の重み付きの多数決を表します.

すると \[ f_m(\mathbf{x}) = f_{m-1}(\mathbf{x}) + \frac{1}{2}\alpha_m g_m(\mathbf{x}) \] より \[ \begin{aligned} J &= \sum_{n=1}^N\exp\left\{-t_nf_{m-1}(\mathbf{x}_n)-\frac{1}{2}t_n\alpha_m g_m(\mathbf{x}_n)\right\}\\ &= \sum_{n=1}^N w_n\exp\left\{-\frac{1}{2}t_n\alpha_m g_m(\mathbf{x}_n)\right\} \end{aligned} \] となります. 但し \[ w^{(m)}_n \stackrel{\mathrm{def}}{=} \exp\left\{-t_nf_{m-1}(\mathbf{x}_n)\right\} \] であり，$g_1,\ldots,g_{m-1},\alpha_1,\ldots,\alpha_{m-1}$ を固定して $g_m,\alpha_m$ だけを動かす場合にはこれは定数となります.

ここで $g_m(\mathbf{x})$ が $\mathbf{x}_n$ を正しく識別したときは $t_ng_m(\mathbf{x}_n)=1$，そうでない時は $t_ng_m(\mathbf{x}_n)=-1$ となるので \[ J= \left(e^{\alpha_m/2}-e^{-\alpha_m/2}\right)\sum_{n=1}^Nw_n^{(m)}E(g_m(\mathbf{x}_n), t_n) + e^{-\alpha_m/2}\sum_{n=1}^Nw_n^{(m)} \] と書くことが出来ます。よってこれを最小化する $g_m$ は経験的単純損失 \[ \sum_{n=1}^Nw_n^{(m)}E(g_m(\mathbf{x}_n), t_n) \] を最小化するものであり，

ここで \[ \varepsilon_m = \frac{\sum_{n=1}^Nw^{(m)}_n E(g_m(\mathbf{x}_n), t_n)}{\sum_{n=1}^N w^{(m)}_n} \] と置くと \[ J = \left(e^{\alpha_m/2}-e^{-\alpha_m/2}\right)\varepsilon_m\sum_{n=1}^N w_n + e^{-\alpha_m/2}\sum_{n=1}^Nw_n^{(m)} \] となるので，$J$ を最小化する $\alpha_m$ は \[ (e^{\alpha_m/2}-e^{-\alpha_m/2})\varepsilon_m + e^{-\alpha_m/2} \] を最小化する \[ \alpha_m = \log\frac{1-\varepsilon_m}{\varepsilon_m} \] となります.

最後に重み $w_n$ の更新規則は \[ \begin{aligned} w_n^{(m+1)} &= \exp\{-t_nf_m(\mathbf{x}_n)\}\\ &= \exp\{-t_n\left(f_{m-1}(\mathbf{x}_n)+\alpha_mg_m(\mathbf{x}_n)/2\right)\}\\ &= w_n^{(m)}\exp\{-t_n\alpha_mg_m(\mathbf{x}_n)/2\} \end{aligned} \] と \[ t_ng_m(\mathbf{x}_n)= 1 - 2E(g_m(\mathbf{x}_n),t_n) \] より \[ \begin{aligned} w_n^{(m+1)} &= w_n^{(m)}\exp\{\alpha_mE(g_m(\mathbf{x}_n),t_n)\}\exp(-\alpha_m/2) \end{aligned} \] となります. $\exp(-\alpha_m/2)$ の部分はデータ $(\mathbf{x}_n,t_n)$ によらない定数で，$f_m$ の符号には影響しないため除去しても良いです.

以上の「弱学習器の線形和モデルで指数損失を反復的に最小化する」というアイデアに基づけば、様々なブースティングアルゴリズムの拡張を導出する事が出来ます.

例えばAdaBoostを回帰に用いる例は以下の論文などで紹介されています.

• Freund, Yoav, and Robert E. Schapire. "A desicion-theoretic generalization of on-line learning and an application to boosting." Computational learning theory. Springer Berlin Heidelberg, 1995.

そもそも「指数損失の最小化」とは一体どういう事なのか補足します.

経験損失ではなく期待損失は \[ \mathbb{E}[\exp(-tf(\mathbf{x}))] = \sum_{t=1,-1}\int \exp(-tf(\mathbf{x}))p(t|\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x} \] となりますが，これを最小とする $f$ を変分法で求めると(次頁) \[ f(\mathbf{x}) = \frac{1}{2}\log \frac{p(t=1|\mathbf{x})}{p(t=-1|\mathbf{x})} \] となります. これは 対数オッズ(log odds) や ロジット (logit) と呼ばれる量(割る2)になっています.

【前頁の導出】
$f$ に微小変化 $\varepsilon \eta(\mathbf{x})$ を加えると \[\sum_{t=1,-1}\int \exp\{-t(f+\varepsilon \eta)\}p(t|\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x} \] これを $\varepsilon$ で微分すると \[\sum_{t=1,-1}\int \exp(-t\eta)\exp\{-t(f+\varepsilon \eta)\}p(t|\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x} \] となりこれが $\varepsilon=0$ で $0$ となる条件を求めれば良い. \[-\sum_{t=1,-1}\int t\eta\exp(-tf)p(t|\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x} = 0 \] $\eta(\mathbf{x})$ は任意に取れるのでこれが $0$ になるためには \[\sum_{t=1,-1}t \exp(-tf)p(t|\mathbf{x})p(\mathbf{x}) = 0 \] が必要. これを解いて \[ f(\mathbf{x}) = \frac{1}{2}\log \frac{p(t=1|\mathbf{x})}{p(t=-1|\mathbf{x})} \]

決定木

決定木

集団学習とは異なる学習器の組み合わせ方として 決定木 (decision tree) というものも使われます.

決定木とは2つの識別器 $f_1(\mathbf{x})$ と $f_2(\mathbf{x})$ のどちらを使うのかを他の識別器 $g(\mathbf{x})$ で選び，選ばれたもので識別を行うというものです.

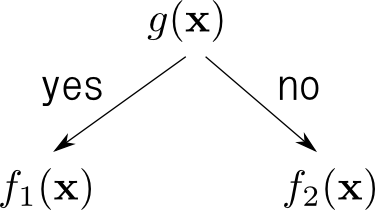
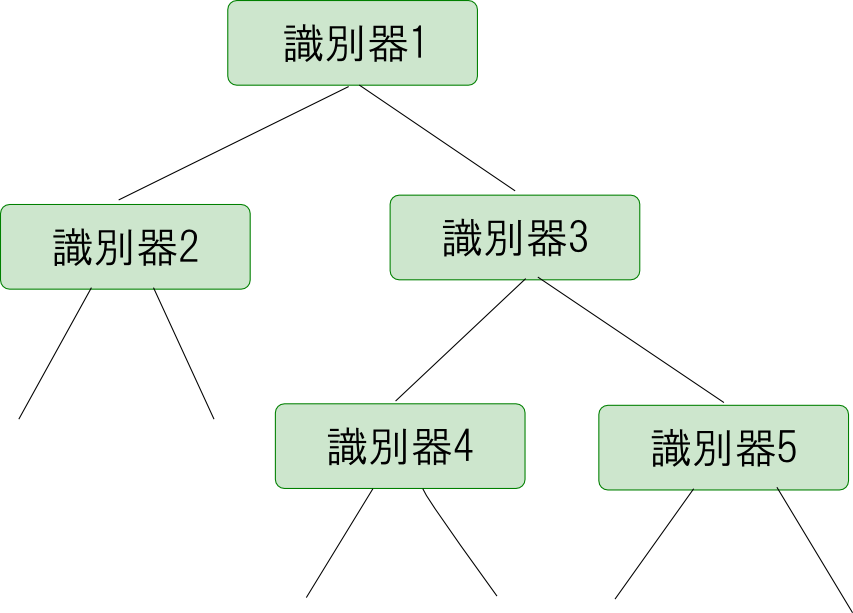
$f_1,f_2$ に再び決定木を用いれば下図のような木構造の識別器となります.

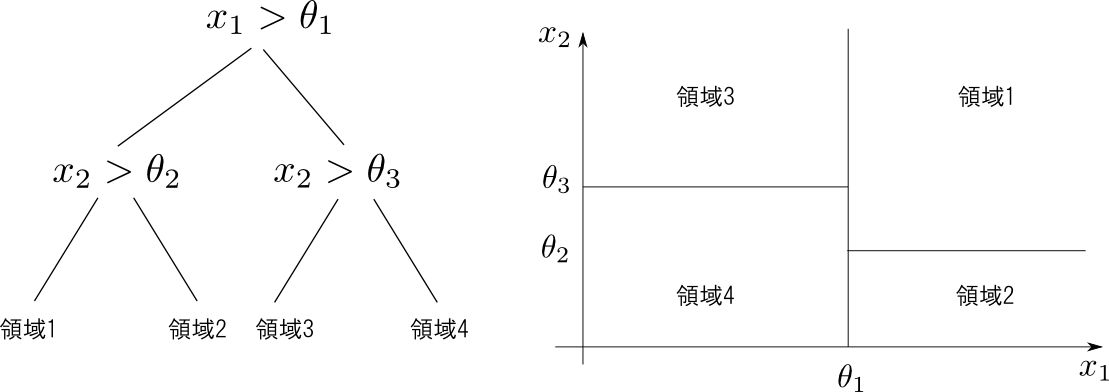
決定木は特徴空間を再帰的に幾つかの領域に分割し，各領域毎に別々の学習で回帰や識別を行うというものです.

下図のようにある軸，もしくは数本の軸に平行な面で分割していく方法が一般的です.

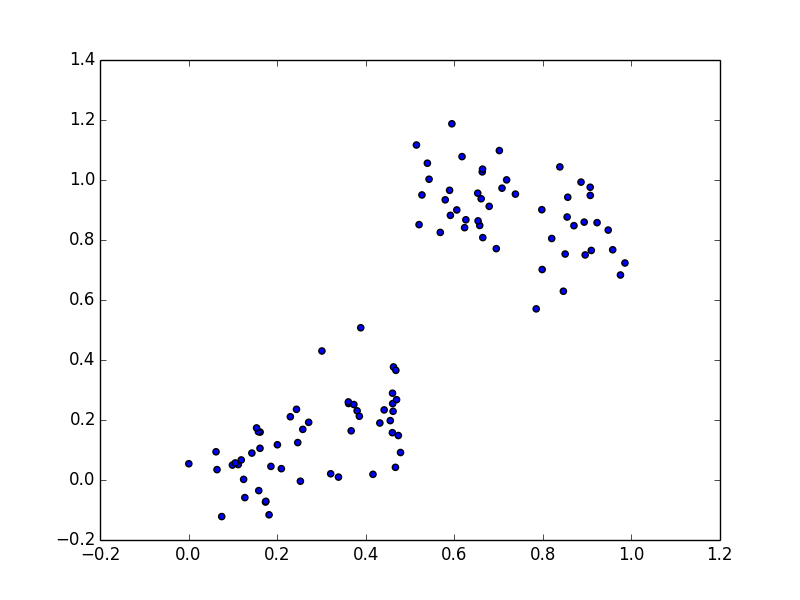
例えば下図の様に途中で不連続的にパターンが変化するようなデータに対しても

prog23-3.py

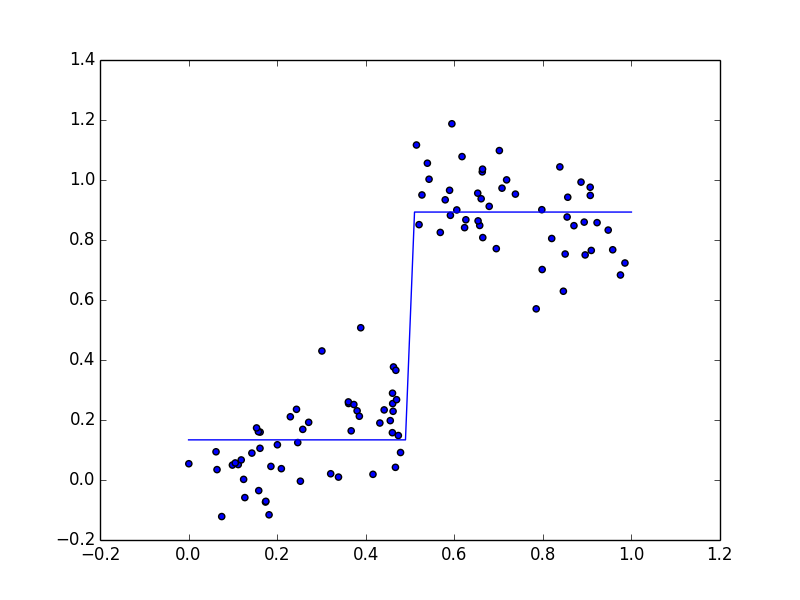
以下のように領域を分割して個別に回帰を行うという事が出来ます.

prog23-3.py

分割された個々の領域毎の学習はこれまでに紹介しましたいろいろな方法をそのまま使えば良いので，決定木の学習は木構造の学習が中心になります.

決定木を構築する場合には領域を再帰的に分割する事を繰り返していきますので，

1. 領域を分割する基準
2. 分割を停止する基準

が必要です. これらの選択によって様々なアルゴリズムを考える事が出来ます.

決定木の構造は離散的なものなので解析的にその構造を学習する事は難しいです. 従いまして 貪欲法(greedy algorithm) などが用いられます.

分割基準

「最も良く分割する」という基準も幾つか考え方がありますが， 相互情報量 (mutual information) などが使われます.

二つの確率変数 $\mathbf{X}_1,\mathbf{X}_2$ に対する相互情報量は \[ I(\mathbf{X}_1,\mathbf{X}_2) = \sum_{\mathbf{x}_1\in\mathbf{X}_1,\mathbf{x}_2\in\mathbf{X}_2}p(\mathbf{x}_1,\mathbf{x}_2)\log \frac{p(\mathbf{x}_1,\mathbf{x}_2)}{p(\mathbf{x}_1)p(\mathbf{x}_2)} \] で定義され，これは $\mathbf{X}_2$ を知ることで $\mathbf{X}_1$ に関して得る情報量と解釈する事が出来ます.

これを用いて，分割を行う事によってクラスの割り当てに関して得る情報量を測る事が出来ます. (授業当日ではこの点について誤った説明をしてしまいました.)

停止基準

分割を停止する際に考慮すべき事は

1. 十分な識別精度を達成出来るほど細かいか？
2. サンプル数が少なくなりすぎていないか？

という２点です. これらはトレードオフの関係にあります.

そこで，もともとの空間が $T$ 個の領域に分割されたとし， $Q_t(T)\quad (t=1,\ldots,T)$ を $t$ 番目の領域 $t$ における誤差の和とした際に \[ C(T) = \sum_{t=1}^TQ_t(T) + \lambda T \quad (\lambda > 0)\] という量を停止基準のしきい値として用いる事が出来ます.

$\lambda T$ は分割が細かくなりすぎることに対するペナルティ項です.

回帰の場合には $Q_t(T)$ として残差平方和などを用いれば良いです.

一方，識別の場合にはノード $t$ がクラス $k$ に所属する確率を $p(k|t)$ とした場合に交差エントロピー \[ Q_t(T) = \sum_{k=1}^Kp(k|t)\log p(k|t) \] や Giniインデックス (Gini index) \[ Q_t(T) = \sum_{k=1}^K p(k|t)(1-p(k|t)) \] を用います. これらは $p(k|t)=0$ は $p(k|t)=1$ となる $k$ が存在した場合に $0$ になります. ノード $t$ のデータが1つのクラスに対応する場合にはそれ以上分割する必要がないというわけです.

ランダムフォレスト

ランダムフォレスト (random forest) という手法は新しいのでPRML本では説明がないですが非常に精度が高く有名です.

これは弱学習器として決定木を用いて集団学習を行うアルゴリズムです. 弱学習器の学習にはブートストラップで生成したサンプルを利用する為，並列に学習を行わせる事が可能です.

まとめ

では最後にPRML本の各章で学んだ事を振り返りたいと思います.

第3・4章

線形回帰モデル・線形識別モデルという話題を扱いました.

学習データを $\mathbf{x}$，それの基底変換関数を $\Psi$ として \[ y = f(\mathbf{w}^T\Psi(\mathbf{x})) \] の形で表されるものを扱いました.

線形モデルは解析的に取り扱える物が多く，他の全ての手法の基礎となるモデルです.

識別問題については特にロジスティックモデルが重要です. \[ y = \frac{1}{1 + \exp(\mathbf{w}^T\Psi(\mathbf{x})}) \]

第5章

ニューラルネットワークの紹介をしました.

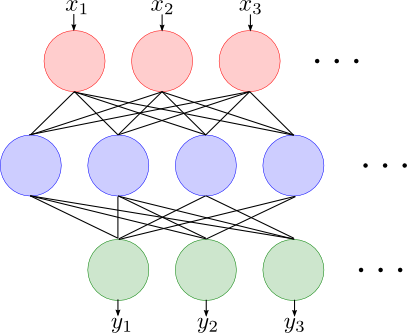
ニューラルネットワークは隠れ層が十分にある場合，任意の連続な非線形関数を表現出来るという極めて重要な特徴がありました.

その学習には誤差逆伝播法という手法を用います.

第6,7章

カーネル法という手法の紹介を行いました.

カーネル法は特徴ベクトル $\Psi(\mathbf{x})$ を明示的に扱う代わりに，その内積 $\Psi(\mathbf{x}_i)^T\Psi(\mathbf{x}_j)$ やそれを一般化したカーネル関数 \[ k(\mathbf{x}_i,\mathbf{x}_j) \] をプリミティブとして用いる手法です. カーネル法では複雑な特徴ベクトルを用いても計算量がデータ数 $N$ のみに依存するようにする事が出来ます. 特に無限次元の特徴ベクトルを用いる事が出来ます.

一方で識別関数を構築する為には基本的に学習データを全て保持しておく必要があります。

カーネル法を用いる最も重要な識別器はサポートベクターマシンです。

これはマージン最大化という考え方によって，汎化性能を高める仕組みがあらかじめ内包されたモデルで非常に使い勝手が良いです。

また，識別器の構築にサポートベクターしか必要ないという大きな特徴があり，保持すべき学習データ数を減らす事が可能になります.

第8章

グラフィカルモデルという確率モデルの表現方法を紹介しました.確率変数間の因果関係をグラフ構造を用いて表現する事により，他のモデルも含む非常に広範なモデルを表現する事が出来ます.

有向グラフを用いるベイジアンネットワークや無向グラフを用いるマルコフ確率場などを紹介しました.

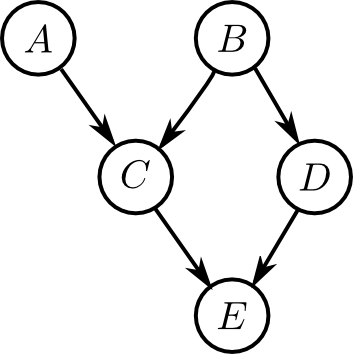
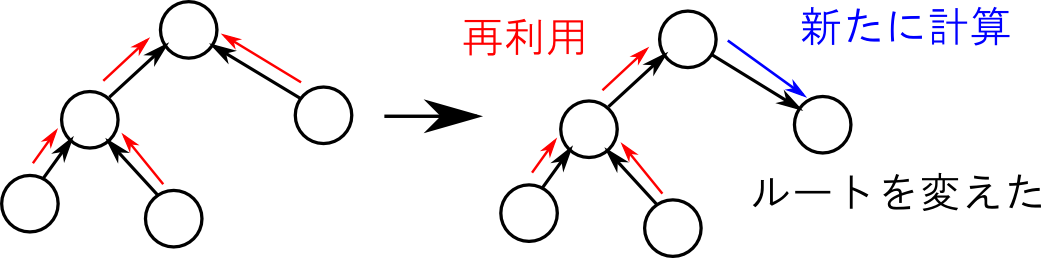
グラフィカルモデルの学習には変数消去法やメッセージパッシングなどの方法を用います. これは根と葉の間でメッセージを一回伝播させるだけで，全てのクラスタに対する同時確率を求める事が出来てしまうというものです.

第9, 10章

教師なし学習のタスクの１つであるクラスタリングやディリクレ配分問題のアルゴリズムを紹介しました.

これらの問題は隠れ変数を持つモデルを用いて解く事が出来，厳密な反復解法であるEM法や近似解法である変分ベイズ法，ギブスサンプリングなどの紹介をしました.

第11章

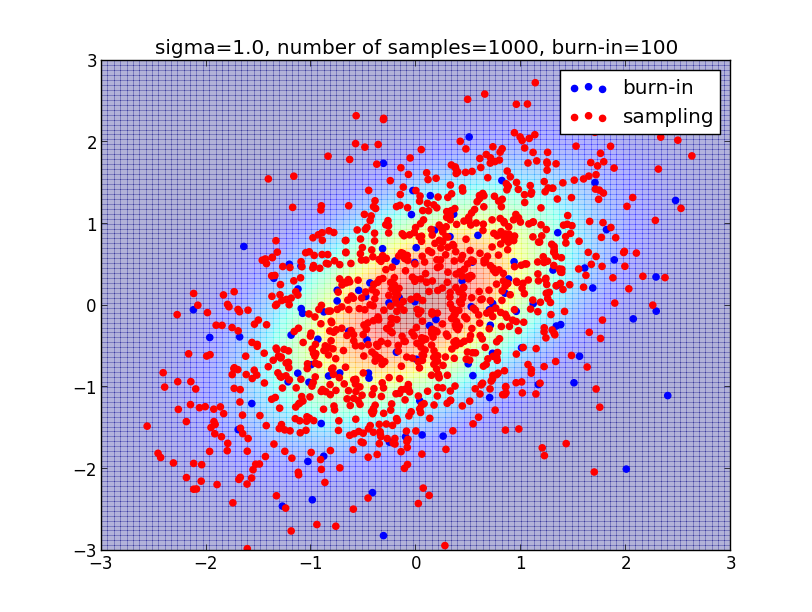
ランダムサンプリング，特にマルコフ連鎖モンテカルロ法の一種であるメトロポリスヘイスティングス法を紹介しました.

非常に高次元の変数に対する期待値の計算，積分の計算などを効率的に解く為にはサンプリングベースの方法が必要になります.

第12章

高次元の空間内でのデータが比較的低次元の多様体上にしか分布していないというケースは非常に良く有ります.

そういったデータに対しては次元削減や多様体学習などの手法を用いた変換が有効です. 具体的なアルゴリズムとしては主成分分析のみを紹介しました.

第13章

系列データの確率モデルの１つである隠れマルコフモデルを紹介しました. 観測データの系列の裏に隠れ変数の一次の系列を考える事によって，モデルの複雑さの増加を抑えつ，任意の離れた観測データ間の相関を表現出来るように工夫したものです.

パラメータの学習には前向き後ろ向きアルゴリズム，パラメータを既知とした隠れ変数の推定にはビタビアルゴリズムを用います.

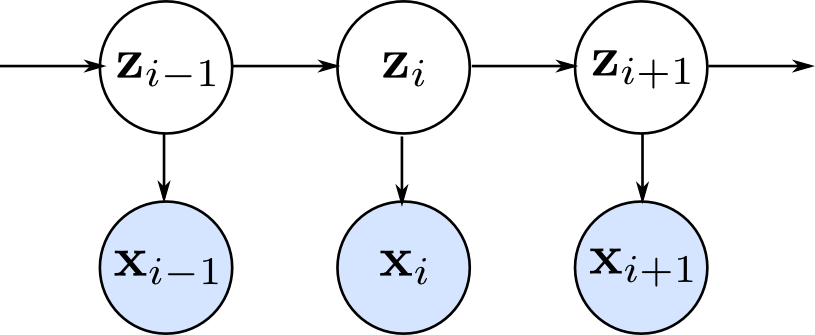
第14章

弱学習器を組み合わせて１つでは達成出来ない性能を持つ学習器を作り上げる集団学習・決定木という手法を紹介しました.

１つの非常に複雑な学習器を用いると過学習や計算コストの増加の問題が生じます. 集団学習には多数の弱い学習器の結果を平均化する事によって過学習を抑制する効果があり，またバギングなどは並列化を容易に行う事が出来ます.

以上でこの勉強会を終了します.

全23回お疲れ様でした. 数学的な部分の説明が殆どでしたが，実際のデータの分析では理論通りには上手くはいかない事が多数ありますので，まずは実際にやってみるという事が大事だと思います. 何か困難な問題にぶつかった時には，数学的な理解がその解決に役に立つと思います.

資料の不足や不備が多数あり大変申し訳ありませんでした. 資料は今後も随時更新していきます.