パターン認識・
機械学習勉強会
第22回

@ナビプラス

謝辞

会場・設備の提供をしていただきました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.

ビタビアルゴリズム

前回は系列データ $\mathbf{x}$ から, 隠れマルコフモデル(HMM)の３つのパラメータ $\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}$ をEM法で推定するアルゴリズムの紹介を行いました.

続いて興味のある問題は，モデルパラメータ $\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}$ が既知の状況で観測データ $\mathbf{x}$ から，隠れラベルの系列 $\mathbf{z}$ を推定する事です.

この問題は $\mathbf{z}$ の事後確率が最大となる系列 $\hat{\mathbf{z}}$ を見つけるという問題であり， \[ \begin{aligned} \hat{\mathbf{z}} &= \mathop{\rm arg~max}\limits_{\mathbf{z}}p(\mathbf{z}|\mathbf{x}) \\ &= \mathop{\rm arg~max}\limits_{\mathbf{z}}\frac{p(\mathbf{x},\mathbf{z})}{p(\mathbf{x})} \\ &= \mathop{\rm arg~max}\limits_{\mathbf{z}}p(\mathbf{x},\mathbf{z}) \\ &= \mathop{\rm arg~max}\limits_{\mathbf{z}}\log p(\mathbf{x},\mathbf{z}) \\ \end{aligned} \] を解けば良いです.

これを動的計画法に基いて計算するアルゴリズムを ビタビアルゴリズム (Viterbi algorithm) と呼びます.

まず， \[ \mathop{\rm max}\limits_{\mathbf{z}}\log p(\mathbf{x},\mathbf{z}) \] について考えます.

これに，前回導きました \[ p(\mathbf{x},\mathbf{z}|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) = \left\{\pi_{z_1} \prod_{i=2}^N A_{z_{i-1},z_{i}}\right\}\left\{\prod_{i=1}^Np(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\right\} \] を代入すると \[ \begin{aligned} \mathop{\rm max}\limits_{\mathbf{z}}\log p(\mathbf{x},\mathbf{z}) = \mathop{\rm max}\limits_{\mathbf{z}}\left\{ \log \pi_{z_1} + \sum_{i=2}^N\log A_{z_{i-1},z_{i}} + \sum_{i=1}^N \log p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\right\} \end{aligned} \] となります.

そこで \[ \omega(z_n) = \mathop{\rm max}\limits_{z_1,\ldots,z_{n-1}}\left\{ \log \pi_{z_1} + \sum_{i=2}^n\log A_{z_{i-1},z_{i}} + \sum_{i=1}^n \log p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\right\} \] と置くと \[ \mathop{\rm max}\limits_{\mathbf{z}}\log p(\mathbf{x},\mathbf{z}) = \mathop{\rm max}\limits_{z_N}\omega(z_N) \] となり，

$\omega$ は以下の漸化式を満たします. \[ \begin{aligned} \omega(z_{n+1}) &= \mathop{\rm max}\limits_{z_1,\ldots,z_n}\left\{ \log \pi_{z_1} + \sum_{i=2}^{n+1}\log A_{z_{i-1},z_{i}} + \sum_{i=1}^{n+1} \log p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\right\} \\ &= \mathop{\rm max}\limits_{z_1,\ldots,z_n}\left\{ \log \pi_{z_1} + \sum_{i=2}^n\log A_{z_{i-1},z_{i}} + \sum_{i=1}^n \log p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\right. \\ &\qquad \left. + \log A_{z_n,z_{n+1}} + \log p(\mathbf{x}_{n+1}|\boldsymbol{\phi}_{z_{n+1}}) \right\} \\ &= \log p(\mathbf{x}_{n+1}|\boldsymbol{\phi}_{z_{n+1}}) + \mathop{\rm max}\limits_{z_n}\left\{\log A_{z_{n},z_{n+1}} + \omega(z_n)\right\} \end{aligned} \]

但し，初期値は \[ \omega(z_1) = \log \pi_{z_1} + \log p(\mathbf{x}_1|\boldsymbol{\phi}_{z_1}) \] となります.

ここまでを，一旦まとめると以下のようになります.

ここで，漸化式 \[ \omega(z_{n+1}) = \log p(\mathbf{x}_{n+1}|\boldsymbol{\phi}_{z_{n+1}}) + \mathop{\rm max}\limits_{z_n}\left\{\log A_{z_{n},z_{n+1}} + \omega(z_n)\right\} \] において，$z_{n+1}$ が決まると $\mathop{\rm max}$ の部分の $z_n$ の値が決まります.

この関数関係 $z_{n+1}\longmapsto z_n$ を $\mathrm{pred}$ と書く事にしましょう. つまり \[ \mathrm{pred}(z_{n+1}) = \mathop{\rm arg~max}\limits_{z_n}\left\{\log A_{z_{n},z_{n+1}} + \omega(z_n)\right\} \] です.

ここまでの様子を絵にしてみると以下のようになります. 左から右に順番に「$z_i=k$ の時に，そこより左の部分の対数尤度が最大となるようなラベルの系列」が計算されていきます. 赤いエッジは $\mathrm{pred}:z_{n+1}\rightarrow z_n$ に対応しています.

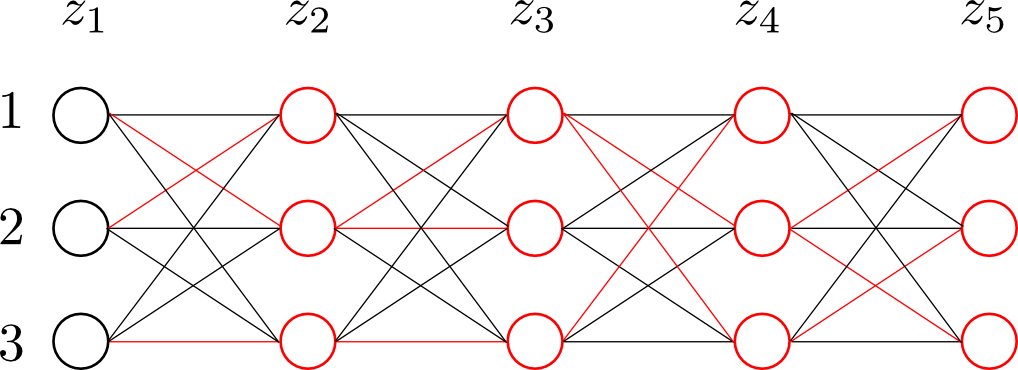
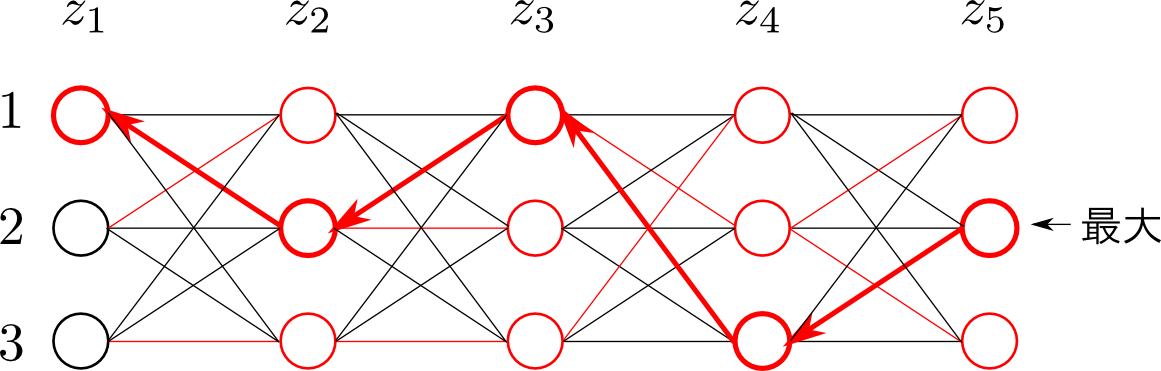
求める隠れ変数の系列は \[ \begin{aligned} \hat{\mathbf{z}} &= \mathop{\rm arg~max}\limits_{\mathbf{z}}\log p(\mathbf{x},\mathbf{z}) \\ &= \mathop{\rm arg~max}\limits_{z_N}\omega(z_N) \end{aligned} \] だったので，まず $z_{N}$ が決まります. すると $\mathrm{pred}$ によって $z_{N-1}=\mathrm{pred}(z_N)$ が決まります. これを繰り返していくと系列 \[ z_1 \rightarrow z_2 \rightarrow \cdots \rightarrow z_{N-1} \rightarrow z_N \] が右から順番に求まります. 所謂 バックトラッキング(backtracking)という計算です.

この様子を絵にすると以下のようになります. この場合 $\mathbf{z}=(1,2,1,3,2)$ という系列が求める系列となります.

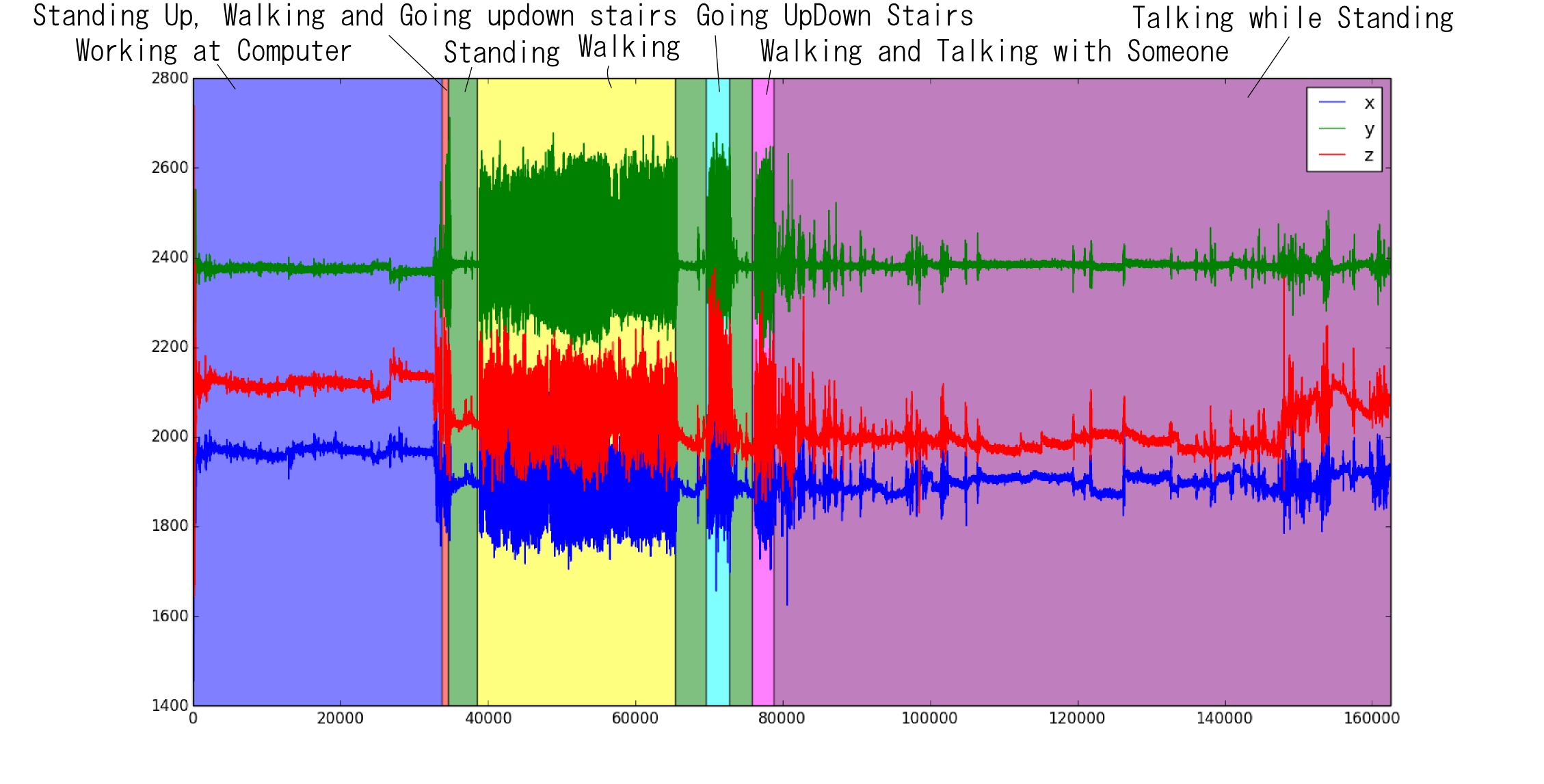
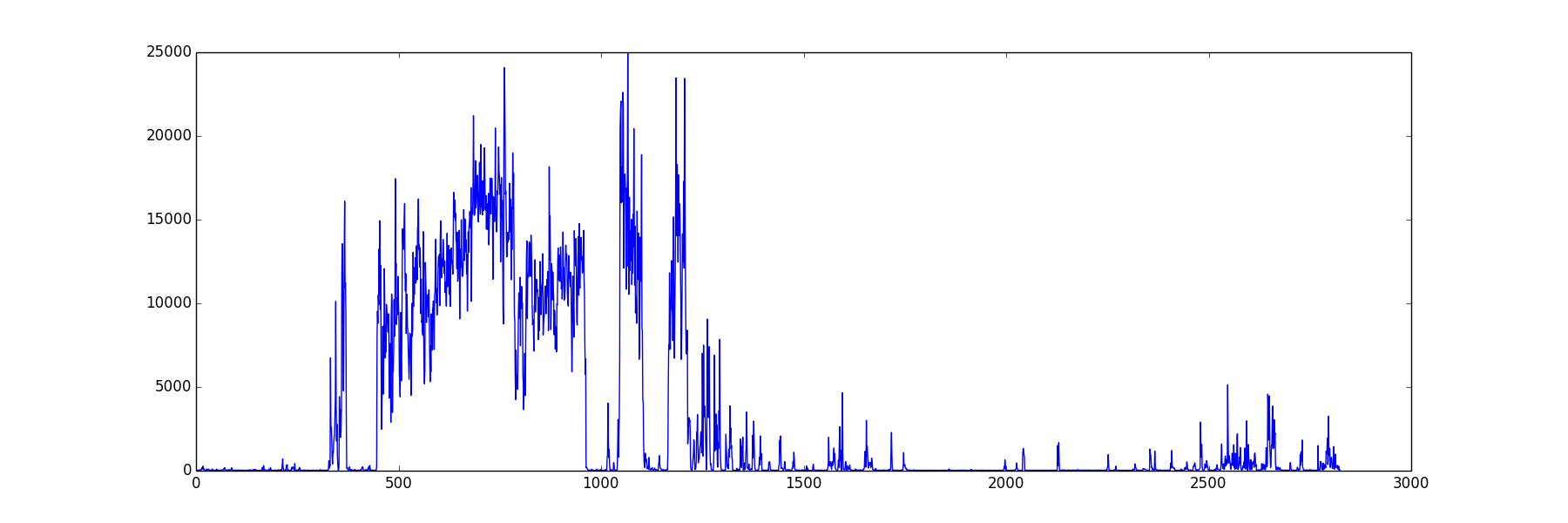
前回使った腰に付けた加速度計 のデータでやってみます.

prog21-1.py

Casale, P. Pujol, O. and Radeva, P. 'Personalization and user verification in wearable systems using biometric walking patterns' Personal and Ubiquitous Computing, 16(5), 563-580, 2012

11人分のデータがあるので，10人分を学習し11人目の行動の推測をしてみます.

主成分分析

テキスト第12章を少しだけやります. 章題は連続潜在変数(continuous latent variables)となっていますが，内容はほぼ主成分分析(principal component analysis)です.

より一般には次元削減(dimentionality reduction)や 多様体学習 (manifold learning) といった話題に関係します.

多様体とは

局所的に見れば $m$ 次元ユークリッド空間と見なせるような空間を $m$次元の多様体(manifold)と呼びます.

例えば地球と地図をイメージして下さい. 地球表面のどの点も局所的に見れば2次元の地図に連続性を保ってマッピングする事が出来ます. 従って地球表面は2次元多様体であるという事になります.

高次元の観測データ $\mathbf{x}$ がより低次元の多様体上に分布しているという事が良くあります.

例えば平面振り子を考えましょう. 各時刻の観測データはおもりの座標 $(x,y)$ とすると,これは2次元のデータです.

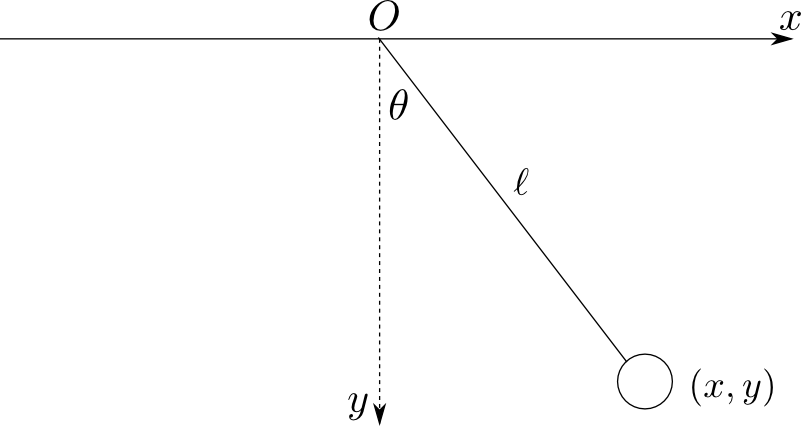
しかし，観測データは $x^2+y^2=\ell^2$ という円周上(1次元多様体)上にのみ分布する事になります.

$D$ 次元の観測データ $\mathbf{x}$ が $d$ 次元の多様体上に分布しているとします. すると，ある範囲(開集合)内の $\mathbf{x}$ は双方向に連続で一対一な写像 $\varphi: \mathbb{R}^d \rightarrow \mathbb{R}^D$ によって \[ \mathbf{x} = \varphi(\mathbf{z}) \qquad (\mathbf{z} \in \mathbb{R}^d)\] と書くことが出来ます.

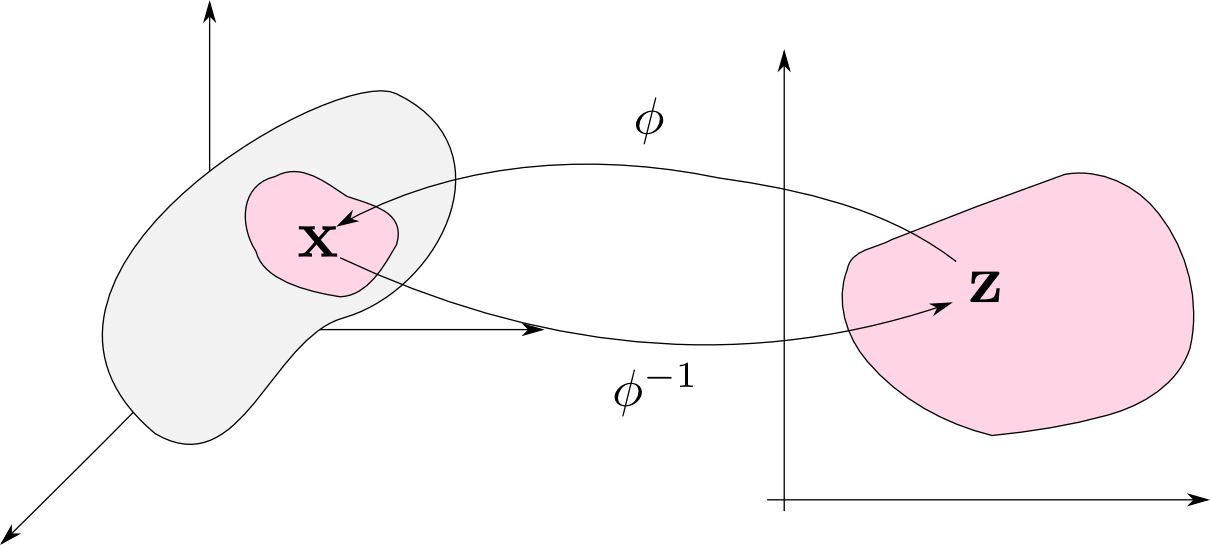
多様体学習 (manifold learning) とは，観測データ $\mathbf{x}$ から変数 $\mathbf{z}$ や写像 $\phi$ を求める事を目標とする機械学習の分野です.

これによって高次元のデータをより低次のデータへ移して分析する事が出来る様になります.

主成分分析

主成分分析 (principal component analysis, PCA) は多様体学習の特別な場合と考える事が出来ます.

これは観測データが線形な空間上に分布していると仮定するものです. (普通、多様体と言うと非線形な空間を考えるので若干奇妙ですが.)

$D$次元の観測データ $\{\mathbf{x}_1,\ldots,\mathbf{x}_N\}$ は 適当な正規直交基底 $\{\mathbf{u}_1,\ldots,\mathbf{u}_D\}$ によって \[ \mathbf{x}_n = \sum_{i=1}^D \alpha_{ni}\mathbf{u}_i \] と書くことが出来ます.

この時 \[ \mathbf{x}_n^T\mathbf{u}_i = \alpha_{ni} \] であるので \[ \mathbf{x}_n = \sum_{i=1}^D (\mathbf{x}_n^T\mathbf{u}_i)\mathbf{u}_i \] が成り立つ事に注意しましょう.

今，観測データがより低次の $d$ 次元空間上に近似的に分布していると仮定します. 先ほどの基底の最初の $d$ 個がこの空間を張るように選べば \[ \tilde{\mathbf{x}}_n = \sum_{i=1}^d z_{ni}\mathbf{u}_i + \sum_{i=d+1}^{D}b_i\mathbf{u}_i \] と書くことが出来ます.

$(z_{n1},\ldots,z_{nd})$ を $\mathbf{x}_n$ の 主成分 (principal component) と呼びます. $\sum_{i=d+1}^{D}b_i\mathbf{u}_i$ は定数項部分なので係数 $b_i$ は全データに対して共通です.

基底 $\mathbf{u}_i$ 及び係数 $z_{ni},b_i$ を求める為に，元の観測データ $\mathbf{x}_n$ と近似したデータ $\tilde{\mathbf{x}}_n$ の残差平方の平均 \[ J = \frac{1}{N}\sum_{n=1}^N||\mathbf{x}_n - \tilde{\mathbf{x}}_n||^2 \] を最小化する事を考えます.

いつもと同じく，これを $z_{ni}$ や $b_i$ などで微分したものを $0$ と置けば良いです.

まず $z_{ni}$ で微分すると \[ \frac{\partial \tilde{\mathbf{x}}_n}{\partial z_{ni}} = \mathbf{u}_i \] なので \[ \frac{\partial J}{\partial z_{ni}} = \frac{2}{N}\mathbf{u}_i^T(\mathbf{x}_n - \tilde{\mathbf{x}}_n) = \frac{2}{N}(\mathbf{u}_i^T\mathbf{x}_n - z_{ni})\] となるので \[ z_{ni} = \mathbf{x}_n^T\mathbf{u}_i \] となります.

$b_i$ についても同様の計算を行うと \[ b_i = \overline{\mathbf{x}}^T\mathbf{u}_i \] となります. ただし $\overline{\mathbf{x}} = \frac{1}{N}\sum_{n=1}^N\mathbf{x}_n$ です.

以上を用いると \[\begin{aligned} \mathbf{x}_n-\tilde{\mathbf{x}}_n &= \sum_{i=1}^N(\mathbf{x}_n^T\mathbf{u}_i)\mathbf{u}_i - \sum_{i=1}^d(\mathbf{x}_n^T\mathbf{u}_i)\mathbf{u}_i - \sum_{i=d+1}^D(\overline{\mathbf{x}}^T\mathbf{u}_i)\mathbf{u}_i \\ &= \sum_{i=d+1}^D\left((\mathbf{x}_n-\overline{\mathbf{x}})^T\mathbf{u}_i\right)\mathbf{u}_i \end{aligned} \] と書くことが出来るので

\[ \begin{aligned} J &= \frac{1}{N}\sum_{n=1}^N\sum_{i=d+1}^D\left((\mathbf{x}_n-\overline{\mathbf{x}})^T\mathbf{u}_i\right)^2\\ &= \frac{1}{N}\sum_{n=1}^N\sum_{i=d+1}^D \mathbf{u}_i^T(\mathbf{x}_n-\overline{\mathbf{x}})(\mathbf{x}_n-\overline{\mathbf{x}})^T\mathbf{u}_i \end{aligned} \] となります. つまり，共分散行列 \[ \mathbf{S} = \frac{1}{N}\sum_{n=1}^N(\mathbf{x}_n-\overline{\mathbf{x}})(\mathbf{x}_n-\overline{\mathbf{x}})^T \] を用いて \[ J = \sum_{i=d+1}^D \mathbf{u}_i^T\mathbf{S}\mathbf{u}_i \] と書くことが出来ます.

ここで各 $\mathbf{u}_i$ が共分散行列 $\mathbf{S}$ の固有ベクトルになる場合を考えると，固有ベクトルを $\lambda_i$ として \[ \mathbf{S}\mathbf{u}_i = \lambda_i\mathbf{u}_i \] が成り立ちます. これを先ほどの式に代入すると \[ J = \sum_{i=d+1}^D \lambda_i \] となるので，固有値が小さい順に $\mathbf{u}_{d+1},\ldots,\mathbf{u}_D$ を選ぶとこれが最小になります. そして，残りの固有ベクトルを $\mathbf{u}_1,\ldots,\mathbf{u}_d$ とすれば良いです.

(何故 $\mathbf{u}_i$ が $\mathbf{S}$ の固有ベクトルの場合だけを考える事が出来るのかについては面倒なのでテキストを参照して下さい.)

時間の関係上詳しくは省略しますが，PRML本では主成分分析の確率的な取り扱いが紹介されています.

立式は線形回帰と同様に変数 $\mathbf{z}$ から $\mathbf{x}$ への変換が $D\times d$ 行列 $\mathbf{W}$ と，$d$ 次元ベクトル $\boldsymbol{\mu}$ とホワイトノイズ $\boldsymbol{\varepsilon}$ によって \[ \mathbf{x} = \mathbf{W}\mathbf{z} + \boldsymbol{\mu} + \boldsymbol{\varepsilon} \] と記述出来ると考えます.

異なる点は $\mathbf{z}$ が隠れ変数であるという点で， \[ p(\mathbf{x}|\mathbf{W},\boldsymbol{\mu}) = \int p(\mathbf{x},\mathbf{z}|\mathbf{W},\boldsymbol{\mu})\mathrm{d}\mathbf{z} \] の最大化を計算する必要があります. 従ってEM法を使う事になります.

今回はここで終了します．

次回は第14章に入りましてブースティングや決定木など，単純なモデルを複数組み合わせてより大きなモデルを構築するという話題をやります.