パターン認識・
機械学習勉強会
第16回
@ワークスアプリケーションズ
中村晃一2014年6月19日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
ジョインツリーアルゴリズム(続き)
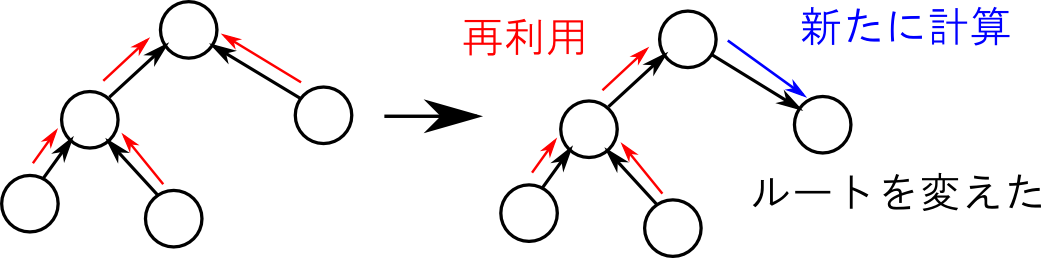
前回は, ファクター消去によってベイジアンネットワークに対する推論を行う場合, エリミネーションツリーという木構造の上で一回メッセージパッシングを行うだけで全てのクラスターについての同時分布を厳密に計算する事が出来るという所まで説明しました.
残る問題は具体的にどのようなエリミネーションツリーを用いると効率的であるかという事になります. そこでジョインツリーという概念が登場します.
グラフ $G=(V,E)$ のノードの部分集合 $\mathbf{C}\subset V$ を クラスター (cluster) と呼びます.
エリミネーションツリーに対して定義されたクラスター \[ \mathbf{C}_i \stackrel{\mathrm{def}}{=} \mathrm{vars}(i)\cup\bigcup_{j}\mathbf{S}_{ij} \] はこの一種です.
無向グラフのクラスター $\mathbf{C}$ 内の全てのノードが互いに接続されているならば $\mathbf{C}$ を クリーク(clique) と呼び, クリーク $\mathbf{C}$ が他のクリークに含まれないならばそれを 極大クリーク (maximal clique) と呼びます.
以下はあるグラフの極大クリークの例です.
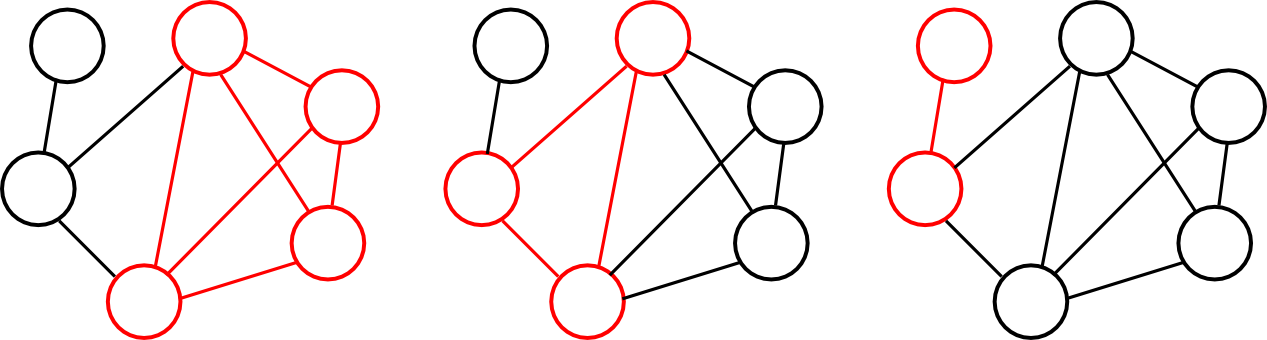
無向グラフ $G$ に対して, $G$ の極大クリークをノードとし, \[ \text{辺$(\mathbf{C}_i,\mathbf{C}_j)$が存在}\Rightarrow \mathbf{C}_i\cap\mathbf{C}_j\neq\emptyset \] を満たすグラフを 極大クリークグラフ (maximal clique graph) と呼び,
\[ \text{辺$(\mathbf{C}_i,\mathbf{C}_j)$が存在}\Leftrightarrow \mathbf{C}_i\cap\mathbf{C}_j\neq\emptyset \] を満たすグラフを ジョイングラフ (join graph) もしくは ジャンクショングラフ (junction graph) と呼びます.
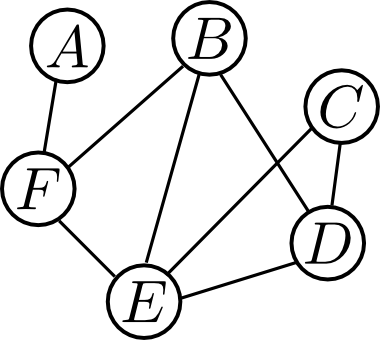
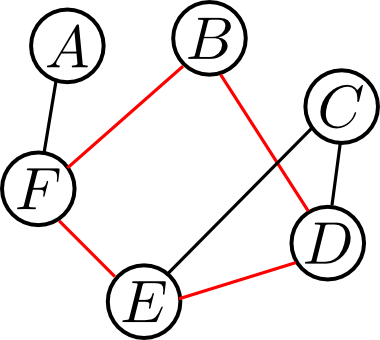
例えば以下のグラフの極大クリークは \[ \{A,F\}, \{B,D,E\}, \{B,E,F\}, \{C,D,E\} \] が全てです.
すると, ジョイングラフは右下のようになります. ジョイングラフは無向グラフ $G$ に対して一意的に定まります.
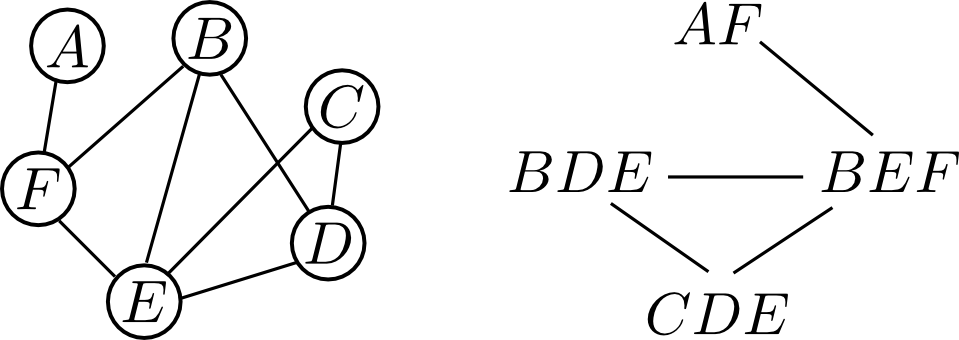
ジョイングラフから $0$ 本以上のエッジを除いた物が極大クリークグラフです. 右下その例です.
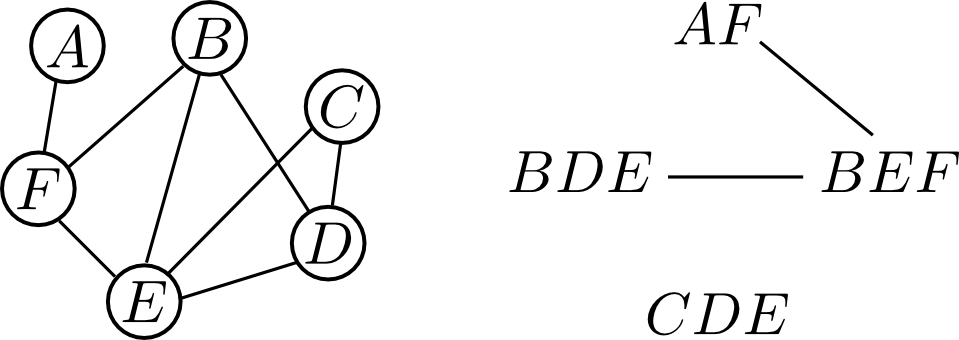
以上の準備の元にジョインツリーが以下の様に定義されます.
ジョインツリーの定義
無向グラフ $G$ の ジョインツリー (jointree) もしくは ジャンクションツリー (junction tree) とは $G$ の極大クリークグラフ $\mathcal{T}$ であって以下の条件を満たすもの.
- $\mathcal{T}$ は木である.
- 任意の2つの極大クリーク $\mathbf{C}_i,\mathbf{C}_j$ について, $A\in\mathbf{C}_i\cap\mathbf{C}_j$ なるノードが存在するならば, $A$ は $\mathcal{T}$ 内の $\mathbf{C}_i$ から $\mathbf{C}_j$ への路上の全ての極大クリークに含まれる.
右下の木は左下のグラフのジョインツリーになっています.
例えば, $E$ は $BEF$ と $CDE$ の両方に含まれますが, この2つを結ぶ路上にある $BDE$ にも含まれています.
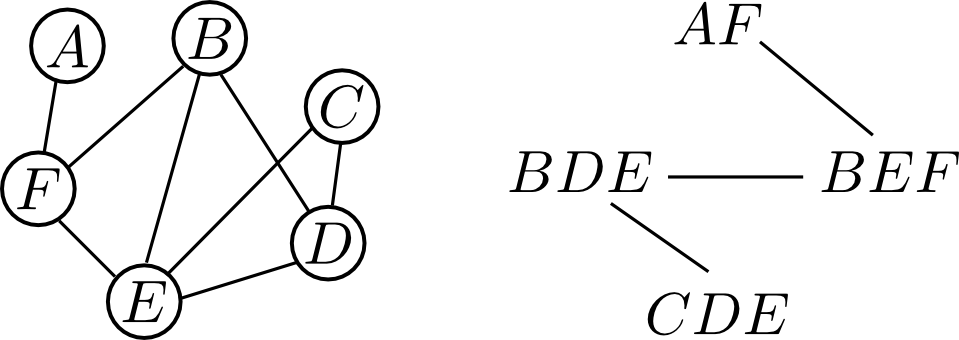
こちらはジョインツリーではないツリーの例です.
$B$ は $BDE$ と $BEF$ に含まれますが, この2つを結ぶ路上にある $CDE$ には含まれないからです.
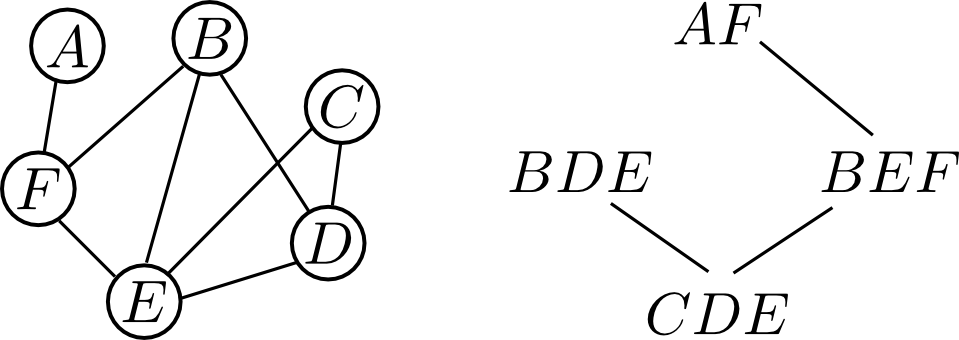
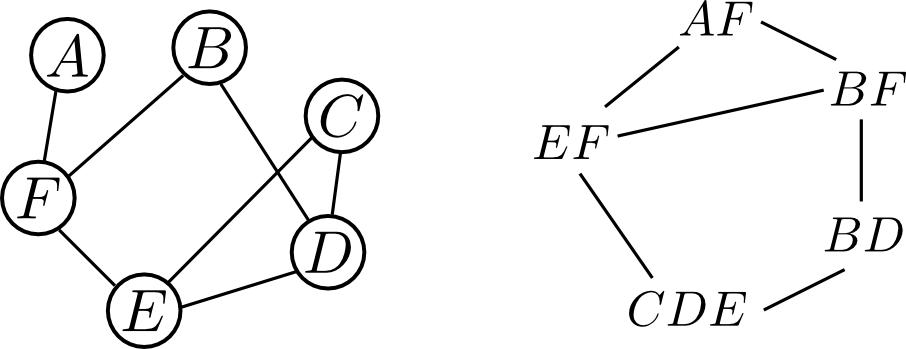
ジョインツリーは任意の無向グラフ $G$ に対して存在するわけではありません.
例えば左下のグラフのジョイングラフは右下のようになりますが, ここからどのように辺を除いてもジョインツリーにはなりません.
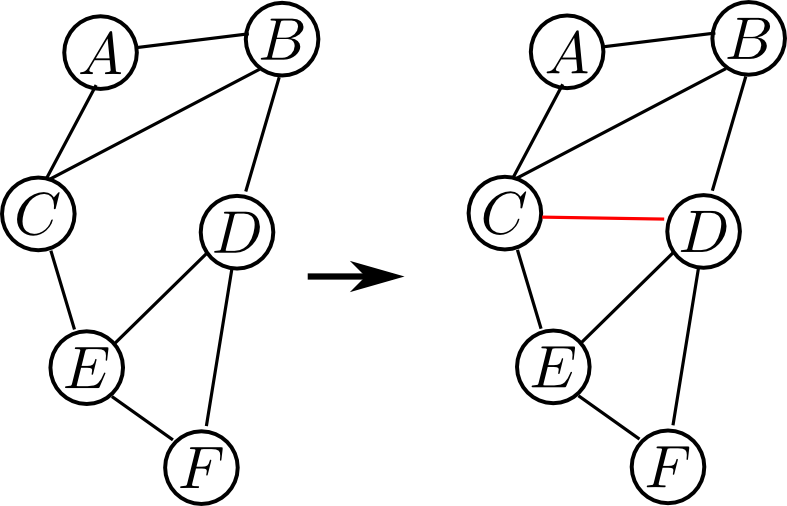
「長さ $4$ 以上の弦を持たないループ」が存在しないグラフを コーダルグラフ (chordal graph) もしくは 三角グラフ (triangulated graph) と呼びます.
先ほどのグラフは以下の様に弦を持たない長さ $4$ 以上のループが存在するのでコーダルグラフではありません.
実は \[ \text{$G$ のジョインツリーが存在}\Leftrightarrow\text{$G$ がコーダルグラフ} \] であるという事が知られています.
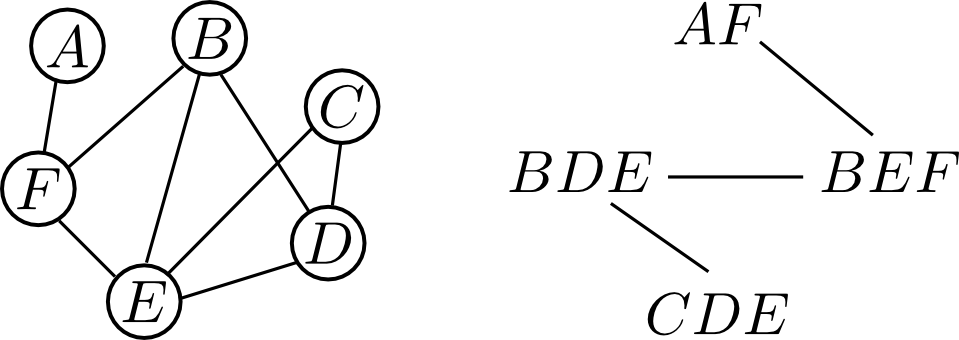
続いて, ベイジアンネットワークからコーダルグラフを得る方法の説明をします.
有向グラフ構造 $G$ に対して以下の操作を行って得られる無向グラフを $G$ の モラルグラフ (moral graph) と呼びます.
- 各ノード $A$ について $\mathrm{pa}(A)$ の全てのノード間に辺を引く.
- $G$ の各辺から向きを除去する

これはコーダルグラフになっていませんが長さ $4$ 以上のループに新たに弦を追加すればコーダルグラフになります. この操作を フィルイン (fill-in) と呼びます.
フィルインの仕方は一意的ではなく, フィルインの良し悪しが推論の効率に影響します.
ここでは MCS (maximum cardinality search) フィルイン というアルゴリズムを紹介します. これはベイジアンネットワークの計算量について最適なフィルインを保証するものではありません.
無向グラフ $G$ に対して \[ \mathrm{Nbr}(A) \stackrel{\mathrm{def}}{=}\{\text{$A$ に隣接するノード}\} \] を $A$ の 近傍 (neighbours) と呼びます.
MCSフィルイン
$G$ を無向グラフとする. ノードに対するナンバリングを $\alpha$ とする. $G$ のノードのうち番号付けが行われたノード集合を $N$ とする.
- 適当にノード $V_1$ を選び, $\alpha(1) = V_1$ とする.
- $i = 2$ とする.
- $|\mathrm{Nbr}(V_k)\cap N|$ が最大の $V_k$ を選び, $\alpha(i) = V_k$ とする.
- $\mathrm{Nbr}(V_k)\cap\{\alpha(1),\ldots,\alpha(i-1)\}$ がクリークでないならば, これをクリークにする為に必要なエッジを追加し, $3$ に戻る.
- $i = \text{(ノード数)}$ ならば終了. そうでなければ$i = i + 1$ として $3$ に戻る.
先ほどのグラフでやってみます. $\alpha(1) = A$ からスタートしてみましょう.
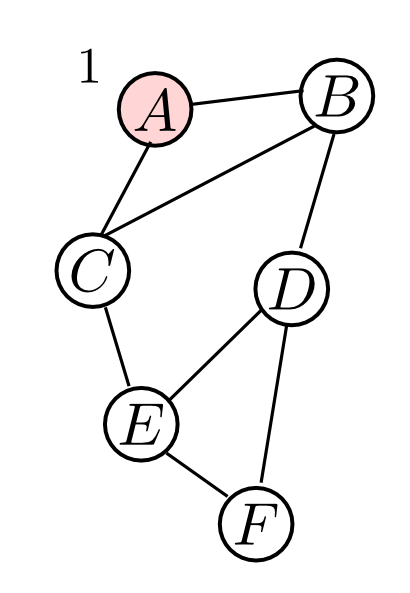
$N = \{A\}$ と隣接するのは $B,C$ のみで, どちらも $|\mathrm{Nbr}(V_k)\cap N|=1$ だから互角です.
そこで $\alpha(2)=B$ としてみましょう. $\mathrm{Nbr}(B)\cap N=\{A\}B$ はクリークなので次に進みます.
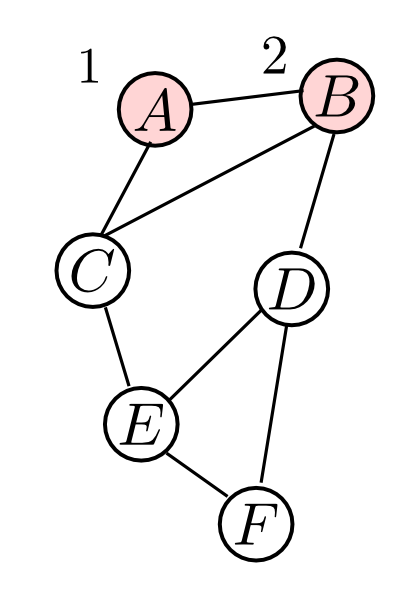
$N = \{A,B\}$ と隣接するのは $C,D$ ですが, $C$ の方が(既に番号付けられた)近傍が多いので $\alpha(3) = C$ です. $\{A,B\}$ はクリークなので次に進みます.
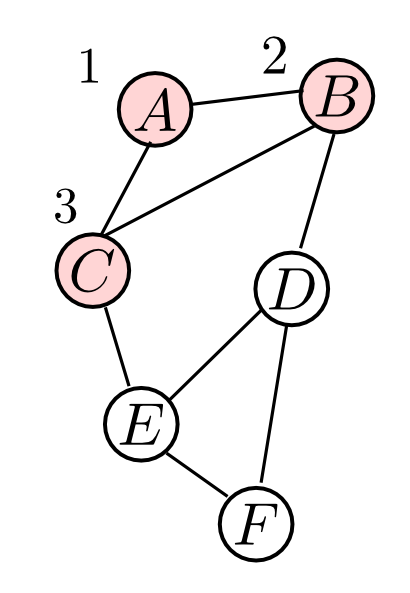
$N = \{A,B,C\}$ と隣接するのは $D,E$ ですが, どちらも近傍は1つなのでどちらでも良いです. そこで $\alpha(4)=D$ としましょう. $D$ の近傍である $\{B\}$ はクリークなので次に進みます.
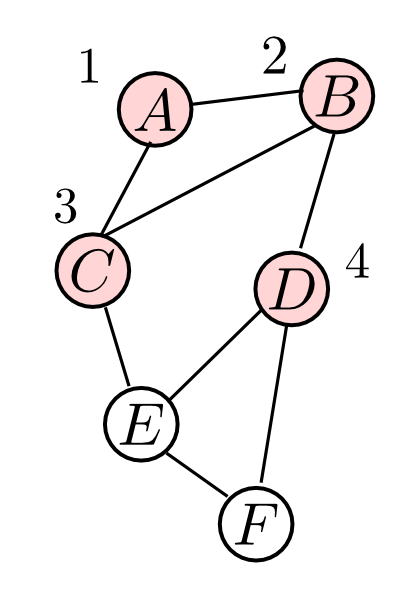
$N = \{A,B,C,D\}$ と隣接するのは $E,F$ ですが, $E$ の方が近傍が多いので $\alpha(5)=E$ です. ところが $E$ の近傍 $\{C,D\}$ はクリークになっていないので辺を追加します.
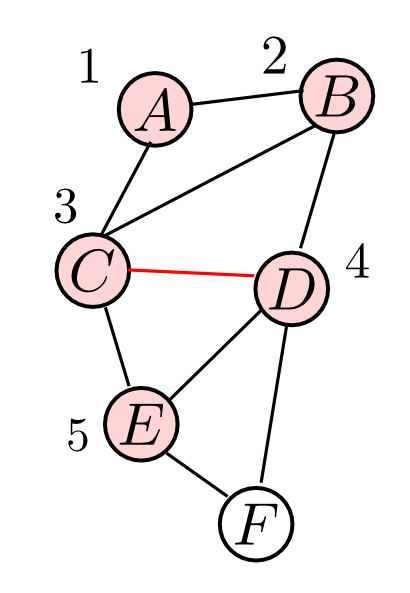
$N = \{A,B,C,D,E\}$ と隣接するのは $F$ のみなので $\alpha(6)=F$ とします. $F$ の近傍 $\{D,E\}$ はクリークになっているので辺の追加はありません.
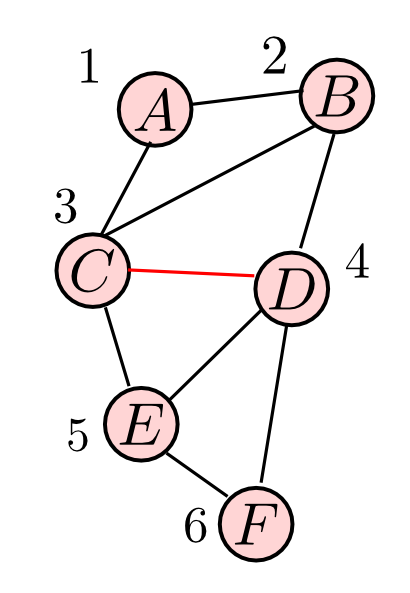
出来上がったコーダルグラフの極大クリークは \[ ABC, BCD, CDE, DEF \] の4つです. これらをMCSフィルインで付けられた番号 $\alpha$ の最大値が小さい順番に並べると \[ ABC \rightarrow BCD \rightarrow CDE \rightarrow DEF \] となります.
これを得られたコーダルグラフの クリークチェーン (clique chain) と言います.

以上で \[ \text{ベイジアンネットワーク}\rightarrow \text{モラルグラフ}\rightarrow\text{コーダルグラフ} \] という所まで来ました. あとはこれからジョインツリーを導出すれば終わりです.
ジョインツリーの生成
- コーダルグラフ $G$ を構築する. そのクリークチェーンを $\mathbf{C}_1,\mathbf{C}_2,\ldots,\mathbf{C}_m$ とする.
- 各 $\mathbf{C}_i, (i=m,m-1,\ldots,2)$ について $\{\mathbf{C}_1,\ldots,\mathbf{C}_{i-1}\}$ の中で $|\mathbf{C}_i\cap\mathbf{C}_k|$ が最大となる $\mathbf{C}_k$ を選び, 辺 $(\mathbf{C}_i,\mathbf{C}_k)$ をジョインツリーに追加する.
先ほどの例ではクリークチェーンが \[ ABC \rightarrow BCD \rightarrow CDE \rightarrow DEF \] であるので $DEF$ から辺を追加します.
$\{ABC,BCD,CDE\}$ のうち共通するノードが最も多いので $CDE$ なので辺 $(CDE, DEF)$ を追加します.
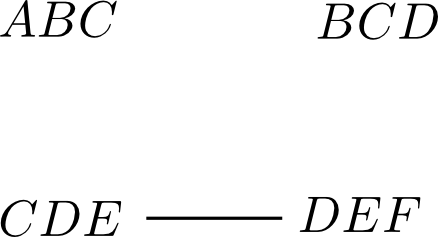
続いて $CDE$ と $\{ABC,BCD\}$ では $BCD$ との共通ノードが最も多いので辺 $(BCD,CDE)$ を追加します.
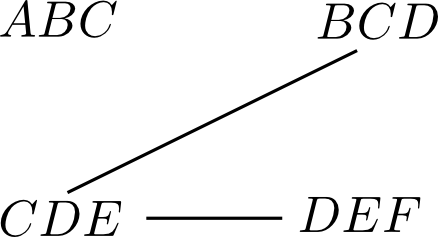
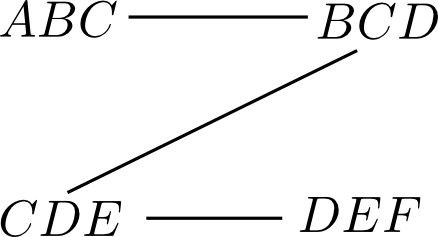
これを繰り返すと以下のグラフを得ます. これがジャンクションツリーです.
あるDAG(非循環有向グラフ) $G$ のノード $A$ に対して \[ \{A\}\cup\mathrm{pa}(A) \] つまり, $A$ と $A$の親ノードの集合を $A$ の ファミリー (family) と呼びます.

例えば, 以下のベイジアンネットワークに対するファミリーは \[ A, B, ABC, BD, CE, DEF \] となります. これは \[ P(A,B,C,D,E,F) = P(A)P(B)P(C|A,B)P(D|B)P(E|C)P(F|D,E) \] という同時分布の各因子と対応しています.
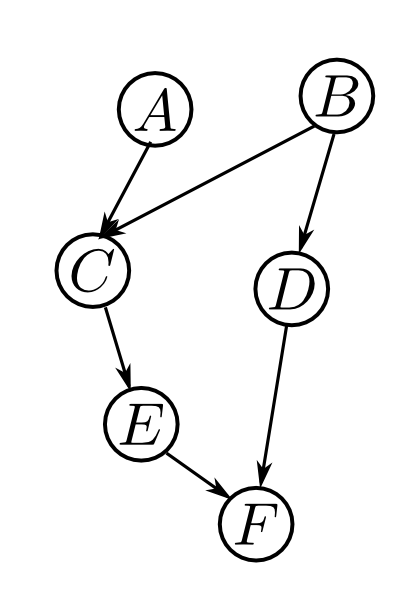
この時, 以下の事実が言えます.
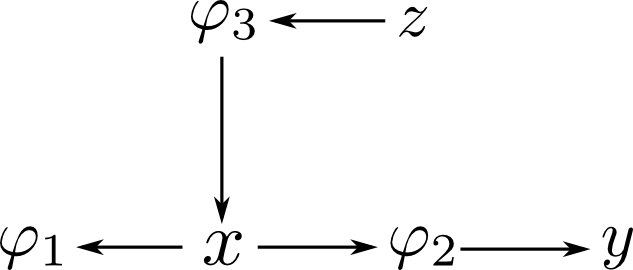
そこで, 各ファミリー $\varphi_i$ をそれを含むジョインツリーのノードに割り当てる事によってエリミネーションツリーを得る事が出来ます.
先ほどの例でやってみると, 例えば
- $P(A)P(B)P(C|A,B)$ をノード $ABC$ に
- $P(D|B)$ をノード $BCD$ に
- $P(E|C)$ をノード $CDE$ に
- $P(F|D,E)$ をノード $DEF$ に
に割り当てる事によって以下のエリミネーションツリーを得る事が出来ます.
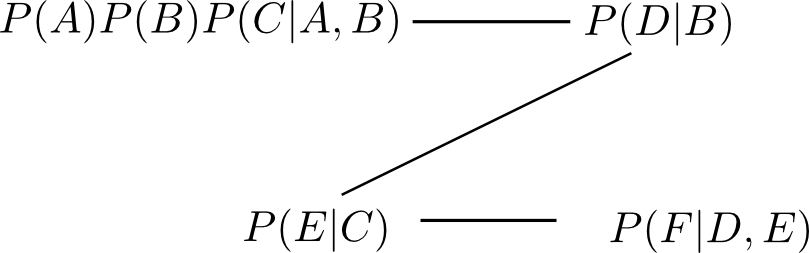
ジョインツリーを用いてエリミネーションを構築した場合, ノード $\mathbf{C}_i,\mathbf{C}_j$ を結ぶ辺に関するセパレータは \[ \mathbf{S}_{ij} = \mathbf{C}_i\cap\mathbf{C}_j \] と, 非常に簡単な形になります.
あとは, メッセージパッシングを行うのみという事になります.
MCSフィルインはその最適性が保証されないので, もっと良いフィルイン方法を考えたいのですが, 最適なフィルインを求める事はNP困難な問題となります.
そこでやはり何らかのヒューリスティクスを用いたいのですが, 変数消去法の際に用いた最小次数法をここで用いる事も可能です.
復習すると, まず インタラクショングラフ (interaction graph) というものが必要でした.
インタラクショングラフ
ファクターの集合 $\mathcal{S}=\{\varphi_1,\ldots,\varphi_n\}$ に対するインタラクショングラフ $\mathcal{G}_i$ とは無向グラフであり, 頂点集合 $\mathbf{V}$と辺集合 $\mathbf{E}$ は以下のように定める.
\[ \begin{aligned} \mathbf{V} &= \{\varphi_1,\ldots\varphi_n\text{に含まれる各変数}\}\\ \mathbf{E} &= \{(x,y) \,|\, \text{$x,y$ が同一のファクターに含まれる}\} \end{aligned}\]例えば, 以下のベイジアンネットワークのインタラクショングラフは
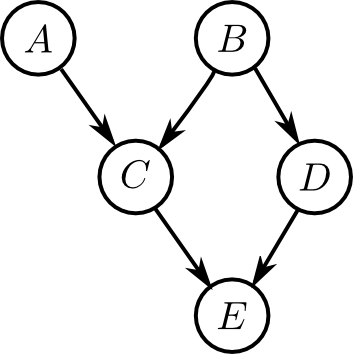
以下のようになるのでしたが, 実はこれはモラルグラフと同じものです.
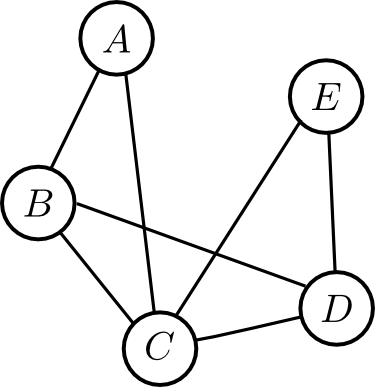
最小次数法というヒューリスティクス的な方法では, 最も隣接するノードの数が少ないノードから消去していくのでした.
この時, 消去するノード及びその隣接ノードを1つのクラスター $\mathbf{C}_i$ とすると, クリークの列を得る事が出来ます.
例えば, 先ほどの消去順の場合には \[ ABC \rightarrow BCD \rightarrow CDE \rightarrow DE \rightarrow D\] となります.

このクリークチェインに基づいてジョインツリーを構築すると以下のようになります.
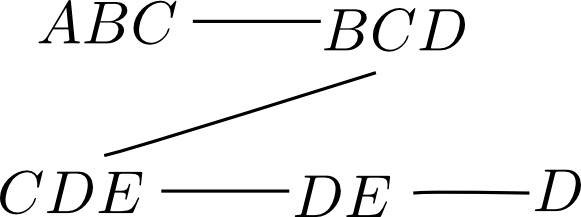
第16回はここで終わります
次回はマルコフ確率場の紹介をします.