パターン認識・
機械学習勉強会
第15回
@ワークスアプリケーションズ
中村晃一2014年6月12日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
ベイジアンネットワーク上での推論(続き)
前回は単純な変数消去法による推論アルゴリズムを紹介しましたが, これは効率が悪いです.
本日と来週の冒頭を使ってより効率的な厳密推論アルゴリズムであるジョインツリー法の解説を行います. この辺りもPRMLではあまり解説されていないので以下の参考書を用いました.
- 植野 真臣著「ベイジアンネットワーク」コロナ社
以下が前回紹介したアルゴリズムです.
変数消去による周辺事後分布の計算
クエリを $\mathbf{Q}$, エビデンスを $E$ とする. \[ \mathcal{S} = \{ p(X_i|\mathrm{pa}(X_i))\}_i \] とする. $\mathcal{S}$ 内の各テーブルについて $E$ と一致しない行を $0$ にする. $\mathbf{Q}$ に含まれない変数 $X$ に対して以下を繰り返す.
- $\mathbf{S}$ 内の$X$を含むファクターを全て除く.
- ファクターを掛けて $X$ について足し合わせる.
- それを $\mathbf{S}$ に追加する.
$\mathbf{S}$ 内のファクターを全て掛け合わせて出力する.
このアルゴリズムは確率密度関数の因数分解 \[ p(\mathbf{X}) = \prod_i p(X_i|\mathrm{pa}(X_i)) \]
このアルゴリズムはネットワークのグラフ構造を一切考慮していないという点が問題です. グラフ理論的な考察によって計算量を削減する事が可能となります.
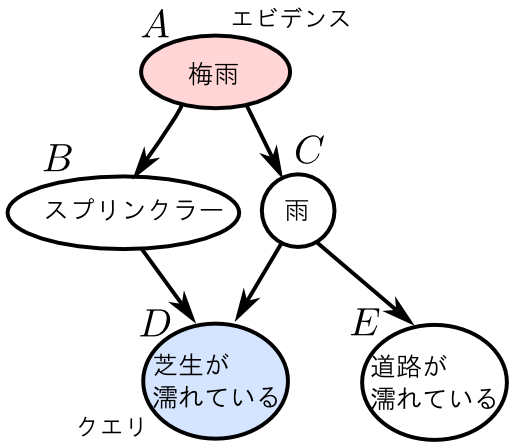
簡単に出来るのが 枝刈り (pruning)です.
前回の例において $\mathbf{Q}=\{D\}$, $\mathbf{E}=\{A\}$ である場合を考えましょう.
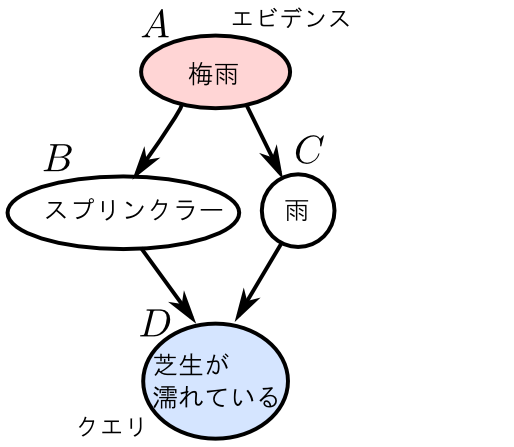
まず, ノード $E$ は $D$ に関する推論とは全く無関係であるので除去出来ます.
\[ \begin{aligned} p(A,D)&=\sum_{B,C,E}p(E|C)p(D|B,C)p(C|A)p(B|A)p(A) \\ &=\sum_{B,C}p(D|B,C)p(C|A)p(B|A)p(A)\sum_EP(E|C) \end{aligned} \] において $\sum_EP(E|C) = 1$ であるからです.

続いてエビデンスノード $A$ も除去してしまう事が出来ます.
例えば, $A$ の観測値が $a$ であるならば \[ \begin{aligned} p(A=a,D) &=\sum_{B,C}p(D|B,C)p(C|A= a)p(B|A= a)p(A= a) \\ \end{aligned} \] であり $p(A=a)=1$ となる為です.
枝刈り
クエリ集合 $\mathbf{Q}$ とエビデンス集合 $\mathbf{E}$ が与えられた時,
- $\mathbf{Q}$ に含まれない葉ノード(子を持たないノード)へ向かうエッジ
- $\mathbf{E}$ に含まれるノードから張られたエッジ
を除去する事が出来る. これを除去出来るノードがなくなるまで繰り返えす.
また, 枝刈りの結果孤立した$\mathbf{Q},\mathbf{E}$に含まれないノードも除去する事が出来る.
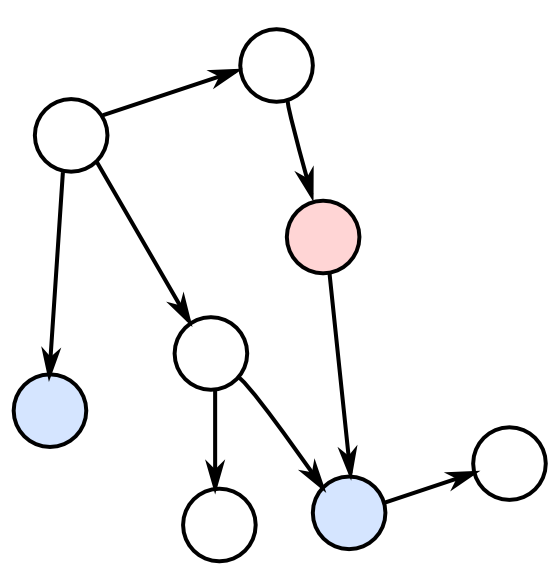
例えば, 右図のような状況(青がクエリ, 赤がエビデンス)ならば
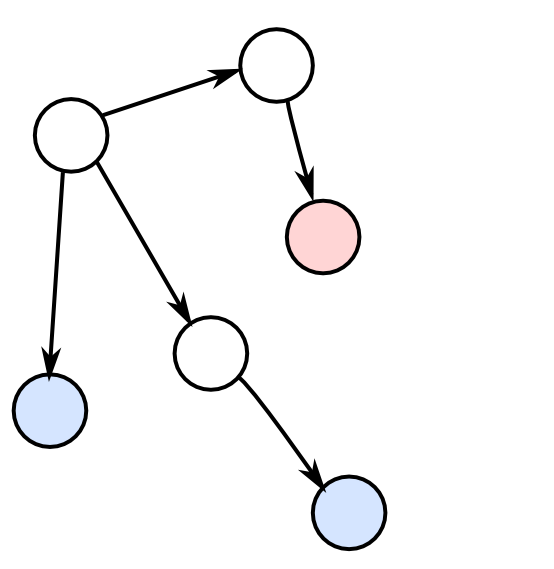
こうなります.
prog15-1.py に枝刈りの実装を行ってみましたので参考にしてください.
変数消去法の計算量
変数消去法の計算量には変数の数 $N$ はもちろんですが, 変数を消去する順番も関係します.
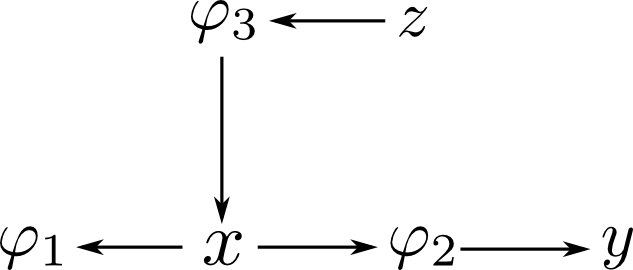
例として, \[ p(A,B,C) = p(C|B)p(B|A)p(A) \] から$A,B$を消去する場合, 消去順によって以下のような違いが出ます.
【$A\rightarrow B$の順に消した場合】
- $\varphi(B) = \sum_{A}p(B|A)p(A)$ を計算.
- $p(C) = \sum_{B}p(C|B)\varphi(B)$ を計算.
【$B\rightarrow A$の順に消した場合】
- $\varphi(A,C) = \sum_{B}p(C|B)p(B|A)$ を計算.
- $p(C) = \sum_A\varphi(A,C)p(A)$ を計算.
$B\rightarrow A$ の順に消去してしまった場合は \[ \varphi(A, C) \] という因子が残り計算量が増加してしまっています.
一般に以下の事が言えます.
変数消去法の計算量
変数の数を $N$, 変数消去の途中に出現する因子の変数の数の最大値を $w$ (width) とすると, 変数消去法の計算量は \[ \mathcal{O}(N^2\mathrm{exp}(w)) \] となる.従って $w$ が最小となるような変数消去順序を求めれば良いのですが, 残念ながらこの問題はNP困難である事が解っています.
そこで, ヒューリスティックスによる 最小次数法 (minimum degree method) を紹介します.
まず, インタラクショングラフ (interaction graph) というものが必要です. これは以下のように定義されます.
インタラクショングラフ
ファクターの集合 $\mathcal{S}=\{\varphi_1,\ldots,\varphi_n\}$ に対するインタラクショングラフ $\mathcal{G}_i$ とは無向グラフであり, 頂点集合 $\mathbf{V}$と辺集合 $\mathbf{E}$ は以下のように定める.
\[ \begin{aligned} \mathbf{V} &= \{\varphi_1,\ldots\varphi_n\text{に含まれる各変数}\}\\ \mathbf{E} &= \{(x,y) \,|\, \text{$x,y$ が同一のファクターに含まれる}\} \end{aligned}\]前回やった \[ p(A,B,C,D,E) = p(A)p(B)p(C|A,B)p(D|B)p(E|C,D) \] を例に考えてみます.
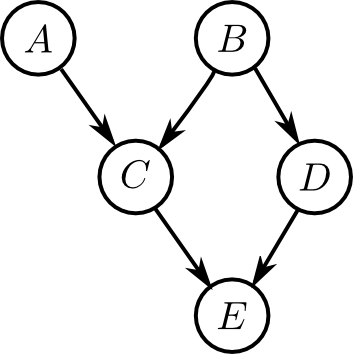
最初の $\mathbf{S}$ の状態は以下のようになるのでした \[ \mathcal{S} = \{p(A),p(B),p(C|A,B),p(D|B),p(E|C,D)\} \]
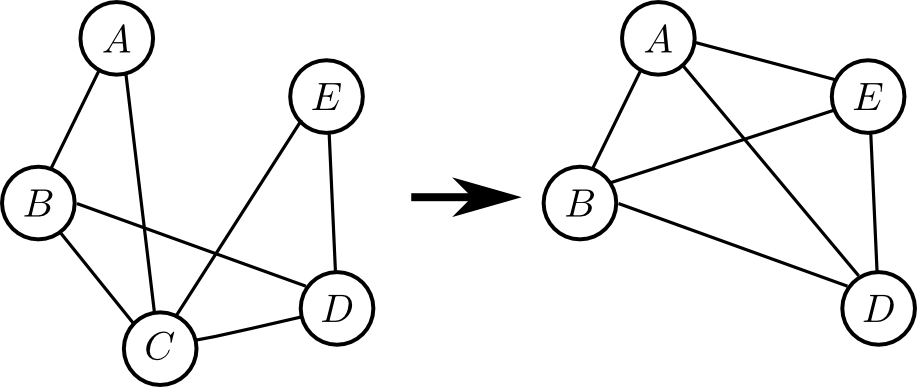
そして, これと対応するインタラクショングラフは下図のようになります.
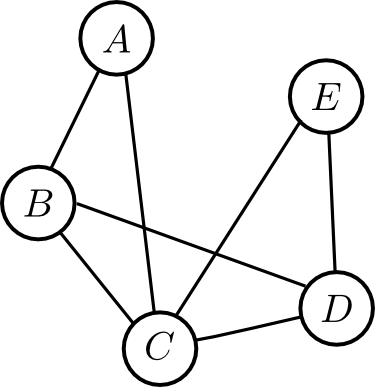
次にここから $B$ を消去してみると \[ \varphi(A,C,D)= \sum_Bp(B)p(C|A,B)p(D|B) \] より \[ \mathcal{S}' = \{p(A),\varphi(A,C,D),p(E|C,D)\} \] となります.
これに対応するインタラクショングラフは以下です.
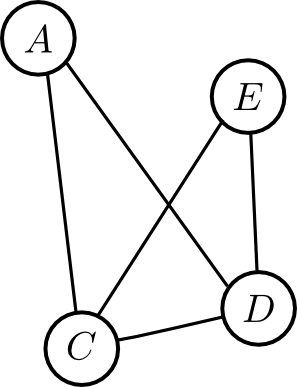
この推移は
- $B$ に隣接していたノード同士を新たに繋ぎ直す
という事によって行う事が出来ます.
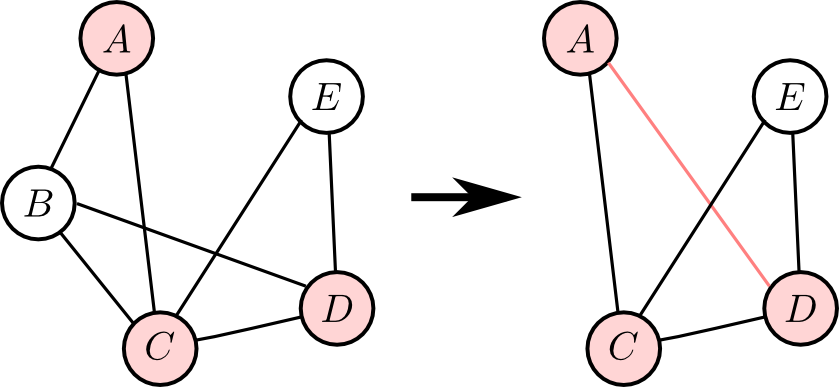
この時, \[ \text{$X$を消去して出来る因子の変数の数} = \text{$X$の$\mathcal{G}_i$での次数} \] となります.
例えば最初に $C$ を消去すると \[ \varphi(A,B,D,E) = \sum_{C}p(C|A,B)p(E|C,D) \] という大きな因子が出来てしまいます.
そこで,
- 常にインタラクショングラフ上で次数が最小の変数を消去する
というヒューリスティクス的な手法を考える事が出来ます. これが最小次数法です.
先ほどの問題で最小次数法を適用すると以下のように \[ A\rightarrow B\rightarrow C\rightarrow E \] などの順番で消去することになり, この場合 $w=3$ です.
ジョインツリーアルゴリズム
ジョインツリーアルゴリズム (jointree algorithm は $\mathcal{O}(N\mathrm{exp}(w))$ の計算量で厳密な推論を行う事が出来るアルゴリズムです.
ジョインツリーアルゴリズムは ファクター消去法 (factor elimination) というものの特別な場合ですので, まずこれから説明します.
例として再び \[ p(A,B,C,D,E) = p(A)p(B)p(C|A,B)p(D|B)p(E|C,D) \] において $p(D)$ を計算する問題を考えます.
変数消去法では$D$ 以外の変数を1つずつ消す事によってこれを計算しました.
ファクター消去法では $D$ を含む適当な1つのファクター(例えば $p(D|B)$) 以外のファクターを1つずつ消す事によってこれを計算します.
やってみます. \[ \mathcal{S} = \{\varphi(A),\varphi(B),\varphi(A,B,C),\varphi(B,D),\varphi(C,D,E)\} \] から $\varphi(B,D)$ 以外を消去する事にします.
まず $\varphi(A)$ を消去します. どれか別の適当なファクター(例えば $\varphi(B)$)に $\varphi(A)$ を掛けた \[ \varphi(A,B)=\varphi(A)\varphi(B) \] を計算して $\varphi(B)$ をこれで置換えます. \[ \mathcal{S} = \{\varphi(A,B),\varphi(A,B,C),\varphi(B,D),\varphi(C,D,E)\} \]
次に $\varphi(C,D,E)$ を消去してみましょう. まず $E$ はこのファクターにしか含まれないので 消しちゃいます. \[ \sum_E \varphi(C,D,E) \] これを別のどれか(例えば $\varphi(B,D)$)に掛けた \[ \varphi(B,C,D) = \varphi(B,D)\sum_E\varphi(C,D,E) \] で $\varphi(B,D)$ を置換えます. \[ \mathcal{S} = \{\varphi(A,B), \varphi(A,B,C),\varphi(B,C,D)\} \]
同様に, 次は $\varphi(A,B)$ を $\varphi(A,B,C)$ に掛けて消去しましょう. \[ \varphi'(A,B,C) = \varphi(A,B)\varphi(A,B,C) \] として \[ \mathcal{S} = \{\varphi'(A,B,C),\varphi(B,C,D)\} \] とします.
次は $\varphi'(A,B,C)$ を消しますが $A$ はこのファクターにしか含まれないので消してしまいます. \[ \sum_A \varphi'(A,B,C) \] そして $\varphi(B,C,D)$ にかけてこのファクターを消します. つまり \[ \varphi'(B,C,D) = \varphi(B,C,D)\sum_A\varphi'(A,B,C) \] として \[ \mathcal{S} = \{\varphi'(B,C,D)\} \] とします.
最後に残ったファクター $\varphi'(B,C,D)$ には求める $D$ 以外のファクター $B,C$ が含まれていますがこれを足し合わせれば \[ p(D) = \sum_{B,C}\varphi'(B,C,D) \] となります. 以上でファクター消去法による確率計算が終わりました.
ファクター $\varphi$ の変数 $\mathbf{Q}$ 以外を足しあわせて消去するという操作は良く使うので \[ \mathrm{proj}(\varphi, \mathbf{Q}) \stackrel{\mathrm{def}}{=} \sum_{\mathrm{vars}\varphi-\mathbf{Q}}\varphi \] と書きます. 但し $\mathrm{vars}\varphi$ は $\varphi$ に含まれる変数の集合です.
まとめると以下の様になります.
ファクター消去による事前周辺確率の計算
クエリ集合を $\mathbf{Q}$ とする.
- $\mathcal{S} = \{ p(X_i|\mathrm{pa}(X_i)) \}_{1\leq i \leq N}$ とする.
- $\varphi_r\in\mathcal{S}$ を $\mathbf{Q}$ の変数を全て含む適当なファクターとする.
- $|\mathcal{S}|>1$の間以下を繰り返す.
- $\varphi_i \in \mathcal{S}, \varphi_i\neq \varphi_r$ を選び $\mathcal{S}$ から除く.
- $\mathbf{V}$ を $\varphi_i$ のみが持つ変数の集合とする.
- $\varphi_j \in \mathcal{S}$ を選ぶ.
- $\varphi_j$ を$\varphi_j\sum_V \varphi_i$で置き換える.
- 以下が求める確率分布. \[ \mathrm{proj}(\varphi_r,\mathbf{Q}) \]
ファクター消去法ではどの順番でファクターを消去するのかが重要となります. これを指定するものが エリミネーションツリー (elimination tree) です.
エリミネーションツリー
エリミネーションツリー $\mathcal{T}$ とは, 各ファクター $\varphi_r$ をノードとする木構造(閉路のない単連結な無向グラフ)である.
エリミネーションツリーを用いたファクター消去法を簡単に書くと以下のようになります.
エリミネーションツリーによるファクター消去
残すファクター $\varphi_r$ をエリミネーションツリー $\mathcal{T}$ のルートとみなして以下を繰り返してファクターを消去する.
- 葉ノードを消去し, 親ノードに掛け合わせる
例えば先ほどの例のファクター消去手順に対応するエリミネーションツリーは下図のようになります.
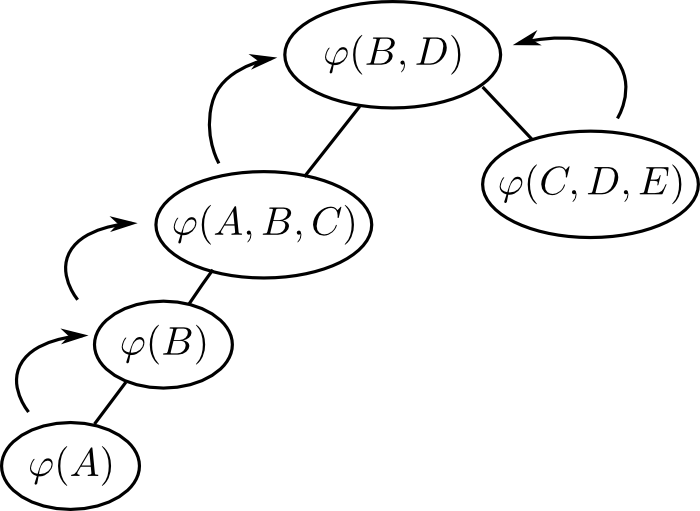
ファクター消去法はどのようなエリミネーションツリーを用いても必ず正しい答えを得る事が出来ます.
そこで問題となるのが「どのようなエリミネーションツリーを用いれば効率的に計算出来るか?」という事です.
ジョインツリーアルゴリズムとはジョインツリーと呼ばれるものをエリミネーションツリーの構成に利用するものです.
もう少し準備が必要です.
エリミネーションツリー $\mathcal{T}$ の辺 $(i,j)$ に対して \[ \mathbf{S}_{ij} \stackrel{\mathrm{def}}{=} \{\text{$\mathcal{T}$の$i$ 側にある変数}\}\cap\{\text{$\mathcal{T}$の$j$側にある変数}\} \] をこの辺の セパレータ(separator) と呼びます.
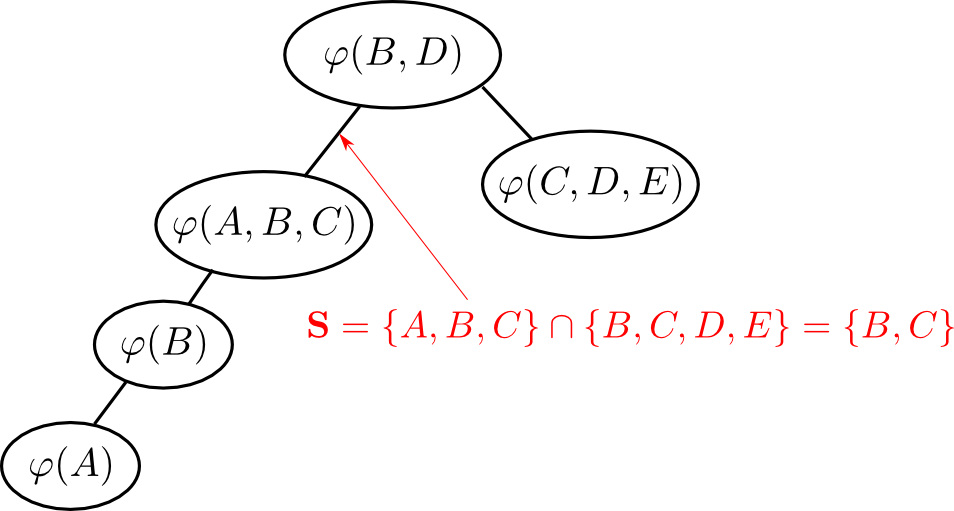
ファクター $\varphi_i$ を消去し $\varphi_j$ にまとめる時には \[ \mathrm{vars}\varphi_i - \mathbf{S}_{ij} \] が $\varphi_i$ のみに含まれる変数となります.
つまり, $\varphi_j$ の更新ルールは \[ \varphi_j \leftarrow \varphi_j\mathrm{proj}(\varphi_i, \mathbf{S}_{ij}) \] と書くことが出来ます.
エリミネーションツリー $\mathcal{T}$ のノード $i$ に対して \[ \mathbf{C}_i \stackrel{\mathrm{def}}{=} \mathrm{vars}(i)\cup\bigcup_{j}\mathbf{S}_{ij} \] をこのノードに対応する クラスター (cluster) と呼びます.
クラスターとは, ファクターを消去していってそのノードが葉になった時に含まれる変数の集合です.
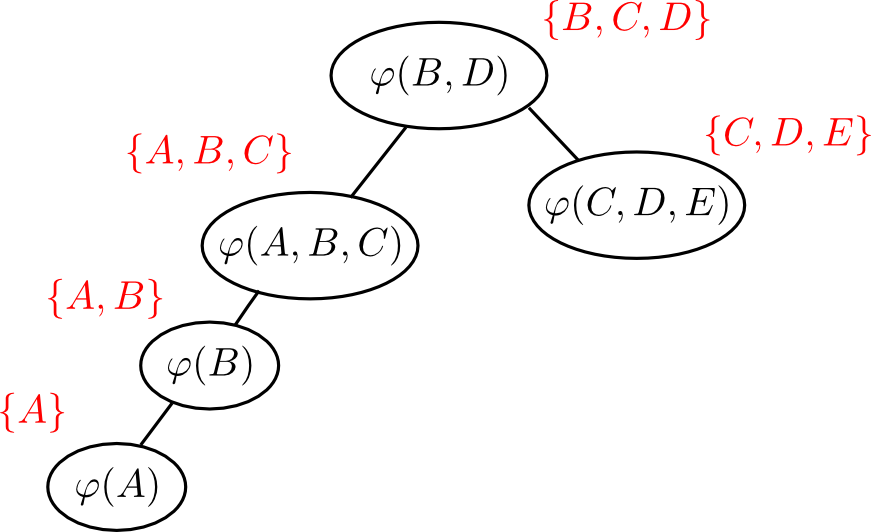
\[ w \stackrel{\mathrm{def}}{=} \mathop{\rm max}\limits_{i}|\mathbf{C}_i|-1 \] をエリミネーションツリーの幅(width)と言います.
変数消去法の時と同様に $w$ に関して指数的に計算量が増加します. 従って $w$ を出来るだけ小さくする事が目標になります.
メッセージパッシング
ファクター消去法では, エリミネーションツリーの辺に沿ってファクターを流して行くわけですが, これをメッセージ(message) と呼びます.

子ノード $i$ から親ノード $j$ へのメッセージは $m_{ij}$以下の様に定義されます. \[ m_{ij} \stackrel{\mathrm{def}}{=} \mathrm{proj}\left(\varphi_i\prod_{k}m_{ki}, \mathbf{S}_{ij}\right) \] 但し $k$ はノード $i$ の子ノードです.
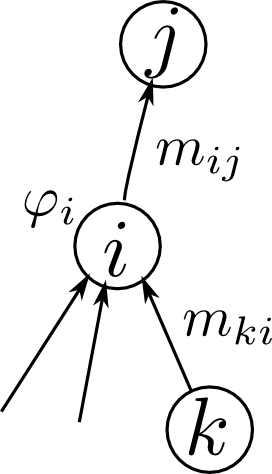
葉ノード $i$ では子が存在しませんから \[ m_{ij} \stackrel{\mathrm{def}}{=} \mathrm{proj}(\varphi_i, \mathbf{S}_{ij}) \] となります.
このメッセージをルートノード $r$ まで流していった時 \[ p(\mathbf{C}_r) = \varphi_r\prod_{k}m_{kr}\] となります. つまりクラスターの同時確率が計算されます.
これを周辺化すれば求める確率 \[ p(\mathbf{Q}) = \mathrm{proj}(p(\mathbf{C}_r),\mathbf{Q}) \] を得る事が出来ます.
メッセージパッシングというアルゴリズム, ルートを変えて再計算したい時に, メッセージを再利用出来る というとても良い特徴を持っています.
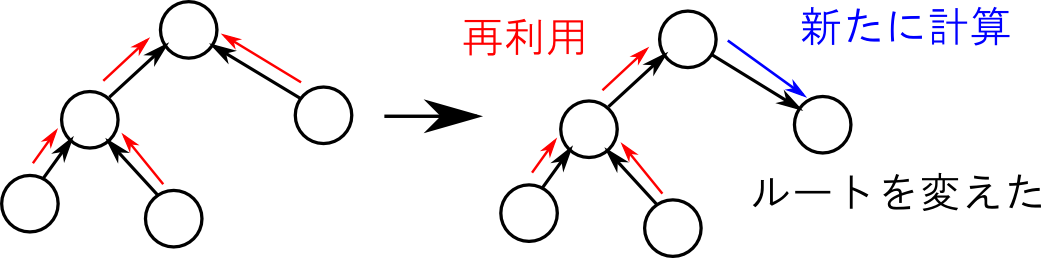
つまり, 一回ルートまでメッセージを流して, その後ルートから逆にメッセージを再分配すれば一辺に全てのクラスター $\mathbf{C}_i$ に関する同時確率を計算してしまうという事が可能です. これによって計算量を削減する事が出来ます.
メッセージパッシング
エリミネーションツリーのルート $r$ を決める.
- 【集積フェーズ】葉ノードからルートに向かってメッセージを流す.
- 【分配フェーズ】ルートノードから葉ノードに向かってメッセージを流す.
ノード $i$ から $j$ へのメッセージ $m_{ij}$ は以下によって定義される. \[ m_{ij} \stackrel{\mathrm{def}}{=} \mathrm{proj}\left(\varphi_i\prod_{k}m_{ki}, \mathbf{S}_{ij}\right) \] 但し, $k$ はメッセージが流れて来た方向の隣接ノード.
第15回はここで終わります
次回前半はジョインツリーの解説を行いジョインツリーアルゴリズムを完成させます. 後半はマルコフ確率場の紹介をします.