パターン認識・
機械学習勉強会
第14回
@ワークスアプリケーションズ
中村晃一2014年6月5日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
ベイジアンネットワーク
グラフィカルモデル (graphical model) とは有向グラフや無向グラフを用いて確率分布を表現したものです。
この際, 確率分布の 条件付き独立性 (conditional independence) の構造をグラフ構造として表す事が出来、これを利用して周辺分布の計算などを効率的に行う事が出来ます。
例として, 離散的な確率変数 $A,B,C$ からなる同時分布 \[ p(A, B, C) \] について考えます. それぞれの変数は $N_A,N_B,N_C$ 通りの値を取るとします.
値の組合せは $N_AN_BN_C$ 通りになるので, この分布を表現する為には同じ数だけの実数値が必要になります. (確率の和が1である事を使えば多少減らせます)
つまり, 以下の様なテーブルで表されます. \[ \begin{array}{cccc} A & B & C & p(A,B,C) \\ \hline a_1 & b_1 & c_1 & p(A=a_1,B=b_1,C=c_1) \\ \vdots & \vdots & \vdots & \vdots \\ a_i & b_j & c_k & p(A=a_i,B=b_j,C=c_k)\\ \vdots & \vdots & \vdots & \vdots \\ a_{N_A} & b_{N_B} & c_{N_C} & p(A=a_{N_A},B=b_{N_B},C=c_{N_C}) \\ \end{array}\]
$p(A,B,C)$ を $A,B$ に関して周辺化して $p(C)$ を求めたいならば \[ p(C) = \sum_{A,B}p(A,B,C) \] という計算を行います.
これは \[ p(C=c_k) = \sum_{i=1}^{N_A}\sum_{j=1}^{N_B}p(A=a_i,B=b_j,C=c_k) \] の略記です. これを $k=1,2,\ldots,N_C$ それぞれに関して計算するので $\mathcal{O}(N_AN_BN_C)$ の計算量が必要となります.
つまり, $p(C=c_k)$ を求める為には以下の部分を全て足します. \[ \begin{array}{cccc} A & B & C & p(A,B,C) \\ \hline \vdots & \vdots & \vdots & \vdots \\ a_{N_A} & b_{N_B} & c_{k-1} & p(A=a_{N_A},B=b_{N_B},C=c_{k-1})\\ a_1 & b_1 & c_k & \color{red}{ p(A=a_1,B=b_1,C=c_k) }\\ a_2 & b_1 & c_k & \color{red}{ p(A=a_2,B=b_1,C=c_k) }\\ \vdots & \vdots & \vdots & \color{red}{ \vdots }\\ a_{N_A} & b_{N_B} & c_k & \color{red}{ p(A=a_{N_A},B=b_{N_B},C=c_k) }\\ a_1 & b_1 & c_{k+1} & p(A=a_1 ,B=b_1,C=c_{k+1})\\ \vdots & \vdots & \vdots & \vdots \\ \end{array}\]
続いて分布 $p(A,B,C)$ に何らかの条件付き独立性が存在する場合を考えます.
まず, 確率の乗法定理より \[ p(A,B,C) = p(C|A,B)p(B|A)p(A) \] と書くことが出来ます.
ここで例えば \[ p(C|A,B) = p(C|B) \] が成り立っている場合を考えましょう. この事を $B$ を所与として $A,C$ が独立と言います.
条件付き独立性
確率変数 $X,Y,C$ に対して \[ p(Y|X,C) = p(Y|C) \] が成り立つ時, $C$ を所与として $X,Y$ は独立 であるという. また, これは \[ p(X,Y|C) = p(X|C)p(Y|C) \] が成り立つ事と同値である.
これは以下のように一般化出来ます.
条件付き独立性
確率変数の集合 $\mathbf{X},\mathbf{Y},\mathbf{C}$ に対して \[ p(\mathbf{Y}|\mathbf{X},\mathbf{C}) = p(\mathbf{Y}|\mathbf{C}) \] が成り立つ時, $\mathbf{C}$ を所与として $\mathbf{X},\mathbf{Y}$ は独立 であるという. また, これは \[ p(\mathbf{X},\mathbf{Y}|\mathbf{C}) = p(\mathbf{X}|\mathbf{C})p(\mathbf{Y}|\mathbf{C}) \] が成り立つ事と同値である.

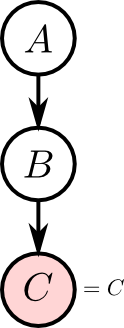
\[ p(A,B,C) = p(C|A,B)p(B|A)p(A) \] において $B$ を所与として $A,C$ が独立ならば \[ p(C|A,B) = p(C|B) \] なので \[ p(A,B,C) = p(C|B)p(B|A)p(A) \] となります. この状況を右のようなグラフで表現する事が出来ます. これをこの分布の ベイジアンネットワーク (Bayesian network) と呼びます. 一般的な定義は後でやります.
簡単な例で, どんな状況かイメージしてみましょう.
ネットショップの登録ユーザーにある商品を紹介する事を考えます. そして, 過去のアンケート結果や国の出している統計から, 以下の事が解っているとしましょう.
- あるユーザーが主婦(主夫)であるか否か$(B)$と, その商品を買ってもらえるか否か$(C)$の関係 $p(C|B)$
- ある人が女性であるか否か $(A)$ と, 主婦(主夫)であるか否か $(B)$ の関係 $p(B|A)$
- ユーザーに占める女性の割合 $p(A)$
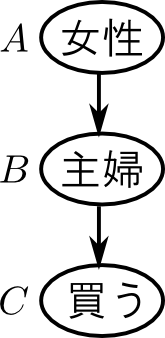
この時 $B$ を所与として $A,C$ が独立というのは \[ p(\text{買う}|\text{女性},\text{主婦}) = p(\text{買う}|\text{主婦}) \] つまり, 主婦(主夫)であるか否かが解っている場合には性別の情報は役に立たないという様子を表します.
$B$ であるか否かが分かっていない場合には $A$ が $B$ に影響を及ぼし, 間接的に $C$ にも影響します. 一方, $B$ が所与の場合には $A\rightarrow B\rightarrow C$ のパスがブロックされて, $A$ が $C$ に影響しないという事になります.
次に, 条件付き独立性を利用してどのようにデータ量・計算量を減らせるのか見てみましょう.
$B$ を所与として $A,C$ が独立の場合, \[ p(A,B,C) = p(C|B)p(B|A)p(A) \] ですから,これを表現する為には, $P(A),P(B|A),P(C|B)$ それぞれを表すテーブルがあれば良いです. よって, テーブルサイズの和は \[ N_A + N_AN_B + N_BN_C \] となります.
先ほどと同様に $p(C)$ の計算を考えてみると \[ p(C) = \sum_{A,B}p(C|B)p(B|A)p(A) \] となりますが, $p(C|B)$ は $A$ に依存しない為 \[ p(C) = \sum_{B}p(C|B)\sum_{A}p(B|A)p(A) \] とくくりだす事が出来ます.

これを計算する為には, まず \[ p(B) = \sum_{A}p(B|A)p(A) \] を各 $B$ に対して計算します. $\sum_{A}$ の部分は $\mathcal{O}(N_A)$ の計算量となるので併せて $\mathcal{O}(N_AN_B)$ となります.
続いて \[ p(C) = \sum_{B}p(C|B)p(B) \] を各 $C$ に対して計算します. この計算量は $\mathcal{O}(N_BN_C)$ となりますので, 上と併せて \[ \mathcal{O}(N_AN_B+N_BN_C) \] となります. 元々 $\mathcal{O}(N_AN_BN_C)$ だったので大分計算量が減っています.
さっきの例でやってみましょう.
例えば条件付き確率が以下のようになっていたとします(数値は適当). \[ \begin{aligned} &\begin{array}{cc} A & p(A) \\ \hline \text{男性} & 0.3 \\ \text{女性} & 0.7 \end{array} \quad \begin{array}{ccc} A & B & p(B|A) \\ \hline \text{男性} & \text{主夫} & 0.1 \\ \text{男性} & \text{主夫じゃない} & 0.9 \\ \text{女性} & \text{主婦} & 0.4 \\ \text{女性} & \text{主婦じゃない} & 0.6 \\ \end{array} \\ & \begin{array}{ccc} B & C & p(C|B) \\ \hline \text{主婦(主夫)} & \text{買う} & 0.3 \\ \text{主婦(主夫)} & \text{買わない} & 0.7 \\ \text{主婦(主夫)じゃない} & \text{買う} & 0.1 \\ \text{主婦(主夫)じゃない} & \text{買わない} & 0.9 \\ \end{array} \end{aligned} \]
まず, \[ \begin{array}{cc} A & p(A) \\ \hline \text{男性} & 0.3 \\ \text{女性} & 0.7 \end{array} \quad \begin{array}{ccc} A & B & p(B|A) \\ \hline \text{男性} & \text{主夫} & 0.1 \\ \text{男性} & \text{主夫じゃない} & 0.9 \\ \text{女性} & \text{主婦} & 0.4 \\ \text{女性} & \text{主婦じゃない} & 0.6 \\ \end{array} \] から \[ \begin{array}{cc} B & p(B) \\ \hline \text{主婦(主夫)} & 0.1\cdot 0.3 + 0.4\cdot 0.7 = 0.31 \\ \text{主婦(主夫)じゃない} & 0.9\cdot 0.3 + 0.6\cdot 0.7 = 0.69 \end{array} \] となります.
続いて, \[ \begin{array}{cc} B & p(B) \\ \hline \text{主婦(主夫)} & 0.31 \\ \text{主婦(主夫)じゃない} & 0.69 \end{array} \quad \begin{array}{ccc} B & C & p(C|B) \\ \hline \text{主婦(主夫)} & \text{買う} & 0.3 \\ \text{主婦(主夫)} & \text{買わない} & 0.7 \\ \text{主婦(主夫)じゃない} & \text{買う} & 0.1 \\ \text{主婦(主夫)じゃない} & \text{買わない} & 0.9 \\ \end{array} \] から \[ \begin{array}{cc} C & p(C) \\ \hline \text{買う} & 0.3\cdot 0.31 + 0.1\cdot 0.69 = \color{red}{ 0.162 }\\ \text{買わない} & 0.7\cdot 0.31 + 0.9\cdot 0.69 = \color{red}{ 0.838 } \end{array} \] となります. 16%くらいの人が買ってくれるだろうという事が分かります.
もうちょっと練習してみましょう.

今度は同じモデル \[ p(A,B,C) = p(C|B)p(B|A)p(A) \] において, \[ p(C|A) \] を計算する方法を考えましょう.
\[ p(C|A) = \frac{p(A,C)}{p(A)} \] なので, $p(A,C)$ と $p(A)$を計算出来れば良いです.
$p(A,B,C)$ を $B$ に関して周辺化して \[ p(A,C) = \sum_B p(A,B,C) \] つまり, \[ p(A,C) = \sum_B p(C|B)p(B|A)p(A) = p(A)\sum_B p(C|B)p(B|A) \] となりますから \[ p(C|A) = \sum_B p(C|B)p(B|A) \] です.
従って, \[ \begin{array}{ccc} A & B & p(B|A) \\ \hline \text{男性} & \text{主夫} & 0.1 \\ \text{男性} & \text{主夫じゃない} & 0.9 \\ \text{女性} & \text{主婦} & 0.4 \\ \text{女性} & \text{主婦じゃない} & 0.6 \\ \end{array} \quad \begin{array}{ccc} B & C & p(C|B) \\ \hline \text{主婦(主夫)} & \text{買う} & 0.3 \\ \text{主婦(主夫)} & \text{買わない} & 0.7 \\ \text{主婦(主夫)じゃない} & \text{買う} & 0.1 \\ \text{主婦(主夫)じゃない} & \text{買わない} & 0.9 \\ \end{array} \] より \[ \begin{array}{ccc} A & C & p(C|A) \\ \hline \text{男性} & \text{買う} & 0.3\cdot 0.1 + 0.1\cdot 0.9 = \color{red}{ 0.12 } \\ \text{男性} & \text{買わない} & 0.7\cdot 0.1 + 0.9\cdot 0.9 = \color{red}{ 0.88 }\\ \text{女性} & \text{買う} & 0.3\cdot 0.4 + 0.1\cdot 0.6 = \color{red}{ 0.18 }\\ \text{女性} & \text{買わない} & 0.7\cdot 0.4 + 0.9\cdot 0.6 = \color{red}{ 0.82 } \end{array} \] となります. 女性の方が買ってもらえる可能性が若干高いです.
今度は, $C$ の値が $c$ であると既に解っている場合の \[ p(A|C=c) \] を考えてみましょう.
$C$ の様にその値が観測された確率変数に対応するノードをエビデンスノード (evidence node) と呼びます. また, この時 $C$ は インスタンス化 (instantiated) されていると言います.
\[ p(A|C=c) = \frac{p(A,C=c)}{p(C=c)} \] ですが, $p(C)$ の計算は既にやりました. また, \[ \begin{aligned} p(A,C=c) & =\sum_B p(A,B,C=c) \\ &= \sum_B p(C=c|B)p(B|A)p(A) \\ &= p(A)\sum_B p(C=c|B)p(B|A) \end{aligned} \] となります.
先ほどの例で $p(A|\text{買う})$ を計算してみましょう. まず \[ \begin{array}{ccc} A & B & p(B|A) \\ \hline \text{男性} & \text{主夫} & 0.1 \\ \text{男性} & \text{主夫じゃない} & 0.9 \\ \text{女性} & \text{主婦} & 0.4 \\ \text{女性} & \text{主婦じゃない} & 0.6 \\ \end{array} \quad \begin{array}{cc} B & p(\text{買う}|B) \\ \hline \text{主婦(主夫)} & 0.3 \\ \text{主婦(主夫)じゃない} & 0.1 \\ \end{array} \] より \[ \begin{array}{cc} A & \sum_Bp(\text{買う}|B)p(B|A) \\ \hline \text{男性} & 0.3\cdot 0.1 + 0.1\cdot 0.9 = 0.12 \\ \text{女性} & 0.3\cdot 0.4 + 0.1\cdot 0.6 = 0.18 \end{array} \] となります.
これに $p(A)$ を掛けて \[ \begin{array}{cc} A & p(A,\text{買う}) \\ \hline \text{男性} & 0.3\cdot 0.12 = 0.036\\ \text{女性} & 0.7\cdot 0.18 = 0.126 \end{array} \] です. これを既に計算した $p(\text{買う}) = 0.162$ で割って \[ \begin{array}{cc} A & p(A|\text{買う}) \\ \hline \text{男性} & 0.036/0.162 \approx \color{red}{ 0.222 } \\ \text{女性} & 0.126/0.162 \approx \color{red}{ 0.778 } \end{array} \] となります. つまり,商品を買ってくれた人が男性である可能性は約22%です.
ベイジアンネットワークがどんなものであるのか大体イメージが掴めたと思いますので, 一般的な説明をしていきます.
ベイジアンネットワーク
確率変数 $\mathbf{X}=(X_1,X_2,\ldots,X_n)$ からなる ベイジアンネットワーク(Bayesian network) は以下により定まる.
- $\mathbf{X}$ をノード集合とする 非循環有向グラフ (directed acyclic graph, DAG)
- 各変数 $X_i$ に対する条件付き確率 \[ p(X_i|\mathrm{pa}(X_i)) \] 但し $\mathrm{pa}(X_i)$ はノード $X_i$ の親ノードの集合
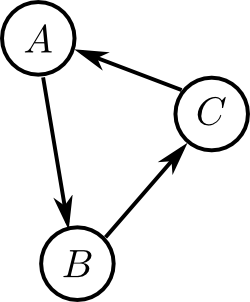
有向グラフというのは辺(エッジ)に向きが付いたグラフ構造の事で, 非循環というのは右図のように(辺の向きを考慮した)閉路が存在しないという事です.
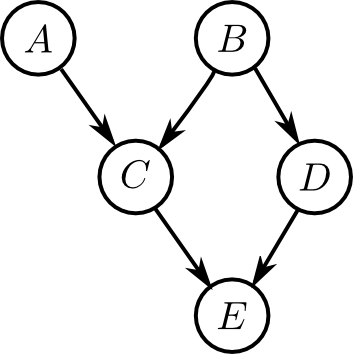
例えば, 右図のようなものがベイジアンネットワークのグラフ構造の例です. このベイジアンネットワークは $A,B,C,D,E$ の5つの確率変数からなり \[ \begin{aligned} \mathrm{pa}(A) &= \emptyset \\ \mathrm{pa}(B) &= \emptyset \\ \mathrm{pa}(C) &= \{A,B\} \\ \mathrm{pa}(D) &= \{B\} \\ \mathrm{pa}(E) &= \{C,D\} \end{aligned} \] となります.
ベイジアンネットワークの中には確率変数間の条件付き独立性が埋め込まれているわけですが, これを説明するのが d分離 (d-separation) という性質です.
目標は \[ \text{グラフ上でd分離} \Rightarrow \text{分布上で独立} \] となるようにグラフを作る事です.

グラフ中の右図のような部分を 逐次結合 (serial connection) と呼びます.
逐次結合に対しては \[ \text{$B$を所与として $A,C$ は d分離である} \] と言います. このグラフは先ほどやったのでイメージ出来ると思います.
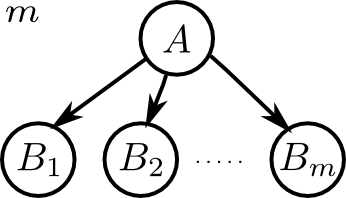
右図のような部分は 分岐結合 (diverging connection) と呼びます.
分岐結合に対しては \[ \text{$A$を所与として $B_1,B_2,\ldots,B_m$ は d分離である} \] と言います.
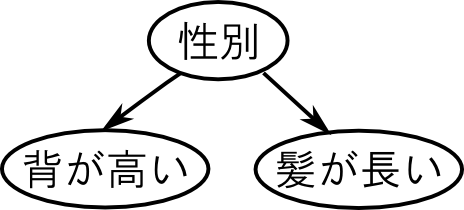
右図を見て下さい.
ある人の性別が所与でない場合 \[ \text{背が高い}\rightarrow\text{きっと男性だろう}\rightarrow\text{きっと髪が短いだろう} \] というように背が高い事と髪が長い事には間接的な従属性があります.
しかし, その人の性別が既に判明しているならば, 背が高い事と髪の長さは関係なさそうです(本当かどうかは知りません).
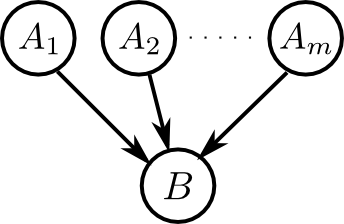
右図のような部分は 合流結合 (converging connection) と呼びます.
合流結合に対しては \[ \begin{aligned} &\text{$B$もしくは $B$の子孫が所与でないとき,}\\ &\text{$A_1,A_2,\ldots,A_m$ はd分離である} \end{aligned} \] と言います. これまでより若干複雑なので注意して下さい.
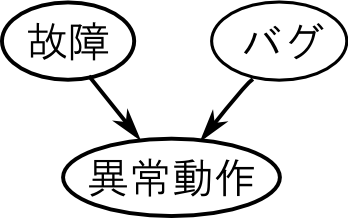
右図を見て下さい.
普通, ソフトウェアにバグがある事とマシンが故障する事は無関係です. つまり「異常動作」が所与でない場合には「バグ」と「故障」は独立です.
しかし, 異常動作が発生した場合 \[ \text{マシンが故障していないならバグがあるはず} \] などの推論が可能になります. つまり「異常動作」が所与の時に「バグ」と「故障」が従属となります.
以上を元にして一般的な状況におけるd分離性が定義されます.
d分離
ノード集合 $E$ が所与である時, ノード $X,Y$ を結ぶ(辺の向きを無視した)全てのパス上に, 以下の条件を満たすノードが存在する時, $X,Y$ は $E$ を所与としてd分離であると言う.
- 逐次結合・分岐結合部のノードであって $E$ に含まれるもの
- 合流結合部のノードもしくはその子孫であって $E$ に含まれないもの
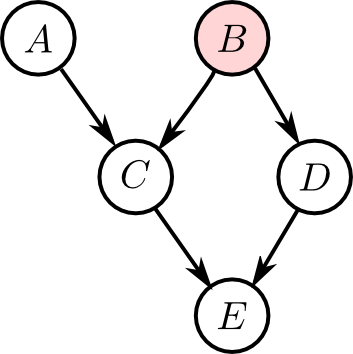
例えば$B$にエビデンスが与えられた右図において, $A$ と $D$ はd分離の関係にあるでしょうか?
$A$から$D$へのパスは2つありますが
- パス $A\rightarrow C\rightarrow B\rightarrow D$ は分岐結合 $B$ でインスタンス化されている.
- パス $A\rightarrow C\rightarrow E\rightarrow D$ は合流結合 $E$ でインスタンス化されていない
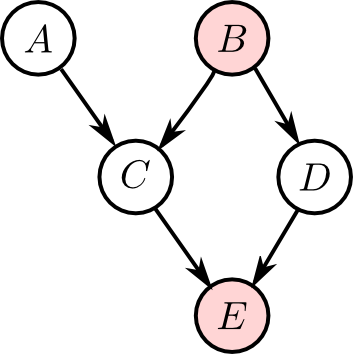
こちらではどうでしょうか?
こんどはパス $A\rightarrow C\rightarrow E\rightarrow D$ が($E$ でインスタンス化されている為に)繋がっています. 従って $A,D$ は $B,E$ を所与とするとd分離ではありません.
ノード集合 $\mathbf{X},\mathbf{Y},\mathbf{C}$ に対するd分離性も同様に定義されます.
つまり $\mathbf{X}$と$\mathbf{Y}$ 内の全てのノードのペアが $\mathbf{C}$ を所与として d分離になる時に $\mathbf{X},\mathbf{Y}$ はd分離であると言います.
さて, あるベイジアンネットワークのグラフ構造が \[ \text{グラフ上でd分離} \Rightarrow \text{確率分布上で条件付き独立} \] を全ての $\mathbf{X},\mathbf{Y},\mathbf{C}$ の組合せに対して満たす時, このグラフを インデペンデントマップ (independent map, I-map) と呼びます.
\[ \text{確率分布上で条件付き独立} \Rightarrow \text{グラフ上でd分離} \] は一般に成り立たないので, I-mapとは確率分布の条件付き独立性の構造の一部を表現したものです.
さて, ベイジアンネットワークのグラフがI-mapであれば, これを用いて確率分布を厳密に表現する事が出来ます.
ベイジアンネットワークの表現する分布
ベイジアンネットワークのグラフがI-mapであるならば \[ p(\mathbf{X}) = \prod_i p(X_i|\mathrm{pa}(X_i)) \] が成立する.例えば下のネットワークに対しては(これがI-mapであると仮定すると), \[ p(A,B,C,D,E) = p(A)p(B)p(C|A,B)p(D|B)p(E|C,D) \] となります.

ベイジアンネットワーク上での推論
ベイジアンネットワーク上で, 幾つかの変数の集合 $Q$ (クエリ) の対して 同時確率 \[ p(Q) \] を計算する事がベイジアンネットワークにおける基本的な推論の形式です.
条件付き確率も \[ p(\mathbf{X}|\mathbf{Y}) = \frac{p(\mathbf{X},\mathbf{Y})}{p(\mathbf{Y})} \] によって同時確率の計算に帰着する事が出来ます.
エビデンスが全くない状態での $p(Q)$ を 周辺事前分布 (marginal prior distribution) , エビデンス $E$ が与えられた状態での $p(Q|E)$ を 周辺事後分布 (marginal posterior distribution) と呼びます.
まずは周辺事前分布の計算を考えます.
下のグラフに対して $p(B,E)$ を計算する事を考えてみましょう.
\[ p(A,B,C,D,E) = p(A)p(B)p(C|A,B)p(D|B)p(E|C,D) \] だったので \[ p(B,E) = \sum_{A,C,D}p(A)p(B)p(C|A,B)p(D|B)p(E|C,D) \] となります.

$\sum$ に関して分配すると例えば \[ p(B,E) = p(B)\sum_{D}p(D|B)\sum_{C}p(E|C,D)\sum_{A}p(A)p(C|A,B) \] となります.
つまり, $A$に関する因数を全部掛けて足す $\rightarrow$ $C$に関する因数を全部掛けて足す $\rightarrow$ $D$に関する因数を全部掛けて足す. という流れで計算を行う事が出来ます.
具体的に書き下してみましょう.
- $\mathcal{S} = \{p(A),p(B),p(C|A,B),p(D|B),p(E|C,D)\}$ とする.
- $A$を含むもの全てを掛けあわせて足して,それらを $\mathcal{S}$ から除く. 計算した \[ \varphi(B,C) = \sum_{A}p(A)p(C|A,B) \] を追加して$\mathcal{S} = \{p(B),p(D|B),p(E|C,D),\varphi(B,C)\}$ とする.
- $C$ を含むもの全てを掛けあわせて足して, それらを $\mathcal{S}$ から除く. 計算した \[ \varphi(B,D,E) = \sum_{C}p(E|C,D)\varphi(B,C) \] を追加して$\mathcal{S} = \{p(B),p(D|B),\varphi(B,D,E)\}$ とする.
- $D$ を含むもの全てを掛けあわせて足して, それらを $\mathcal{S}$ から除く. 計算した \[ \varphi(B,E) = \sum_{D}p(D|B)\varphi(B,D,E) \] を追加して$\mathcal{S} = \{p(B),\varphi(B,E)\}$とする.
- 最後に残った $\mathcal{S}$ の要素を全て掛けたものを出力する. \[ p(B,E) = p(B)\varphi(B,E) \]
途中計算に現れた因数, つまり $\mathcal{S}$ の要素を ファクター(factor) と呼びます.
ファクターの集合からは \[ \begin{aligned} &\{p(A),p(B),p(C|A,B),p(D|B),p(E|C,D)\}\\ \rightarrow& \{p(B),p(D|B),p(E|C,D),\varphi(B,C)\}\\ \rightarrow& \{p(B),p(D|B),\varphi(B,D,E)\}\\ \rightarrow& \{p(B),\varphi(B,E)\} \end{aligned} \] と一文字ずつ変数が消えていきます. そこで, このアルゴリズムを 変数消去アルゴリズム(variable elimination) と呼びます.
まとめましょう.
変数消去による周辺事前分布の計算
クエリを $\mathbf{Q}$ とする. \[ \mathcal{S} = \{ p(X_i|\mathrm{pa}(X_i))\}_i \] とし, $\mathbf{Q}$ に含まれない変数 $X$ に対して以下を繰り返す.
- $\mathbf{S}$ 内の$X$を含むファクターを全て除く.
- ファクターを掛けて $X$ について足し合わせる.
- それを $\mathbf{S}$ に追加する.
$\mathbf{S}$ 内のファクターを全て掛け合わせて出力する.
これをエビデンス $E$ が与えられたものに修正する事は簡単です. 各ファクター$\varphi(\mathbf{X})$について \[ \varphi(\mathbf{X})' = \left\{\begin{array}{cl} \varphi(\mathbf{X}) & (\text{$\mathbf{X}$と$E$が $E$内の変数に関して一致する}) \\ 0 & (それ以外) \end{array}\right. \] と修正を行ってから変数消去を行えば良いです.
変数消去による周辺事後分布の計算
クエリを $\mathbf{Q}$, エビデンスを $E$ とする. \[ \mathcal{S} = \{ p(X_i|\mathrm{pa}(X_i))\}_i \] とする. $\mathcal{S}$ 内の各テーブルについて $E$ と一致しない行を $0$ にする. $\mathbf{Q}$ に含まれない変数 $X$ に対して以下を繰り返す.
- $\mathbf{S}$ 内の$X$を含むファクターを全て除く.
- ファクターを掛けて $X$ について足し合わせる.
- それを $\mathbf{S}$ に追加する.
$\mathbf{S}$ 内のファクターを全て掛け合わせて出力する.
ベイジアンネットワークの例題としてよく使われる以下のものでやってみようと思います.
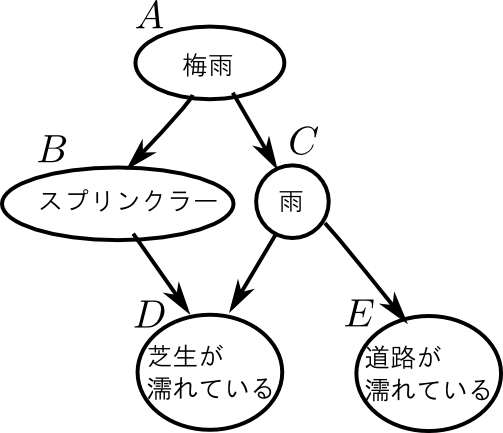
\[ \small{\begin{aligned} &p(A) = 0.6\\ &p(B|A) = 0.2,\,p(B|\overline{A}) = 0.75\\ &p(C|A) = 0.8,\,p(C|\overline{A}) = 0.1\\ &p(D|B,C) = 0.95,\,p(D|B,\overline{C})=0.9,\,p(D|\overline{B},C)=0.8,\,p(D|\overline{B},\overline{C})=0.0\\ &p(E|C) = 0.7,\, p(E|\overline{C}) = 0.0 \end{aligned}} \]
例として, $E$ が偽である事が解っている時の $D$ の確率を求めましょう. つまり \[ p(D|E=F) = \frac{p(D, E=F)}{p(E=F)} \] を計算します. ($F$は偽の意味)
ファクターの集合 $\mathcal{S}$ の変化の様子が解りやすいようにexcelで様子を描いてみました.
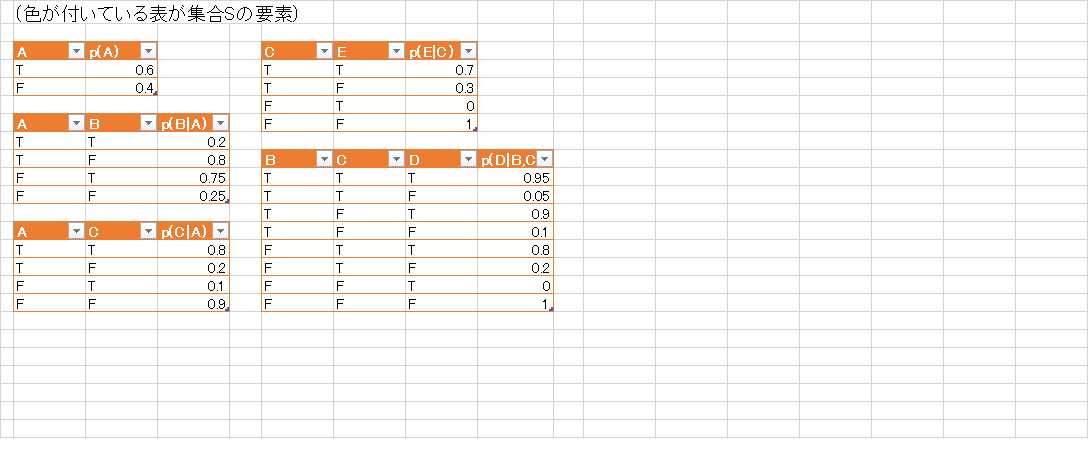
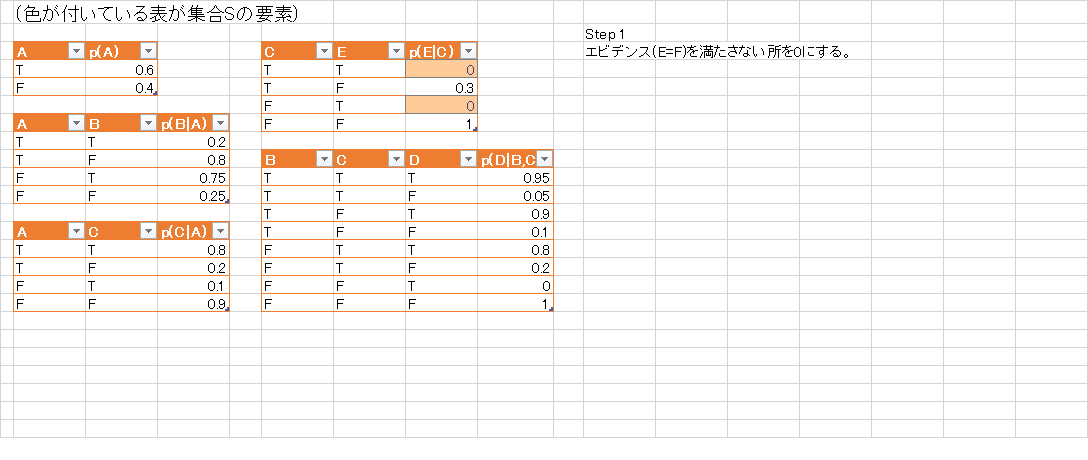
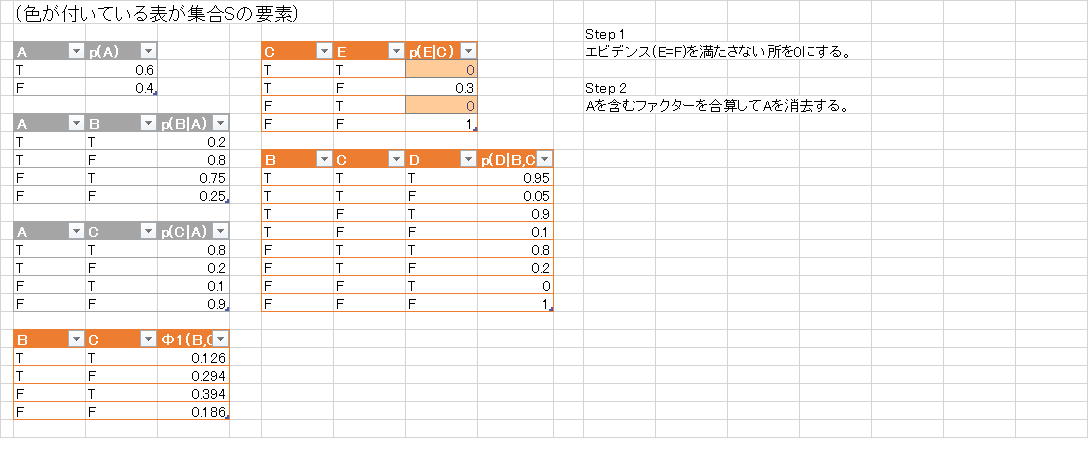
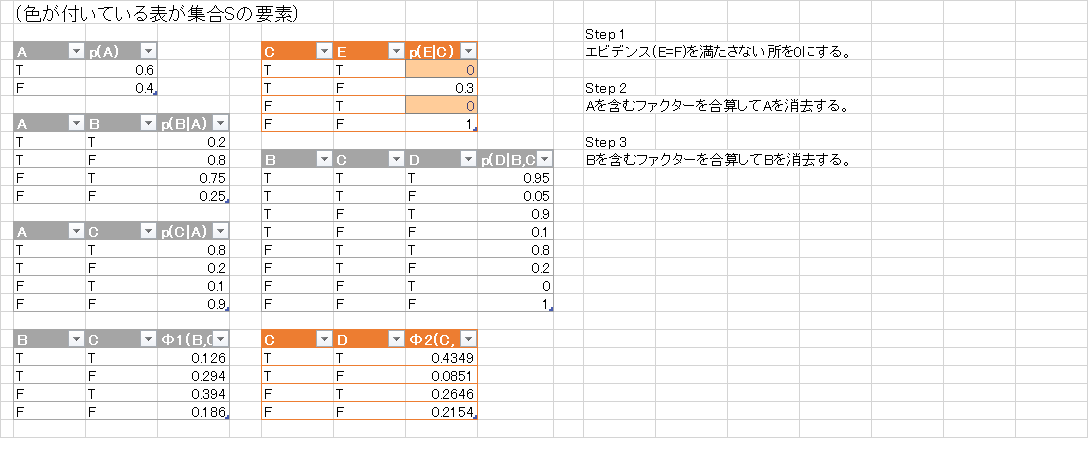
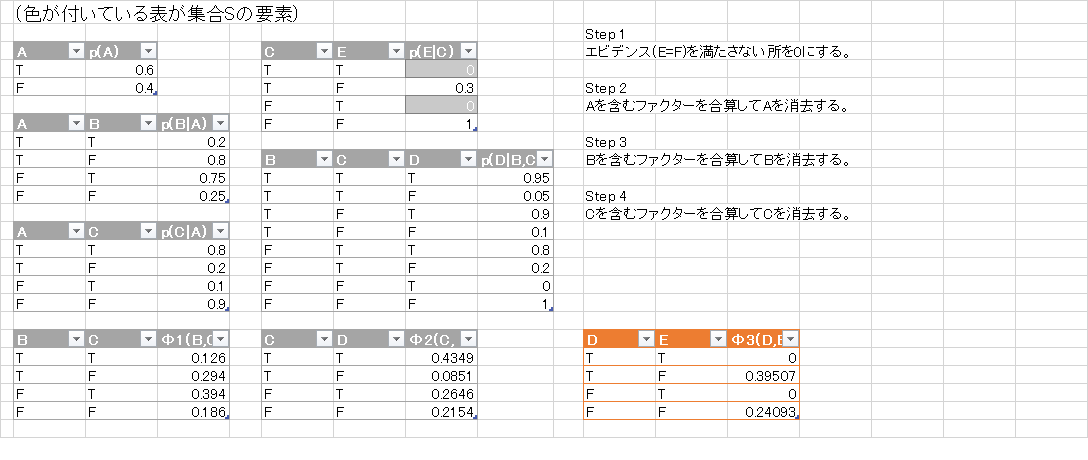
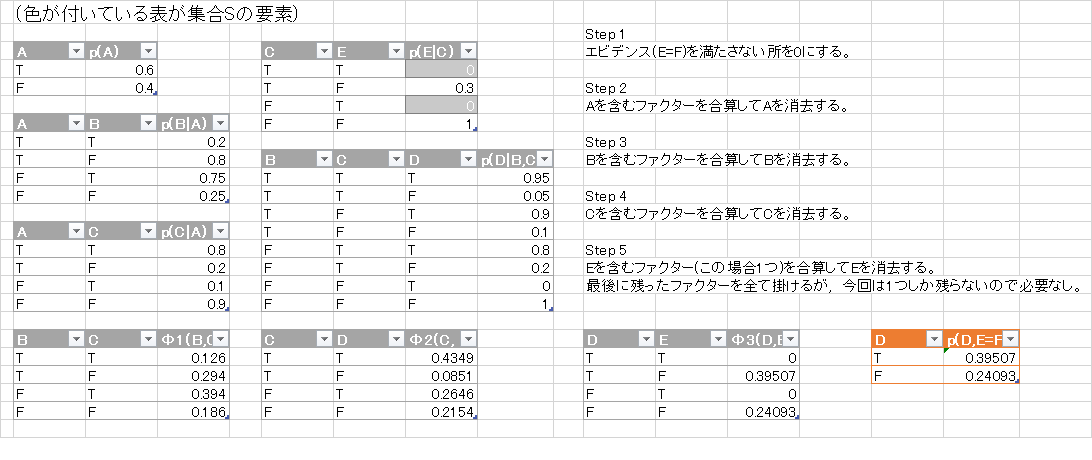
従って \[ p(D=T, E=F) = 0.39507, p(D=F,E=F) = 0.24093 \] が得られました. これを $D$ に関して周辺化して \[ p(E=F) = 0.39507 + 0.24093 = 0.636 \] となりますので, \[ p(D=T|E=F) = \frac{p(D=T,E=F)}{p(E=F)} = \frac{0.39507}{0.636} \approx 0.62 \] つまり, 道路が濡れていない時は62%の確率で芝が濡れているという事になります.
道路が濡れているか否かの情報がない場合の周辺事前分布 $p(D)$ を同様に計算してみると \[ p(D=T) = 0.6995 \] となります.
つまり, 道路が濡れていないという情報を得る事によって, 芝が濡れている確率が減少している事が分かります.
prog14-1.py に今回紹介した単純な変数消去アルゴリズムによるベイジアンネットワークを実装してみました. 先ほどのネットワークはsample_netという変数名で既に作ってあります.
こんな感じで使います. メソッドqueryの引数にクエリ集合・条件集合・エビデンス集合 (Q,C,E)を渡すと $p(Q|C,E)$ を返します. 変数の取る値は $0,1,\ldots$ という連番で扱います. 以下の場合 $0$ が真, $1$ が偽です.
遊んでみてください.
>>> execfile("prog14-1.py")
# 道路が濡れていない(E=1)時も62%の確率で芝は濡れている(D=0)
>>> sample_net.query(Q = ['D'], E = {'E':1})
D | p(D|E=1)
---+--------------
0 | 0.6211792453
1 | 0.3788207547
# 無情報の時は70%の確率で芝が濡れていると推論される.
>>> sample_net.query(Q = ['D'])
D | p(D)
---+--------------
0 | 0.6995000000
1 | 0.3005000000
# 芝が濡れている(D=0)時に, スプリンクラーが作動していた可能性は55%.
>>> sample_net.query(Q = ['B'], E={'D':0})
B | p(B|D=0)
---+--------------
0 | 0.5493924232
1 | 0.4506075768
# 梅雨(A=0)だとスプリンクラーが作動していた可能性は低下.
>>> sample_net.query(Q = ['B'], E={'A':0, 'D':0})
B | p(B|A=0,D=0)
---+--------------
0 | 0.2685714286
1 | 0.7314285714
# 逆に, 梅雨でないなら可能性が高くなる.
>>> sample_net.query(Q = ['B'], E={'A':1, 'D':0})
B | p(B|A=1,D=0)
---+--------------
0 | 0.9713774597
1 | 0.0286225403
# 梅雨(A=0)のスプリンクラーと雨の状態.
# グラフ上でAを所与としてB,Cはd分離なので,
# p(B|C,A=0) = p(B|A=0)
# になっているはず. 実際, 以下のようになる.
>>> sample_net.query(Q = ['B'], C = ['C'], E={'A':0})
B | C | p(B|C,A=0)
---+---+--------------
0 | 0 | 0.2000000000
0 | 1 | 0.2000000000
1 | 0 | 0.8000000000
1 | 1 | 0.8000000000
# 梅雨(A=0)で芝が濡れている(D=0)時のスプリンクラーと雨の状態.
# Dが所与だと, B -> D -> C のパスでd分離になっていない為B,Cは従属(の可能性がある).
# 実際,雨が降ったか否かによってスプリンクラーが作動した確率が変化している.
>>> sample_net.query(Q = ['B'], C = ['C'], E={'A':0, 'D':0})
B | C | p(B|C,A=0,D=0)
---+---+----------------
0 | 0 | 0.2289156627
0 | 1 | 1.0000000000
1 | 0 | 0.7710843373
1 | 1 | 0.0000000000
# 全変数の同時分布は以下のようになる.
# これは (A,B,C,D,E) = (1,0,1,0,1) で最大, つまり
# 無情報下では
# 「梅雨でなく」「スプリンクラーが作動し」「雨が振らず」
# 「芝が濡れており」「道路は濡れていない」
# という状態にある可能性が最も高いと推論される.
#
# 次いで可能性が高いのは (A,B,C,D,E) = (0,1,0,0,0) つまり
# 「梅雨であり」「スプリンクラーが作動せず」「雨が振り」
# 「芝が濡れており」「道路も濡れている」
# という状態.
>>> sample_net.query(Q = ['A', 'B', 'C', 'D', 'E'])
A | B | C | D | E | p(A,B,C,D,E)
---+---+---+---+---+--------------
0 | 0 | 0 | 0 | 0 | 0.0638400000
0 | 0 | 0 | 0 | 1 | 0.0273600000
0 | 0 | 0 | 1 | 0 | 0.0033600000
0 | 0 | 0 | 1 | 1 | 0.0014400000
0 | 0 | 1 | 0 | 0 | 0.0000000000
0 | 0 | 1 | 0 | 1 | 0.0216000000
0 | 0 | 1 | 1 | 0 | 0.0000000000
0 | 0 | 1 | 1 | 1 | 0.0024000000
0 | 1 | 0 | 0 | 0 | 0.2150400000
0 | 1 | 0 | 0 | 1 | 0.0921600000
0 | 1 | 0 | 1 | 0 | 0.0537600000
0 | 1 | 0 | 1 | 1 | 0.0230400000
0 | 1 | 1 | 0 | 0 | 0.0000000000
0 | 1 | 1 | 0 | 1 | 0.0000000000
0 | 1 | 1 | 1 | 0 | 0.0000000000
0 | 1 | 1 | 1 | 1 | 0.0960000000
1 | 0 | 0 | 0 | 0 | 0.0199500000
1 | 0 | 0 | 0 | 1 | 0.0085500000
1 | 0 | 0 | 1 | 0 | 0.0010500000
1 | 0 | 0 | 1 | 1 | 0.0004500000
1 | 0 | 1 | 0 | 0 | 0.0000000000
1 | 0 | 1 | 0 | 1 | 0.2430000000
1 | 0 | 1 | 1 | 0 | 0.0000000000
1 | 0 | 1 | 1 | 1 | 0.0270000000
1 | 1 | 0 | 0 | 0 | 0.0056000000
1 | 1 | 0 | 0 | 1 | 0.0024000000
1 | 1 | 0 | 1 | 0 | 0.0014000000
1 | 1 | 0 | 1 | 1 | 0.0006000000
1 | 1 | 1 | 0 | 0 | 0.0000000000
1 | 1 | 1 | 0 | 1 | 0.0000000000
1 | 1 | 1 | 1 | 0 | 0.0000000000
1 | 1 | 1 | 1 | 1 | 0.0900000000
PRMLはベイジアンネットワークの説明が若干軽めなので, 今回は以下のテキストを参考にしました.
- 植野 真臣著「ベイジアンネットワーク」コロナ社
第14回はここで終わります
次回も引き続きベイジアンネットワークの話をします. 変数消去アルゴリズムに関してもう少し話をした後, ジョインツリーアルゴリズムというより効率の良い手法や近似推論アルゴリズムの紹介をする予定です.