パターン認識・
機械学習勉強会
第10回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

カーネル法

本日はテキスト第6章の カーネル法 (kernel method) に進みます.

カーネル法とは カーネル関数 (kernel function) \[ k(\mathbf{x}, \mathbf{x}') \] を用いる統計的学習法の総称です.

$k(\mathbf{x},\mathbf{x}')$ は 入力 $\mathbf{x},\mathbf{x}'$ の類似度を何らかの意味で数量化した物であると考える事が出来ます. 従って少なくとも \[ k(\mathbf{x},\mathbf{x}') = k(\mathbf{x}',\mathbf{x}) \] が成立する事が要請されます.

簡単なカーネル関数は, 特徴ベクトル $\Psi(\mathbf{x})$ の内積 \[ k(\mathbf{x},\mathbf{x}') = \Psi(\mathbf{x})^T\Psi(\mathbf{x}') \] として定まるものです.

他にも様々なカーネル関数を構成する事が出来ますが, まずはどのようにしてカーネル関数が登場するのか簡単な例を見てみましょう.

最小二乗法による正則化項付きの線形再帰, つまり \[ E(\mathbf{w}) = \sum_{i=1}^n ||\mathbf{w}^T\Psi(\mathbf{x}_i)-y_i||^2 + \lambda||\mathbf{w}||^2 \] の最小化問題を考えます.

この勾配は \[ \nabla E(\mathbf{w}) = 2\sum_{i=1}^n (\mathbf{w}^T\Psi(\mathbf{x}_i)-y_i)\Psi(\mathbf{x}_i) + 2\lambda\mathbf{w} \] であるので, $\nabla E = \mathbf{0}$ と置くことにより \[ \mathbf{w} = -\frac{1}{\lambda}\sum_{i=1}^n (\mathbf{w}^T\Psi(\mathbf{x}_i)-y_i)\Psi(\mathbf{x}_i) \] が成立します.

ここで新たなパラメータとして \[ a_i = -\frac{1}{\lambda}(\mathbf{w}^T\Psi(\mathbf{x}_i)-y_i) \] を導入すると \[ \mathbf{w} = \sum_{i=1}^n a_i\Psi(\mathbf{x}_i) = \mathbf{X}^T\mathbf{a} \] と置くことが出来ます. 但し $\mathbf{X}$ は計画行列で $X_{ij} = \psi_j(\mathbf{x}_i)$ です.

これを元の誤差関数に代入すると \[ \begin{aligned} E(\mathbf{a}) &= \sum_{i=1}^n ||\mathbf{a}^T\mathbf{X}\Psi(\mathbf{x}_i)-y_i||^2 + \lambda||\mathbf{X}^T\mathbf{a}||^2 \\ &= \mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{X}\mathbf{X}^T\mathbf{a} - 2\mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{y} + \mathbf{y}^T\mathbf{y}+\lambda \mathbf{a}^T\mathbf{X}\mathbf{X}^T\mathbf{a} \end{aligned} \] となるので, $\mathbf{K}=\mathbf{X}\mathbf{X}^T$ と置けば \[ E(\mathbf{a}) = \mathbf{a}^T\mathbf{K}^2\mathbf{a} - 2\mathbf{a}^T\mathbf{K}\mathbf{y} + \mathbf{y}^T\mathbf{y}+\lambda \mathbf{a}^T\mathbf{K}\mathbf{a} \] となります. これを誤差関数の 双対表現 (dual representation) と呼びます.

行列 $\mathbf{K}$ は(線形代数の用語で)グラム行列 (Gram matrix) と呼ばれます.

この$(i,j)$ 成分は \[ K_{ij} = \Psi(\mathbf{x}_i)^T\Psi(\mathbf{x}_j) \] となっているので, 先ほどのカーネル関数を用いれば以下のように表す事が出来ます. \[ \mathbf{K} = \begin{pmatrix} k(\mathbf{x}_1,\mathbf{x}_1) & k(\mathbf{x}_1,\mathbf{x}_2) & \cdots & k(\mathbf{x}_1,\mathbf{x}_n) \\ k(\mathbf{x}_2,\mathbf{x}_1) & k(\mathbf{x}_2,\mathbf{x}_2) & \cdots & k(\mathbf{x}_2,\mathbf{x}_n) \\ \vdots & \vdots & \ddots & \vdots \\ k(\mathbf{x}_n,\mathbf{x}_1) & k(\mathbf{x}_n,\mathbf{x}_2) & \cdots & k(\mathbf{x}_n,\mathbf{x}_n) \\ \end{pmatrix} \]

双対表現 \[ E(\mathbf{a}) = \mathbf{a}^T\mathbf{K}^2\mathbf{a} - 2\mathbf{a}^T\mathbf{K}\mathbf{y} + \mathbf{y}^T\mathbf{y}+\lambda \mathbf{a}^T\mathbf{K}\mathbf{a} \] を $\mathbf{a}$ について微分すると $\mathbf{K}^T=\mathbf{K}$ である事に注意して \[ \nabla E(\mathbf{a}) = 2\mathbf{K}^2\mathbf{a}-2\mathbf{K}\mathbf{y} + 2\lambda\mathbf{K}\mathbf{a} \] となるので, \[ (\mathbf{K}^2+\lambda\mathbf{K})\mathbf{a} = \mathbf{K}\mathbf{y} \] を解けば $\mathbf{a}$ が求まります.

$\mathbf{K}$ 及び $\mathbf{K}+\lambda\mathbf{I}$ が正則ならば \[ \mathbf{a} = (\mathbf{K}+\lambda\mathbf{I})^{-1}\mathbf{y} \] です. (これは$\mathbf{K}$ が正定値ならば十分です. 後述します.)

以上の結果得られるモデルは \[ y = \Psi(\mathbf{x})^T\mathbf{w} = \Psi(\mathbf{x})^T\mathbf{X}^T\mathbf{a} = \sum_{i=1}^n a_ik(\mathbf{x}_i,\mathbf{x}) \] となります.

まとめると以下の様になります.

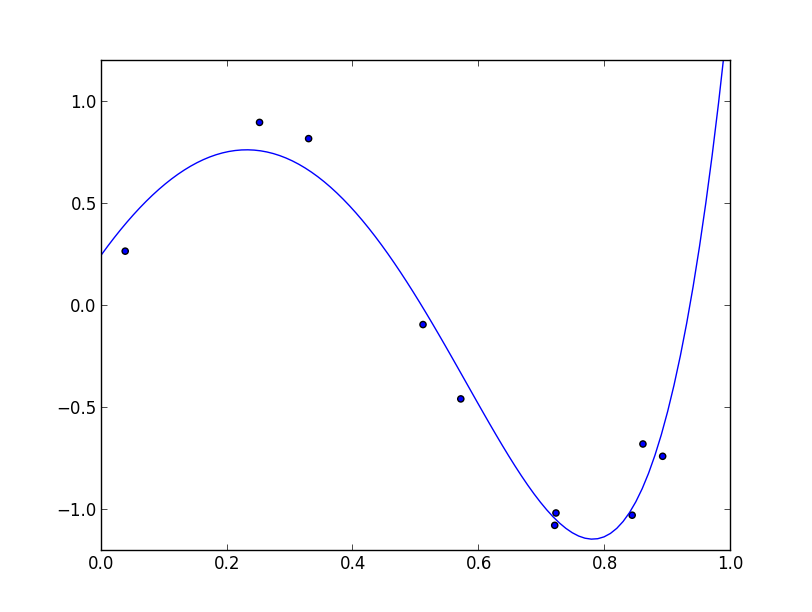
以下は多項式フィッティングのカーネル法による実装例です.
($10$次式, $\lambda=0.001$)

prog10-1.py

カーネル法の利点

先ほど使ったカーネル関数 \[ k(\mathbf{x},\mathbf{x}') = \Psi(\mathbf{x})^T\Psi(\mathbf{x}') \] の値は $\Psi(\mathbf{x})$ が如何に高次元でもスカラーとなります.

計画行列 $\mathbf{X}$ は特徴空間の次元 $M$ とデータ数 $N$ に対して $N\times M$ 行列なので, 計画行列を使う手法はモデルが複雑になるほど計算量が増えます. 一方, グラム行列 $\mathbf{K}$ は常に $N\times N$ 行列です.

この仕組みによって, 非常に高次元もしくは無限次元の特徴ベクトルを利用する事が可能になります.

カーネル関数の満たす条件

関数 $k(\mathbf{x},\mathbf{x}')$ が適切なカーネル関数である為には, 何らかの変換関数 $\Psi$ を用いて \[ k(\mathbf{x},\mathbf{x}') = \sum_{i=1}^\infty \psi_i(\mathbf{x})\psi_i(\mathbf{x}') \] と表せる事が必要です.

例えば, 2次元の入力ベクトルに対して \[ k((x_1,x_2),(y_1,y_2)) = x_1^2y_1^2+2x_1y_1x_2y_2+x_2^2y_2^2 \] はカーネル関数と見なす事が出来るでしょうか？

これは \[ k((x_1,x_2),(y_1,y_2)) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)(y_1^2, \sqrt{2}y_1y_2, y_2^2)^T \] と書き直す事が出来るので, 変換関数 $\Psi((x_1,x_2)) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)^T$ に対するカーネル関数と見なす事が出来ます.

正定値カーネル

Mercerの定理によって半正定値カーネルは前頁の条件を満たす事が保証されます.

テキスト6.2節では半正定値カーネルを構成する技法が紹介されています.

$k_1,k_2,k_3,k_a,k_b$ は既に与えられたカーネル関数, $c$ は実数定数, $\Psi$ は何らかの変換関数, $f$ は任意の連続関数, $q$ は非負係数の多項式関数, $A$ は半正定値対称行列, $\mathbf{x}_a,\mathbf{x}_b$ は $\mathbf{x}$ の成分を適当な２つの空間に分解した物.

代表的なカーネル関数

線形カーネル (linear kernel) \[ k(\mathbf{x},\mathbf{x}') = \mathbf{x}^T\mathbf{x}' \]

ガウスカーネル (Gaussian kernel) \[ k(\mathbf{x},\mathbf{x}') = \exp\left(-\frac{||\mathbf{x}-\mathbf{x}'||^2}{2\sigma^2}\right) \]

多項式カーネル (polynomial kernel) \[ k(\mathbf{x},\mathbf{x}') = (\mathbf{x}^T\mathbf{x}'+c)^d,\quad c \geq 0, d \in \mathbb{N} \]

シグモイドカーネル (sigmoid kernel) \[ k(\mathbf{x},\mathbf{x}') = \tanh (a\mathbf{x}^T\mathbf{x}'+b) \]

注: これは一般に半正定値カーネルではありませんが, ニューラルネットワークにおいて $\tanh$ が利用される事との関連から, 他のモデルにおいても利用される事があります.

他にも確率的生成モデルに基づいて \[ k(\mathbf{x}, \mathbf{x}') = p(\mathbf{x}, \mathbf{x}') \] を正定値カーネルとして扱う事もあります. 同時に出現する確率の高いデータは類似性が高いという考え方です.

例えばデータ $\mathbf{x}$ の出現が, 何らかの状態変数 $\mathbf{z}$ に依存して決まるならば \[ k(\mathbf{x}, \mathbf{x}') = \int p(\mathbf{x}|\mathbf{z})p(\mathbf{x}'|\mathbf{z})p(\mathbf{z})\mathrm{d}\mathbf{z} \] となります.

確率的生成モデルに基づいた他のカーネルに フィッシャーカーネル (Fisher kernel) があります.

データ $\mathbf{x}$ の生成確率がパラメータ $\boldsymbol{\theta}$ によって $p(\mathbf{x}|\boldsymbol{\theta})$ と表される場合を考えます. この時 \[ \mathbf{g}(\boldsymbol{\theta},\mathbf{x})=\nabla_{\boldsymbol{\theta}}\ln p(\mathbf{x}|\boldsymbol{\theta}) \] を フィッシャースコア (Fisher score) と呼びます.

$\ln p(\mathbf{x}|\boldsymbol{\theta})$ は $\mathbf{x}$ から得る情報量(の $-1$ 倍)なので, $\mathbf{g}(\boldsymbol{\theta},\mathbf{x})$ は各パラメータ $\theta_i$ に関して得る情報の大きさを表しています. 従ってフィッシャースコアの類似度が高いならば $\mathbf{x},\mathbf{x}'$ の類似度も高いと考える事が出来ます.

そこで, \[ k(\mathbf{x}, \mathbf{x}') = \mathbf{g}(\boldsymbol{\theta},\mathbf{x})^T\mathbf{g}(\boldsymbol{\theta},\mathbf{x}') \] をカーネル関数として利用する事が出来ます. もっと厳密には, 各ベクトルの共分散を考慮して \[ k(\mathbf{x}, \mathbf{x}') = \mathbf{g}(\boldsymbol{\theta},\mathbf{x})^T\mathbf{F}^{-1}\mathbf{g}(\boldsymbol{\theta},\mathbf{x}') \] とします. 但し $\mathbf{F}$ は フィッシャー情報行列 (Fisher information matrix) と呼ばれる共分散行列 \[ \mathbf{F} = \mathbb{E}_{\mathbf{x}}\left[\mathbf{g}(\boldsymbol{\theta},\mathbf{x})\mathbf{g}(\boldsymbol{\theta},\mathbf{x})^T\right] \] です.

カーネル密度推定法

カーネル密度推定法は母集団の分布を推定するノンパラメトリックな手法です. カーネル法はカーネル密度推定法との関連で登場する事があるので, 先に進む前に簡単に紹介します.

但し,カーネル法の「カーネル」とカーネル密度推定法の「カーネル」は基本的に異なる概念ですので注意して下さい.

カーネル密度推定法のアイデアは非常にシンプルです. 各データ点 $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n$ を中心に正規分布などを置き, それらを重ねあわせた分布によって母分布を近似します.

prog10-3.py

具体的には, サンプル $\{\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n\}$ に対して, その母分布を \[ p(\mathbf{x}) = \frac{1}{nh^d}\sum_{i=1}^n K\left(\frac{\mathbf{x}-\mathbf{x}_i}{h}\right) \] と近似します. $K$ を カーネル関数 (kernel function) , $h$ を平滑化パラメータと呼びます. $d$ は入力空間の次元です.

カーネル関数は \[ \int K(\mathbf{x})\mathrm{d}\mathbf{x} = 1 \] を満たす必要があります.

先ほどの例では標準正規分布 \[ K(\mathbf{x}) = \left(\frac{1}{\sqrt{2\pi}}\right)^D\exp\left(-\frac{||\mathbf{x}||^2}{2}\right) \] をカーネルとして使いました.

prog10-3.py

他には窓関数 \[ K(\mathbf{x}) = \left\{\begin{array}{cl} 1 & (|x_i|\leq 1/2, i=1,2,\ldots,d) \\ 0 & (\text{上記以外}) \end{array}\right. \] を使う場合もあります.

prog10-3.py

カーネル回帰分析

これまでは「何らかの基底関数を固定して」という形で基底関数を用いて来ましたが, 「どのような基底関数を用いるべきであるか？」という事については一切説明をしませんでした.

テキスト6.3節ではこの問題について解説していますが, その一部を紹介します.

どのような基底関数を用いるべきかについて厳密に考える為には, データの組 $\mathbf{x},y$ の生成モデル, つまり同時分布 \[ p(\mathbf{x}, y) \] を考えます.

カーネル密度推定法を用いるならば, 学習データ $\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\}$ に対して \[ p(\mathbf{x}, y) = \frac{1}{n}\sum_{i=1}^n f(\mathbf{x}-\mathbf{x}_i,y-y_i) \] とモデル化されます.

$\mathbf{x}$ に対する $y$ の予測値として $p(y|\mathbf{x})$ の平均を用いると \[ \begin{aligned} &y(\mathbf{x}) = \mathbb{E}[y|\mathbf{x}]= \int_{-\infty}^{\infty}yp(y|\mathbf{x})\mathrm{d} y\\ =&\frac{\displaystyle\int_{-\infty}^{\infty}yp(y,\mathbf{x})\mathrm{d} y} {\displaystyle \int_{-\infty}^{\infty}p(y,\mathbf{x})\mathrm{d} y} = \displaystyle\frac{\displaystyle \sum_i\int_{-\infty}^{\infty}yf(\mathbf{x}-\mathbf{x}_i, y-y_i)\mathrm{d} y} {\displaystyle \sum_i\int_{-\infty}^{\infty}f(\mathbf{x}-\mathbf{x}_i, y-y_i)\mathrm{d} y} \\ \end{aligned} \] となります.

ここで \[ \int_{-\infty}^{\infty}yf(\mathbf{x},y)\mathrm{d}y = 0 \] が任意の $\mathbf{x}$ について成立する場合を考えると, \[ \int_{-\infty}^{\infty}(y-y_i)f(\mathbf{x}-\mathbf{x}_i, y-y_i)\mathrm{d} y = 0 \] なので \[ \int_{-\infty}^{\infty}yf(\mathbf{x}-\mathbf{x}_i,y-y_i)\mathrm{d}y = y_i\int_{-\infty}^{\infty}f(\mathbf{x}-\mathbf{x}_i,y-y_i)\mathrm{d}y \] となりますから

\[ y(\mathbf{x}) = \frac{\displaystyle \sum_i y_i g(\mathbf{x}-\mathbf{x}_i)}{\displaystyle \sum_i g(\mathbf{x}-\mathbf{x}_i)}\qquad\left(\text{但し} g(\mathbf{x}) = \int_{-\infty}^{\infty}f(\mathbf{x},y)\mathrm{d}y\right) \] となり, さらにカーネル関数 $k$ を \[ k(\mathbf{x}, \mathbf{x}') = \frac{g(\mathbf{x}-\mathbf{x}')}{\displaystyle \sum_i g(\mathbf{x}-\mathbf{x}_i)} \] と置けば \[ y(\mathbf{x}) = \sum_i k(\mathbf{x},\mathbf{x}_i)y_i \] となります. これをナダラヤ=ワトソンモデル (Nadaraya-Watson model) または カーネル回帰モデル (kernel regression) と呼びます.

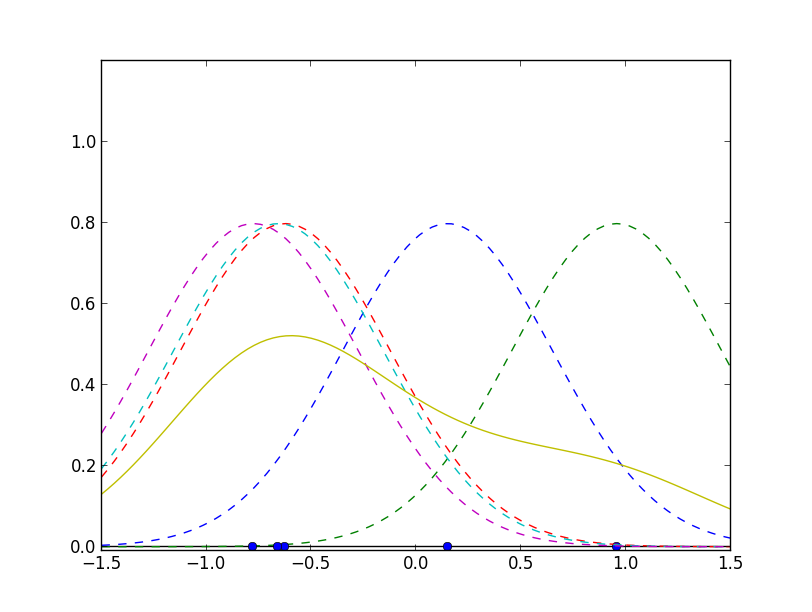
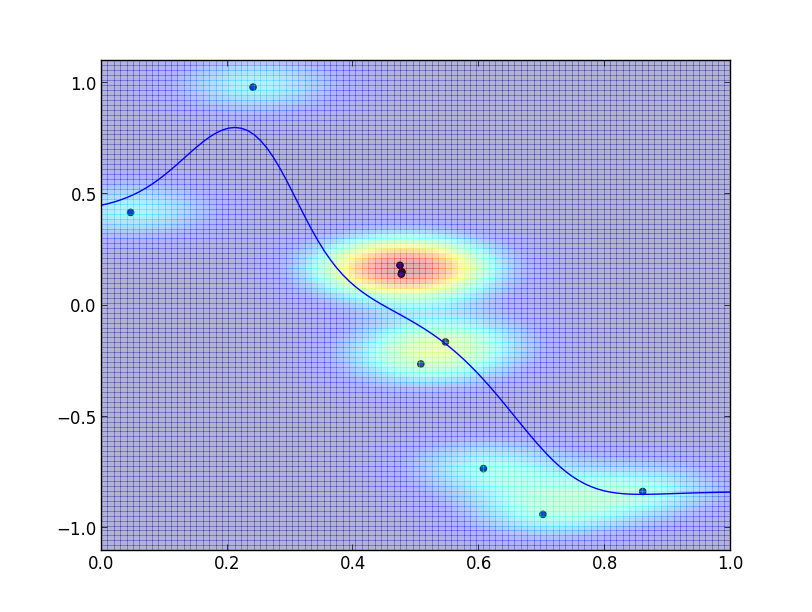
以下は $g(\mathbf{x})$ に正規分布 $\sigma=0.1$ を用いた場合のカーネル回帰の実装例です.

prog10-4.py

以下はこの時の $p(x, y)$ の様子です. 各データ点を中心に正規分布が配置されています.

prog10-4.py

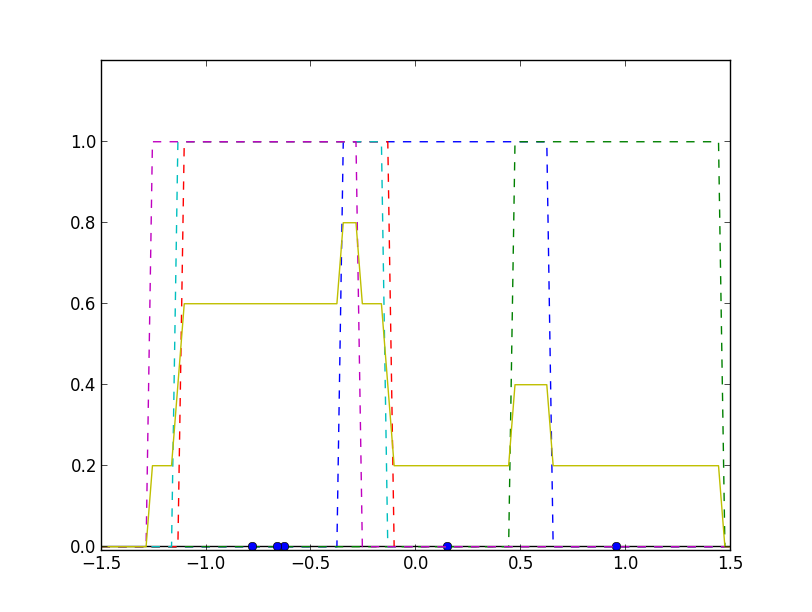
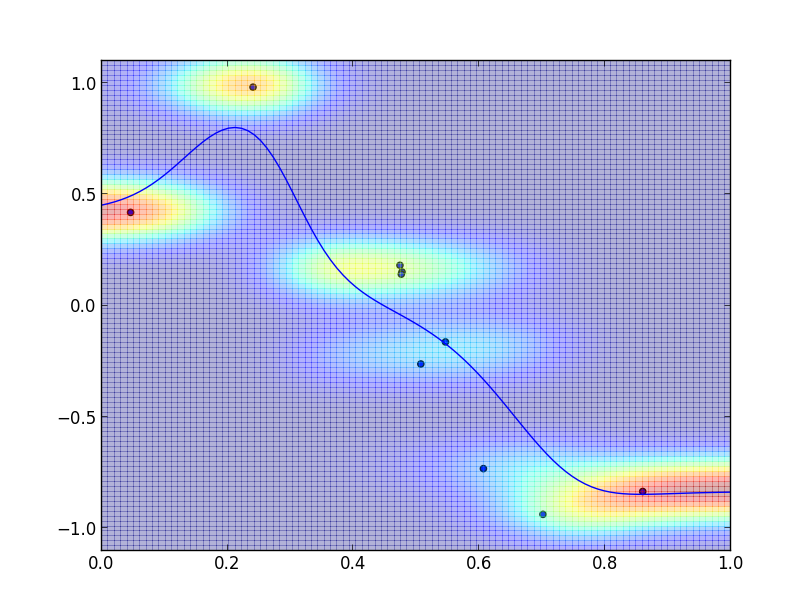
以下は $p(y|x)$ の様子です.

prog10-4.py

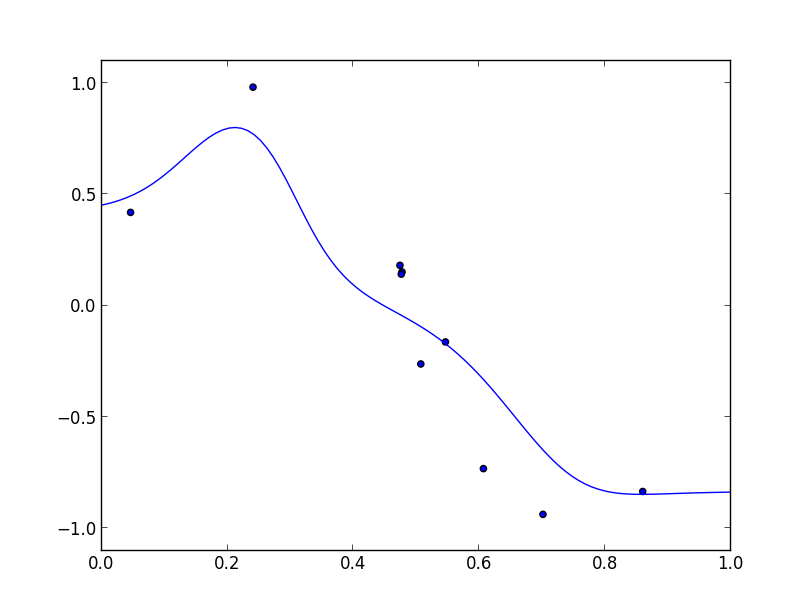
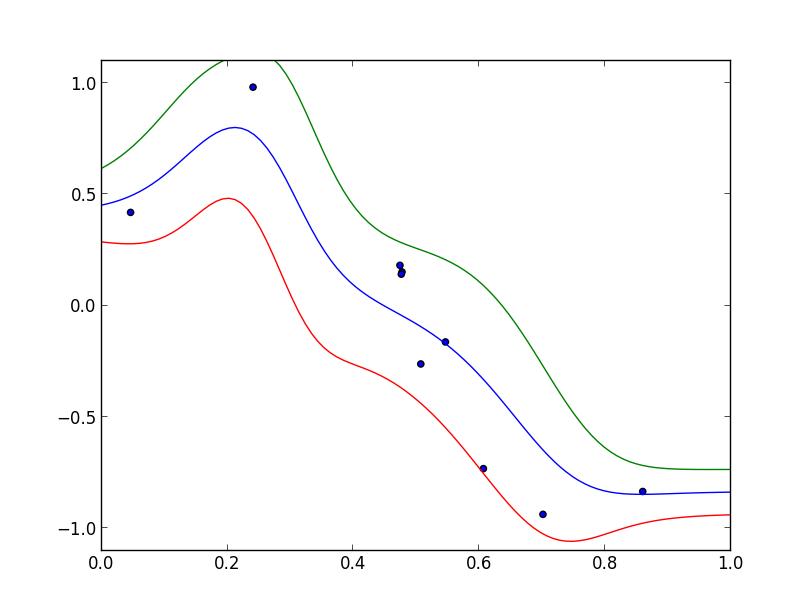
そして予測値 $\pm$ 標準偏差は以下の様になります.

prog10-4.py

途中で \[ \int_{-\infty}^{\infty}yf(\mathbf{x},y)\mathrm{d}y = 0 \] という仮定が登場しましたが, $f(\mathbf{x}, y)$が$|y|$ のみに依存する時(つまり $y$ について偶関数の時)には常にこれが成立する事に注意しましょう.

また、 $g(\mathbf{x}-\mathbf{x}_i)$ の値は $\mathbf{x}$ と $\mathbf{x}_i$ が近いほど大きな値を取るであろうと考える事が出来ます.

原点に極大値を持つ単峰型で対称的な関数はこの両方の性質を満たす為本アプローチに適していると考えられます.

放射基底関数

その値がある点からの距離のみに依存して定まる関数を 放射基底関数 (radial basis function) と呼びます. つまり, 放射基底関数とは適当な関数 $h$ を用いて \[ \psi_i(\mathbf{x}) = h(||\mathbf{x}-\boldsymbol{\mu}_i||) \] と表されるものです.

例えば, ガウス基底関数は放射基底関数の例です. \[ \psi_i(\mathbf{x}) = \exp\left(-\frac{||\mathbf{x}-\boldsymbol{\mu}_i||^2}{2\sigma^2}\right) \]

以上の議論より, 放射基底関数を基底に取った \[ y = \sum_{i=1}^n w_i h(||\mathbf{x}-\boldsymbol{\mu}_i||) \] というモデルが導出されます.

ガウス基底関数を用いた例はこれまでにも利用しましたが, その妥当性が確率的生成モデルの考察から示されました.

第10回はここで終わります

次回はテキストの6.4節 ガウス過程・ガウスランダム場をやり第6章を終了します. 時間が余れば第7章スパースカーネルマシンに進みます.