圏論勉強会
第7回
@ワークスアプリケーションズ
中村晃一2013年6月27日 $$ \newcommand\banana[1]{{(\hspace{-.2em}|#1|\hspace{-.2em})}} $$
謝辞
この勉強会の企画,会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この会について
- 圏論(category theory)を題材にいろんなことを学びます。
- 分かり易さを重視して初歩的な例を多用します。
- 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
- 中高生も数人見ているらしいのでプログラミングと関係が浅い内容も取り上げます。
- この資料はhttp://nineties.github.com/category-seminarに置いてあります。
第7回
様々な極限
代数的データ型
第7回の内容
前半は前回定義した「極限・余極限」の続き,後半は代数的データ型の圏論的な定式化とプログラム運算について紹介します。
復習
インデックス圏$\mathbf{J}$からの函手$D$を底とする二種類の「錐のなす圏」における,終対象と始対象を極限$\displaystyle\lim_{\leftarrow}D$・余極限$\displaystyle\lim_{\rightarrow}D$と呼ぶのでした。
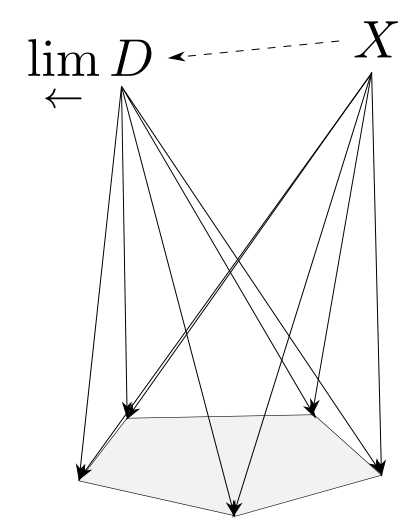
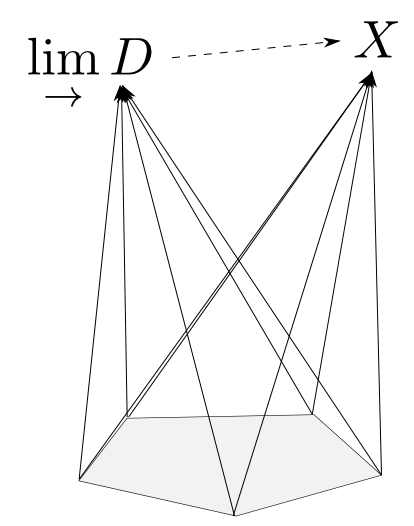
$\mathbf{J}$が空圏の時
底$D:\mathbf{J}\rightarrow \mathbf{C}$は唯一つ存在して $$ \lim_{\leftarrow}D \cong 1,\ \lim_{\rightarrow}D\cong 0$$
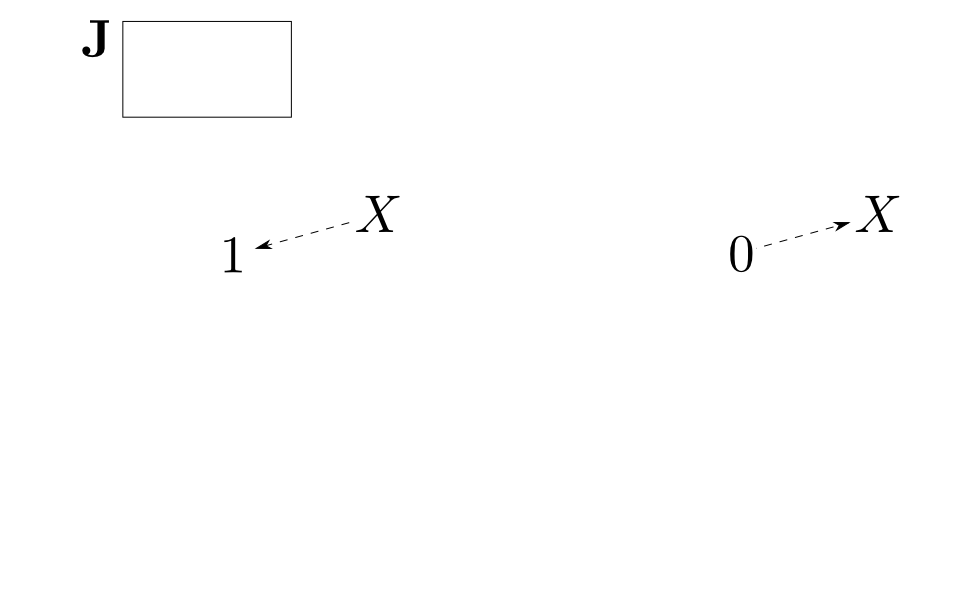
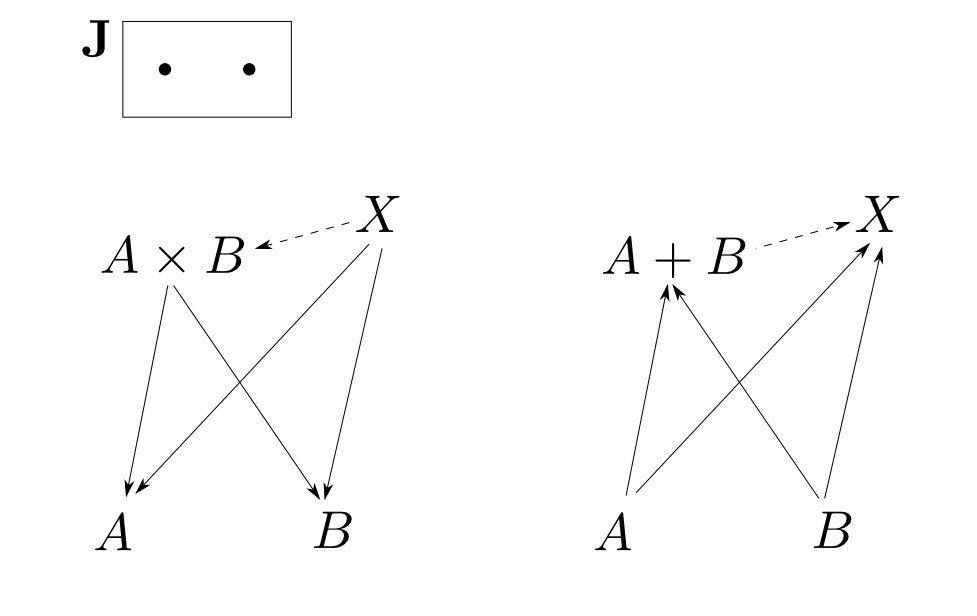
$\mathbf{J}$が二点集合の時
底$D:\mathbf{J}\rightarrow \mathbf{C}$が$A$,$B$の対だとすると $$ \lim_{\leftarrow}D \cong A\times B,\ \lim_{\rightarrow}D\cong A+B$$
$\mathbf{J}$が三点集合の時
底$D:\mathbf{J}\rightarrow \mathbf{C}$が$A$,$B$,$C$の組だとすると $$ \lim_{\leftarrow}D \cong A\times B\times C,\ \lim_{\rightarrow}D\cong A+B+C$$
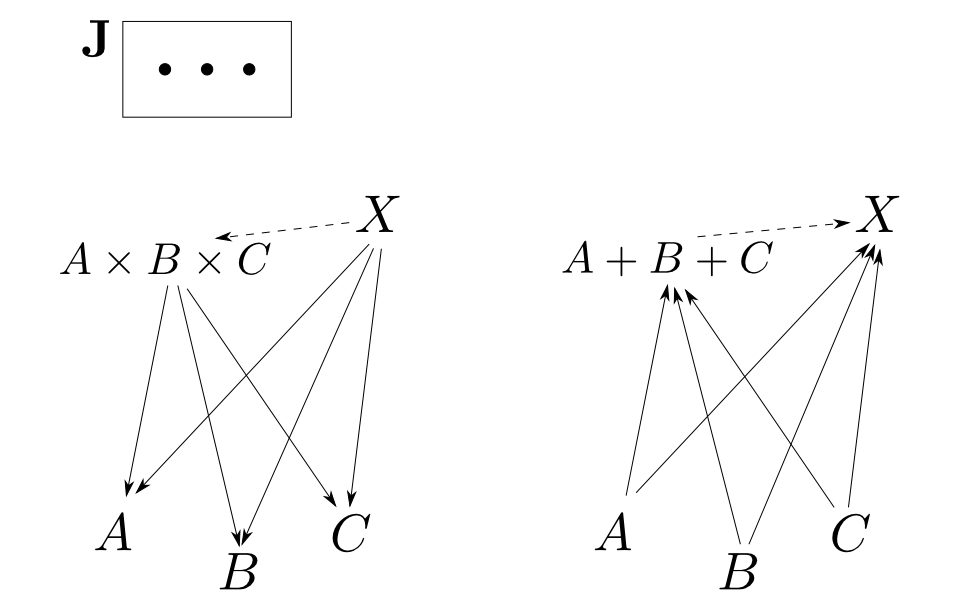
イコライザ・コイコライザ
イコライザ・コイコライザとは
インデックス圏$\mathbf{J}$を下図の様な平行射からなる圏
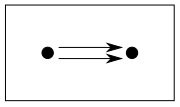
とした時の極限をイコライザ,余極限をコイコライザと言います。
簡単な絵を描いて見ると下図の様な状況です。$E$が頂点の錐がイコライザ,$Q$が頂点の錐がコイコライザです。
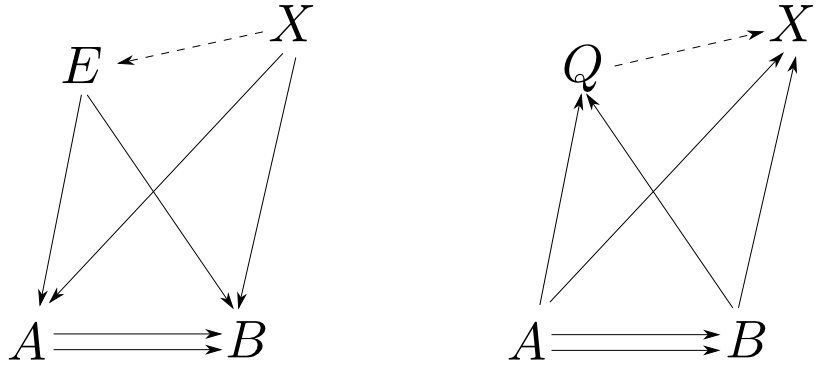
錐の様子
底への錐の様子を詳しく見ます。底からの錐も同様です。
底$D:\mathbf{J}\rightarrow\mathbf{C}$は二本の射$f,g: A\rightarrow B$で定まります。この時,射$x: X\rightarrow A$が与えられると錐の側面の三角形は全て可換でなければいけなかったので$X$から$B$への射は自動的に決まります。
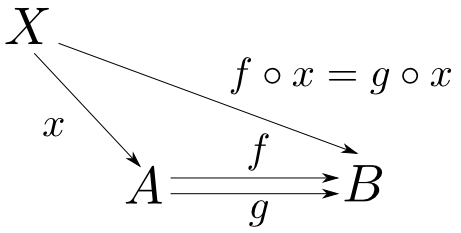
イコライザ
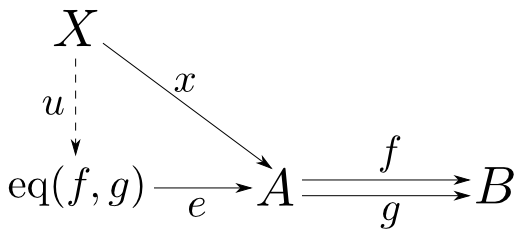
$f,g:A\rightarrow B$のイコライザ(equaliser)とは対象$\mathrm{eq}(f,g)$と$f\circ e=g\circ e$を満たす$e:\mathrm{eq}(f,g)\rightarrow A$からなり,任意の$f\circ x=g\circ x$を満たす$x:X\rightarrow A$に対して$x=e\circ u$を満たす$u:X\rightarrow \mathrm{eq}(f,g)$が唯一つ存在するものである。
$e$の事を単にイコライザと言うこともある。
コイコライザ
$f,g:A\rightarrow B$のコイコライザ(coequaliser)とは対象$\mathrm{coeq}(f,g)$と$q\circ f=q\circ g$を満たす$q:B\rightarrow \mathrm{coeq}(f,g)$からなり,任意の$x\circ f=x\circ g$を満たす$x:B\rightarrow X$に対して$x=u\circ q$を満たす$u:\mathrm{coeq}(f,g)\rightarrow X$が唯一つ存在するものである。
$q$の事を単にコイコライザという事もある。
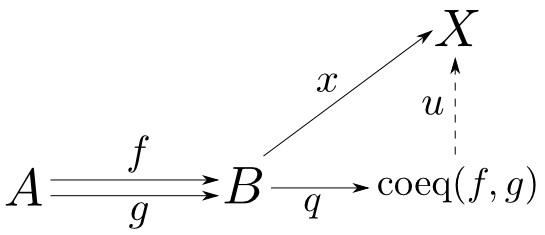
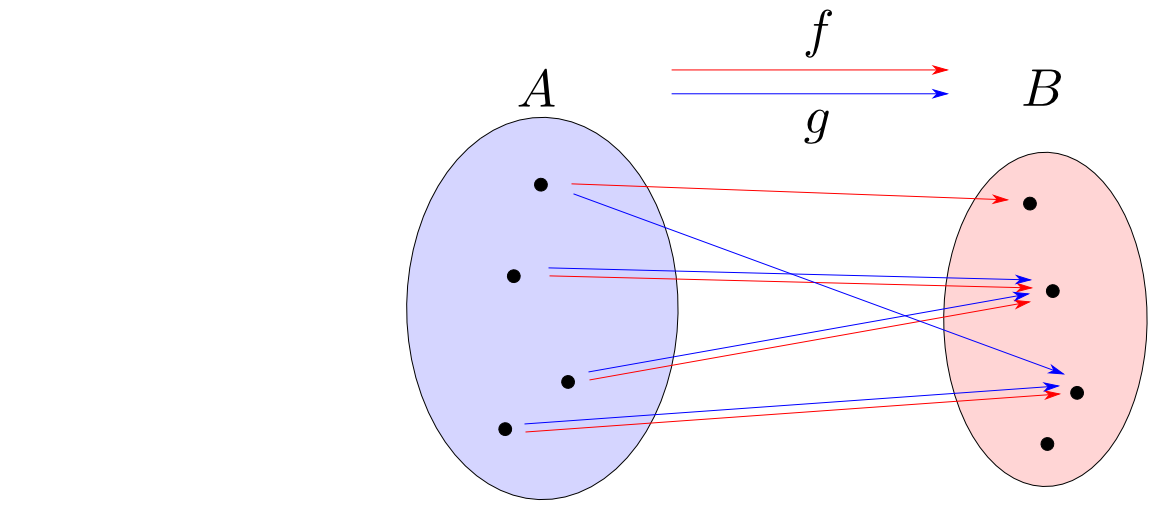
$\mathbf{Sets}$でのイコライザ
$f,g:A\rightarrow B$とすると $$ \mathrm{eq}(f,g) = \{ x \in A | f(x) = g(x) \} $$ 及び包含写像$e(x) = x$がイコライザとなります。
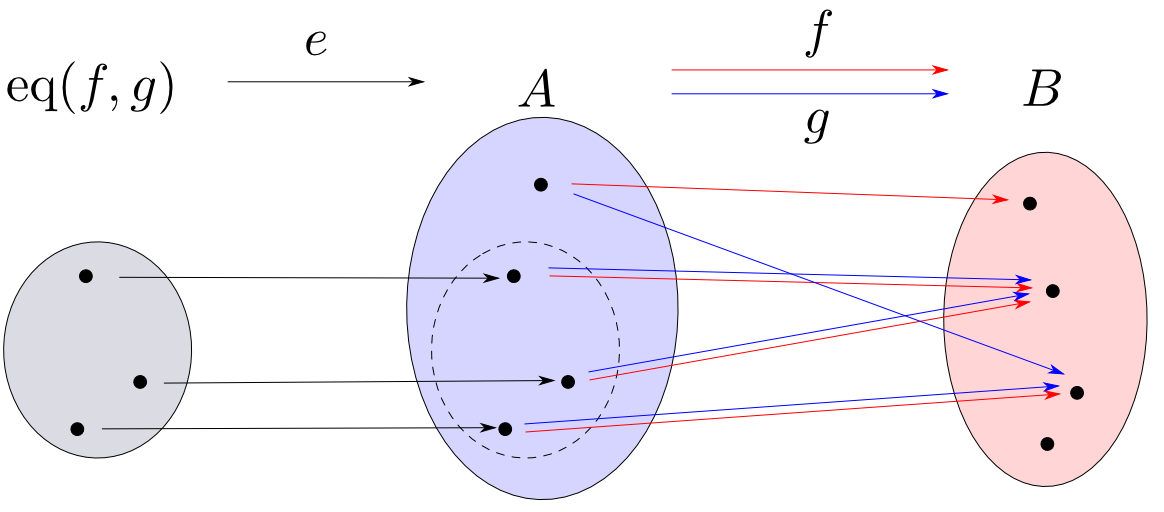
$\mathbf{Sets}$でのイコライザ
$f,g:A\rightarrow B$とすると $$ \mathrm{eq}(f,g) = \{ x \in A | f(x) = g(x) \} $$ 及び包含写像$e(x) = x$がイコライザとなります。
具体例
$f,g: \mathbb{R}\times \mathbb{R}\rightarrow \mathbb{R}$を $$ f(x,y) = x^2+y^2,\ g(x,y) = 1 $$ とすると $$ \mathrm{eq}(f,g) = \{ (x,y) | x^2 + y^2 = 1 \}$$ すなわち単位円周となります。
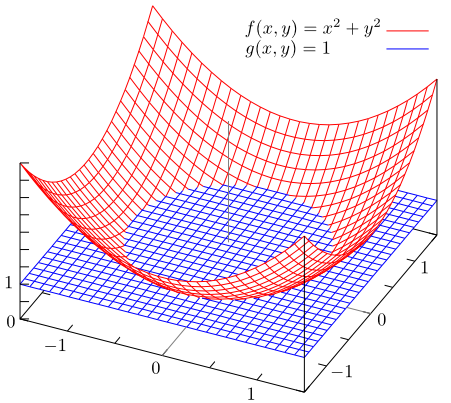
$\mathbf{Sets}$でのコイコライザ
$f,g: A\rightarrow B$に対して,各$a\in A$について$f(a)$と$g(a)$が同一の類に入るように $B$を類別する操作がコイコライザに対応します。
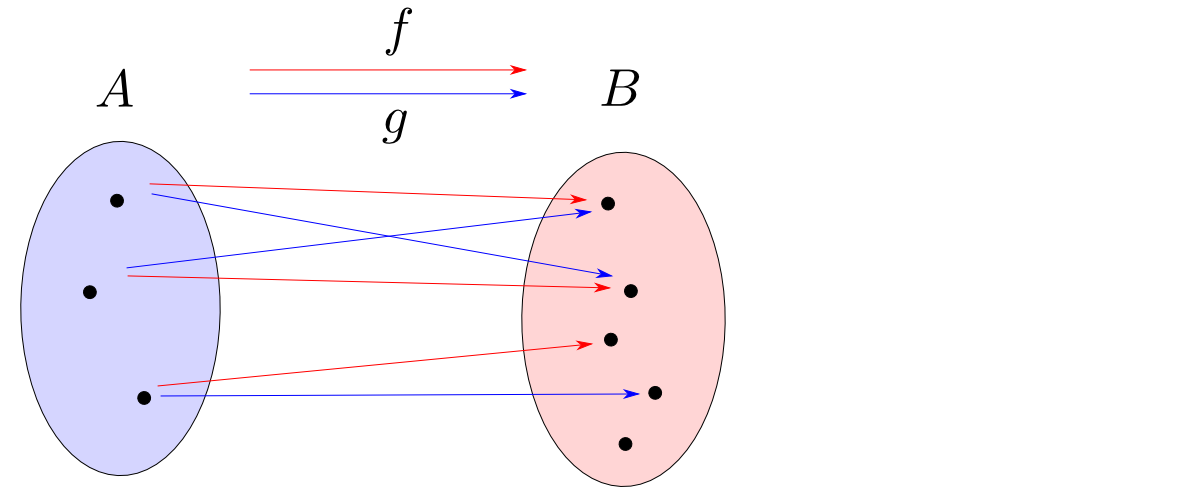
$\mathbf{Sets}$でのコイコライザ
$f,g: A\rightarrow B$に対して,各$a\in A$について$f(a)$と$g(a)$が同一の類に入るように $B$を類別する操作がコイコライザに対応します。
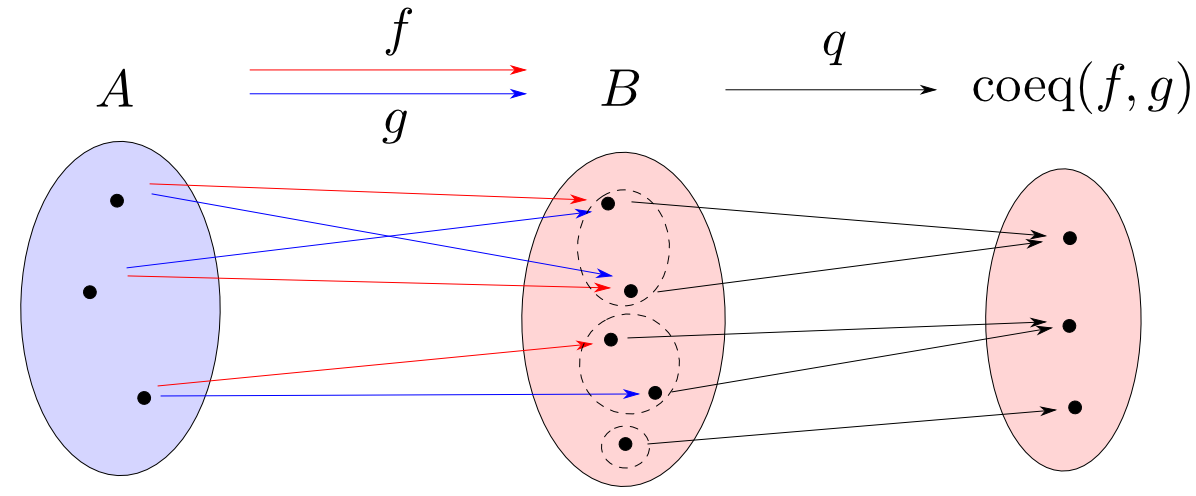
具体例
$f,g: \mathbb{N}\rightarrow\mathbb{N}$を $$ f(n) = n,\ g(n) = n + 3$$ とします。すると任意の$n$について$n$と$n+3$が同じ類に入るように$\mathbb{N}$を類別するので例えば, $$ \begin{aligned} & \mathrm{coeq}(f,g) = \{0,1,2\} \\ & e(n) = n \bmod 3 \ (\text{$n$を$3$で割った余り}) \end{aligned} $$ がコイコライザとなります。
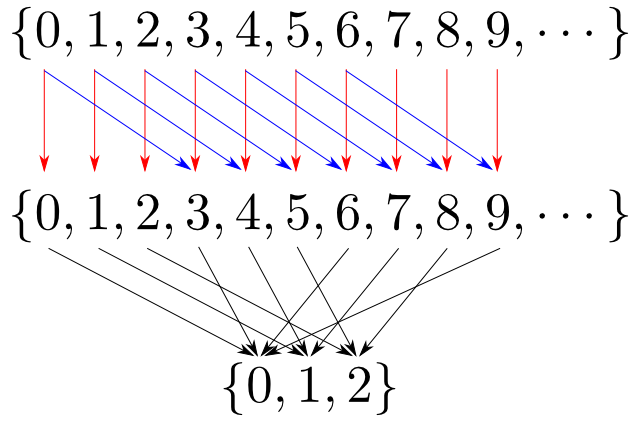
定理: イコライザはモノ,コイコライザはエピ
イコライザ$e:\mathrm{eq}(f,g)\rightarrow A$はモノ射,
コイコライザ$q:B\rightarrow\mathrm{coeq}(f,g)$はエピ射である。
$\mathbf{Sets}$の場合はモノ射は単射,エピ射は全射でした。
モノ射の復習
射$m: A\rightarrow B$がモノ射(monomorphism)であるとは,任意の対象$X$と射$f,g: X\rightarrow A$について
$$ m\circ f = m\circ g \ \Rightarrow\ f = g $$
が成り立つ事である。
$m$がモノ射である事をモニックであるとも言い,記号では$m: A\rightarrowtail B$と表す。
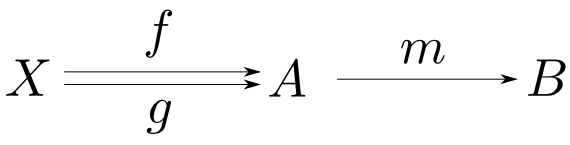
また,エピ射はこの双対でした。
イコライザはモノ
任意の$x,y:X\rightarrow\mathrm{eq}(f,g)$について $$ e\circ x = e\circ y\ \Rightarrow\ x = y$$ である事を示せば良いです。
【証明】
任意の$x,y:X\rightarrow\mathrm{eq}(f,g)$について$ e\circ x = e\circ y$であると仮定し,$z = e\circ x = e\circ y$とおく。$e$はイコライザなので$f\circ e=g\circ e$であるから
$$ f\circ z = f\circ e\circ x = g\circ e\circ x = g\circ z$$
となる。従って$(X,z)$は錐になっており$z = e\circ u$を満たす$u$は唯一に定まることから$x = y$となる。
すなわち$e$はモノ射である。 □
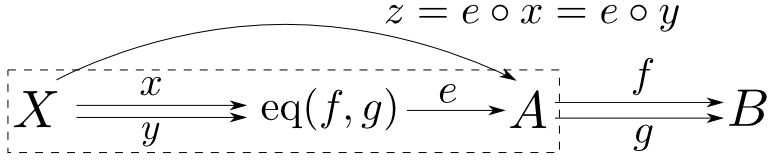
コイコライザはエピ
【証明】
双対性□
イコライザ・コイコライザは重要な用途が多くありますので是非Awodey本の第3章を読んでみて下さい。
引き戻し・押し出し
引き戻し・押し出しとは
インデックス圏$\mathbf{J}$を下図の様な圏
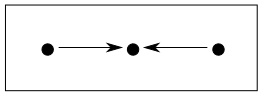
とした時の極限を引き戻しと言います。
引き戻しの双対,つまり$\mathbf{J}$を下図の様な圏
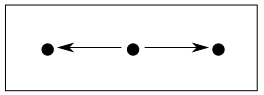
とした時の余極限を押し出しと言います。
引き戻し
$f:A\rightarrow C$,$g:B\rightarrow C$の引き戻し(pullback)とは対象$A\times_{C} B$と$f\circ p_1 = g\circ p_2$を満たす$p_1:A\times_{C}B\rightarrow A$,$p_2: A\times_{C} B\rightarrow B$からなり,任意の$f\circ x=g\circ y$を満たす$x:X\rightarrow A$,$y:X\rightarrow B$に対して$x = p_1\circ u$,$y = p_2\circ u$を満たす$u: X\rightarrow A\times_{C}B$が唯一つ存在するものである。
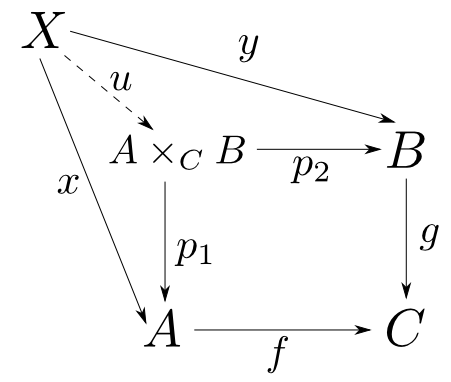
押し出し
$f:C\rightarrow A$,$g:C\rightarrow B$の押し出し(pushout)とは対象$A+_{C} B$と$q_1\circ f = q_2\circ g$を満たす$q_1:A\rightarrow A+_{C}B$,$q_2: B\rightarrow A+_{C} B$からなり,任意の$x\circ f=y\circ g$を満たす$x:A\rightarrow X$,$y:B\rightarrow X$に対して$x = u\circ q_1$,$y = u\circ q_2$を満たす$u: A+_{C}B\rightarrow X$が唯一つ存在するものである。
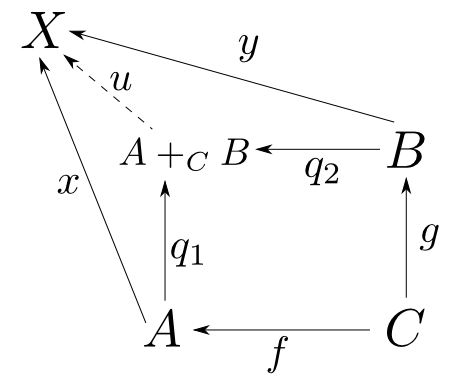
$\mathbf{Sets}$での引き戻し
$f:A\rightarrow C$,$g:B\rightarrow C$に対して $$ A\times_C B = \{(a,b) \in A\times B | f(a) = g(b) \}$$ となります。直積$A\times B$の$f(a)=g(b)$を満たす部分集合です。
$\mathbf{Sets}$での引き戻し:具体例
関数$\chi:A\rightarrow\{\mathrm{true},\mathrm{false}\}$と定数$\mathrm{true}:1\rightarrow\{\mathrm{true},\mathrm{false}\}$の引き戻しは
$$ U = \{a \in A | \chi(a) = \mathrm{true}\}$$
です。$A\times 1 \cong A$であった事に注意しましょう。
つまり,条件$\chi$を満たす要素からなる集合$U$を構成する事を表現できます。この$\chi$の事を$U$の特性関数(characteristic function)などと言います。
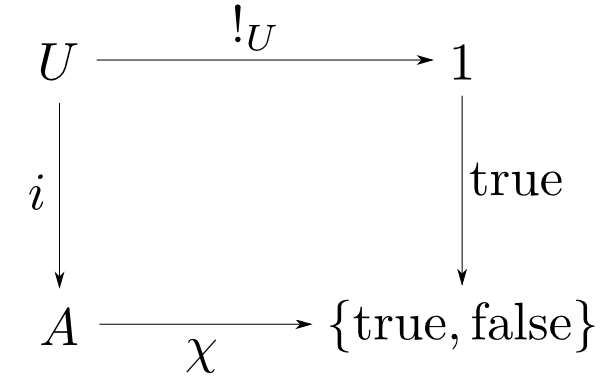
この場合の$p_1$は包含写像$i(x) = x$,$p_2$は$U$から$1$への唯一の写像($!_U$と表す)です。
積+等式 = 引き戻し?
$\mathbf{Sets}$では積$A\times B$の$f(a) = g(b)$を満たす部分集合が引き戻し$A\times_C B$となっていました。そして,ある等式を満たす部分集合はイコライザで表せました。
実は任意の圏においても,引き戻しは積とイコライザで表せます。

定理
任意の二対象の積,任意の並行射に対するイコライザが存在する圏において, $A\times B$からの$A$,$B$への射影を$\pi_1,\pi_2$とすると $$ A\times_C B \cong \mathrm{eq}(f\circ\pi_1, g\circ\pi_2) $$ が成り立つ。 $A\times_C B$から$A$,$B$への射影$p_1,p_2$は $$ p_1 = \pi_1\circ e,\ p_2 = \pi_2\circ e$$ で与えられる。

【証明】
$x: X\rightarrow A, y:X\rightarrow B$を$f\circ x = g\circ y$を満たす任意の射とする。
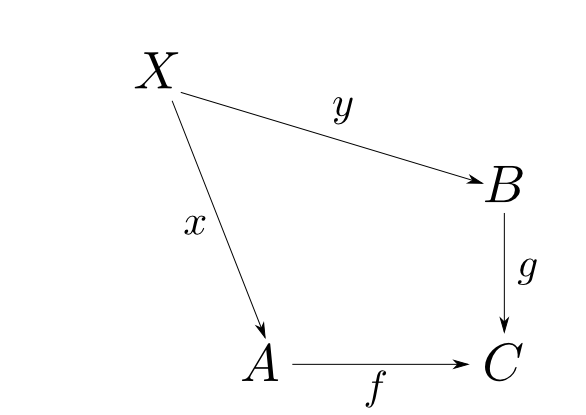
これは $$ f\circ\pi_1\circ\langle x,y \rangle = g\circ\pi_2\circ\langle x,y\rangle $$ が成り立つ事と同値である。
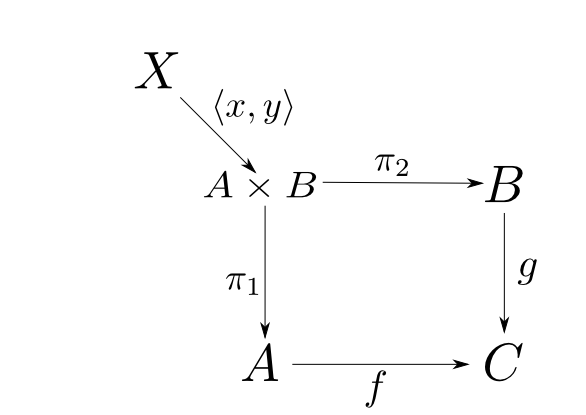
従って$(X,\langle x,y\rangle)$は平行射$f\circ\pi_1,g\circ\pi_2: A\times B\rightarrow C$を底とする錐になっている。
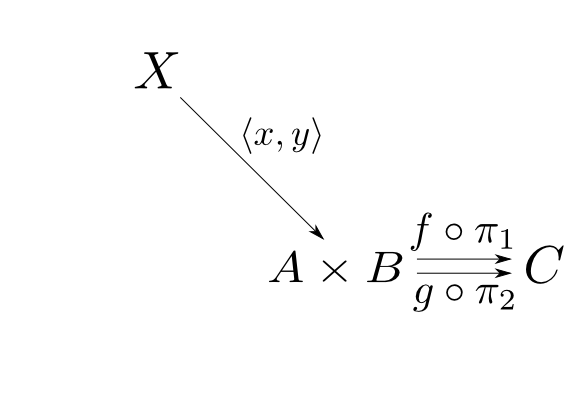
よってイコライザ$(E, e)$が存在する。すなわち$e$は$f\circ\pi_1\circ e = g\circ\pi_2\circ e$を満たし, $$ \langle x,y \rangle = e\circ u$$ を満たす$u:X\rightarrow E$が唯一つ存在する。積の普遍性より,この等式は $$ x = \pi_1\circ e\circ u,\ y = \pi_2\circ e\circ u$$ と同値である。
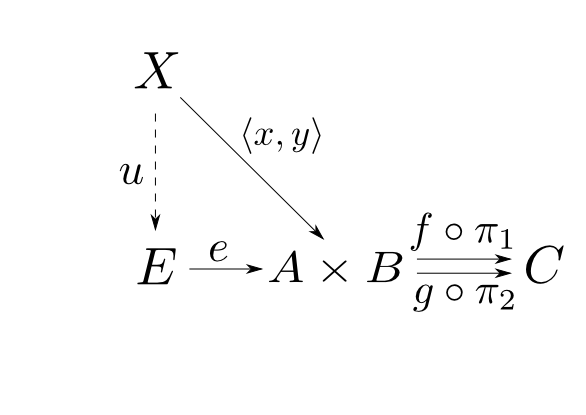
ここで$p_1 = \pi_1\circ e, p_2 = \pi_2\circ e$とおいて等式を書き直すと,$ f\circ p_1 = g\circ p_2$ を満たし, $$ x = p_1\circ u,\ y = p_2\circ u$$ を満たす$u$が唯一つ存在する事が示される。すなわち $$ A\times_C B \cong E = \mathrm{eq}(f\circ\pi_1,g\circ\pi_2)$$ である。□
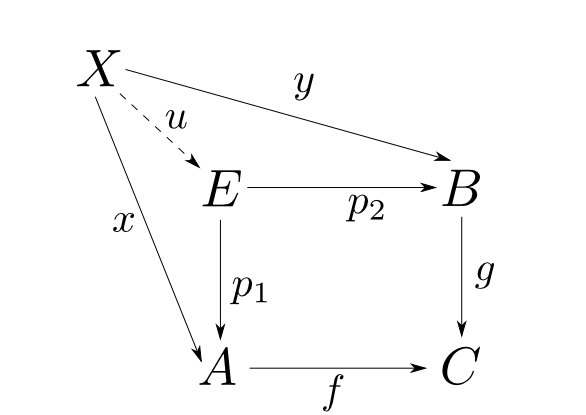
双対性より押し出しも余積,コイコライザで表せます。
$\mathbf{Sets}$の場合は$A+_C B$は直和$A + B$を$f(c)$,$g(c)$を同一視する事によって類別した集合に対応します。
時間の関係上具体例の説明は省略します。
実は引き戻しに限らず,任意の極限は積とイコライザで表せます。
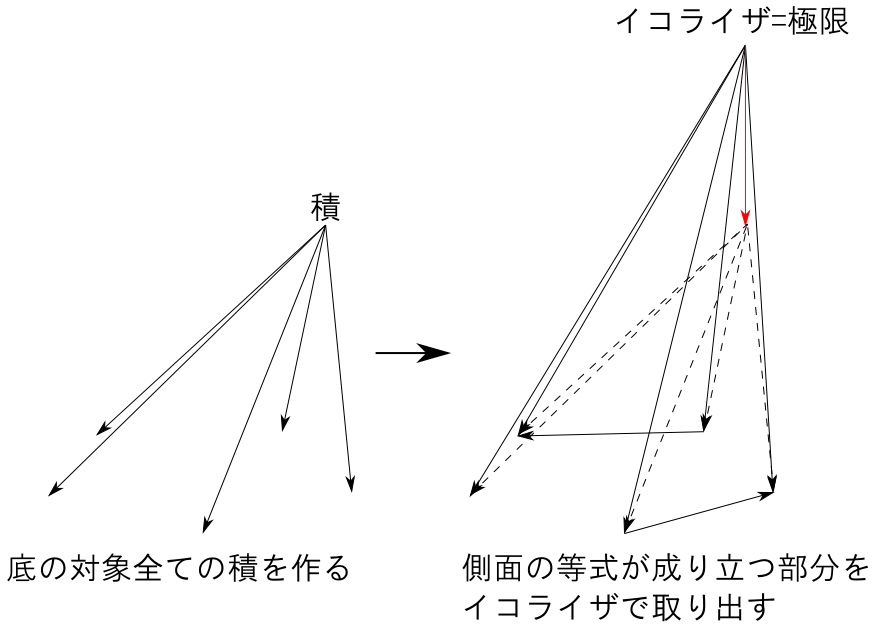
定理
圏$\mathbf{C}$において
- 任意の対象の集合の積
- 任意の平行射のイコライザ
が存在するならば任意の極限が存在する。
また,そのような圏$\mathbf{C}$は完備(complete)であるという。
双対性より,任意の余積とコイコライザを持つ圏は任意の余極限を持ち,そのような圏は余完備(cocomplete)であると言います。
一旦ここまで
今の定理の証明は是非やりたい所なのですが時間がありません。Awodey本のProposition 5.21を参照して下さい。引き戻しを積とイコライザに分解する例を良く理解すると,この定理の証明も読めると思います。
ある種の余完備な圏がプログラムの意味論を構築する上で必要になりますので,次回も引き続き極限の話題を取り上げる予定です。
代数的データ型
代数的データ型
第3回に半群やマグマのなす圏において自由対象という普遍的な対象を考えるとデータ構造が出てくるという話をしました。
これらの特別な場合として,$F$代数,$F$余代数というもののなす圏において関数型言語の代数的データ型が説明されます。
自然数
一旦「型」から離れて,自然数の集合を考えます。
自然数の集合$N$は以下の条件を満たす集合である。
- ある定数$\mathrm{zero}\in N$が存在。
- 関数$\mathrm{succ}: N\rightarrow N$が存在。
- 任意の$n$について$\mathrm{zero} \neq \mathrm{succ}(n)$である。
- $n\neq m$ならば$\mathrm{succ}(n) \neq \mathrm{succ}(m)$である。
- 以上の他に$N$の要素は存在しない。
$\mathrm{zero}=0$,$\mathrm{succ}(n)=n + 1$とすると$N$が通常の自然数の集合$\mathbb{N}$になります。
他にも,$\mathrm{zero}=1$, $\mathrm{succ}(n)=2n$などとすると定義を満たす別の集合ができますが,全て同型になります。
自然数を射で表す
今の定義を圏論の言葉で述べる方法を考えます。
定数$\mathrm{zero}$は$N$の要素なので終対象$1$から$N$への射で表せ,$\mathrm{succ}$は$N$から$N$への関数で表せます。
この状況を下の様な図式で表しましょう。
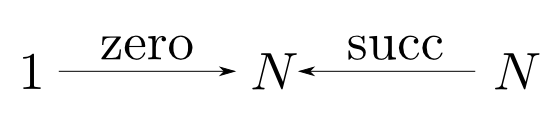
実際には対象・射の中身を覗く事は出来ないので以下の図式が自然を表しているか否かを直接知ることはできません。
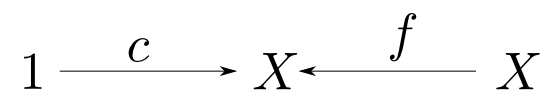
この図式と外部との関係性によって自然数を特定する必要があります。
その為にこの形の図式を対象とする圏を考える必要があります。
自然数の属す圏
下図の様な図式(射$c,f$で定まる)を対象とし
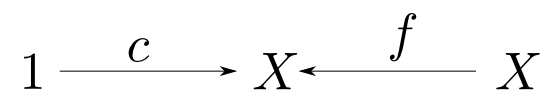
下図を可換とする射$h: X\rightarrow Y$を図式間の射とすると,これらは圏をなします。(恒等射の存在・結合律を確かめてみて下さい)。
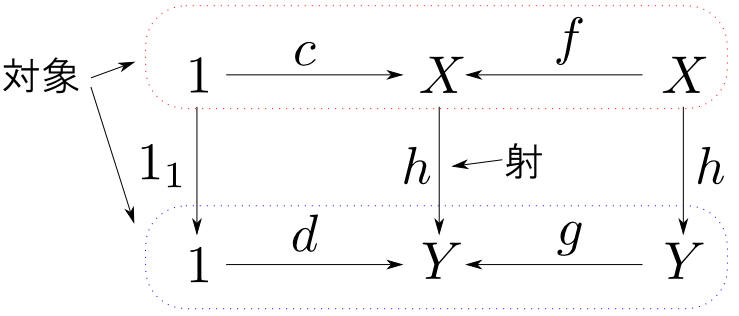
$h$は準同型
今の可換図式を等式で表すと $$ h\circ c = d,\ h\circ f = g\circ h$$ となります。
これをpointwiseに書き表すと($c,d$は対応する定数に直して) $$ h(c) = d,\ h(f(x)) = g(h(x)) $$ となります。これは$h$が準同型である事を表しています。

自然数
今の圏における始対象が自然数を与えます。$\mathbf{Sets}$以外の任意の圏$\mathbf{C}$に一般化して定義を書き下します。
$\mathbf{C}$を任意の有限積を持つ圏とする。
対象$N$,射$\mathrm{zero}:1\rightarrow N,\mathrm{succ}:N\rightarrow N$が$\mathbf{C}$における自然数であるとは,
任意の対象$X$,射$c:1\rightarrow X,f:X\rightarrow X$に対して
$$ u\circ\mathrm{zero}=c,\ u\circ\mathrm{succ} = f\circ u$$
を満たす$u:N\rightarrow X$が唯一つ存在する事である。
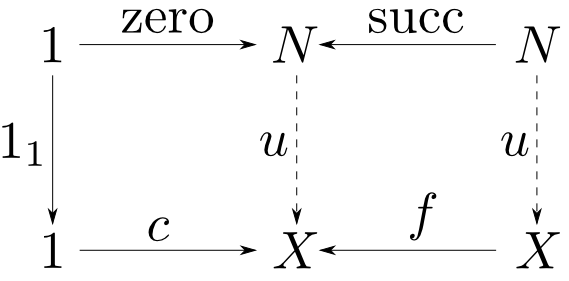
$\mathbf{Sets}$における自然数
$\mathbf{Sets}$で解釈すると$N$はまさしく自然数の集合となっています。
【証明】
$$ N = \{0,1,2,3,\cdots\},\ \mathrm{zero} = 0,\ \mathrm{succ}(n) = n+1$$
とする。任意の集合$X$,$c\in X$,$f:X\rightarrow X$に対して
$$ u(\mathrm{zero}) = c,\ u\circ\mathrm{succ} = f\circ u$$
を満たすとする。すなわち,任意の$n\in N$について
$$ \color{red}{u(0) = c,\ u(n+1) = f(u(n))} $$
を満たすとすると帰納的に
$$ u(n) = f^{n}(c) = f\circ f\circ\cdots\circ f(c)$$
となる。すなわち$u$が一意に定まるので$N$は(圏論的な)自然数の定義を満たす。
□
関数型言語における自然数型には$\bot$という未定義値を表す特殊な値が存在する事から,擬数や無限数と呼ばれる値が発生し複雑です。
その為に他の圏が必要になりますが難しい話は後に回します。
自然数の例を一般化
自然数の定義を圏論的に一般化していきます。
圏$\mathbf{C}$が余積を持つならば,先ほどの左下の可換図式を折り畳んで等価な右下の可換図式に変換出来ます。
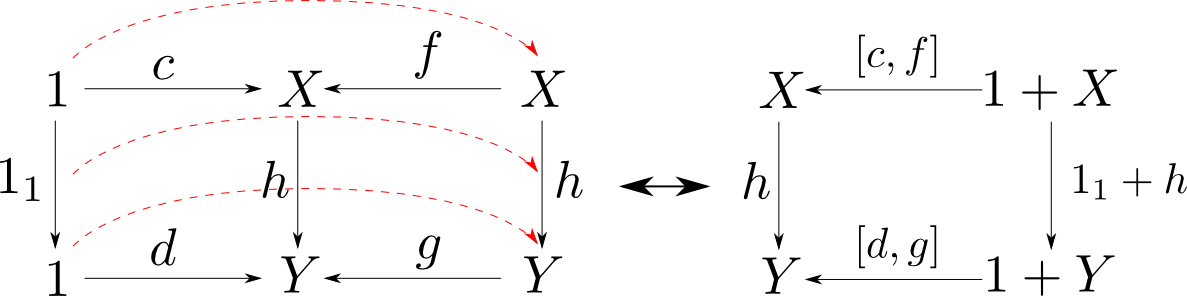
(左右の図式で成り立つ等式を書きだして,それらが一致する事を確かめてみて下さい。)
余積からの任意の射$f: A+B\rightarrow X$は$f = [a,b]$の形に表す事ができますから,先ほどの図式の$[c,f],[d,g]$は任意の射$x,y$としてしまって良いです。
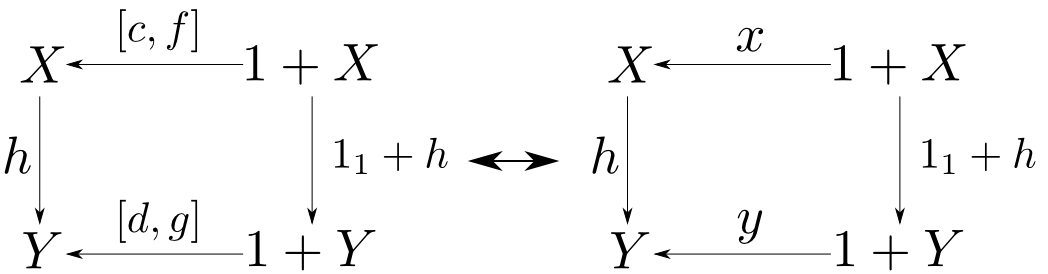
結局,下図の赤線で囲った部分のパターンを一般化できれば良さそうです。

これは対象$X$を$F(X) = 1+X$に移し,射$f$を$F(f) = 1+f$に移す函手$F$で表現できます。(この$F$が函手である事の確認は練習問題。)
$F$代数
函手$F:\mathbf{C}\rightarrow\mathbf{C}$に対して射$x: F(X)\rightarrow X$を$F$代数($F$-algebra)という。 この$F$代数を$(X,x)$とも表す。
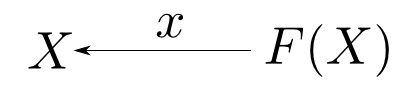
$F$代数は,下の図式を可換とする射$h:X\rightarrow Y$を$(X,x)$から$(Y,y)$への射として圏をなす。
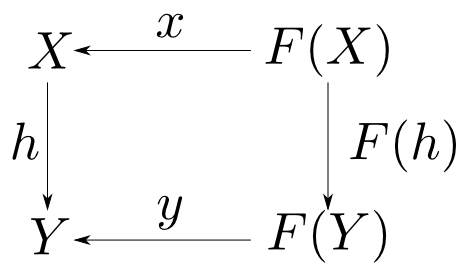
$F$始代数, catamorphism
$F$代数の圏に始対象が存在するならばそれを$F$始代数(initial $F$-algebra)という。
$F$始代数$(T, \mathrm{in})$から任意の$F$代数$(X,\varphi)$への射は$\varphi$に対して唯一つに定まるのでこれを$\banana{\varphi}$と表し, catamorphismと呼ぶ。
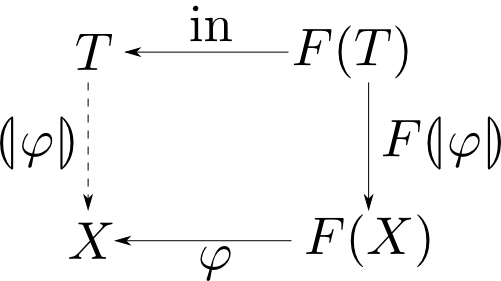
多項式函手
積・余積で構成される函手を多項式函手(polynomial functor)と言います。これは $$ F(X) = 1 + A\times X\times X $$ などと表され任意の対象$X$を $$ X\longmapsto 1 + A\times X\times X$$ 任意の射$f: X\rightarrow Y$を $$ f\longmapsto 1_1 + 1_A\times f \times f$$ のように移します。
様々な$F$始代数
以下の様な多項式関手による$F$始代数が各データ型に対応します。
- 自然数 $$F(X) = 1 + X$$
- $A$型のリスト $$F(X) = 1 + A\times X$$
- 長さが$1$以上の$A$型のリスト $$F(X) = A + A\times X$$
- 葉に$A$型の値を持つ二分木 $$F(X) = A + X\times X$$
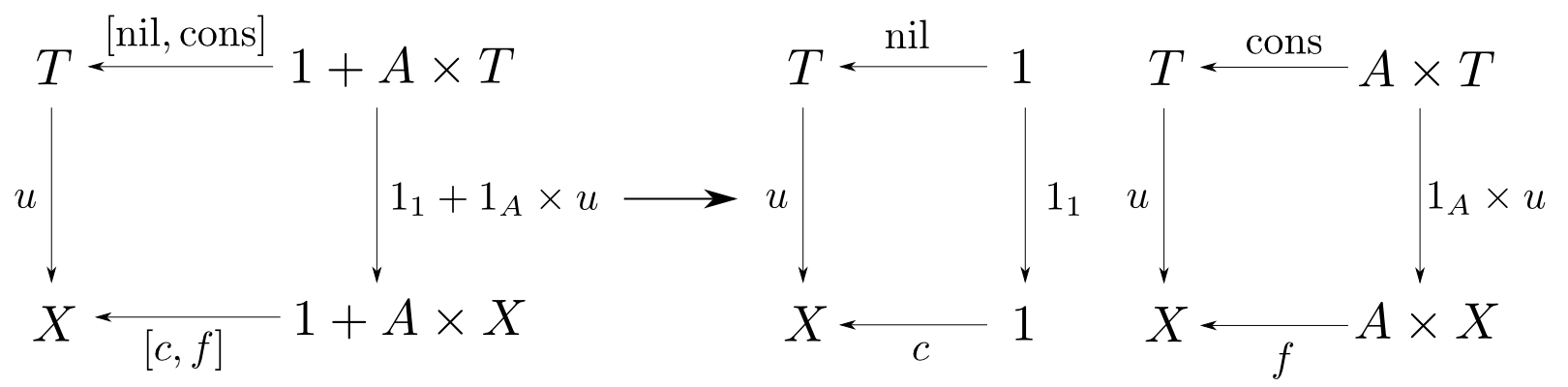
リストに対するcatamorphism
$F(X) = 1 + A\times X$として$F$始代数の図式を右下の様に展開します。 するとcatamorphismを$u$とすると等式 $$ \begin{aligned} & u(\mathrm{nil}) = c \\ & u(\mathrm{cons}(a,as)) = f(a,u(as)) \\ \end{aligned} $$ が得られます。これは所謂$\mathrm{foldr}(f,c)$の定義になっています。 $$ \color{red}{\banana{[c,f]} = \mathrm{foldr}(f,c)} $$
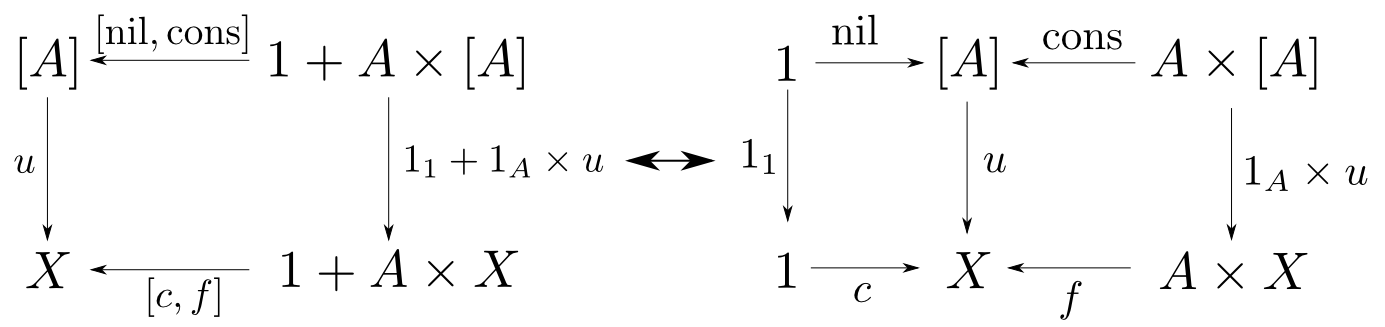
catamorphism=畳み込み
今みたようにcatamorphismは$\mathrm{foldr}$に代表される畳み込み系の再帰関数を統一するものです。catamorphismの様なある種の再帰関数を表す射を再帰スキームと言います。
プログラム運算の初歩
反射則,融合則
$0$を始対象,$0$から対象$A$への唯一の射を$!_A:0\rightarrow A$と表す事にすると,以下が成り立つ。
- 反射則(reflection law) $$ !_0 = 1_0 $$
- 融合則(fusion law)
任意の$f: A\rightarrow B$に対して $$ f\circ !_A = !_B $$
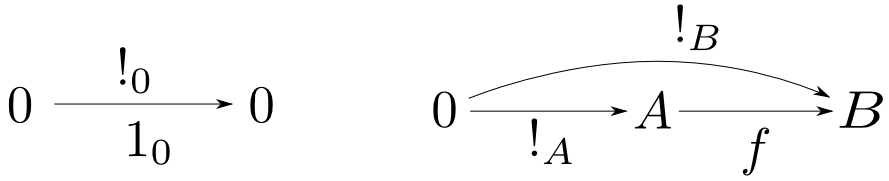
catamorphismの反射則,融合則
catamorphismは始対象からの射ですので,今の法則がそのまま成り立ちます。
$(T,\mathrm{in})$が$F$始代数ならば $$ \banana{\mathrm{in}} = 1_T \quad\text{(反射則)}$$ また$h\circ f=g\circ F(h)$が成り立つならば $$h\circ\banana{f}=\banana{g} \quad\text{(融合則)}$$
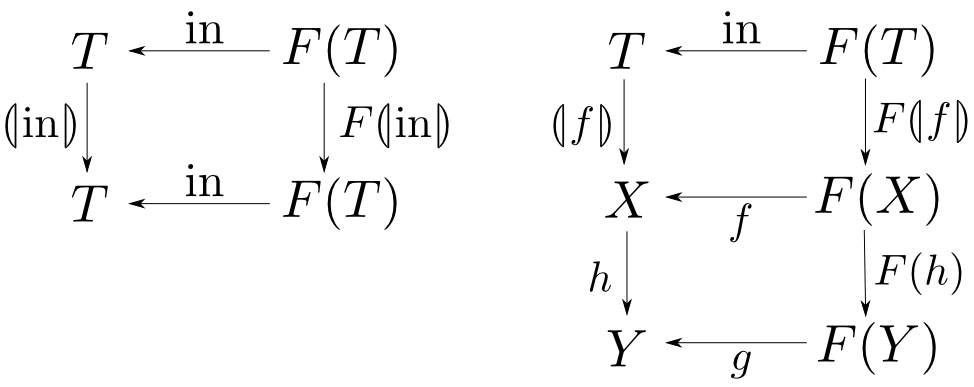
例題
$\mathrm{sum}\circ\mathrm{filter}(\mathrm{even})$を一つの$\mathrm{foldr}$で表せ。
まず $$ p(a,as) = \left\{\begin{array}{ll} \mathrm{cons}(a,as)&(\mathrm{even}(a) = \mathrm{true}\text{の時}) \\ as&(\text{それ以外}) \end{array}\right. $$ とすると$\mathrm{filter}(\mathrm{even}) = \banana{[\mathrm{nil},p]}$となります。 よって$\mathrm{sum}\circ [\mathrm{nil},p] = [c,g]\circ(1_1+1_A\times\mathrm{sum})$を満たす$c,g$を見つければ融合則が使えます。これをpointwiseな等式に書き直すとまず$c = \mathrm{sum}(\mathrm{nil}) = 0$であり, $$ g(a, \mathrm{sum}(as)) = \left\{\begin{array}{ll} \mathrm{sum}(\mathrm{cons}(a, as)) = a + \mathrm{sum}(as) & (\mathrm{even}(a) = \mathrm{true}\text{の時}) \\ \mathrm{sum}(as) & (\text{それ以外}) \end{array}\right. $$ が成り立てば良いので, $$ g(a,x) = \left\{\begin{array}{ll} a+x & (\mathrm{even}(a) = \mathrm{true}\text{の時}) \\ x & (\text{それ以外}) \end{array}\right.$$ とすれば良いです。すなわち$\banana{[0,g]}=\mathrm{foldr}(g, 0)$が求める関数です。
Lambekの補題
$(T,\mathrm{in})$が$F$始代数ならば$\mathrm{in}$は同型射
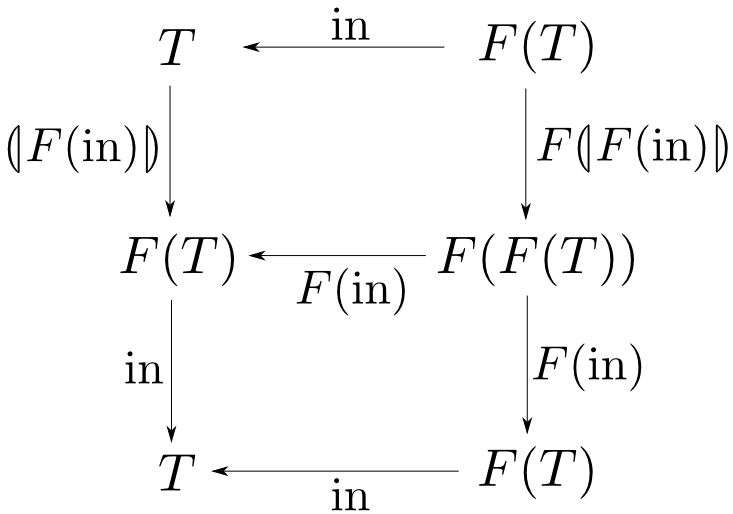
【証明】
下の四角形において$\mathrm{in}\circ F(\mathrm{in}) = \mathrm{in}\circ F(\mathrm{in})$が成り立つから融合則より
$$ \mathrm{in}\circ \banana{F(\mathrm{in})} = \banana{\mathrm{in}} $$
である。さらに反射則より$$\mathrm{in}\circ\banana{F(\mathrm{in})} = 1_T$$
また,上の四角形の可換性より
$$ \banana{F(\mathrm{in})}\circ\mathrm{in} = F(\mathrm{in})\circ F\banana{F(\mathrm{in})} $$
$F$は函手なので
$$ \banana{F(\mathrm{in})}\circ\mathrm{in} = F(\mathrm{in}\circ \banana{F(\mathrm{in})}) = F(1_T) = 1_{F(T)} $$
となる。従って$\mathrm{in}$は同型射であり$\mathrm{in}^{-1} = \banana{F(\mathrm{in})}$
□
練習問題
練習として以下の様な事をやってみると良いと思います。
- 自然数・リスト以外のcatamorphismの導出
- 様々な再帰関数をcatamorphismで表す練習(全てが単純なcatamorphismで表せる訳ではありません。)
-
適当な関数を選んで以下の事実(証明は来週)を確認してみて下さい。$\pi_1$は積からの射影($\mathrm{fst}$)です。
- 任意の$f: N \rightarrow X$という型の関数($N$は自然数)は,適当な$g$によって $$ f = \pi_1\circ\banana{g} $$ と表せる。
- 任意の$f: [A] \rightarrow X$という型の関数は,適当な$g$によって $$ f = \pi_1\circ\banana{g} $$ と表せる。
第7回はここで終わります
お疲れ様でした。
来週の前半はプログラム意味論を目指して極限の続きをやります。
後半はより発展的・実用的なプログラム運算に関する各種定理について紹介します。
練習問題解答
catamorphismの導出を(本文中でも挙げましたが)自然数・リスト・二分木の例について説明します。
自然数のcatamorphism
自然数は函手$F(X) = 1+X$の始代数ですので、catamorphism $u$は左下の図を右の様に展開して $$ \begin{aligned} & u(\mathrm{zero}) = c \\ & u(\mathrm{succ}(n)) = f(u(n)) \end{aligned} $$ となります。

実装例
以下のfoldNが自然数に対するcatamorphismです。
--代数的データ型として自然数を定義する場合
-- data Nat = Zero | Succ Nat deriving (Show,Eq)
--
-- foldN :: (a -> a) -> a -> Nat -> a
-- foldN f c = u
-- where
-- u Zero = c
-- u (Succ n) = f (u n)
-- 組み込みの整数を使った場合
foldN :: (a -> a) -> a -> Int -> a
foldN f c = u
where
u 0 = c
u n = f (u (n-1))
-- 反射則より(xが自然数なら)
-- x == foldN (+ 1) 0 x
-- が成立します。
-- foldNでの他の関数の実装例
add x = foldN (+ 1) x
mul x = foldN (+ x) 0
pow x = foldN (* x) 1
-- 漸化式 a(n+1) = f(a(n)), a(0) = c
-- の一般解がfoldN c fとなります。
sqrt2 = foldN (\x -> (x+2/x)/2) 2
-- a(n+1) = (n+1)*a(n), a(0) = 1
-- の様なより一般的な漸化式は、foldNのみでは書けないですが、
-- fst . foldN f cの形に書くことが可能です。
fact = fst . foldN (\(c,n) -> (c*n, n+1)) (1, 1)
リストのcatamorphism
リストは函手$F(X) = 1+A\times X$の始代数ですので、catamorphism $u$は左下の図を右の様に展開して $$ \begin{aligned} & u(\mathrm{nil}) = c \\ & u(\mathrm{cons}(a,as)) = f(a,u(as)) \end{aligned} $$ となります。
実装例
以下のfoldrがリストに対するcatamorphismです。
import Prelude hiding (foldr,length,sum,product)
--代数的データ型としてリストを定義する場合
--data List a = Nil | Cons a (List a) deriving (Show,Eq)
--
--foldr :: (a -> b -> b) -> b -> List a -> b
--foldr f c = u
-- where
-- u Nil = c
-- u (Cons a as) = f a (u as)
-- 組み込みのリストを使った場合
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f c = u
where
u [] = c
u (a:as) = f a (u as)
-- 反射則より
-- x == foldr (:) [] x
-- が成立します。
-- foldrでの他の関数の実装例
length = foldr (\_ x -> x + 1) 0
sum = foldr (+) 0
product = foldr (*) 1
二分木のcatamorphism
葉(leaf)に値を持つタイプの二分木は函手$F(X) = A+X\times X$の始代数ですので、catamorphism $u$は左下の図を右の様に展開して $$ \begin{aligned} & u(\mathrm{leaf}(a)) = c(a) \\ & u(\mathrm{node}(l,r)) = f(u(l), u(r)) \end{aligned} $$ となります。
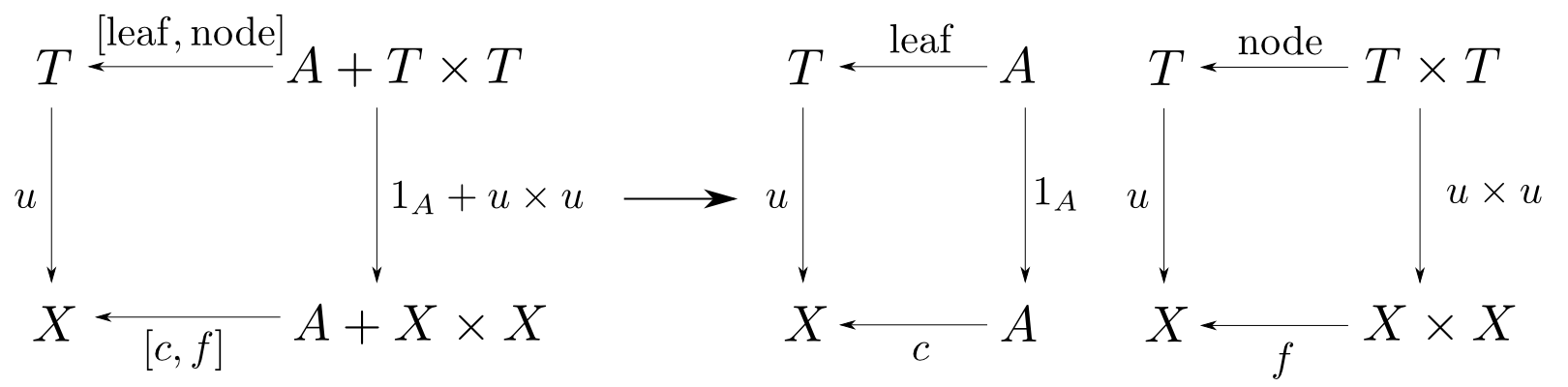
実装例
以下のfoldTが二分木に対するcatamorphismです。
import Prelude hiding (sum,product)
data BTree a = Leaf a | Node (BTree a) (BTree a) deriving (Show,Eq)
foldT :: (b -> b -> b) -> (a -> b) -> BTree a -> b
foldT f c = u
where
u (Leaf a) = c a
u (Node l r) = f (u l) (u r)
-- 反射則より
-- x == foldT Node Leaf x
-- が成立します。
size = foldT (+) (const 1)
sum = foldT (+) id
product = foldT (*) id