圏論勉強会
第4回
@ワークスアプリケーションズ
中村晃一2013年6月6日
謝辞
この勉強会の企画,会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この会について
- 圏論(category theory)を題材にいろんなことを学びます。
- 分かり易さを重視して初歩的な例を多用します。
- 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
- 中高生も数人見ているらしいのでプログラミングと関係が浅い内容も取り上げます。
- この資料はhttp://nineties.github.com/category-seminarに置いてあります。
第4回: 射で考える
第4回の内容
今回と次回は様々な概念を「圏論の言葉のみで述べる」方法について見ていきます。
記法について
- 第2回と同じく,2項演算子$\star$の第1引数,第2引数を定数に固定した関数を便宜的に以下の様に表す事にします。 $$ \color{red}{(a\ \star)} : x \mapsto a \star x $$ $$ \color{red}{(\star\ a)} : x \mapsto x \star a $$ 例えば $$ (2\ +)(3) = 2 + 3 \qquad (+\ 2)(3) = 3 + 2$$ という感じです。
Hom集合
クイズ
要素が1つの集合を単集合(singleton, unit set)と呼び$1$と表す事にします。
さて,$1$から他の集合$A$への関数はいくつあるでしょうか?
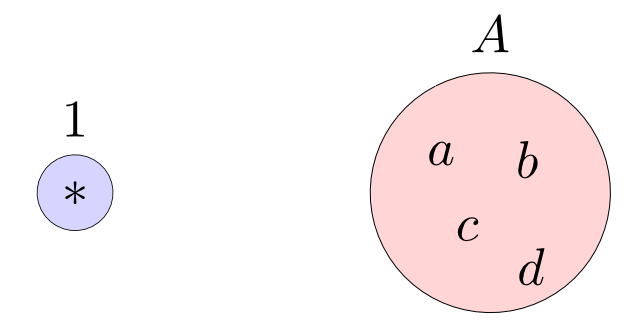
答え: $A$の要素と同じ数だけ存在する。
クイズ
要素が1つの集合を単集合(singleton, unit set)と呼び$1$と表す事にします。
さて,$1$から他の集合$A$への関数はいくつあるでしょうか?
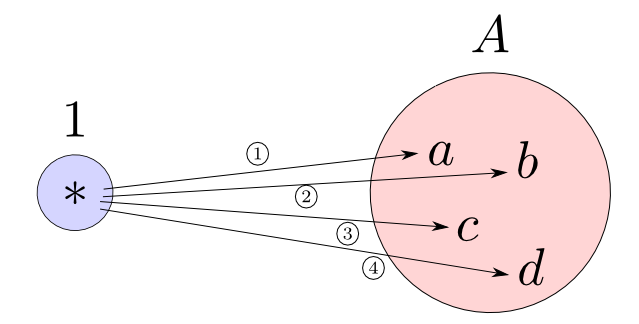
答え: $A$の要素と同じ数だけ存在する。
クイズ
では集合$A$から$1$への関数はいくつあるでしょうか?
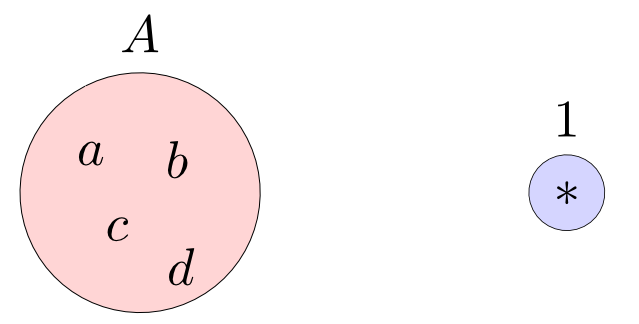
答え: 全ての要素を一点に移す唯一つの関数しか存在しない。
クイズ
では集合$A$から$1$への関数はいくつあるでしょうか?
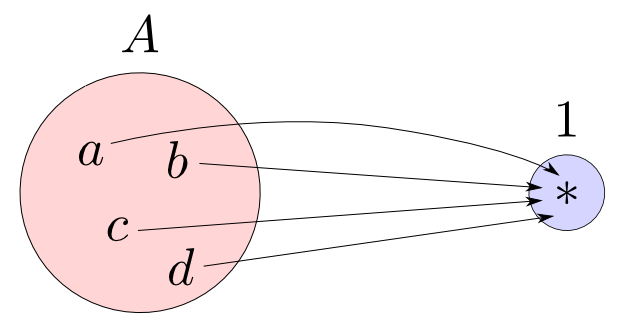
答え: 全ての要素を一点に移す唯一つの関数しか存在しない。
クイズ
要素が2つの集合$2$から他の集合$A$への関数はいくつあるでしょうか?
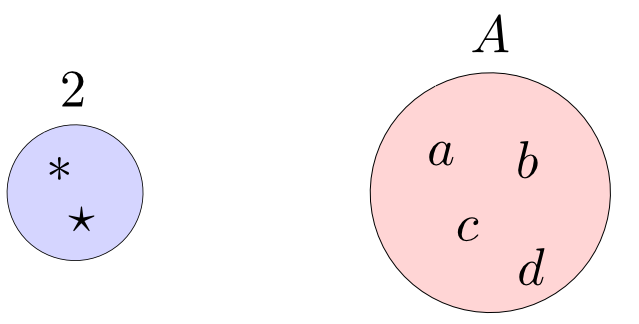
答え: $A$の要素の対(重複を許す)と同じ数だけ存在する。
クイズ
要素が2つの集合$2$から他の集合$A$への関数はいくつあるでしょうか?
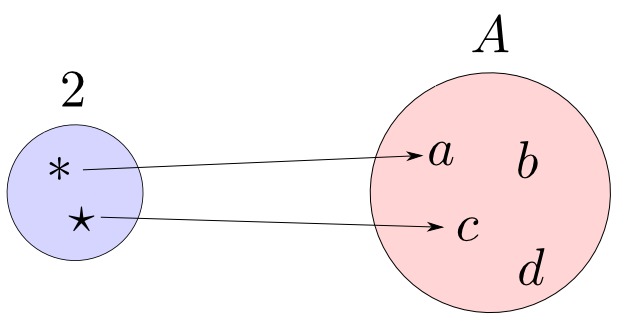
答え: $A$の要素の対(重複を許す)と同じ数だけ存在する。
クイズ
最後に,集合$A$から$2$への関数はいくつあるでしょうか?
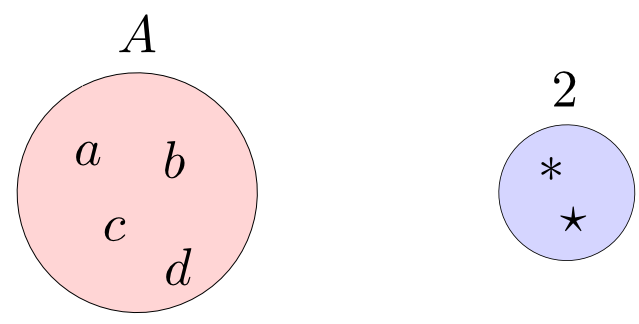
答え: $A$の部分集合の数だけ存在する。
クイズ
最後に,集合$A$から$2$への関数はいくつあるでしょうか?
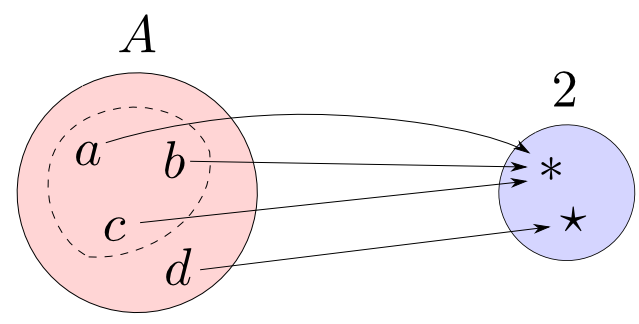
答え: $A$の部分集合の数だけ存在する。
関数空間
集合$A$から$B$への全ての関数の集合を関数空間(function space)と呼ぶ事にします。
今見た様に,関数空間の構造は$A$,$B$の構造により定まるということが言えます。今の場合の構造とは「要素の数」(正確には濃度)です。

Hom集合
圏$\mathbf{C}$において,対象$A$から対象$B$への射全てからなる集合を $$ \mathrm{Hom}_{\mathbf{C}}(A,B) $$ と表し,Hom集合(hom-set)と言う。 文脈から圏が明らかな場合には単に$\mathrm{Hom}(A,B)$と表す。
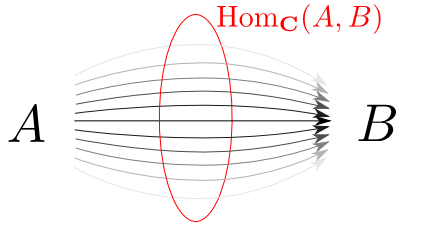
何故Hom集合が重要か
先ほど見たように$A$の要素と$\mathrm{Hom}_{\mathbf{Sets}}(1, A)$の要素を同一視出来ます。つまり,同型対応 $$ A \cong \mathrm{Hom}_{\mathbf{Sets}}(1, A) \quad \text{in $\mathbf{Sets}$}$$ があります。

何故Hom集合が重要か
ところで,圏論の基本語彙である「対象・射・合成」によって「$A$の要素(対象$A$の内部)」について述べる事はできません。
一方,$\mathrm{Hom}_{\mathbf{Sets}}(1, A)$の要素は射ですので,その中身については圏論の言葉で説明できます。つまり,この仕組みによって「圏論の言葉」のみで「対象の内部」について述べる事が出来るようになるのです。
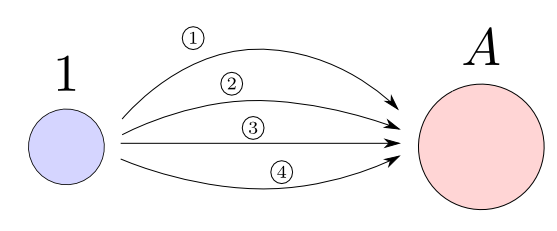
対象の内部構造が,それを取り囲む射の集合の構造として圏の中に見える形で顕れます。
逆に言うと,圏が定まるとその中で観察可能な事象が決まります。
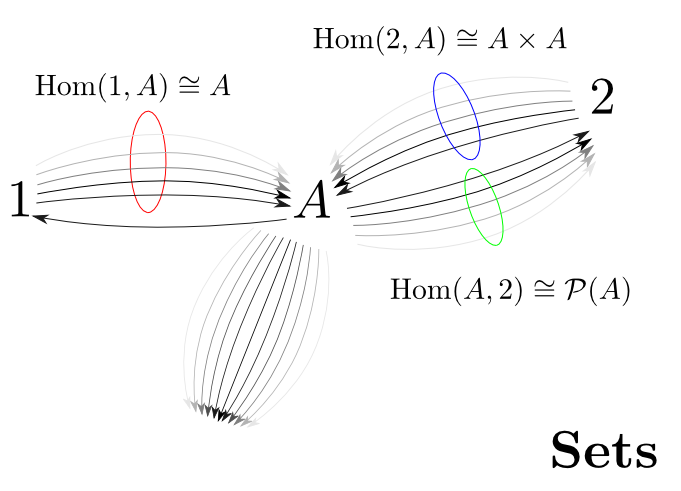
何故Hom集合が重要か
このように$\mathrm{Hom}(A,B)$は「射」によって「$A$や$B$の内部構造」について述べる為の道具となります。
また一般に,$\mathrm{Hom}(A,B)$は$A$,$B$自体よりも豊かな構造を持ちますので,Hom集合自体が探求の対象となる事もあります。
最後に,任意の圏$\mathbf{C}$の任意の対象$A$,$B$について$\mathrm{Hom}_{\mathbf{C}}(A,B)$は$\mathbf{Sets}$の対象つまり集合である事に注意しましょう。$\mathbf{C}$に関する議論の舞台を$\mathbf{Sets}$に移すという役割にも使います。
Hom集合の例
例1
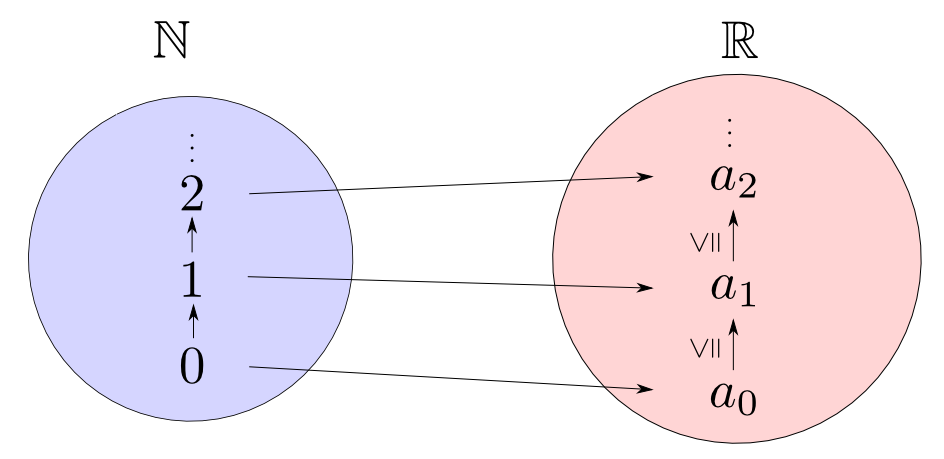
$$ \mathrm{Hom}_{\mathbf{Sets}}(\mathbb{N},\mathbb{R}) $$ の要素は任意の無限長の実数列と一対一に対応(以後省略)します。
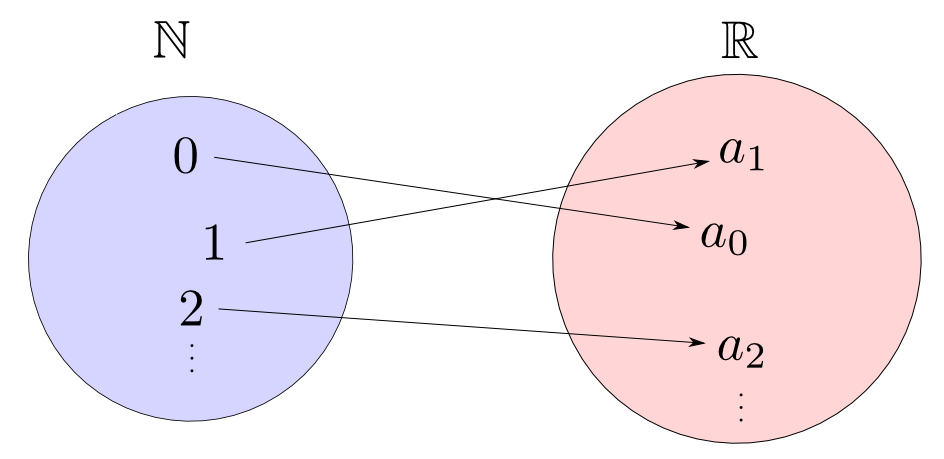
例2
半順序集合と単調関数からなる圏を$\mathbf{Pos}$(Category of partially ordered sets)と表す事にすると $$ \mathrm{Hom}_{\mathbf{Pos}}(\mathbb{N},\mathbb{R}) $$ の要素は任意の単調増加実数列です。
例3
【線形代数既習者向けの例】
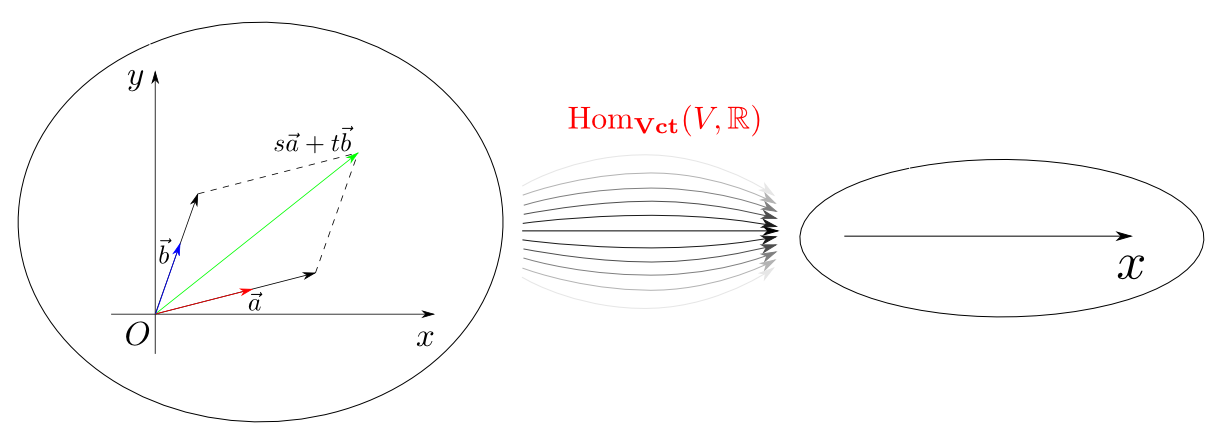
ベクトル空間(とりあえず実数係数)と線形写像からなる圏を$\mathbf{Vct}$と表す事にします。
すると任意のベクトル空間$V$について $$ \mathrm{Hom}_{\mathbf{Vct}}(V, \mathbb{R})$$ は$V$の双対ベクトル空間$V^{*}$です。
例4
$\mathbb{N}_{+}$を自然数と加法からなるモノイド, $\mathbb{Z}_{\times}$を整数と乗法からなるモノイドとして, $$ \mathrm{Hom}_{\mathbf{Mon}}(\mathbb{N}_{+},\mathbb{Z}_{\times}) $$ つまり$\mathbb{N}_{+}$から$\mathbb{Z}_{\times}$への全ての準同型写像の集合を考えます。
さて,$ \mathrm{Hom}_{\mathbf{Mon}}(\mathbb{N}_{+},\mathbb{Z}_{\times}) $は$\mathbb{N}_{+}$や$\mathbb{Z}_{\times}$の構造をどう反映しているでしょうか?

例えばある準同型$f \in \mathrm{Hom}_{\mathbf{Mon}}(\mathbb{N}_{+},\mathbb{Z}_{\times})$が $$ f(1) = 2 $$ を満たすとしましょう。
このような準同型は $$ f(n) = 2^n $$ しか有り得ません。(何故でしょうか?)
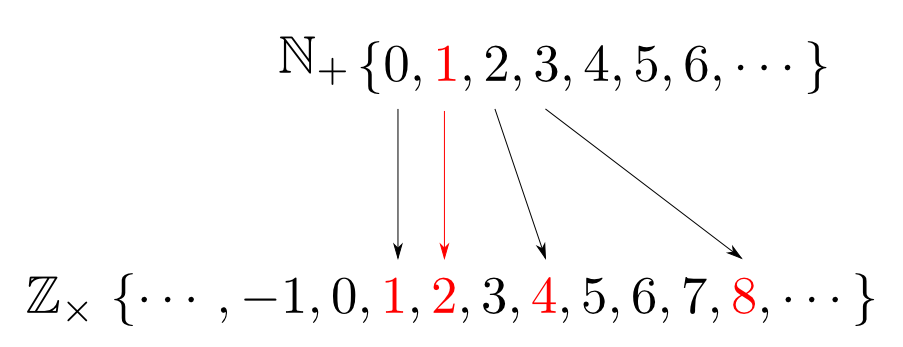
詳しい証明は省略しますが,任意の整数$a \in \mathbb{Z}$に対して $$ f(1) = a $$ を満たす$f \in\mathrm{Hom}_{\mathbf{Mon}}(\mathbb{N}_{+},\mathbb{Z}_{\times})$が唯一つ存在します。
つまり, $$\mathrm{Hom}_{\mathbf{Mon}}(\mathbb{N}_{+},\mathbb{Z}_{\times}) \cong \mathbb{Z} \qquad\text{in $\mathbf{Sets}$}$$ という事です。
$\mathbb{N}_{+}$と$\mathbb{Z}_{\times}$の構造がHom集合の構造を決めている事がよくわかります。
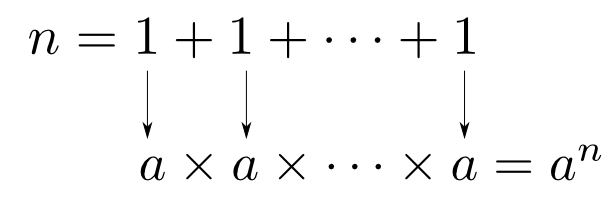
例5
$\mathbf{Hask}$圏におけるHom集合 $$ \mathrm{Hom}_{\mathbf{Hask}}(A,B) $$ は$A\rightarrow B$型の関数の集合となります。
関数型言語のHom集合を観察すると面白い事が解ります。 同時にプログラミング言語特有の厄介さにも触れておきます。
-- 以下の説明では、有限時間で停止して値を返し副作用なども持たない関数のみを考えます。
-- まず Integer -> () という型の関数を考えます。
-- ()というのは同じ記号()で表される値を一つしか持たない型です。
-- f :: Integer -> ()
-- f x = ..... どんな実装が可能か? ...
-- 字面の違いはあれ、どのような実装も以下の実装と等価である事が判ると思います。
f :: Integer -> ()
f x = ()
-- 同様に () -> Integerという型の関数は
one :: () -> Integer
one () = 1
-- のように定数値を返す関数しか存在しません。
-- 「全ての関数が~の形である」と述べられる事になります。
-- これらの例から判る事は「型」が具体的な実装方法にまで、思いの外影響している
-- という事です。
-- 上手く型を設計する事によって実装の複雑性が増加するのを防ぐ事が出来ます。
-- また,関数の性質について調べる事が容易になります。
-- 有限時間で停止しない関数なども考えると
g :: Integer -> ()
g x = g x
-- のような新たな関数を考える事が出来てしまいます。
-- プログラミングにおける関数は「部分関数」といって,常に値を返すものばかりでは
-- 無いためこのような事が起きます。詳しくは後の回に改めて説明します。
Hom集合に構造を入れる
Hom集合に構造を入れる
$\mathrm{Hom}_{\mathbf{C}}(X,A)$はただの集合です。
しかし,$A$がモノイドや群や順序などの構造を持っている場合 $\mathrm{Hom}_{\mathbf{C}}(X,A)$にも同じ構造を入れる事が出来ます。

$M$がモノイド$\Rightarrow$$\mathrm{Hom}(X,M)$もモノイド
例えば集合$M$が演算$\cdot$によってモノイドになるとしましょう。また集合$X$を固定します。
この時,任意の$f, g \in \mathrm{Hom}_{\mathbf{Sets}}(X,M)$に対して $$ (f \cdot g)(x) = f(x)\cdot g(x) $$ によって各点ごとに(pointwiseに)演算$f\cdot g$を定義します。
例1
例えば自然数の集合$\mathbb{N}$に加法によってモノイドの構造を入れると,$\mathrm{Hom}_{\mathbf{Sets}}(2,\mathbb{N})$の要素にも加法を定義出来ます。
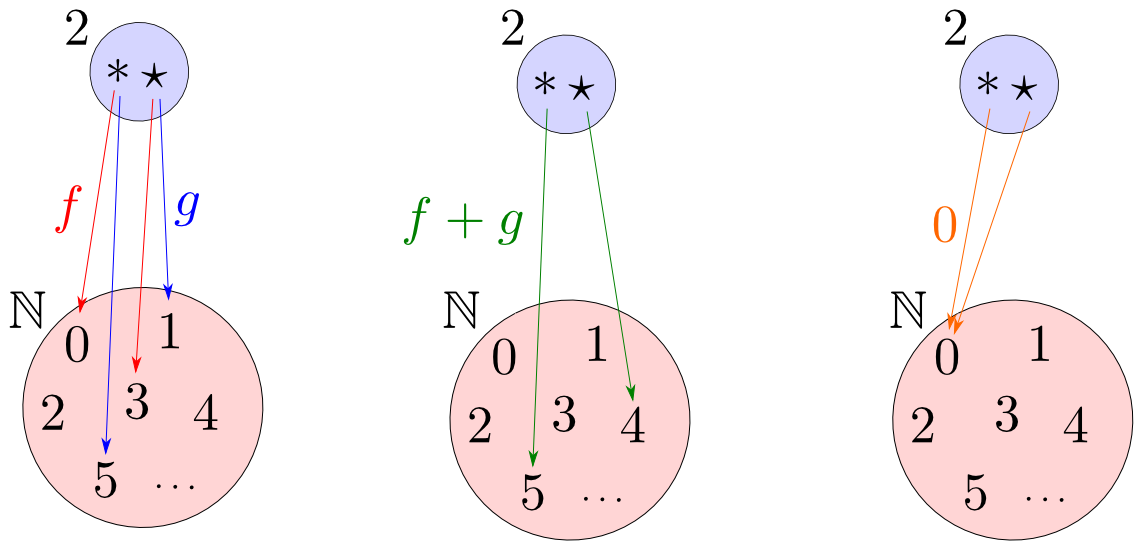
$A$が半順序集合$\Rightarrow$$\mathrm{Hom}(X,A)$も半順序集合
集合$A$が何らかの順序$\leqq$によって半順序集合になるとします。
この時,任意の$f, g \in \mathrm{Hom}_{\mathbf{Sets}}(X,A)$に対して $$\text{任意の$x$について}f(x) \leqq g(x) \text{の時のみ} f\leqq g$$ と定義する事によって$\mathrm{Hom}_{\mathbf{Sets}}(X,A)$が半順序集合になります。
例2
例えば下図において$\mathbb{N}$に自然数の通常の順序を入れると,$f(*)\leqq g(*)$かつ$f(\star)\leqq g(\star)$なので$f \leqq g$となります。
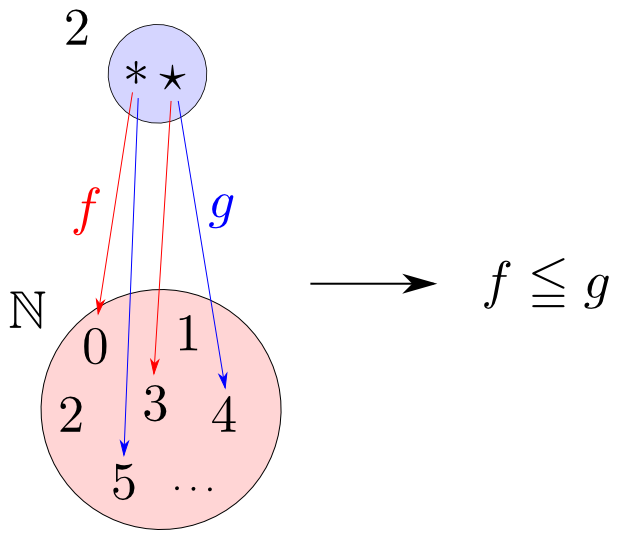
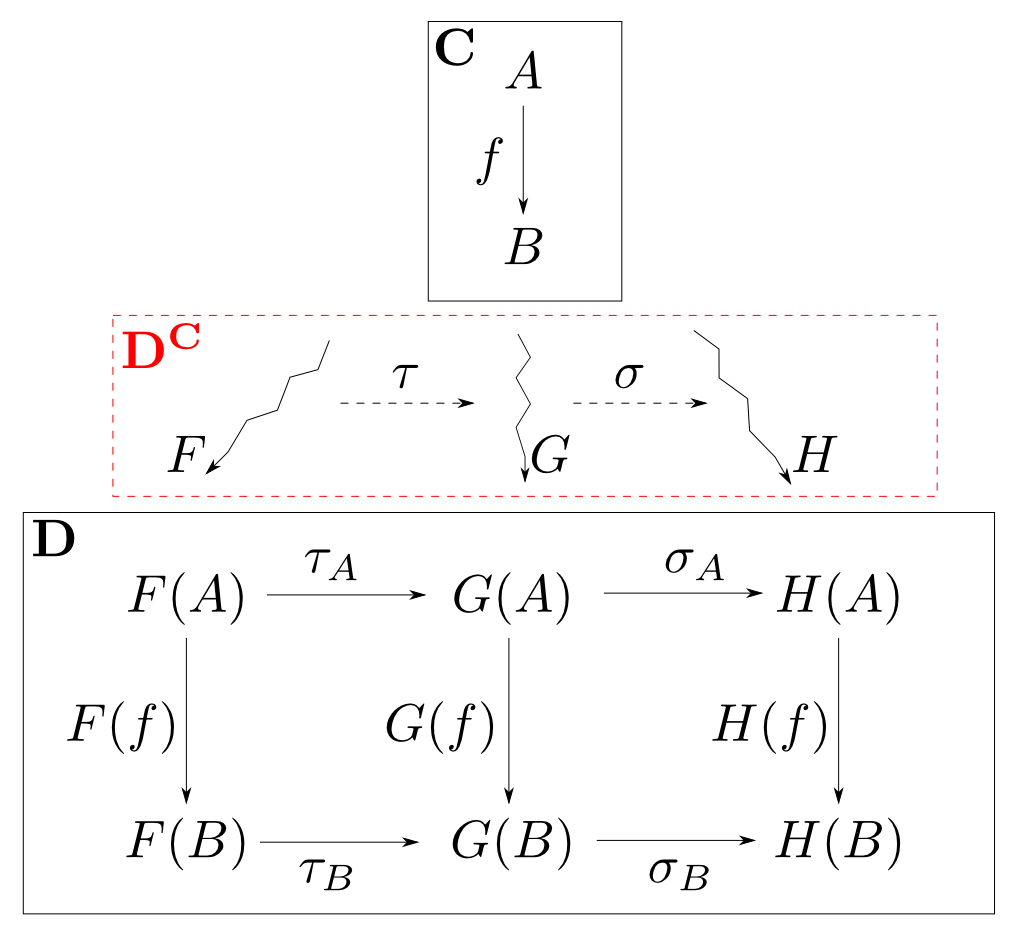
前回やった函手圏$\mathbf{D}^{\mathbf{C}}$の構成は,$\mathrm{Hom}(A,B)$に$B$の構造を入れるという事の圏論的な一般化になっています。
今の2例を函手圏として説明する事は良い練習になると思います。時間があれば,当日確認してみます。
generalized element
様々なセッティングによって$\mathrm{Hom}(X,A)$を「$A$そのもの」「$A$の対の集合」「モノイド」「半順序集合」などと見なせる事を見ました。 もはや$\mathrm{Hom}(X,A)$の要素を「射」のイメージでは考えていません。
特に任意の射$a: X\rightarrow A$を$A$の構成要素と思う視点は重要で,この意味で射$a$の事を$A$のgeneralized elementと呼ぶ事があります。
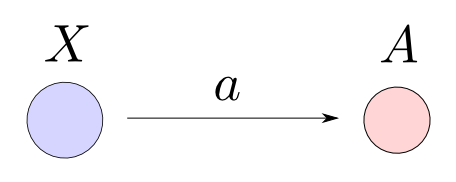
point-free style
ところで関数型言語ではpoint-free styleという関数と合成でプログラムを書くスタイルがあります。言い方を変えればpoint-free styleとは型の圏の「射」のみでプログラムを表現するという事に他なりません。
人間が読むのには適していない場合もありますが,プログラムを圏論の枠組みで扱う場合に必要となります。
h x = f (g x) -- not point-free
h = f . g -- point-free
Hom函手
対象$X$を固定して,$A$を$\mathrm{Hom}_{\mathbf{C}}(X, A)$に移して考えるということの重要性は何となく解ってもらえたのではないかと思います。 この$\mathbf{C}$の対象と$\mathbf{Sets}$の対象の対応を $$ \mathrm{Hom}_{\mathbf{C}}(X, -): \mathbf{C}\rightarrow \mathbf{Sets} $$ と表す事にします。

次は$\mathbf{C}$の射と$\mathbf{Sets}$の射の上手い対応を考えましょう。 $\mathbf{C}$を$\mathbf{Sets}$に移す函手が得られるはずです。
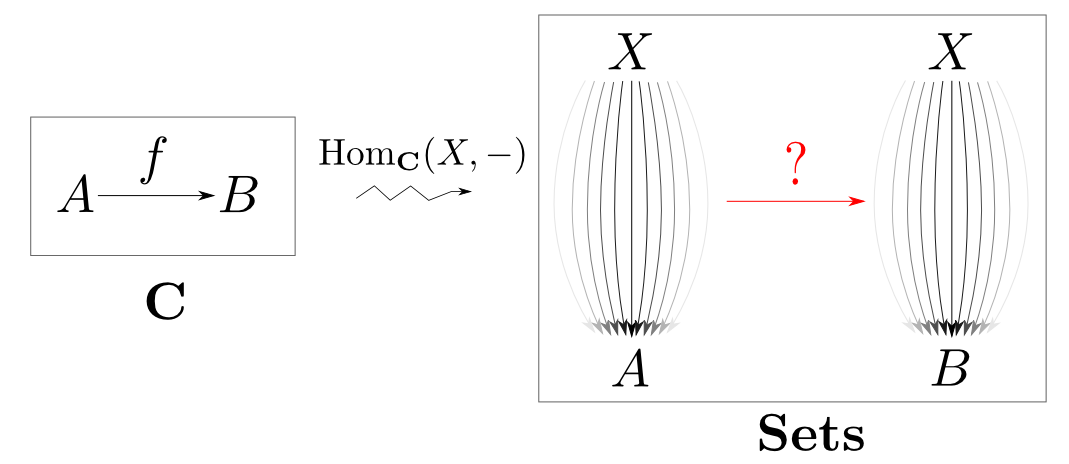
まず,$\mathbf{C} = \mathbf{Sets}$,$X = 1$のケースを考えてみます。
$\mathrm{Hom}_{\mathbf{Sets}}(1, A)$の射は$A$の要素と一対一に対応するのでした。 そこで下図の関数$a$がどのような関数に移るべきか?を考えます。
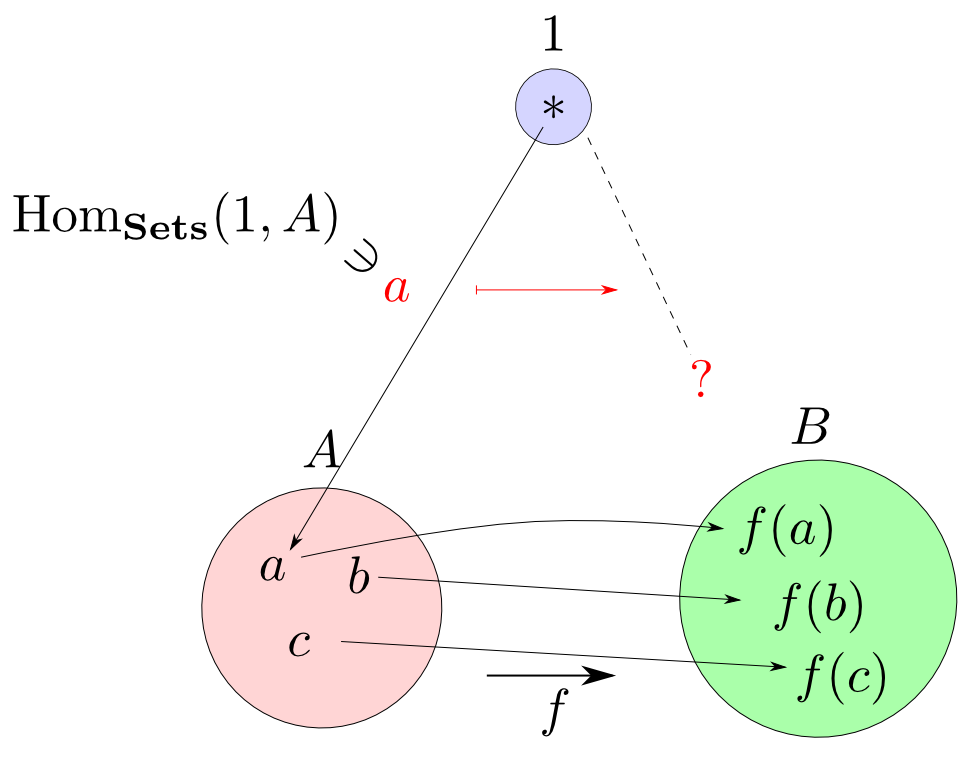
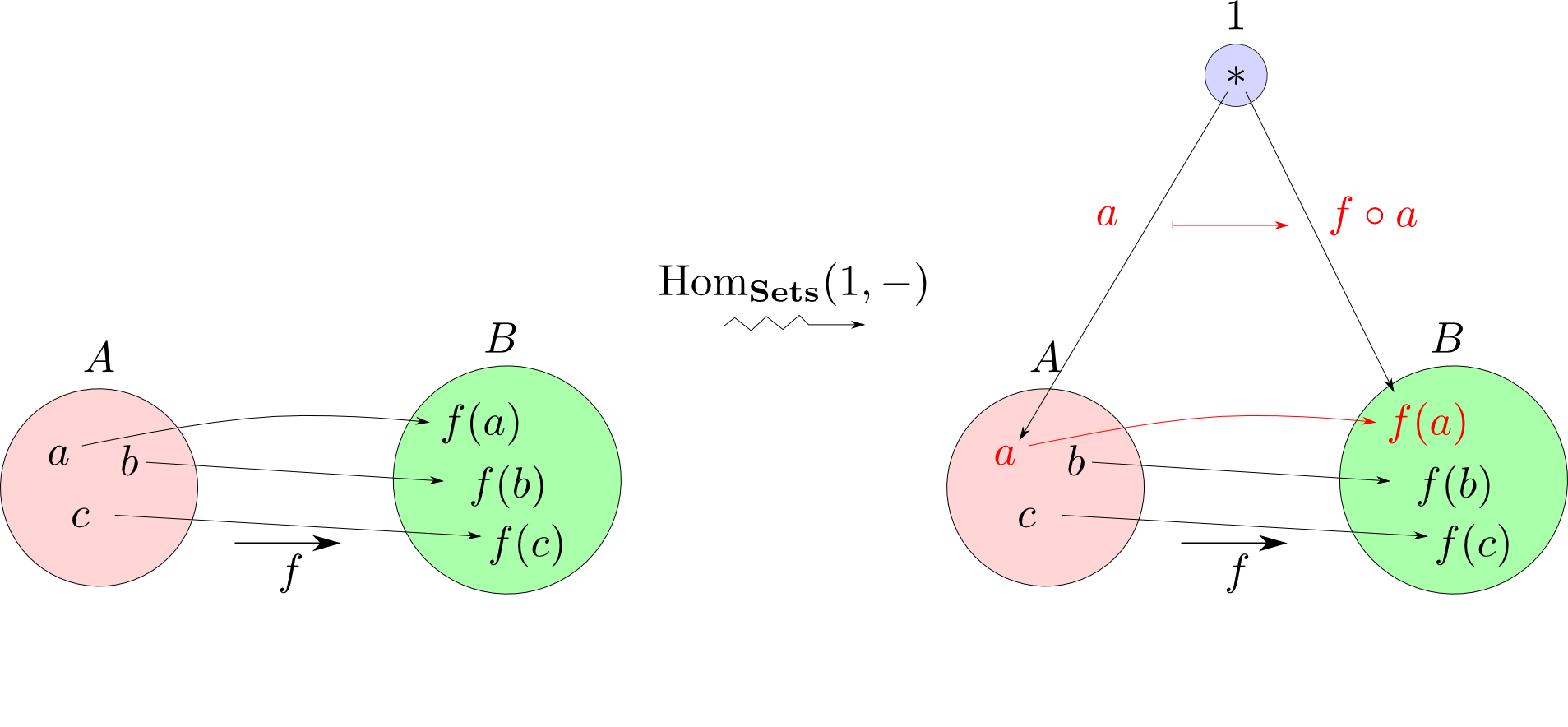
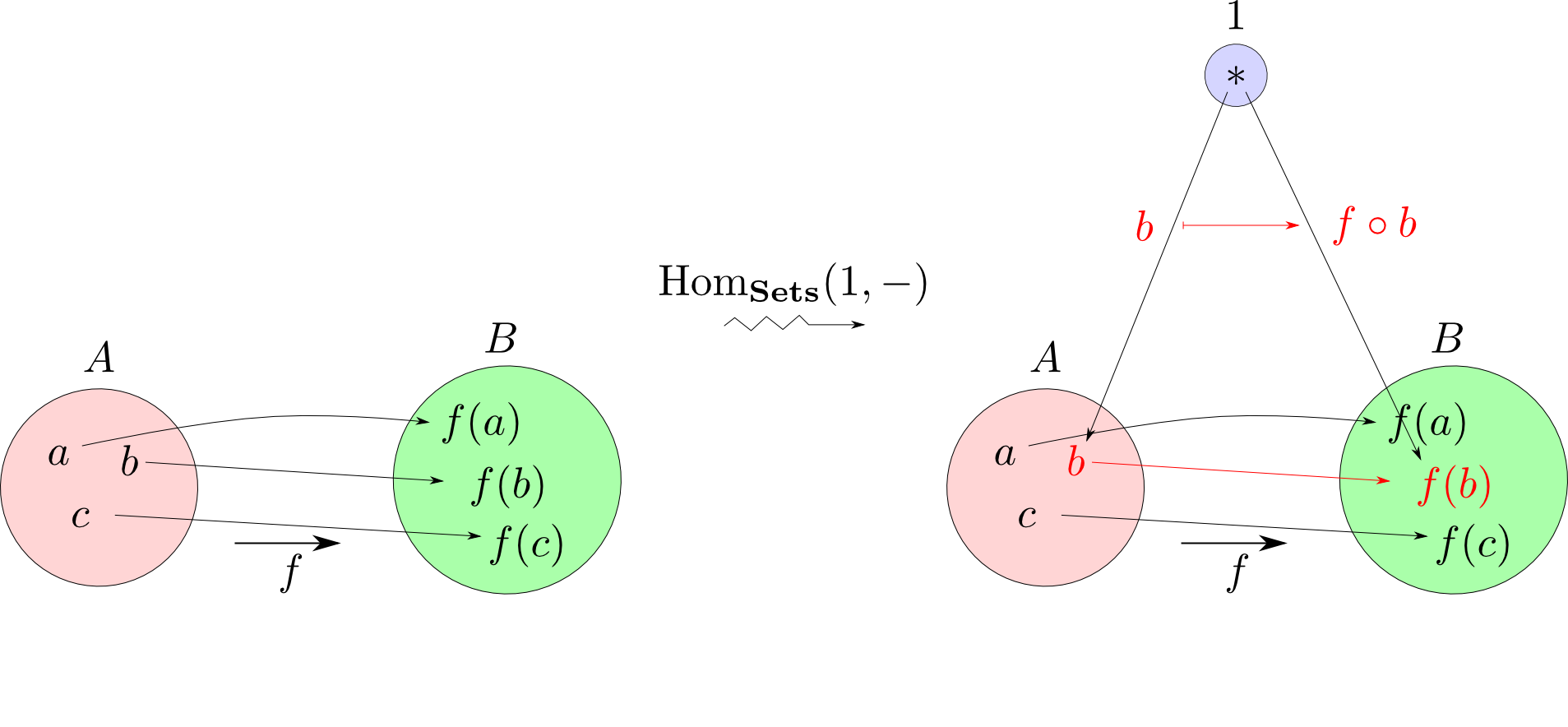
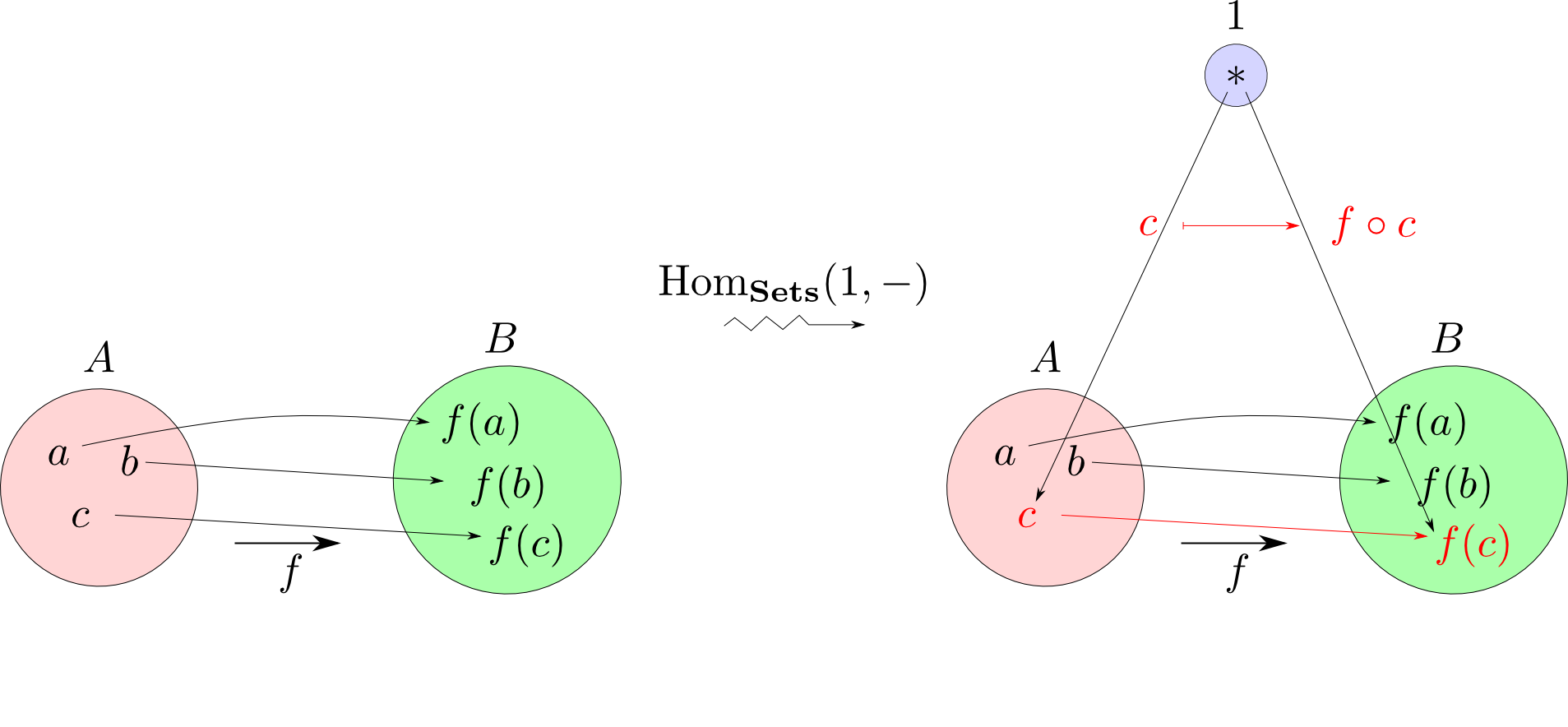
まとめると $$ \begin {align} & a \longmapsto f\circ a \\ & b \longmapsto f\circ b \\ & c \longmapsto f\circ c \\ \end{align} $$ などと移される事になります。
つまり,射$f: A\rightarrow B$をHom集合の世界に自然に移すと左から$f$を合成するという関数$(f\ \circ)$に移る事になります。
$1$の代わりに任意の集合$X$を取った場合の状況を絵にしてみると,下のようになります。
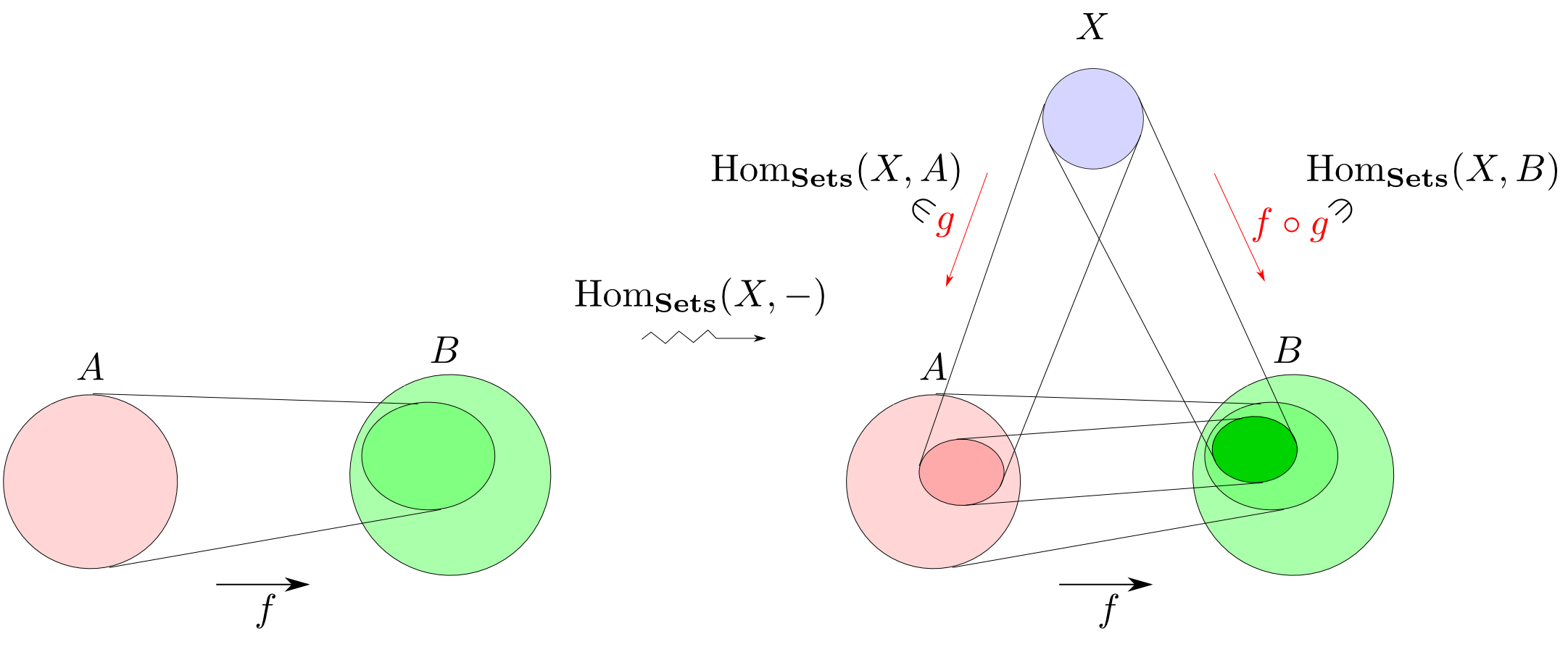
射$f$を「左から$f$を合成する関数」に移すという話は第2回にも登場しました。
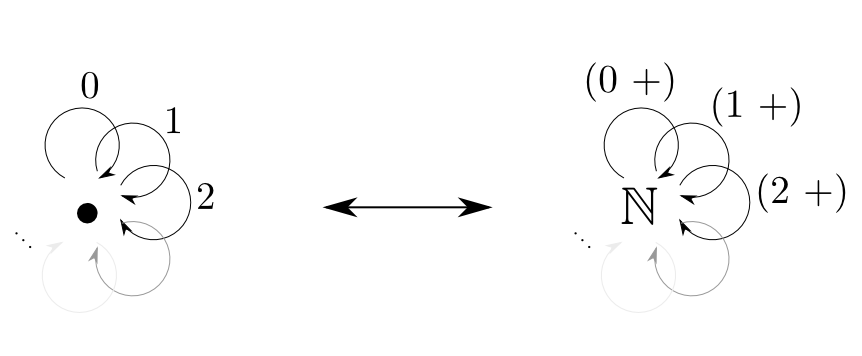
$\mathbf{C}$として対象が一つ($\bullet$とします)の圏,つまりモノイドを取った場合を考えます。対象が一つしかないのでドメインには$\bullet$を固定し $$ \mathrm{Hom}_{\mathbf{C}}(\bullet, -): \mathbf{C} \rightarrow \mathbf{Sets} $$ を考えます。$\mathbf{C}$における射の合成演算子を$\cdot$と表す事にします。
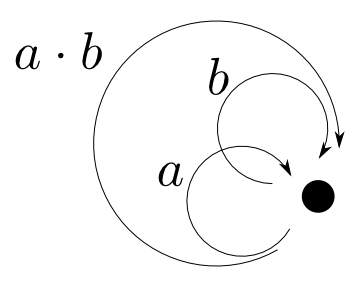
すると$\mathbf{C}$の対象$\bullet$は$\mathrm{Hom}_{\mathbf{C}}(\bullet, \bullet)$,つまり$\mathrm{End}_{\mathbf{C}}(\bullet)$に移り,$\mathbf{C}$の射$a$が関数$(a\ \ \cdot)$に移ることになります。

具体例を2つ見ましたが,まとめると$\mathbf{C}$に対象$X$を固定し
- $\mathbf{C}$の対象$A$を集合$\mathrm{Hom}_{\mathbf{C}}(X,A)$に移し,
- $\mathbf{C}$の射$f$を関数$(f\ \ \circ)$に移す
という対応は函手になりそうです。
定義を確認し,証明をしてみましょう。
共変Hom函手
$\mathbf{C}$の対象$X$を固定して
- $\mathbf{C}$の対象$A$に集合$\mathrm{Hom}(X, A)$を対応させ
- $\mathbf{C}$の射$f: A\rightarrow B$に,「左から$f$を合成する」という関数 $$ \mathrm{Hom}(X, f) = (f\ \ \circ): \mathrm{Hom}(X,A) \rightarrow \mathrm{Hom}(X, B)$$ を対応させる
事は函手である。これを共変Hom函手(covariant hom-functor)と言い,$ \mathrm{Hom}(X, -): \mathbf{C} \rightarrow \mathbf{Sets} $と表す。

函手である事の証明
$\mathbf{C}$での射の合成を$\cdot$,$\mathbf{Sets}$での合成を$\circ$と表す事にする。
【射の合成関係を保つ事】
任意の$\mathbf{C}$の射$g:A\rightarrow B$,$f:B\rightarrow C$と任意の射$h: X\rightarrow A$について
$$\begin{aligned}
& \mathrm{Hom}_{\mathbf{C}}(X, f\cdot g)(h) = ((f\cdot g)\ \ \cdot)(h) = f\cdot g\cdot h \\
& \mathrm{Hom}_{\mathbf{C}}(X, f)\circ \mathrm{Hom}_{\mathbf{C}}(X, g)(h) = (f\ \ \cdot)\circ(g\ \ \cdot)(h) = (f\ \ \cdot)(g\cdot h) = f\cdot g\cdot h
\end{aligned} $$
すなわち$\mathrm{Hom}_{\mathbf{C}}(X,f\cdot g)=\mathrm{Hom}_{\mathbf{C}}(X,f)\circ\mathrm{Hom}_{\mathbf{C}}(X,g)$
【恒等射を保つ事】
任意の$\mathbf{C}$の恒等射$1_A:A\rightarrow A$と任意の射$h:X\rightarrow A$について
$$ \mathrm{Hom}_{\mathbf{C}}(X,1_A)(h) = 1_A\cdot h = h$$
すなわち$\mathrm{Hom}_{\mathbf{C}}(X,1_A) = 1_{\mathrm{Hom}_{\mathbf{C}}(X,A)}$
以上より$\mathrm{Hom}_{\mathbf{C}}(X,-)$は函手である。□
アナロジー的に
- 対象$A$を$\mathrm{Hom}_{\mathbf{C}}(A, X)$に移し
- 射$f$を「右から$f$を合成する」という関数に移す
という対応$\mathrm{Hom}_{\mathbf{C}}(-, X)$を考えて見ましょう。
第2回にも似た事をしました。モノイドの要素を右からの作用に移した時は関数合成の順番を逆にする事によって演算の順序を保ったのでした。
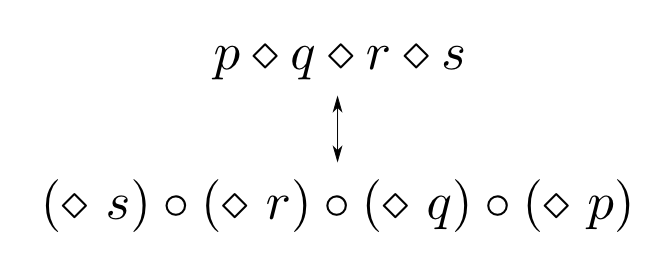
射$f: A\rightarrow B$を右から合成するということはBの側に繋げるという事になります。

すると$\mathrm{Hom}_{\mathbf{C}}(-,X)$による対応付けの様子は下図の様になり, $A$から$B$への射が$\mathrm{Hom}_{\mathbf{C}}(B,X)$から$\mathrm{Hom}_{\mathbf{C}}(A,X)$への射に移ります。
ドメインとコドメインの順序を保っていないので,これは(今までの意味での)函手になっていません。
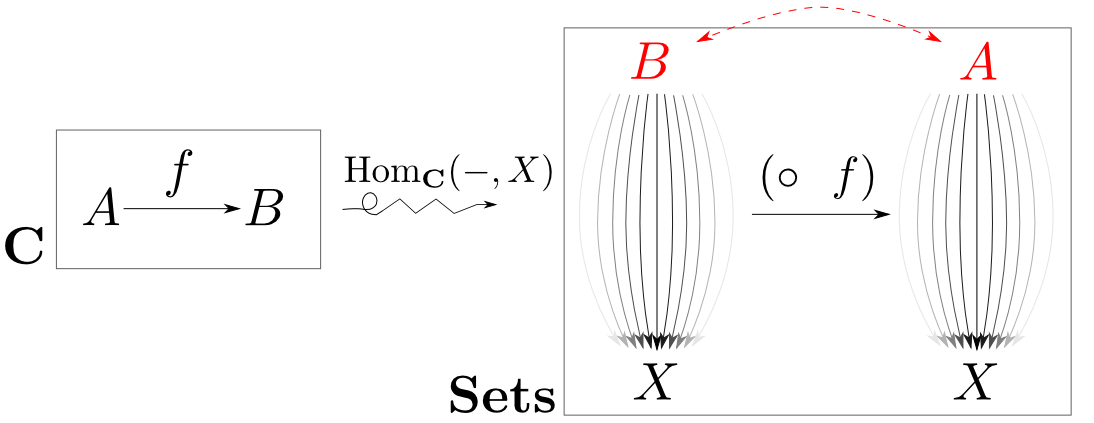
ここで$\mathbf{C}$の射の向きを全て逆向きにした双対圏(opposite category)$\mathbf{C}^{\mathrm{op}}$を考えると,ドメインとコドメインの順序が保たれた対応関係になります。

このように一方を双対圏にすると函手$F:\mathbf{C}^{\mathrm{op}}\rightarrow \mathbf{D}$となる対応$F$を$\mathbf{C}\rightarrow\mathbf{D}$への反変函手(contravariant functor)と言います。
今まで函手と呼んでいたものは正確には共変函手(covariant functor)と呼ばれます。
反変Hom函手
$\mathbf{C}$の対象$X$を固定して
- $\mathbf{C}$の対象$A$に集合$\mathrm{Hom}(A, X)$を対応させ
- $\mathbf{C}$の射$f: A\rightarrow B$に,「右から$f$を合成する」という関数 $$ \mathrm{Hom}(f, X) = (\circ\ \ f): \mathrm{Hom}(B,X) \rightarrow \mathrm{Hom}(A,X)$$ を対応させる
事は反変函手である。これを反変Hom函手(contravariant hom-functor)と言い,$ \mathrm{Hom}(-, X): \mathbf{C}^{\mathrm{op}} \rightarrow \mathbf{Sets} $と表す。

反変Hom函手が実際に$\mathbf{C}^{\mathrm{op}}$から$\mathbf{Sets}$への函手になっている事の証明は,共変Hom函手の場合と殆ど同じなので省略します。良い練習になりますのでやってみて下さい。
第4回はここで終わります
お疲れ様でした。
非常に難しい内容だったと思いますが,ここを乗り越えると今後の学習が大分楽になると思います。本資料では情報量が少ないですので、テキストを読み練習問題を解く事をお薦めします。
今回はHom集合という形で様々な射をひっくるめて考えましたが,射には同型射・モノ射・エピ射・(様々な)普遍射など特徴的なものが沢山あります。次回はそのような話をする予定です。