パターン認識・
機械学習勉強会
第4回
@ワークスアプリケーションズ
中村晃一2014年3月6日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
ギブスサンプリング
技術的な話題が続いて申し訳ないのですが, 大変重要なランダムサンプリング手法である ギブスサンプリング (Gibbs sampling, GS) を紹介します.
ギブスサンプリングは前回紹介したメトロポリス・ヘイスティングス法(MH法)の特別な場合と見なす事が出来ます.
二変数の分布 $\pi(x,y)$ からサンプリングを行いたいとします.
MCMCでは, マルコフ連鎖 \[ (x_0,y_0)\rightarrow (x_1,y_1)\rightarrow (x_2,y_2)\rightarrow\cdots \] を生成しますが, この1ステップ $(x_n,y_n) \rightarrow (x_{n+1},y_{n+1})$ を
\[ (x_n,y_n) \rightarrow (x_{n+1},y_n) \rightarrow (x_{n+1},y_{n+1}) \] と分解します.
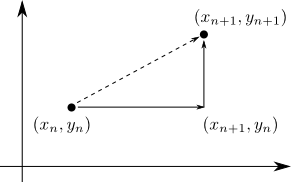
$\pi(x,y)$ において $y=y_n$ と固定すれば \[ \pi(x, y_n)\propto \pi(x|y_n) \] となります. これから $x_{n+1}$ をサンプリングして, $(x_n,y_n)\rightarrow (x_{n+1},y_n)$ の推移を行います.
$(x_n,y_n)\rightarrow (x_{n+1},y_n)$ の推移では, (目標分布からサンプルを生成しているので当然)詳細釣り合い条件が成立します.
$(x_{n+1},y_n)\rightarrow (x_{n+1},y_{n+1})$ の推移でも同様です.
まとめると
- $\pi(x|y_n)$ に従って $x_{n+1}$ を選ぶ.
- $\pi(y|x_{n+1})$ に従って $y_{n+1}$ を選ぶ.
という手順によって $(x_n,y_n)\rightarrow (x_{n+1},y_{n+1})$ の推移を行います.

2変数以外の場合に一般化すると, 以下のようになります.
ギブスサンプリング
目標分布 $\pi(x_1,x_2,\ldots,x_m)$ に対して, マルコフ連鎖の1ステップ $(x_1,x_2,\ldots,x_m)\rightarrow (x_1',x_2',\ldots,x_m')$ を以下の手順で行う.
- $\pi(x_1'|x_2,x_3,x_4,\ldots,x_m)$ に従い $x_1'$ を生成
- $\pi(x_2'|x_1',x_3,x_4,\ldots,x_m)$ に従い $x_2'$ を生成
- $\pi(x_3'|x_1',x_2',x_4,\ldots,x_m)$ に従い $x_3'$ を生成
- $\cdots$
- $\pi(x_m'|x_1',x_2',x_3',\ldots,x_{m-1}')$ に従い $x_m'$ を生成
ギブスサンプリングは, 条件付き分布 \[ \pi(x_i'|x_1',x_2',\ldots,x_{i-1}',x_{i+1},\ldots,x_m) \] に従うサンプリングが可能であるならば,
- 提案分布 $q(\mathbf{x}'|\mathbf{x})$ が不要.
- サンプルが全て採択される.
という非常に単純なMH法です.
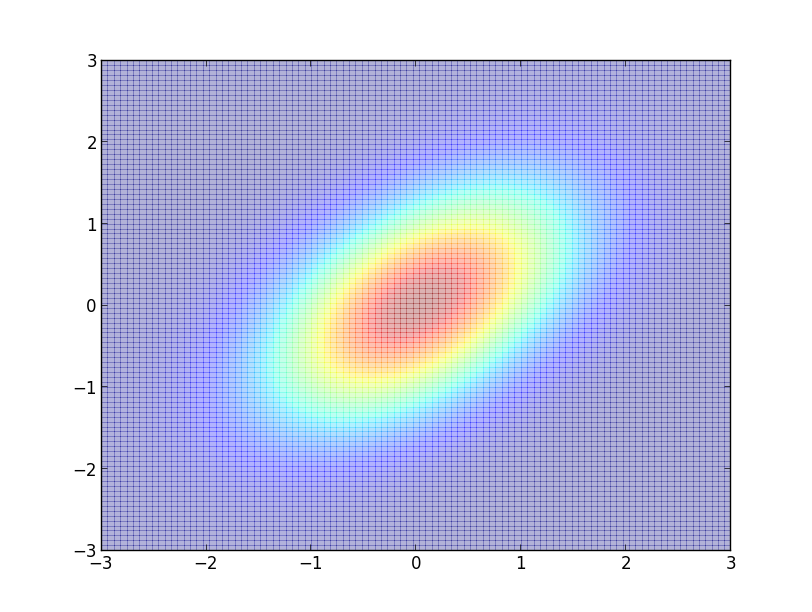
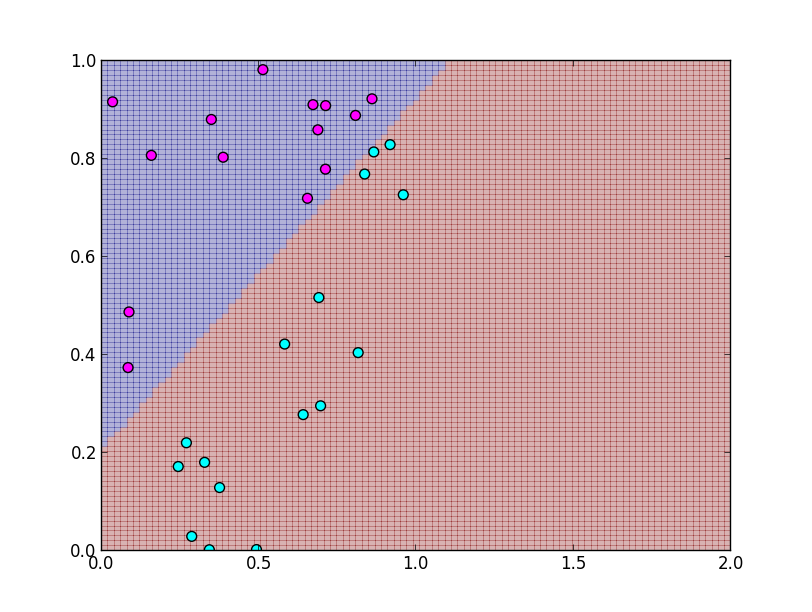
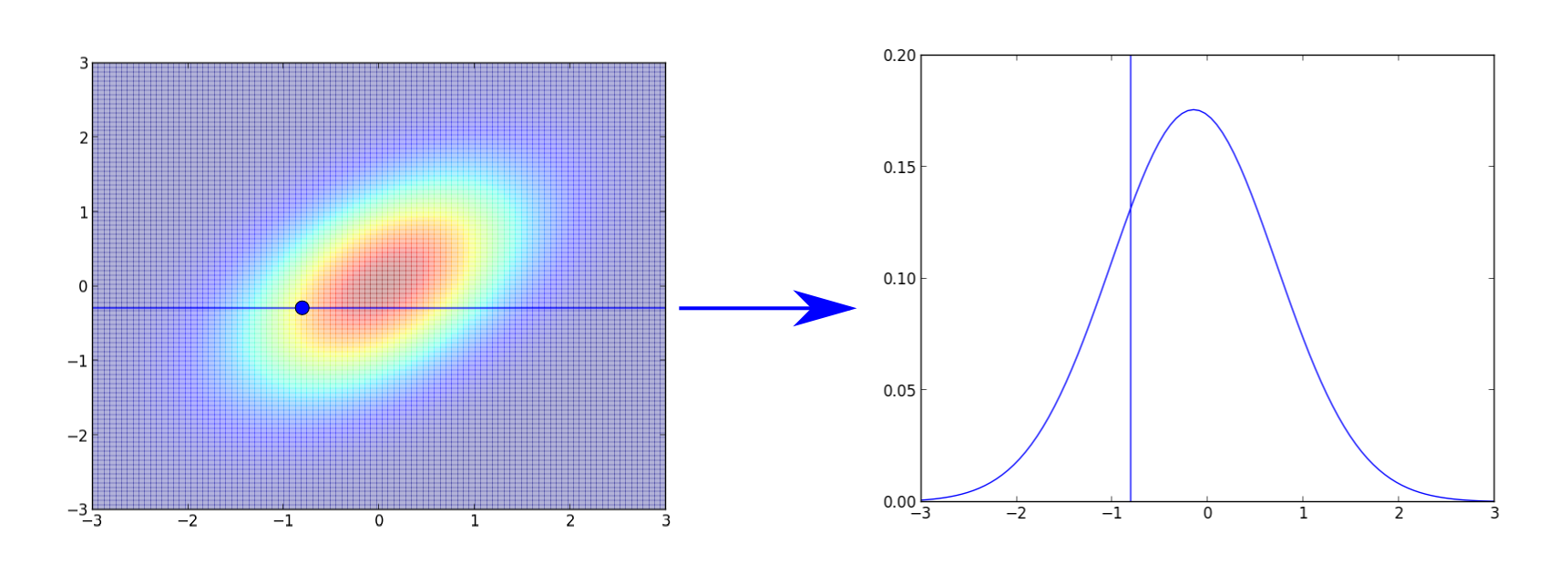
簡単な例として, 前回と同じく二次元正規分布 \[ \small{ \mathcal{N}\left(\mathbf{0}, \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \right)} \] からサンプリングしてみます(下図は $\rho=0.5$).

この場合 \[ \pi(x,y) \propto \exp\left\{-\frac{1}{2(1-\rho^2)}(x^2-2\rho xy+y^2)\right\} \] なので, $y$ を固定すると \[ \pi(x|y)\propto\pi(x,y)\propto\exp\left\{-\frac{1}{2(1-\rho^2)}(x-\rho y)^2\right\} \] つまり, $\pi(x|y)=N(\rho y, 1-\rho^2)$ となります. 同様に $\pi(y|x)=N(\rho x, 1-\rho^2)$ です.
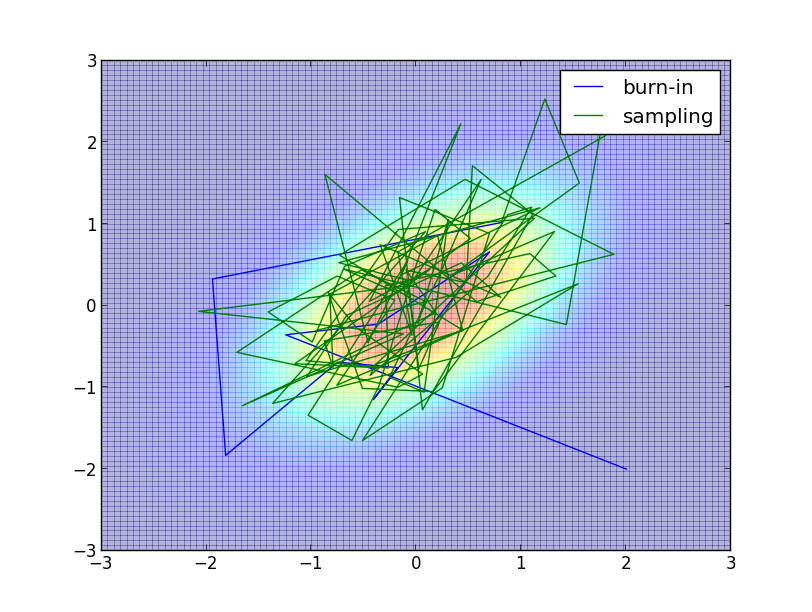
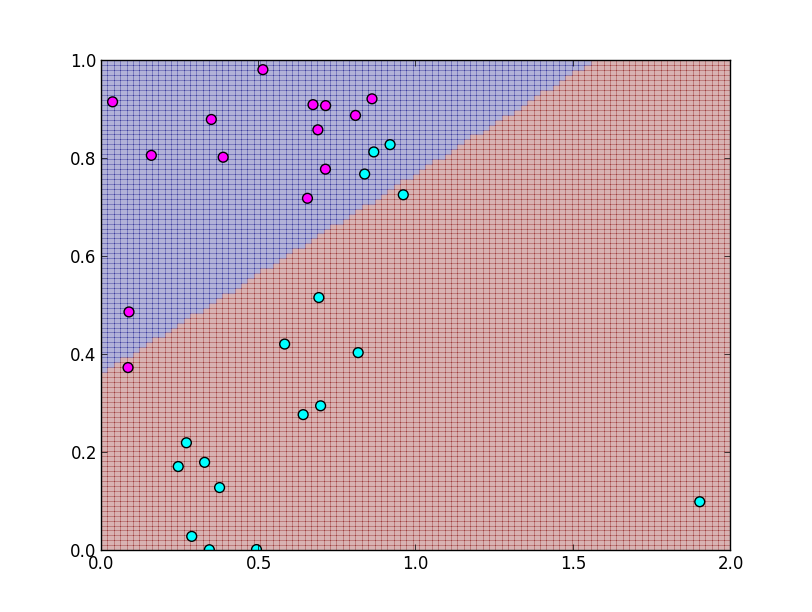
以下が $\rho=0.5$, $(x_0,y_0)=(2,-2)$, バーンイン期間 $10$、 サンプル数 $100$ での例です.
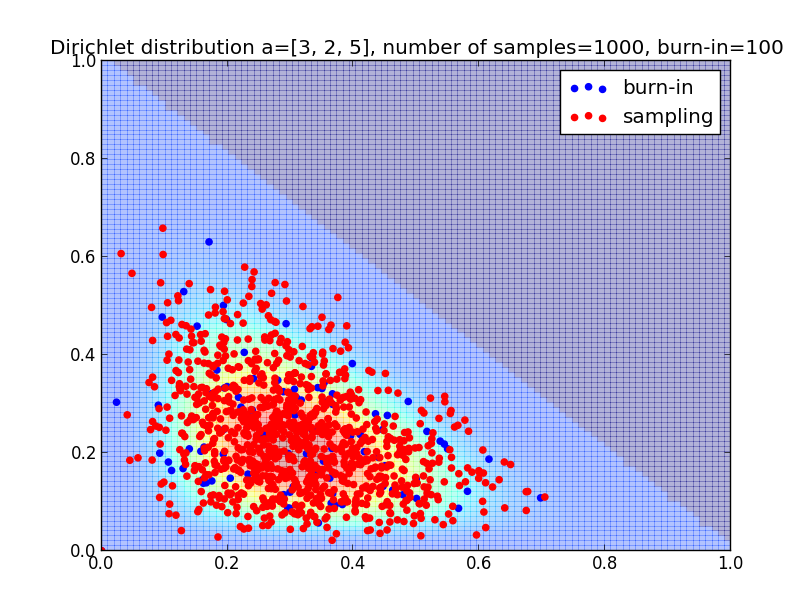
別の例として, ベータ分布を多次元に拡張した ディリクレ分布 (Dirichlet distribution) からのサンプリングをやってみましょう.
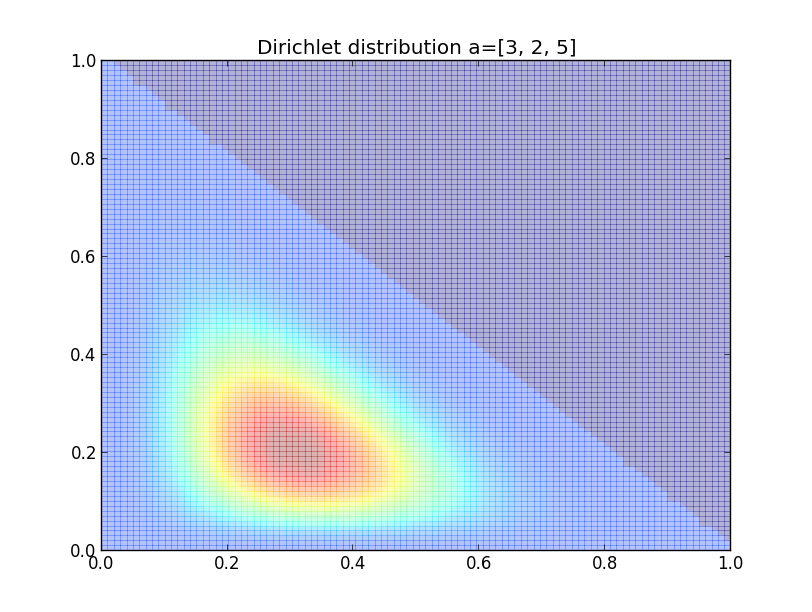
$k-1$ 次のディリクレ分布は, パラメータ $\mathbf{a}=(a_1,a_2,\ldots,a_k)$ と変数 $\mathbf{x}=(x_1,x_2,\ldots,x_k)$ に対して \[ \pi(\mathbf{x}) \propto \prod_{i=1}^k x_i^{a_i}\qquad \small{(x_i\geq 0, x_1+x_2+\cdots+x_k=1)} \] と表されます.
例えば $\mathbf{a}=(a,b,c)$ に対する $2$ 次のディリクレ分布は \[ \pi(x,y)\propto x^ay^b(1-x-y)^c \] となります.
すると \[ \pi(x|y)\propto x^a(1-x-y)^c \propto x^a\{(1-y)-x\}^c \] より $\pi(x|y)$ は変域 $[0,1-y]$ 上のベータ分布 $Be(a+1,c+1)$ となります.
同様に $\pi(y|x)$ は変域 $[0,1-x]$ 上のベータ分布 $Be(b+1,c+1)$ となります.
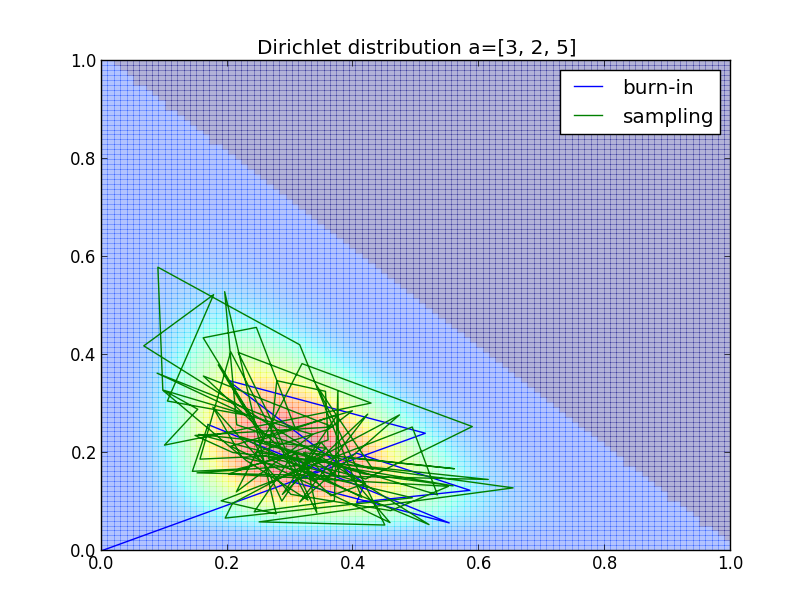
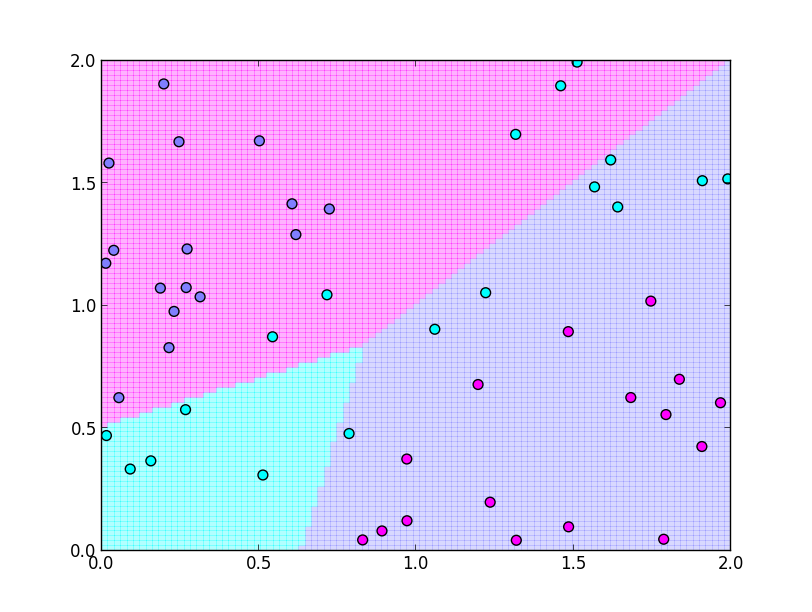
以下が $\mathbf{a}=(3,2,5)$, $(x_0,y_0)=(0,0)$, バーンイン期間 $10$、 サンプル数 $100$ での例です.
同分布でサンプル数を増やした場合はこんな様子です.
MCMC法の応用例
MCMC法は様々な問題に利用しますが, とりあえず最も簡単なベイズ線形回帰の問題を考えましょう.解析的に解ける例もあえてランダムサンプリングを使う形で解いてみます.
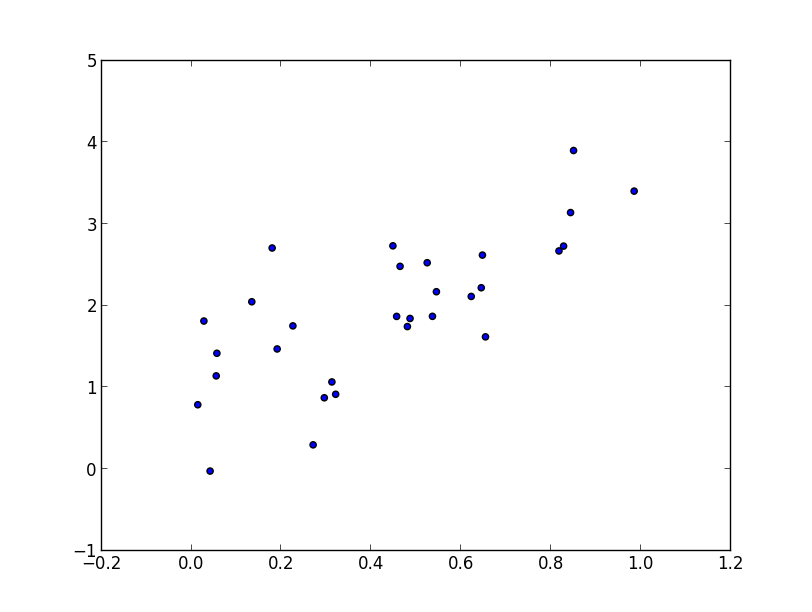
以下のような30組のデータ(prog4-4.dat)に対する回帰分析を行いましょう. これは$y=2x+1$ に従って生成しています.
モデルは $y_i = ax_i+b+\varepsilon_i\quad (\varepsilon_i\sim N(0, \sigma^2))$ とします. つまり \[ \mathbf{a}=(a,b)^T,\quad \mathbf{X}= \begin{pmatrix} x_1 & x_2 & \cdots & x_n \\ 1 & 1 & \cdots & 1 \end{pmatrix}^T \] とおいて, \[ \mathbf{y} \sim \mathcal{N}(\mathbf{X}\mathbf{a},\sigma^2I) \] というモデルを考えます. $\mathbf{a}$ と $\sigma^2$ の事後分布を求める事が目標です.
まず,データ $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\}$ が与えられた時の尤度は \[ \begin{aligned} L(\mathbf{a},\sigma^2|D)&=\mathcal{N}(\mathbf{y}|\mathbf{X}\mathbf{a},\sigma^2I)\\ & \propto (\sigma^2)^{-n/2}\exp\left\{-\frac{1}{2\sigma^2}||\mathbf{y}-\mathbf{X}\mathbf{a}||^2\right\} \end{aligned} \] です.
$\mathbf{a}$ の事前分布は $\mathcal{N}(\mathbf{a}_0, \sigma_0^2I)$ としましょう.
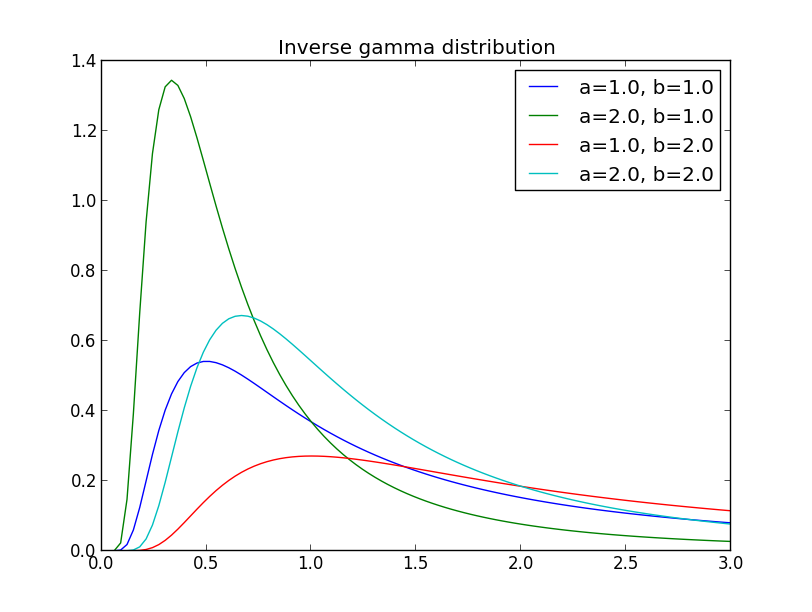
$\sigma^2$ の事前分布は $[0,\infty)$ 上の分布とすべきですが, 逆ガンマ分布 (inverse gamma distribution) $IG(\alpha_0/2,\beta_0/2)$ が用いられる事が多いです.
[参考] 逆ガンマ分布 $IG(\alpha/2,\beta/2)$ とは密度関数が \[ IG(x|\alpha/2,\beta/2) \propto x^{-\alpha/2-1}\exp\left(-\frac{\beta}{2x}\right) \] と表される分布です. \[ L(\mathbf{a},\sigma^2)\propto (\sigma^2)^{-n/2}\exp\left\{-\frac{1}{2\sigma^2}||\mathbf{y}-\mathbf{X}\mathbf{a}||^2\right\} \] の $\mathbf{a}$ を固定すると, 逆ガンマ分布と同じ形の関数になるため計算が容易です.
ベイズの定理より,$\mathbf{a},\sigma^2$ の事後分布は \[ \pi(\mathbf{a},\sigma^2|D)\propto L(\mathbf{a},\sigma^2|D)\mathcal{N}(\mathbf{a}|\mathbf{a}_0,\sigma_0^2I)IG(\sigma^2|\alpha_0/2,\beta_0/2) \] となり,これは各変数についての条件付き分布を求める事が出来るのでギブスサンプリングが使えます.
$\sigma^2$ を固定すると \[ \begin{aligned} \pi(\mathbf{a}|\sigma^2,D)&\propto L(\mathbf{a},\sigma^2|D)\mathcal{N}(\mathbf{a}|\mathbf{a}_0,\sigma_0^2I) \\ &\propto \exp\left\{-\frac{1}{2\sigma^2}||\mathbf{y}-\mathbf{X}\mathbf{a}||^2-\frac{1}{2\sigma_0^2}||\mathbf{a}-\mathbf{a}_0||^2\right\} \\ \end{aligned} \] となるので, これを $\mathbf{a}$ について平方完成(もしくは微分)すると, \[ \begin{aligned} & \pi(\mathbf{a}|\sigma^2,D) = \mathcal{N}(\mathbf{a}', \mathbf{\Sigma}) \\ & \mathbf{\Sigma}^{-1} = \frac{1}{\sigma^2}\mathbf{X}^T\mathbf{X}+\frac{1}{\sigma_0^2}I\\ & \mathbf{a}' = \mathbf{\Sigma}\left(\frac{1}{\sigma^2}\mathbf{X}^T\mathbf{y}+\frac{1}{\sigma_0^2}\mathbf{a}_0\right) \end{aligned} \] となります.
$\mathbf{a}$ を固定すると \[ \begin{aligned} \pi(\sigma^2|\mathbf{a},D) &\propto L(\mathbf{a},\sigma^2|D)IG(\sigma^2|\alpha_0/2,\beta_0/2) \\ &\propto (\sigma^2)^{-n/2-\alpha_0/2-1}\exp\left\{-\frac{1}{2\sigma^2}||\mathbf{y}-\mathbf{X}\mathbf{a}||^2-\frac{1}{2\sigma^2}\beta_0\right\} \end{aligned} \] となるので, \[ \begin{aligned} &\pi(\sigma^2|\mathbf{a},D) = IG(\alpha/2,\beta/2) \\ &\alpha = \alpha_0 + n\\ &\beta = \beta_0 + ||\mathbf{y}-\mathbf{X}\mathbf{a}||^2 \end{aligned} \] となります.
以上に基づいてギブスサンプラーを実装して走らせてみましょう.
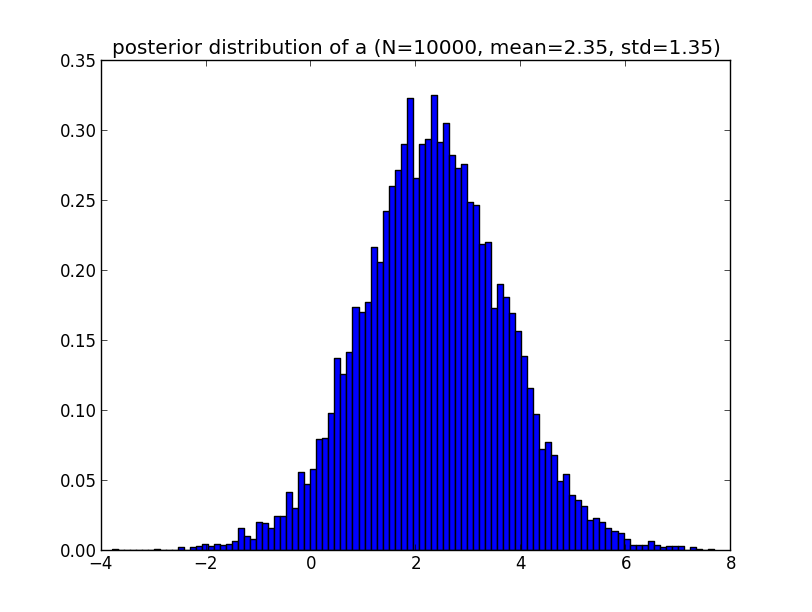
まず, $y=ax+b$ の $a$ の事後分布です.
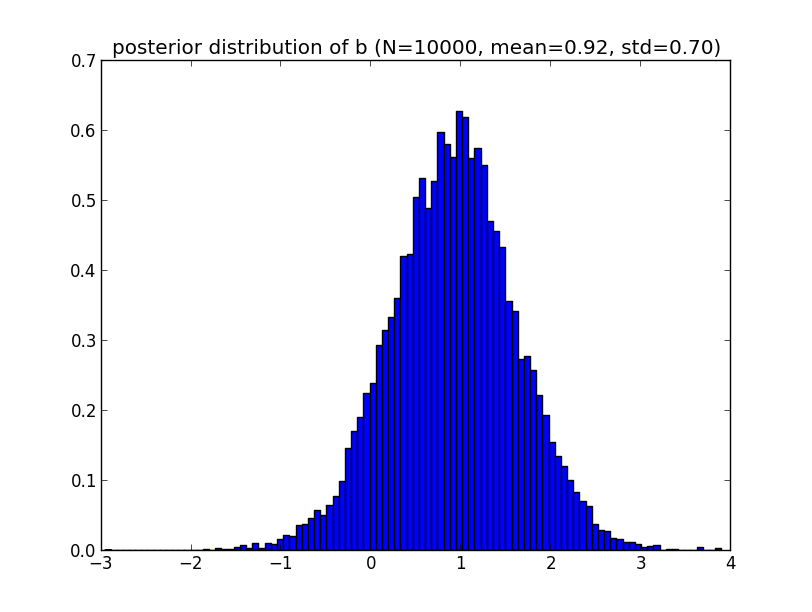
続いて $b$ の事後分布です.
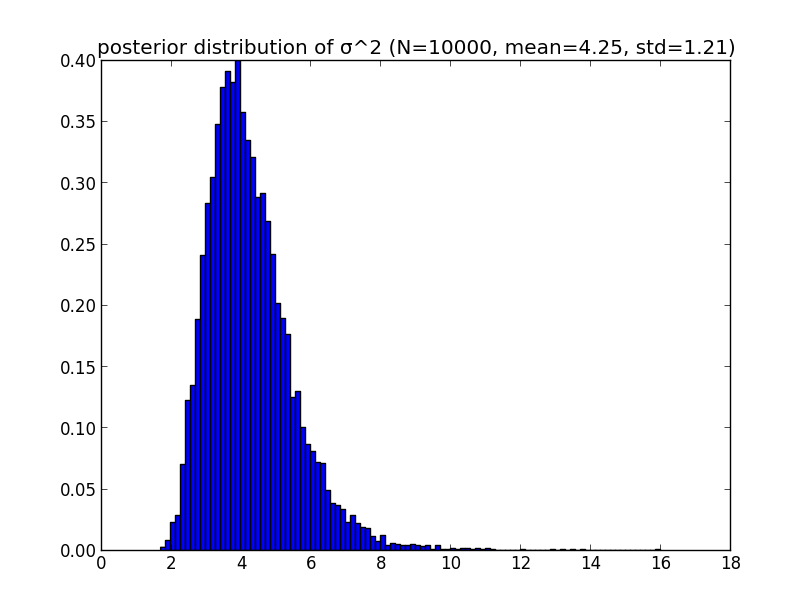
最後に $\sigma^2$ の事後分布です.
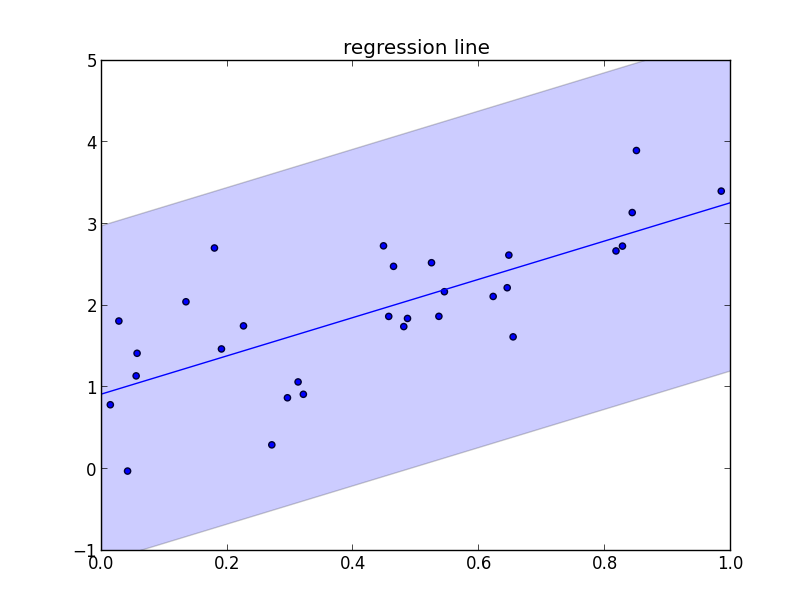
パラメータのMAP推定値は各分布の最頻値であり, 正規分布では標本平均と一致しますから \[ \hat{a}=2.35, \hat{b}=0.92 \] となります.
今の例ではMAP推定値を利用しましたが, 折角 $\mathbf{a},\sigma^2$ の分布が得られているのにもったいないです.
$\mathbf{a},\sigma^2$ に関して畳み込みを行って得られる分布を 予測分布 (predictive distribution) と呼びます. つまり, \[ \pi(y|x,D)=\int\int \pi(y|x,\mathbf{a},\sigma^2)\pi(\mathbf{a},\sigma^2|D)\mathrm{d}\mathbf{a}\mathrm{d}(\sigma^2) \] と計算される分布です. (解析的に求められるならそれがベストですが) $\pi(\mathbf{a},\sigma^2|D)$ に従うサンプルを生成し, それを使って $\pi(y|x,\mathbf{a},\sigma^2)$ からサンプリングを行えば予測分布からのサンプリングが出来ます.
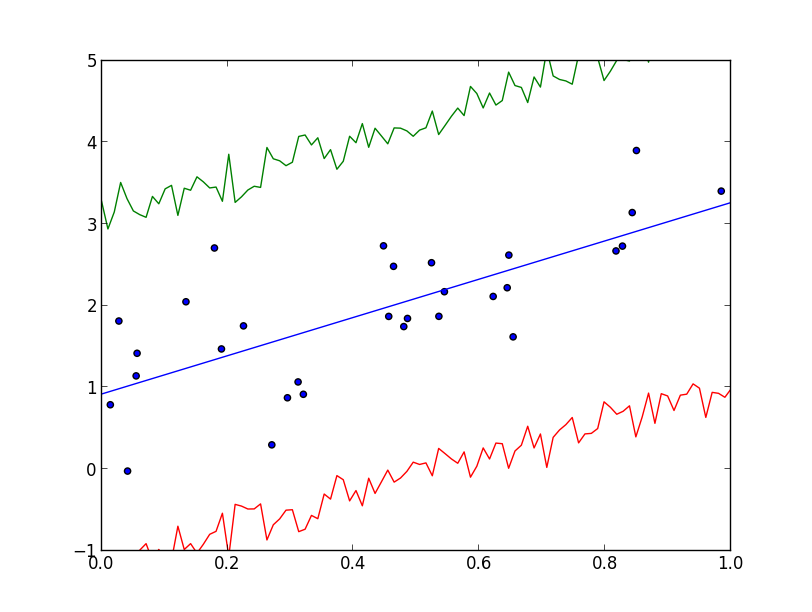
以下は予測分布からのサンプリングによって 標準偏差 を推定した例です.
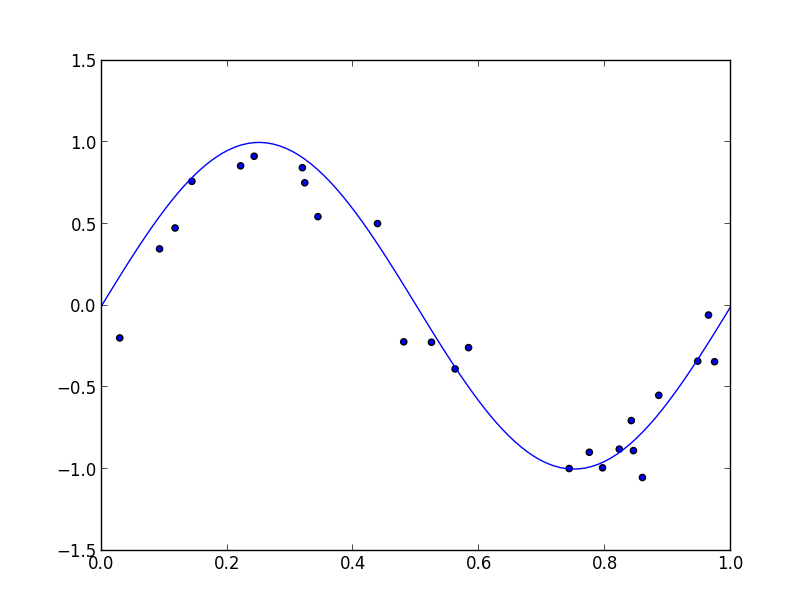
もう少し複雑な例として, PRMLの3.3.2節の問題を解いてみます. 入力データとして $y_i=\sin(2\pi x_i)+\varepsilon_i\quad (\varepsilon_i \sim N(0,\sigma^2))$ というモデルで生成したものを利用します.
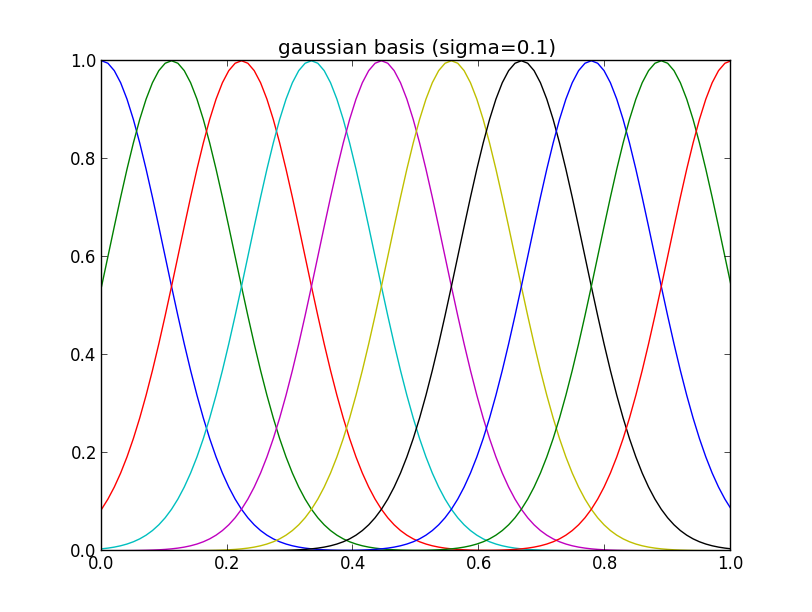
ガウス基底関数を $[0,1]$ に等間隔に10個 (分散パラメータは $\beta=0.1$ と固定) 配置して使う事にします.
ガウス基底を $\Psi(x)=(\psi_1(x),\psi_2(x),\ldots,\psi_{10}(x))^T$ と書くと, パラメータ $\mathbf{a}=(a_1,a_2,\ldots,a_{10})^T$ に対して \[ y_i \sim N(\Psi(x_i)^T\mathbf{a}, \sigma^2) \] と仮定する事になります. 例によって \[ \mathbf{X} = (\Psi(x_1),\Psi(x_2),\ldots,\Psi(x_n))^T,\quad \mathbf{y}=(y_1,y_2,\ldots,y_n)^T \] と置けば \[ \mathbf{y} \sim \mathcal{N}(\mathbf{X}\mathbf{a}, \sigma^2I) \] となって, 先ほどの問題と全く同じ様に解くことができます.
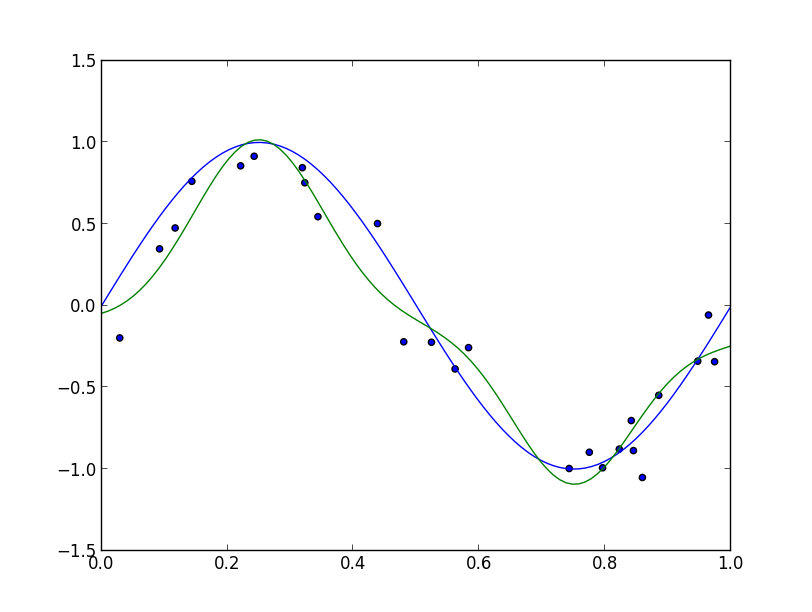
ギブスサンプラーを走らせ, $\hat{\mathbf{a}}$ をMAP推定で求めると以下のような曲線が得られます.
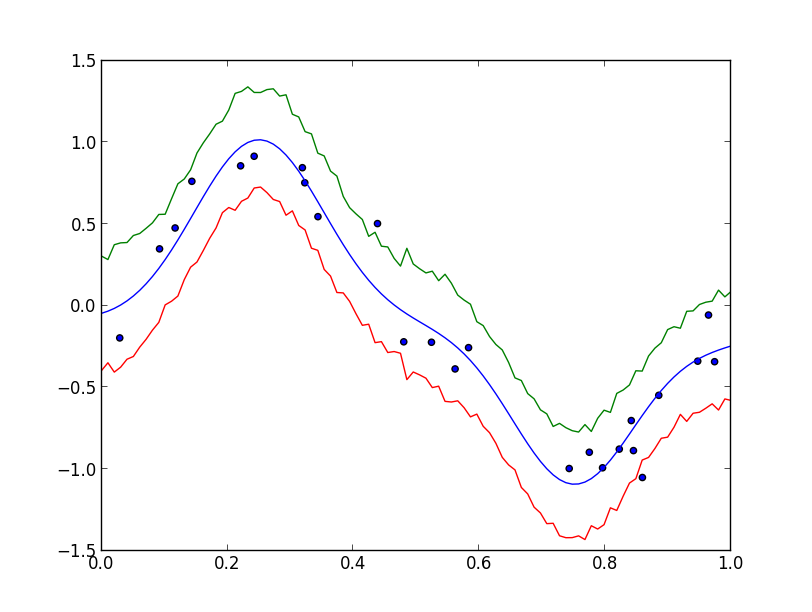
予測分布の標準偏差を推定してみると以下のようになります.
MCMC法を利用したパラメータ推定・回帰分析の例は一旦ここで終了します.
いろいろと細かい話(事前分布をどうするかなど)が残っていますが, 大体の様子はつかめたのではないかと思うので識別の問題に進みます.
線形識別モデル
PRMLの第4章に相当する内容を進めていきます.
特徴空間 $\Omega$ を $K\geq 2$ 個の領域に分割する際の境界を 決定面 (decision surface) と呼びます. 線形識別モデル (linear discriminant model) とは決定面が超平面となるようなモデルです.
例えば第一回に紹介したテンプレートマッチング法は線形識別モデルの一種です.
2クラスの場合
クラスが $C_1,C_2$ の2つの場合を考えます. (特徴空間の $\Psi$ による変換を考えない場合)線形識別関数は \[ f(\mathbf{x}) = \mathbf{w}^T\mathbf{x}+w_0 \] と書くことができ, $\mathbf{w}$ を 重み (weight) $w_0$ を バイアス (bias) と呼びます.
\[ f(\mathbf{x}) = \mathbf{w}^T\mathbf{x}-\theta \] の用に書いて $\theta$ を しきい値 (threshold) と呼ぶ場合もあります.
これまでもやって来ましたように, 特徴ベクトル $\mathbf{x}$ にダミー変数を \[ \mathbf{x}=(\color{red}{1}, x_1,x_2,\ldots,x_m) \] のように入れてしまえば, 線形識別関数はもっと単純に \[ f(\mathbf{x})=\mathbf{w}^T\mathbf{x} \] と書くことが出来ます.
さて, $2$ クラスの場合は
- $f(\mathbf{x})> 0$ ならば $C_1$
- $f(\mathbf{x})< 0$ ならば $C_2$
というように識別を行います.
従って決定面は \[ \mathbf{w}^T\mathbf{x} = 0 \] という $\mathbf{w}$ と直交する超平面となります.
多クラスの場合
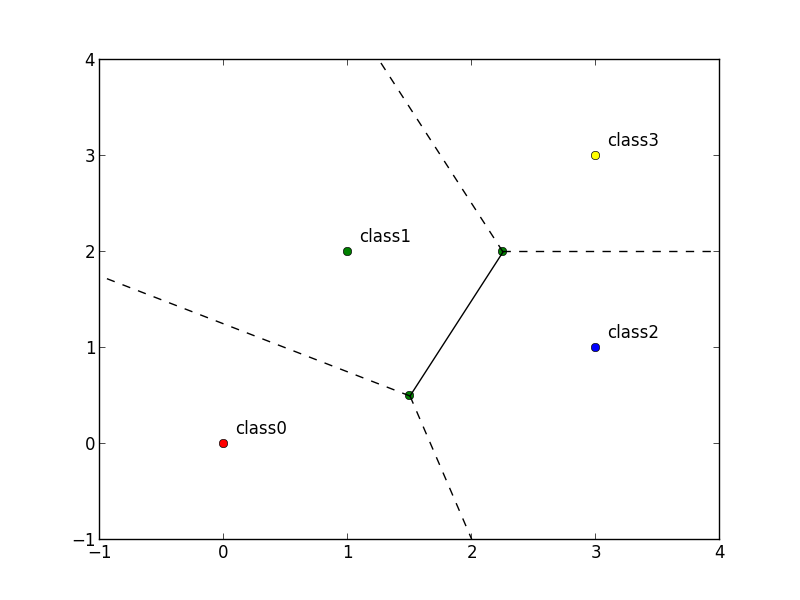
クラスの数 $K$ が $3$ 以上の場合,「 $f(\mathbf{x})$ の正負で識別する」という方針では問題が生じます.
例えば $K=3$ の場合に $f(\mathbf{x}) > 0$ ならクラス1, $g(\mathbf{x})>0$ ならクラス3とした場合, $f(\mathbf{x})>0\text{かつ}g(\mathbf{x})>0$ の領域のクラスが確定しません.
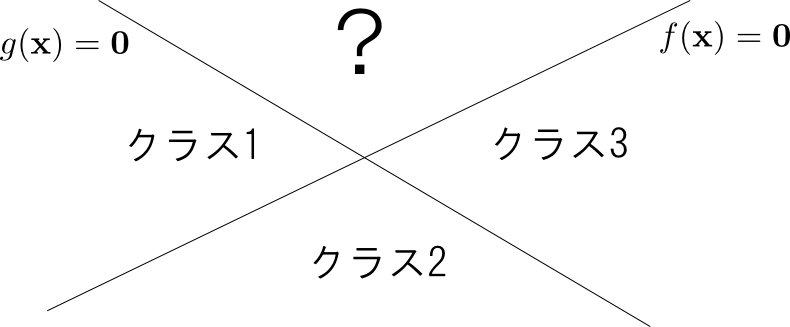
そこで, 多クラス識別の場合には各クラス $c$ 毎に識別関数 \[ f_c(\mathbf{x})=\mathbf{w}_c^T\mathbf{x} \] を定め,「$f_c(\mathbf{x})$ が最大の $c$ を選ぶ」という方法をとります.
今の様なルールにすると, 領域の形状が想像しづらくなるかもしれませんが線形識別モデルで得られる領域は全て凸領域であるという一般的な事実が言えます.

1-of-K 符号化
クラス数が $K$ であるとき, クラス $C_i$ に対して \[ \mathbf{t}=(0,\ldots,0,1,0,\ldots,0)\quad\text{($i$番目だけ $1$)} \] というベクトルを目標のベクトルとする符号化を 1-of-K 符号化 と呼びます.
ここで $t_1+t_2+\cdots+t_K=1, t_i\geq 0$ を満たすようにとるならば, $t_i$ を $\mathbf{x}$ がクラス $C_i$ に属する確率と解釈する事が可能です.
最小二乗法による線形識別の問題点
第1回には識別関数 $f_c(\mathbf{x})$ を束にした \[ \mathbf{f}(\mathbf{x})=(f_{c_1}(\mathbf{x}),f_{c_2}(\mathbf{x}),\ldots,f_{c_K}(\mathbf{x}))^T \] を考え, 最小二乗法によって $\mathbf{f}(\mathbf{x})$ が目標ベクトル $\mathbf{t}$ に近づくように最適化する方法を紹介しました.
実は, この方法にはいくつかの問題があります.
まず, $\mathbf{t}$ を確率として解釈する場合には \[ t_1+t_2+\cdots+t_K = 1,\quad t_i\geq 0 \] を満たすように制約を加える必要があります.
また, 単純な最小二乗法は外れ値に敏感に反応してしまいます.
また, 単純な最小二乗法は外れ値に敏感に反応してしまいます.
そして,目標ベクトルとの差 $\mathbf{t} - \mathbf{f}(\mathbf{x})$ は明らかに正規分布には従わない為, 線形識別可能なデータでも正しく識別出来ません.
最後の問題は特に本質的です. $\mathbf{t}$ は正規分布ではなくどのような分布に従って生成されるのか, その 確率的生成モデル (probabilistic generative model) をしっかりと考える必要があります.
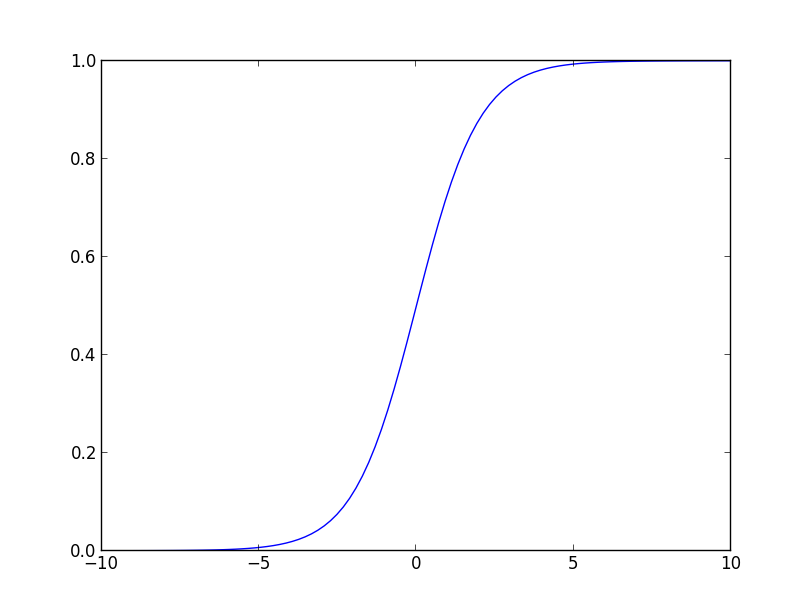
$K=2$ の場合を考えましょう. 既に述べたように $t_1$ は $\mathbf{x}$ がクラス $C_1$ である確率と解釈出来るので,ベイズの定理より \[ t_1 = p(C_1|\mathbf{x}) = \frac{\pi(\mathbf{x}|C_1)p(C_1)}{\pi(\mathbf{x})} \] と書くことが出来ます. ここで \[ \pi(\mathbf{x})= \pi(\mathbf{x}|C_1)p(C_1) + \pi(\mathbf{x}|C_2)p(C_2) \] であるので, \[ a = \ln\frac{\pi(\mathbf{x}|C_1)p(C_1)}{\pi(\mathbf{x}|C_2)p(C_2)} \] と置き直せば \[ p(C_1|\mathbf{x})=\frac{1}{1+\exp(-a)} \] となります.
ここで登場した \[ \sigma(a) = \frac{1}{1+\exp(-a)} \] は前回紹介しました, ロジスティック・シグモイド基底 (logistic sigmoid basis) に他なりません.
ここで \[ a = \ln\frac{\pi(\mathbf{x}|C_1)p(C_1)}{\pi(\mathbf{x}|C_2)p(C_2)} \] が $\mathbf{x}$ の関数である事に注意して, 適当な基底の変換 $\Psi$ を行った後に \[ a = \mathbf{w}^T\Psi(\mathbf{x}) \] と表すならば, \[ p(C_1|\mathbf{x}) = \sigma(\mathbf{w}^T\Psi(\mathbf{x})) \] となります. この確率的生成モデルを $K > 2$ の場合に拡張すると ロジスティック回帰 (logistic regression) という手法が得られます.
第4回はここで終わります
という所で時間が無くなってしまいましたので続きは次回にまわします. MCMC法をよく練習しておいて下さい.
次回はロジスティック回帰,ベイジアンロジスティック回帰, パーセプトロン, フィッシャーの線形判別など線形識別の理論を勉強していきます.