パターン認識・
機械学習勉強会
第21回

@ナビプラス

謝辞

会場・設備の提供をしていただきました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.

系列データ

テキスト第12章を一旦飛ばして、テキスト第13章「系列データ」をやります. 所謂「時系列データ解析」の話題ではなく隠れマルコフモデル(hidden markov model)の紹介が中心になります.

系列データとは

何らかの順序を持つデータの列を 系列データ (sequential data) と呼びます. 特に時間軸に沿って観測されるデータ列は 時系列データ (time series) と呼ばれます.

例えば以下のようなものを系列データと考える事が出来ます.

• 株価の変動
• 音声データ
• 文章(文字・単語の列)
• ユーザーの行動履歴
• センサーデータ

これまで紹介した手法では，学習データ $\{\mathbf{x}_1,\ldots,\mathbf{x}_N\}$ がi.i.d.，つまり独立に同一の分布に従う場合を主に考えてきました. この場合は \[ p(\mathbf{x}_1,\ldots,\mathbf{x}_n) = \prod_{i=1}^Np(\mathbf{x}_i)=p(\mathbf{x}_1)\cdot p(\mathbf{x}_2)\cdots p(\mathbf{x}_n)\] と分解できます.

しかし，系列データの多くではi.i.d.性を仮定出来ず，このような単純な分解は出来ません.

マルコフモデル

系列データ $\{\mathbf{x}_1,\ldots,\mathbf{x}_N\}$ において \[ p(\mathbf{x}_{i}|\mathbf{x}_{i-1},\mathbf{x}_{i-2},\ldots,\mathbf{x}_1) = p(\mathbf{x}_{i}|\mathbf{x}_{i-1})\qquad (i=2,\ldots,N) \] が成り立つとするモデルを 1次のマルコフモデル(first-order Markov model) と呼びます.

各時点のデータは一ステップ前のデータのみに依存し，それより前のデータとは独立であるとするモデルです.

1次のマルコフモデルの同時分布は \[ \begin{aligned} p(\mathbf{x}_1,\ldots,\mathbf{x}_N) &= p(\mathbf{x}_1)\prod_{i=2}^Np(\mathbf{x}_i|\mathbf{x}_{i-1}) \\ & =p(\mathbf{x}_1)p(\mathbf{x}_2|\mathbf{x}_1)p(\mathbf{x}_3|\mathbf{x}_2)\cdots p(\mathbf{x}_N|\mathbf{x}_{N-1}) \end{aligned} \] となります.

ここで， $p(\mathbf{x}_i|\mathbf{x}_{i-1})$ が全て同一の分布，つまり \[ p(\mathbf{x}_i=\mathbf{x}'|\mathbf{x}_{i-1}=\mathbf{x}) = p(\mathbf{x}_2=\mathbf{x}'|\mathbf{x}_1=\mathbf{x}) \quad (i=2,\ldots,N)\] が成り立つモデルを斉次マルコフモデル(homogeneous Markov model)，そうでないモデルを非斉次マルコフモデル(inhomogeneous Markov model)と呼びます.

2次，3次・・・のマルコフモデルも同様に定義されます. 例えば2次のマルコフモデルは \[ \begin{aligned} p(\mathbf{x}_1,\ldots,\mathbf{x}_N) &= p(\mathbf{x}_1,\mathbf{x}_2)\prod_{i=3}^Np(\mathbf{x}_i|\mathbf{x}_{i-1},\mathbf{x}_{i-2}) \\ &= p(\mathbf{x}_1,\mathbf{x}_2)p(\mathbf{x}_3|\mathbf{x}_1,\mathbf{x}_2)\cdots p(\mathbf{x}_N|\mathbf{x}_{N-1},\mathbf{x}_{N-2}) \end{aligned} \] と表されます. 斉次性も同様に定義されます.

マルコフモデルの典型例は 自己回帰モデル (autoregressive model, ARモデル) で, 現時点の値は過去 $p$ 時点の値の線形和+ホワイトノイズ(正規ノイズ)であるとするものです. \[ x_{i} = a_1x_{i-1} + \cdots + a_px_{i-p} + a_0 + \varepsilon_i \qquad \varepsilon_i \sim N(0,\sigma^2) \] これは $p$ 次の(斉次)自己回帰モデルと呼ばれ $\mathrm{AR}(p)$ などと書かれます.

他には 移動平均モデル (moving average model, MAモデル) というものも有名です. これは現時点の値は過去 $q$ 時点のホワイトノイズの線形和+現時点のホワイトノイズであるとするものです. \[ x_{i} = b_1\varepsilon_{i-1}+\cdots + b_q\varepsilon_{i-q}+b_0 + \varepsilon_i \qquad \varepsilon_i \sim N(0,\sigma^2) \] これは $\mathrm{MA}(q)$ などと書かれます.

時系列のモデルにはその他ARとMAを組み合わせた 自己回帰移動平均モデル (ARMAモデル) や，更に和分という操作を入れた 自己回帰和分移動平均モデル (ARIMAモデル)，周期性を取り入れた 季節性自己回帰和分移動平均モデル (SARIMAモデル) など様々な物があります.

テキストではあまり詳しく説明がありませんので，これらに興味がありましたら他の書籍をあたって下さい.

隠れマルコフモデル

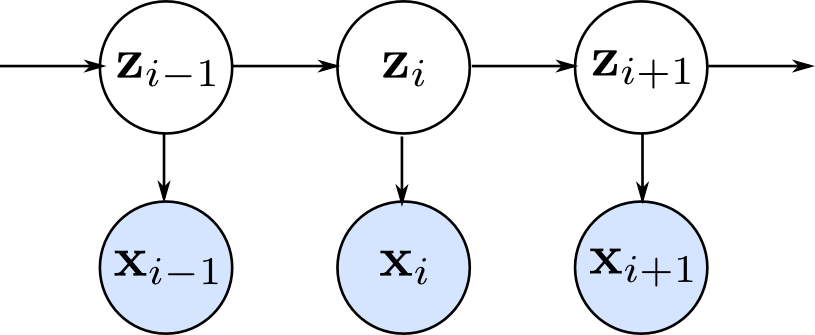
下のグラフィカルモデルの様に，観測変数 $\mathbf{x}_i$ 毎に隠れ変数 $\mathbf{z}_i$ を割り当て，隠れ変数がマルコフ過程に従うとするモデルを(広い意味での) 隠れマルコフモデル (hidden Markov model, HMMモデル) と呼びます. 一般に隠れマルコフモデルと言った場合には隠れ変数がカテゴリカル変数である物を指します.

隠れマルコフモデルでモデル化出来る事例を紹介します.

典型的な例は単語列に対する品詞タグ付けです. 観測変数 $x_i$ は各単語で，隠れ変数 $z_i$ が品詞タグとなります.

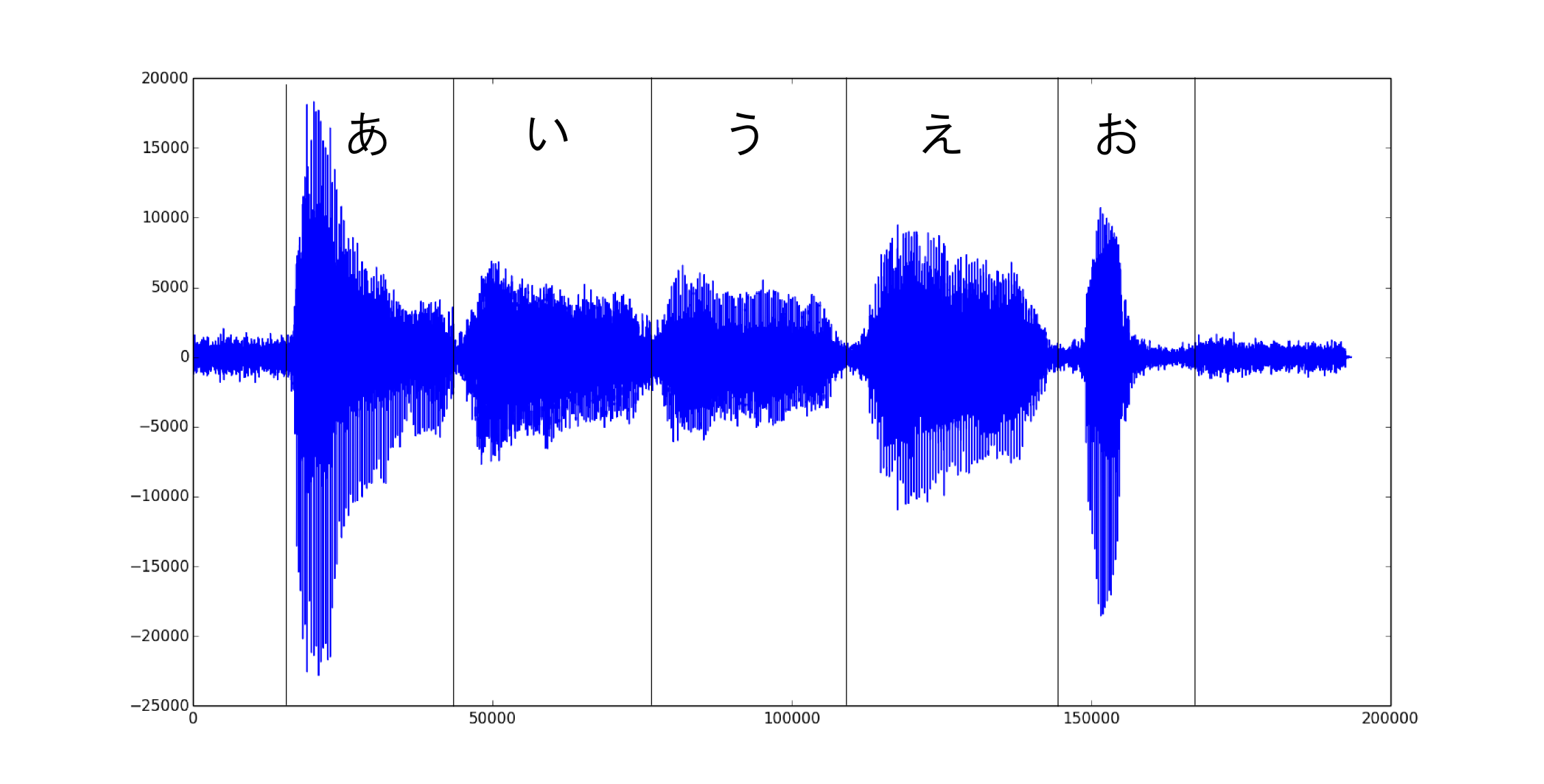
音声認識の場合 $\mathbf{x}_i$ は音声データであり，隠れ変数 $z_i$ は発声されている音声を表すタグとなります.

(実際には $\mathbf{x}_i$ は下図のようなものではなく周波数領域に変換したもの，$z_i$ は「あいうえお」より更に細かい音の単位を使うと思います.多分.)

以下はある人の 腰に付けた加速度計 の約50分間のデータ(ただしキャリブレーションなし)です. このようなセンサーデータから行動を判定するという問題は，Activity recognitionと呼ばれます.

加速度データを観測変数 $\mathbf{x}_i$，その時の行動ラベルを $z_i$ としてHMMでモデル化出来そうです. (以下の論文では別の方法を使っています.)

prog21-1.py

Casale, P. Pujol, O. and Radeva, P. 'Personalization and user verification in wearable systems using biometric walking patterns' Personal and Ubiquitous Computing, 16(5), 563-580, 2012

今例に挙げた様な問題では主に隠れ変数を特定する事に興味があります. この様な問題は一般に 系列ラベリング (sequence labelling) と呼ばれます.

隠れマルコフモデルと言った場合，多くの場合は「ラベルが未知」の場合を指すと思います. しかし，系列ラベリングの問題ではラベルが教えられた状況での学習も良く行われ，その時も隠れマルコフモデルと呼ぶ場合があります.

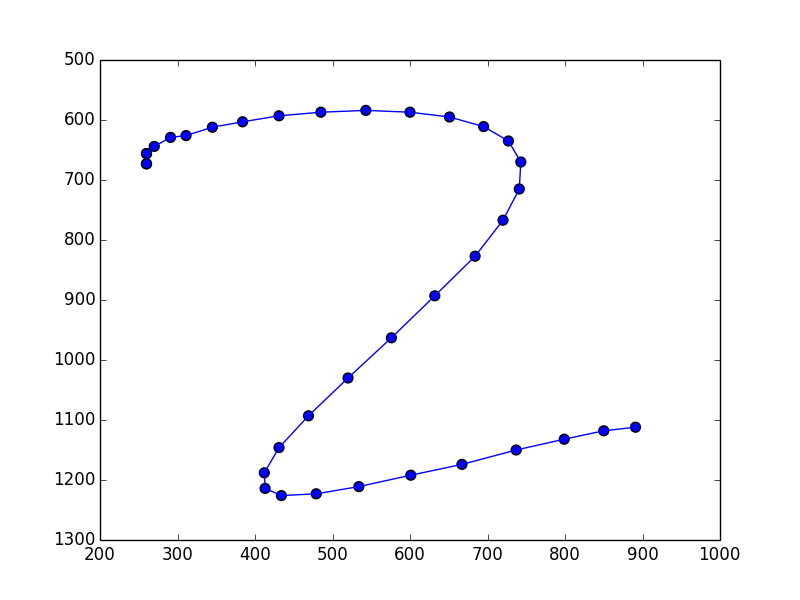
以下は 手書き文字のストローク のデータ例です. 以前やったようなピクセル単位のデータと異なり， \[ (557, 844) \rightarrow (550, 803) \rightarrow (550, 803) \rightarrow \cdots \] の様な座標列からなるデータとなります.

このようなデータは「今，文字のどのあたりを描いているのか？」を表すラベルを隠れ変数として教師なし学習をするモデル化する事が出来ます.

prog21-2.py

隠れ変数を持たない1次のマルコフモデルでは $\mathbf{x}_{i}$ が観測されると $\mathbf{x}_{i-1}$ と $\mathbf{x}_{i+1}$ が独立になります. 高次のマルコフモデルでも，やはりある程度離れた観測データ同士の間に条件付き独立性が存在します.

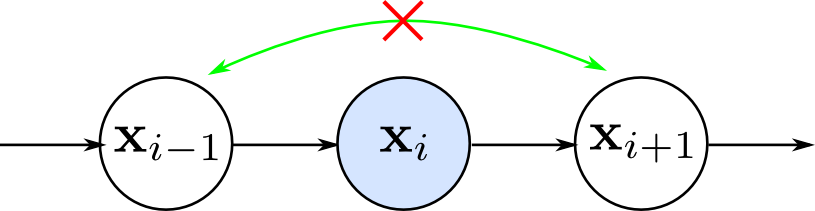
一方，隠れ変数を持つマルコフモデルでは隠れ変数の系列を通るパスが存在するので遠く離れた $\mathbf{x}_i$ と $\mathbf{x}_j$ も従属となります.

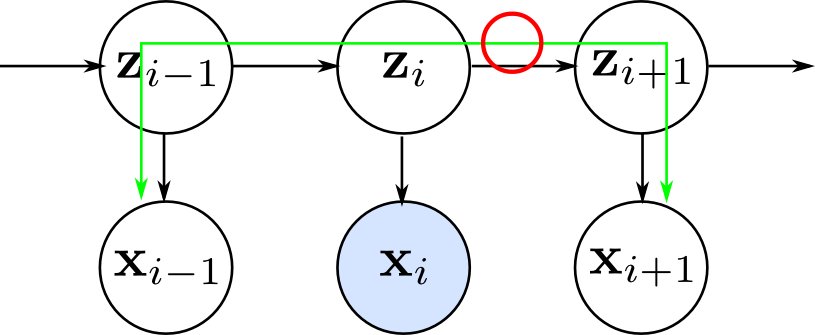
離れた $\mathbf{x}_i$ と $\mathbf{x}_j$ の関係をマルコフモデルで表現したければ，

• 高次のマルコフモデルを使う
• 隠れ変数を持つマルコフモデルを使う

という2通りの方法がありますが，前者では次数が高くなるほどパラメータの数が増え計算量が増大してしまいます.

隠れマルコフモデルではモデルの複雑さを抑えつつ，離れた観測データ間の関係を表現する事が出来ます.

また，間隔の伸び縮みする様な系列データ列に対しても隠れマルコフモデルは有効です.

HMMのパラメータ

HMMに従う観測データ $\mathbf{x}=\{\mathbf{x}_i\}$, 隠れ変数 $\mathbf{z}=\{\mathbf{z}_i\}$ の同時分布は \[ p(\mathbf{x},\mathbf{z}) = \left\{p(\mathbf{z}_1)\prod_{i=2}^Np(\mathbf{z}_{i}|\mathbf{z}_{i-1})\right\}\left\{\prod_{i=1}^Np(\mathbf{x}_i|\mathbf{z}_i)\right\} \] となります.

従って斉次モデルならば, 以下の三種類のパラメータが必要となります.

• $p(\mathbf{z}_1)$ を記述するパラメータ $\boldsymbol{\pi}$
• $p(\mathbf{z}_{i}|\mathbf{z}_{i-1})$ を記述するパラメータ $\mathbf{A}$
• $p(\mathbf{x}_i|\mathbf{z}_i)$ を記述するパラメータ $\boldsymbol{\phi}$

隠れ変数 $\mathbf{z}_i$ は 状態 (state) と解釈する事ができます. 隠れた状態があり，それに基いて観測データが生成されるという考え方です. この意味で 状態空間モデル (state space model) と呼ばれる場合もあります.

$p(\mathbf{z}_1)$ は初期状態の分布です. 状態数が $K$ のHMMの場合は $\sum_{k=1}^K\pi_k = 1$ を満たすパラメータ $\boldsymbol{\pi}$ を用いて \[ p(z_1 = k) = \pi_k \] と書く事が出来ます.

\[ p(\mathbf{z}_i | \mathbf{z}_{i-1}) \] は状態 $\mathbf{z}_{i-1}$ から 状態 $\mathbf{z}_{i}$ への 遷移確率 (transition probability)です.

状態数 $K$ のHMMの場合は $K\times K$ 行列を用いて \[ p(z_i = k | z_{i-1} = j) = A_{jk} \] と表す事が出来ます. この $\mathbf{A}$ を 遷移行列 (transition matrix) と呼びます.

$\mathbf{A}$ は \[ \sum_{k=1}^KA_{jk} = 1 \qquad (j=1,\ldots,K) \] を満たす必要があります.

以下が隠れ変数の状態遷移図の例と，対応する遷移行列です.

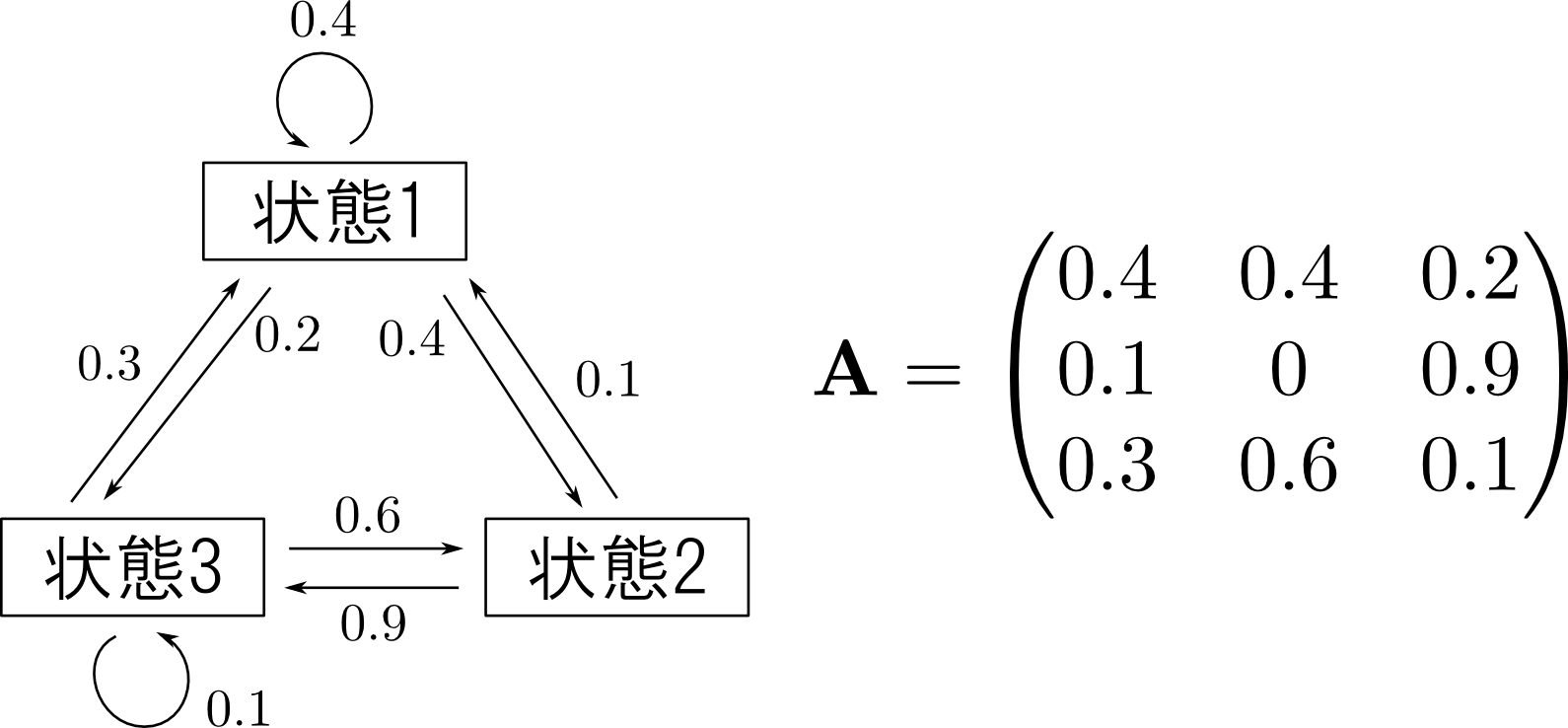
\[ p(\mathbf{x}_i | \mathbf{z}_i) \] は隠れ状態と観測値の関係を表しており， emission probability と呼ばれます.

$ p(\mathbf{x}_i | \mathbf{z}_i) $ はどのような分布も考える事が出来ます. HMMの場合は $z_i = k$ の場合の分布のパラメータを $\boldsymbol{\phi}_k$ とすれば \[ p(\mathbf{x}_i | z_i = k) = p(\mathbf{x}_i | \boldsymbol{\phi}_k) \] という事になります.

まとめると，HMMは以下のように記述されます.

HMMの学習(ラベルが隠れていない場合)

PRMLでは続いて状態(ラベル)が隠れている場合の学習に進みますが，まずは簡単なラベルが与えられている状況での学習を先に紹介します. 隠れてないのでHMMという呼び方は妥当じゃないと思うのですが，HMMと呼ぶ事にします.

学習データを $D= \{(\mathbf{x}^{(1)},\mathbf{z}^{(1)}),\ldots, (\mathbf{x}^{(N)},\mathbf{z}^{(N)})\}$ とおきます. 第 $i$ 番目のデータ列の長さを $N_i$ とします. すると，尤度は \[ p(D|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) = \prod_{i=1}^N\left[ \left\{\pi_{z^{(i)}_1} \prod_{l=2}^{N_i} A_{z^{(i)}_{j-1},z^{(i)}_{j}}\right\}\left\{\prod_{j=1}^{N_i}p(\mathbf{x}^{(i)}_j|\boldsymbol{\phi}_{z^{(i)}_j})\right\}\right] \] となりますので， \[ \log p(D|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) = \sum_{i=1}^N\left[\log \pi_{z^{(i)}_1} + \sum_{l=2}^{N_i} \log A_{z^{(i)}_{j-1},z^{(i)}_{j}} + \sum_{j=1}^{N_i}\log p(\mathbf{x}^{(i)}_j|\boldsymbol{\phi}_{z^{(i)}_j})\right] \] の最大化を行えば良いです.

ただし，$\boldsymbol{\pi},\mathbf{A}$ には制約条件が付くのでラグランジュの未定乗数を導入し \[ \begin{aligned} \log p(D|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) &= \sum_{i=1}^N\left[\log \pi_{z^{(i)}_1} + \sum_{l=2}^{N_i} \log A_{z^{(i)}_{j-1},z^{(i)}_{j}} + \sum_{j=1}^{N_i}\log p(\mathbf{x}^{(i)}_j|\boldsymbol{\phi}_{z^{(i)}_j})\right] \\ & - \alpha (\sum_{k=1}^K \pi_k - 1) - \sum_{j=1}^K\beta_j (\sum_{k=1}^K A_{jk} - 1) \end{aligned} \] の極値問題を解く必要があります.

難しく見えますが， $\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}$ を含む項は別々になっているので微分計算は非常に単純です.

これは簡単に解くことが出来ます. まず $\boldsymbol{\pi}$ で微分すると \[ \frac{\partial}{\partial \pi_k}\log p(D|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) = \sum_{i=1}^N\frac{[z_1^{(i)}=k]}{\pi_k} - \alpha \] となります. ただし $[z_1^{(i)} = k]$ は中が真ならば $1$, そうでなければ $0$ とします.

これが $0$ になれば良いので \[ \pi_k = \frac{1}{\alpha}\sum_{i=1}^N[z_1^{(i)}=k] \] となります. これと $\sum_{k=1}^K \pi_k = 1$ を合わせて \[ \pi_k = \frac{1}{N}\sum_{i=1}^N[z_1^{(i)}=k] = \frac{\text{(初期状態が $k$ である系列数)}}{\text{(全系列数)}} \] となります.

全く同様にして \[ \begin{aligned} A_{jk} &= \frac{\sum_{i=1}^N\sum_{\ell=1}^{N_i-1}[z^{(i)}_\ell=j][z^{(i)}_{\ell+1}=k]}{\sum_{i=1}^N\sum_{\ell=1}^{N_i-1} [z^{(i)}_\ell = j]}\\ &= \frac{\text{(状態 $j$ から $k$ へ遷移した回数)}}{\text{((最後を除き)状態 $j$ になった回数)}} \end{aligned} \] となります.

emission確率のパラメータ $\boldsymbol{\phi}_k$ ですが， $\boldsymbol{\phi}$ に依存する項だけ取り出すと \[ \begin{aligned} \log p(D|\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}) &= \sum_{i=1}^N\sum_{j=1}^{N_i}\log p(\mathbf{x}^{(i)}_j|\boldsymbol{\phi}_{z^{(i)}_j})+\mathrm{const}. \\ &= \sum_{k=1}^K\sum_{i=1}^N\sum_{j=1}^{N_i}[z^{(i)}_j=k]\log p(\mathbf{x}^{(i)}_j|\boldsymbol{\phi}_{k}) + \mathrm{const}.\\ &= \sum_{k=1}^K(\text{ラベルが $k$ の観測データの対数尤度の和}) + \mathrm{const}. \end{aligned} \] となりますので，各ラベル毎に観測データを分けて通常の最尤法の計算を行えば良いです.

先ほどの加速度センサの例を使ってサンプルプログラム(prog21-3.py)を書いてみました. このデータセットには11人分のデータが入っています. これからパラメータ $\boldsymbol{\pi}, \mathbf{A}, \boldsymbol{\phi}$ を学習する事が目標です.

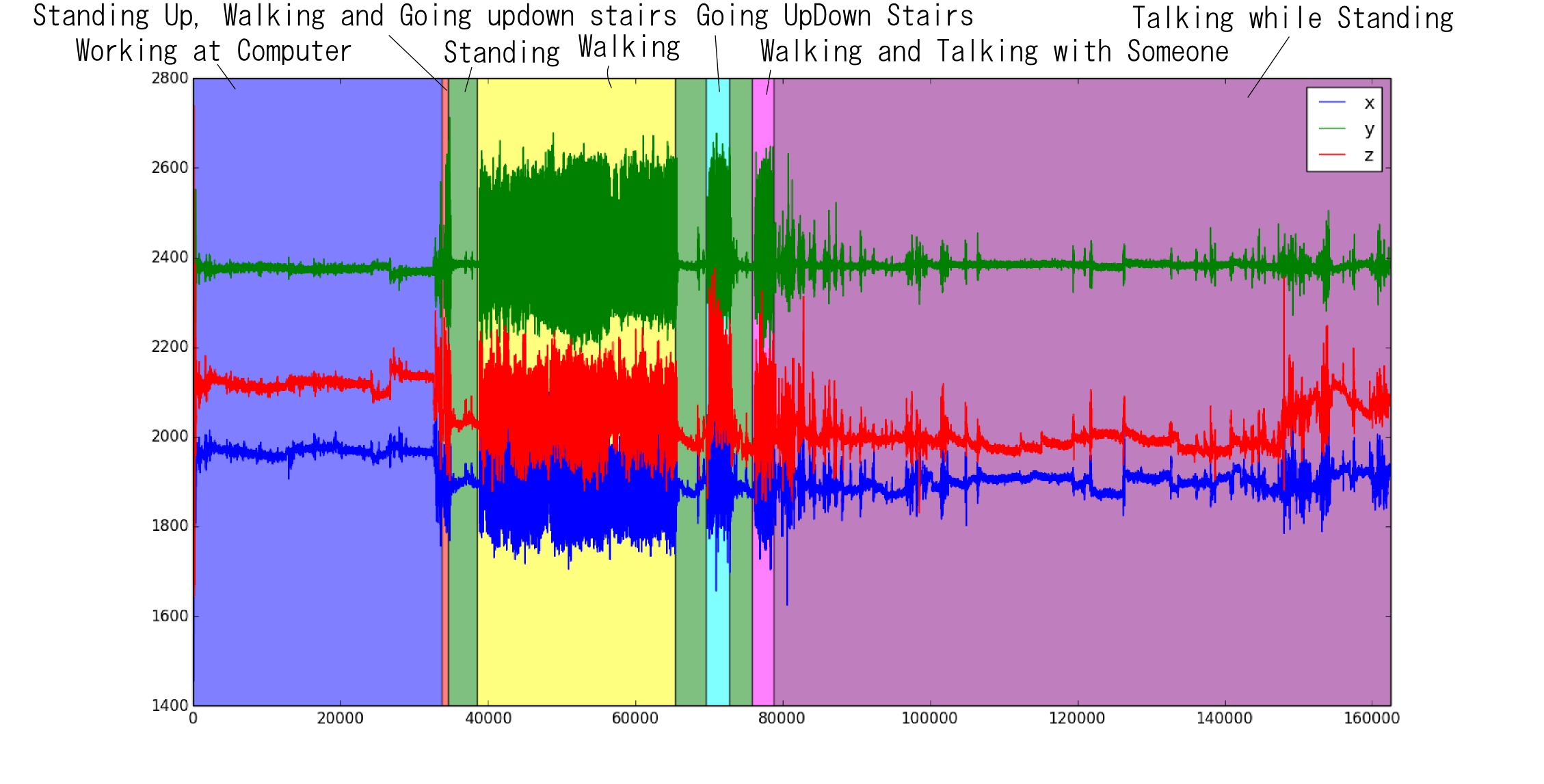
【データセットの注意】
公開されているデータは以下の図のように一部の被験者の教師ラベルが明らかにずれていました. このズレは手作業で測って修正する事にしました. また，測定開始時直後にセンサの取り付けの際の大きなノイズが見られますので，最初の10秒ほどは学習データから削りました.

【学習データの前処理】
加速度センサのデータには人の動きに起因する加速度と重力に起因する加速度が混ざっており，後者はセンサーの取り付け位置や身長などで微妙に変わりますので除去する必要があります. また，センサーの取り付け角度や姿勢の影響を除去する為に加速度のノルムだけを考える事にします. また元データのサンプリングレート52Hzは高すぎるので1Hzまで減らしました. すると下図のような系列データが得られます. 詳しい処理内容はプログラムのコメントに書いてあります.

prog21-3.py

以下が状態遷移の様子です. このデータセットは全員が大体同じシナリオでやるみたいで, あまりおもしろくありませんでした. コンピュータで仕事をしている所から開始し，歩いたり階段の昇り降りをした後，人と立ち話をして終わるという流れの様です.

基本的には同じ状態にとどまり続ける確率が高い事，異なる動作と動作の間には必ずstandingが入る事などの特徴が学習されています.

以下はemission分布の学習結果です. 分布の種類はガンマ分布としました. 前処理が正しければ，横軸は動加速度のノルムの二乗になっているはずです. スケーリング調整はしてません.

working at computer → standing → talking while standing → … → walking と順に加速度が大きくなる傾向がある事が分かります.

パラメータ学習が完了したら，次はそれを使って新しい系列データに対するラベリングなどを行いたいですが，その為のアルゴリズムの紹介は次回にまわします.

HMMの学習(ラベルが隠れている場合)

本題のラベルが隠れている場合の学習に進みます. 隠れ変数がありますのでEM法や変分ベイズやランダムサンプリングを使う事になります.

以下，HMM(隠れ状態がカテゴリカル)の場合の汎用的なEM法のアルゴリズムの導出を行います.

$\boldsymbol{\pi},\mathbf{A},\boldsymbol{\phi}$ を全て合わせて $\boldsymbol{\theta}$ と書く事にします.

EM法を復習すると，$\boldsymbol{\theta}$ を適当に初期化し $\mathcal{Q}$ 関数 \[ \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) = \sum_{\mathbf{z}} p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta}^{\mathrm{old}})\log p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) \] が最大となるような $\boldsymbol{\theta}$ にそれを更新するという事を繰り返せば良いのでした.

簡単の為, 系列データが一本の場合を考え \[ \begin{aligned} \gamma_{ik} &= p(z_i =k | \mathbf{x},\boldsymbol{\theta}^{\mathrm{old}}) \\ \xi_{ijk} &= p(z_{i-1}=j,z_i=k|\mathbf{x},\boldsymbol{\theta}^{\mathrm{old}}) \end{aligned} \] とおきます.

すると， $\mathcal{Q}$ 関数は以下のようになります. \[ \begin{aligned} \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) &= \sum_{k=1}^K \gamma_{1k}\log \pi_k + \sum_{i=1}^N\sum_{j=1}^K\sum_{k=1}^K\xi_{ijk}\log A_{jk} \\ &+ \sum_{i=1}^N\sum_{k=1}^K\gamma_{ik}\log p(\mathbf{x}_i|\boldsymbol{\phi}_k) \end{aligned} \]

EM法のM stepでは $\gamma,\xi$ を固定した上でこれが最大となる $\boldsymbol{\theta}$ を求めます. 先ほどのラベルが与えられている場合と全く同様にラグランジュの未定乗数法を用いて計算を行うと \[ \begin{aligned} \pi_k &= \frac{\gamma_{1k}}{\sum_{k=1}^K\gamma_{1k}} \\ A_{jk} &= \frac{\sum_{i=2}^N \xi_{ijk}}{\sum_{i=2}^N\sum_{k=1}^K \xi_{ijk}} \end{aligned} \] となります.

$\boldsymbol{\phi}_k$ の更新式はemission確率 $p(\mathbf{x}_i|\boldsymbol{\phi}_k)$ のモデルに依存しますが， \[ \begin{aligned} \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) &= \sum_{k=1}^K \gamma_{1k}\log \pi_k + \sum_{i=1}^N\sum_{j=1}^K\sum_{k=1}^K\xi_{ijk}\log A_{jk} \\ &+ \sum_{i=1}^N\sum_{k=1}^K\gamma_{ik}\log p(\mathbf{x}_i|\boldsymbol{\phi}_k) \end{aligned} \] の一番最後の項しか $\boldsymbol{\phi}_k$ に依存しないので， \[ \begin{aligned} \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) & = \sum_{i=1}^N\sum_{k=1}^K\gamma_{ik}\log p(\mathbf{x}_i|\boldsymbol{\phi}_k) + \mathrm{const}. \end{aligned} \] の最大化を行えば良いです. これは第19回にやったのと全く同じ形になっているので，更新式も同じです.

例えば $p(\mathbf{x}_i|\boldsymbol{\phi}_k)$ が正規分布 \[ p(\mathbf{x}_i|\boldsymbol{\phi}_k) = \mathcal{N}(\mathbf{x}_i | \boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k) \] ならば, 更新式は \[ \begin{aligned} \boldsymbol{\mu}_k &= \frac{\sum_{i=1}^N \gamma_{ik}\mathbf{x}_i}{\sum_{i=1}^N\gamma_{ik}} \\ \boldsymbol{\Sigma}_k &= \frac{\sum_{i=1}^N \gamma_{ik}(\mathbf{x}_i-\boldsymbol{\mu}_k)(\mathbf{x}_i-\boldsymbol{\mu}_k)^T}{\sum_{i=1}^N \gamma_{ik}} \end{aligned} \] という事になります.

続いてE stepで行う $\gamma_{ik}$ と $\xi_{ijk}$ の学習です. こちらを効率よく計算する為には 前向き後ろ向きアルゴリズム (forward backward algorithm) という動的計画法に基づくアルゴリズムを使います.

まず $\gamma_{ik}$ を求める為には \[ \gamma_{i} = p(z_i|\mathbf{x}) = \frac{p(\mathbf{x}|z_i)p(z_i)}{p(\mathbf{x})} \] より $\boldsymbol{\theta}^{\mathrm{old}}$ を使って $p(\mathbf{x}|z_i)$ を計算する事が出来れば良いです.

ここで $z_i$ の値が定まると， $i$ より過去と未来が独立になります.

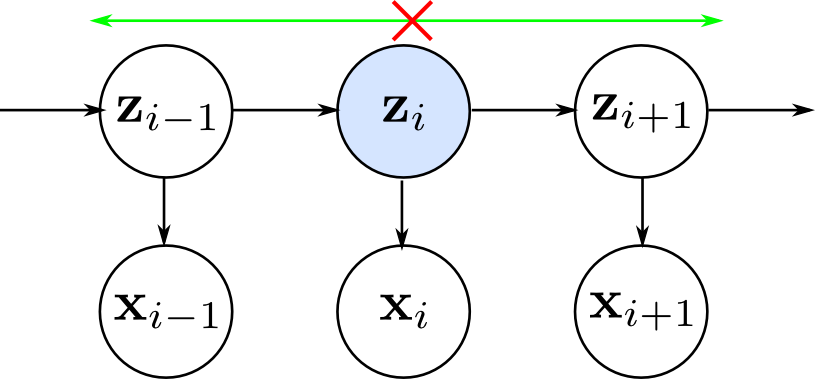
つまり \[ p(\mathbf{x}|z_i) = p(\mathbf{x}_1,\ldots,\mathbf{x}_i|z_i)p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_i) \] という分解が出来ます.

すると, \[ p(\mathbf{x}_1,\ldots,\mathbf{x}_i|z_i)p(z_i) = p(\mathbf{x}_1,\ldots,\mathbf{x}_i,z_i) \] である事を使えば \[ \gamma_{ik} = p(z_i|\mathbf{x}) = \frac{p(\mathbf{x}_1,\ldots,\mathbf{x}_i,z_i)p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_i)}{p(\mathbf{x})} \] となります.

そこで \[ \begin{aligned} \alpha(z_i) &= p(\mathbf{x}_1,\ldots,\mathbf{x}_i,z_i) \\ \beta(z_i) &= p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_i) \end{aligned} \] とおきましょう.

条件付き独立性に注意して変形していくと，$\alpha$ の漸化式を導く事が出来ます. \[ \begin{aligned} \alpha(z_i) &= p(\mathbf{x}_1,\ldots,\mathbf{x}_i,z_i) \\ &= p(\mathbf{x}_1,\ldots,\mathbf{x}_i|z_i) p(z_i) \\ &= p(\mathbf{x}_i|z_i)p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}|z_i)p(z_i) \\ &= p(\mathbf{x}_i|z_i)p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}, z_i) \\ &= p(\mathbf{x}_i|z_i)\sum_{z_{i-1}}p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}, z_i, z_{i-1}) \\ &= p(\mathbf{x}_i|z_i)\sum_{z_{i-1}}p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}, z_i|z_{i-1})p(z_{i-1}) \\ &= p(\mathbf{x}_i|z_i)\sum_{z_{i-1}}p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}|z_{i-1})p(z_i|z_{i-1})p(z_{i-1}) \\ &= p(\mathbf{x}_i|z_i)\sum_{z_{i-1}}p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1},z_{i-1})p(z_i|z_{i-1}) \\ &= p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})\sum_{z_{i-1}}\alpha(z_{i-1})A_{z_{i-1},z_i} \\ \end{aligned} \]

初期値は \[ \alpha(z_1) = p(\mathbf{x}_1|z_1)p(z_1) = p(\mathbf{x}_1|\boldsymbol{\phi}_{z_1})\pi_{z_1} \] となります.

以上が前向き後ろ向きアルゴリズムにおける「前向き」の部分の計算です.

同様にして $\beta$ の漸化式も導けます. \[ \begin{aligned} \beta(z_i) &= p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_i) \\ &= \sum_{z_{i+1}} p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N,z_{i+1} |z_i) \\ &= \sum_{z_{i+1}} p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_{i+1},z_i)p(z_{i+1} |z_i) \\ &= \sum_{z_{i+1}} p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_{i+1})p(z_{i+1} |z_i) \\ &= \sum_{z_{i+1}} p(\mathbf{x}_{i+2},\ldots,\mathbf{x}_N|z_{i+1})p(\mathbf{x}_{i+1}|z_{i+1})p(z_{i+1} |z_i) \\ &= \sum_{z_{i+1}} \beta(z_{i+1})p(\mathbf{x}_{i+1}|\boldsymbol{\phi}_{z_{i+1}})A_{z_i,z_{i+1}} \end{aligned} \]

こちらの初期値ですが，ステップ $N$ 以降の値は存在しないので $\beta(z_N) = 1$ となります.

以上が前向き後ろ向きアルゴリズムにおける「後ろ向き」の部分の計算です.

また $p(\mathbf{x})$ の計算が残っていますがこれは \[ p(\mathbf{x}) = \sum_{z_N} p(\mathbf{x}_1,\ldots,\mathbf{x}_N,z_N) = \sum_{z_N}\alpha(z_N) \] として計算する事が出来ます.

続いて $\xi_{ijk}$ の更新式ですが，先ほどと同様に条件付き独立性に注意して式を変形していくと \[ \begin{aligned} \xi_{i} &= p(z_{i-1},z_i|\mathbf{x}) \\ &= \frac{p(\mathbf{x}|z_{i-1},z_i)p(z_{i-1},z_i)}{p(\mathbf{x})} \\ &= \frac{p(\mathbf{x}_1,\ldots,\mathbf{x}_{i-1}|z_{i-1})p(\mathbf{x}_i|z_i)p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_{N}|z_i)p(z_i|z_{i-1})p(z_{i-1})}{p(\mathbf{x})} \\ &= \frac{\alpha(z_{i-1})\beta(z_{i})p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i})A_{z_{i-1},z_i}}{p(\mathbf{x})} \end{aligned} \] となり，既に計算した $\alpha,\beta$ を用いて求める事が出来ます.

系列が複数 $\mathbf{x}^{(1)},\ldots,\mathbf{x}^{(N)}$ ある場合ですが， E stepで計算する $\gamma_{i},\xi_{i}$ は各系列毎に独立なので別々に前向き後ろ向きアルゴリズムで計算すれば良いです.

一方，M stepで計算する $\boldsymbol{\theta}$ は全系列で共有していますので, $\mathcal{Q}$ 関数を \[ \begin{aligned} \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) &= \sum_{\ell=1}^N\left[ \sum_{k=1}^K \gamma^{(\ell)}_{1k}\log \pi_k + \sum_{i=1}^{N_\ell}\sum_{j=1}^K\sum_{k=1}^K\xi^{(\ell)}_{ijk}\log A_{jk}\right. \\ &+ \left.\sum_{i=1}^{N_\ell}\sum_{k=1}^K\gamma^{(\ell)}_{ik}\log p(\mathbf{x}_i|\boldsymbol{\phi}_k)\right] \end{aligned} \] に直して計算をします. $\Sigma$ が１つ付くだけで計算式は変わりません.

実際に計算する際には浮動小数点数のアンダーフローへの対処が必要です. $\alpha,\beta$ は以下の様に定義されているので，$\alpha(z_i)$ は $i$ が大きいほど $\beta(z_i)$ は $i$ が小さいほど その値が指数的に小さくなっていきます. \[ \begin{aligned} \alpha(z_i) &= p(\mathbf{x}_1,\ldots,\mathbf{x}_i,z_i) \\ \beta(z_i) &= p(\mathbf{x}_{i+1},\ldots,\mathbf{x}_N|z_i) \end{aligned} \]

対数を取って計算する場合には，$\Sigma$ が含まれている為以下のようにして logsumexp 関数を利用します. \[ \log \alpha(z_i) = \log p(\mathbf{x}_i|\boldsymbol{\phi}_{z_i}) + \log \sum_{z_{i-1}} \exp \left\{\log \alpha(z_{i-1}) + \log A_{z_{i-1},z_i} \right\} \] スケーリングを用いる方法もありPRML本ではこちらが紹介されています. 一概にどちらかが優れているという事はありません.

手書き文字のストローク のデータに今のアルゴリズムを適用して，「2」の書き方を学習させてみます. このデータセットには11人分, 22文字のサンプルが含まれています.

prog21-2.py

PRML本で紹介されている方法では「今どの部分を描いているか？」を $K$ 個の値で表します. 状態 $1$ は描き始め, 状態 $K$ は描き終わった事を表します.

部分 $k$ を書いている状態からの遷移は，次も同じ部分であるか続く部分 $k+1$ に進むかの2通りしかないと考える事が出来ます. つまり状態遷移図は下のようになります. このようなモデルを left-to-right HMM と呼びます.

この場合，遷移行列 $A$ の成分の多くが $0$ になりパラメータ数を減らす事が出来ます.

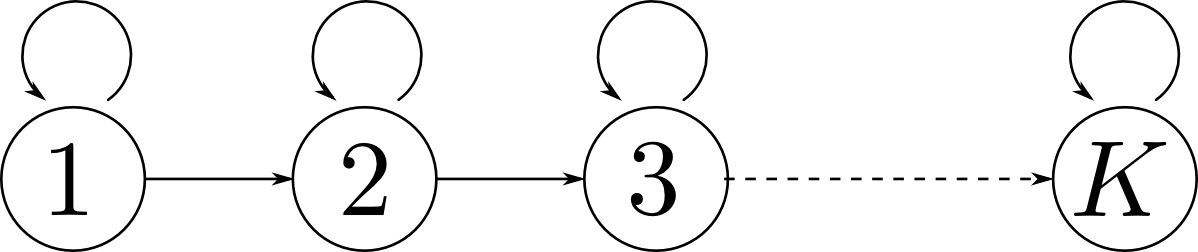
emission分布には分散を固定した対称的な二次元正規分布を使うことにしました. つまり \[ p(\mathbf{x}_i|z_i=k) = N(\mathbf{x}_i|\boldsymbol{\mu}_k,\sigma^2I) \] です. 今回は学習データ数が非常に少ない為モデルの自由度を下げました.

以下が学習された $\boldsymbol{\mu}_k$ の様子です. $\sigma=300$ としました.

prog21-4.py

よりデータ数が多いならば，emissionをもっと複雑にしたりleft-to-rightモデルよりも自由度の高い遷移を考える事が出来ると思います.

今回はここで終了します．

次回はHMMの続きと，テキスト第12章「連続潜在変数」をやります.