パターン認識・
機械学習勉強会
第20回
@ナビプラス
中村晃一2014年9月18日
謝辞
会場・設備の提供をしていただきました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.
変分ベイズ
テキスト第10章「近似推論」に進みます. 内容は変分推論(variational inference)または変分ベイズ(variational Bayes)と呼ばれる手法の解説です. 非常にボリュームがある内容なので問題を1つだけやってみます. たった1つと言えども非常に難しいです.しかし,これを理解出来れば実用的な様々な複雑なモデルを解けるようになります.
その後,変分ベイズに変わるアプローチであるランダムサンプリング(random sampling)を用いて同じ問題を解く方法を解説します.
確率的なモデリングに基づく機械学習の問題の多くは,現象を観測変数 $\mathbf{x}$, 隠れ変数 $\mathbf{z}$ とパラメータ $\boldsymbol{\theta}$ で記述される分布 \[ p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) \] でモデリングし, $\mathbf{x}$ を観測した結果から $\boldsymbol{\theta}$ や $\mathbf{z}$ を推定するという問題に帰着します.
$\boldsymbol{\theta}$ の推定には尤度 \[ p(\mathbf{x}|\boldsymbol{\theta}) \] $\mathbf{z}$ の推定には事後分布 \[ p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta}) \] の計算が必要です.
問題は $p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta})$ が複雑だとこれらを解析的に計算できなくなってしまうという事です.
$p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta})$ が複雑な場合には
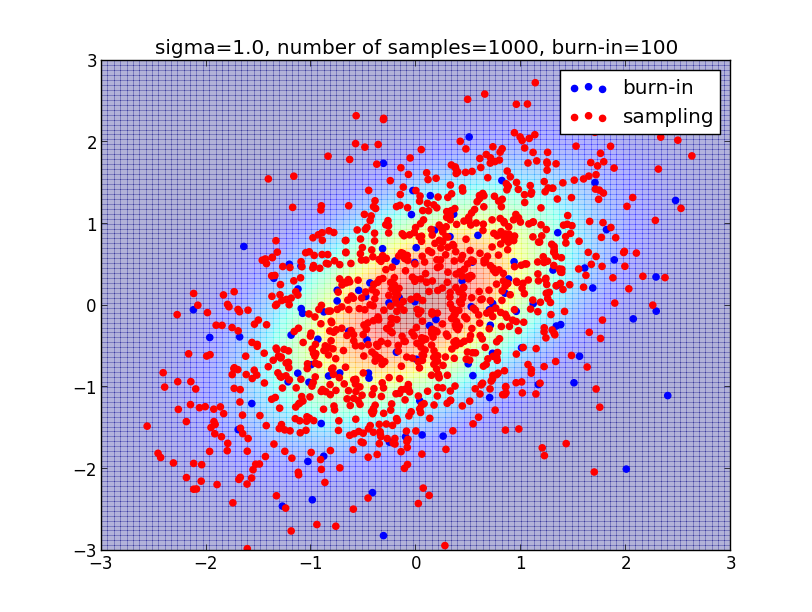
- マルコフ連鎖モンテカルロ法(MCMC法)などを使って数値的に計算を行う
- 何らかの近似を行って,解析的に計算できるようにする
という方法を取ることが出来ます.
数値計算の利点は,原理的には任意の精度で正確な計算が出来るという事です. 欠点は,高い計算機性能が必要になるという事です.
近似を用いる場合の利点・欠点はこれとは正反対で, 正確さを犠牲にする代わりにより大きな問題を解くことが出来るようになります.
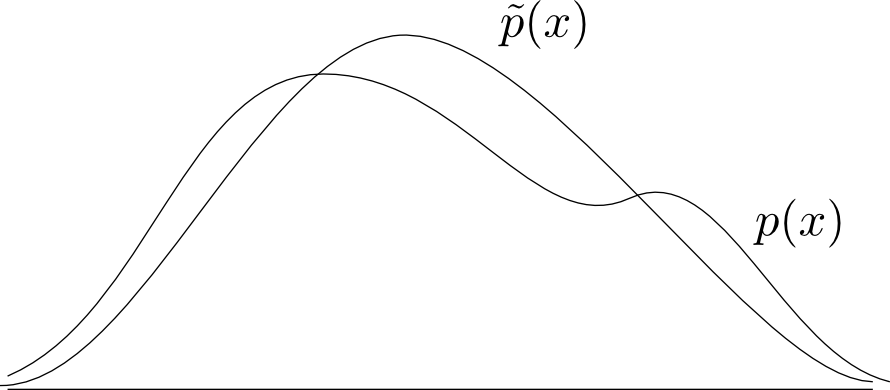
変分ベイズは 変分法 (calculus of variations) という,物理学の分野で生まれた手法を基にしています.
変分法とは関数 $f$ を変数として取り実数値等を返す 汎関数 (functional) $I[f]$ が極値または停留点を取るような $f$ を求める手法です.
変分法を用いる問題を1つ紹介します. 但し,変分ベイズでは今からやるようないわゆる変分法の計算は使わないのでスキップしても良いです.
【問題】
$\mathbb{R}$ 上の連続分布 $p(x)$ で平均が $0$, 分散が $1$ であるもののうち,
エントロピー
\[ I[p] = -\int p(x)\log p(x)\mathrm{d} x \]
が最大になるようなものは何でしょうか?
通常の極値問題と同じく \[ \text{$I[p]$ が極値ならば, $p$ に微小変化を加えても $I[p]$ は変化しない} \] という事を使います.
しかし, $p(x)$ は関数ですから,無数の微小変化の方法があります. そこで,関数 $\eta(x)$ を任意に固定し, $\varepsilon$ を実数値変数として
\[ p(x) \rightarrow p(x) + \varepsilon \times \eta(x) \]
と書けるものだけを考え,$\varepsilon=0$ 付近で変化率が $0$ になる条件を求めます.
(直感的には, 点 $p$ での方向微分係数が任意の方向ベクトル $\eta$ に関して $0$ となれば良いという事です.)

確率の和が $1$, 平均が $0$, 分散が $1$ という制約条件があるのでラグランジュの未定乗数 $\alpha,\beta,\gamma$ を導入して \[ \begin{aligned} F[p] &= -\int p(x)\log p(x)\mathrm{d} x + \alpha\left(\int p(x)\mathrm{d}x - 1\right) + \beta\int xp(x)\mathrm{d}x + \gamma\left(\int x^2p(x)\mathrm{d}x - 1 \right)\\ &= - \int \left\{ \log p(x) - \alpha - \beta x- \gamma x^2\right\}p(x)\mathrm{d} x - \alpha - \gamma \end{aligned} \] が停留点を取る条件を求めます.
$p$ に微小変化を加えると, \[ - \int \left\{ \log \color{red}{(p+\varepsilon\eta)} - \alpha - \beta x- \gamma x^2\right\}\color{red}{(p+\varepsilon\eta)}\mathrm{d} x - \alpha - \gamma \] となります. これを $\varepsilon$ で微分すると \[ - \int\left\{ \log (p+\varepsilon\eta) - \alpha - \beta x- \gamma x^2\right\}\eta\mathrm{d} x - \int \eta\mathrm{d} x \] となり,$\varepsilon=0$ でこれが $0$ となる事が必要です. \[ - \int\left\{ \log p - \alpha - \beta x- \gamma x^2 + 1 \right\}\eta\mathrm{d} x = 0 \]
これが任意の $\eta(x)$ で成立するので \[ \log p - \alpha - \beta x- \gamma x^2 + 1 = 0 \Leftrightarrow p(x) = \exp\left\{\alpha+\beta x+\gamma x^2-1\right\}\] となります. 発散しない為には $\gamma < 0$ が必要であることに注意します. ここで \[ \int p'(x)\mathrm{d} x = \left[p(x)\right]_{-\infty}^{\infty} = 0 \] ですが, \[ \text{(左辺)} = \int \{\beta + 2\gamma x\}p(x)\mathrm{d}x = \beta \] なので $\beta = 0$ です.
すると, 制約条件より \[ \int p(x)\mathrm{d} x = \sqrt{\frac{\pi}{-\gamma}}e^{\alpha-1}= 1 \Leftrightarrow e^{\alpha-1} = \sqrt{\frac{-\gamma}{\pi}} \] から \[ p(x) = \sqrt{\frac{-\gamma}{\pi}}\exp(\gamma x^2) \] となり,さらに \[ \int x^2p(x)\mathrm{d} x = \frac{1}{-2\gamma} = 1\Leftrightarrow \gamma = -\frac{1}{2} \] となります.
以上より,平均が $0$で分散が $1$ の連続分布でエントロピー \[ -\int p(x)\log p(x)\mathrm{d} x \] が最大となる分布は標準正規分布 \[ N(x|0,1) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right) \] である事が証明されました. 平均を $\mu$, 分散を $\sigma^2$ と一般化した場合,多次元の場合も全く同様です.
ある母集団についてその平均と分散以外に一切の事前知識がない場合,エントロピーという観点ではそれを正規分布だと仮定すると余計な構造が入らないので妥当だと考える事が出来ます.
話を変分ベイズに戻します. 前回紹介した対数尤度 $\log p(\mathbf{x})$ の分解公式 \[ \begin{aligned} \log p(\mathbf{x}) &= \mathcal{L}(q) + \mathrm{KL}(q||p) \\ \mathcal{L}(q) &= \int q(\mathbf{z})\log \frac{p(\mathbf{x},\mathbf{z})}{q(\mathbf{z})}\mathrm{d}\mathbf{z} \\ \mathrm{KL}(q||p) &= -\int q(\mathbf{z}) \log \frac{p(\mathbf{z}|\mathbf{x})}{q(\mathbf{z})}\mathrm{d}\mathbf{z} \end{aligned} \] を考えます.
$\log p(\mathbf{x})$ を最大化する為には $\mathcal{L}(q)$ を最大化すれば良く,その時 $\mathrm{KL}(q||p)$ は最小値 $0$ を取ります.
\[ \mathrm{KL}(q||p)=0 \Leftrightarrow \color{red}{ p(\mathbf{z}|\mathbf{x}) = q(\mathbf{z}) } \] なので,$\mathcal{L}(q)$ の最大化を行うことによって求めたかった $\mathbf{z}$ の事後分布 $p(\mathbf{z}|\mathbf{x})$ を求める事が出来ます.
$\mathcal{L}(q)$ は関数 $q(\mathbf{z})$ を変数とする汎関数であるので,対数尤度の最大化及び事後分布の導出が変分問題に帰着しました.
ここで \[ \text{$\mathcal{L}(q)$ を最大にする $q(\mathbf{z})$ をありとあらゆる関数から探す} \] 事が難しいとしましょう.
変分ベイズでは $q(\mathbf{z})$ の探索範囲を制限する事によって,近似的に $\mathcal{L}(q)$ の最大化を行います. 過学習を抑制する効果もあります.
平均場近似
$q(\mathbf{z})$ が \[ q(\mathbf{z}) = \prod_{i=1}^C q_i(\mathbf{z}_i) \] と幾つかの独立な分布の積に分解出来る場合のみを考えるという近似を 平均場近似(mean field approximation) と呼びます. この近似では分解可能性のみを仮定し,各 $q_i(\mathbf{z}_i)$ がどのような分布であるかは一切仮定しません.
平均場(mean field) という用語は物理学に由来しており,もともとは解析的に解けない多体問題を解析的に解ける一体問題や二体問題に帰着させる為の近似モデルです.
$\mathcal{L}(q)$ に平均場近似を用いると \[ \begin{aligned} \mathcal{L}(q) &= \int q(\mathbf{z})\log \frac{p(\mathbf{x},\mathbf{z})}{q(\mathbf{z})}\mathrm{d}\mathbf{z} \\ &= \int q(\mathbf{z})\left\{\log p(\mathbf{x},\mathbf{z}) - \log q(\mathbf{z}) \right\}\mathrm{d}\mathbf{z} \\ &= \int \prod_{i=1}^C q_i(\mathbf{z}_i)\left\{\log p(\mathbf{x},\mathbf{z}) - \sum_{i=1}^C \log q_i(\mathbf{z}_i)\right\}\mathrm{d}\mathbf{z} \end{aligned} \] となり,
因子 $q_j(\mathbf{z}_j)$ だけを別にすれば \[ \mathcal{L}(q) = \int q_j\left\{\int \log p(\mathbf{x},\mathbf{z})\prod_{i\neq j}q_i(\mathbf{z}_i)\mathrm{d}\mathbf{z}_i\right\}\mathrm{d}\mathbf{z}_j - \int q_j\log q_j\mathrm{d}\mathbf{z}_j + \mathrm{const}. \] となります.
この $\{\cdots \}$ の部分は $\mathbf{z}_j$ 以外の変数群に関する $\log p(\mathbf{x},\mathbf{z})$ の期待値なので,これを \[ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] = \int \log p(\mathbf{x},\mathbf{z})\prod_{i\neq j}q_i(\mathbf{z}_i)\mathrm{d}\mathbf{z}_i \] と書くことにします.
ここで新しい確率分布 $\tilde{p}(\mathbf{x},\mathbf{z}_j)$ を \[ \tilde{p}(\mathbf{x},\mathbf{z}_j) \propto \exp\left\{ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] \right\} \] によって定めれば \[ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] = \log\tilde{p}(\mathbf{x},\mathbf{z}_j) + \mathrm{const}. \] となるので, \[ \begin{aligned} \mathcal{L}(q) &= \int q_j \log \tilde{p}(\mathbf{x},\mathbf{z}_j)\mathrm{d}\mathbf{z}_j - \int q_j \log q_j\mathrm{d}\mathbf{z}_j + \mathrm{const}. \\ &= \int q_j(\mathbf{z}_j)\log\frac{\tilde{p}(\mathbf{x},\mathbf{z}_j)}{q_j(\mathbf{z}_j)}\mathrm{d}\mathbf{z}_j + \mathrm{const}. \\ &= -\mathrm{KL}(q_j || \tilde{p}) + \mathrm{const}. \end{aligned} \] と書けます.
従って,$q_i(i\neq j)$ を固定して $q_j$ のみを動かした時に $\mathcal{L}(q)$ が最大となる条件は カルバックライブラー情報量 \[\mathrm{KL}(q_j || \tilde{p}) \] が最小となる条件で,それは \[ q_j(\mathbf{z}_j) = \tilde{p}(\mathbf{x},\mathbf{z}_j) \] となります. 明示的に書き下せば \[ q_j(\mathbf{z}_j) = \tilde{p}(\mathbf{x},\mathbf{z}_j) = \frac{\exp\left\{ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] \right\}}{\int \exp\left\{ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] \right\}\mathrm{d}\mathbf{z}_j } \] となります. この右辺の期待値計算は $q(\mathbf{z})$ に依存するので,反復計算が必要です.
平均場近似による変分ベイズ
観測変数 $\mathbf{x}$, 隠れ変数 $\mathbf{z}$ に対する同時分布のモデル \[ p(\mathbf{x},\mathbf{z}) \] について $\mathbf{z}$ の事後分布 $p(\mathbf{z}|\mathbf{x})$ を計算する為には,
$\mathbf{z}$ を幾つかの変数群 $\mathbf{z}_i$ に分け,それらの分布 $q_i(\mathbf{z}_i)$ を適当に初期化し, \[ q_j^{\mathrm{new}}(\mathbf{z}_j) \propto \exp\left\{ \mathbb{E}_{i\neq j}\left[\log p(\mathbf{x},\mathbf{z}) \right] \right\} \] によって収束するまで反復を行う.
求めた $q_i(\mathbf{z}_i)$ が事後分布 $p(\mathbf{z}_i|\mathbf{x})$ を近似する分布となる.
では具体的な問題に適用してみます.
最初は自然言語処理におけるトピックモデルの1つである潜在的ディリクレ配分モデル(latent dirichlet allocation, LDAモデル) をやる予定でしたが,入門用としては難しいと思うので「ディリクレ配分」のアイデアを使ったもっと簡単な問題を考えてみました.
UCI Machine Learning Repository で見つけた Zoo Data Setを使って動物のカテゴリを教師なしで学習させてみようと思います.
データセットの内容
- データ数: 101種
- 属性数: 16
- 全てカテゴリカル変数
- 「体毛があるか?」などの二値属性が15種類 と 足の数(0,2,4,5,6,8本)
オリジナルの問題は生物種を独立な $K$ クラスに分離せよという問題です.
しかしここでは,ちょっと趣向を変えて 各生物 $\mathbf{x}_i$ は複数のクラスを配合して出来ると考えてみましょう.
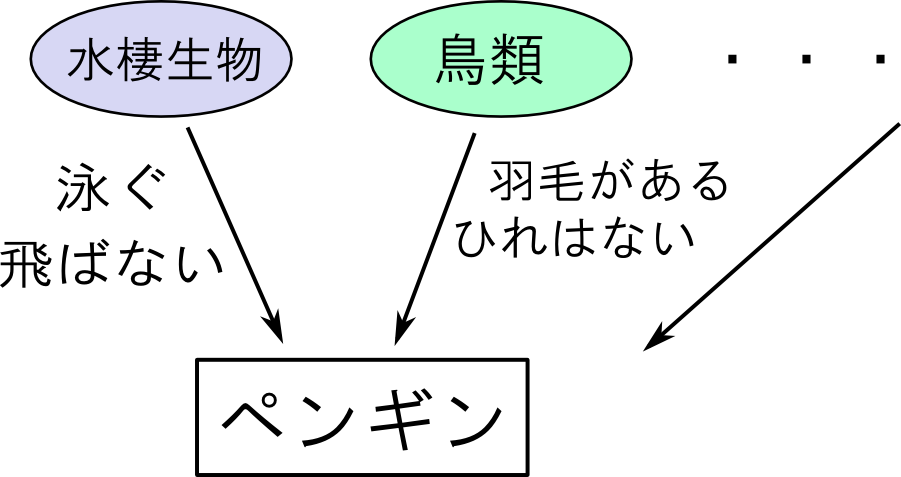
どういう事かと言うと,まず「水棲生物」や「鳥類」などの大きなカテゴリが $K$ 個あるとします. 各カテゴリ毎に「泳ぐ」とか「飛ぶ」など属性値が異なります.
次に,各カテゴリをいくらかずつ配合して生物が作られると考えます.
観測データを $\mathbf{x}=\{\mathbf{x}_1,\ldots,\mathbf{x}_N\}$ とします. 各 $\mathbf{x}_i$ は $M$ 個の属性値からなるベクトルで, 第 $j$ 成分は $1,\ldots,n_j$ のいずれかの値を取るとします.
$\mathbf{x}_i$ は $K$ 個のクラスを比率 \[ \boldsymbol{\theta}_i = (\theta_{i1},\ldots,\theta_{iK}) \] で配合して作られるとします. $\boldsymbol{\theta}_i$ は \[ \theta_{i1},\ldots,\theta_{iK}\geq 0, \quad \theta_{i1} + \cdots + \theta_{iK} = 1 \] を満たす確率変数です.
このような変数に対する事前分布には ディリクレ分布(Dirichlet distribution) を使うと後の計算が楽になります( 共役事前分布(conjugate prior)と呼ばれる性質を持ちます).
今回も各 $\boldsymbol{\theta_i}$ はパラメータが $\boldsymbol{\alpha}$ のディリクレ分布に従うと仮定しましょう.
\[ \boldsymbol{\theta_i} \sim \mathrm{Dir}(\boldsymbol{\alpha}) \]
次は各属性 $j=1,\ldots,M$ をどのクラスから持ってくるかを決めます.
確率変数 \[ \mathbf{z}_{i}=(z_{i1},\ldots,z_{iM}) \] を \[ z_{ij} = k \stackrel{\mathrm{def}}{\Leftrightarrow} \text{(データ $i$ の属性 $j$ はクラス $k$ から持ってくる)} \] と定義します.
どのクラスから持ってくるかは先ほどの配合比 $\boldsymbol{\theta}_i$ に従って選ぶとしましょう. \[ p(z_{ij}=k) = \theta_{ik} \] これはカテゴリ分布(categorical distribution)と呼ばれる分布で,以下のように書きます. \[ z_{ij} \sim \mathrm{Cat}(\boldsymbol{\theta}_i) \]
属性 $j$ が$1,\ldots,n_j$ のどの値を取るかは,その属性を持ってきたクラス毎に異なるとしましょう. そこで,属性 $j$ の値が $\ell$ となる確率を \[ p(x_{ij}=\ell) = \boldsymbol{\phi}_{jk\ell}\qquad \text{($z_{ij}=k$のとき)} \] と置きます. これもやはりカテゴリ分布で \[ x_{ij} \sim \mathrm{Cat}(\boldsymbol{\phi}_{j,z_{ij}}) \] と書けます.
各 $\boldsymbol{\phi}_{jk}$ は \[ \boldsymbol{\phi}_{jk1},\ldots,\boldsymbol{\phi}_{jkn_j}\geq 0,\quad \boldsymbol{\phi}_{jk1}+\cdots + \boldsymbol{\phi}_{jkn_j} = 1 \] を満たす必要があるので,その事前分布はやはりディリクレ分布とします. この分布は属性の種類 $j$ のみに依存するとして,以下のように置きます. \[ \boldsymbol{\phi}_{jk} \sim \mathrm{Dir}(\boldsymbol{\beta}_j) \]
まとめると以下のようになります.
- $N$: データ数, $M$:属性数, $K$: クラス数
- $n_j\,(j=1,\ldots,M)$: 属性 $j$ のカテゴリ数
- パラメータ:$\boldsymbol{\alpha}, \boldsymbol{\beta}_{j}\,(j=1,\ldots,M)$
- クラスの配合比 $\boldsymbol{\theta}_i\,(i=1,\ldots,N)$
- クラス毎の属性値の分布 $\phi_{jk}\,(k=1,\ldots,K,j=1,\ldots,M)$
- 属性の所属クラス $z_{ij}\,(i=1,\ldots,N,j=1,\ldots,M)$
- 観測データ $x_{ij}\,(i=1,\ldots,N,j=1,\ldots,M)$
- モデル \[ \begin{aligned} \boldsymbol{\theta}_i &\sim \mathrm{Dir}(\boldsymbol{\alpha})\\ \boldsymbol{\phi}_{jk} &\sim \mathrm{Dir}(\boldsymbol{\beta}_j)\\ z_{ij} &\sim \mathrm{Cat}(\boldsymbol{\theta}_i)\\ x_{ij} &\sim \mathrm{Cat}(\boldsymbol{\phi}_{j,z_{ij}})\\ \end{aligned} \]
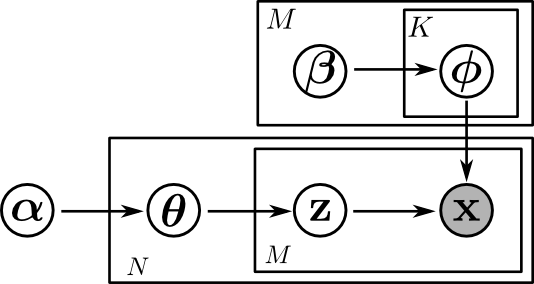
グラフィカルモデルは下図のようになります. 四角い囲みはプレート(plate)と呼ばれ,実際にはプレート内部と同じ形のノードが多数ある事を表しています.
$\boldsymbol{\theta}$ と $\mathbf{z}$ はもちろん独立ではありませんが, 合流部の $\mathbf{x}$ がインスタンス化されている為 $\boldsymbol{\phi}$ もこれらと独立では無いという事がわかります.(第14回資料のd分離性を復習して下さい)
$\mathbf{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}$ の同時分布を計算すると以下のようになります. \[ \begin{aligned} p(\mathbf{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}) &= p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})p(\mathbf{z}|\boldsymbol{\theta})p(\boldsymbol{\theta})p(\boldsymbol{\phi})\\ &= \prod_{i=1}^Np(\boldsymbol{\theta}_i)\prod_{j=1}^M p(x_{ij}|z_{ij},\boldsymbol{\phi})p(z_{ij}|\boldsymbol{\theta}_i)\times \prod_{j=1}^M\prod_{k=1}^Kp(\boldsymbol{\phi}_{jk})\\ &= \prod_{i=1}^N\mathrm{Dir}(\boldsymbol{\theta}_i|\boldsymbol{\alpha})\prod_{j=1}^M \mathrm{Cat}(x_{ij}|\boldsymbol{\phi}_{j,z_{ij}})\mathrm{Cat}(z_{ij}|\boldsymbol{\theta}_i)\times \prod_{j=1}^M\prod_{k=1}^K\mathrm{Dir}(\boldsymbol{\phi}_{jk}|\boldsymbol{\beta}_{j})\\ &\propto \prod_{i=1}^N\left(\prod_{k=1}^K\theta_{ik}^{\alpha_{k}-1}\right)\prod_{j=1}^M\phi_{j,z_{ij},x_{ij}}\theta_{i,z_{ij}}\times \prod_{j=1}^M\prod_{k=1}^K\prod_{\ell=1}^{n_j}\phi_{jk\ell}^{\beta_{j\ell}-1} \end{aligned} \] 目標は隠れ変数の事後分布 \[ q(\mathrm{z},\boldsymbol{\theta},\boldsymbol{\phi}) = p(\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}|\mathbf{x}) \] を求める事です. 工夫なしでは結構大変そうですね.
では変分ベイズの計算に進みます.
先ほど説明したように,真の事後分布 $p(\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}|\mathbf{x})$ において $\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}$ は互いに従属です. しかし,$\mathbf{z}$ と $\{\boldsymbol{\theta},\boldsymbol{\phi}\}$ が独立であると仮定して \[ \color{red}{ q(\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}) = q(\mathbf{z})q(\boldsymbol{\theta},\boldsymbol{\phi}) } \] を満たす $q$ で真の事後分布を近似する事を考えましょう.
本モデルに対する近似はこの一箇所だけです. また,繰り返しになりますが $q(\mathbf{z})$ と $q(\boldsymbol{\theta},\boldsymbol{\phi})$ が具体的にどのような分布であるかは自然に導かれるので考えなくて良いです.
まず $\mathbf{z}$ に関する更新式は以下のようになります. $\mathbf{z}$ を含まない項は定数である事に注意して下さい. \[ \begin{aligned} \log q^{\mathrm{new}}(\mathbf{z}) &= \mathbb{E}_{\boldsymbol{\theta},\boldsymbol{\phi}}[\log p(\mathbb{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi})] +\mathrm{const}.\\ &= \mathbb{E}_{\boldsymbol{\theta},\boldsymbol{\phi}}[\log p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})p(\mathbf{z}|\boldsymbol{\theta})p(\boldsymbol{\theta})p(\boldsymbol{\phi})]+\mathrm{const}.\\ &= \mathbb{E}_{\boldsymbol{\theta}}[\log p(\mathbf{z}|\boldsymbol{\theta})] + \mathbb{E}_{\boldsymbol{\phi}}[\log p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})]+\mathrm{const}.\\ &= \sum_{i=1}^N\sum_{j=1}^M\left\{\mathbb{E}_{\boldsymbol{\theta}_i}[\log p(z_{ij}|\boldsymbol{\theta}_i)] + \mathbb{E}_{\boldsymbol{\phi}}[\log p(x_{ij}|z_{ij},\boldsymbol{\phi})]\right\}+\mathrm{const}.\\ &= \sum_{i=1}^N\sum_{j=1}^M\left\{\mathbb{E}_{\boldsymbol{\theta}_i}[\log \theta_{i,z_{ij}}] + \mathbb{E}_{\boldsymbol{\phi}}[\log \phi_{j,z_{ij},x_{ij}}]\right\}+\mathrm{const}.\\ \end{aligned} \]
式を簡単にする為に新たな定数 $\gamma_{ijk}$ を \[ \log \gamma_{ijk} \stackrel{\mathrm{def}}{=} \mathbb{E}_{\boldsymbol{\theta}_i}[\log \theta_{ik}] + \mathbb{E}_{\boldsymbol{\phi}}[\log \phi_{jk,x_{ij}}] \] を満たすように取れば \[ \log q^{\mathrm{new}}(\mathbf{z}) = \sum_{i=1}^N\sum_{j=1}^M\log \gamma_{ij,z_{ij}} + \mathrm{const}. \] つまり \[ q^{\mathrm{new}}(\mathbf{z}) \propto \prod_{i=1}^N\prod_{j=1}^M \gamma_{ij,z_{ij}} \] となるので, \[ r_{ijk}\stackrel{\mathrm{def}}{=} q^{\mathrm{new}}(z_{ij}=k) = \frac{\gamma_{ijk}}{\sum_{k=1}^K\gamma_{ijk}} \] が得られます.
$\gamma_{ijk}$ の定義に出てくる期待値の計算は $\boldsymbol{\theta},\boldsymbol{\phi}$ の分布が分かった後です.
次は $\boldsymbol{\theta},\boldsymbol{\phi}$ の更新式を計算していきます. \[ \begin{aligned} \log q^{\mathrm{new}}(\boldsymbol{\theta},\boldsymbol{\phi}) &= \mathbb{E}_{\mathbf{z}}[\log p(\mathbb{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi})] +\mathrm{const}.\\ &= \mathbb{E}_{\mathbf{z}}[\log p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})p(\mathbf{z}|\boldsymbol{\theta})p(\boldsymbol{\theta})p(\boldsymbol{\phi})]+\mathrm{const}.\\ &= \log p(\boldsymbol{\theta})p(\boldsymbol{\phi}) + \mathbb{E}_{\mathbf{z}}[\log p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})p(\mathbf{z}|\boldsymbol{\theta})]+\mathrm{const}.\\ \end{aligned} \] となり,期待値の部分は今定義した $r_{ijk}$ を使えば \[ \begin{aligned} \mathbb{E}_{\mathbf{z}}[\log p(\mathbf{x}|\mathbf{z},\boldsymbol{\phi})p(\mathbf{z}|\boldsymbol{\theta})] &= \sum_{i=1}^N\sum_{j=1}^M \mathbb{E}_{z_{ij}}[\log \phi_{j,z_{ij},x_{ij}}\theta_{i,z_{ij}}]\\ &= \sum_{i=1}^N\sum_{j=1}^M\sum_{k=1}^Kr_{ijk} \log \phi_{jk,x_{ij}}\theta_{ik} \\ &= \sum_{i=1}^N\sum_{j=1}^M\sum_{k=1}^K\sum_{\ell=1}^{n_j}[x_{ij}=\ell]r_{ijk} \log \phi_{jk\ell}\theta_{ik} \\ \end{aligned} \] となります. 但し $[x_{ij}=\ell]$ は等式が成り立つなら $1$, そうでなければ $0$ です.
よって \[ \begin{aligned} \log q^{\mathrm{new}}(\boldsymbol{\theta},\boldsymbol{\phi}) &= \sum_{i=1}^N\sum_{k=1}^K\log \theta_{ik}^{\alpha_k-1}+\sum_{j=1}^M\sum_{k=1}^K\sum_{\ell=1}^{n_j}\log \phi_{jk\ell}^{\beta_{j\ell}-1}\\ &+ \sum_{i=1}^N\sum_{j=1}^M\sum_{k=1}^K\sum_{\ell=1}^{n_j}[x_{ij}=\ell]r_{ijk} \log \phi_{jk\ell}\theta_{ik}+\mathrm{const}. \\ \end{aligned} \] つまり, \[ \begin{aligned} q^{\mathrm{new}}(\boldsymbol{\theta},\boldsymbol{\phi}) &\propto \prod_{i=1}^N\left\{\prod_{k=1}^K\theta_{ik}^{\alpha_k+\sum_{j=1}^Mr_{ijk}-1}\right\}\times \prod_{j=1}^M\prod_{k=1}^K\left\{\prod_{\ell=1}^{n_j}\phi_{jk\ell}^{\beta_{j\ell}+\sum_{i=1}^N[x_{ij}=\ell]r_{ijk}-1}\right\} \end{aligned} \] となります. これから,更新後も $\boldsymbol{\theta}_i$ や $\boldsymbol{\phi}_{jk}$ はディリクレ分布に従う事が解ります.
よって,見やすくする為に新しい変数を \[ \begin{aligned} A_{ik} &\stackrel{\mathrm{def}}{=} \alpha_k+\sum_{j=1}^Mr_{ijk} \\ B_{jk\ell} &\stackrel{\mathrm{def}}{=} \beta_{j\ell}+\sum_{i=1}^N[x_{ij}=\ell]r_{ijk} \end{aligned} \] と定義すれば \[ \begin{aligned} q^{\mathrm{new}}(\boldsymbol{\theta}_i) &= \mathrm{Dir}(\boldsymbol{\theta}_i|\mathbf{A}_i) \\ q^{\mathrm{new}}(\boldsymbol{\phi}_{jk}) &= \mathrm{Dir}(\boldsymbol{\phi}_{jk}|\mathbf{B}_{jk}) \\ \end{aligned} \] となります.
$\boldsymbol{\theta},\boldsymbol{\phi}$ の分布が分かったので,保留していた \[ \log \gamma_{ijk} \stackrel{\mathrm{def}}{=} \mathbb{E}_{\boldsymbol{\theta}_i}[\log \theta_{ik}] + \mathbb{E}_{\boldsymbol{\phi}}[\log \phi_{jk,x_{ij}}] \] の計算を進める事が出来ます.
ディリクレ分布 $\mathrm{Dir}(\mathbf{x}|\boldsymbol{\alpha})$ における $\log x_i$ の期待値は解析的に求める事ができて \[ \mathbb{E}[\log x_i] = \psi(\alpha_i) - \psi\left(\sum_{i}\alpha_i\right) \] となります. $\psi(x)$ は ディガンマ関数(digamma function)と呼ばれる関数です.
よって \[ \mathbb{E}_{\boldsymbol{\theta}_i}[\log \theta_{ik}] = \psi(A_{ik}) - \psi\left(\sum_{k=1}^KA_{ik}\right) \] また \[ \begin{aligned} \mathbb{E}_{\boldsymbol{\phi}}[\log \phi_{jk,x_{ij}}] &= \sum_{\ell=1}^{n_j}[x_{ij}=\ell]\mathbb{E}_{\boldsymbol{\phi}}[\log \phi_{jk\ell}] \\ &= \sum_{\ell=1}^{n_j}[x_{ij}=\ell]\left\{\psi(B_{jk\ell})-\psi\left(\sum_{\ell}^{n_j}B_{jk\ell}\right)\right\} \\ &= \sum_{\ell=1}^{n_j}[x_{ij}=\ell]\psi(B_{jk\ell})-\psi\left(\sum_{\ell}^{n_j}B_{jk\ell}\right) \\ \end{aligned} \] となります.
以上全てをまとめると以下のようになります.
\[ A_{ik} = \alpha_k,\quad B_{jk\ell} = \beta_{j\ell} \] と初期化し収束するまで以下の反復を繰り返す. \[ \begin{aligned} \log\gamma^{\mathrm{new}}_{ijk} &= \psi(A_{ik}) - \psi\left(\sum_{k=1}^KA_{ik}\right) + \sum_{\ell=1}^{n_j}[x_{ij}=\ell]\psi(B_{jk\ell})-\psi\left(\sum_{\ell}^{n_j}B_{jk\ell}\right) \\ A^{\mathrm{new}}_{ik} &= \alpha_k + \sum_{j=1}^Mr_{ijk} \qquad \left(r_{ijk} = \frac{\gamma_{ijk}}{\sum_{k=1}^K\gamma_{ijk}}\right) \\ B^{\mathrm{new}}_{jk\ell} &= \beta_{j\ell} + \sum_{i=1}^N[x_{ij}=\ell]r_{ijk} \end{aligned} \]
求める事後分布(の近似)は以下のようになる. \[ \begin{aligned} \boldsymbol{\theta}_i &\sim \mathrm{Dir}(\mathbf{A}_i)\\ \boldsymbol{\phi}_{jk} &\sim \mathrm{Dir}(\mathbf{B}_{jk}) \\ q(z_{ij} = k) &= r_{ijk} \end{aligned} \]
では学習を行わせてみます. 今回は学習データが $101$ 個しかない為過学習に注意が必要です.
最初は非常に少ないクラス数 $K=3$ にし, クラスの配合比率 $\boldsymbol{\theta}_i$, 属性値の分布 $\boldsymbol{\phi}$ に関する事前知識はないとします. その為には事前分布を一様分布にすれば良いです.
ディリクレ分布 $\mathrm{Dir}(\boldsymbol{\alpha})$ は $\boldsymbol{\alpha}=(1,\ldots,1)$ の時に一様分布になります. 但し,事前分布が全て同じだと学習が全く進まないので,乱数で少しだけ $1$ からずらした物を事前分布として採用します.
以下が学習された3つのクラスの属性値の組み合わせの様子で,$\boldsymbol{\phi}_i$の分布からわかります.
$99$% 以上の確率で確実にその値を取る属性には色をつけています.
| 体毛 | 羽毛 | 卵 | 乳 | 飛ぶ | 水棲 | 肉食 | 歯 | 脊椎 | 呼吸 | 毒 | ひれ | 足 | 尾 | 家畜化 | 猫サイズ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| クラス0 | N | N | Y | N | N | Y | Y | Y | Y | N | N | Y | 0本 | Y | N | N |
| クラス1 | Y | N | N | Y | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | Y |
| クラス2 | N | Y | Y | N | Y | N | N | N | N | Y | N | N | 2本 | N | N | N |
クラス0は「水棲生物っぽいカテゴリ」,クラス1は「哺乳類っぽいカテゴリ」,クラス2は「鳥類っぽいカテゴリ」という感じでしょうか. (prog20-1.py)
以下はクラスの配合比の学習例で, $\boldsymbol{\theta}_i$ の分布からわかります. なかなか面白い結果が出たと思います.
| 水棲生物? | 哺乳類? | 鳥類? | |
|---|---|---|---|
| コイ | 80.0% | 9.6% | 10.4% |
| クマ | 4.9% | 90.3% | 4.8% |
| ニワトリ | 4.2% | 5.8% | 90.1% |
| イルカ | 52.8% | 44.6% | 2.7% |
| ペンギン | 32.8% | 16.2% | 50.9% |
| コウモリ | 4.6% | 62.1% | 33.3% |
| カエル | 56.2% | 25.0% | 18.9% |
| ハマグリ | 47.9% | 5.4% | 46.7% |
| 女の子 | 4.2% | 83.6% | 12.2% |
| 吸血鬼 | 4.6% | 62.1% | 33.3% |
各属性がどのクラスに由来するかは $p(\mathbf{z})$ を見ればわかります.
【問題】
例えば,今の結果では「女の子」の属性の12.2%が「鳥類っぽいカテゴリ」に由来するという結果が出ましたがそれは何故でしょうか?
【答え】
足が2本である点.
$K=10$ でやってみると以下のようになりました(prog20-2.py).こちらでは95%で値が確定している属性に色をつけています.
教師無しでもそれなりに妥当な分類が出来たように思います. 基のデータセットでは区別していない肉食動物と草食動物が区別出来ました. また草食動物は肉食動物よりも家畜化される傾向があるなど新しい発見もあります.
| 体毛 | 羽毛 | 卵 | 乳 | 飛ぶ | 水棲 | 肉食 | 歯 | 脊椎 | 呼吸 | 毒 | ひれ | 足 | 尾 | 家畜化 | 猫サイズ | カテゴリ(予想) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| クラス0 | Y | N | N | Y | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | Y | 肉食動物(クラス9と同じ) |
| クラス1 | Y | N | N | Y | N | N | N | Y | Y | Y | N | N | 4本 | Y | Y | Y | 草食動物 |
| クラス2 | N | N | Y | N | Y | N | N | N | N | Y | N | N | 6本 | N | N | N | 昆虫 |
| クラス3 | N | N | Y | N | N | Y | Y | Y | Y | N | N | Y | 0本 | Y | N | N | 魚類 |
| クラス4 | N | N | Y | N | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | N | 特徴なし |
| クラス5 | N | Y | Y | N | Y | N | N | N | Y | Y | N | N | 2本 | Y | N | N | 鳥類 |
| クラス6 | N | N | Y | N | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | N | 特徴なし |
| クラス7 | N | N | Y | N | N | Y | Y | N | N | N | N | N | 0本 | N | N | N | クラゲとかヒトデとか |
| クラス8 | N | N | Y | N | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | N | 特徴なし |
| クラス9 | Y | N | N | Y | N | N | Y | Y | Y | Y | N | N | 4本 | Y | N | Y | 肉食動物 |
今回は事前分布に特に工夫を施しませんでしたが,事前分布の設計によって私達の知識を取り入れたり過学習を抑制するといった事が出来ます.
例えば,$K$ クラスのうちの幾つかを「主要クラス」,残りを「瑣末クラス」として学習させたいとします. これは例えば,配合比 $\boldsymbol{\theta}_i$ の値が主要クラスの方が大きめの値になるように事前分布のパラメータ $\boldsymbol{\alpha}$ を調整するなどの方法でモデルに取り入れる事が出来ます.
確率的生成モデルの良い所は,学習されたパラメータを使えば同時分布 \[ p(\mathbf{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}) \] を変形して様々な計算が出来るという所です.
例えば,ある特定の配合 $\boldsymbol{\theta}'$ の観測データ $\mathbf{x}'$ はどんなものか?を知りたければ条件付き分布 \[ p(\mathbf{x}'|\boldsymbol{\theta}') \] を計算すれば良いですし,未知の観測データ $\mathbf{x}'$ については 予測分布 (predictive distribution) \[ p(\mathbf{x}'|\mathbf{x}) \propto \int\int\int\int p(\mathbf{x}',\mathbf{z}',\boldsymbol{\theta}',\mathbf{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi})\mathrm{d}\mathbf{z}'\mathrm{d}\boldsymbol{\theta}'\mathrm{d}\mathbf{z}\mathrm{d}\boldsymbol{\theta}\mathrm{d}\boldsymbol{\phi} \] を計算すればその分布がわかります.
周辺化ギブスサンプリング
同じ問題をMCMC法でもやってみたいと思います. サンプリングアルゴリズムは第3・4回に既にやっていますのでアルゴリズムの解説は省略します.
繰り返しになりますが,ランダムサンプリングの利点は近似をせずに事後分布を直接調べる事が出来る事です. 欠点は,何の工夫もせずに事後分布 $p(\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}|\mathbf{x})$ から直接サンプリングを行うと非常に長い時間がかかってしまうという事です.
工夫出来るポイントは主に以下の2点です.
- 各変数毎に数百~数千サンプルが必要. 従って変数の数を出来るだけ減らしたい.
- ディリクレ分布からの1回のサンプリングには内部的に複数回の乱数生成が必要. もっと単純な分布からサンプリング出来るようにしたい.
そこで,サンプリングの前に興味のない隠れ変数は周辺化して消してしまいましょう. 今回の場合,例えば $\mathbf{z}$ に興味があるならば \[ \begin{aligned} p(\mathbf{z}|\mathbf{x}) &= \int\int p(\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}|\mathbf{x})\mathrm{d}\boldsymbol{\theta}\mathrm{d}\boldsymbol{\phi}\\ &\propto \int\int p(\mathbf{x}, \mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi})\mathrm{d}\boldsymbol{\theta}\mathrm{d}\boldsymbol{\phi}\\ \end{aligned} \] としてからサンプリングを行います.
更に,$p(\mathbf{z}|\mathbf{x})$ に対してギブスサンプリングを行います. つまり $\{z_{ij}\}_{(i,j)\neq (i',j')}$ を固定して $z_{i'j'}$ だけをサンプリングするという事を繰り返します. サンプリングする次元を1つに絞る事によって,ディリクレ分布などよりずっと単純な分布からサンプリングする事が出来ます.
この方法は周辺化ギブスサンプリング(collapsed gibbs sampling)と呼ばれます.
まず,同時分布の式を整理すると \[ \begin{aligned} p(\mathbf{x},\mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi}) &\propto \prod_{i=1}^N\left(\prod_{k=1}^K\theta_{ik}^{\alpha_{k}-1}\right)\prod_{j=1}^M\phi_{j,z_{ij},x_{ij}}\theta_{i,z_{ij}}\times \prod_{j=1}^M\prod_{k=1}^K\prod_{\ell=1}^{n_j}\phi_{jk\ell}^{\beta_{j\ell}-1} \\ &\propto \prod_{i=1}^N\prod_{k=1}^K\theta_{ik}^{\alpha_k + M_{ik}-1} \times \prod_{j=1}^M\prod_{k=1}^K\prod_{\ell=1}^{n_j}\phi_{jk\ell}^{\beta_{j\ell}+N_{jk\ell} - 1} \end{aligned} \] となります. 但し \[ \begin{aligned} M_{ik} &\stackrel{\mathrm{def}}{=} \sum_{j=1}^M[z_{ij}=k]\qquad(\text{データ$i$ の属性でクラス $k$ に由来するものの数}) \\ N_{jk\ell} &\stackrel{\mathrm{def}}{=} \sum_{i=1}^N[z_{ij}=k][x_{ij}=\ell]\qquad (\text{属性 $j$ がクラス $k$ に由来しその値が $\ell$ であるようなデータの数}) \end{aligned} \] です.
ここで以下の積分公式を使います. \[ \int \prod_{k=1}^Kx_k^{\alpha_k-1}\mathrm{d}\mathbf{x} = \frac{\prod_{k=1}^K\Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K\alpha_k)}\qquad (x_1,\ldots,x_K\geq 0, x_1+\cdots+x_K = 1) \] 但し $\Gamma(x)$ は ガンマ関数(gamma function) です.
すると \[ \begin{aligned} p(\mathbf{z}|\mathbf{x}) &\propto \int\int p(\mathbf{x}, \mathbf{z},\boldsymbol{\theta},\boldsymbol{\phi})\mathrm{d}\boldsymbol{\theta}\mathrm{d}\boldsymbol{\phi}\\ & = \prod_{i=1}^N\frac{\prod_{k=1}^K\Gamma(\alpha_k+M_{ik})}{\Gamma(\sum_{k=1}^K(\alpha_k+M_{ik}))}\times \prod_{j=1}^M\prod_{k=1}^K\frac{\prod_{\ell=1}^{n_j}\Gamma(\beta_{j\ell}+N_{jk\ell})}{\Gamma(\sum_{\ell=1}^{n_j}(\beta_{j\ell}+N_{jk\ell}))} \end{aligned} \] となります.
難しく見えますが,これを単純化する事が出来ます. まず \[ \sum_{k=1}^KM_{ik} = (\text{データ $i$ の属性の数}) = M \] でこれは定数です. また新たな変数・定数を \[ \begin{aligned} N_{jk} &\stackrel{\mathrm{def}}{=} \sum_{\ell=1}^{n_j}N_{jk\ell}\qquad (\text{属性 $j$ がクラス $k$ に由来するデータの数})\\ \beta_{j} &\stackrel{\mathrm{def}}{=} \sum_{\ell=1}^{n_j}\beta_{j\ell} \end{aligned} \] と定義すれば \[ \begin{aligned} p(\mathbf{z}|\mathbf{x}) &\propto \prod_{i=1}^N\prod_{k=1}^K\Gamma(\alpha_k+M_{ik})\times \prod_{j=1}^M\prod_{k=1}^K\frac{\prod_{\ell=1}^{n_j}\Gamma(\beta_{j\ell}+N_{jk\ell})}{\Gamma(\beta_j+N_{jk})} \end{aligned} \] となります.
次はギブスサンプリングを行う為に $z_{i'j'}$ 以外の $z$ 全てを固定した条件付き分布 \[ p(z_{i'j'}=k'|\{z_{ij}\}_{(i,j)\neq (i',j')}\mathbf{x}) \] を導出します.
そこで, $\tilde{M_{ik}}, \tilde{N_{jk\ell}},\tilde{N_{jk}}$ を既に定義した変数から $z_{i'j'}$ に依存する部分を全て取り除いたものとします. これらは定数値になる事に注意しましょう.
すると, $z_{i'j'}=k'$ の時 \[\begin{aligned} \prod_{k=1}^K\Gamma(\alpha_k + M_{i'k}) &= \Gamma(\alpha_{k'}+M_{i'k'})\times \prod_{k\neq k'}\Gamma(\alpha_k + M_{i'k})\\ &= \Gamma(\alpha_{k'}+\tilde{M}_{i'k'}+1)\times \prod_{k\neq k'}\Gamma(\alpha_k + \tilde{M}_{i'k})\\ \end{aligned} \] となり,ガンマ関数の性質 $\Gamma(x+1)=x\Gamma(x)$ を使うと \[ \begin{aligned} \prod_{k=1}^K\Gamma(\alpha_k + M_{i'k}) &= (\alpha_{k'}+\tilde{M}_{i'k'})\Gamma(\alpha_{k'}+\tilde{M}_{i'k'})\times \prod_{k\neq k'}\Gamma(\alpha_k + \tilde{M}_{i'k})\\ &= (\alpha_{k'}+\tilde{M}_{i'k'})\prod_{k=1}^K\Gamma(\alpha_k + \tilde{M}_{i'k})\\ \end{aligned} \] となります. この $\prod$ 以降は定数値です.
他の因子も同様の変換をしていくと \[ \begin{aligned} p(z_{i'j'}=k'|\{z_{ij}\}_{(i,j)\neq (i',j')},\mathbf{x})\propto (\alpha_{k'}+\tilde{M}_{i'k'})\frac{\beta_{j'x_{i'j'}}+\tilde{N}_{j'k'x_{i'j'}}}{\beta_j'+\tilde{N}_{j'k'}} \end{aligned} \] という四則演算のみで計算出来る式に辿りつきます. これに基いて $z_{i'j'}$ のサンプリングを行います.
実際に計算する時は,毎回 $\tilde{M}_{jk}$ や $\tilde{N}_{jk\ell}$ を再計算すると遅いのでその差分のみを更新しながら計算していきます. サンプル実装はprog20-3.pyです.
今回はここで終了します.
次回はちょっと飛びましてテキスト第13章の隠れマルコフモデルをやろうと思います.