パターン認識・
機械学習勉強会
第2回
@ワークスアプリケーションズ
中村晃一2014年2月20日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.
第2回の内容
本日は基礎的な話題であるベイズ確率論,ベイズ識別,モデル選択について進めていきます.
記法・用語について
多変数関数 $f(\mathbf{x})=f(x_1,x_2,\ldots,x_n)$ の領域 $D$ での重積分を \[ \int_Df(\mathbf{x})\mathrm{d}\mathbf{x}\overset{\mathrm{def}}{=} \int\cdots\int f(x_1,\ldots,x_n)\mathrm{d}x_1\ldots\mathrm{d}x_n \] と書きます.
離散変数に関する和も \[ \sum_{\mathbf{x}}f(\mathbf{x}) \overset{\mathrm{def}}{=} \sum_{x_1}\ldots\sum_{x_n}f(x_1,\ldots,x_n) \] の様に書きます.
どちらも $\mathbf{x}$ の範囲が書いていない場合には $\mathrm{x}$ の変域全体について積分・和を取ることとします.
確率変数 $\mathbf{x}$ が連続の場合, 確率分布は 確率密度関数 (probability density function) $\pi(\mathbf{x})$ によって表され, 確率 $p(A)$ は \[ p(A) = \int_A \pi(\mathbf{x})\mathrm{d}\mathbf{x} \] となります.
確率変数 $\mathbf{x}$ が離散的の場合の確率 $p(A)$ は, 各点での確率の和 \[ p(A) = \sum_{\mathbf{a} \in A}p(\mathbf{x}=\mathbf{a}) \] と表されますが, $\pi(\mathbf{t})=p(\mathbf{x}=\mathbf{t})$ と定めれば, \[ p(A) = \sum_{\mathbf{x}\in A}\pi(\mathbf{x}) \] と書くことが出来ます. この $\pi(\mathbf{x})$ は 確率質量関数 (probability mass function) と呼ばれます.
連続変数と離散変数の場合で記法を使い分けるのは面倒なので, 変数が離散的の場合も \[ p(A) = \sum_{\mathbf{x}\in A}\pi(\mathbf{x}) \] を \[ p(A) = \int_A \pi(\mathbf{x})\mathrm{d}\mathbf{x} \] と書きます.
測度論が必要ですが程度が過ぎるので勉強会ではやりません.
ベイズ確率論
ベイズ確率
データ $\mathbf{x}$ のクラスが $c$ である確率 \[ p(\mathrm{class}(\mathbf{x})=c) \] のようなものを頻度主義的に解釈する事は出来ません. $\mathrm{class}(\mathbf{x})=c$ であるか否かは既に確定している事柄だからです.
しかし, $\mathbf{class}(\mathbf{x})=c$ である否かが私達には分からない場合があるという, 主観的な不確かさが存在します.
このような「不確かさ」を定量的に扱う為の代表的な体系が ベイズ確率論 (Bayesian probability theory) です.
ベイズ的解釈では 確率 $p(A)$ を \[ \text{「事象 $A$ が起こるという事の確信度」} \] と考えます.
但し, $p(A)$ は確率論の公理を満たす様に数量化します.
ベイズ確率は主観的に定まるわけですが, 新たな情報を取り入れて ベイズ改訂 (Belief revision) を行う事によってその客観性を高めていく事が出来ます.

ベイズ改訂にはベイズの定理を利用します.
ベイズの定理
\[ p(X|D) = \frac{p(D|X)p(X)}{p(D)} \] が成立する。
$p(X)$ を事前確率 (priori probability), $p(X|D)$ を事後確率 (posterior probability)と呼ぶ.
例えば, 「ある日本人$A$ さん」が男性である確率を考えましょう.
事前確率 $p(\text{男})$ は可能な限り客観的に考えながら, 最終的には主観で定めます.
今, $A$ さんについて一切の情報が無いけども, 日本人の男女比が $95:100$ (数値は適当) である事を知っているとしましょう. そこで \[ p(\text{男}) = \frac{95}{195} \approx 0.487 \] と事前確率を設定する事にします.
ここで「$A$さんの身長が 170cm以上」という新情報が得られたとしましょう. 日本人男性の 60%が170cm以上, 女性では5% であるとします.
するとベイズの定理より \[ \small{\begin{aligned} &p(男|\text{170cm以上})\propto p(\text{170cm以上}|男)p(男) = 0.6\times 0.487 \approx 0.292 \\ &p(女|\text{170cm以上})\propto p(\text{170cm以上}|女)p(女) = 0.05\times 0.525 \approx 0.0257 \end{aligned}} \] となります. (分母の $p(\text{170cm以上})$ は共通なので計算は不要)
最後に確率の和が $1$ になるように正規化を行えば事後確率 \[ p(\text{男}|\text{170cm以上}) \approx 0.919 \] が得られます.
男女比率を考えずに $p(\text{男})=0.5$ として計算すると \[ p(\text{男}|\text{170cm以上}) \approx 0.923 \] となります.
前頁の \[ p(\text{男}|\text{170cm以上}) \approx 0.919 \] では男性の方が少ないという事が加味されて確率が少し小さくなっています.
以下は確率分布に対するベイズの定理です.
確率分布のベイズ改訂
\[ \pi(\mathbf{x}|\mathbf{d}) = \frac{p(\mathbf{d}|\mathbf{x})\pi(\mathbf{x})}{p(\mathbf{d})}\propto p(\mathbf{d}|\mathbf{x})\pi(\mathbf{x}) \] が成立する。
$\pi(\mathbf{x})$ を事前分布 (priori distribution), $\pi(\mathbf{x}|\mathbf{d})$ を事後分布 (posterior distribution)と呼ぶ.
また, \[ L(\mathbf{x}|\mathbf{d})=p(\mathbf{d}|\mathbf{x}) \] を $\mathbf{x}$ の関数とみなした時これを 尤度関数 (likelihood function) と呼ぶ.
頻度主義による分析手法はデータ数が十分にないと極端な結論を導いてしまう事があります.
ベイズ確率論では事前知識を事前分布として取り込むことで, そうした極端な結論を回避する事が出来ます.
例えばあるコインを投げて表が出る確率 $\theta$ について考えましょう.
コインを $3$ 回投げて全て表が出たならば尤度関数は \[ L(\theta|\text{$3$連続表}) = p(\text{$3$連続表}|\theta) = \theta^3 \] となります. 最尤法 (maximum liklihood estimation, MLE) では $L$ が最大となるようにパラメータを推定するので $\theta = 1$ という結論が得られます.
「$3$ 連続表が出る」という事象が最も起こりやすいのは「表しかでないコイン」の場合であるというわけです.
では, 事前知識として 「$\theta=0,1$ という事は無いだろう」「$\theta=0.5$の近辺だろう」という事を取り入れてみましょう.
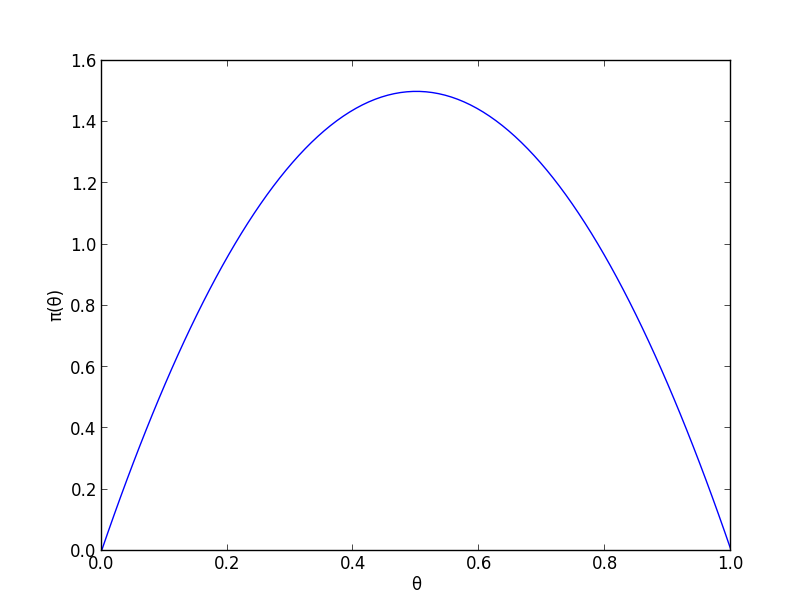
そこで, 事前分布 $\pi(\theta)$ としてベータ分布 $Be(2,2)$ つまり \[ \pi(\theta)\propto\theta(1-\theta) \] を使ってみます.
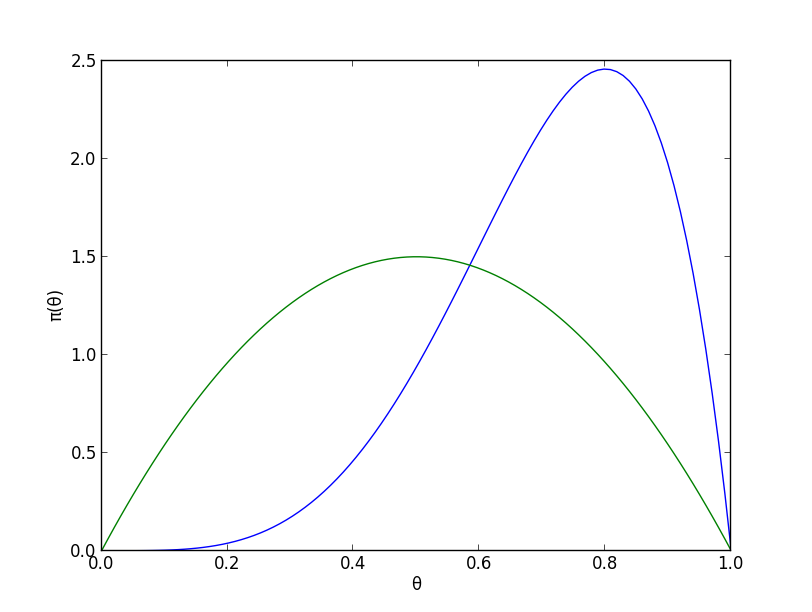
ベイズの定理より事後分布は \[ \small{\pi(\theta|\text{$3$連続表}) \propto p(\text{$3$連続表}|\theta)\pi(\theta) \propto \theta^3\cdot \theta(1-\theta) = \theta^4(1-\theta)} \] つまりベータ分布 $Be(5,2)$ となります.
事前知識を加味しつつ, 実験結果を考慮して分布が右に動いています.事後分布の密度は $\theta=0.8$ のとき最大値をとります.
MAP推定値
データ $\mathbf{x}$ を所与として, 事後分布 $\pi(\theta|\mathbf{x})$ を最大にするような $\hat{\theta}$, すなわち \[ \hat{\theta} = \mathop{\rm arg~max}\limits_{\theta}\pi(\theta|\mathbf{x}) \] を 事後分布最大化推定量 (maximum a posterior estimator, MAP推定値) と呼ぶ.
先ほどの例では計算の容易な分布を利用しましたが, 実際にはもっと複雑な分布を利用する必要があります.
そこで マルコフ連鎖モンテカルロ法 (Markov chain Monte Carlo methods, MCMC法) というランダムサンプリングに基づく数値積分法や, 変分ベイズ法 (variational Bayesian methods, VB法) などの近似推定法が必要となります. 後の回に解説を行う予定です.
ベイズ識別
様々な識別手法を互いに比較したりする為には, 数学的な検討が必要不可欠ですので, ベイズ確率論を利用してパターン識別の問題について詳しく見ていきます.
特徴ベクトルの分布
まず, クラスの集合 $C=\{c_1,c_2,\ldots\}$ の各パターンが出現する確率を $p(c_i)$ としましょう.
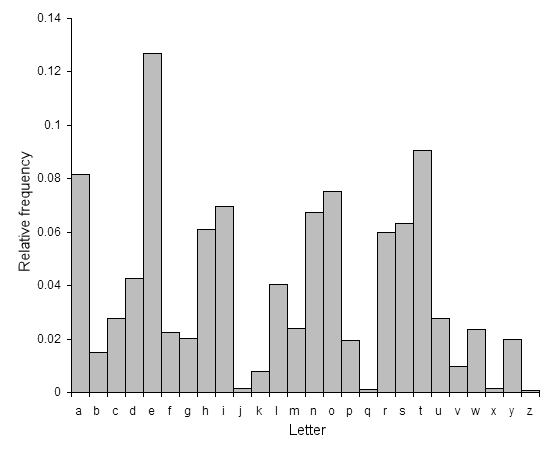
例えば英文ではアルファベット e が最も頻繁に登場し, z が最も少ないという傾向がありますが, こういった各パターンの出現頻度の偏りを $p(c)$ で表現します.
続いて, パターン $c$ が選ばれた時に観測される特徴ベクトル $\mathbf{x}$ の分布を $\pi(\mathbf{x} | c)$ としましょう. これは クラス分布 (class-conditional distribution) と呼ばれます.
すると, 特徴ベクトル $\mathbf{x}$ の分布は \[ \pi(\mathbf{x}) = \sum_c \pi(\mathbf{x}|c)p(c) \] となります.
損失関数
識別器はクラスを返す関数 $\varphi(\mathbf{x})$ と表す事が出来ます.
ここで問題となるのは $\varphi(\mathbf{x})$ の「良さ」をどのように評価するかです.
まず, クラス $c'$ のデータを誤って $c$ と識別してしまった場合の損失の大きさを表す 損失関数 (loss function) $L(c, c')$ を定めます.
最も簡単なのが 0-1損失関数 (0-1 loss function) \[ L(c, c') = \left\{\begin{array}{cc} 0 & (c = c') \\ 1 & (c \neq c') \end{array}\right. \] です.
$\varphi$ を最適化する簡単な方法として, 学習データ $\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\}$ に対する平均損失 \[ \frac{1}{n}\sum_i L(\varphi(\mathbf{x}_i), y_i) \] を最小化する方法が考えられますが, これはデータ数が少ない場合に上手く行きません.
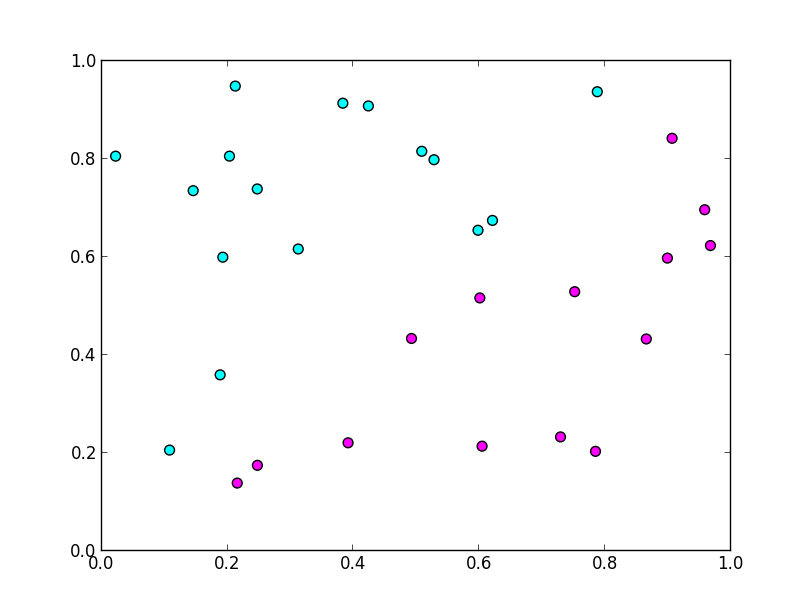
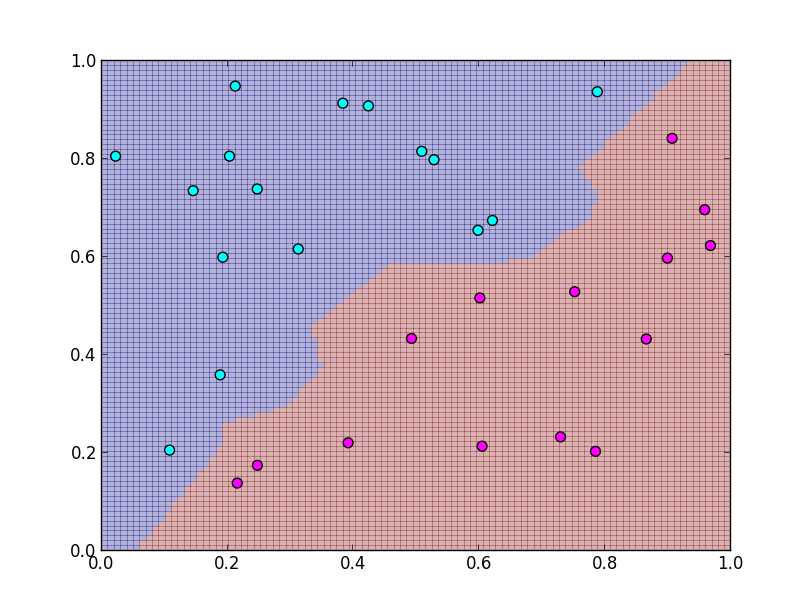
例えば1-NN法では学習データに対する損失が全て $0$ になりますが
以下のような歪な境界面になって,未知のデータに対する識別能力が低下します.
学習データに基いて作られた識別器の, 未知の新しいデータに対する識別能力を 汎化能力 (generalization performance) と呼びます. これを最適化する事が本当に必要な事です.
期待損失最小化
特徴ベクトル $\mathbf{x}$ は分布 $\pi(\mathbf{x})=\sum_c \pi(\mathbf{x}|c)p(c)$ に従うので, 損失の期待値は \[ EL(\varphi) = \int \sum_c L(\varphi(\mathbf{x}),c)\pi(\mathbf{x}|c)p(c)\mathrm{d}\mathbf{x} \] となります. これを 期待損失 (expected loss) と呼びます.
これを最小化するように識別器を最適化する事を 期待損失最小化 (expected loss minimization) と呼びます.
ベイズ識別
0-1損失関数の場合を考えます. \[ EL(\varphi) = \int\sum_c L(\varphi(\mathbf{x}),c)\pi(\mathbf{x}|c)p(c)\mathrm{d}\mathbf{x} \] の $\pi(\mathbf{x}|c)p(c)$ が最大の所の損失を $0$ にすれば良いので, \[ \varphi(\mathbf{x}) = \mathop{\rm arg~max}\limits_{c} \pi(\mathbf{x}|c)p(c) \] とするのが最適です.
ここで, ベイズの定理より \[ p(c|\mathbf{x}) \propto \pi(\mathbf{x}|c)p(c) \] なので, 今述べた方法はクラス $c$ の事前確率 $p(c)$ に対する事後確率 $p(c|\mathbf{x})$ を最大化する方法であると言えます. その為 事後確率最大化識別 (maximum a posterior probability discrimination, MAP識別) または ベイズ識別 (Bayesian classification) と呼ばれます.
まとめましょう.
ベイズ識別
\[ \varphi(\mathbf{x}) = \mathop{\rm arg~max}\limits_{c}\pi(\mathbf{x}|c)p(c) \] を識別関数とすると, これは 0-1損失関数に対する期待損失を最小化する.
多くの場合 $\pi(\mathbf{x}|c)p(c)$ は非常に小さな値になるので \[ \ln\pi(\mathbf{x}|c)p(c) = \ln\pi(\mathbf{x}|c)+\ln p(c) \] を考える事も多いです.
$p(c)$ と $\pi(\mathbf{x}|c)$ は実際には分からないので, 推定を行う必要があります.
$p(c)$ は各クラスの出現頻度の統計をとって推定する事が出来ます. 十分な統計が取れないならば $p(c)=\mathrm{const}.$ とします.
クラス分布 $\pi(\mathbf{x}|c)$ は学習データから推定するということになります. 様々な分布の推定方法が存在します.
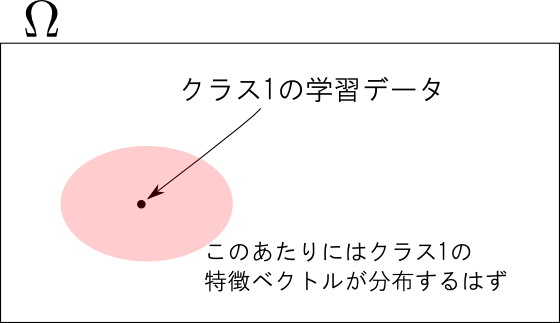
ここで1つだけ簡単な例を紹介します.
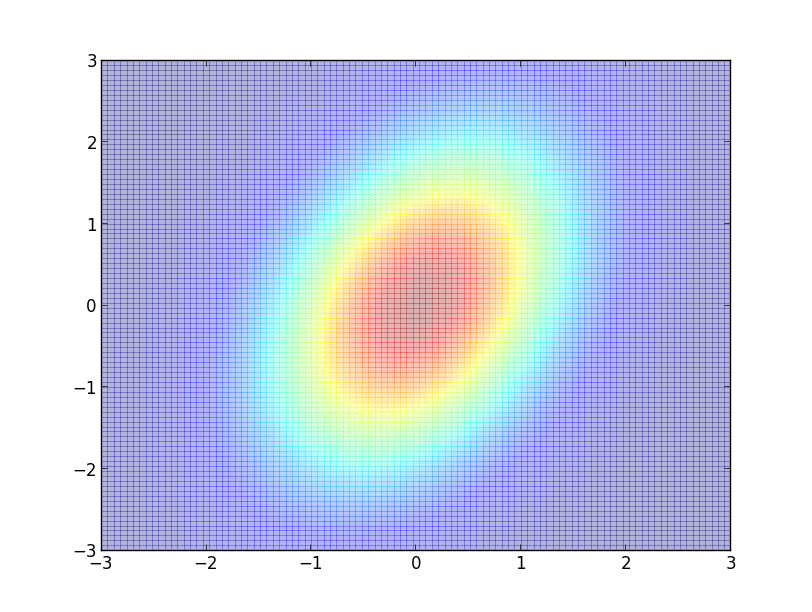
各クラス $c$ に対する特徴ベクトルの分布 $\pi(\mathbf{\mathbf{x}}|c)$ が多変量正規分布 $\mathcal{N}(\mathbf{\mu}_c,\mathbf{\Sigma}_c)$ であるとしましょう.
すなわち, \[ \pi(\mathbf{\mathbf{x}}|c) = \frac{1}{(\sqrt{2\pi})^n\sqrt{|\mathbf{\Sigma}_c|}}\exp\left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu}_c)^T\mathbf{\Sigma}_c^{-1}(\mathbf{x}-\mathbf{\mu}_c)\right\} \] とおきます.
すると \[ \begin{aligned} &\ln \pi(\mathbf{x}|c)p(c) \\ = &-\frac{1}{2}(\mathbf{x}-\mathbf{\mu}_c)^T\mathbf{\Sigma}_c^{-1}(\mathbf{x}-\mathbf{\mu}_c) - \frac{1}{2}\ln |\mathbf{\Sigma}_c| +\ln p(c) + \mathrm{const.} \end{aligned} \] となります.
今の結果からテンプレートマッチング法について前回よりも良く理解する事が出来ます.
まず, $p(c)=\mathrm{const}., \mathbf{\Sigma}_c = \sigma^2I$ であるならば \[ \ln \pi(\mathbf{x}|c)p(c) = -\frac{1}{2\sigma^2}||\mathbf{x}-\mathbf{\mu}_c||^2 + \mathrm{const}. \] となるので, $c$ のベイズ推定値はユークリッド距離 \[ ||\mathbf{x}-\mathbf{\mu}_c || \] を最小化するものです.
つまり, ユークリッド距離によるテンプレートマッチング法とは
- 特徴ベクトルが多変量正規分布に従うと仮定.
- 各クラスの出現頻度が等しい.
- 分散が等方的で等しい.
という仮定の下, 0-1損失関数による期待損失を最小化する識別方法であるという事が分かりました.
同様に $p(c)=\mathrm{const}., |\mathbf{\Sigma}_c| = \mathrm{const}.$ であるならば \[ \ln \pi(\mathbf{x}|c)p(c) = -\frac{1}{2}(\mathbf{x}-\mathbf{\mu}_c)^T\mathbf{\Sigma}_c^{-1}(\mathbf{x}-\mathbf{\mu}_c) + \mathrm{const}. \] となってマハラノビス距離によるテンプレートマッチング法と一致します.
この場合は出現頻度が等しい事と, 一般化分散 $|\mathbf{\Sigma}_c|$ が等しい事を仮定している事になります.
モデルの検証
今の例では 「$\pi(\mathbf{x},c)$ が多変量正規分布というモデルに従っていると仮定する」という部分が本質的でした.
識別の理論ではクラス分布 $\pi(\mathbf{x},c)$ のモデルの選択が重要となります.
過学習
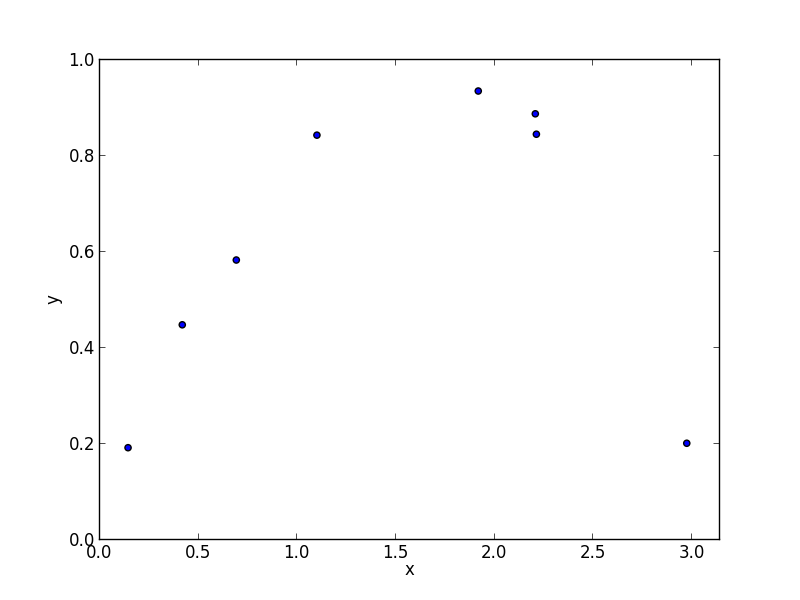
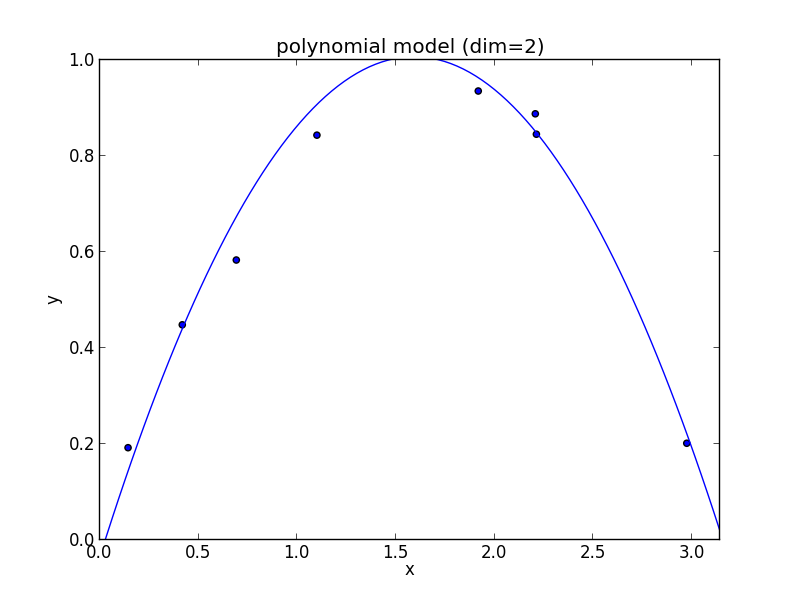
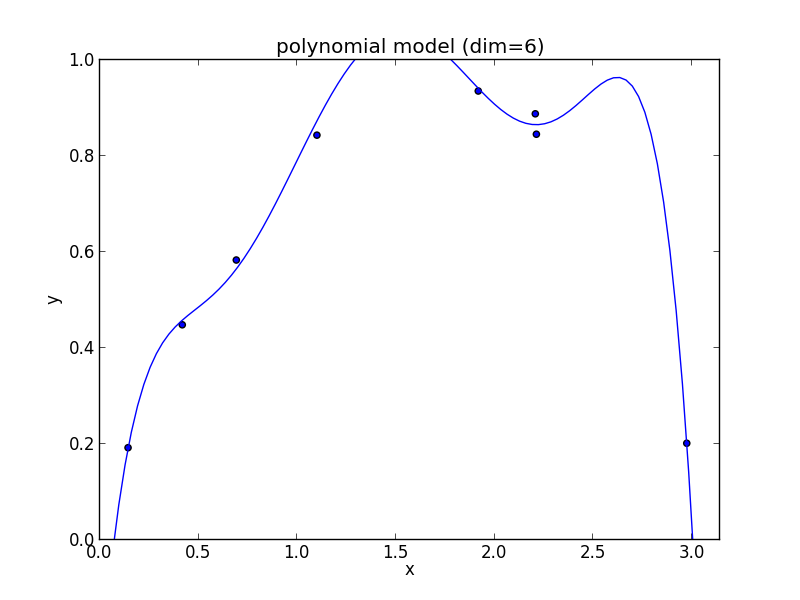
モデル選択の例題として, 以下のデータに 多項式モデル (polynomial model) \[ y=a_dx^d+a_{d-1}x^{d-1}+\cdots+a_1x+a_0 \] を当てはめる問題を考えます.
フィッティングは最小二乗法で行います. つまり学習データ $\{(x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\}$ に対して残差平方和 (residual sum of squares, RSS) \[ RSS=\sum_i(a_dx_i^d+a_{d-1}x_i^{d-1}+\cdots+a_1x_i+a_0-y_i)^2 \] を最小化する様に多項式の係数を決定します.
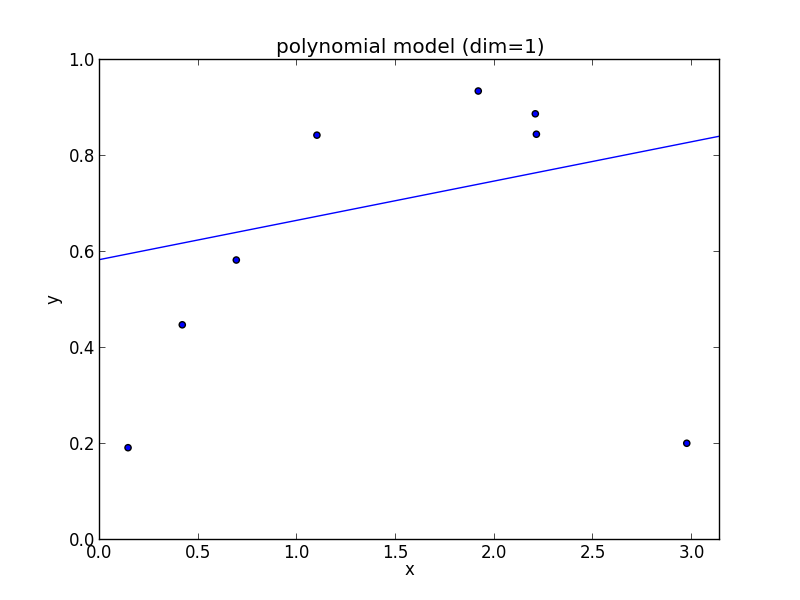
1次式の場合
2次式の場合
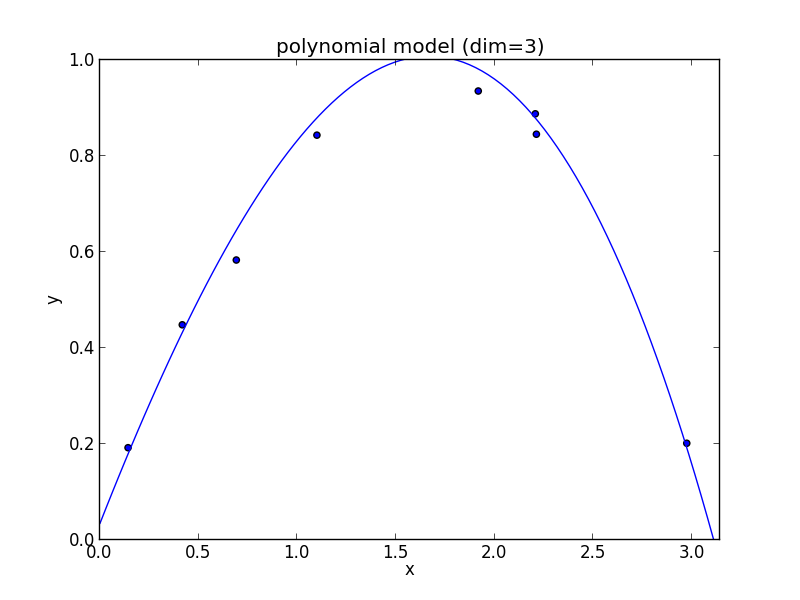
3次式の場合
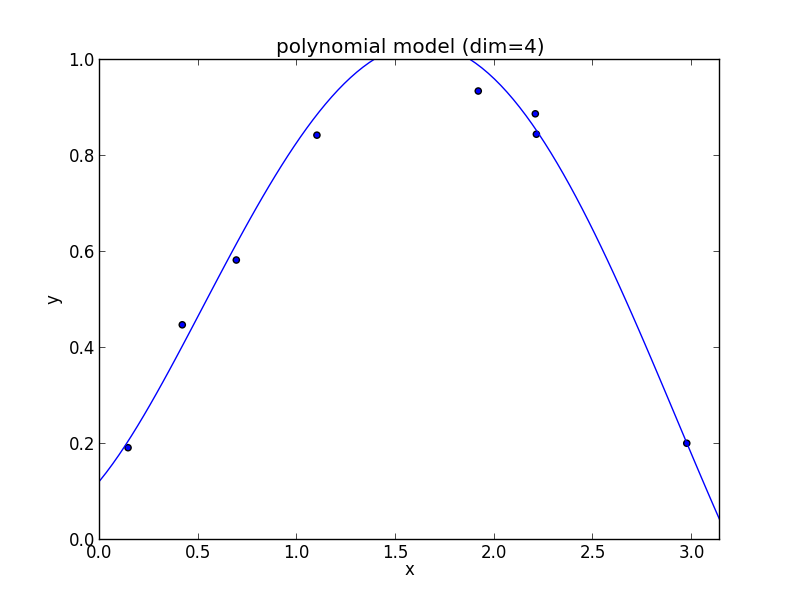
4次式の場合
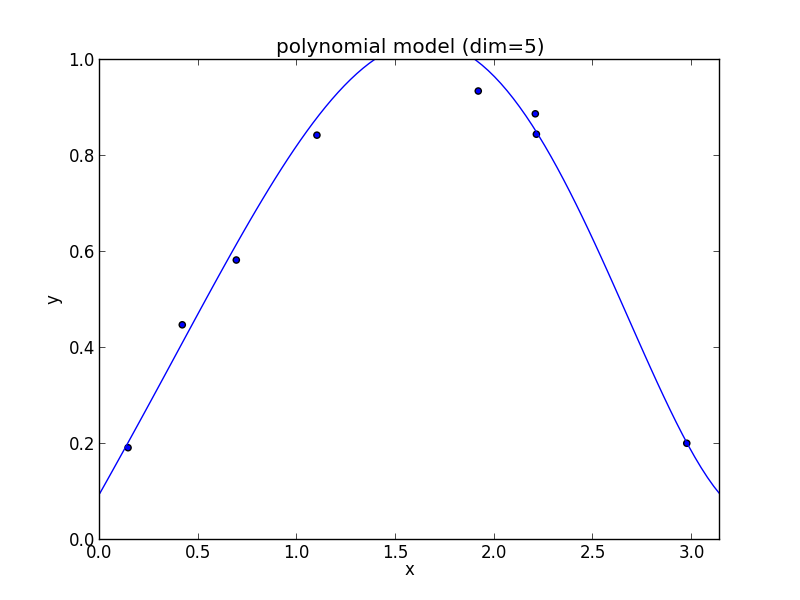
5次式の場合
6次式の場合
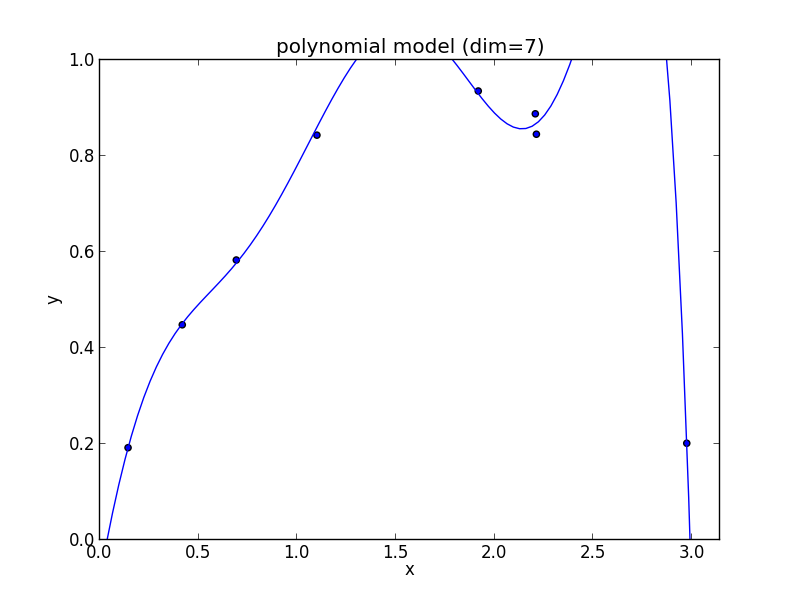
7次式の場合
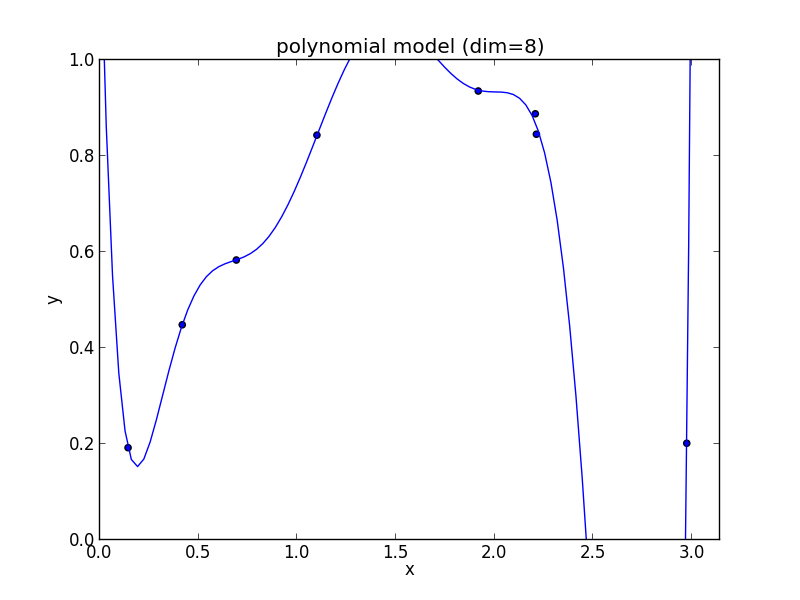
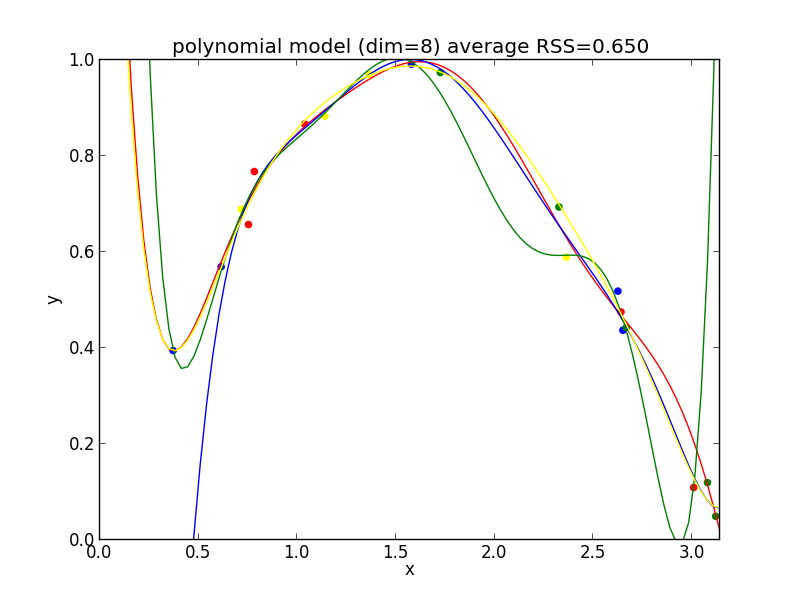
8次式の場合
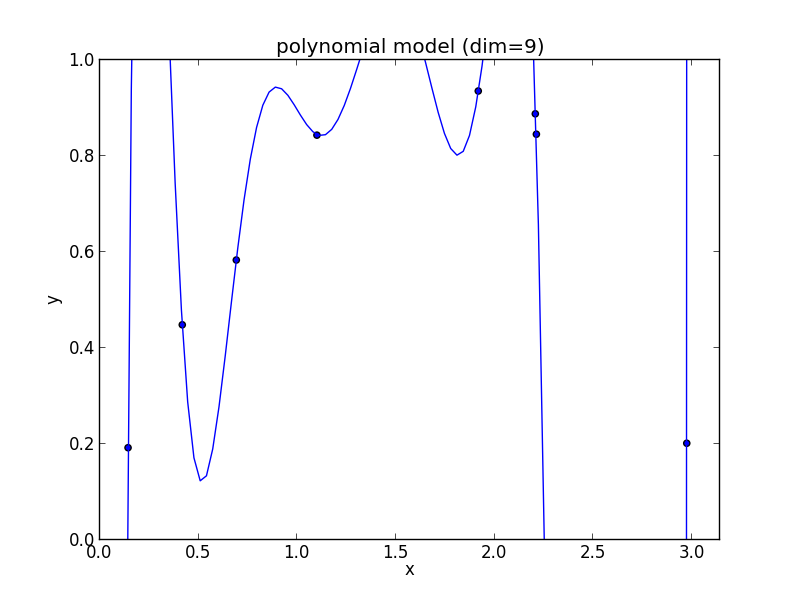
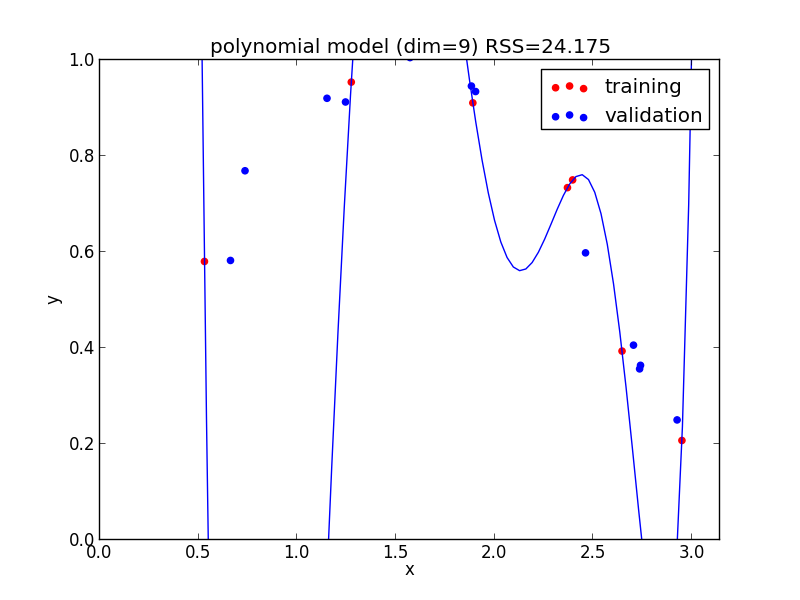
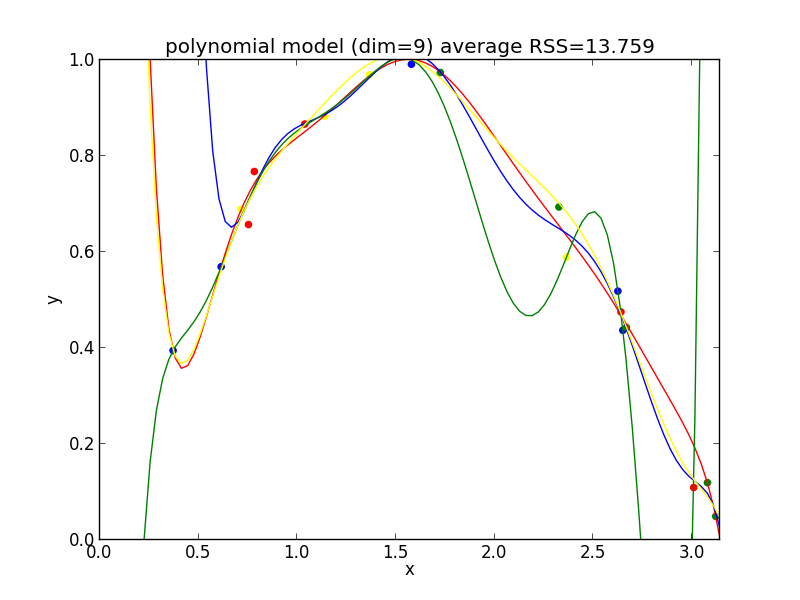
9次式の場合
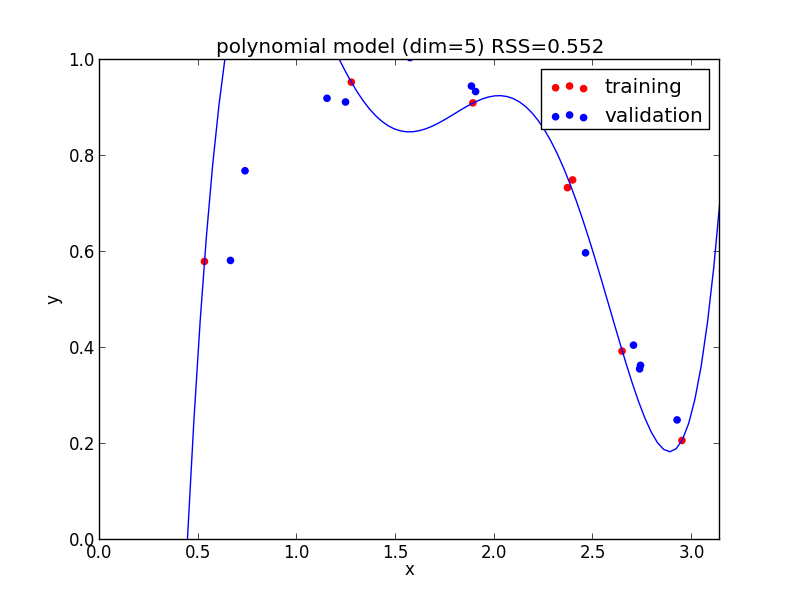
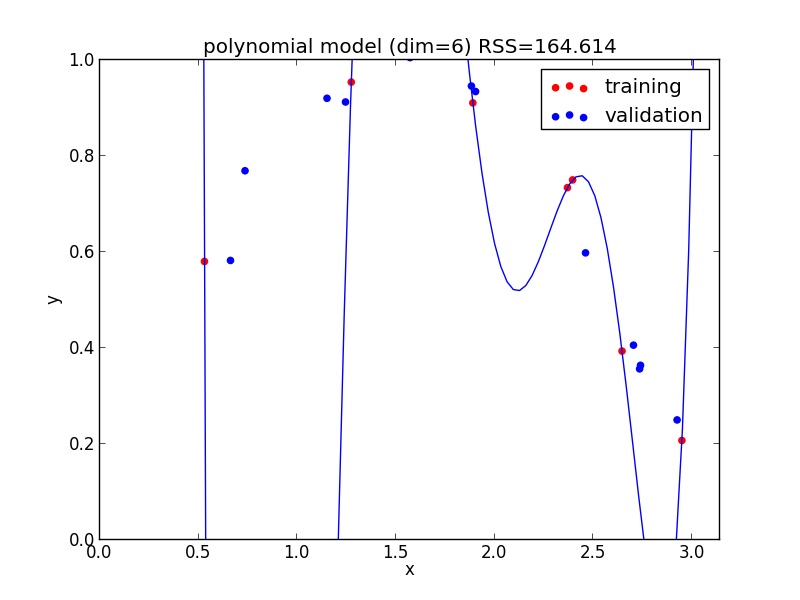
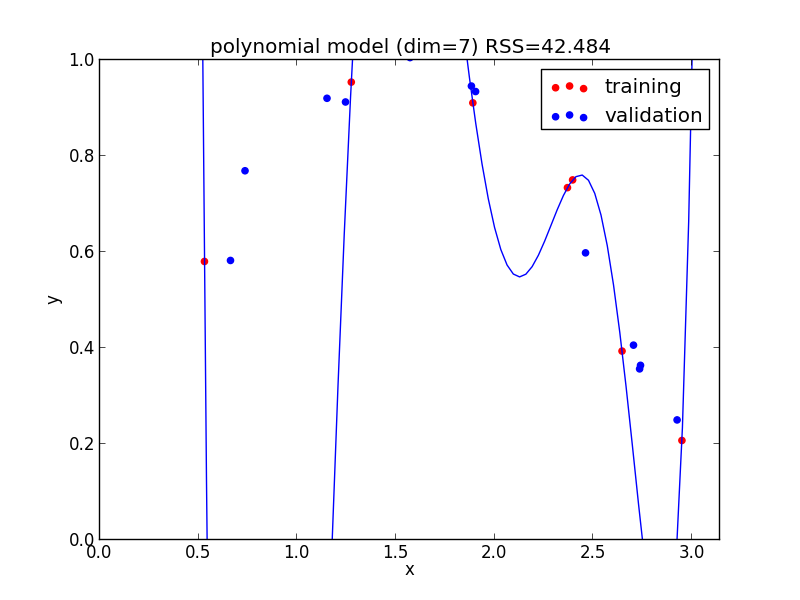
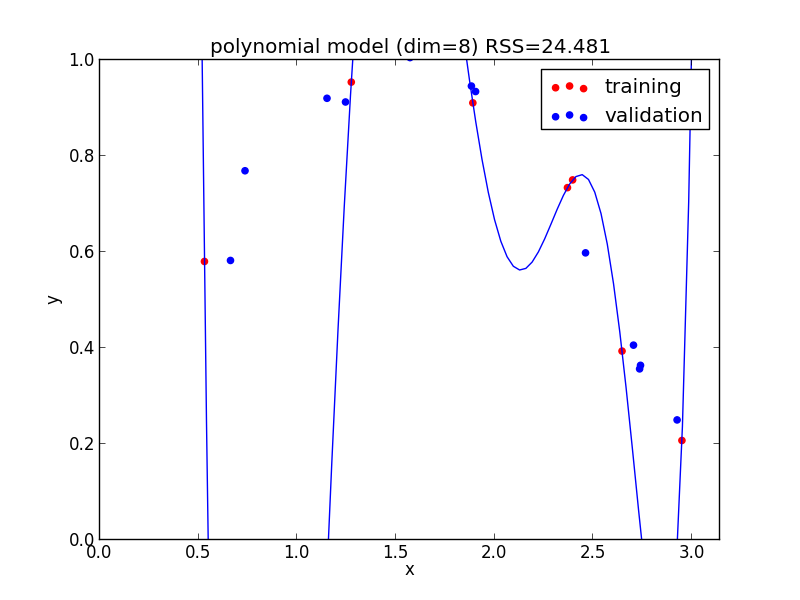
高次の多項式モデルでは, 学習データの確率的変動を忠実に拾ってしまい汎化能力が低下していることが判ります. これが 過学習 (overfitting) と呼ばれる現象です.
過学習の問題に対処する為には,
- 学習結果の汎化能力を評価する
- モデルの複雑さを評価する
- 過学習を起こさない学習方法を利用する
など方法があります.
ホールドアウト検証
学習用データが十分にある場合には, それを学習用データと 検証用データ (validation set) の2つにわけ
- 学習用データで学習を行う.
- 検証用データに対する誤り率などによって評価をする.
という検証が出来ます. これはホールドアウト検証 (hold-out validation) と呼ばれます.
検証用データに対しても過学習してしまわない様に気をつける必要があります. 場合によっては3つ目の最終的な確認を行うデータセットを用意する場合もあります.
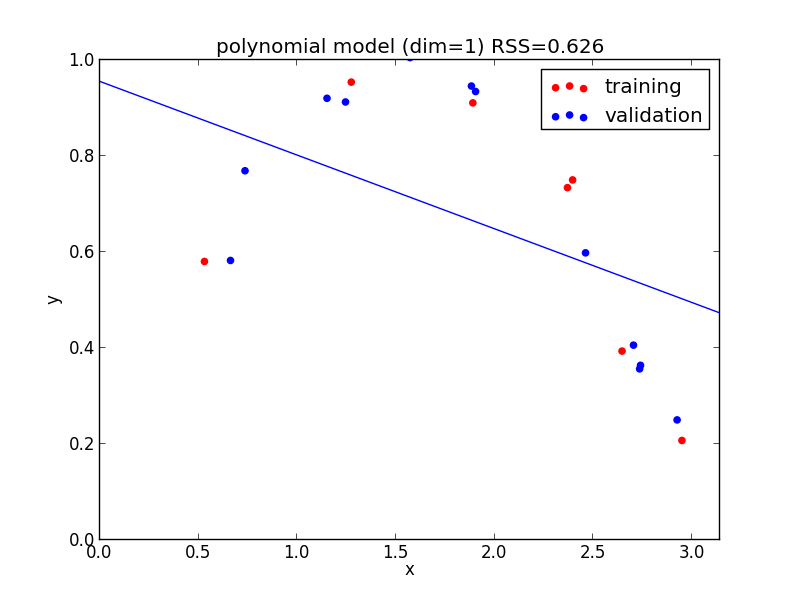
1次式の場合
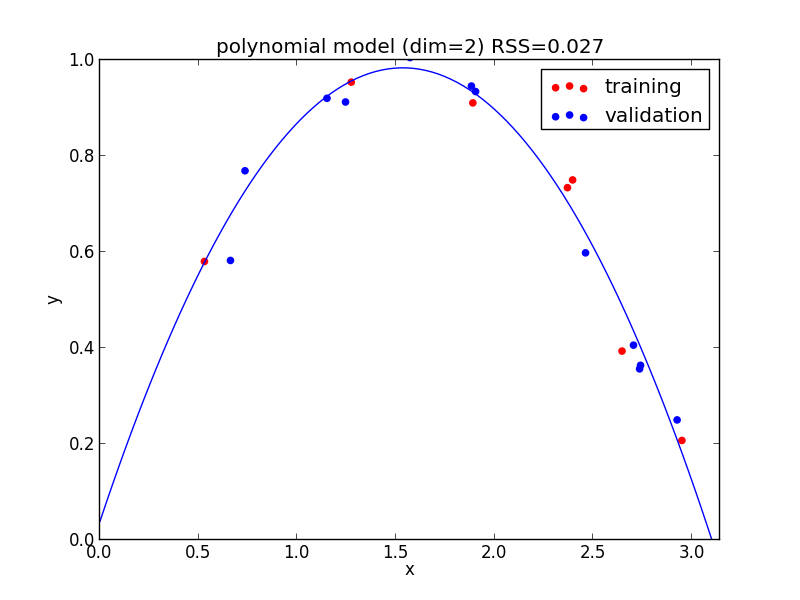
2次式の場合
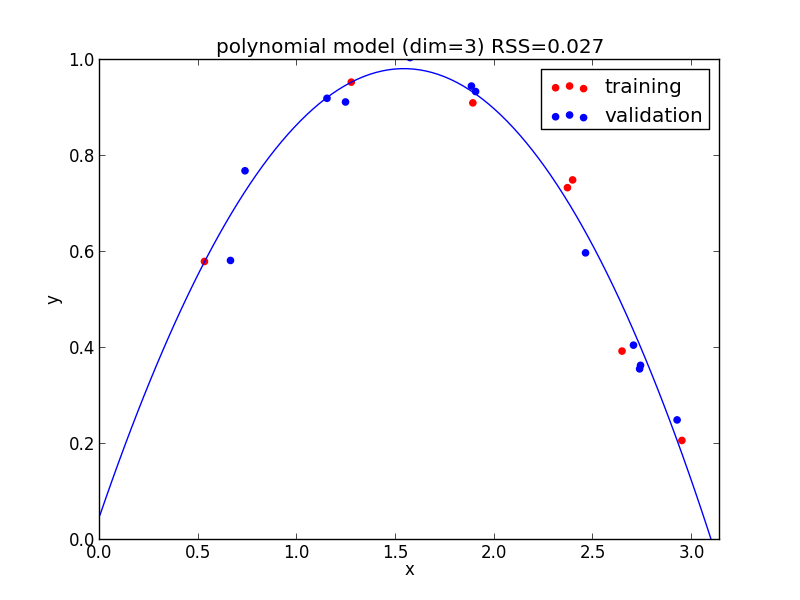
3次式の場合
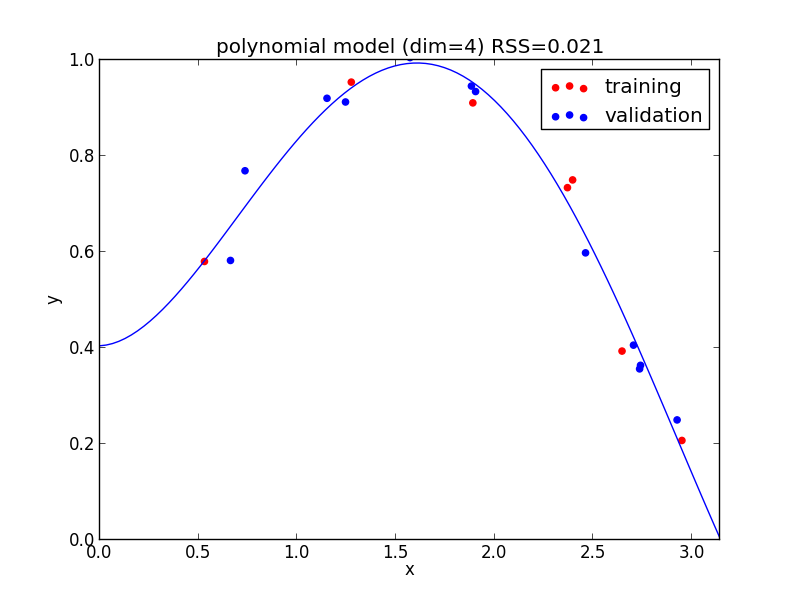
4次式の場合
5次式の場合
6次式の場合
7次式の場合
8次式の場合
9次式の場合
今の例では $4$ 次のモデルでの検証用セットに対する$RSS$ が最小となりました.
$K$-交差検証
学習用データが少ない場合には学習用データの出来るだけ多くを利用して訓練を行いたいので, 以下の方法が使えます.
- 学習用データを $K$ 組に分割する.
- $K-1$組を使って学習し, 残りの$1$組で検証を行う.
- 上記を $K$ パターン行ってその平均をとる.
これは $K$-交差検証 ($K$-cross validation) と呼ばれます.
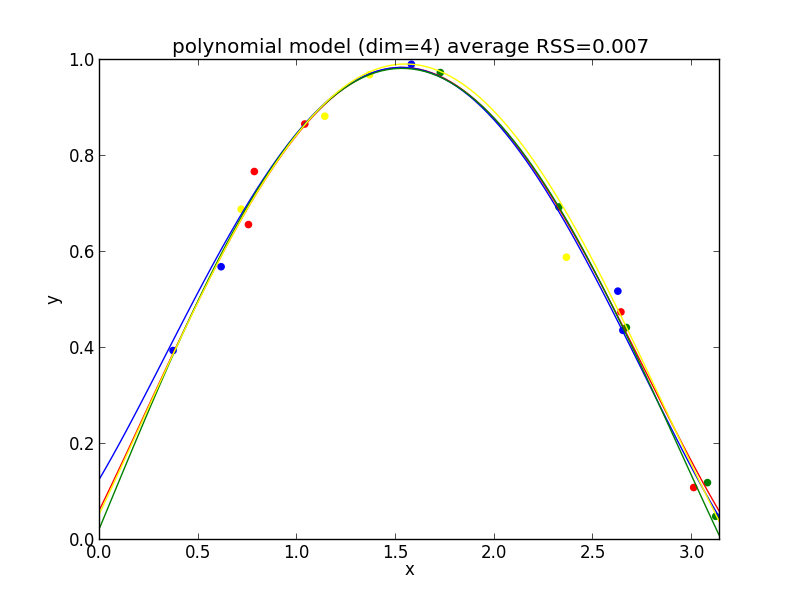
次頁以降 $K=4$ の場合のサンプルを載せてあります.
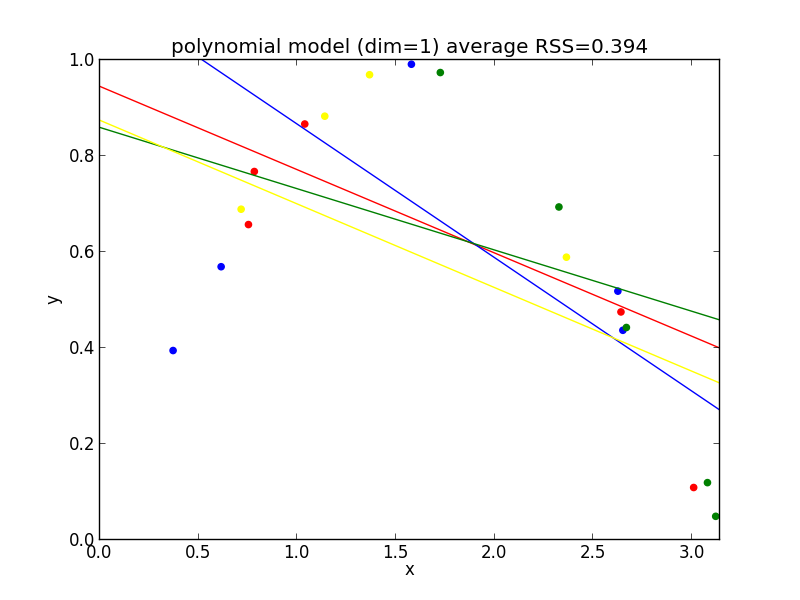
1次式の場合
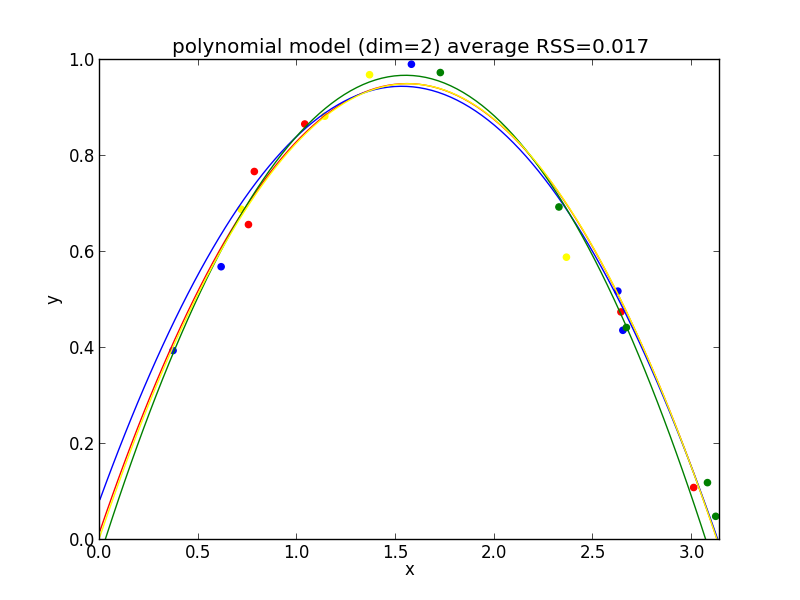
2次式の場合
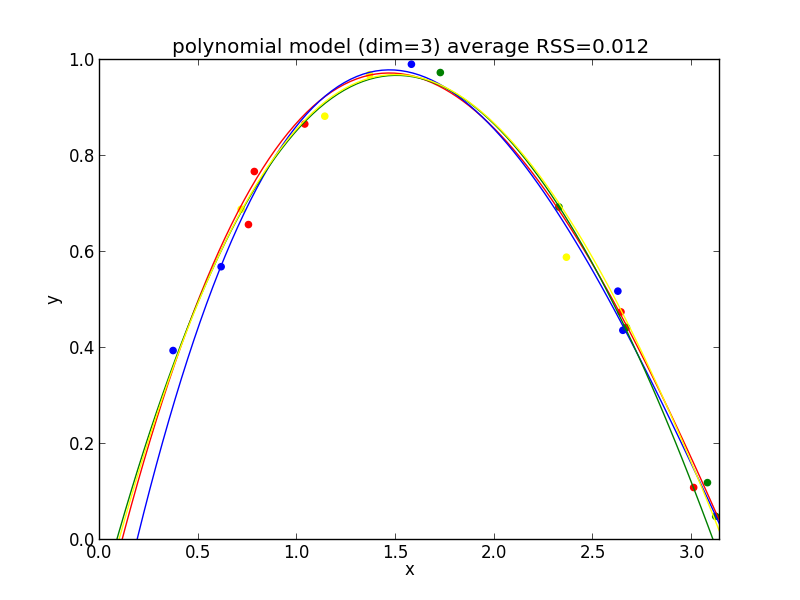
3次式の場合
4次式の場合
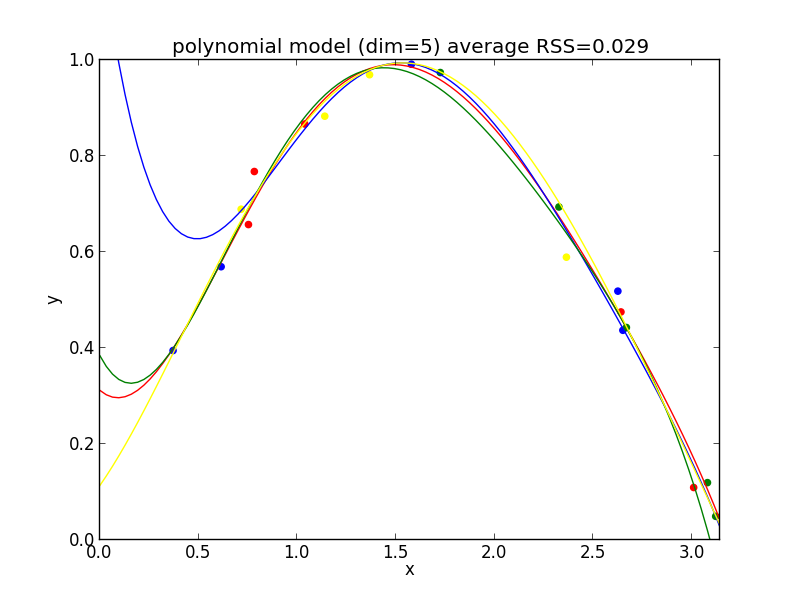
5次式の場合
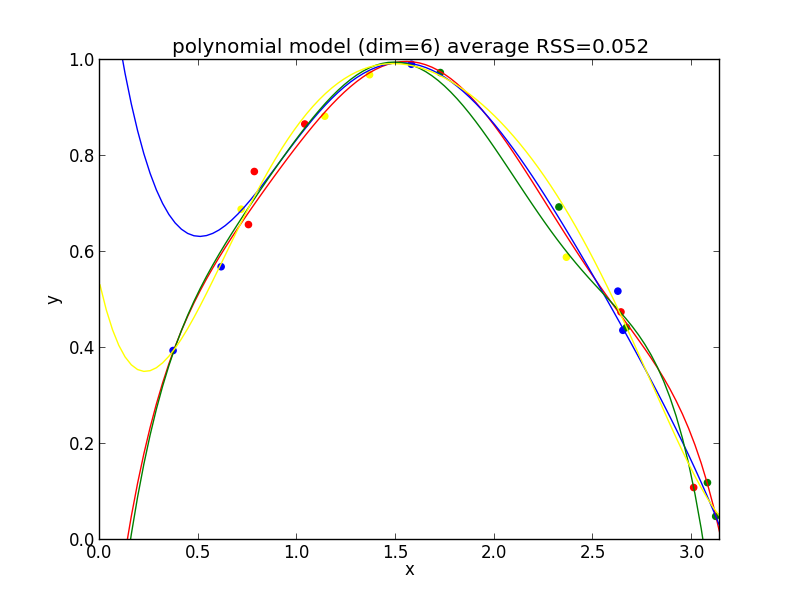
6次式の場合
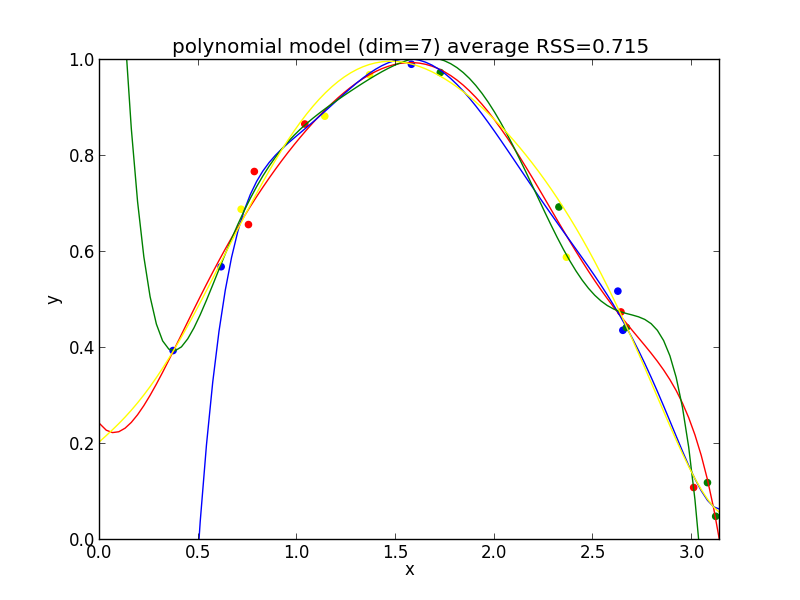
7次式の場合
8次式の場合
9次式の場合
今の例では $4$ 次のモデルでの残差平方和の平均が最も小さくなりました.
検証に基づく方法ではモデルの複雑さは考慮していないので, データ数が増えていくとより複雑なモデルが選ばれる様になります.
モデルの複雑さを測る為には来週説明する指標を利用する事となります.
leave-one-out 交差検証
$K$-交差検証の極端な場合として $K=(\text{学習データ数})$ とするものがあります. これは leave-one-out 交差検証 (leave-one-out cross validation, LOOCV法) と呼ばれます.
交差検証では $K$ を大きくした方がより多くの学習データを利用できるわけですが, それに応じて必要な計算量が増加するという問題もあります.
第2回はここで終わります
時間が無くなりそうなのでここまでにします. 次回も前半はモデル選択について解説します. 赤池情報量基準などのモデルの評価指標や, ベイズ線形回帰などの過学習を防ぐ学習方法について説明します.
その後, 本日お話したMCMC法や変分ベイズ法の解説をしようかと思っていますが,内容を変更する可能性があります.