パターン認識・
機械学習勉強会
第19回

@ナビプラス

謝辞

会場・設備の提供をしていただきました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.

ガウス分布以外でのEM法

前回は混合ガウス分布 \[ p(\mathbf{x}) = \sum_{c=1}^K \pi_c\mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] に対するEM法の紹介をしましたが，今回は多変数ベルヌーイ分布や多項分布を混合した分布に対するEM法も紹介します．

多変数ベルヌーイ分布

久しぶりなので復習すると，確率 $p$ で $x=1$， $1-p$ で $x=0$ となる確率分布をベルヌーイ分布(Bernoulli distribution) と呼びます． $$ \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline p(x) & 1-p & p \\ \hline \end{array} $$ これは簡潔に \[ p(x) = p^x(1-p)^{1-x} \] と書くことが出来ます．

これの多変数バージョンが多変数ベルヌーイ分布(multivariate Bernoulli distribution)です．つまり \[ \mathbf{x} = (1,0,0,1,0,\ldots,0,1) \] の様な $d$ 次元の二値ベクトルで表現され，各変数は独立であり，第 $i$ 成分が $1$ となる確率が $p_i$ であるような確率変数の従う分布が $d$ 変数ベルヌーイ分布です.

多変数ベルヌーイ分布の例を紹介します．

文書 $d$ 内に単語 $w_i$ が出現したか否かを $1,0$ で表現し，各単語の出現は独立だと仮定すればこれは多変数ベルヌーイモデルとなります． $$ \begin{array} \hline \text{単語} & w_1 & w_2 & w_3 & w_4 & \cdots \\ \hline \text{文書}d & 1 & 0 & 0 & 1 & \cdots \\ \hline \end{array} $$

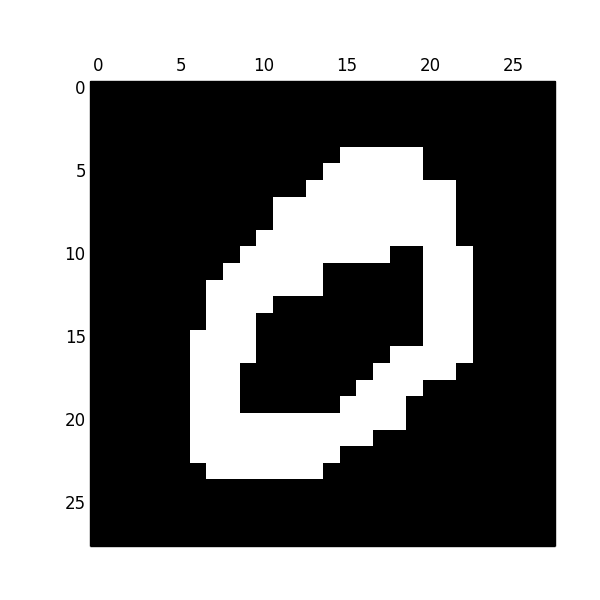
下図はmldata.orgからダウンロード出来る$28\times 28$ の手書き数字データを二値化したものです．これを $784$ 次元のベルヌーイ分布に従う確率変数としてモデリングすることが出来ます.

prog19-1.py

その他，yes/noで答えるタイプのアンケート結果など，二値変数が複数ある場合のもっともシンプルなモデル化が多変数ベルヌーイ分布です．

再び数式に戻ると，$d$変数ベルヌーイ分布とは変数の変域が $\mathbf{x} \in \{0,1\}^d$ であり， \[ \mathbf{x} = (x_1,x_2,\ldots,x_d) \] を取る確率が \[ p(\mathbf{x}|\mathbf{p}) = \prod_{i=1}^d p_i^{x_i}(1-p_i)^{1-x_i} \] と表されるような確率分布です．この分布のパラメータは \[ \mathbf{p} = (p_1,p_2,\ldots,p_d) \qquad (0\leq p_i \leq 1)\] となります.

分布の平均・共分散は \[ \begin{aligned} E[\mathbf{x}] &= \mathbf{p}\\ \mathrm{cov}[\mathbf{x}] &= \mathrm{diag}\{p_i(1-p_i)\} = \begin{pmatrix} p_1(1-p_1) & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & p_d(1-p_d) \end{pmatrix} \end{aligned}\] となります.各変数は独立なので，分散共分散行列は対角行列になります.

【証明】
各変数は独立なので1変数の場合を示せば十分. \[ \begin{aligned} E[x] &= 1\cdot p + 0 \cdot (1-p) = p \\ V[x] &= E[(x-p)^2] = (1-p)^2\cdot p + (0-p)^2\cdot (1-p) = p(1-p) \end{aligned} \]

$K$ 個の $d$変数ベルヌーイ分布を比率 $\boldsymbol{\pi}$で混ぜあわせれば混合ベルヌーイ分布 \[ p(\mathbf{x}|\mathbf{p},\boldsymbol{\pi}) = \sum_{k=1}^K \pi_k p(\mathbf{x}|\mathbf{p}_k) \] が出来上がります．

混合ベルヌーイ分布の平均・共分散は次のようになります． \[ \begin{aligned} E[\mathbf{x}] &= \sum_{k=1}^K\pi_k\mathbf{p}_k \\ \mathrm{cov}[\mathbf{x}] &= \sum_{k=1}^K\pi_k\left\{\mathrm{diag}\{p_{ki}(1-p_{ki})\}+\mathbf{p}_k\mathbf{p}_k^T\right\}\\ & - E[\mathbf{x}]E[\mathbf{x}]^T \end{aligned} \]

【証明】
\[ E[\mathbf{x}] = \sum_{\mathbf{x}}\mathbf{x}\sum_{k=1}^K\pi_kp(\mathbf{x}|\mathbf{p}_k) = \sum_{k=1}^K\pi_k\sum_{\mathbf{x}}\mathbf{x}p(\mathbf{x}|\mathbf{p}_k) = \sum_{k=1}^K\pi_k\mathbf{p}_k \] また， \[ \mathrm{cov}[\mathbf{x}] = E[\mathbf{x}\mathbf{x}^T]-E[\mathbf{x}]E[\mathbf{x}]^T \] と \[ \begin{aligned} E[\mathbf{x}\mathbf{x}^T] &= \sum_{\mathbf{x}}\mathbf{x}\mathbf{x}^T\sum_{k=1}^K\pi_kp(\mathbf{x}|\mathbf{p}_k) = \sum_{k=1}^K\pi_k\sum_{\mathbf{x}}\mathbf{x}\mathbf{x}^Tp(\mathbf{x}|\mathbf{p}_k) \\ &= \sum_{k=1}^K\pi_k\left\{ \mathrm{cov}_k[\mathbf{x}] - E_k[\mathbf{x}]E_k[\mathbf{x}]^T\right\} \end{aligned} \] より(但し，$\mathrm{cov}_k,E_k$は $p(\mathbf{x}|\mathbf{p}_k)$ における共分散・平均)

面白いポイントは，混合ベルヌーイ分布の分散共分散行列 \[ \mathrm{cov}[\mathbf{x}] = \sum_{k=1}^K\pi_k\left\{\mathrm{diag}\{p_{ki}(1-p_{ki})\}+\mathbf{p}_k\mathbf{p}_k^T\right\} - E[\mathbf{x}]E[\mathbf{x}]^T \] はもはや対角行列ではないという事です.

あるデータ $\mathbf{x}$ の一部だけ観測出来たとしましょう．すると，そのデータがどのカテゴリ $k$ のデータであるかある程度推測する事が出来，$\mathbf{x}$ の他の部分も予測する事が可能になる為です.

では，混合ベルヌーイ分布に対するEM法を導出しましょう.

今の場合，学習データは二値ベクトルの集合 $D=\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}$，モデルのパラメータは $\boldsymbol{\theta} = (\mathbf{p},\boldsymbol{\pi})$ です.

また，隠れ変数 $\mathbf{z}$ は各データ $\mathbf{x}_i$ がクラス $k$ のデータか否かを表す二値変数で，これを \[ z_{ik} = \left\{\begin{array}{ll} 1 & (\text{$\mathbf{x}_i$ がクラス $k$ のデータ}) \\ 0 & (\text{それ以外}) \end{array}\right. \] と置きます．

ベイズの定理より \[ p(z_{ik}=1|D)\propto p(z_{ik}=1)p(\mathbf{x}_i|z_{ik}=1) \] であり， \[p(z_{ik}=1) = \pi_k,\quad p(\mathbf{x}_i|z_{ik}=1) = p(\mathbf{x}_i|\mathbf{p}_k) \] なので，正規化すると \[ p(z_{ik}=1|D) = \frac{\pi_kp(\mathbf{x}_i|\mathbf{p}_k)}{\sum_{k=1}^K\pi_kp(\mathbf{x}_i|\mathbf{p}_k)} \] となります．(パラメータは省略して書いています．)

これを $r_{ik}$ と略記します.

続いて,

を計算します.

まず， \[ \begin{aligned} \log p(\mathbf{D},\mathbf{z}) &= \sum_{i=1}^n \log p(\mathbf{x}_i,\mathbf{z}_i) \end{aligned} \] で，$\mathbf{z}_i$ は１つの成分だけが $1$ になるので \[ \log p(\mathbf{D},\mathbf{z}) = \sum_{i=1}^n\sum_{k=1}^K z_{ik} \log p(\mathbf{x}_i,z_{ik}=1) \] と書くことが出来ます.

そして \[ \begin{aligned} \log p(\mathbf{x}_i,z_{ik}=1) &= \log p(\mathbf{x}_i|z_{ik}=1)p(z_{ik}=1) \\ &= \log p(z_{ik}=1) + \log p(\mathbf{x}_i|z_{ik}=1) \\ &= \log \pi_k + \log \prod_{j=1}^d p_{kj}^{x_{ij}}(1-p_{kj})^{1-x_{ij}}\\ &= \log \pi_k + \sum_{j=1}^d\left(x_{ij}\log p_{kj} + (1-x_{ij})\log (1-p_{kj}) \right) \end{aligned} \] となるので

\[ \begin{aligned} &\log p(\mathbf{D},\mathbf{z}) \\ &= \sum_{i=1}^n\sum_{k=1}^K z_{ik}\left\{\log \pi_k + \sum_{j=1}^d\left(x_{ij}\log p_{kj} + (1-x_{ij})\log (1-p_{kj}) \right)\right\} \end{aligned} \] となります. これに $r_{ik}$ を掛けて足しあわせますが， $z_{ik}=1$ の項しか残らない為，最終的に $\mathcal{Q}$ 関数は \[ \sum_{i=1}^n\sum_{k=1}^Kr_{ik}\left\{\log \pi_k + \sum_{j=1}^d\left(x_{ij}\log p_{kj} + (1-x_{ij})\log (1-p_{kj}) \right)\right\} \] となります.次はこれを最大にする $\mathbf{p},\boldsymbol{\pi}$ を求めます.

まず, \[\begin{aligned} \frac{\partial\mathcal{Q}}{\partial p_{kj}} &= \sum_{i=1}^nr_{ik}\left(\frac{x_{ij}}{p_{kj}}-\frac{1-x_{ij}}{1-p_{kj}}\right)\\ &= \frac{1}{p_{kj}(1-p_{kj})}\left(\sum_{i=1}^nr_{ik}x_{ij}-p_{kj}\sum_{i=1}^n r_{ik}\right) \end{aligned}\] が $0$ となる条件より \[ p_{kj}^{\mathrm{new}} = \frac{\sum_{i=1}^n r_{ik}x_{ij}}{\sum_{i=1}^n r_{ik}} \] つまり \[ \mathbf{p}_k^{\mathrm{new}} = \frac{\sum_{i=1}^n r_{ik}\mathbf{x}_i}{\sum_{i=1}^n r_{ik}} \] となります.

$\boldsymbol{\pi}$ については $\sum_{k=1}^K\pi_k=1$ が必要なので，ラグランジュの未定乗数を導入した \[ F = \mathcal{Q} - \lambda(\sum_{k=1}^K\pi_k - 1) \] を $\pi_k$ で微分すると \[ \frac{\partial F}{\partial \pi_k} = \sum_{i=1}^n \frac{r_{ik}}{\pi_k} - \lambda \] なのでこれが $0$ となる条件より \[ \pi_k = \frac{1}{\lambda}\sum_{i=1}^n r_{ik} \] となります.

従って \[ 1 = \sum_{k=1}^K\pi_k = \frac{1}{\lambda}\sum_{i=1}^n\sum_{k=1}^Kr_{ik} = \frac{n}{\lambda} \] だから \[ \lambda = n \] となり， \[ \pi_k^{\mathrm{new}} = \frac{1}{n} \sum_{i=1}^n r_{ik} \] となります.

まとめると以下のようになります.

例として手書き文字学習の問題をやってみます. mldata.orgから以下のような $28\times 28$ の手書き数字画像をダウンロード出来ます. どれが何の数字であるか一切指定する事なく学習をさせてみましょう.

prog19-2.py

全7万画像から，12クラスを学習させた結果が下図です. 各画像は各クラスの平均ベクトルです.

prog19-3.py

各クラスに所属すると判定された画像の例は以下のようになりました.

多項分布

$M$ 個の値 $w_1,\ldots,w_M$ のいずれかの値をそれぞれ確率 $p_1,\ldots,p_M$ で取る試行を考えます.もちろん$p_1+\cdots+p_M=1$です.

この試行を $L$ 回繰り返した時に各 $w_i$ が出現する回数を $k_i$ とした時， \[ \mathbf{x} = (k_1, \ldots, k_M)\qquad (k_1 + \cdots + k_M = L) \] の従う分布を多項分布(multinomial distribution)と呼びます. 多項分布のパラメータは $L$ と $\mathbf{p}=(p_1,\ldots,p_M)$ となります.

文書 $d$ 内に単語 $w_i$ が出現した回数をベクトルにしたものを文書のbag-of-words表現と呼びます. $$ \begin{array} \hline \text{単語} & w_1 & w_2 & w_3 & w_4 & w_5 &\cdots \\ \hline \text{文書}d & 1 & 0 & 0 & 3 & 2 & \cdots \\ \hline \end{array} $$

このベクトルは多項分布に従う確率変数と見なす事が出来ます．この場合の $L$ は文書の長さ(=単語数)です.

多項分布の確率質量関数は \[ p(\mathbf{x}|\mathbf{p}) = \frac{L!}{x_1!\cdots x_M!}p_1^{x_1}\cdots p_M^{x_M} \qquad \left(L=\sum_{i=1}^Mx_i\right)\] であり，これを $K$ クラス混合した分布は \[ p(\mathbf{x}) = \sum_{k=1}^K\pi_k p(\mathbf{x}|\mathbf{p}_k) \] となります.

ではEM法を導出しますが詳細は省略します. まずデータ $\mathbf{x}_i$ がクラス $k$ に所属する確率は \[ r_{ik} = \frac{\pi_kp(\mathbf{x}_i|\mathbf{p}_k)}{\sum_{k=1}^K\pi_kp(\mathbf{x}_i|\mathbf{p}_i)} \] となります.

続いて $\mathcal{Q}$ 関数は次のようになります. \[ \sum_{i=1}^n\sum_{k=1}^Kr_{ik}\left\{\log \pi_k + \sum_{j=1}^M x_{ij}\log p_{kj} + \log \frac{L_i!}{x_{i1}!\cdots x_{iM}!}\right\} \] 但し $L_i = \sum_{j=1}^Mx_{ij}$ です.

これを制約 $\sum_{j=1}^Mp_{kj} = 1$ と $\sum_{k=1}^K\pi_k = 1$ の下で最大化すると \[ \mathbf{p}_k^{\mathrm{new}} = \frac{\sum_{i=1}^n r_{ik}\mathbf{x}_i}{\sum_{i=1}^n r_{ik}L_i} \] 及び \[ \pi_k^{\mathrm{new}} = \frac{1}{n}\sum_{i=1}^n r_{ik} \] となります.

sklearn.datasetsに用意されている20 newsgroupsというデータに利用してみます. このデータセットには異なるニュースグループの記事が1万1千件ほど入っています.

文書を単語に分割し，ステミングを行い，極端に出現回数の低い単語や多い単語を除去すると約1万6千単語が抽出されました. これら単語のカウントデータを解析して，10グループに分けてみます.

学習された各グループ毎に出現頻度の高い上位50単語のうち，各グループに固有の単語のみをリストアップしてみると以下のようになりました.上手くトピックが抽出されているでしょうか. (prog19-4.py)

1. leagu, didn, pitch, got, home, better, basebal, season, let, score, start, lot, fan, happen, hit, won, gui,
2. format, sun, user, jpeg, ftp,
3. claim, life, human, moral, turkish, person, live, kill, reason, gun,
4. nhl, messag, list, period, power, hockei, pt,
5. giz, bike, gov, bhj, nasa, max, screen, monitor, manag, chang,
6. cleveland, ohio, engin, price, appl, book, jew, usa, order, john,
7. secur, presid, health, american, clinton, nation, clipper,
8. server, set, mit, connect, wire, current, widget, ground, font, displai,
9. scsi, port, hard, video, machin, id, control, bu, driver, card, disk, mac,
10. launch, christ, word, bibl, church,

今行った解析は，文書の意味を確率統計的に調べるものだと考える事が出来ます.

この様な，文書や画像や音声等に対する意味解析に利用するモデルはトピックモデル(topic model)と呼ばれ様々なものが開発されています.今日やった混合多項分布モデルはその中でも非常にシンプルなモデルです.

PRMLは自然言語処理や画像処理などは深く扱っていないので，興味のある方は専門書(何がありますか？)を読んでみて下さい.

クラスタ分析以外への応用

ここまではEM法を混合分布を用いた教師なしのクラスタ学習に用いて来ましたが，テキストでは他にベイズ線形回帰への応用が紹介されています. 軽く紹介します.

データ列 $D=\{(\mathbf{x}_1,y_1),\ldots,(\mathbf{x}_n,y_n)\}$ に回帰方程式 \[ y_i = \mathbf{a}^T\boldsymbol{\Psi}(\mathbf{x}_i) + \varepsilon_i, \qquad \varepsilon_i \sim N(0,\beta^{-1}) \] を当てはめる事を考えます. $\boldsymbol{\Psi}$ は適当な基底変換関数で，$\boldsymbol{\Psi}(\mathbf{x})$ の次元は $M$ であるとします.

また，$\mathbf{a}$ の事前分布を \[ \mathbf{a} \sim N(0,\alpha^{-1}I) \] とします.

ここで，与えられたデータ $D$ からハイパーパラメータ $\alpha,\beta$ を学習するという問題を考えましょう．

この時 \[ p(D,\mathbf{a}|\alpha,\beta) = p(D|\mathbf{a},\beta)p(\mathbf{a}|\alpha) \] であるので, \[ p(D|\alpha,\beta) = \int p(D|\mathbf{a},\beta)p(\mathbf{a}|\alpha)\mathrm{d}\mathbf{a} \] となり，$\mathbf{a}$ を隠れ変数と見なす事ができます.

すると，$D$ と隠れ変数 $\mathbf{a}$ が与えられた下での $\alpha,\beta$ の対数尤度は \[ \begin{aligned} \log p(D,\mathbf{a}|\alpha,\beta) &= \log p(D|\mathbf{a},\beta) + \log p(\mathbf{a}|\alpha)\\ &= \log \prod_{i=1}^n \sqrt{\frac{\beta}{2\pi}}\exp\left\{-\frac{\beta}{2}|y_i-\mathbf{a}^T\boldsymbol{\Psi}(\mathbf{x}_i)|^2\right\}\\ & + \log \left(\frac{\alpha}{2\pi}\right)^{M/2}\exp\left\{-\frac{\alpha}{2}||\mathbf{a}||^2\right\}\\ &= \frac{n}{2}\log\left(\frac{\alpha}{2\pi}\right)-\frac{\beta}{2}||\mathbf{y}-\mathbf{X}\mathbf{a}||^2\\ & + \frac{M}{2}\log\left(\frac{\beta}{2\pi}\right)-\frac{\alpha}{2}||\mathbf{a}||^2 \end{aligned}\] ($\mathbf{X}$ は計画行列)となりますので

$\mathbf{a}$ の事後分布に関して期待値を取れば \[ \begin{aligned} E[\log p(D,\mathbf{a}|\alpha,\beta)] &= \frac{n}{2}\log\left(\frac{\beta}{2\pi}\right)-\frac{\beta}{2}E[||\mathbf{y}-\mathbf{X}\mathbf{a}||^2]\\ & + \frac{M}{2}\log\left(\frac{\alpha}{2\pi}\right)-\frac{\alpha}{2}E[||\mathbf{a}||^2] \end{aligned} \] となります.よってこれを $\alpha,\beta$ に関して最大化してやれば良いです.

まず $\alpha$ に関して微分してみれば \[ \frac{M}{2\alpha} - \frac{1}{2}E[||\mathbf{a}||^2] = 0 \] となるので \[ \alpha^{\mathrm{new}} = \frac{M}{E[||\mathrm{a}||^2]} \] となります.

$\mathbf{a}$ に関する事後分布の計算は第3回あたりの資料でやっているので詳しくは省略しますが \[ p(\mathbf{a}|D) \propto p(\mathbf{a})p(D|\mathbf{a}) \] を計算して \[ \begin{aligned} p(\mathbf{a}|D) &= N(\mathbf{w}|\mathbf{m}, \mathbf{S})\\ \mathbf{m} &= \beta\mathbf{S}\mathbf{X}^T\mathbf{y} \\ \mathbf{S}^{-1} &= \alpha I + \beta \mathbf{X}^T\mathbf{X} \end{aligned} \] となります. 従って \[ \alpha^{\mathrm{new}} = \frac{M}{||\mathbf{m}||^2 + \mathrm{Tr}(\mathbf{S})} \] です. $\beta$ に関しても同様です.

EM法の理論

最後にEM法で何故尤度を最大化する事が出来るのかについて理論的な説明をします. 次回やる 変分推論(variational inference) でもここで説明する事実を使います.

そもそも，EM法を使って何を達成したいのかというと与えられたデータ $\mathbf{x}$ に基づくパラメータ $\boldsymbol{\theta}$ の尤度 \[ p(\mathbf{x} | \boldsymbol{\theta}) \] を最大化する事です.

ここで $p(\mathbf{x}|\boldsymbol{\theta})$ を実際に最大化する事は非常に難しいので，隠れ変数 $\mathbf{z}$ を導入したより扱い易い分布 \[ p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) \] を考える事にします.

この二つの分布には \[ p(\mathbf{x}|\boldsymbol{\theta}) = \sum_{\mathbf{z}} p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) \] の関係があります.

ここで, $\mathbf{z}$ の事前分布 $q(\mathbf{z})$ を導入すると \[ \color{red}{ \log p(\mathbf{x}|\boldsymbol{\theta}) = \mathcal{L}(q,\boldsymbol{\theta}) + \mathrm{KL}(q||p) } \] という分解が出来ます. 但し， \[ \begin{aligned} \mathcal{L}(q,\boldsymbol{\theta}) &= \sum_{\mathbf{z}}q(\mathbf{z})\log \frac{p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta})}{q(\mathbf{z})} \\ \mathrm{KL}(q||p) &= - \sum_{\mathbf{z}} q(\mathbf{z})\log \frac{p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta})}{q(\mathbf{z})} \end{aligned} \] であり， $\mathrm{KL}(q||p)$ は カルバック・ライブラー情報量(Kullback-Leibler divergence)と呼ばれます.

【証明】
乗法定理より \[ \log p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) = \log p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta}) + \log p(\mathbf{x}|\boldsymbol{\theta}) \] であるから \[ \begin{aligned} \mathcal{L}(q,\boldsymbol{\theta}) &= \sum_{\mathbf{z}}q(\mathbf{z})\left\{\log p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta}) + \log p(\mathbf{x}|\boldsymbol{\theta}) - \log q(\mathbf{z})\right\} \\ &= \log p(\mathbf{x}|\boldsymbol{\theta})\sum_{\mathbf{z}}q(\mathbf{z}) + \sum_{\mathbf{z}}q(\mathbf{z})\log \frac{p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta})}{q(\mathbf{z})} \\ &= \log p(\mathbf{x}|\boldsymbol{\theta}) - \mathrm{KL}(q||p) \end{aligned} \]

カルバック・ライブラー情報量というのは初出だと思うので説明します.確率分布 $p(\mathbf{x}),q(\mathbf{x})$ に対するカルバックライブラー情報量 $\mathrm{KL}(q||p)$ は \[ \mathrm{KL}(q||p) = \sum_{\mathbf{x}}q(\mathbf{x})\log \frac{q(\mathbf{x})}{p(\mathbf{x})} = - \sum_{\mathbf{x}}q(\mathbf{x})\log \frac{p(\mathbf{x})}{q(\mathbf{x})} \] と定義されます.

よくある直感的な説明は，事前分布が $p(\mathbf{x})$ である状態から何らかの学習を行って事後分布が $q(\mathbf{x})$ になった場合の学習によって得た情報量であるというものです.

もっと単純に，2つの分布 $p,q$ がどのくらい異なっているかを表していると考えてKL距離と呼ばれる事もあります. 数学的な意味での距離にはなっていませんので注意して下さい.

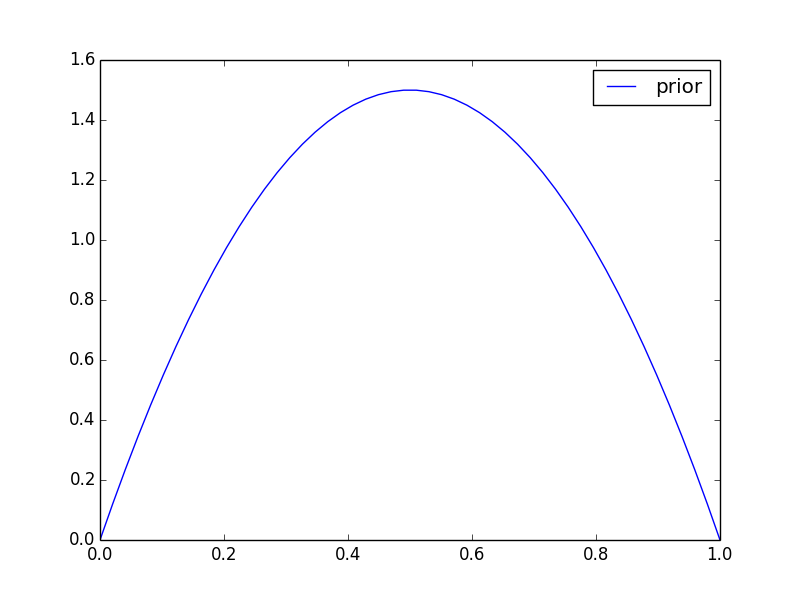
簡単な例で実際にKL情報量を計算してみましょう．あるコインの表が出る確率 $\theta$ をMAP推定したいとします. 事前分布として $\mathrm{Beta}(2,2)$ \[ p(\theta) \propto \theta(1-\theta) \] を採用したとします.

ここで実験を行い$D=\text{「表、裏、裏、表」}$という結果が出たとしましょう。この時の事後分布は \[ p(\theta|D) \propto p(\theta)p(D|\theta) = \theta(1-\theta)\cdot \theta^2 (1-\theta)^2 = \theta^3(1-\theta)^3 \] となります.

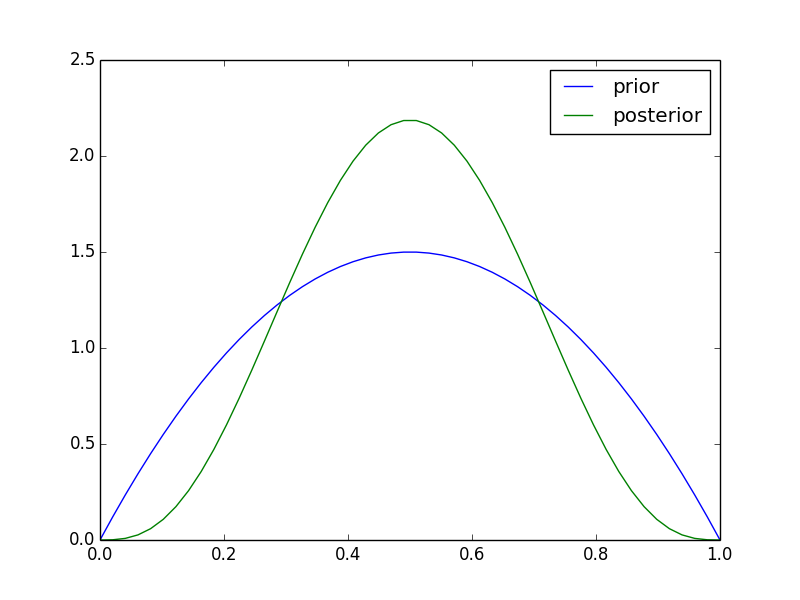
この学習で$p(\theta)\rightarrow p(\theta|D)$ という分布の変化が生じましたが，この時のKL情報量を実際に計算してみると \[ \begin{aligned} \mathrm{KL}(p(\theta|D)||p(\theta)) &= \int_0^1 p(\theta|D) \log \frac{p(\theta|D)}{p(\theta)} \mathrm{d}\theta\\ &= \int_0^1 140\theta^3(1-\theta)^3\log \frac{140\theta^3(1-\theta)^3}{6\theta(1-\theta)}\mathrm{d}\theta \\ & \approx 0.111 \end{aligned} \] となります.

別の実験では $D'=\text{「表、表、表、表」}$ という結果が出たとします. この時のKL情報量を同様に計算すると \[ \mathrm{KL}(p(\theta|D')||p(\theta)) \approx 0.708 \] となり，先ほどより得た情報量が大きくなっています.

$D'$ から得る情報量の方が大きかったのは次のように解釈出来ます. まず，事前分布では大体 $\theta=1/2$ あたりだろうと予想をしています. 結果 $D$ では4回中2回表が出ましたがこれはある程度予想通りだったので学習で得た情報はそれほど大きくありません. 一方, $D'$ は予想外の結果だったので $\theta$ の推定値を大きく修正する必要がありました. この意味でより大きな情報を得たと考える事が出来ます.

話を戻します. KL情報量は必ず $0$ 以上になる事が証明出来ます. 従って \[ \mathcal{L}(q,\boldsymbol{\theta}) \leq \log p(\mathbf{x}|\boldsymbol{\theta}) \] が成り立ちます.

EM法で最大化している値は，実はこの左辺の量です. 左辺を大きくしていくと，実際に最大化を行いたい右辺の値も大きくなっていきます. $\boldsymbol{\theta}^{\mathrm{old}}$ の下で $q(\mathbf{z})$ を固定すると \[ \mathcal{L}(q,\boldsymbol{\theta}) = \sum_{\mathbf{z}}q(\mathbf{z})\log \frac{p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta})}{q(\mathbf{z})} \] を最大化する事は \[ \sum_{\mathbf{z}}q(\mathbf{z})\log p(\mathbf{x},\mathbf{z}|\boldsymbol{\theta}) \] を最大化する事と同値です.

【KL情報量の非負性の証明】
$y=\log x$ は上に凸の関数であるから \[ \begin{aligned} \mathrm{KL}(q||p) &= -\sum_{\mathbf{x}}q(\mathbf{x})\log \frac{p(\mathbf{x})}{q(\mathbf{x})} \\ &\geq -\log\left\{\sum_{\mathbf{x}}q(\mathbf{x})\frac{p(\mathbf{x})}{q(\mathbf{x})}\right\} \\ &= -\log\left\{\sum_{\mathbf{x}}p(\mathbf{x})\right\} \\ &= -\log 1 \\ &= 0 \end{aligned} \]

反復を繰り返して 隠れ変数 $\mathbf{z}$ の分布に変化がなくなったとします. つまり \[ q(\mathbf{z}) \] と \[ p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta}) \] が等しくなったとします.

すると \[ \mathrm{KL}(q||p) = -\sum_{\mathbf{z}} q(\mathbf{z})\log \frac{p(\mathbf{z}|\mathbf{x},\boldsymbol{\theta})}{q(\mathbf{z})} = 0 \] となります.

従って，反復が停止した時点では \[ \log p(\mathbf{x}|\boldsymbol{\theta}) = \mathcal{L}(q,\boldsymbol{\theta}) \] が成立する為，$\mathcal{L}$ を最大化する事と実際の対数尤度を最大化する事が一致するわけです.

今回はここで終了します．

次回はテキスト第10章に進み変分推論法の解説をします.少しペースを挙げて一回でほぼ全部を終了させるつもりです.