パターン認識・
機械学習勉強会
第18回
@ナビプラス
中村晃一2014年9月4日
2ヶ月ほど間が空きましたが、場所を変えまして再開します.テキストの第9章「Mixture Models and EM」から開始します。
謝辞
前回終了後,新たに会場の提供を申し出て下さいました
㈱ ナビプラス様
にこの場をお借りして御礼申し上げます.
K-meansクラスタリング
これまでに紹介した識別手法では,特徴ベクトルとラベルからなるデータ $D=\{(\mathbf{x}_1,t_1),(\mathbf{x}_2,t_2),\ldots,(\mathbf{x}_n,t_n)\}$ を基に学習を行いました.各特徴ベクトル $\mathbf{x}_i$ に対して、正解のラベル $t_i$ が与えられていますので,このような学習を教師付き学習(supervised learning)と呼びます.
一方,正解のラベル $t_i$ が与えられない状態でも特徴ベクトルの分布の特徴に基いて分類等のパターン認識タスクを行う事が出来ます.このような学習を教師なし学習(unsupervised learning)と呼びます.
クラスター分析
すごく簡単に言えば「$\mathbf{x}_i$ と $\mathbf{x}_j$ が似ている時は同じグループに分類する」という作業によって,特徴ベクトルの集合を幾つかのクラスター(cluster)に分類する事が出来ます.このような分析手法をクラスター分析(cluster analysis)と言います.
識別したいパターンを教師データとして与える教師付き問題と異なり,クラスター分析はデータの分布が持つ本質的な特徴を調べる為に利用出来ます.
様々な集団の混ざったデータを分析する際の標準的な手法です.
K-meansアルゴリズム
K-means アルゴリズムは代表的な非階層的クラスタリングの手法です.非階層的というのはクラスタ間の階層的な構造(例:人間クラスタは生物クラスタの一部)は調べないという事です.
このアルゴリズムではクラスタの数 $K$ をあらかじめ与えると,データを $K$ 個の集団に分類します.
数学的な話の前にアルゴリズムの説明をします.まずテンプレート法を思い出しましょう.
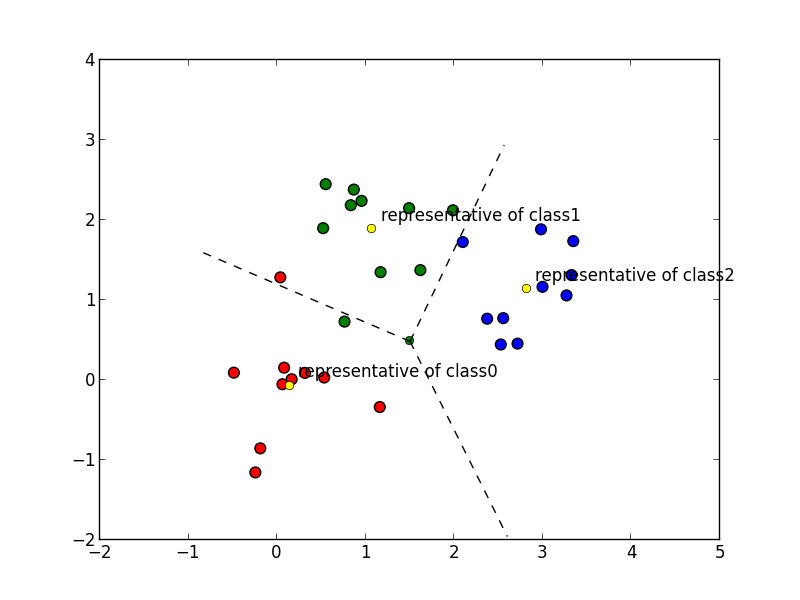
テンプレート法では,各クラス $C$ を代表ベクトル $\boldsymbol{\mu}_C$ によって表現し,各特徴ベクトル $\mathbf{x}$ は最も距離の近い代表ベクトル所属するクラスに分類するのでした. \[ \mathrm{classof}(\mathbf{x}) = \mathop{\rm arg~min}\limits_{C}|| \mathbf{x}-\boldsymbol{\mu}_C||^2 \]
また,代表ベクトルの推定値は $C$ に属す学習ベクトル達の重心とすると良いのでした. \[ \boldsymbol{\mu}_C = \frac{1}{|C|}\sum_{\mathbf{x}_i\in C}\mathbf{x}_i \qquad \small{(\text{$C$はクラス $C$ に属す学習ベクトルの集合})}\]
教師なしで分類を行う際の問題は各学習ベクトル $\mathbf{x}_i$ がどのクラス $C$ に所属するのか分からないという事です.
そこで,一番最初は代表ベクトルを ランダムに $K$ 個選び,
- それに基いて分類を行う
- 得られた分類に基いて代表ベクトルを計算し直す
という事を反復します.
まとめると次のようになります. E-step,M-stepという呼び方については後で説明します.
K-meansアルゴリズム
クラスタの数 $K$ を決め,代表ベクトル $\boldsymbol{\mu}_c\quad (c=1,2,\ldots,K)$ をランダムに決める.
以下を収束するまで繰り返す.
- 【E-step】各学習ベクトルを $\boldsymbol{\mu}_c$ に基づいて分類する.
- 【M-step】得られた各クラスタに基いて $\boldsymbol{\mu}_c$ を再計算する.
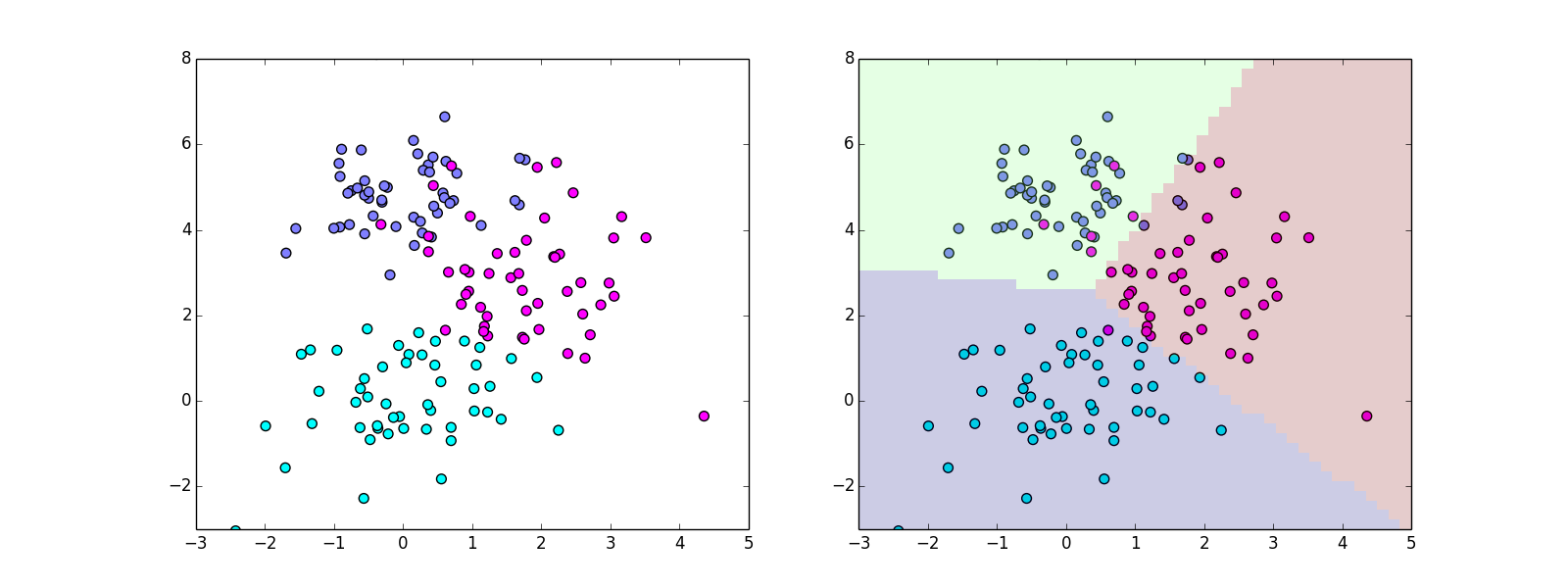
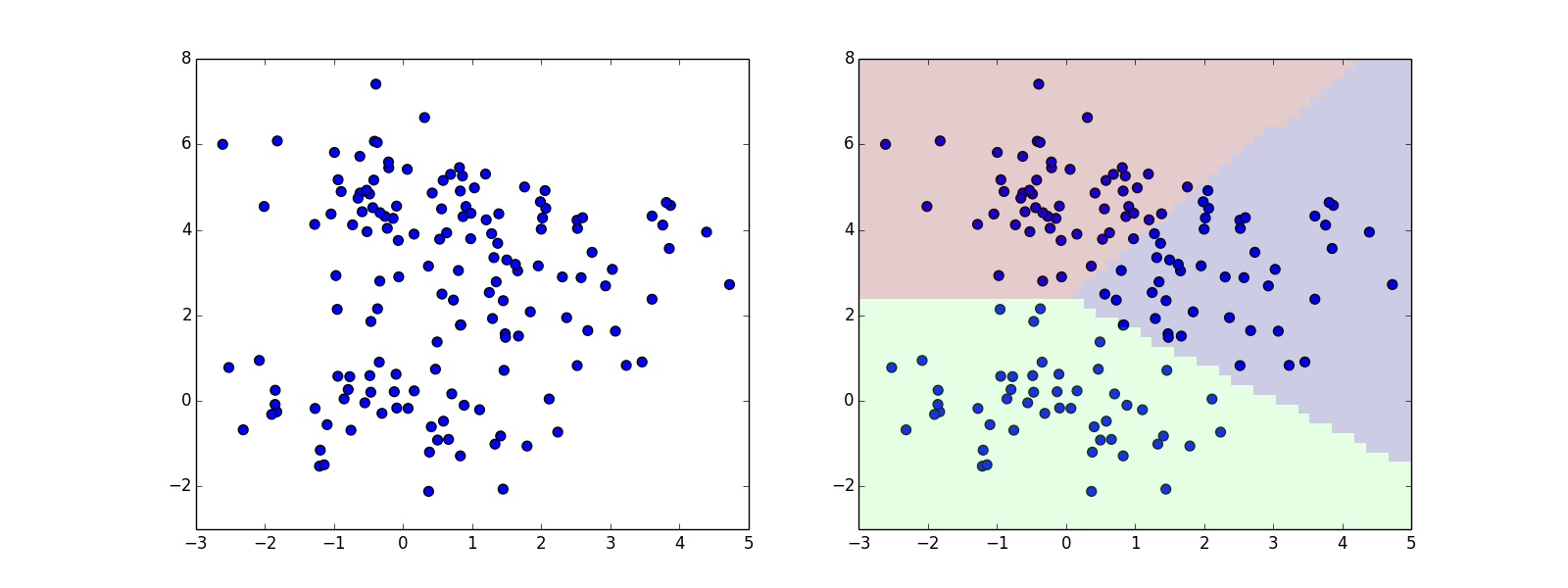
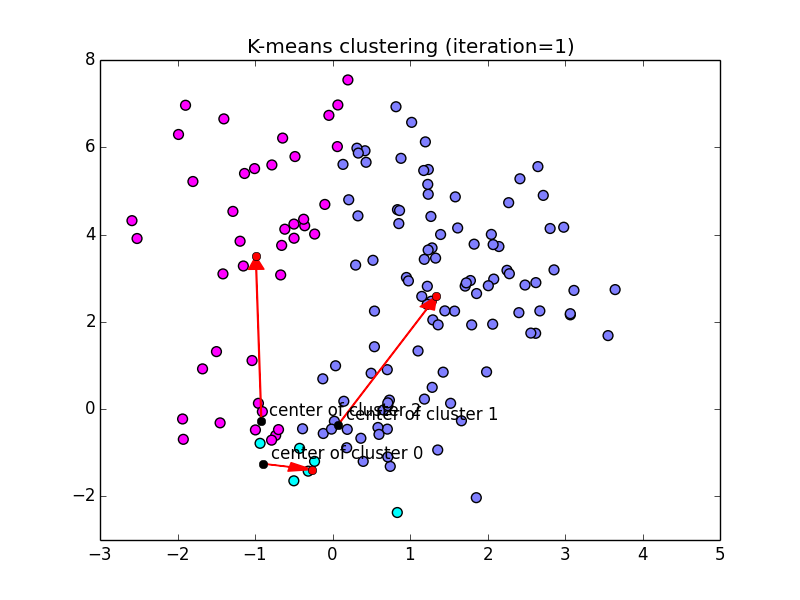
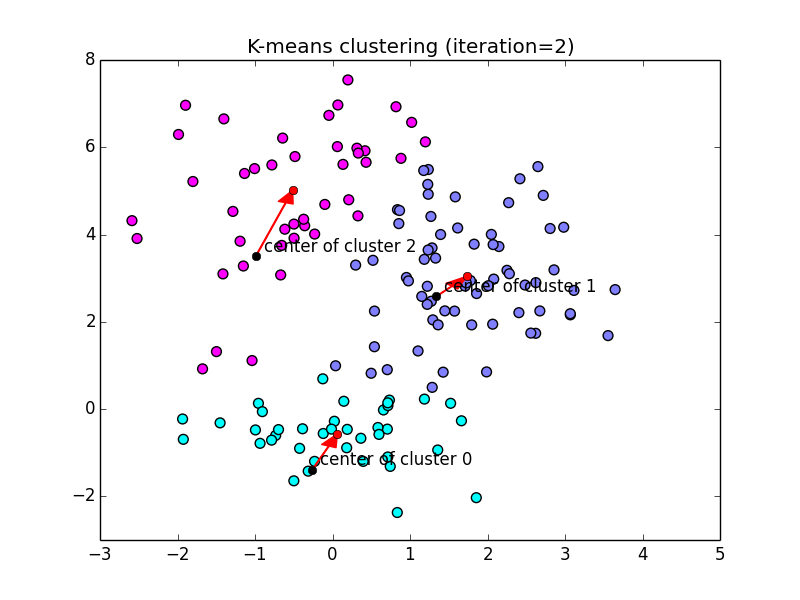
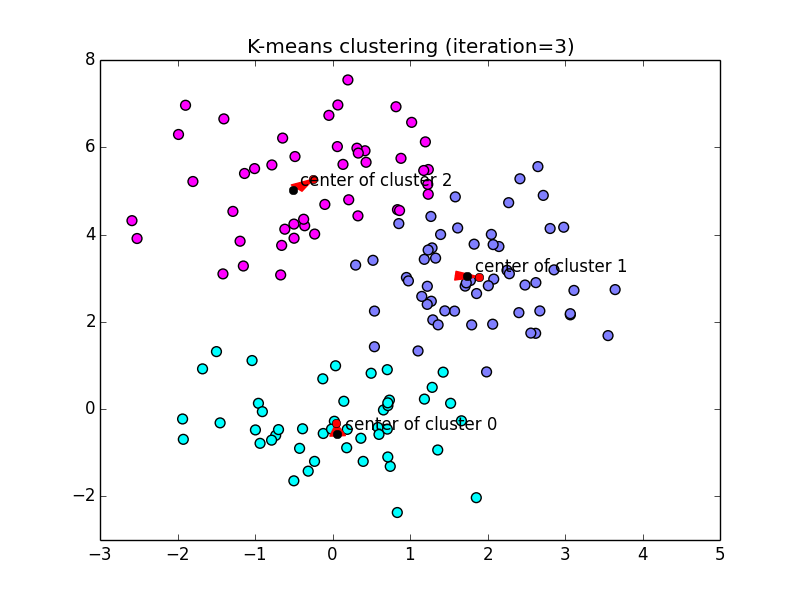
以下が実装例です. (黒点:現在の重心, 赤点:新しい重心)
以下が実装例です. (黒点:現在の重心, 赤点:新しい重心)
以下が実装例です. (黒点:現在の重心, 赤点:新しい重心)
代表ベクトル $\boldsymbol{\mu}=\{\boldsymbol{\mu}_1,\ldots,\boldsymbol{\mu}_K\}$ と,各学習ベクトルのクラスへの割り当て $r_{ic}$ \[ r_{ic} = \left\{\begin{array}{ll} 1 & (\text{$\mathbf{x}_i$ をクラス $c$ に割り当てた時})\\ 0 & (\text{そうでない時}) \end{array}\right. \] に基いて計算される以下の量を歪み測度(distortion measure)と言います. \[ J(r, \boldsymbol{\mu}) = \sum_{c=1}^K\sum_{i=1}^n r_{ic}||\mathbf{x}_i-\boldsymbol{\mu}_c||^2 \] 各クラス毎のバラつき具合の総和を表しています.
K-meansアルゴリズムはこの $J(r,\boldsymbol{\mu})$ が最小となるような割り当て $r$ と代表ベクトル $\boldsymbol{\mu}$ を反復的に求めるアルゴリズムです.
【E-step】
代表ベクトル $\boldsymbol{\mu}$ が与えられた時は
\[ J(r, \boldsymbol{\mu}) = \sum_{c=1}^K\sum_{i=1}^n r_{ic}||\mathbf{x}_i-\boldsymbol{\mu}_c||^2 \]
の $||\mathbf{x}_i-\boldsymbol{\mu}_c||$ は定数になるのでこれが最小となる $i,c$ に対して $r_{ic} = 1$ ,それ以外は0とする時に $J$ は最小になる.
【M-step】
クラスの割り当て $r$ が与えられた時は,各 $\boldsymbol{\mu}_c$ について
\[ \frac{\partial}{\partial\boldsymbol{\mu}_c}J(r,\boldsymbol{\mu}) = -2\sum_{i=1}^n r_{ic}(\mathbf{x}_i-\boldsymbol{\mu}_c) \]
となるので,これが $0$ となる $\boldsymbol{\mu}_c$ は
\[ \boldsymbol{\mu_c} = \frac{\sum_{i=1}^n r_{ic}\mathbf{x}_i}{\sum_{i=1}^n r_{ic}} \]
つまりクラス $c$ に割り当てられたベクトルの重心となる.
歪み測度 \[ J(r, \boldsymbol{\mu}) = \sum_{c=1}^K\sum_{i=1}^n r_{ic}||\mathbf{x}_i-\boldsymbol{\mu}_c||^2 \] の $||\mathbf{x}_i-\boldsymbol{\mu}_c||^2$ の部分はベクトル $\mathbf{x}_i$ と $\boldsymbol{\mu}_c$ の非類似度を表していると考える事ができます。値が大きいほど(距離が遠いほど)似ていないという事です.
この考え方を一般化すれば,ユークリッド距離以外の何らかの非類似度の尺度 $\mathcal{V}$ を用いて \[ J(r, \boldsymbol{\mu}) = \sum_{c=1}^K\sum_{i=1}^n r_{ic}\mathcal{V}(\mathbf{x}_i, \boldsymbol{\mu}_c) \] を最小化するというようにアルゴリズムを一般化する事が出来ます.
この場合,これを最小化する $\boldsymbol{\mu}$ は平均(mean)ではなくなり,medoidsと呼ばれる、クラス内の他のベクトルとの非類似度の総和が最小になる点になります.そこで、この一般化された手法はK-medoidsアルゴリズムと呼ばれます.
K-means法の応用としてテキストで紹介されている画像のセグメンテーションをやってみましょう.
画像の各ピクセルは3色の画素値 $(R,G,B)$ からなりますが,これを3次元ベクトルとみなしてK-means法を適用します.
以下の画像に適用してみます.

$K = 10$ の場合
$K = 5$ の場合
$K = 2$ の場合
K-means法については一旦終了します.
テキストにはK-means法の計算量を改良する手法や、画像のセグメンテーションを応用して圧縮を行う手法などが紹介されていますが、そちらはテキストを参照して下さい.
混合ガウスモデル
K-meansと同様の複数の集団が混合した分布の分析を確率論的に行う方法として混合分布モデル(mixture model)というものを説明します.
混合ガウスモデル
平均が $\boldsymbol{\mu}_c$、分散共分散行列が $\boldsymbol{\Sigma}_c$ である複数の正規分布を重み $\pi_c$ で足しあわせた分布 \[ p(\mathbf{x}) = \sum_{c=1}^K \pi_c\mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] を混合ガウス分布(gaussian mixture distirbution)または混合正規分布(normal mixture distribution)と呼びます.
重みは \[ 0\leq \pi_c \leq 1,\qquad \sum_{c=1}^K\pi_c = 1 \] を満たす必要があります.
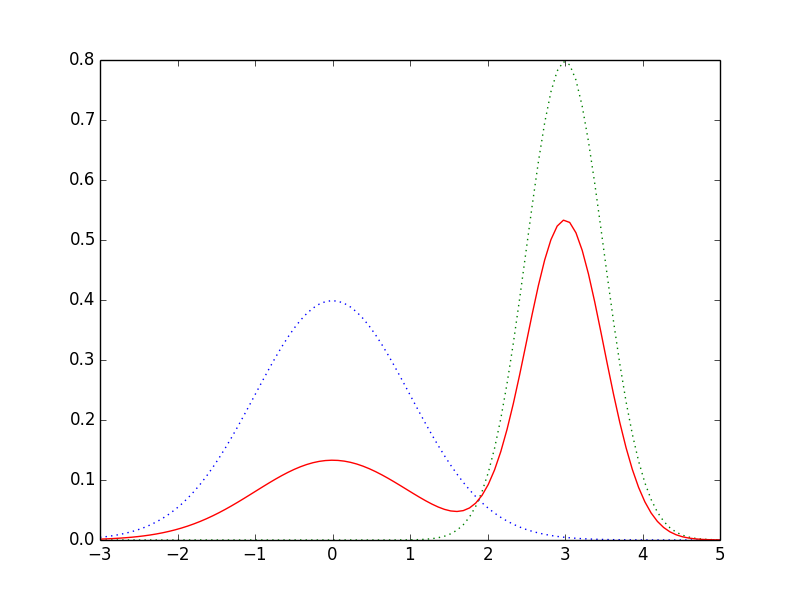
例えば一次元の $N(0, 1)$ と$N(3, 0.5)$ を重み $1:2$ で混合した分布は以下のようになります.
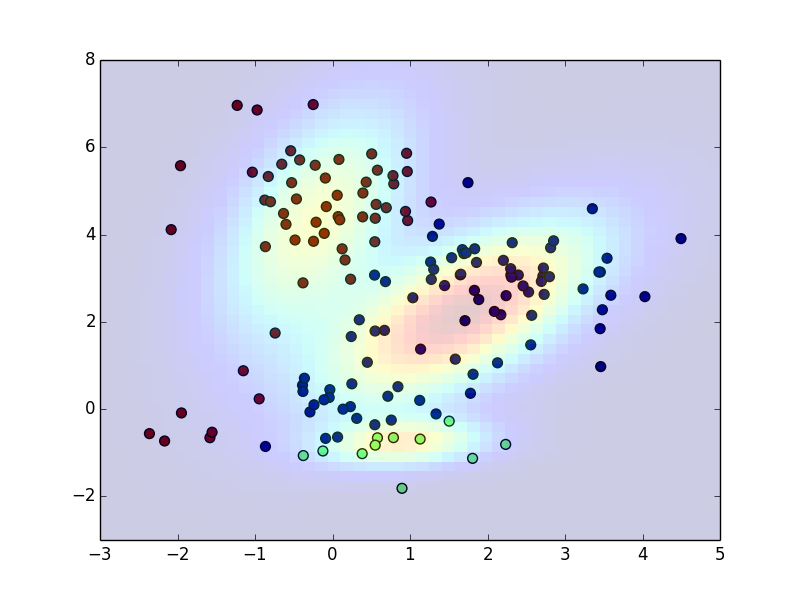
以下は,二次元の \[ \mathcal{N}\left(\begin{pmatrix} 0 \\ 0\end{pmatrix}, I\right), \mathcal{N}\left(\begin{pmatrix} 3 \\ 3\end{pmatrix}, 2I\right), \mathcal{N}\left(\begin{pmatrix} 2 \\ 5\end{pmatrix}, 3I\right) \] を等しい重みで混合した例です.
さて,この混合ガウス分布
\[ p(\mathbf{x}) = \sum_{c=1}^K \pi_c\mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \]は隠れ変数モデル(latent variable model)の一種として考える事が出来ます.
隠れ変数モデル
隠れ変数モデルというのは観測出来る変数 $\mathbf{x}$ の他に,観測が出来ない変数 $\mathbf{z}$ の効果も考慮にいれたモデリングの事です.
隠れ変数モデルでは,観測出来る $\mathbf{x}$ の分布 $p(\mathbf{x})$ は,隠れ変数 $\mathbf{z}$ も考慮した分布 $p(\mathbf{x}, \mathbf{z})$ を周辺化して得られるものだと考えます. \[ \begin{aligned} p(\mathbf{x}) &= \int p(\mathbf{x},\mathbf{z})\mathrm{d}\mathbf{z}\\ p(\mathbf{x}) &= \sum_{\mathbf{z}} p(\mathbf{x},\mathbf{z}) \end{aligned} \]
クラスタリングの文脈でこの事を考えましょう.今,$K$ クラスが存在するとして,各クラスタは正規分布であると仮定します.つまり,データ $\mathbf{x}$ のクラスが $c$ だと分かっているならば \[ p(\mathbf{x} | c) = \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] と表されます.
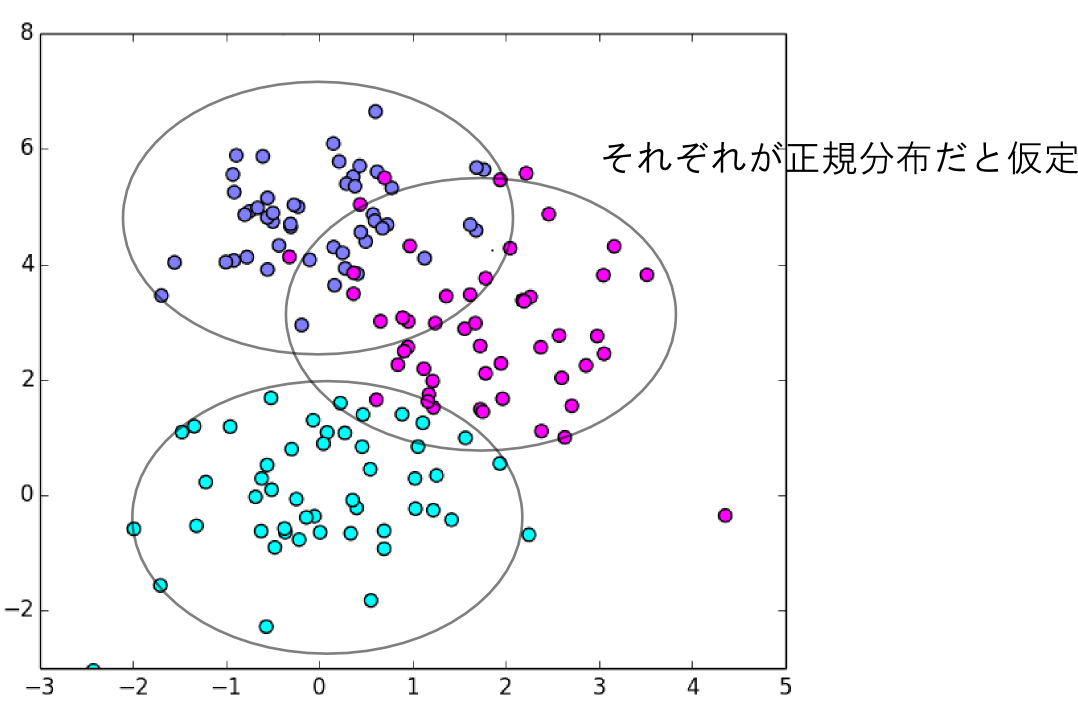
教師無し学習の場合,実際には $\mathbf{x}$ のクラスが $c$ であるという事は分かりません.従って $c$ は隠れ変数になります.
今, 各クラスのデータの出現確率 $p(c)$ が分かっているならば \[ p(\mathbf{x},c) = p(\mathbf{x}|c)p(c) \] と書くことが出来るので, $\mathbf{x}$ の分布は \[ p(\mathbf{x}) = \sum_c p(\mathbf{x}|c)p(c) = \sum_c \pi_c\mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \qquad (\pi_c = p(c)) \] となります.すなわち,各データのクラス $c$ が隠れ変数である時の出現データ $\mathbf{x}$ の分布は混合ガウス分布としてモデリングする事が出来ます.
まとめましょう.
混合ガウスモデル
$K$ クラスある各クラス $c$ について,所属するベクトルの分布が平均 $\boldsymbol{\mu}_c$,分散共分散行列が $\boldsymbol{\Sigma}_c$ の正規分布であると仮定し, 各クラス $c$ の出現確率が $\pi_c$ であるとする.各データ $\mathbf{x}$ のクラス $c$ が未知である場合には, $\mathbf{x}$ の分布は \[ p(\mathbf{x}) = \sum_c \pi_c \mathcal{N}(\mathbf{x}|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] とモデル化出来る.
学習データ $D=\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}$ の出現確率をモデル化する事が出来たので,あとは最尤推定やMAP推定等を行えば $\boldsymbol{\mu}_c$ や $\boldsymbol{\Sigma}_c$ や $\pi_c$ を求める事が出来るはずです.
例えば最尤法を行う為には, $D$ に対する対数尤度関数 \[\begin{aligned} \log L(\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}|D) &= \log p(D|\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}) \\ &=\sum_{i=1}^n \ln \left\{\sum_c \pi_c \mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)\right\} \end{aligned} \] が最大となるような $\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}$ を求めれば良いです
が、これは非常に複雑な形状をしており素直に解くことは出来ません.
EM法
今の問題を解くためには Expectation Maximization法(EM法) を用いる事が出来ます.
EM法は隠れ変数モデルに対するパラメータ推定に用いられる標準的なアルゴリズムです.
基本的な考え方はK-means法の場合と同じです.
まず $\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}$ を適当に初期化します.
それに基いて,各データ $\mathbf{x}_i$ がクラス $c$ に所属する確率 \[ p(c|\mathbf{x}_i) \] を計算する事が出来ます.
計算された $p(c|\mathbf{x}_i)$ に基いて,$\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}$ を更新します.これを変化がなくなるまで繰り返します.
では,実際の計算をしていきましょう.まず $\pi,\boldsymbol{\mu},\boldsymbol{\Sigma}$ が与えられているという条件下で,データ $\mathbf{x}_i$ がクラス $c$ に所属する確率 \[ r_{ic} \stackrel{\mathrm{def}}{=} p(c|\mathrm{x}_i) \] を求めます.
ベイズの定理より \[ r_{ic} \propto p(c)p(\mathrm{x}_i|c) = \pi_c\mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] なので,和が1になるように正規化を行えば \[ r_{ic} = \frac{\pi_c\mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)}{\sum_{k}\pi_k\mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)} \] となります.
次は,$r_{ic}$ が与えられているという条件下で,各パラメータを推定します.まず,対数尤度 \[ \log L =\sum_{i=1}^n \ln \left\{\sum_c \pi_c \mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)\right\} \] を $\boldsymbol{\mu}_c$ で微分すれば \[ \begin{aligned} \frac{\partial}{\partial\boldsymbol{\mu}_c}\log L &= \sum_{i=1}^n \frac{\pi_c\mathcal{N}(\mathcal{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)}{\sum_k \pi_k \mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)}\boldsymbol{\Sigma}_c^{-1}(\mathbf{x}_i-\boldsymbol{\mu}_c)\\ &= \boldsymbol{\Sigma}_c^{-1}\sum_{i=1}^n r_{ic}(\mathbf{x}_i-\boldsymbol{\mu}_c) \end{aligned} \] となります.
従ってこれが $\mathbf{0}$ となる条件を考えて \[ \boldsymbol{\mu}_c = \frac{\sum_{i=1}^n r_{ic}\mathbf{x}_i}{\sum_{i=1}^n r_{ic}} \] となります.
K-means法との類似性に注目しましょう.
K-means法ではクラス $c$ に所属するベクトルの平均を $\boldsymbol{\mu}_c$ としましたが,混合分布クラスタリングの場合には,$c$ に所属する確率 $r_{ic}$ で重み付けした平均を $\boldsymbol{\mu}_c$ とするという事になります.
全く同様の計算を共分散行列 $\boldsymbol{\Sigma}_c$ に対しても行えば \[ \boldsymbol{\Sigma}_c = \frac{\sum_{i=1}^n r_{ic}(\mathbf{x}_i-\boldsymbol{\mu}_c)(\mathbf{x}_i-\boldsymbol{\mu}_c)^T}{\sum_{i=1}^n r_{ic}} \] が得られます.但し $\boldsymbol{\mu}_c$ は更新後の値を使います.
パラメータ $\pi_c$ については \[ \sum_{c=1}^K \pi_c = 1 \] という制約が付いているので,ラグランジュの未定乗数 $\lambda$ を導入した \[ \log L + \lambda\left(\sum_{c=1}^K \pi_c - 1\right) \] の導関数が $0$ となる条件を求める事になります.
詳しい計算は省略しますが,実際にやってみると \[ \pi_c = \frac{1}{n}\sum_{i=1}^n r_{ic} \] となります.
今の計算において最大化した \[ \log L =\sum_{i=1}^n \ln \left\{\sum_c \pi_c \mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)\right\} \] の \[ \sum_c \pi_c \mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c) \] の部分はデータ $\mathbf{x}_i$ に対する尤度の期待値と解釈する事が出来ます.これがExpectation Maximization法という名前の由来です.
まとめましょう.
混合ガウスモデルによるクラスタリング
クラスの数を $K$ とし,各クラスは正規分布に従うと仮定する.
各クラスの出現確率 $\pi_c$,平均 $\boldsymbol{\mu}_c$,分散共分散行列 $\boldsymbol{\Sigma}_c$ を適当に初期化し,以下を収束するまで繰り返す.
- 【E step】データ $\mathbf{x}_i$ がクラス $c$ に所属する確率 \[ r_{ic} = \frac{\pi_c\mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_c,\boldsymbol{\Sigma}_c)}{\sum_{k}\pi_k\mathcal{N}(\mathbf{x}_i|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)} \] を計算する.
- 【M step】平均・分散共分散行列・クラスの出現確率を更新する. \[ \begin{aligned} \boldsymbol{\mu}_c &= \frac{\sum_{i=1}^n r_{ic}\mathbf{x}_i}{\sum_{i=1}^n r_{ic}},\quad \boldsymbol{\Sigma}_c = \frac{\sum_{i=1}^n r_{ic}(\mathbf{x}_i-\boldsymbol{\mu}_c)(\mathbf{x}_i-\boldsymbol{\mu}_c)^T}{\sum_{i=1}^n r_{ic}} \\ \pi_c &= \frac{1}{n}\sum_{i=1}^n r_{ic} \end{aligned} \] ($\boldsymbol{\Sigma}_c$ の計算には更新後の平均を使う.)
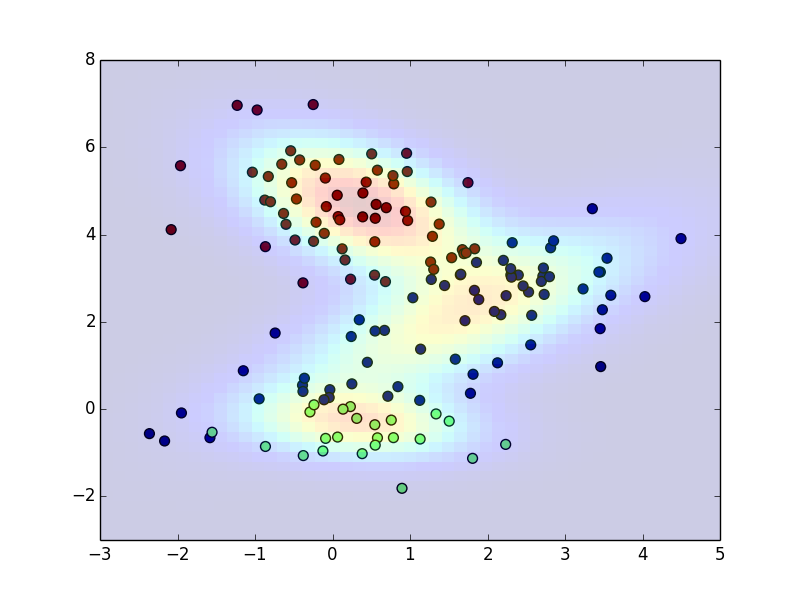
以下が実装例です.初期状態
以下が実装例です.反復10回目
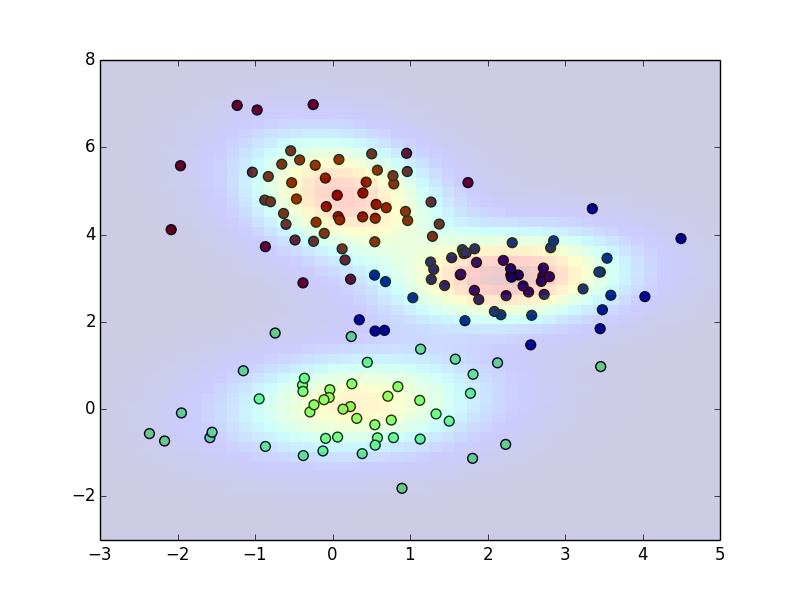
以下が実装例です.反復50回目
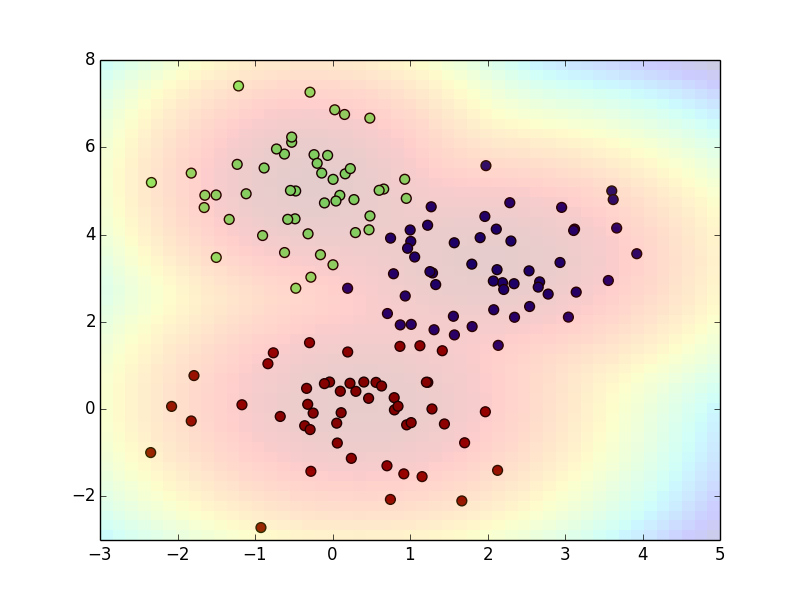
以下は自前の実装ではなく,scikit-learnのライブラリを用いた場合です.この計算ではデフォルトのセッティングを使っていて, $\boldsymbol{\Sigma}$ が対角行列(各変数が無相関)のモデルが使われています.
一般的なEM法
EM法はクラスタリング問題に限らず,隠れ変数を持つ様々なモデルのパラメータ推定に利用する事が出来るアルゴリズムです.
観測出来る変数 $\mathbf{x}$ と 隠れ変数 $\mathbf{z}$ を持つモデルにおいてパラメータ $\boldsymbol{\theta}$ を推定する問題を考えます.$\mathbf{x}$ の観測データを $D$ とします。
まずパラメータ $\boldsymbol{\theta}$ を初期化します.E step開始時の値を $\boldsymbol{\theta}^{\mathrm{old}}$ とすると,これを用いて$\mathbf{z}$ の値の分布 \[ p(\mathbf{z}|D,\boldsymbol{\theta}^{\mathrm{old}}) \] を計算する事が出来ます.
すると,「新しい$\boldsymbol{\theta}$に対する」対数尤度の期待値を計算する事が出来ます.これを $\mathcal{Q}$関数 と呼びます. \[ \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) = \sum_{\mathbf{z}}p(\mathbf{z}|D,\boldsymbol{\theta}^{\mathrm{old}})\log p(D,\mathbf{z}|\boldsymbol{\theta}) \]
最後に,この $\mathcal{Q}$関数を最大にする様な値に $\boldsymbol{\theta}^{\mathrm{old}}$ を更新します。 \[ \boldsymbol{\theta}^{\mathrm{new}} = \mathop{\rm arg~max}\limits_{\boldsymbol{\theta}}\mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) \] 以上をパラメータの値が収束するまで反復すれば完了です.
EM法
学習データを $D$, 隠れ変数を $\mathbf{z}$,モデルのパラメータを$\boldsymbol{\theta}$とする. $\boldsymbol{\theta}$ を推定する為には,これを初期化して以下を収束するまで反復する.
- 【E step】 $\boldsymbol{\theta}^{\mathrm{old}}$ を用いて以下を計算する. \[ p(\mathbf{z}|D,\boldsymbol{\theta}^{\mathrm{old}}) \]
- 【M step】以下によって $\boldsymbol{\theta}$ を更新する. \[ \boldsymbol{\theta}^{\mathrm{new}} = \mathop{\rm arg~max}\limits_{\boldsymbol{\theta}}\mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) \] 但し, \[ \mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{\mathrm{old}}) = \sum_{\mathbf{z}}p(\mathbf{z}|D,\boldsymbol{\theta}^{\mathrm{old}})\log p(D,\mathbf{z}|\boldsymbol{\theta}) \]
今回はここで終了します.
次回もEM法の続きをやります.混合ガウス分布以外のモデルを用いた場合,EM法の応用の紹介をする予定でした.