パターン認識・
機械学習勉強会
第17回

@ワークスアプリケーションズ

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます.

マルコフ確率場

これまではベイジアンネットワークという有向グラフ構造を持つグラフィカルモデルの説明をしてきましたが, 本日は無向グラフによるグラフィカルモデルである マルコフ確率場 (Markov random field, MRF) の説明をします.

MRFの構造は無向グラフ $G=(V, E)$ により定まります。各頂点には異なる確率変数を割り当てます.

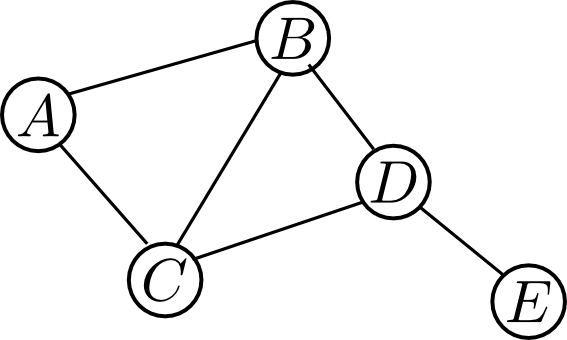
この際, グラフの構造とどのような条件付き確率性が対応するのかという事が重要となります.

そこで, MRFでは, $\mathbf{X}$ から $\mathbf{Y}$ への任意のパスが $\mathbf{Z}$ によってブロックされている時に, $\mathbf{X}$ と $\mathbf{Y}$ が $\mathbf{Z}$ を所与として独立であるという条件を要請します. (これを大域的マルコフ性といいますが, 実際にはもう少し弱めた局所的マルコフ性という性質を満たせばMRFと呼ぶ事が出来ます.)

例えば, 以下のグラフで $\{C,D\}$ にエビデンスが与えられると $\{A,B\}$ から $\{E\}$ への全てのパスがブロックされます. 従って, 以下のグラフでは $\{C,D\}$ を所与として$\{A,B\}$ と $\{E\}$ が条件付き独立であるという事が表現されています.

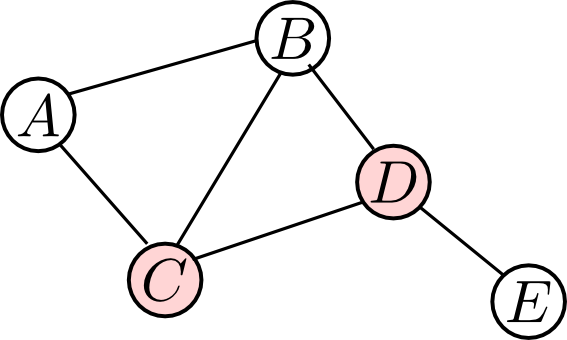
従って, 同時分布上では \[ P(A,B,E|C,D) = P(A,B|C,D)P(E|C,D) \] つまり, \[ P(A,B,C,D,E) = P(A,B|C,D)P(E|C,D)P(C,D) \] という因数分解が可能になります.

今の例だと, サイズ4のファクター $P(A,B|C,D)$ があるのでもっと小さく分解出来ないか考えてみましょう.

まず, $\{B,C\}$ を所与として$\{A\}$ と $\{D,E\}$ は独立なので \[ \begin{aligned} P(A,B,C,D,E) &= P(A|B,C,D,E)P(B,C,D,E) \\ &= P(A|B,C)P(B,C,D,E) \end{aligned}\] となります.

続いて, $\{D\}$ を所与として $\{B,C\}$ と $\{E\}$ は独立なので \[ P(B,C,D,E) = P(B,C|D,E)P(D,E) = P(B,C|D)P(D,E) \] と出来ます.

つまり, \[ P(A,B,C,D,E) = P(A|B,C)P(B,C,|D)P(D,E) \] と出来ます. ファクターサイズが最大で3なので, さっきよりも良い分解です.

今の \[ P(A,B,C,D,E) = \varphi(A,B,C)\varphi(B,C,D)\varphi(D,E) \] という分解においてノード集合 $\{A,B,C\}$, $\{B,C,D\}$, $\{D,E\}$ は極大クリークになっています. これをMRFにおける クリーク因子分解 (clique factorization) と言います.

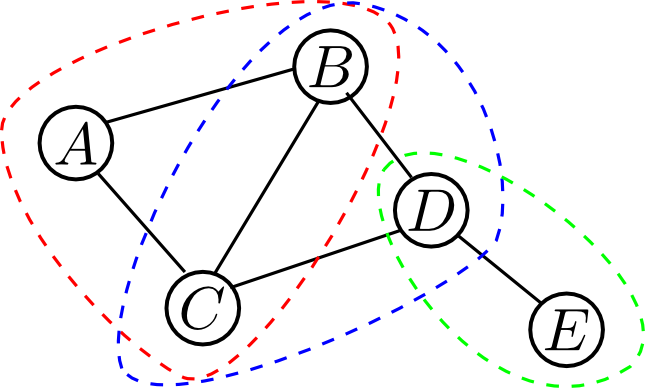
クリーク $C$ 内の変数集合 $\mathbf{X}_C$ の間にはいかなる条件付き独立性も成り立ちません. 従って, 同時分布 \[ P(\mathbf{X}_C) \] はこれ以上小さなファクターに分解する事が出来ないので, クリーク因子分解を行った時に最大ファクターのサイズが最小となる事が解ります.

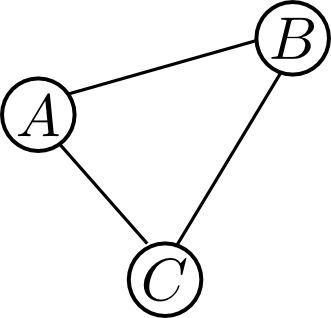
一般にクリーク因子分解を以下のように定める事が出来ます.

ここで登場したポテンシャル関数 $\varphi(\mathbf{X}_C)$ は必ずしも $P(A|B,C)$ の様な特定の形をしている必要はありません.

むしろ, $P(\mathbf{X})$ よりもポテンシャル関数 $\varphi(\mathbf{X}_C)$ の方が主役であり(だから特別な名前が付いている), $\varphi(\mathbf{X}_C)$ を定める事によって同時分布 $P(\mathbf{X})$ の形が定まるのだと考えます.

ポテンシャル関数 $\varphi(\mathbf{X}_C)$ は \[ \varphi(\mathbf{X}_C) > 0 \] の場合を考える事が多いです.

この場合は \[ \varphi(\mathbf{X}_C) = \exp\{-E(\mathbf{X}_C)\} \] を満たす関数 $E(\mathbf{X}_C)$ が存在しますが, これを エネルギー関数 (energy function) と呼びます.

エネルギー関数を用いるとMRF上の確率分布は \[ P(\mathbf{X}) = \frac{1}{Z}\prod_C\exp\{-E(\mathbf{X}_C)\} = \frac{1}{Z}\exp\left\{- \sum_C E(\mathbf{X}_C)\right\} \] となりますが, \[ E(\mathbf{X}) \stackrel{\mathrm{def}}{=} \sum_C E(\mathbf{X}_C) \] を 全エネルギー (total energy) と呼びます.

全エネルギーを用いると \[ P(\mathbf{X}) = \frac{1}{Z}\exp\left\{- E(\mathbf{X})\right\} \] と書くことが出来ますが, この形で分布を書き表した時これを ボルツマン分布 (Boltzmann distribution) と呼びます.

上の式から, 最も生じやすい状態 $\mathbf{X}$ というのはエネルギー $E(\mathbf{X})$ が最小の状態であるという事が解ります.

元々, マルコフ確率場は統計力学の分野で生まれた概念であり, ポテンシャルやエネルギー等の用語はこれに由来しています.

マルコフ確率場:画像処理への応用

画像のノイズ除去はMRFの有名な応用の１つです.

今, 2値画像だけを考えて黒を $-1$, 白を $1$ とします. $D$ をピクセル数とすると, ノイズ入りの画像はベクトル \[ y = (y_1,y_2,\ldots,y_D)\quad (y_i \in \{-1, 1\}) \] として表す事が出来ます.

同様に, ノイズの無い元画像を \[ x = (x_1,x_2,\ldots,x_D)\quad (x_i \in \{-1, 1\}) \] とします.

$y$ は観測出来て $x$ は観測出来ません. $y$ から $x$ を復元する事が目標です.

一般に, あるピクセル $x_i$ の値は観測値 $y_i$ 及び隣接するピクセル $x_j$ と強い相関があると考えられます. これを以下のようなグラフで表現する事にしましょう. これをMRFと見なします.

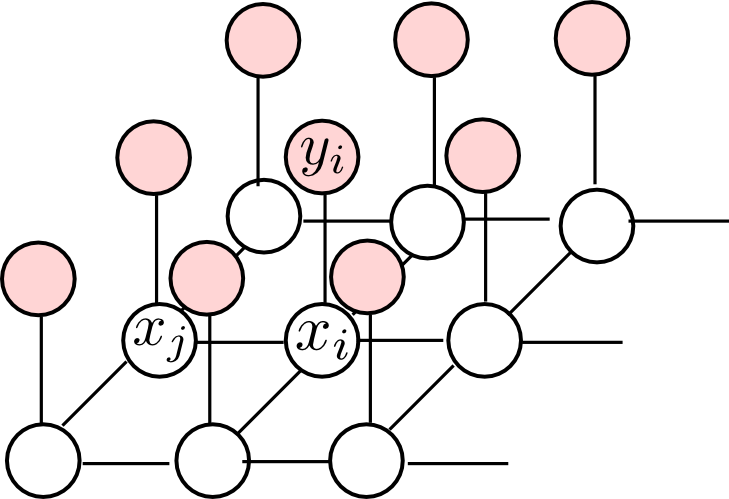
このMRFの極大クリークは $\{x_i,x_j\} \quad \text{($x_i,x_j$ は隣接)}$ というものと $\{x_i,y_i\}$ というものです. 従ってエネルギー関数 \[ E(x_i,x_j)\text{と}E(x_i,y_i) \] を定めれば良いです.

そこで $h$ を実数, $\eta > 0$ として \[ E(x_i,y_i) = hx_i - \eta x_iy_i \] また, $\beta > 0$ として \[ E(x_i,x_j) = -\beta x_ix_j \] とおいてみます.

エネルギーが小さい状態の方が実現しやすい事を思い出しましょう. $x_i$ と $y_i$ が同じ色の時, $x_i$ と $x_j$ が同じ色の時にそれぞれのエネルギー関数の値は小さくなります. $hx_i$ は黒と白のピクセルのどちらの方が実現しやすいかに関する項です.

すると, 全エネルギーは各クリークに関するエネルギーの和なので \[ E(\mathbf{x},\mathbf{y}) = h\sum_i x_i - \beta \sum_{i,j:\text{隣接}}x_ix_j - \eta \sum_i x_iy_i \] となります.

このモデルは統計力学においては イジングモデル (ising model) と呼ばれるものです. 色の代わりに原子のスピンの向きを割り当てて, 磁性体の振る舞いをモデル化する事が出来ます.

各ピクセルの値 $x_i$ を推定する為には, エネルギー \[ E(\mathbf{x},\mathbf{y}) = h\sum_i x_i - \beta \sum_{i,j:\text{隣接}}x_ix_j - \eta \sum_i x_iy_i \] が最小となるような $x_i$ を求めれば良いです.

確率的勾配降下法を使えば簡単に局所最適解を得る事が出来ます. つまり, 各 $x_i$ についてその他のピクセルを固定した上で $x_i = 1$ の場合と $x_i = -1$ の場合を比べてより小さい方を採用するという事を変化が無くなるまで繰り返します.

勾配法による実装例です.(prog17-2.py ) パラメータは $h = 0, \beta = 3,\eta = 2$ としています.

ファクターグラフ

ベイジアンネットワークもマルコフ確率場も, 確率分布の因子分解 \[ P(\mathbf{X}) = \prod_i \varphi_i(\mathbf{X}_i) \] に基づくものでした.

そこで, ファクターグラフ (factor graph) という概念を考える事によって, どちらも統一的に取り扱う事が出来ます.

ファクターグラフは二部グラフであって, 一方のノード群は確率変数, 他方のノード群はファクターからなります. ファクター $\varphi$ が変数 $x$ を含む場合にのみ辺 $(x, \varphi)$ を引きます.

例えば, 以下のファクターグラフは \[ P(x,y,z) = \varphi_1(x)\varphi_2(x,y)\varphi_3(x,z) \] という因子分解を表しています.

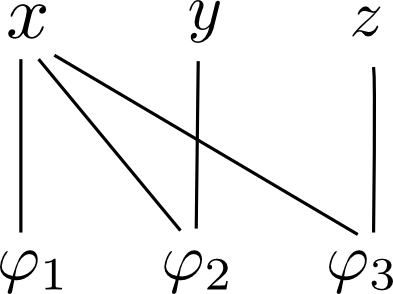
ベイジアンネットワークと同様にして, メッセージパッシング法によってファクターグラフ上での確率推論を行う事が出来ます. Sum-Productアルゴリズム とも呼ばれます.

ファクターグラフ上でのメッセージパッシングでは変数からファクターへのメッセージと, ファクターから変数へのメッセージを考えます.

簡単の為, ファクターグラフが木である場合を考えます. ルートを定め集積フェーズでは葉からルート, 分配フェーズではルートから葉に向かってメッセージを流します.

ファクター $\varphi$ から変数 $x$ へのメッセージ \[ \mu_{\varphi \rightarrow x}(x) \] はプライベート変数に関する畳込みを表しており, \[ \mu_{\varphi\rightarrow x}(x) = \sum_{\mathbf{X}}F(x, \mathbf{X}) \] となります. $F(x,\mathbf{X})$ は $\varphi$ をルートとするサブツリーのファクターの積で, $\mathbf{X}$ は $\varphi$ に隣接する $x$ 以外の変数集合です.

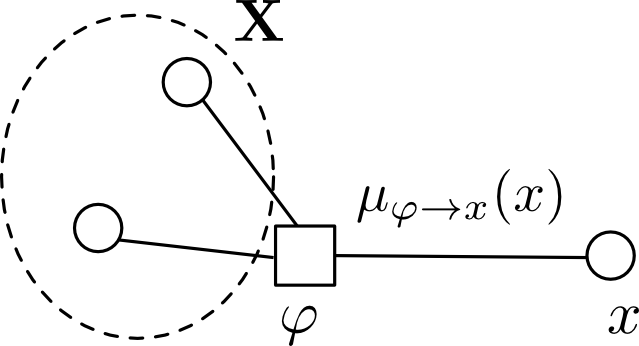
ここで, $F(x,\mathbf{x})$ というのはファクター $\varphi$ に流れて来たメッセージと $\varphi$ の積を取れば良く \[ F(x, \mathbf{x}) = \varphi\prod_{y \in \mathrm{Ne}(\varphi)\setminus x} \mu_{y\rightarrow\varphi}(y) \] となります.($\mathrm{Ne}(\varphi)$ は $\varphi$ の隣接ノード集合)

従って, \[ \mu_{\varphi\rightarrow x}(x) = \sum_{\mathbf{X}}\varphi\prod_{y \in \mathrm{Ne}(\varphi)\setminus x} \mu_{y\rightarrow\varphi}(y) \] となります. これが Sum-Product アルゴリズムという命名の由来です.

変数 $x$ から ファクター $\varphi$ へのメッセージは $x$ へ流れてきたメッセージの合算となります. つまり \[ \mu_{x \rightarrow \varphi}(x) =\prod_{\psi \in \mathrm{Ne}(x)\setminus \varphi} \mu_{\psi\rightarrow x}(x) \] となります.

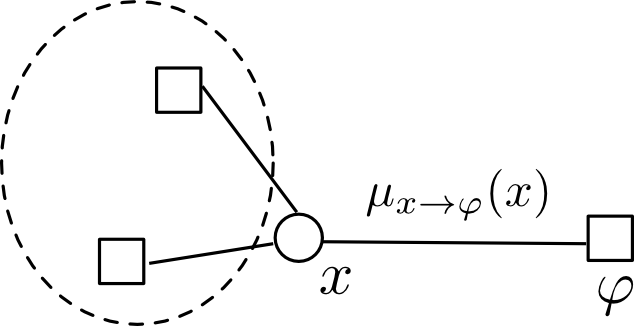
$x$ がファクターグラフの葉である場合には \[ \mu_{x\rightarrow\varphi} = 1 \] $\varphi$ がファクターグラフの葉である場合には \[ \mu_{\varphi\rightarrow x}=\varphi(x) \] と初期化します.

あとは、ベイジアンネットワークの際にやった時にルートまでのメッセージ伝播と再分配を行えば各クリークに関する厳密な確率分布を求める事が出来ます.

先ほどのファクターグラフはちょうど木になっているので, これでやってみましょう. $z$ をルートにしてみます.

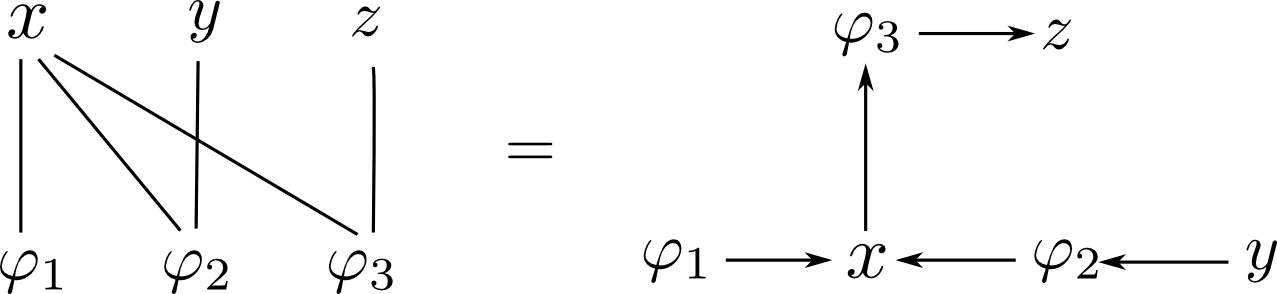
$y$ から出発すると \[ \begin{aligned} \mu_{y\rightarrow\varphi_2} &= 1 \\ \mu_{\varphi_2 \rightarrow x} &= \sum_{y}\varphi_2\mu_{y\rightarrow\varphi_2}=\sum_{y}\varphi_2 \end{aligned} \] です. また \[ \mu_{\varphi_1\rightarrow x} = \varphi_1 \] です.

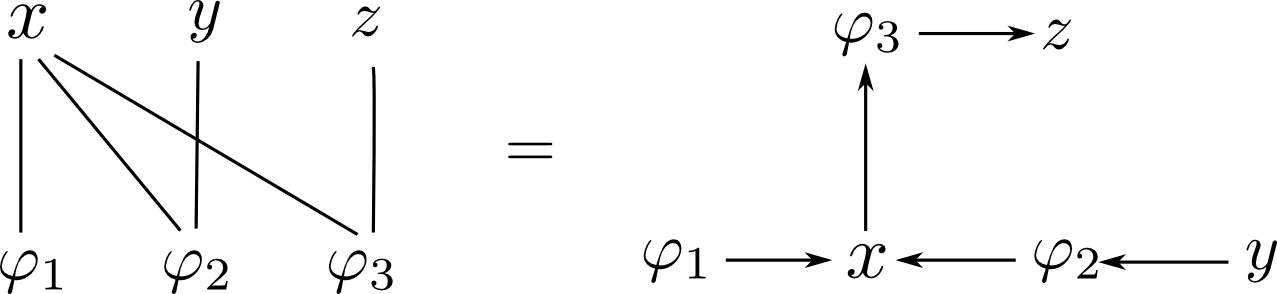
これを掛けあわせて \[ \mu_{x\rightarrow \varphi_3} = \mu_{\varphi_1\rightarrow x}\mu_{\varphi_2\rightarrow x}=\varphi_1\sum_{y}\varphi_2 \] となり, \[ \mu_{\varphi_3\rightarrow z} = \sum_x\varphi_3 \mu_{x\rightarrow\varphi_3} = \sum_x\varphi_3\varphi_1\sum_{y}\varphi_2 \] となります.

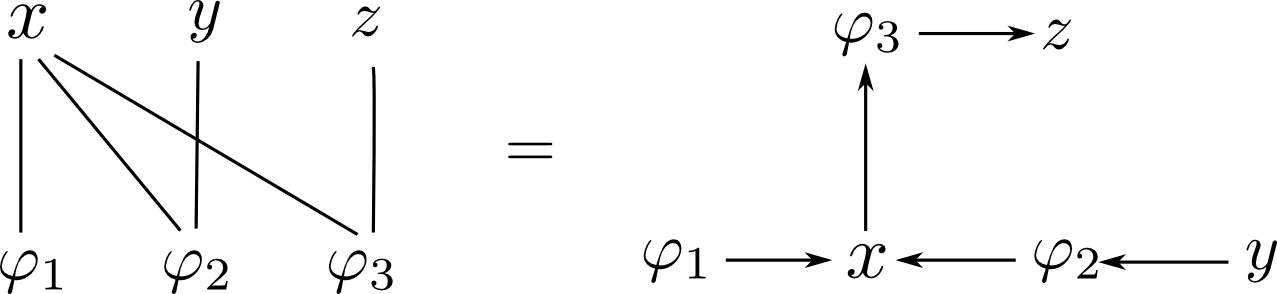
次は辺の向きを逆にしてルートから葉に向かってメッセージを流します. この際, 既に計算されたメッセージは再利用する事が出来ます.

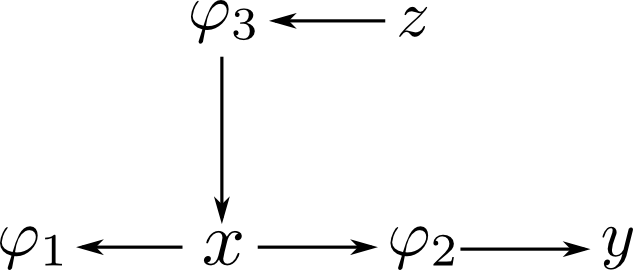
実際にやってみると \[ \begin{aligned} \mu_{z\rightarrow\varphi_3} &= 1 \\ \mu_{\varphi_3\rightarrow x} &= \sum_z\varphi_3 \\ \mu_{x\rightarrow\varphi_1} &= \mu_{\varphi_3\rightarrow x}{\color{red}{\mu_{\varphi_2\rightarrow x}}} = \sum_z\varphi_3\sum_{y}\varphi_2 \\ \mu_{x\rightarrow\varphi_2} &= \mu_{\varphi_3\rightarrow x}{\color{red}{\mu_{\varphi_1\rightarrow x}}} = \sum_z\varphi_3\varphi_1 \\ \mu_{\varphi_2\rightarrow y} &= \sum_x\varphi_2\sum_z\varphi_3\varphi_1 \end{aligned} \] となります. 赤いファクターは既に計算したものの再利用です.

変数ノード $x$ に到達したメッセージは $P(x)$ となります. 例えば $z$ に到達したメッセージは \[ P(z) = \mu_{\varphi_3\rightarrow z} = \sum_x\varphi(x,z)\varphi_1(x)\sum_y\varphi(x,y) \]

ファクターノード $\varphi(\mathbf{X})$ に到達したメッセージと $\varphi$ 自信の積は $\mathbf{X}$ に関する同時分布となります. 例えば $\varphi_2$ に到達したメッセージと $\varphi_2$ の積は \[ P(x,y) = \varphi_2(x,y)\mu_{x\rightarrow\varphi_2}\mu_{y\rightarrow\varphi_2} = \varphi_2(x,y)\sum_z\varphi_3(x,z)\varphi_1(x) \] となります.

以上の方法は, ファクターグラフが木でない場合には利用する事が出来ません. その場合には, \[ \mu_{\phi\rightarrow x} \] を一様分布などで初期化しておいて, 収束するまでメッセージを流すという方法があります. これは loopy belief propagation と呼ばれます.

本勉強会は以上で終了します.

全17回お疲れ様でした. やり残した内容(主にEM法などの近似推論)がありますので, 今後資料に追加する予定です. その場合は @9_ties で告知しますのでよろしくお願いします.