プログラマの為の
数学勉強会
第7回

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。

この資料について

• http://nineties.github.com/math-seminar に置いてあります。
• SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
• 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
• サンプルプログラムはPythonで記述しています。

線型代数

本日から線型代数学を学んでいきます。微積分学と同様に,理工学の様々な問題に取り組む上で必須の学問です。

線型代数は大きく分けて

• 行列・行列式と連立一次方程式の理論
• 線型空間・線型写像の理論

からなりますが,まず前者から解説を始めます。

行列とベクトル

行列とベクトル

まず,行列とベクトルについての基本的な知識をざっと確認します。

行列

以下のように\(m\times n\)個の数・式を縦横に並べたものを\((m,n)\)型行列と言い,アルファベットの大文字を用いて \[ A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \] と表します。

\(a_{ij}\)を\((i,j)\)成分と呼び, \( a_{i1}, a_{i2}, \cdots, a_{in} \)を第\(i\)行, \( a_{1j}, a_{2j}, \cdots, a_{mj} \)を第\(j\)列と呼びます。

また\((n,n)\)型行列を\(n\)次正方行列と呼び,\((i,i)\)成分を対角成分と呼びます。

また,\((i,j)\)成分が\(a_{ij}\)である\((m,n)\)型行列を \[ (a_{ij})_{m,n} \] や,添字の範囲を明示して \[ (a_{ij})_{1\leq i\leq m, 1\leq i\leq n} \] と書きます。前者の場合,添字は1から始める事にします。

例えば \[ \begin{aligned} (i+2j)_{2,3} &= \begin{pmatrix} 1+2\cdot 1 & 1+2\cdot 2 & 1+2\cdot 3 \\ 2+2\cdot 1 & 2+2\cdot 2 & 2+2\cdot 3 \\ \end{pmatrix}\\ &= \begin{pmatrix} 3 & 5 & 7 \\ 4 & 6 & 8 \end{pmatrix} \end{aligned} \] という感じです。

成分が全て\(0\)の行列 \[ O = (0)_{m,n} = \begin{pmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \\ \end{pmatrix} \] を零行列と言います。型を明示して\(O_{m,n}\)と書く場合もあります。

対角成分が全て\(1\),それ以外が\(0\)である\(n\)次正方行列を単位行列と呼び\(E\)や\(E_n\)と表します。 \[ E_n = (\delta_{ij})_{n,n} = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{pmatrix} \] 但し,\(\delta_{ij}\)はクロネッカーのデルタ \[\delta_{ij} = \left\{ \begin{array}{ll} 1 & (i = j) \\ 0 & (i \neq j) \end{array} \right.\] です。

行列の演算

これらの成立は明らかなので証明は省略します。

具体的な行列では,以下のようになります。 \[ \begin{aligned} &\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} e & f \\ g & h \end{pmatrix} = \begin{pmatrix} ae+bg & af+bh \\ ce+dg & cf+dh \end{pmatrix} \\ &\begin{pmatrix} a & b & c\\ d & e & f \end{pmatrix} \begin{pmatrix} g \\ h \\ i \end{pmatrix} = \begin{pmatrix} ag+bh+ci \\ dg+eh+fi \end{pmatrix} \\ &\begin{pmatrix} a & b & c\\ \end{pmatrix} \begin{pmatrix} d \\ e \\ f\\ \end{pmatrix} = ad+be+cf \end{aligned} \]

最後の例のように\((1,1)\)型行列は一つの数と同一視出来るので,括弧を外して書くこともあります。

例えばPythonだとNumPyというライブラリを利用できます。練習として自前で実装すると以下のようなコードとなります。

# -*- coding: utf-8 -*-
import numpy as np

def mat_add(a, b):    # 行列の和
    if a.shape != b.shape:
        raise ArithmeticError, u"行列の型の不一致"
    (m,n) = a.shape   # 行列の型
    r = np.zeros( (m,n) )
    for i in xrange(m):
        for j in xrange(n):
            r[i,j] = a[i,j] + b[i,j]
    return r

def mat_scale(k, a):  # 行列の定数倍
    (m,n) = a.shape
    r = np.zeros( (m,n) )
    for i in xrange(m):
        for j in xrange(n):
            r[i,j] = k * a[i,j]
    return r

def mat_mul(a, b):    # 行列の積
    (l, m) = a.shape
    (m2, n) = b.shape
    if m != m2:
        raise ArithmeticError, u"行列の型の不整合"

    c = np.zeros( (l,n) )
    for i in xrange(l):
        for j in xrange(n):
            v = 0
            for k in xrange(m):
                v += a[i,k] * b[k,j]
            c[i,j] = v
    return c

a = np.array([[1,2,3],[4,5,6]])
b = np.array([[2,1,4],[5,2,1]])

print mat_add(a, b)
print mat_scale(2, a)

a = np.array([[1,2,3],[4,5,6]])
b = np.array([[2,1,4],[5,2,1],[0,1,3]])
print mat_mul(a, b)

行列演算の計算量

少し話題を変えて,行列演算の計算量について考えて見ましょう。

\((m,n)\)型行列の和・差・定数倍はもちろん\(\color{yellow}{\mathcal{O}(mn)}\)です。

\((l,m)\)型行列と\((m,n)\)型行列の積 \[ (a_{ij})_{l,m}(b_{ij})_{m,n} = \left( \sum_{k=1}^m a_{ik}b_{kj} \right)_{l,n} \] の計算では,\( \sum_{k=1}^m a_{ik}b_{kj} \)の計算に\(m\)回の加算と乗算が必要で,これが\(ln\)要素あるので\(\color{yellow}{\mathcal{O}(lmn)}\)の計算量となります。

現実の問題では,数万とか数億といった次元の行列を扱わなければならなくなりますが, 例えば倍精度浮動小数点数の百万次正方行列を使う場合

• 行列一つあたり, \[ \text{8バイト}\times(\text{百万}\times \text{百万})\text{要素} \approx \text{7.3テラバイト} \] のメモリが必要で
• 行列を二つ掛ける為に \( \text{百万}^3 = \text{百京}\)回の加算・乗算が必要

という事になります。

こんな計算を力技で行う事は困難ですので,問題を数学的に良く考察し適切にデータ構造・アルゴリズムを選択する事が重要となります。

話題を戻して,行列積の性質を確認していきます。

\( A = (a_{ij})_{m,n}\)という表記を利用して記述する証明に慣れておきましょう。

【\(A(BC)=(AB)C\)の証明】
\[ \begin{aligned} A(BC) &= (a_{ij})_{s,t}((b_{ij})_{t,u}(c_{ij})_{u,v})= (a_{ij})_{s,t}\left(\sum_{l=1}^ub_{il}c_{lj}\right)_{t,v} \\ &= \left(\sum_{k=1}^ta_{ik}\sum_{l=1}^ub_{kl}c_{lj}\right)_{s,v} = \left(\sum_{l=1}^u(\sum_{k=1}^ta_{ik}b_{kl})c_{lj}\right)_{s,v} \\ &= \left(\sum_{k=1}^ta_{ik}b_{kj}\right)_{s,u}(c_{ij})_{u,v} = ((a_{ij})_{s,t}(b_{ij})_{t,u})(c_{ij})_{u,v} \\ &= (AB)C \end{aligned} \] □

【\(A(B+C)=AB+AC\)の証明】
\[ \begin{aligned} A(B+C) &= (a_{ij})_{l,m}(b_{ij}+c_{ij})_{m,n} \\ &= \left(\sum_{k=1}^ma_{ik}(b_{kj}+c_{kj})\right)_{m,n}\\ &= \left(\sum_{k=1}^ma_{ik}b_{kj}+\sum_{k=1}^ma_{ik}c_{kj}\right)_{m,n}\\ &= \left(\sum_{k=1}^ma_{ik}b_{kj}\right)_{m,n}+\left(\sum_{k=1}^ma_{ik}c_{kj}\right)_{m,n}\\ &= AB+AC \end{aligned} \] □

\((A+B)C=AC+BC\)の証明も同様です。

正方行列\(A\)を\(n\)個掛ける場合,結合則より掛ける順番は任意なので単純に\(A^n\)と書くことが出来ます。

【証明】
零行列の方は明らかに成立します。単位行列の方は \[ E_m A = \left(\sum_{k=1}^m\delta_{ik}a_{kj}\right)_{m,n} = (a_{ij})_{m,n} = A \quad\text{($\because \delta_{ii}$のみ1,他は0)} \] となります。\(AE_n = A\)も同様です。 □

以上の性質から解る様に,行列の計算規則は通常の文字式の計算規則と殆ど同じです。但し,以下の二点に関しては注意が必要です。

例えば \[ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 2 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 3 \\ 8 & 7 \end{pmatrix} ,\qquad \begin{pmatrix} 0 & 1 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 3 & 4 \\ 5 & 8 \end{pmatrix} \]

例えば \[ \begin{pmatrix} -2 & 1 \\ 4 & -2 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \]

非可換性によって,数式の展開公式は使えなくなります。 \[ \begin{aligned} (A+B)^2 &= (A+B)(A+B) \\ &= A^2+AB+BA+B^2 \\ &\neq A^2+2AB+B^2 \end{aligned} \] また,方程式を因数分解によって解くことも出来ません。 \[ \begin{aligned} X^2-3X+2E = O\ &\Leftrightarrow\ (X-E)(X-2E) = O\\ &\not\Rightarrow\ X = E, 2E \end{aligned} \]

行列の転置

最初の3つは自明だと思います。最後の一つだけ証明しましょう。
【\((AB)^T=B^TA^T\)の証明】
\(A\)が\((l,m)\)型,\(B\)が\((m,n)\)型のとき \[ (AB)^T = \left(\sum_{k=1}^m a_{ik}b_{kj}\right)^T_{l,n} = \left(\sum_{k=1}^m a_{jk}b_{ki}\right)_{n,l} = (b_{ji})_{n,m}(a_{ji})_{m,l} = B^TA^T \] □

【答え】
\[ \begin{pmatrix} 1 & 5 & 2 \\ 2 & 1 & 3 \\ 4 & 2 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac72 & 3 \\ \frac72 & 1 & \frac52 \\ 3 & \frac52 & 1 \end{pmatrix} + \begin{pmatrix} 0 & \frac32 & -1 \\ -\frac32 & 0 & \frac12 \\ 1 & -\frac12 & 0 \end{pmatrix} \]

ベクトル

数や式を\(n\)個を縦に並べたものを\(n\)次元列ベクトルと言い,ボールド体を用いて \[ \mathbf{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \] と表します。また全ての成分が\(0\)の列ベクトルを零ベクトルと言い0と表します。

同様に\(n\)個を横に並べたものを\(n\)次元行ベクトルと言い, \[ \mathbf{x}^T = \begin{pmatrix} x_1 & \cdots & x_n \end{pmatrix} \] などと表します。

\(x_i\)をこれらベクトルの第\(i\)成分と呼びます。

\(n\)次元列ベクトルは\((n,1)\)型行列,行ベクトルは\((1,n)\)型行列でもあります。行列と全く同じ演算規則が適用されます。

この勉強会では主に実数成分のベクトル(実ベクトル)を考えます。実数成分の\(n\)次元列ベクトルの集合を \(\mathbb{R}^n\) と表します。

列ベクトルと行ベクトルは常に区別されますので注意して下さい。 今後,単に「ベクトル」と言った場合,それは列ベクトルの事であるとします。

【注】 ベクトルの内積・ノルムという概念は実際にはその性質によって抽象的に定義され,上の定義以外にも様々な内積・ノルムが存在します。しかし,よく使われる上の定義だけをここでは考える事にします。

ベクトルの内積・ノルムは,行列の記法を利用すれば \[ \begin{aligned} (\mathbf{x}, \mathbf{y}) &= \begin{pmatrix}x_1&\cdots&x_n\end{pmatrix} \begin{pmatrix}y_1\\ \vdots \\ y_n\end{pmatrix} = \color{yellow}{\mathbf{x}^T\mathbf{y}} \\ ||\mathbf{x}||^2 &= (\mathbf{x},\mathbf{x}) = \color{yellow}{\mathbf{x}^T\mathbf{x}} \end{aligned} \] と記述する事が出来ます。

【証明】 \[ (A\mathbf{x}, \mathbf{y}) = (A\mathbf{x})^T\mathbf{y} = \mathbf{x}^TA^T\mathbf{y}=(\mathbf{x}, A^T\mathbf{y}) \] □

【証明】
\[ (tx_i-y_i)^2 = x_i^2t^2-2x_iy_it+y_i^2\geq 0 \] を\(i = 1,\cdots,n\)について加えて \[ (x_1^2+\cdots+x_n^2)t^2-2(x_1y_1+\cdots+x_ny_n)t+(y_1^2+\cdots+y_n^2)\geq 0 \] が任意の実数\(t\)について成立する。従って左辺の判別式を考えて \[ D\leq 0\ \Leftrightarrow\ (x_1y_1+\cdots+x_ny_n)^2-(x_1^2+\cdots+x_n^2)(y_1^2+\cdots+y_n^2)\leq 0 \] である。 □

【三角不等式の証明】
\[ \begin{aligned} ||\mathbf{x}+\mathbf{y}||^2 &= (x_1+y_1)^2 + \cdots + (x_n+y_n)^2 \\ &= x_1^2+\cdots+x_n^2 + y_1^2 + \cdots + y_n^2 + 2(x_1y_1 + \cdots + x_ny_n) \\ &= ||\mathbf{x}||^2 + ||\mathbf{y}||^2 + 2(\mathbf{x},\mathbf{y}) \\ &\leq ||\mathbf{x}||^2+||\mathbf{y}||^2 + 2||\mathbf{x}|| ||\mathbf{y}|| \qquad\text{(コーシー・シュワルツの不等式)}\\ &= (||\mathbf{x}|| + ||\mathbf{y}||)^2 \end{aligned} \] □

その他の性質の証明は省略します。

小行列への分解

\[ \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \] \[ A = \begin{pmatrix} a & b \\ d & e \end{pmatrix}, B = \begin{pmatrix} c \\ f \end{pmatrix}, C = \begin{pmatrix} g & h \end{pmatrix}, D = (i) \] の様に行列を小行列へ分解する操作もよく行われます。

行列\(X,Y\)を小行列\(A,B,C,D,E,F,G,H\)へ分解したとき,以下の各演算が定義されるならば \[ \begin{aligned} XY &= \begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} E & F \\ G & H \end{pmatrix} \\ &= \begin{pmatrix} AE+BG & AF+BH \\ CE+DG & CF+DH \end{pmatrix} \end{aligned} \] が成立します。これの成立も明らかでしょう。

例えば,行列\(A\)を各列ベクトルに分解して \[ BA = B(\mathbf{a_1}, \cdots, \mathbf{a_n}) = (B\mathbf{a_1},\cdots,B\mathbf{a_n}) \] と書くといった事が良く行われます。

行列・ベクトルで何を表すのか？

さて,行列・ベクトルの定義と演算を確認しましたが,これらを一体どのように利用するのかイメージが湧かない方もいるでしょう。

そこで,行列・ベクトルで表すことの出来る様々な問題を紹介します。様々な読者を想定していろんな話をしますが、個別の話は解らない事があっても良いです。線型代数はほぼありとあらゆる場面で必要となるのだということが解ってもらえれば結構です。

連立一次方程式

連立一次方程式 \[ \left\{\begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n = b_m \end{array}\right. \] は \[ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix} \] と表す事が出来ます。多くの問題が連立一次方程式を解く事に帰着します。

連立一次漸化式

全く同じ事ですが,連立漸化式 \[ \left\{\begin{array}{c} x_1(i+1) = a_{11}x_1(i)+a_{12}x_2(i)+\cdots+a_{1n}x_n(i) \\ x_2(i+1) = a_{21}x_1(i)+a_{22}x_2(i)+\cdots+a_{2n}x_n(i) \\ \vdots \\ x_n(i+1) = a_{n1}x_1(i)+a_{m2}x_2(i)+\cdots+a_{nn}x_n(i) \end{array}\right. \] も \[ \begin{pmatrix} x_1(i+1) \\ x_2(i+1) \\ \vdots \\ x_n(i+1) \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{pmatrix} \begin{pmatrix} x_1(i) \\ x_2(i) \\ \vdots \\ x_n(i) \end{pmatrix} \] と表されます。

漸化式が \[ \mathbf{x}_{i+1} = A\mathbf{x}_i \] と表される場合, \[ \mathbf{x}_i = A\mathbf{x}_{i-1} = AA\mathbf{x}_{i-2} = \cdots = A^i\mathbf{x}_0 \] となりますから,一般項を求める事が行列の累乗を計算する事に帰着します。

フィボナッチ数列の漸化式は \[ \begin{pmatrix}a_{n+2} \\ a_{n+1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} a_{n+1} \\ a_n \end{pmatrix} \] と表されるので \[ \begin{pmatrix} a_{n+1} \\ a_n \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n \begin{pmatrix} 1 \\ 0 \end{pmatrix} \] となります。つまり \[ \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n \] の\((2,1)\)成分が\(a_n\)となります。

\[a_{100} = 354224848179261915075\] の計算例です。

>>> import numpy as np
>>> from numpy import linalg as LA
>>> A = np.array([[1,1],[1,0]], dtype=object)   # dtype=objectは多倍長整数を使う為
>>> LA.matrix_power(A, 100)
array([[573147844013817084101, 354224848179261915075],
       [354224848179261915075, 218922995834555169026]], dtype=object)

良くある再帰的な定義では指数オーダーの時間が掛かりますが,この方法の場合 ナイーブに実装しても\(\mathcal{O}(n)\),工夫すれば\(\mathcal{O}(\log n)\)(二進累乗算)で計算出来ます。

微分方程式

第1回には,連成ばねの微分方程式が \[ m\frac{\mathrm{d}^2}{\mathrm{d}t^2}\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{array}\right) = -k\left(\begin{array}{ccccc} 2 & -1 & 0 & 0 & \cdots & \\ -1 & 2 & -1 & 0 & \cdots & \\ 0 & -1 & 2 & -1 & \cdots & \\ \vdots & \vdots & \ddots& \ddots & \ddots & \\ & & & & & \\ \end{array}\right) \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{array}\right) \] と表せるといった話題を紹介しました。この例に限らず,様々な微分方程式が行列で表され,差分化によって連立一次漸化式に帰着されます。

ベクトル値関数

ベクトル\(\mathbf{x}\)を引数とし,ベクトル\(\mathbf{y}\)を返すベクトル値関数 \[ \mathbf{y} = f(\mathbf{x}) \] を考えましょう。

このような\(f\)のうち,もっともシンプルなものは一次式であり \[ \mathbf{y} = A\mathbf{x}\ \text{や}\ \mathbf{y} = A\mathbf{x}+\mathbf{b} \] といった形で表すことが出来ます。

適切な近似によって一次式で表せる関数が多いこと,理論的な取り扱いが容易であることからこのモデルがよく利用されます。

例えば,画像の識別の問題を考えてみましょう。

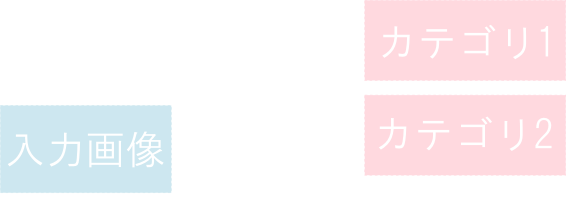
この場合,入力\(\mathbf{x}\)は画像のピクセル値のベクトルとなり, 出力\(\mathbf{y}=(y_1,\cdots,y_m)^T\)の\(y_i\)はカテゴリ\(i\)である確率などとなり,識別器がベクトル値関数 \[ \mathbf{y} = f(\mathbf{x}) \] となります。

識別器の最もシンプルなモデルが \[ \mathbf{y} = A\mathbf{x} \] で,トレーニングデータ\((\mathbf{x_1},\mathbf{y_1}),\cdots,(\mathbf{x_k},\mathbf{y_k})\)から\(A\)を決定する問題は連立一次方程式を解く問題に帰着します。 もちろん,性能はあまり良くないのですが全ての基本となります。

信号解析の分野から別の問題を紹介しましょう。

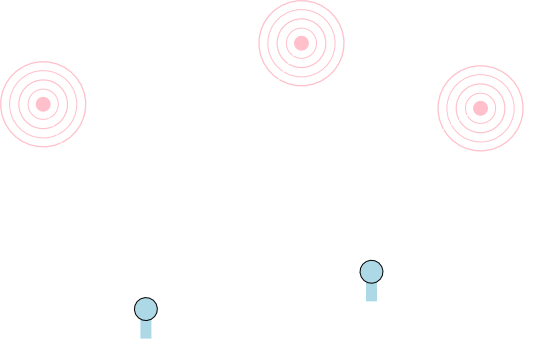
今,3箇所の音源が何らかの波形\(a(t),b(t),c(t)\)で音を出しているとします。\(t\)は時刻を表します。 この音を2箇所のマイクで拾ったら\(x(t),y(t)\)という波形が得られたとしましょう。

すると,当然(音の伝達時間を無視すれば) \[ (x(t), y(t))^T = f(a(t), b(t), c(t)) \] というベクトル値関数が存在するはずで,最もシンプルなモデルは \[ \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = A \begin{pmatrix} a(t) \\ b(t) \\ c(t) \end{pmatrix} \] となります。観測データに基づいて\(A\)や\(a(t),b(t),c(t)\)を求める事が出来れば,個々の信号源を分離することが出来ます。

先ほどまでと異なるのは\(A\)も\(a(t),b(t),c(t)\)も未知なので,連立一次方程式としてそのまま解くことは出来ず,統計学的な手法を利用する必要があります。

次は,入出力と状態の更新を行う何らかのシステム(ロボットとか)を考えましょう。

この場合は,時刻が\(\Delta t\)経過した時の状態の更新が \[ \mathbf{u}(t+\Delta t) = f(\mathbf{u}(t), \mathbf{x}(t)) \] と表され,出力が \[ \mathbf{y}(t+\Delta t) = g(\mathbf{u}(t), \mathbf{x}(t)) \] となりますから,線型なモデルを仮定すれば \[ \begin{pmatrix} \mathbf{u}(t+\Delta t) \\ \mathbf{y}(t+\Delta t) \end{pmatrix} = A \begin{pmatrix} \mathbf{u}(t) \\ \mathbf{x}(t) \end{pmatrix} \] と表せます。このモデルに基づいて,望ましい出力を得る為に最適な\(\mathbf{x}\)を計算するといった事を行います。

テーブル

今までとは異なる例として,行列\(A\)をテーブルと思う事も出来ます。例えば試験の成績表 \[ \left[ \begin{array}{cccc} & \text{国語} & \text{英語} & \text{数学} \\ \text{A君} & 60 & 75 & 80 \\ \text{B君} & 50 & 40 & 50 \\ \text{C君} & 80 & 100 & 95 \\ \end{array}\right] \] を行列だと見なす事が出来ます。

テーブルの上での様々な集計は積和算になりますから,結局行列演算で表現する事が出来ます。例えば,生徒毎の得点の平均値は \[ \frac{1}{3} \begin{pmatrix} 60 & 75 & 80 \\ 50 & 40 & 50 \\ 80 & 100 & 95 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \] となるといった具合です。

グラフ

Webページや鉄道網などのリンク構造,状態の遷移,物事の因果の構造などを表現したりする為に用いられるグラフも行列と密接に関係します。

例えば\((i,j)\)成分の値をノード\(i\)からノード\(j\)への辺が存在するときに\(1\),それ以外は\(0\)とすれば,下のようにグラフを行列で表す事が出来ます。

そして,各ノードに入るエッジ・各ノードから出るエッジに関する積和算はやはり行列演算で記述する事が出来ます。

連立一次方程式

連立一次方程式 \[ \left\{\begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n = b_m \end{array}\right. \] の理論を説明します。

連立方程式の様々な表現

まず,先ほどの連立方程式と等価な表現を覚えて下さい。まず, \[ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix} \] すなわち, \[ A\mathbf{x} = \mathbf{b} \] という表現があります。

一般に \[ AX = B \] という方程式は, \[ A(\mathbf{x}_1,\cdots,\mathbf{x}_n)=(\mathbf{b}_1,\cdots,\mathbf{b}_n)\] すなわち \[ A\mathbf{x}_1=\mathbf{b}_1,\cdots,A\mathbf{x}_n=\mathbf{b}_n\] と分解出来るので,係数行列\(A\)が同一の連立一次方程式の組と等価です。

また,元の連立一次方程式を \[ x_1\begin{pmatrix} a_{11} \\ \vdots \\ a_{m1} \end{pmatrix} + x_2\begin{pmatrix} a_{12} \\ \vdots \\ a_{m2} \end{pmatrix} + \cdots x_n\begin{pmatrix} a_{1n} \\ \vdots \\ a_{mn} \end{pmatrix} = \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix} \] と書き直す事もできます。

すなわち,係数行列を\(A = (\mathbf{a}_1,\cdots,\mathbf{a}_n)\)と分解したとき \[ x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n = \mathbf{b} \] と等価です。これは線型空間・線型写像の話題の時によく登場する形です。

最後に \[ \left\{\begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n = b_m \end{array}\right. \] を \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ a_{21}&a_{22}&\cdots&a_{2n}&:& b_2 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ a_{m1}&a_{m2}&\cdots&a_{mn}&:& b_m \\ \end{array}\right] \] と表す方法を良く利用します。これを拡大係数行列と言います。

連立一次方程式の同値表現まとめ

以上,

• 連立一次方程式
• 行列の一次方程式\[ A\mathbf{x} = \mathbf{b} \]
• 一次結合の等式\[ x_1\mathbf{a}_1+\cdots+x_n\mathbf{a}_n=\mathbf{b} \]
• 拡大係数行列表現

は全て同じ方程式となります。頭の中ですぐに変換出来るようしておいて下さい。

行基本変形

連立一次方程式を解くには,それを同値変形して\(x_1 = \alpha_1, \cdots, x_n = \alpha_n\)という連立方程式に直せば良いわけですが, 行基本変形と呼ばれる変形で,これを実行する事が出来ます。

具体例として \[\left\{\begin{array}{c} 3x + y = 2\\ 2x + 4y = 2\\ \end{array}\right. \] を考えましょう。

まず,明らかに \[\left\{\begin{array}{c} 3x + y = 2\\ 2x + 4y = 2\\ \end{array}\right. \ \Leftrightarrow\ \left\{\begin{array}{c} 2x + 4y = 2\\ 3x + y = 2\\ \end{array}\right. \] です。このように2つの行を入れ替える事は同値変形です。

そこで第\(i\)行と第\(j\)行を入れ替える操作を \[ P_{i,j} \] と書くことにしましょう。

次に,1行目を\(\frac12\)倍しましょう。 \[\left\{\begin{array}{r} 2x + 4y = 2\\ 3x + y = 2\\ \end{array}\right. \ \Leftrightarrow\ \left\{\begin{array}{r} x + 2y = 1\\ 3x + y = 2\\ \end{array}\right. \] このように行を\(c\neq 0\)倍する事も同値変形です。\(c\)で割れば元に戻るからです。

そこで第\(i\)行を\(c\)倍する操作を \[ Q_{i,c} \] と書くことにしましょう。

次に,1行目の\(-3\)倍を２行目に足しましょう。 \[ \left\{\begin{array}{r} x + 2y = 1\\ 3x + y = 2\\ \end{array}\right. \ \Leftrightarrow\ \left\{\begin{array}{r} x + 2y = 1\\ - 5y = -1\\ \end{array}\right. \] このようにある行を\(c\)倍したものを別の行に足す事も同値変形となります。\(-c\)倍したものを再び足せば元に戻るからです。

そこで第\(i\)行を\(c\)倍し,第\(j\)列に足すという操作を \[ R_{i,j,c} \] と表す事にしましょう。

以上の3種類の変形を次々に行うことによって連立一次方程式を(それが唯一の解を持つ場合には)解くことが出来ます。

\[ \begin{aligned} \left\{\begin{array}{r} 3x + y = 2\\ 2x + 4y = 2\\ \end{array}\right. &\xrightarrow{P_{1,2}} \left\{\begin{array}{r} 2x + 4y = 2\\ 3x + y = 2\\ \end{array}\right. \xrightarrow{Q_{1,\frac{1}{2}}} \left\{\begin{array}{r} x + 2y = 1\\ 3x + y = 2\\ \end{array}\right. \\ &\xrightarrow{R_{1,2,-3}} \left\{\begin{array}{r} x + 2y = 1\\ -5y = -1\\ \end{array}\right. \xrightarrow{Q_{2,-\frac{1}{5}}} \left\{\begin{array}{r} x + 2y = 1\\ y = \frac15\\ \end{array}\right. \\ &\xrightarrow{R_{2,1,-2}} \left\{\begin{array}{r} x = \frac{3}{5}\\ y = \frac15\\ \end{array}\right. \end{aligned} \]

以上,

• \(P_{i,j}\): 第\(i\)行と第\(j\)行を入れ替える
• \(Q_{i,c}\): 第\(i\)行を\(c \neq 0\)倍する
• \(R_{i,j,c}\): 第\(i\)行を\(c\)倍したものを第\(j\)行に加える

を行基本変形と言い,これらを組み合わせる事によって連立一次方程式を解くことが出来ます。

\[ \begin{aligned} \left[\begin{array}{cccc} 3& 1 & : &2\\ 2& 4 & : &2\\ \end{array}\right] &\xrightarrow{P_{1,2}} \left[\begin{array}{cccc} 2& 4 & : &2\\ 3& 1 & : &2\\ \end{array}\right] \xrightarrow{Q_{1,\frac{1}{2}}} \left[\begin{array}{cccc} 1& 2 & : &1\\ 3& 1 & : &2\\ \end{array}\right] \\ &\xrightarrow{R_{1,2,-3}} \left[\begin{array}{cccc} 1& 2 & : &1\\ 0&-5 & : &-1\\ \end{array}\right] \xrightarrow{Q_{2,-\frac{1}{5}}} \left[\begin{array}{cccc} 1& 2 & : &1\\ 0& 1 & : &\frac15\\ \end{array}\right] \\ &\xrightarrow{R_{2,1,-2}} \left[\begin{array}{cccc} 1& 0 & : &\frac{3}{5}\\ 0& 1 & : &\frac15\\ \end{array}\right] \end{aligned} \]

連立一次方程式の数値解法

さて,連立一次方程式を計算機で解く為には大きく分けて

• 直接法
• 反復法

の２つの解法があります。

直接法は掃き出し法のように,連立方程式の同値変形によって解を求める手法です。一方,反復法は 微積分の回にやった様な,反復計算によって真の回に収束させていく方法です。

今回は直接法の解説をします。反復法は次回以降に説明します。

直接法:ガウス消去法

直接法の全てのアルゴリズムの基本となるガウス消去法を紹介します。係数行列が正方行列(未知変数と方程式の数が同じ)場合だけを考えます。

ガウス消去法は

1. 前進消去
2. 後退代入

の2ステップからなります。

前進消去

まず,拡大係数行列 \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ a_{21}&a_{22}&\cdots&a_{2n}&:& b_2 \\ a_{31}&a_{32}&\cdots&a_{3n}&:& b_3 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&:& b_n \\ \end{array}\right] \] の第1行を\(\frac{a_{i1}}{a_{11}}\)倍して,\(i=2,3,\cdots,n\)行から引けば \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ 0 &a'_{22}&\cdots&a'_{2n}&:& b'_2 \\ 0 &a'_{32}&\cdots&a'_{3n}&:& b'_3 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ 0 &a'_{n2}&\cdots&a'_{nn}&:& b'_n \\ \end{array}\right] \] となり,第1列目の\(a_{11}\)以外を\(0\)にする事が出来ます。

次は第２行を\(\frac{a'_{i2}}{a'_{22}}\)倍して,\(i=3,4,\cdots,n\)行から引けば, \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ 0 &a'_{22}&\cdots&a'_{2n}&:& b'_2 \\ 0 &0 &\cdots&a''_{3n}&:& b''_3 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ 0 &0 &\cdots&a''_{nn}&:& b''_n \\ \end{array}\right] \] となります。この作業を繰り返していけば,係数行列を対角成分より下が全て\(0\)の上三角行列 \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ 0 &a'_{22}&\cdots&a'_{2n}&:& b'_2 \\ 0 &0 &\cdots&a''_{3n}&:& b''_3 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ 0 &0 & &a^{(n-1)}_{nn}&:& b^{(n-1)}_n \\ \end{array}\right] \] にすることが出来ます。以上のステップを前進消去と言います。 また,消去に用いる行をピボット行,係数\(a^{(i-1)}_{ii}\)をピボットと言います。

実装例は以下のようになります。

import numpy as np

def forward_elimination(A, b):
    # A,bの型チェックは省略
    n = b.size
    for k in xrange(n-1):
        pivot = A[k,k]

        for i in xrange(k+1, n):
            l = A[i, k]/pivot

            for j in xrange(k+1):
                A[i, j] = 0

            for j in xrange(k+1, n):
                A[i, j] -= l * A[k, j]
            b[i] -= l * b[k]

A = np.array([[8,4,-3],[6,1,-2],[2,-3,1]], dtype=float)
b = np.array([7,2,-1], dtype=float)

print "before forward-elimination"
print A
print b

forward_elimination(A, b)
print "after forward-elimination"
print A
print b

後退代入

前進消去の結果 \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1n}&:& b_1 \\ 0 &a'_{22}&\cdots&a'_{2n}&:& b'_2 \\ 0 &0 &\cdots&a''_{3n}&:& b''_3 \\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ 0 &0 & &a^{(n-1)}_{nn}&:& b^{(n-1)}_n \\ \end{array}\right] \] から,まず \[ x_n = \frac{b^{(n-1)}_n}{a^{(n-1)}_{nn}} \] が得られます。

これを元の連立方程式に代入すれば \[ \left[\begin{array}{cccccc} a_{11}&a_{12}&\cdots&a_{1,n-1}&:& b_1 -a_{1n}x_n\\ 0 &a'_{22}&\cdots&a'_{2,n-1}&:& b'_2 -a'_{2n}x_n\\ 0 &0 &\cdots&a''_{3,n-1}&:& b''_3 - a''_{3n}x_n\\ \vdots&\vdots&\ddots&\vdots&:&\vdots\\ 0 &0 & &a^{(n-2)}_{n-1,n-1}&:& b^{(n-1)}_n - a^{(n-2)}_{n-1,n}x_n\\ \end{array}\right] \] となって,\(n-1\)元のやはり係数行列が上三角な方程式になります。

従って,以上の作業を再帰的に繰り返せば, \[ x_n, x_{n-1}, \cdots, x_1 \] が順番に求まります。これを後退代入と言います。

実装例は以下のようになります。

import numpy as np

def forward_elimination(A, b):
    # A,bの型チェックは省略
    n = b.size
    for k in xrange(n-1):
        pivot = A[k,k]

        for i in xrange(k+1, n):
            l = A[i, k]/pivot

            for j in xrange(k+1):
                A[i, j] = 0   # この行は無くしても良い。

            for j in xrange(k+1, n):
                A[i, j] -= l * A[k, j]
            b[i] -= l * b[k]

def backward_substitution(U, b):
    # U,bの型チェックは省略
    n = b.size
    x = np.zeros(n)
    for i in reversed(xrange(n)):
        x[i] = b[i]/U[i, i]
        for j in xrange(i):
            b[j] -= A[j,i]*x[i]
    return x


A = np.array([[8,4,-3],[6,1,-2],[2,-3,1]], dtype=float)
b = np.array([7,2,-1], dtype=float)

print "before forward-elimination"
print A
print b

forward_elimination(A, b)
print "after forward-elimination"
print A
print b

print "the answer"
print backward_substitution(A, b)

【答え】
\[ (x,y,z) = (2.6, 3.4, -2.8) \]

ガウス消去法の計算量

今のプログラムの加算・乗算・除算の回数をカウントしてみて下さい。

すると加算が約\(\frac{n^3}{3}\)回,乗算が約\(\frac{n^3}{3}\)回,除算が約\(2n\)回となります。従って(係数も無視できないのですが)ざっくりと言えば\(\color{yellow}{\mathcal{O}(n^3)}\)のオーダーの計算量という事になります。

という事で,反復法は変数の数が数百～数千くらいの比較的小さな連立一次方程式の解法に適しています。それ以上のサイズの場合には,後で説明する反復法を利用する事になります。

ピボット選択

気づいた人もいると思いますが,ガウス消去法においてピボット\(a^{(i-1)}_{ii}\)が\(0\)だと除算が出来ません。また,\(0\)でなくても\(0\)に非常に近い数だと逆数が非常に大きくなりますから,前進消去時に桁落ちが発生してしまいます。

そこで

• ピボットの絶対値が大きい行とピボット行を交換する(部分ピボット選択)
• ピボットが小さすぎる時はエラーにする

といった処理が必要になります。

以下が実装例です。

# -*- coding: utf-8 -*-
import numpy as np

def solve(A, b):
    # 前進消去
    n = b.size
    p = np.arange(n)    # [0,1,2,...,n-1] 
    for k in xrange(n-1):

        # ピボット選択
        pivot_idx = p[k]
        pivot_max = 0
        for i in xrange(k, n):
            v = abs(A[p[i], k])
            if v > pivot_max:
                pivot_max = v
                pivot_idx = i

        if pivot_max < 1e-10:
            raise ArithmeticError, u'ピボットが小さすぎ'

        # ピボット行の交換
        if p[k] != pivot_idx:
            p[k], p[pivot_idx] = p[pivot_idx], p[k]

        pivot = A[p[k],k]
        for i in xrange(k+1, n):
            l = A[p[i], k]/pivot

            for j in xrange(k+1, n):
                A[p[i], j] -= l * A[p[k], j]
            b[p[i]] -= l * b[p[k]]

    # 後退代入
    x = np.zeros(n)
    for i in reversed(xrange(n)):
        x[i] = b[p[i]]/A[p[i], i]
        for j in xrange(i):
            b[p[j]] -= A[p[j],i]*x[i]
    return x


A = np.array([[8,4,-3],[6,1,-2],[2,-3,1]], dtype=float)
b = np.array([7,2,-1], dtype=float)

print solve(A, b)

簡単な応用として,以前もやった最小二乗法を取り上げましょう。

\[ \frac{\partial E}{\partial a} = \frac{\partial E}{\partial b} = \frac{\partial E}{\partial c} = 0 \] を解けば良いです。 \[ \begin{aligned} \frac{\partial E}{\partial a} &= \sum 2x_i (ax_i + by_i + cz_i - w_i) \\ &= 2(\sum x_i^2)a + 2(\sum x_iy_i) b + 2(\sum z_ix_i)c - 2\sum x_iw_i \end{aligned} \] であるので,１つ目の方程式は \[ (\sum x_i^2)a + (\sum x_iy_i) b + (\sum z_ix_i)c = \sum x_iw_i \] です。\(b,c\)についても同様にすれば \[ \left[\begin{array}{ccccc} \sum x_i^2 & \sum x_iy_i & \sum z_ix_i & : & \sum x_iw_i \\ \sum x_iy_i & \sum y_i^2 & \sum y_iz_i & : & \sum y_iw_i \\ \sum z_ix_i & \sum y_iz_i & \sum z_i^2 & : & \sum z_iw_i \\ \end{array} \right] \] を解けば良いという事になります。

従って,(綺麗なコードではないですが)以下のプログラムで求める事が出来ます。

このデータを試してみて下さい。これは \[ w=x+2y+3z \] というモデルにノイズを加えて作っていますので,\((1,2,3)\)に近いパラメータが出力されるはずです。

import csv
import numpy as np
from numpy import linalg as LA

reader = csv.reader(open("test-data.csv", "rb"), delimiter=",")

sum_x2 = 0.0
sum_y2 = 0.0
sum_z2 = 0.0
sum_xy = 0.0
sum_yz = 0.0
sum_zx = 0.0
sum_xw = 0.0
sum_yw = 0.0
sum_zw = 0.0

for x,y,z,w in reader:
    x = float(x)
    y = float(y)
    z = float(z)
    w = float(w)

    sum_x2 += x*x
    sum_y2 += y*y
    sum_z2 += z*z
    sum_xy += x*y
    sum_yz += y*z
    sum_zx += z*x
    sum_xw += x*w
    sum_yw += y*w
    sum_zw += z*w

A = np.array([[sum_x2, sum_xy, sum_zx],
              [sum_xy, sum_y2, sum_yz],
              [sum_zx, sum_yz, sum_z2]])
b = np.array([sum_xw, sum_yw, sum_zw])
print LA.solve(A, b)    # [a,b,c]

今の事実を使って、先ほどのコードを書き直すと以下のようになります。

import csv
import numpy as np
from numpy import linalg as LA

reader = csv.reader(open("test-data.csv", "rb"), delimiter=",")
arr = np.array(list(reader), dtype=float) # (x y z w)

X = arr[...,0:3]    # (x y z)
w = arr[...,3:4]    # w
XT = X.T            # (x y z)^T

print LA.solve(np.dot(XT, X), np.dot(XT, w))

先ほどと同様に \[ X = \begin{pmatrix} 1 & x_1 & \cdots & x_1^{m-1} & x_1^m \\ 1 & x_2 & \cdots & x_2^{m-1} & x_2^m \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & x_n & \cdots & x_n^{m-1} & x_n^m \\ \end{pmatrix} \] とおけば解くべき方程式は \[ X^TX\mathbf{a}=X^T\mathbf{y} \] となります。但し\(\mathbf{a} = (a_0, a_1, \cdots, a_m)^T\)です。 プログラムは例題と同様です。

今回はここで終わります。

次回も連立一次方程式の理論を中心に学習していきます。行列式・逆行列・LU分解,固有値・固有ベクトル,連立一次方程式の反復解法,未知変数と方程式の数が異なる問題の解法などを紹介する予定です。