プログラマの為の
数学勉強会
第2回
(於)ワークスアプリケーションズ中村晃一
2013年9月19日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPythonで記述しています。
浮動小数点数と誤差
浮動小数点数と誤差
浮動小数点数を利用した計算結果には誤差が含まれます。 複雑な計算をしたり多数のデータを扱う場合にはその影響が目に見えて現れますので, 最初に浮動小数点数と誤差に関する基礎知識の確認を行います。
浮動小数点数の規格
最も広く使用されている浮動小数点数の規格はIEEE 754です。
以下のデータ形式に加え,丸めの方式などが定義されています。
- 正規化数
- 非正規化数
- \(0\)と\(-0\)
- \(\infty\)と\(-\infty\)
- 非数(NaN)
IEEE754では3種類の二進小数,2種類の十進小数の形式が基本形式として定義されていますが,以下では二進形式のみ説明をします。
正規化数
二進形式の正規化数は
- 符号\(s\) (1bit)
- 指数\(e\) (整数)
- 仮数\(1.m_1m_2\cdots m_n\) (1以上2未満の有限二進小数)
からなり, \[ (-1)^s\times 1.m_1m_2\cdots m_n \times 2^e \] という形で表されます。
例えば,小数の\(1001.01001_2 = 9.28185_{10}\)は \[ 1.00101001\times 2^3 \] と正規化され,符号\(0\),指数\(3\),仮数\(1.00101001_2\)となります。
二進小数の精度・範囲
二進小数については単精度,倍精度,四倍精度という3種類の精度の形式が定義されています。
| 指数の範囲 | 仮数の桁数(精度\(p\)) | |
|---|---|---|
| 単精度(binary32形式) | -126~127 | 1 + 23 |
| 倍精度(binary64形式) | -1022~1023 | 1 + 52 |
| 四倍精度(binary128形式) | -16382~16383 | 1 + 112 |
\(\log_{10}2 \approx 0.3010\)をこれらに掛ければ十進数でのおおよその精度・指数の範囲が解ります。例えば倍精度の場合,仮数の精度は十進数で\(15\)~\(16\)桁程度,指数は\(10^{-308}\)から\(10^{308}\)程度の範囲となります。
好きな処理系で精度・指数の限界について実験してみると良いでしょう。 以下は,Python 2.7.3(デフォルトでは倍精度)の例です。
>>> 1.0 + 1e-15
1.000000000000001
>>> 1.0 + 1e-16 # 仮数の精度より細かくは値を表現出来ない
1.0
>>> 1e308
1e+308
>>> 1e309 # 指数のオーバーフロー
inf
>>> 1e-307
1e-307
>>> 1e-308 # 非正規化数(後述)に切り替わり0.0にはならない
1e-308
>>> 1e-323
1e-323
>>> 1e-324 # 指数のアンダーフロー
0.0
非正規化数
正規化数の \[ (-1)^s\times 1.m_1m_2\cdots m_n \times 2^e \] という表現では0周辺の値の扱いに問題が発生します。
十進小数の方が分り易いので,\(a = 1.1\times 10^e\)と\(b = 1.0\times 10^e\)を考えます。これらの差をとって正規化すると \[ a - b = 0.1\times 10^e = 1.0\times 10^{e-1} \] となり指数が減ってしまいます。\(e\)が指数の範囲の最小値の時は\(e-1\)がアンダーフローするので,\(a \neq b\)なのに\(a - b = 0\)となってしまいます。
非正規化数
そこで,0の周辺では正規化をせず \[ (-1)^s\times \color{pink}{0}.m_1m_2\cdots m_n \times 2^{\text{最小指数}} \] という固定小数点数で表すことにします。これを非正規化数と言います。指数のアンダーフローが無くなる替わりに,仮数の有効桁数が減少するので注意してください。
これによって,例えば倍精度の場合は \[ 0.000\cdots0001\times 2^{-1022} = 2^{-1074} \approx 4.941\times 10^{-324} \] という所まで表せる事になります。
マシンイプシロン
精度\(p\)の正規化数では\(\epsilon = \frac{1}{2^{p-1}}\) より小さい仮数の差を表現出来ません。この\(\epsilon\)はマシンイプシロンと呼ばれます。注
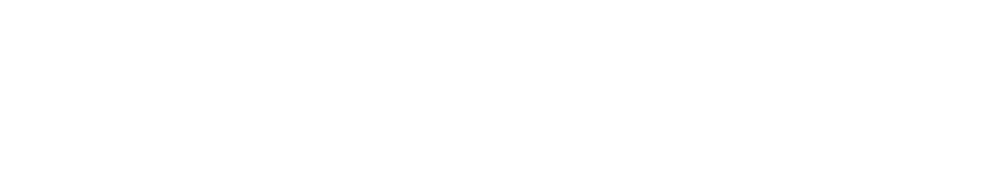
| 単精度 | \(\epsilon = 2^{-23} \approx 1.19\times 10^{-7}\) |
|---|---|
| 倍精度 | \(\epsilon = 2^{-52} \approx 2.22\times 10^{-16}\) |
| 四倍精度 | \(\epsilon = 2^{-112} \approx 1.93\times 10^{-34}\) |
注: マシンイプシロンはIEEEで定義されている訳ではなく様々な定義が存在しますが,ここでは 「\(1\)より大きい最小の浮動小数点数が\(1+\epsilon\)と表される時の\(\epsilon\)」という事にします。
丸め
計算機は内部的に多めの桁数で演算を行ったあと,実際の桁数に収まるように結果を丸めます。
IEEEではいくつかの丸めの方式が定義されていますが,再近接偶数丸めが標準的な方式です。
再近接偶数丸め
- 最も近い値へ丸める
- ちょうど中間の値は結果が偶数となるように丸める
何故,偶数丸め?
中間の値の丸めを切り上げ,切り捨ての一方に定めると誤差の出方の偏りが生じてしまいます。偶数丸めを行うことによって誤差の累積を抑える事が出来ます。
十進小数の四捨五入を例に説明します。整数\(x\)と\(x+1\)の間の9つの小数 \[ x.1,\ x.2,\ x.3,\ x.4,\ x.5,\ x.6,\ x.7,\ x.8,\ x.9\] を四捨五入すると4つが切り捨て,5つが切り上げとなります。
自前で丸めを行う場合には,処理系の用意する丸め関数の仕様をよく調べるようにしましょう。
絶対誤差と相対誤差
実数\(x\)とその近似値\(\widetilde{x}\)に対して \[ E_A(x) = |x-\widetilde{x}| \] を絶対誤差と言います。
一方,浮動小数点数だと誤差は仮数部に現れるので,その大きさは相対誤差 \[ E_R(x) = \frac{|x-\widetilde{x}|}{|x|} \] によって評価する事が出来ます。注
注: \(x=0\)の時には\(E_R(x)\)が定義されないので,絶対誤差を用いて議論する必要があります。
丸めの相対誤差
\(f\times 2^e\)を\(\widetilde{f}\times 2^e\)で近似した場合の相対誤差は \[ \frac{|f\times 2^e-\widetilde{f}\times 2^e|}{|f\times 2^e|} = \frac{|f-\widetilde{f}|}{|f|} \] となります。
仮数の間隔は\(\epsilon\)なので,再近接丸めの場合\(|f-\widetilde{f}|\leqq \frac{\epsilon}{2}\)が成り立ちます。また\(1\leqq |f| < 2\)なので \[ \frac{|f-\widetilde{f}|}{|f|} \leqq \frac{\epsilon}{2} \] となります。これが丸めの相対誤差の上限となります。
丸め以外の誤差
丸め以外にも以下のような要因によって誤差が生じます。これらは丸め誤差よりも影響が大きいので十分に気をつけなければいけません。
- オーバーフロー・アンダーフロー
- 情報落ち
- 桁落ち
- 打ち切り誤差
- 二進と十進の変換
オーバーフロー・アンダーフロー
指数がオーバーフローすると\(\pm \infty\),アンダーフローすると\(\pm 0\)になってしまいます。仮数の一切の情報が失われてしまうので,発生させないように十分気をつける必要があります。
対処
オーバーフロー・アンダーフローは巨大な数・微小な数の乗除累乗算などによって発生します。典型的な回避方法は対数を利用する事です。 \[ \begin{aligned} \log AB &= \log A + \log B \\ \log \frac{A}{B} &= \log A - \log B \\ \log A^k &= k\log A \end{aligned} \]
確率計算からの事例
確率\(p_1,p_2,\cdots,p_n\)で生じる独立な事象が,全て生じる確率(同時確率)は \[ P = \prod_{i}p_i = p_1p_2\cdots p_n \] となります。\(0\leqq p_i \leqq 1\)なので,\(n\)が大きいと容易にアンダフローを起こします。
これを回避する為には \[ \log P = \sum_{i}\log p_i = \log p_1 + \log p_2 + \cdots + \log p_n \] と計算すれば良いです。
計算例
>>> from math import log10
>>> from random import random
>>> ps = [random() for i in range(1000)] # 1未満正数を1000個用意
>>> P = 1.0
>>> for p in ps:
... P *= p
...
>>> P
0.0 # アンダーフロー発生
>>> logP = 0.0
>>> for p in ps:
... logP += log10(p)
...
>>> logP
-428.5221443182958 # アンダーフロー回避
>>> 10**(logP - round(logP))
3.005077533929242 # つまりPの値は約3.0e-429
桁落ち
非常に近い2数の差を取ると,有効桁数が大きく減少してしまう現象です。
>>> 1.2345678 - 1.2345677
1.0000000005838672e-07 # 10桁しか合っていない
有効桁数が4桁の十進小数\(1.234\times 10^2\)と\(1.233\times 10^2\)を用いて説明します。 \[ 1.234\times 10^2 - 1.233\times 10^2 = 1\times 10^{-1} \] となり有効桁数が1桁に落ちてしまいます。
足りなくなった桁は計算機内部で余分に持っている桁の数値で埋めるので,上のように一見デタラメな数値が出てきます。
桁落ちの対処
数式の変形によって回避出来る場合があります。いつでも出来る訳ではないので,必要ならば精度の高い浮動小数点数を利用するといった対処をします。どうしようもない場合もあります。
数式の変形による対処の例
例えば以下の左辺では\(h\)が小さい時に桁落ちの影響が大きくなりますが,右辺のように変形すればこれを回避出来ます。 \[ \frac{\sqrt{x+h}-\sqrt{x}}{h} = \frac{1}{\sqrt{x+h}+\sqrt{x}} \]
情報落ち
絶対値の大きく異なる2数の加減算によって,絶対値の小さい方の情報が無視されてしまう現象です。
>>> 100 + 1e-15
100.0
>>> 100 - 1e-15
100.0
対処
上の様なケースで情報落ちを防ぎたいならば,精度の高い浮動小数点数を利用する他ありません。
また,絶対値の異なる多数の数を加えていく場合には絶対値の小さい数から加えたり,大小毎に分けて計算結果を持っておくなどの対処が考えられます。
打ち切り誤差
反復計算などを途中で打ち切る事によって生じる誤差です。解析には微積分や線型代数の知識が必要になるので,随時説明をしていきます。
例えば, \[ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \] が成り立ちます(後でやる)が,これを途中で打ち切って \[ \sin x \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots + (-1)^n\frac{x^{2n+1}}{(2n+1)!}\] とすると\(n\)に応じて大小の誤差が生じます。
\(\sin\frac{\pi}{2} = 1\)を今の公式で計算してみます。
>>> from math import pi
>>> v = 0.0
>>> x = pi/2
>>> term = x
>>> for k in range(1, 10):
... v += term
... print "{0}: {1:.16f}".format(k, v)
... term *= -x*x/((2*k)*(2*k+1))
...
1: 1.5707963267948966
2: 0.9248322292886504
3: 1.0045248555348174
4: 0.9998431013994987
5: 1.0000035425842861
6: 0.9999999437410509
7: 1.0000000006627803
8: 0.9999999999939768
9: 1.0000000000000437
二進と十進の変換
私達が使う十進小数と,計算機が使う二進小数を相互に変換すると誤差が発生します。
例:十進の0.1
十進の\(0.1\)は二進では無限小数となりますので誤差が生じます。例えば倍精度での\(0.1\)は \[\frac{1}{10} + \color{pink}{\frac{1}{5\times 2^{55}}} \] という値になり\(5.55\times 10^{-18}\)程度の誤差を含みます。字面上では正確な小数に見えてしまう為,気をつけないと以下のようなミスをします。実際には\(0.1\)には誤差が含まれ,加算の誤差の累積も生じています。
>>> t = 0.0
>>> while (t < 1.0): # 0.0, 0.1, 0.2, ..., 0.9と回すつもり
... print t
... t += 0.1
...
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0 # t < 1.0を通過している??
この場合,誤差の生じない整数を利用して回すのが正解です。
>>> for i in range(10): # i = 0, 1, 2, ..., 9
... t = i*0.1
... print t
...
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
誤差の伝播
\( f(x_1,\cdots,x_n) \)という値を計算する為に近似値\(\widetilde{x_1},\cdots,\widetilde{x_n}\)と,\(f\)を近似した関数\(\widetilde{f}\)を用いることにしましょう。
この場合の誤差は \[ \begin{aligned} &f(x_1,\cdots,x_n) - \widetilde{f}(\widetilde{x_1},\cdots,\widetilde{x_n}) \\ = &\left\{f(\widetilde{x_1},\cdots,\widetilde{x_n}) - \widetilde{f}(\widetilde{x_1},\cdots,\widetilde{x_n})\right\} \\ + & \left\{f(x_1,\cdots,x_n) - f(\widetilde{x_1},\cdots,\widetilde{x_n})\right\} \end{aligned} \] となるので,近似演算が原因である第1項と,引数の誤差が原因である第2項(伝播誤差)からなります。
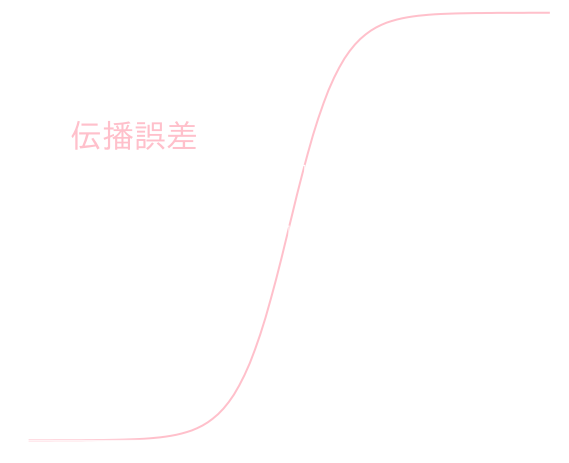
伝播誤差の大きさ
伝播誤差の詳しい記述には微積分の知識が必要となりますが,直感的には下図の様に変化率の大きい所で伝播誤差も大きくなるという事が言えます
極限・微分
「微分」では何をしたいのか?
微積分学における微分分野では,一変数関数\(f(x)\)や多変数関数\(f(x_1, x_2, \cdots, x_n)\)の連続的な変化の様子が考察の対象となります。
関数の変化の様子を記述には導関数や偏導関数を利用し,その定義の為に極限という概念が必要となります。
導関数とは,直感的には関数\(f(x)\)のグラフ\(y=f(x)\)の各点での接線の傾き(微分係数)を与える関数であると言えます。
上図は\(y=\sin x\)とその導関数\(y=\cos x\)という例です。
2点\((x, f(x))\)と\((x+h, f(x+h))\)を通る直線の傾きは \[ \frac{f(x+h)-f(x)}{h} \] となります。直感的には\(h\)を\(0\)に近づけていくと,この値が点\((x, f(x))\)での傾きに限りなく近づくという事が言えそうです。
極限
今考察した事を正確に述べる為に極限という概念を導入します。
数列の極限の素朴な定義
数列\(a_1,a_2,a_3,\cdots\)の値がある定数\(\alpha\)に限りなく近づいていくならば,\(\{a_n\}\)は\(\alpha\)に収束すると言い,以下の様に表す。 \[ \lim_{n\rightarrow\infty}a_n = \alpha \]
関数の極限の素朴な定義
\(x\)を\(a\)に近づけた時,\(f(x)\)の値がある定数\(\alpha\)に限りなく近づいていくならば,\(f(x)\)は\(x\rightarrow a\)で\(\alpha\)に収束すると言い,以下のように表す。 \[ \lim_{x\rightarrow a}f(x) = \alpha\]
数列の極限の例
例えば\( a_n = \frac{1}{n} \)という数列は \[ 1, \frac{1}{2}, \frac{1}{3}, \cdots, \frac{1}{10000},\cdots \] と限りなく\(0\)に近づいていくので \[ \lim_{n\rightarrow\infty}\frac{1}{n} = 0\] となります。
関数の極限の例
例えば\(f(x) = \frac{1}{1+x}\)という関数は\(x\rightarrow 0\)の時,限りなく\(1\)に近づいていくので \[ \lim_{x\rightarrow 0}\frac{1}{1+x} = 1 \] となります。
高校数学では以上の様に説明されますが,なんだか怪しいと思った人もいるのではないかと思います。
素朴な定義では限りなく近づくという事の意味が曖昧になってしまっています。
そこで\(\varepsilon-N\)論法,\(\varepsilon-\delta\)論法と呼ばれる定義を紹介します。
「限りなく近づいていく」とは
まず,\(a_n\)の値を\(\alpha\)に限りなく「近づける事が出来る」というのは, どのような距離の限界\(\varepsilon > 0\)を用意してもそれより近づけるということなので,
そして,限りなく「近づいていく」というのは限界\(\varepsilon\)が与えられた時に \[ a_1,a_2,a_3,a_4,a_5\cdots, \] のある所から先は常に\(|a_n-\alpha|<\varepsilon\)を満たすことだと言えます。
\(\varepsilon-N\)論法
\(\varepsilon-N\)論法による数列の極限の定義
任意の\(\varepsilon > 0\)に対してある自然数\(N\)が存在して, \[ n > N\ \text{ならば}\ |a_n - \alpha| < \varepsilon\] となる時\(\{a_n\}\)は\(\alpha\)に収束すると言い,下のように表す \[ \lim_{n\rightarrow\infty}a_n = \alpha \]
\(\displaystyle\lim_{n\rightarrow\infty}\frac{1}{n} = 0\)を\(\varepsilon-N\)論法で証明してみます。
[証明]
任意の\(\varepsilon > 0\)に対して自然数\(N\)を
\[ N > \frac{1}{\varepsilon} \]
を満たすようにとれば\(n > N\)の時
\[ \left|\frac{1}{n}-0\right| = \frac{1}{n} < \frac{1}{N} < \varepsilon \]
を満たす。従って
\[ \lim_{n\rightarrow\infty}\frac{1}{n} = 0 \]
である。□
\(\varepsilon-\delta\)論法
同様にして関数の極限も定義されます。
\(\varepsilon-\delta\)論法による関数の極限の定義
任意の\(\varepsilon > 0\)に対してある\(\delta > 0\)が存在して, \[ 0 < |x-a| < \delta\ \text{ならば}\ |f(x)-\alpha|<\varepsilon\] となる時\(f(x)\)は\(x\rightarrow a\)で\(\alpha\)に収束すると言い,下のように表す \[ \lim_{x\rightarrow a}f(x) = \alpha \]
練習問題
\(\varepsilon-\delta\)論法で\(\displaystyle\lim_{x\rightarrow 0}\frac{1}{1+x} = 1\)を証明して下さい。
微分係数
以上の準備によって微分係数を定義する事が出来ます。
微分係数
関数\(f(x)\)に対して極限 \[ \lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h} \] が収束する時,この値を\(x=a\)における\(f(x)\)の微分係数と言い \[ f'(a),\ \frac{\mathrm{d}f}{\mathrm{d}x}(a),\ \left.\frac{\mathrm{d}}{\mathrm{d}x}f(x)\right|_{x=a} \] などと表す。
\(f'(a)\)が存在する時,\(f(x)\)は\(x=a\)で微分可能であると言います。
導関数
導関数
微分係数\(f'(a)\)は\(x=a\)を変化させる事により\(x\)の関数, \[ f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \] となる。これを\(y=f(x)\)の導関数と言い, \[ f'(x),\ y',\ \frac{\mathrm{d}}{\mathrm{d}x}f(x),\ \frac{\mathrm{d}y}{\mathrm{d}x}\] などと表す。
先ほど説明したように,\(f'(x)\)は\(y=f(x)\)の各点での傾きと解釈する事ができます。
導関数の例
\(f(x) = x^2\)の導関数を計算してみると,
\[\begin{aligned} f'(x) &= \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0}\frac{(x+h)^2-x^2}{h}\\ &= \lim_{h\rightarrow 0}\frac{2xh+h^2}{h}= \lim_{h\rightarrow 0}(2x+h)\\ &= 2x \end{aligned} \] となります。
【練習問題】\(\left(\frac{1}{x}\right)' = -\frac{1}{x^2}\)を示して下さい。
基本的な関数の導関数
以下,よく使う基本的な関数の導関数を紹介します。
導出は省略するので教科書を参照してください。
グラフは\((x^2)'=2x\)の例
その他三角関数の導関数
自然対数の底
自然対数の底
\[ e = \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n \] という極限値として定義される\(e\)を自然対数の底,もしくはネイピア数と言う。その値は無理数であり \[ e = 2.718281828459045\cdots \] となる。\(\left(1+\frac{1}{n}\right)^n\)が収束する事,\(e\)が無理数である事の証明は教科書を参照して下さい。
指数関数・対数関数
ネイピア数\(e\)を底とする指数関数,対数関数は重要なので以下の記法がよく使われます。
指数・対数関数
ネイピア数\(e\)を底とする指数関数,対数関数を以下の様に表す。 \[ \begin{aligned} \color{pink}{\exp x} &= e^x\\ \color{pink}{\ln x} &= \log_e x \end{aligned} \]
微分の公式
導関数の定義より以下の公式を示す事が出来ます。
公式を利用した計算の例
\(f(x) = \exp\left(-\frac{x^2}{2}\right)\)の導関数を求めてみます。
合成関数の微分法により \[ \begin{aligned} f'(x) &= \exp\left(-\frac{x^2}{2}\right)\times \left(-\frac{x^2}{2}\right)' \\ &= -x\exp\left(-\frac{x^2}{2}\right) \end{aligned} \] となります。
こういった計算はスラスラ出来るように良く練習しておいて下さい。
高階導関数
関数\(f(x)\)を繰り返し微分して得られる関数も重要です。
高階導関数
関数\(f(x)\)を\(n\)回微分した関数を\(f(x)\)の\(n\)階導関数といい, \[ f^{(n)}(x),\ \frac{\mathrm{d}^n}{\mathrm{d}x^n}f(x),\ \left(\frac{\mathrm{d}}{\mathrm{d} x}\right)^nf(x) \] などと表す。
【練習問題】\( f(x)=e^x\sin x \)の\(n\)階導関数を求めて下さい。
今回はここで終わります。
次回は微分法の応用として,極値・テイラー展開・近似・差分法などの説明をします。時間があれば,多変数関数の微分法の説明もします。