プログラマの為の
数学勉強会
第18回
(於)ワークスアプリケーションズ中村晃一
2014年1月30日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
ベイズ統計
今回はベイズ主義に基づく ベイズ統計学 の基礎事項を紹介します.
復習すると, ベイズ主義では確率 \(P(A)\) を 事象 \(A\) が起こるという事の確信度の大きさとして解釈するのでした. そしてベイズの定理が中心的な役割を果たします.
ベイズ統計では, 考察の対象 \(A\) に対して予め事前確率\(P(A)\)を定めておきます. \(A\) と関係する事象\(B\)が生起したならば ベイズ改訂 を行って 事後確率 \(P(A|B)\) へと確率を更新する事が出来ます. これを繰り返せば確率の客観性を高めていく事が出来ます.
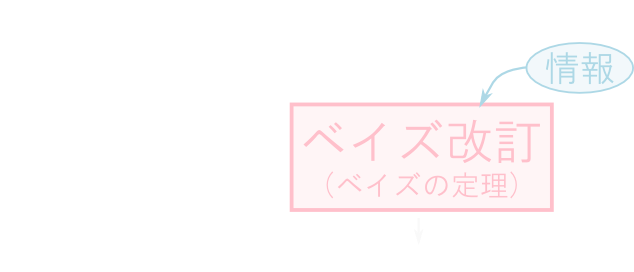
ベイズの定理
\(P(A),P(B)>0\)の時 \[ P(A|B) = \frac{P(A)P(B|A)}{P(B)} \] が成立する。
ベイズ主義の立場では, \(P(A)\) を事前確率, \(P(A|B)\) を \(B\) が生じたという情報(証拠)を得たことによる事後確率と解釈します.
注: この定理は公理的確率論の定理であるので, 頻度主義であってもこの定理は利用されます.
以下の形も良く使われます.
ベイズの定理
\(B_1,B_2,\cdots\)が互いに素で,\(\Omega=B_1\cup B_2\cup\cdots\)であるならば \[ P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\displaystyle\sum_{i=1}^{\infty}P(B_i)P(A|B_i)} \] である。
ベイズの定理 \[ P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\displaystyle\sum_{i=1}^{\infty}P(B_i)P(A|B_i)} \] の分母は全確率の値が \(1\) という条件を満たす為の規格化定数と考える事が出来るので, \[ P(B_i|A) \propto P(B_i)P(A|B_i) \] と表記する場合もあります.
有名な問題を考えてみましょう.
3囚人問題
\(A,B,C\)の3人の囚人がいます. 3人のうち2人が処刑される事は分かっており, どの1人が助かるのかは囚人達には全く分かりません.
ここで囚人 \(A\) が看守に「\(B,C\)の少なくとも1人は処刑になるはずだが, その名前を教えてくれ」と質問した所, 「\(B\)は処刑される」と看守が答えました. それを聞いて \(A\) は自分が処刑されない確率が \(1/3\) から \(1/2\) に上がったと喜びましたが, これは正しいでしょうか?
\(A,B,C\)が処刑を免れるという事象をそれぞれ \(A,B,C\) とし, 「\(B\) が処刑される」と看守が証言する事象を \(E\) とします. \(P(A)=P(B)=P(C)=1/3\) として \(P(A|E)\) について考えます.
(看守が正直だとすれば) 明らかに\(P(E|B)=0, P(E|C)=1\) となります. また, \(A\) が処刑を免れる時は「\(B\)が処刑される」と「\(C\)が処刑される」両方の証言が可能です. この場合, 看守がどちらの証言を選ぶかは全く分からないので \(P(E|A)=1/2\) としましょう.
処刑を免れるのは一人と決まっているので \(A,B,C\)は互いに素で \(A\cup B\cup C = \Omega\) ですからベイズの定理より \[ P(A|E) = \frac{P(A)P(E|A)}{P(A)P(E|A)+P(B)P(E|B)+P(C)P(E|C)} \] が成立します.
従って \[ P(A|E) = \frac{\frac{1}{3}\cdot\frac{1}{2}}{\frac{1}{3}\cdot\frac{1}{2}+\frac{1}{3}\cdot 0+\frac{1}{3}\cdot 1} = \frac{1}{3}\] となります. \(P(A)=P(A|E)\) であるので 証言 \(E\) を聞いた所で \(A\) が処刑を免れる確率は変化しません.
理由不十分の原則
今の問題では事前確率を \[ P(A)=P(B)=P(C) \] としましたが, これは\(A,B,C\)のどれが起こるのか全く分からないからです. この様に「どの事象が生起するかについて全く情報がないときは等確率とする」という原則を 理由不十分の原則 と呼びます.
ベイズ改訂と事象の独立性
証拠が沢山ある場合の事後確率の計算は \[ \begin{aligned} & P(A|B_1,B_2,\ldots,B_n) \\ \propto &P(A)P(B_1,B_2,\ldots,B_n|A) \\ =&P(A)P(B_1|A)P(B_2,\ldots,B_n|A,B_1) \\ =&P(A)P(B_1|A)P(B_2|A,B_1)P(B_3,\ldots,B_n|A,B_1,B_2)\\ =&\cdots \\ =&P(A)P(B_1|A)P(B_2|A,B_1)P(B_3|A,B_1,B_2)\\ &\qquad \cdots P(B_n|A,B_1,B_2,\ldots,B_{n-1}) \end{aligned} \] となりますが, この計算は非常に複雑です.
ここで, 証拠\(B_i,B_j (i < j)\) が独立ならば \[ P(B_i|\ldots,B_{j-1},B_j,B_{j+1},\ldots)=P(B_i|\ldots,B_{j-1},B_{j+1},\ldots) \] が成り立ちます(正確には独立性よりも弱い条件付き独立性という性質を持てば十分). 事象の独立性に注目すると計算を簡略化する事が出来ます.
単純ベイズモデル
証拠 \(B_1,B_2,\ldots,B_n\) が全て独立である という強い仮定を置けば, \[ P(A|B_1,B_2,\ldots,B_n) \propto P(A)P(B_1|A)P(B_2|A)\cdots P(B_n|A) \] となるので \[ \color{yellow}{ P(A|B_1,B_2,\ldots,B_n) \propto P(A)\prod_{i=1}^n P(B_i|A) }\] によってベイズ改訂の計算が出来ます. この仮定を適用したモデルを 単純ベイズモデル(ナイーブベイズモデル) と呼びます.
例題
非常に簡単な迷惑メール判定の問題を考えてみましょう. ここでは4つの単語「連絡」「無料」「登録」「経理」のみに注目します. これらがメールの中に出現する確率は以下のようになっているとします. \[ \begin{array}{|c|c|c|c|} \hline & \text{連絡} & \text{無料} & \text{登録} & \text{経理}\\ \hline \text{通常メール} & 0.8 & 0.2 & 0.3 & \text{0.9} \\ \hline \text{迷惑メール} & 0.2 & 0.8 & 0.7 & \text{0.1} \\ \hline \end{array} \] また, 受け取るメールの6割が通常メールであるとします.
あるメールを調べた所「連絡」「無料」「登録」という単語が検出されたとします. このメールが通常メール・迷惑メールのどっちであるか単純ベイズモデルを適用して計算してみましょう.
\[ \begin{aligned} P(\text{通常}|\text{連絡},\text{無料},\text{登録}) &\propto P(\text{通常}) P(\text{連絡}|\text{通常}) P(\text{無料}|\text{通常}) P(\text{登録}|\text{通常})\\ &= 0.6\times 0.8 \times 0.2\times 0.3 = 0.0288 \\ P(\text{迷惑}|\text{連絡},\text{無料},\text{登録}) &\propto P(\text{迷惑}) P(\text{連絡}|\text{迷惑}) P(\text{無料}|\text{迷惑}) P(\text{登録}|\text{迷惑}) \\ &= 0.4\times 0.2 \times 0.8 \times 0.7 = 0.0448 \end{aligned} \] となるので, この場合は迷惑メールである可能性が高いと考えられます.
今の問題では, 文章中の単語が全く無関係にランダムに出現するという, 納得しがたい仮定をおいています.
しかし実際には,単純ベイズモデルに基づく分類器は多くの問題に対して効果的に働くようです. この事については, 事象の従属関係による確率の変動が実際には上手くキャンセルされるからだという 理論的な説明 もあります.計算上の注意ですが \(P(A)\prod_{i=1}^n P(B_i|A) \) の値は \(n\) が大きいとどんどん小さくなりアンダーフローがおきてしまいます. そこで実際には, \[ P(A|B_1,B_2,\ldots,B_n) =\alpha P(A)\prod_{i=1}^n P(B_i|A) \quad (\alpha:\text{規格化定数}) \] の対数をとって \[ \ln P(A|B_1,B_2,\ldots,B_n) =\ln \alpha + \ln P(A) + \sum_{i=1}^n \ln P(B_i|A) \] の形で計算を行います.
ベイジアンネットワーク
今回は詳しい解説をする時間がないのですが, 事象の独立性をベイジアンネットワークというグラフ構造の上で表す事が出来ます. グラフ上の幾つかのノードに対して証拠が与えられた時に,それ以外のノードに関する全確率をベイズの定理に基いて計算する事が出来ます.
ベイズ推定
確率分布の母数\(\theta\)に対する推定を行うには以下の定理を利用します.
母数分布に対するベイズの定理
\(X\) が確率密度関数(もしくは確率質量関数) \(f(X|\theta)\) の表す分布に従い, 母数 \(\theta\) の 事前分布 が \(p(\theta)\) ならば \[ p(\theta|X=x) = \frac{f(X=x|\theta)p(\theta)}{f(X=x)} \] を\(\theta\)の事後分布という.
\(p(\theta|X=x)\) を最大にする\(\theta\)の値を ベイズ推定値 (もしくはMAP(maximum a posterior estimator)推定値)と呼びます.
例題
ある新薬を10人の治験者に使用した所, 7人には効果があり3人には効果がなかった. この薬が効く確率 \(\theta\) は全く分からないとして事後分布とベイズ推定値を計算しましょう.
今回得られた結果を \(A\) としましょう. これは二項分布に従うので \[ f(A|\theta) = \binom{10}{7}\theta^7(1-\theta)^3 \] となります. \(\theta\) の値は全く分からないので事前分布は一様分布とします. \[ p(\theta) = 1\qquad (0\leq \theta \leq 1) \] すると, 事後分布は \[ p(\theta|A) \propto \binom{10}{7}\theta^7(1-\theta)^3\times 1 \propto \theta^7(1-\theta)^3 \] となります.
ここで \[ \int_0^1 \theta^7(1-\theta)^3\mathrm{d}\theta = \frac{1}{1320} \] となるので規格化を行って \[ \color{yellow}{ p(\theta|A) = 1320\theta^7(1-\theta)^3} \] が求める事後分布となります.(後述しますが, これはベータ分布 \(Be(8,4)\) という分布です.)
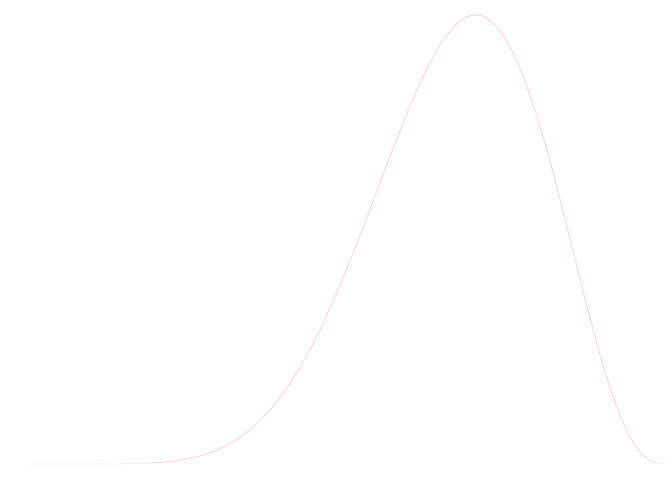
図示してみれば, 以下が \(\theta\) の事前分布です. \(\theta\) の値は全く分からないという様子です.

事後分布は以下のようになります. \(\theta\) の値は0.7付近の値である確率が高いという事になります.
ベイズ推定値は, \[ \frac{\mathrm{d}}{\mathrm{d}\theta}\theta^7(1-\theta)^3 = -\theta^7(\theta-1)^2(10\theta-7) \] より \(\color{yellow}{ \hat{\theta} = 7/10 }\)となります. これは10人中7人に効いたという結果と合致します.
これは当たり前の事で, 事前分布が一様分布ならば \[ p(\theta|X=x) \propto f(X=x|\theta) \] となりますので事後分布は尤度関数に比例します. つまり, 事前分布が一様分布の時はベイズ推定値と最尤推定値は一致します.
ベータ分布
確率密度関数が \[ f(x) = Cx^{m-1}(1-x)^{n-1} \qquad (0\leq x\leq 1,C:\text{規格化定数})\] と表される確率分布をベータ分布と呼び \(Be(m,n)\) と書く.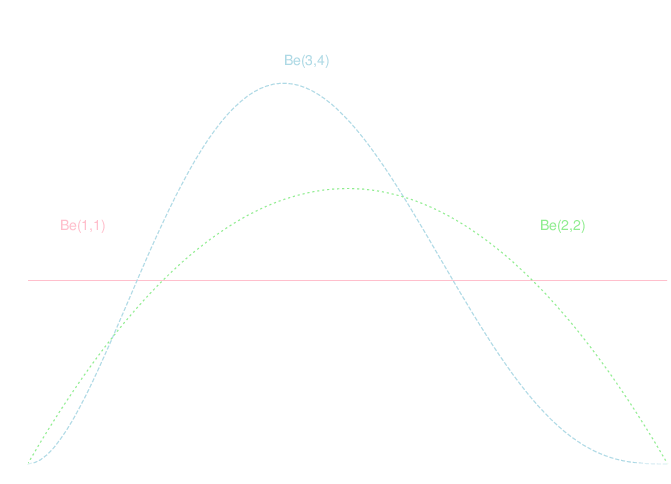
\(Be(m,n)\) の平均・分散は以下の様になります. \[ \text{平均}: \frac{m}{m+n}\quad\text{分散}: \frac{mn}{(m+n)^2(m+n+1)} \] また, 密度関数が最大値を取る点(最頻値)は \[ \frac{m-1}{m+n-2} \] となります. これはベイズ推定値を計算する為に便利です.
また, 標準一様分布はベータ分布 \(Be(1,1)\) と一致します.
最尤推定値とベイズ推定値の違いを見る為に以下の問題を考えましょう.
例題
あるコインを5回投げたら全て表が出た. このコインの表が出る確率 \(p\) を推定しましょう.
例題の事象を \(A\) と書きます. 尤度関数は \[ f(A|p) = p^5 \qquad (0\leq p \leq 1)\] となるので, \(p\) の最尤推定値は \(1\) となります. つまり, 常に表が出るコインであるという事になります.
一方, ベイズ推定では事前分布として私達の常識的な知識を使う事が出来ます. \(p\) の値は \(p=1/2\) の付近にあるはずなので, 事前分布\(\pi(p)\) として \(Be(2,2)\) を仮定しましょう.
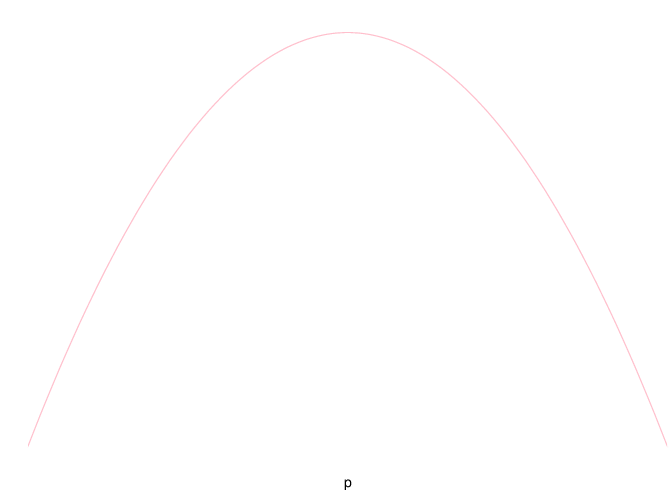
すると, 事後分布 \(\pi(p|A)\) は \[ \pi(p|A)\propto p(1-p)\times p^5 = p^6(1-p) \] より \(B(7,2)\) となるので, \(p\) のベイズ推定量は 6/7 となります.
この例で最尤推定法が上手くいかなかったのは, サンプル数が少なかったからだと言えます. ベイズ推定法ではサンプルの不足を事前知識によって補って意味のある結果を得る事が出来ます.
他の種類の分布の例を見てみましょう.
例題
あるパン屋が新しく売りだしたメロンパンは \(100\mathrm{g}\) の重さらしいです. 過去の調査からこのパン屋が作るパンの重さの分散は 10 である事が分かっています.
試しに 4つのメロンパンを買って調べた所 \(101\mathrm{g},105\mathrm{g},98\mathrm{g},102\mathrm{g}\) でした. メロンパンの重さの母平均 \(\mu\) を推定しましょう.
例題の事象を \(A\) とします. パンの重さは正規分布に従うと仮定すると, 尤度関数は \[\begin{aligned} f(\mu|A) &\propto e^{-\frac{(101-\mu)^2}{20}} e^{-\frac{(105-\mu)^2}{20}} e^{-\frac{(98-\mu)^2}{20}} e^{-\frac{(102-\mu)^2}{20}} \\ &\propto \exp\left\{ -\frac{\mu^2-203\mu}{5}\right\} \end{aligned} \] となります.
\(\mu\) の事前分布 \(p(\mu)\) ですが平均が\(100\)の正規分布としましょう. 分散は大きめに100とします. つまり \[ p(\mu)\propto \exp\left\{-\frac{(\mu-100)^2}{200}\right\} \] となります.
よって, \(\mu\) の事後分布は \[ \begin{aligned} p(\mu|A) &\propto \exp\left\{ -\frac{\mu^2-203\mu}{5}\right\} \exp\left\{-\frac{(\mu-100)^2}{200}\right\} \\ &\propto \exp\left\{-\frac{41\mu^2-8320\mu}{200}\right\} \\ &\propto \exp\left\{-\frac{41(\mu-4160/41)^2}{200}\right\} \end{aligned} \] より 平均 \(4160/41\), 分散 \(100/41\) の正規分布となります. よって \(\mu\) のベイズ推定値は \(4160/41=101.5\) となります.
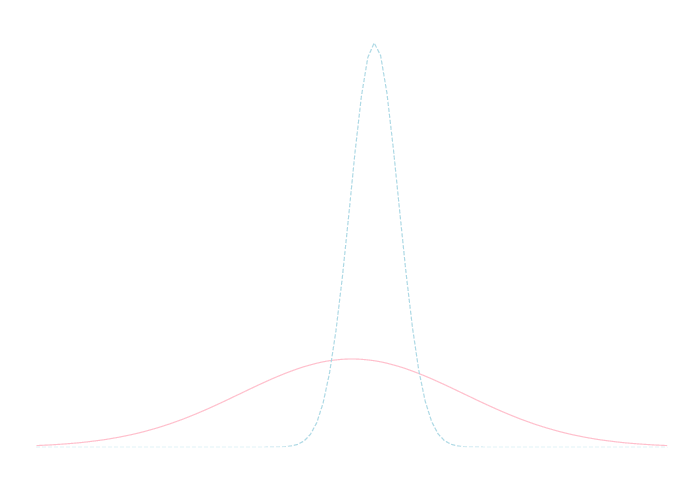
\(\mu\) の事前分布・事後分布は以下の様になります(それぞれピンクと青). 調査によって分散が減少し \(\mu\) の値の不確実性が減少した事がわかります.
自然な共役分布
事前分布の取り方によっては事後分布は非常に複雑になってしまいます. すると積分や最大値の計算が面倒になります.
事前分布と事後分布の種類が一致する 様に分布を選べばこの問題を回避する事が出来ます. そのような条件を満たす分布を(母集団に対する) 自然な共役分布 と呼びます.
これまでの例題で利用したのが
\[ \begin{array}{|c|c|c|} \hline \text{母集団の分布} & \text{事前分布} & \text{事後分布} \\ \hline \text{ベルヌーイ分布・二項分布} & \text{ベータ分布} & \text{ベータ分布} \\ \hline \text{正規分布} & \text{正規分布} & \text{正規分布} \\ \hline \end{array} \]という関係で, 他には
\[ \begin{array}{|c|c|c|} \hline \text{母集団の分布} & \text{事前分布} & \text{事後分布} \\ \hline \text{ポアソン分布} & \text{ガンマ分布} & \text{ガンマ分布} \\ \hline \text{正規分布} & \text{逆ガンマ分布} & \text{逆ガンマ分布} \\ \hline \end{array} \]などがあります. 逆ガンマ分布は母分散の推定に使います. 詳しくは省略します.
公式化してしまいましょう. 証明は練習問題とします.
ベイズ改訂の公式:ベータ分布
母集団分布が試行回数 \(n\), パラメータ \(p\) のベルヌーイ分布もしくは二項分布であるとする. 試行の成功回数が \(r\) であるとき, 事前分布に \(Be(p,q)\) を仮定してベイズ改訂を行うと事後分布は \[ Be(p+r, q+n-r) \] となる.
ベイズ改訂の公式:正規分布
\(N(\mu,\sigma^2)\)に従う独立な確率変数の実現値\(x_1,x_2,\ldots,x_n\)を用いて, 事前分布を \(N(\mu_0,\sigma_0^2)\) としてベイズ改訂を行うと事後分布は \[ N\left(\frac{\sum x_i/\sigma^2+\mu_0/\sigma_0^2}{n/\sigma^2+1/\sigma_0^2}, \frac{1}{n/\sigma^2+1/\sigma_0^2} \right) \] となる.
自然な共役分布ではなく, 他の種類の確率分布を利用したい場合もあるかもしれません. この場合, 解析的に事後分布を計算する事は難しいので数値計算が必要になります.
詳しくは省略しますが, マルコフ連鎖モンテカルロ法(MCMC法) という手法が近似計算に利用されます.
ベイズ線型回帰
線形回帰の問題に事前分布の考え方を導入する事を考えます.
\[ y = a_1g_1(\mathbf{x})+\cdots + a_mg_m(\mathbf{x}) \] という回帰方程式で重回帰を行う事を考えます. 誤差分布の分散を\(\sigma^2\) とします. データセット \((\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots,(\mathbf{x}_n,y_n)\) に対して行列 \(G\), ベクトル \(\mathbf{y}\) を前回設定したようにおきます. また, \(\mathbf{a}\) を係数のベクトルとします.
まず, このデータセット\(D\)に対する尤度は \[ f(D|\mathbf{a}) \propto \exp\left\{-\frac{1}{2\sigma^2}(\mathbf{y}-G\mathbf{a})^T(\mathbf{y}-G\mathbf{a})\right\} \]
また, 事前分布として \(\mathbf{a}\) が多変量正規分布 \(N(\mathbf{\mu}_0,\Sigma_0)\) に従う事を仮定します. すなわち, \[ p(\mathbf{a})\propto \exp\left\{-\frac{1}{2}(\mathbf{a}-\mathbf{\mu}_0)^T\Sigma_0^{-1}(\mathbf{a}-\mathbf{\mu}_0) \right\} \] とします.
すると, 事後分布は \[ p(\mathbf{a}|D) \propto \exp\left\{-\frac{1}{2}\left(\frac{1}{\sigma^2}(\mathbf{y}-G\mathbf{a})^T(\mathbf{y}-G\mathbf{a})+(\mathbf{a}-\mathbf{\mu}_0)^T\Sigma_0^{-1}(\mathbf{a}-\mathbf{\mu}_0)\right) \right\} \] となります. これを整理すると 事後分布は多変量正規分布 \(N(\mathbf{\mu},\Sigma)\) に従う事が判ります. 従って \(\mathbf{\mu}\) が \(\mathbf{a}\) のベイズ推定値となります. 但し \[ \color{yellow}{ \Sigma^{-1} = \frac{1}{\sigma^2}G^TG + \Sigma_0^{-1}, \mathbf{\mu} = \Sigma\left(\frac{1}{\sigma^2}G^T\mathbf{y}+\Sigma_0^{-1}\mathbf{\mu}_0\right) } \] です.
【証明】
分散共分散行列が対称行列 (\(\Sigma^T=\Sigma\)) である事に注意すると
\[ \begin{aligned}
&(\mathbf{a}-\mathbf{\mu})^T\Sigma^{-1}(\mathbf{a}-\mathbf{\mu}) \\
= &\mathbf{a}^T\Sigma^{-1}\mathbf{a} -2\mathbf{a}^T\Sigma^{-1}\mathbf{\mu}+(\text{定数})\\
= &\mathbf{a}^T\left(\frac{1}{\sigma^2}G^TG+\Sigma_0^{-1}\right)\mathbf{a} - 2\mathbf{a}^T\left(\frac{1}{\sigma^2}G^T\mathbf{y}+\Sigma_0^{-1}\mathbf{\mu}_0\right) + (\text{定数}) \\
=& \frac{1}{\sigma^2}(\mathbf{a}^TG^TG\mathbf{a}-2\mathbf{a}^TG^T\mathbf{y})+(\mathbf{a}^T\Sigma_0^{-1}\mathbf{a}-2\mathbf{a}^T\Sigma_0^{-1}\mathbf{\mu}_0)+(\text{定数}) \\
=& \frac{1}{\sigma^2}(\mathbf{y}-G\mathbf{a})^T(\mathbf{y}-G\mathbf{a}) + (\mathbf{a}-\mathbf{\mu}_0)^T\Sigma_0^{-1}(\mathbf{a}-\mathbf{\mu}_0) + (\text{定数})
\end{aligned} \]
となるから. □
先ほどの式から \(\Sigma\) を消去するとベイズ線型回帰の正規方程式 \[ G^TG\mathbf{\mu}-G^T\mathbf{y}+\sigma^2\Sigma_0^{-1}(\mathbf{\mu}-\mathbf{\mu}_0) = 0 \] が得られます.
もしパラメータ \(\mathbf{a}\) について一切の情報がないならば, 分散が無限大となって(\(\Sigma_0^{-1}=0\) となるから)最小二乗法の正規方程式 \[ G^TG\mathbf{\mu}-G^T\mathbf{y}=0 \] と一致する事が判ります.
例題
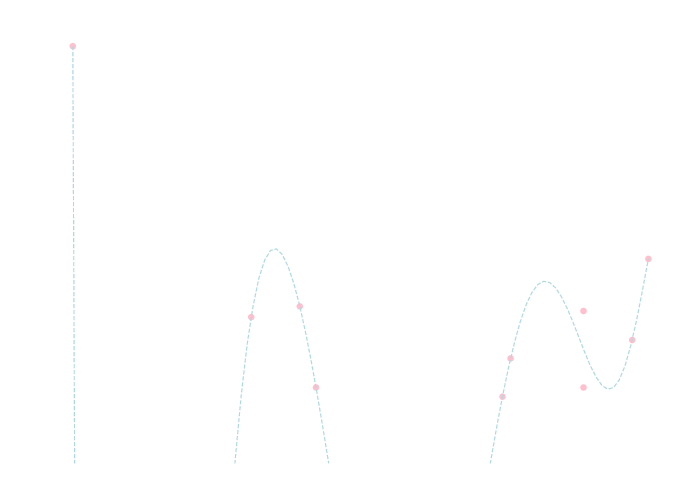
以下のデータセットに対して \(9\)次方程式を当てはめてみましょう. \[ \begin{array}{|c|cccccccccc|} \hline X & -1.2&1.9&-3.4&-0.4&2.9&2.9&3.5&-0.6&2.0&3.7 \\ \hline Y & 4.6& -0.6&22.3&-0.0&-0.0&5.0&3.1&5.3&1.9&8.4 \\ \hline \end{array} \]
単純な最小二乗法では \[\small{ y=-0.01x^9+0.05x^8+0.11x^7-0.39x^6-1.0x^5-2.7x^4+16x^3+7.8x^2-32x-11 } \] となり以下の様にノイズを忠実に拾った回帰方程式となってしまうのでした.
ベイズ線型回帰でやってみます. ここで次数の高い項の係数ほど \(0\) に近いはずという事を事前分布として導入してみましょう.
そこで, \(x^k\) の係数は \(N(0, 10^{-k})\) に従うと仮定します. つまり, \[ \mathbf{\mu}_0 = \mathbf{0}, \Sigma_0 = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 10^{-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & 10^{-9} \end{pmatrix} \] とおきましょう. つまり \[ \Sigma_0^{-1} = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 10 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & 10^9 \end{pmatrix} \] となります. 誤差分布の分散の \(\sigma^2\) の値は分かりませんので適当な値を仮定します.
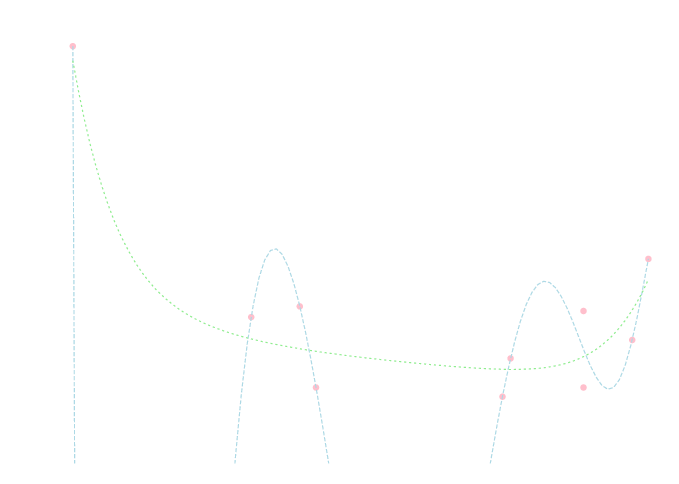
正規方程式を解くと \[\begin{aligned} &\small{ y=-2.3\cdot 10^{-5}x^9+2.4\cdot 10^{-4}x^8 -3.2\cdot 10^{-4}x^7 + 1.9\cdot 10^{-3}x^6}\\ &\quad\small{ - 3.5\cdot 10^{-3}x^5 + 1.5\cdot 10^{-2}x^4 -3.9\cdot 10^{-2}x^3 +0.13x^2 -0.67x + 2.1} \end{aligned} \] となり以下のグラフ(緑の線)のようになります. 高次の急激な変動を除去する事ができている事がわかります.
以上でベイズ統計の基本の説明を終わります.
事前分布を主観的に定めてしまうという考え方は慣れるまでは(慣れても?)奇妙に感じるかもしれませんが, データ数が少ない場合の統計的解析には大変強力です. 是非, 復習を行って下さい.
以上でプログラマの為の数学勉強会を終わります.
全18回お付き合いいただきありがとうございました. 非常に初歩的な所から始めましたが, 結構実用的なレベルの所まで解説する事が出来たと思います.
今後ですが, せっかく統計まで講義を行いましたので最近はやりのパターン認識・機械学習の勉強会を開催したいと思います. そちらではこの勉強会で解説した程度の基礎的な数学知識は前提とし, 積極的に難しいテーマにも取り組んでいこうと思います. 是非お越しください.