プログラマの為の
数学勉強会
第16回
(於)ワークスアプリケーションズ中村晃一
2014年1月16日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
適合度検定・独立性検定
前回は, 母集団分布の形が既知の場合に母平均や母分散の値, それらに差があるかといった事を検定する方法を紹介しました. これらは母数というパラメータを考えるので パラメトリック 手法と呼ばれます.
今回紹介するのは ノンパラメトリック 手法と呼ばれる, 母集団分布の形を仮定しない検定法のうち度数分布に適用出来る手法を紹介します.
検定の基本的な流れは同じです. 復習すると以下のように行うのでした.
- 帰無仮説\(H_0\)と対立仮説\(H_1\)を立てる.
- 有意水準 \(\alpha\) を決める.
- 検定に用いる統計量を定めて, \(H_0,H_1\) に基き棄却域を計算する.
- 実現値(実際に得られたデータ)に基いて, \(H_0\) を棄却するか否かを決める.
\(\chi^2\) 適合度検定
度数分布 , つまり~が \(x\) 回生じたという形の確率分布に対しては \(\chi^2\) 適合度検定を利用する事が出来ます.
定理
ある度数分布に従う確率変数のカテゴリ毎の観測値が \(x_1,x_2,\ldots,x_m\) 回, 理論値が \(e_1,e_2,\ldots,e_m\) である場合
\[ \chi^2 = \frac{(x_1 - e_1)^2}{e_1} + \frac{(x_2-e_2)^2}{e_2} + \cdots + \frac{(x_m-e_m)^2}{e_m} \] は近似的に自由度 \(m-1\) の \(\chi^2\) 分布に従う.\(\chi^2\) の値が大きいほど理論値から外れているという事になりますので, この定理に基いて\(\chi^2\)分布を利用した片側検定を行えば良いです.
例題
サイコロを600回投げた所, それぞれの出目の回数が以下のようになりました. このサイコロは一様分布に従っていると言えるでしょうか? \[ \begin{array}{|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 112\text{回} & 85\text{回} & 120\text{回} & 101\text{回} & 89\text{回} & 93\text{回} \\ \hline \end{array} \]
帰無仮説・対立仮説を \[ \begin{aligned} H_0&: \text{分布は一様である.} \\ H_1&: \text{分布は一様ではない.} \end{aligned} \] と仮定します.
仮説 \(H_0\) の元では, 各目は確率 \(1/6\) なので \[ \begin{aligned} \chi^2 &= \frac{(112 - 100)^2}{100} + \frac{(85-100)^2}{100} + \frac{(120-100)^2}{100} + \frac{(101-100)^2}{100} \\ & + \frac{(89-100)^2}{100} + \frac{(93-100)^2}{100} = 9.4 \end{aligned} \] となります.
ここで, 自由度 \(5\) の \(\chi^2\) 分布の上側 5% 点を求めると
>>> from scipy import stats
>>> stats.chi2.ppf(0.95, 5)
11.070497693516351
となるので, \(H_0\) を棄却する事は出来ません.
練習問題
あるWebサービスへの1秒あたりのアクセス回数の測定を1000回行いました. これはポアソン分布 \(Po(5)\) に従っていると言えるでしょうか? \[ \tiny{ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{0回} & \text{1回} & \text{2回} & \text{3回} & \text{4回} & \text{5回} & \text{6回} & \text{7回} & \text{8回} & \text{9回} & \text{10回} & \text{11回} \\ \hline 5 & 31 & 72 & 135 & 183 & 173 & 162 & 89 & 79 & 41 & 18 & 12 \\ \hline \end{array}} \]帰無仮説 \(H_0\) を母集団分布が \(Po(5)\) である事とします. 1秒間のアクセス回数が \(k\) 回である確率は \(5^k e^{-5}/k!\) であるので理論値は \[ \tiny{ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{0回} & \text{1回} & \text{2回} & \text{3回} & \text{4回} & \text{5回} & \text{6回} & \text{7回} & \text{8回} & \text{9回} & \text{10回} & \text{11回} & \text{12回} & \text{13回} & \text{14回} & \cdots \\ \hline 6.7 & 33.7 & 84.2 & 140.4 & 175.5 & 175.5 & 146.2 & 104.4 & 65.3 & 36.3 & 18.1 & 8.2 & 3.4 & 1.3 & 0 & \cdots\\ \hline \end{array}} \] となります. これから \(\chi^2 = 17.0\) となります. 自由度 \(13\) の\(\chi^2\) 分布の上側 5% 点は \(22.4\) なので, \(H_0\) を棄却する事は出来ません.
独立性検定
適合度検定を応用して 独立性検定 を行う事が出来ます.
定理
2つの独立な度数分布に従う確率変数 \(X(\text{カテゴリ数 $m$})\),\(Y(\text{カテゴリ数 $n$})\) について \[ \chi^2 = \sum \frac{(\text{観測値}-\text{理論値})^2}{\text{理論値}} \]
は近似的に自由度 \((m-1)\times(n-1)\) の \(\chi^2\) 分布に従う.例題
新薬の効果を見るために新薬と古い薬を適当な人数ずつ処方したところ, 以下の結果となった. 新薬に効果はあったと言えるか?
\[ \begin{array}{|c|cc|c|} \hline & 効果あり & 効果なし & \text{計} \\ \hline \text{新しい薬} & 79 & 41 & 120 \\ \text{古い薬} & 43 & 37 & 80 \\ \hline \text{計} & 122 & 78 & 200 \\ \hline \end{array} \]新薬でも古い薬でも効果が変わらないならば, \((\text{効果あり}):(\text{効果なし})\) の比率は一定です. そこで, \((\text{効果あり}):(\text{効果なし}) = 122:78 = 61:39\) であると仮定するならば, 理論値は \[ \begin{array}{|c|cc|c|} \hline & 効果あり & 効果なし & \text{計} \\ \hline \text{新しい薬} & 73.2 & 46.8 & 120 \\ \text{古い薬} & 48.8 & 31.2 & 80 \\ \hline \text{計} & 122 & 78 & 200 \\ \hline \end{array} \] となるはずです. よって \[ \chi^2 = \frac{(79-73.2)^2}{73.2}+\frac{(41-46.8)^2}{46.8}+\frac{(43-48.8)^2}{48.8}+\frac{(37-31.2)^2}{31.2} = 2.9 \] となります. よって自由度 \((2-1)\times(2-1)=1\) の \(\chi^2\) 分布の上側 5% 点は \(3.8\) であるので, 新薬に効果があったとは言えません.
回帰分析
ある結果が幾つかの要因からどのように説明されるかを推定する手法を 回帰分析 といいます. 例えば以下の様な問題を考えます.
数学的には, 確率変数 \(Y\) と確率変数 \(X_1,X_2,\ldots,X_n\) について \[ Y=f(X_1,X_2,\ldots,X_n) \] を満たすような \(f\) を推定する事となります. この \(f\) を \(Y\) の モデル と呼びます.
最小二乗法(1変数)
観測値 \(Y\) と理論値 \(f(X)\) の誤差 \(Y-f(X)\) が正規分布に従うと仮定して最尤推定で \(f(X)\) を決定する手法を 最小二乗法 と呼びます.
誤差 \(E=Y-f(X)\) が正規分布 \( N(0,\sigma^2) \) に従うと仮定します. すると, \(X=x_i\) と値が確定した場合 \(Y\) は \(N(f(x_i),\sigma^2)\) に従います. よって, データ列 \((x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\) が得られたならば, 尤度関数は \[ \begin{aligned} L(f) &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(y_i-f(x_i))^2}{2\sigma^2}\right) \\ &\propto \exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-f(x_i))^2\right) \end{aligned} \] となります. よって \(L(f)\) が最大になるのは 残差平方和 \[ \sum_{i=1}^n(y_i-f(x_i))^2 \] が最小となる場合となります.
最小二乗法(1変数・母分散が一定)
誤差の母分散が一定の場合, データ列 \((x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\) に対して残差平方和 \[ \sum_{i=1}^n\left\{ y_i-f(x_i) \right\}^2 \] を最小とする \(f\) としてモデルを決定する.
最小二乗法:一次関数の場合
モデルが \(y=ax+b\) という形の場合, データ列 \((x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\) に対して残差平方和を最小とする\(a,b\) は \[ a = \frac{n\sum x_iy_i - \sum x_i \sum y_i}{n\sum x_i^2 - \left( \sum x_i\right)^2}, b = \frac{\sum x_i^2 \sum y_i - \sum x_iy_i \sum x_i}{n\sum x_i^2 - \left( \sum x_i \right)^2} \] である.
【証明】
\[ E=\sum_{i=1}^n(y_i-ax_i-b)^2 \]
を \(a,b\) で偏微分すれば
\[ \begin{aligned}
\frac{\partial E}{\partial a} &= -\sum 2x_i(y_i-ax_i-b)=2(\sum x_i^2)a+2(\sum x_i) b - 2\sum x_iy_i \\
\frac{\partial E}{\partial b} &= -\sum 2(y_i-ax_i-b) = 2(\sum x_i)a + 2nb - 2\sum y_i
\end{aligned} \]
となるので, \(E\) が最小となるのは
\[ \begin{aligned}
&\frac{\partial E}{\partial a}=\frac{\partial E}{\partial b} = 0 \\
\Leftrightarrow &
a = \frac{n\sum x_iy_i - \sum x_i \sum y_i}{n\sum x_i^2 - \left( \sum x_i\right)^2}, b = \frac{\sum x_i^2 \sum y_i - \sum x_iy_i \sum x_i}{n\sum x_i^2 - \left( \sum x_i \right)^2}
\end{aligned} \]
の時である. □
練習問題
以下のデータ列に対して \(y=ax+b\) というモデルを仮定して, 最小二乗法によって \(a,b\) を決定して下さい.
\[ \small{\begin{array}{|c|cccccccccc|} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline y & 1.6 & 2.9 & 7.8 & 11.2 & 11.7 & 14.2 & 16.0 & 20.0 & 17.7 & 18.9 \\ \hline \end{array}} \]
(答え) \( a=2.0, b=3.0 \)
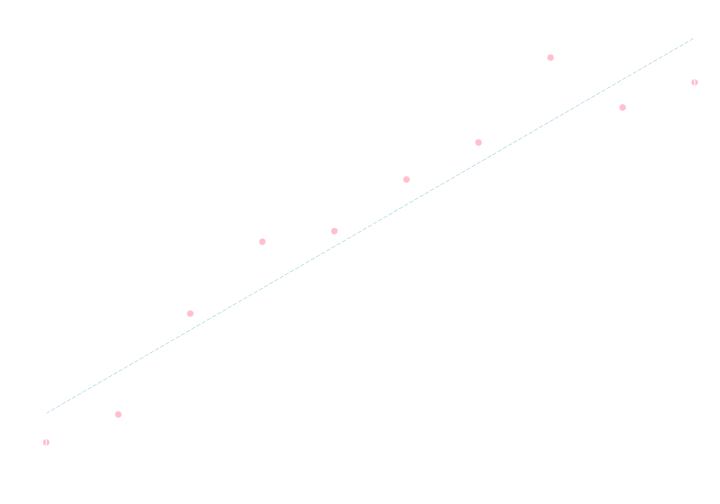
最小二乗法(1変数・母分散が既知)
データ列 \((x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\) に対して, \(i\) 番目のデータの誤差の母分散が \(\sigma_i^2\) であるならば, 残差平方和 \[ \sum_{i=1}^n\frac{\left\{ y_i-f(x_i) \right\}^2}{\sigma_i^2} \] を最小とする \(f\) としてモデルを決定する.
【練習問題】\(y=ax+b\) というモデルの場合に \(a,b\) の値を得る公式を求めて下さい.
数値計算の手法を利用すれば, 一次式でない場合にも最小二乗法を適用する事が可能です.
練習問題
以下のデータ列に対して \(y=\sin ax \) というモデルを仮定して, 最小二乗法によって \(a\) を決定して下さい.
\[ \small{\begin{array}{|c|cccccccccc|} \hline x & 0.0 & 0.5 & 1.0 & 1.8 & 2.1 & 2.6 & 3.1 & 3.7 & 4.2 & 4.7 \\ \hline y & 0.0 & 0.2 & 0.5 & 0.7 & 0.9 & 1.1 & 1.1 & 1.1 & 0.9 & 0.6 \\ \hline \end{array}} \]
第4回にやったニュートン法を復習しておきます.
ニュートン法
方程式\(f(x)=0\)の解を\(\alpha\)とする。
\(x=\alpha\)を含む適当な区間で\(f'(x)\neq 0\),\(f(x),f'(x),f''(x)\)が連続ならば,この区間内に初期値\(x_0\)を取れば数列 \[ x_{n+1} = x_{n} - \frac{f(x_n)}{f'(x_{n})} \] が\(\alpha\)に収束する。
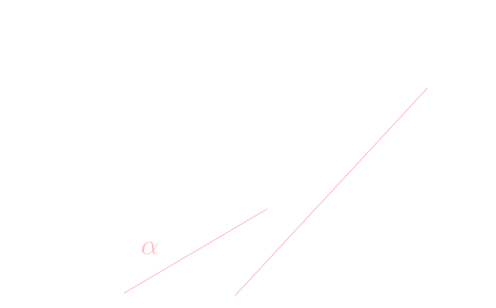
\[ E = \sum (y_i-\sin ax_i)^2 \] を \(a\) について微分すれば \[ \frac{\mathrm{d} E}{\mathrm{d} a} = -2\sum x_i\cos ax_i (y_i-\sin ax_i) = -2 \sum x_iy_i\cos ax_i+\sum x_i\sin 2ax_i \] となるので, 方程式 \[ \sum x_i \sin 2ax_i - 2\sum x_iy_i\cos ax_i = 0\] を解けば良いです. この左辺を \(f(a)\) とおくと \[ f'(a) = \sum 2x_i^2\cos 2ax_i + 2\sum x_i^2y_i\sin ax_i \] となるので, ニュートン法 \[ a_{k+1} = a_k - \frac{f(a_k)}{f'(a_k)}=a_k - \frac{\sum x_i \sin 2a_kx_i - 2\sum x_iy_i\cos a_kx_i}{\sum 2x_i^2\cos 2a_kx_i + 2\sum x_i^2y_i\sin a_kx_i} \] を利用する事が出来ます. 初期値はグラフを見て \(a_0 = 0.4\)くらいにすれば良いでしょう.
以下がコーディング例です.
import numpy as np
x = np.array([0.0, 0.5, 1.0, 1.8, 2.1, 2.6, 3.1, 3.7, 4.2, 4.7])
y = np.array([0.0, 0.2, 0.5, 0.7, 0.9, 1.1, 1.1, 1.1, 0.9, 0.6])
a = 0.4
while True:
next_a = a - (np.sum( x*np.sin(2*a*x) ) - 2 * np.sum( x*y*np.cos(a*x) )) / (np.sum( 2*x*x*np.cos(2*a*x) ) + 2 * np.sum( x*x*y*np.sin(a*x) ))
if abs((next_a-a)/a) < 1.0e-6:
break
a = next_a
print a
計算結果は \(a=0.5\) となります.
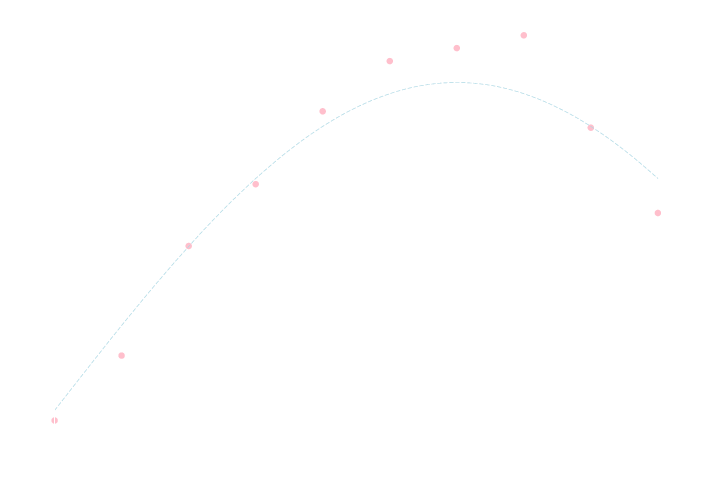
練習問題
以下のデータ列に対して \(y=\sin ax \) というモデルを仮定して, 最小二乗法によって \(a\) を決定して下さい.
\[ \small{\begin{array}{|c|cccccccccc|} \hline x & 0.0 & 0.5 & 1.0 & 1.8 & 2.1 & 2.6 & 3.1 & 3.7 & 4.2 & 4.7 \\ \hline y & 0.0 & 0.2 & 0.5 & 0.7 & 0.9 & 1.1 & 1.1 & 1.1 & 0.9 & 0.6 \\ \hline \end{array}} \]
最小二乗法(線型回帰・母分散が一定)
モデル \(y=f(x)\) が既知の関数 \(g_1(x),g_2(x),\ldots,g_m(x)\)とパラメータ \(a_1,a_2,\ldots,a_m\) によって \[ f(x)=a_1g_1(x) + a_2g_2(x) + \cdots + a_mg_m(x) \] と表される場合, \[\begin{aligned} G&=(g_j(x_i))_{1\leq i \leq n,1\leq j\leq m}\\ \mathbf{a}&=(a_1,a_2,\ldots,a_m)^T\\ \mathbf{y}&=(y_1,y_2,\ldots,y_n)^T \end{aligned} \] とおけば 正規方程式 \[ \color{yellow}{ G^TG\mathbf{a}=G^T\mathbf{y} } \] の解が最小二乗法による \(a_1,a_2,\ldots,a_m\) の推定値を与える.
例えば, \[ f(x)=a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0 \] であるとか, \[ f(x) = a_n\sin nx + a_{n-1}\sin (n-1)x + \cdots + a_1\sin x + a_0 \] などの形のモデルであれば今の方法を使う事が出来ます. \[ f(x)= e^{ax} \] の様に, 関数の中にパラメータが入っている場合には使えないので数値解法を利用したり, モデルの法を近似するなどの工夫を行って下さい.
証明の前に第8回にやったベクトルでの微分法を復習しておきます.
ベクトルでの微分法
多変数スカラー値関数\(f,g\),定数\(k,l\)に関して \[ \frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}(kf+lg) = k\frac{\mathrm{d}f}{\mathrm{d}\mathbf{x}} + l\frac{\mathrm{d}g}{\mathrm{d}\mathbf{x}} \] また\(c\)を定数,\(\mathbf{a}\)を定ベクトル,\(A\)を正方行列とすると \[ \begin{aligned} &\frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}c = \mathbf{0} \\ &\frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}\mathbf{a}^T\mathbf{x} = \frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}\mathbf{x}^T\mathbf{a} = \mathbf{a} \\ &\frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}||\mathbf{x}||^2 = 2\mathbf{x} \\ &\frac{\mathrm{d}}{\mathrm{d}\mathbf{x}}\mathbf{x}^TA\mathbf{x} = (A+A^T)\mathbf{x} \end{aligned} \] が成り立つ。
【証明】
残差平方和
\[ E=\sum(y_i-a_1g_1(x_i)-a_2g_2(x_i)-\cdots-a_mg_m(x_i))^2 \]
はベクトル \(\mathbf{y}-G\mathbf{a}\) のノルムの二乗であるから
\[ \begin{aligned}
E&=(G\mathbf{a}-\mathbf{y})^T(G\mathbf{a}-\mathbf{y}) = (\mathbf{a}^TG^T-\mathbf{y}^T)(G\mathbf{a}-\mathbf{y}) \\
&= \mathbf{a}^TG^TG\mathbf{a}-\mathbf{a}^TG^T\mathbf{y}-\mathbf{y}^TG\mathbf{a}+\mathbf{y}^T\mathbf{y}
\end{aligned} \]
となるので,
\[ \frac{\mathrm{d} E}{\mathrm{d} \mathbf{a}} = (G^TG+(G^TG)^T)\mathbf{a}-2G^T\mathbf{y} = 2(G^TG\mathbf{a}-G^T\mathbf{y}) \]
である. よって \(E\) が最小値を取る点で
\[ G^TG\mathbf{a} = G^T\mathbf{y} \]
が成立する. □
練習問題
以下のデータに対して \(y=ax^2+bx+c\) というモデルを最小二乗法によって当てはめて下さい.
#x y
0.0 3.7
0.5 1.2
1.0 -3.2
1.5 -1.0
2.0 -4.1
2.5 -3.3
3.0 -3.5
3.5 -2.4
4.0 -1.8
4.5 1.7
5.0 2.7
5.5 5.5
6.0 8.5
6.5 11.4
7.0 17.1
7.5 22.4
8.0 26.4
8.5 33.2
9.0 39.2
9.5 46.2
モデルが \(y=ax^2+bx+c\) という形なので, \[ g_1(x) = x^2, g_2(x) = x, g_3(x) = 1 \] とおきます. すると \[ G = \begin{pmatrix} x_1^2 & x_1 & 1 \\ x_2^2 & x_2 & 1 \\ \vdots & \vdots & \vdots \\ x_n^2 & x_n & 1 \end{pmatrix}, \mathbf{a} = \begin{pmatrix} a \\ b \\ c \end{pmatrix}, \mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} \] となります. これに基いて正規方程式を導出し, それを解きます.
以下がコーディング例です.
import numpy as np
from scipy import linalg as LA
N = 20
x = np.array([0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5])
y = np.array([3.7, 1.2, -3.2, -1.0, -4.1, -3.3, -3.5, -2.4, -1.8, 1.7, 2.7, 5.5, 8.5, 11.4, 17.1, 22.4, 26.4, 33.2, 39.2, 46.2])
G = np.array([x*x, x, np.ones(N)]).T
print LA.solve(G.T.dot(G), G.T.dot(y))
結果は \[ a= 1.0, b= -5.2, c=3.1 \] となります.
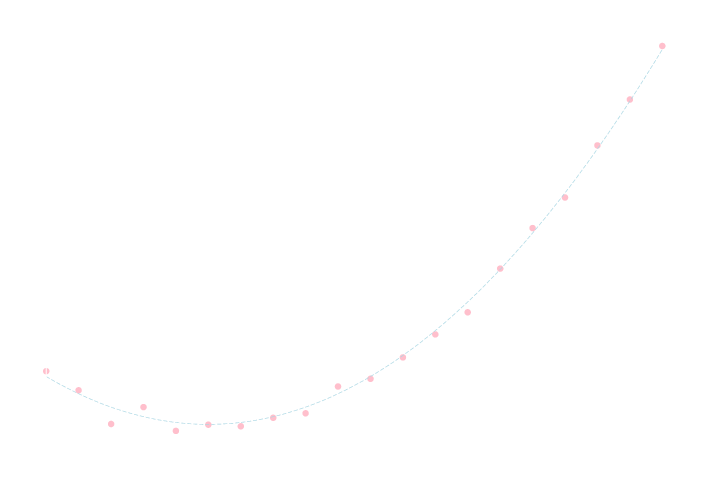
測定誤差の母分散が一定ではないが既知という場合にも, 一変数の場合と同様に解くことが出来ます. 方程式を導出してみてください.
今回はここで終わります。
次回も回帰分析の続きを行います. モデルの当てはまりの良さを判定や, 多変量回帰分析の計算法, 過学習といった問題の紹介を行います.