プログラマの為の
数学勉強会
第15回

(於)ワークスアプリケーションズ
中村晃一
2013年12月19日

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。

この資料について

http://nineties.github.com/math-seminar に置いてあります。
SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
サンプルプログラムはPython及びMaximaで記述しています。

検定

母集団が確率分布 $D$ に従っているか否かを判断したいとします.

その為には, 標本 $X_1,X_2,\ldots,X_n$ を無作為に抽出して \[ X_1,X_2,\ldots,X_n \sim D \] であるという仮説の元で実際のデータ $x_1,x_2,\ldots,x_n$ が得られる確率を考え, 仮説の妥当性を検定します.

母数による仮説検定

母集団の従う分布の種類が既知であり, 母数に対する仮説検定を行う場合を考えます.

帰無仮説と対立仮説

統計的に示したい仮説を対立仮説とか実験仮説などと言い, $H_1$ と書きます. 対立仮説を否定する仮説を帰無仮説と呼び, $H_0$ と書きます.

例

ある会社$X$は$X$社の製品が$Y$社の製品より高性能であると主張しています. この主張を統計的に示したいのならば, \[ \begin{aligned} \text{帰無仮説}H_0&: \text{$X$社の製品は$Y$社の製品と同性能} \\ \text{対立仮説}H_1&: \text{$X$社の製品は$Y$社の製品より高性能} \\ \end{aligned} \] といった仮説を立てて, $H_0$を否定する事を目指します.

有意水準

帰無仮説$H_0$を否定する為には, 仮説$H_0$の元ではめったに起こらない事が起きたという事を示せば良いです.

そこで, 適当な定数 $\alpha$ を定めて, $H_0$ のもとで \[ P(\text{実際に生じた事象}) \leq \alpha \] となった時に, $H_0$ を棄却することにします. この $\alpha$ を 有意水準 と呼び, $H_0$ が棄却された時, 検定の結果は有意であると言います. また, 棄却される事象の範囲を棄却域と言います.

$\alpha$の値としては, $0.05$や$0.01$などがよく利用されます.

検定のやり方をまとめておくと, 以下のようになります.

帰無仮説$H_0$と対立仮説$H_1$を立てる.
有意水準 $\alpha$ を決める.
検定に用いる統計量を定めて, $H_0,H_1$ に基き棄却域を計算する.
実現値(実際に得られたデータ)に基いて, $H_0$ を棄却するか否かを決める.

細かい話をする前に, 簡単な例を１つみてみましょう.

例

コインを100回投げた所, 63回表が出たとします. このコインは表が出やすいと言えるでしょうか？有意水準 5% で検定しましょう.

コインの出る確率を $p$ として帰無仮説・対立仮説を \[ \begin{aligned} H_0&: p = \frac{1}{2} \\ H_1&: p > \frac{1}{2} \end{aligned} \] と設定します. 有意水準は $\alpha=0.05$ です.
検定に用いる統計量には, 標本平均(表の出る頻度) $\overline{X}$ を使うことにします.

$H_0$ の元では, $\overline{X}$は(中心極限定理によって)正規分布 \[ N\left(p,\frac{p(1-p)}{n}\right) = N\left(\frac{1}{2}, \frac{1}{400}\right) \] に従います.

$H_0$が棄却されるのは$p=1/2$ よりも上側に大きく外れる場合ですから, 棄却域は$N(0,1)$ の上側$\alpha$ 点を$z_\alpha$ として \[ \overline{X} \geq \frac{1}{2} + \sqrt{\frac{1}{400}}z_\alpha = 0.58 \] となります. 先ほどの実験結果では $\overline{X}=0.63$ なので, この実験結果に基づけば $H_0$ は棄却され, 例題のコインは表が出やすいものだ結論する事が出来ます.

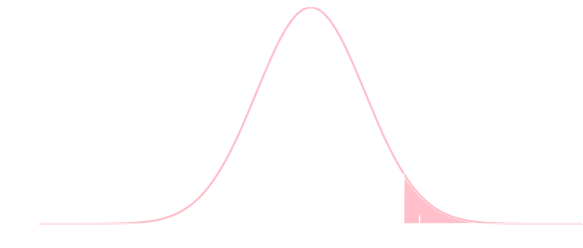
今の例題の様に,対立仮説が \[ \theta > \theta_0\text{とか}\theta_0 < \theta_0 \] の場合には一般に棄却域が下図のようになります. このような検定を片側検定と言います. 棄却域が左右のどちらに来るかを区別して左側検定・右側検定と言う事もあります.

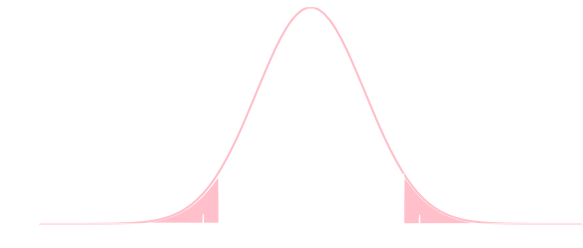
一方,対立仮説が \[ \theta \neq \theta_0 \] のような場合には両側検定と言います.

注意

帰無仮説$H_0$が棄却できなかった場合, $H_0$ が正しいという結論にはならないので注意してください. 「$H_0$が誤っているとは言えない」という事と, 「$H_0$ が正しい」という事は異なります.

意味のある結論を導く為には, 帰無仮説は基本的に棄却される必要があります.

仮説検定の雰囲気はわかったと思うので, 定理をいくつか紹介します.

母分散が既知の正規分布(両側検定)

独立な標本 $X_1,X_2,\ldots,X_n$ が $N(\mu,\sigma^2)$ に従い, $\sigma^2$ が既知であるとする.
$\mu$ に関する仮説 \[ \begin{aligned} H_0&: \mu = \mu_0 \\ H_1&: \mu \neq \mu _0 \end{aligned} \] を標本平均 $\overline{X}$ で検定するときの棄却域は \[ \overline{X} \leq \mu_0 - \frac{\sigma}{\sqrt{n}}z_\alpha, \mu_0 + \frac{\sigma}{\sqrt{n}}z_\alpha \leq \overline{X} \] である. 但し $z_\alpha$ は$N(0,1)$の両側$\alpha$点.

母分散が既知の正規分布(右側検定)

独立な標本 $X_1,X_2,\ldots,X_n$ が $N(\mu,\sigma^2)$ に従い, $\sigma^2$ が既知であるとする.
$\mu$ に関する仮説 \[ \begin{aligned} H_0&: \mu = \mu_0 \\ H_1&: \mu > \mu _0 \end{aligned} \] を標本平均 $\overline{X}$ で検定するときの棄却域は \[ \mu_0 + \frac{\sigma}{\sqrt{n}}z_\alpha \leq \overline{X} \] である. 但し $z_\alpha$ は$N(0,1)$の上側$\alpha$点.

母分散が未知の正規分布(両側検定)

独立な標本 $X_1,X_2,\ldots,X_n$ が $N(\mu,\sigma^2)$ に従い, $\sigma^2$ が未知であるとする.
$\mu$ に関する仮説 \[ \begin{aligned} H_0&: \mu = \mu_0 \\ H_1&: \mu \neq \mu _0 \end{aligned} \] を標本平均 $\overline{X}$ で検定するときの棄却域は \[ \overline{X} \leq \mu_0 - \frac{S}{\sqrt{n}}t_\alpha, \mu_0 + \frac{S}{\sqrt{n}}t_\alpha \leq \overline{X} \] である. 但し $t_\alpha$ は自由度$n-1$の$t$分布の両側$\alpha$点, $S^2$は不偏分散.

片側検定も同様です. 以上の結果は前回やった信頼区間に関する定理とほぼ同じなので, 証明は省略します.

例

あるWebサービスには1分あたり平均$970$回アクセスがあるとします. このWebサービスを改良したことの効果を検証しましょう.
そこで,ランダムに100回(各一分間)アクセス回数を測定した所, 標本平均が$980$回でした. 改良によって平均アクセス回数は有意に増えたと言えるでしょうか？

有意水準を $\alpha=0.05$ とします. 一分あたりのユーザーのアクセス回数はポアソン分布$Po(\lambda)$ に従うと仮定します. 帰無仮説・対立仮説は \[ \begin{aligned} H_0&: \lambda = 970 \\ H_1&: \lambda > 970 \end{aligned} \] となります. 検定は標本平均 $\overline{X}$ で行うことにします. $Po(\lambda)$の平均・分散は共に$\lambda$なので, 中心極限定理より $H_0$ のもとでは, $\overline{X} \sim N\left(970, \frac{970}{100}\right) = N(970, 9.7)$ となります. 母分散が既知なので, 棄却域は$N(0,1)$の上側$\alpha$点$z_\alpha\approx1.64$を用いて \[ \lambda \geq 970 + \sqrt{9.7}\cdot z_\alpha \approx 975 \] となります. よって, $980 \geq 975$ なので $H_0$ を棄却する事が出来ます. ユーザーのアクセス回数は有意に増加したと言えそうです.

母平均の差の検定

以下のような母平均の差に関する検定を行い場合もあります.

例

A高校,B高校のそれぞれから, 7人, 9人の生徒をランダムに抽出して, 数学の試験を行った所以下の結果を得たとします. \[ \begin{aligned} \text{A高校}&: 69, 75, 63, 78, 54, 84, 72\quad\text{(平均$70.7$)} \\ \text{B高校}&: 89, 77, 72, 48, 69, 83, 53, 65, 59\quad\text{(平均$68.3$)} \end{aligned} \]

A高校出身者の方が有意に優れていると言えるでしょうか？

以下の定理が必要となります.

$X_1,X_2$が独立であるとする. $ X_1\sim N(\mu_1,\sigma_1^2),X_2\sim N(\mu_2,\sigma_2^2) $ならば \[ X_1-X_2 \sim N(\mu_1-\mu_2, \sigma_1^2 + \sigma_2^2) \] である.

これは第13回に説明した正規分布の再生性から言えます.

先ほどの問題に利用してみましょう.

例

A高校,B高校のそれぞれから, 7人, 9人の生徒をランダムに抽出して, 数学の試験を行った所以下の結果を得たとします. \[ \begin{aligned} \text{A高校}&: 69, 75, 73, 78, 85, 84, 72\quad\text{(平均$76.6$)} \\ \text{B高校}&: 79, 77, 72, 48, 89, 73, 53, 65, 59\quad\text{(平均$68.3$)} \end{aligned} \]

A高校の生徒の方が有意に優れていると言えるでしょうか？但し, 母分散はそれぞれ60,93であるとします.

有意水準を$\alpha=0.05$とします.
A,B高校の生徒の数学の成績の母集団が正規分布 $N(\mu_A,\sigma_A^2),N(\mu_B,\sigma_B^2)$ に従うと仮定し, 帰無仮説・対立仮説を \[ \begin{aligned} H_0&: \mu_A = \mu_B \\ H_1&: \mu_A > \mu_B \end{aligned} \] とします. A,B高校それぞれの標本平均を$\overline{X}_A,\overline{X}_B$とし, $\overline{X}_A-\overline{X}_B$ で検定を行います. $ \overline{X}_A \sim N(\mu_A,\sigma_A^2/7),\overline{X}_B\sim N(\mu_B,\sigma_B^2/9)$なので, 仮説$H_0$のもとでは \[ \overline{X}_A-\overline{X}_B \sim N(\mu_A-\mu_B,\frac{\sigma_A^2}{7}+\frac{\sigma_B^2}{9}) = N(0, 18.9) \] となるので, 棄却域は$N(0,1)$の上側$\alpha$点$z_\alpha\approx1.64$を用いて \[ \overline{X}_A-\overline{X}_B \geq 0 + \sqrt{18.9}\cdot z_\alpha \approx 7.2 \] となります. 実際には $\overline{X}_A-\overline{X}_B = 8.2$ であったので, $H_0$ を棄却する事が出来ます. よって,この検定ではA高校の生徒の方が優れていると結論できます.

今の問題では母分散を既知としましたが,母分散が未知の場合には以下の定理を利用する事が出来ます.

$X_1,X_2,\ldots,X_m\sim N(\mu_1,\sigma^2)$, $Y_1,Y_2,\ldots,Y_n\sim N(\mu_2,\sigma^2)$ が全て独立な確率変数であるならば, \[ S^2 = \frac{\sum_{i=1}^m(X_i-\overline{X})^2 + \sum_{i=1}^n(Y_i-\overline{Y})^2}{m+n-2} \] として, \[ T = \frac{\overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{S^2/m+S^2/n}} \] で定まる確率変数$T$は自由度$m+n-2$の$t$分布に従う.

先ほどの問題で分散が未知の場合を考えましょう.

例

A高校の生徒の方が有意に優れていると言えるでしょうか？ 母分散はわかりませんが等しいとします.

有意水準を$\alpha=0.05$とします.
A,B高校の生徒の数学の成績の母集団が正規分布 $N(\mu_A,\sigma^2),N(\mu_B,\sigma^2)$ に従うと仮定し, 帰無仮説・対立仮説を \[ \begin{aligned} H_0&: \mu_A = \mu_B \\ H_1&: \mu_A > \mu_B \end{aligned} \] とします. A,B高校それぞれの標本平均を$\overline{X}_A,\overline{X}_B$とし, $\overline{X}_A-\overline{X}_B$ で検定を行います. 仮説$H_0$のもとでは$\mu_A-\mu_B=0$なので, \[ T = \frac{\overline{X}_A-\overline{X}_B}{\sqrt{S^2/7+S^2/9}} \] が自由度 $7+9-2=14$ の$t$分布に従います. よって $t$ 分布の上側 $\alpha$ 点が $t_\alpha = 1.76$ なので棄却域は $ T \geq 1.76 $ となります. 実際に計算してみると, \[ S^2 = \frac{\sum_{i=1}^m(X_i-\overline{X})^2 + \sum_{i=1}^n(Y_i-\overline{Y})^2}{m+n-2} = 116 \] なので, \[ T = \frac{76.6-68.3}{\sqrt{116/7+116/9}} = 1.53 \] となり, この場合は$H_0$を棄却する事が出来ません.

母分散の検定

独立な標本 $X_1,X_2,\ldots,X_n$ が $N(\mu,\sigma^2)$ に従うとする. $\sigma^2$ に関する仮説 \[ \begin{aligned} H_0&: \sigma = \sigma_0 \\ H_1&: \sigma \neq \sigma _0 \end{aligned} \] を標本分散$s^2$で検定するときの棄却域は, \[ s^2 \leq \frac{\chi^2_{n-1}(1-\alpha/2)}{n}, \frac{\chi^2_{n-1}(\alpha/2)}{n}\leq s^2 \] である. 但し $\chi^2_{n-1}(\alpha)$ は自由度$n-1$の$\chi^2$分布の上側$\alpha$点.

先ほど, 母平均の差を検定しましたが, 同様に母分散の差 \[ \sigma_1^2 - \sigma_2^2 \] を検定したい場合もあります.

これを直接考えるのは難しいのですが, 代わりに母分散の比 \[ \frac{\sigma_1^2}{\sigma_2^2} \] を用いて検定が行う事が出来ます.

母分散の比の推定・検定の為には以下の分布が必要になります.

F分布

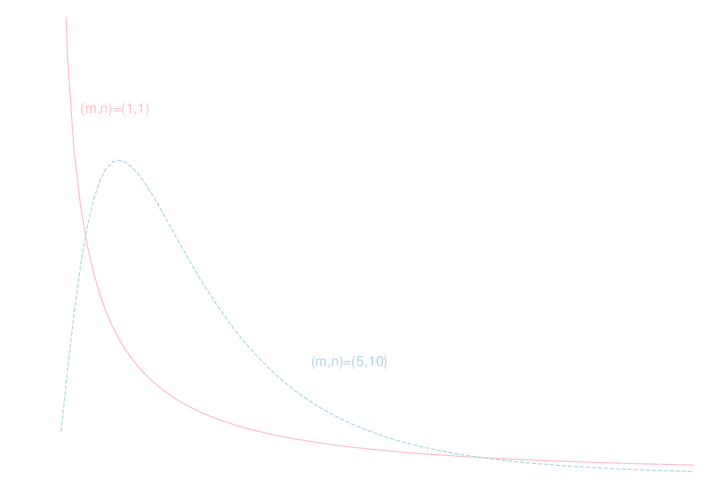
$X\sim \chi^2_m, Y\sim \chi^2_n$で $X,Y$ が独立である時, \[ F = \frac{X/m}{Y/n} \] で定まる確率変数の従う分布を自由度$(m,n)$のF分布と言い, $F(m,n)$ と書く.

F分布の密度関数のグラフは例えば以下のようになります.

$X_1,X_2,\ldots,X_m\sim N(\mu_1,\sigma_1^2),Y_1,Y_2,\ldots,Y_n\sim N(\mu_2,\sigma_2^2)$ で全ての確率変数が独立である時, \[ F= \frac{\sigma_2^2}{\sigma_1^2}\frac{S_1^2}{S_2^2} \] は自由度$(m-1,n-1)$のF分布に従う. ただし, $S_1^2$ は$X_1,X_2,\ldots,X_m$の不偏分散, $S_2^2$は$Y_1,Y_2,\ldots,Y_n$の不偏分散である.

先ほどの問題で分散の検定をしましょう.

例

各高校の数学の成績の母分散は異なると言えるでしょうか？

有意水準を$\alpha=0.05$とします.
A,B高校の生徒の数学の成績の母集団が正規分布 $N(\mu_A,\sigma_A^2),N(\mu_B,\sigma_B^2)$ に従うと仮定し, 帰無仮説・対立仮説を \[ \begin{aligned} H_0&: \sigma_A^2/\sigma_B^2 = 1\\ H_1&: \sigma_A^2/\sigma_B^2 \neq 1 \end{aligned} \] とします. A,B高校それぞれの不偏分散を$S_A^2,S_B^2$ とすると $H_0$ のもとで \[ F=\frac{\sigma_B^2}{\sigma_A^2}\frac{S_A^2}{S_B^2} = \frac{S_A^2}{S_B^2} \] が自由度$(7-1,9-1)=(6,8)$ のF分布に従います. この分布の上側$\alpha$点を$F_{6,8}(\alpha)$と書くと \[ \mathrm{F}_{6,8}(\alpha/2) = 4.65,\mathrm{F}_{6,8}(1-\alpha/2) = 0.18 \] であるので, 棄却域は \[ F\leq 0.18, 4.65\leq F \] となります. ここで, 実際の値は$F=70.3/184.7=0.21$ であるので$H_0$を棄却する事は出来ません.

以上が母数による仮説検定の基本です. 他にも様々な場合があり, 個々の定理を覚えるのは大変なので理屈をよく理解するようにしてください.

今回はここで終わります。

標本数の決定までやろうと思いましたが, 資料作成が間に合いませんでした. すみません.

次回は, 母分散の種類が未知の場合の検定, 標本数の計算, 多変量分布について解説する予定です.

プログラマの為の数学勉強会第15回

謝辞