プログラマの為の
数学勉強会
第13回
(於)ワークスアプリケーションズ中村晃一
2013年12月5日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
情報量・エントロピー
前回,エントロピーの話が中途半端になってしまったのでここから始めます.
情報量とは一体なんでしょうか?直感的に考えて見ます。
分かり易い例として,文章の中の単語の情報量について考えましょう。
「そして」、「しかし」、「例えば」、「本節では」\(\cdots\)
など,他の文章でも頻繁に登場する単語はその文章を理解する上でほとんど役に立ちません。
一方
「確率」、「事象」、「測度」、「分布」、\(\cdots\)
などの単語が登場したら、それだけでその文書は確率論や統計学に関するものであろうと分かってしまいます。これらの単語は情報量が多い単語であると言えるでしょう。
今の例から、 情報量は確率と深く関係しているのではないかと考えられます。更に, 確率が小さい事象の持つ情報量は大きいであろうという事も分かります。
そこで,事象\(A\)の情報量\(I(A)\)は,何らかの単調減少な関数\(f(x)\)によって \[ \color{yellow}{ I(A) = f(P(A)) } \] と表されると仮定してみましょう。
さらに,事象\(A,B\)が独立であるならば,\(A,B\)それぞれの持つ情報に重複は無いであろうと考えられるので, \[ \color{yellow}{ A,B\text{が独立ならば} I(A\cap B) = I(A) + I(B)} \] である事が期待されます。
この時\(P(A\cap B)=P(A)P(B)\)なので, \[ \color{yellow}{ f(P(A)P(B)) = f(P(A))+f(P(B)) } \] が成立しなければなりません。
このような性質を持つ,単調減少な\(f\)であれば良いので \[ \color{yellow}{ f(x) = -\log x } \] などが候補となります。以上の他,様々な考察に基いて情報量が定義されます。
情報量
事象\(A\)の確率が\(P(A)\)である時 \[ I(A) = -\log P(A) \] をこの事象の(選択)情報量という。
\(\log\)の底は(何でも良いが),例えば\(2\)とすればよい。 底が\(2\)の時の情報量の単位をビットという。
例
歪みのないコインを3回振って,表が\(k\)回出たという事象を\(A_k\)とします。\(I(A_k)\)を計算しましょう。
【解答】
\[ P(A_k) = {}_nC_k\left(\frac{1}{2}\right)^3 \]
なので
\[ P(A_0) = \frac{1}{8},\ P(A_1)=\frac{3}{8},\ P(A_2)=\frac{3}{8},\ P(A_3)=\frac{1}{8} \]
となるから,
\[ I(A_0)=I(A_3)=-\log\frac{1}{8}=3,\ I(A_1)=I(A_2)=-\log\frac{3}{8} \approx 1.42 \]
となる。
選択情報量の期待値が情報エントロピーです。
情報エントロピー
有限集合(サイズ\(n\))上の確率分布に対して,
\[ \begin{aligned}
H(X) &= \sum_{i=1}^{n}I(X=x_i)P(X=x_i)\\
&= -\sum_{i=1}^{n}P(X=x_i)\log P(X=x_i)
\end{aligned} \]
を,確率分布の情報エントロピーやシャノン情報量と言う。
ただし\(P(X=x_i)=0\)の時は\(-P(X=x_i)\log P(X=x_i)=0\)とする。
連続的な確率分布に対しても,似た量 \[ h(x) = -\int_{-\infty}^{\infty}\rho(x)\log \rho(x)\mathrm{d} x \] を考えてこれをエントロピーと呼びますが,これはシャノン情報量とは異なるので注意してください。 (\(\rho(x)\)は確率「密度」なので\(-\log\rho(x)\)は選択情報量ではない。)
例
サイコロの出目の確率分布のエントロピーを計算してみましょう。出目に偏りがある場合はどうなるでしょうか?
出目に偏りが無い場合には, \[ H(X) = -\sum_{i=1}^{6}\frac{1}{6}\log\frac{1}{6}=-\log\frac{1}{6}\approx 2.585\] です。出目に偏りがある場合として,例えば1が出る確率を\(\frac{11}{60}\),6が出る確率を\(\frac{9}{60}\)としてみれば \[ \begin{aligned} H(X) &= -4\times \frac{1}{6}\log\frac{1}{6}-\frac{11}{60}\log\frac{11}{60}-\frac{9}{60}\log\frac{9}{60} \\ &\approx 2.583 \end{aligned} \] 少しエントロピーが小さくなりました。
以下の定理が成立します.
エントロピー \[ H(X) = -\sum_{i=1}^{n}P(X=x_i)\log P(X=x_i) \] は\(P(X=x_i)\)が全て等しい時に最大となる。
【証明】
ラグランジュの未定定数法を利用する。\(p_i = P(X=x_i)\)とおいて,
\[ f(p_1,\cdots,p_n,\lambda) = -\sum_{i=1}^{n}p_i\log p_i + \lambda(p_1+\cdots +p_n - 1) \]
とすると,
\[ \frac{\partial f}{\partial p_i} = -\log p_i - 1 + \lambda,\quad \frac{\partial f}{\partial \lambda} = p_1+\cdots +p_n-1 \]
であるので極値において
\[ \lambda = \log p_i + 1,\quad p_1+\cdots + p_n = 1 \]
が成り立つ。従って,\(H(X)\)が極値を取るとき
\[ p_1 = \cdots = p_n = \frac{1}{n},\ \lambda = 1-\log n\]
である。これが最大値である事は明らか。
□
「エントロピー」という言葉を「乱雑さの度合い」と理解している人もいるでしょう。実際,統計力学におけるエントロピーと情報科学におけるエントロピーは定数倍を除いて一致します。
直感的に言えば,今の定理より\(\Omega=\{x_1,\cdots,x_n\}\)上の確率分布のエントロピーが大きくなると,\(X=x_1,\cdots,x_n\)のいずれが出るかが全くのランダムに近づいていく(乱雑になっていく)という事になります。

また,「情報量」と聞いて通常連想するのは「データの圧縮」ではないかと思います。
あるランダムなデータの列のエントロピーが小さい(シャノン情報量が少ない)という事は,そのデータ列が何らかのパターンを持っている(乱雑さが小さい)という事です。 そのパターンを利用してデータの圧縮を行う事が出来ます。
- 出現頻度の高いデータ(選択情報量小)に短いbitを割り当てる
- 出現頻度の低いデータ(選択情報量大)に長いbitを割り当てる
また,情報量は事象の独立性とも関係があります。統計学ではこの視点が特に重要であり、今後も登場すると思います。
2つの事象の間で情報のやり取りがあるならば,それらは確率的に独立ではないはずです。先ほど説明した独立性の定義 \[ P(X,Y)=P(X)P(Y) \] では、「\(X,Y\)が独立か否か」しかわかりませんが、情報量を測る事で「独立性の程度」を数値化出来ます。

今説明した事を定式化します.
結合エントロピー
2つの確率変数 \(X,Y\) (それぞれ \(m,n\) 個の値をとる)に対して \[\small{\begin{aligned} H(X, Y) = -\sum_{\substack{1\leq i \leq m\\ 1\leq j\leq n}}P(X=x_i,Y=y_j)\log P(X=x_i,Y=y_j) \end{aligned}} \] を結合エントロピーという.
相互情報量
2つの確率変数 \(X,Y\) に対して \[ I(X, Y) = H(X)+H(Y) - H(X,Y) \] を 相互情報量 という.
そして以下の定理が成立します.
\[ \text{確率変数 $X,Y$ が独立}\Leftrightarrow I(X,Y) = 0\] (但し, \(X,Y\) が独立であるというのは, それぞれの変数がとる全ての値について \(P(X=x_i,Y=y_j) = P(X=x_i)P(Y=y_j)\) が成り立つこと.)
重要な確率分布
有名な離散的分布・連続的分布の例をいくつか紹介します.
重要なものを除き定理の証明を省略しますので, その証明は練習問題としてください.
離散一様分布
\[ \begin{array}{|c|c|c|c|}\hline X & x_1 & x_2 & \cdots & x_n \\ \hline P(X=x_i) & \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \\ \hline \end{array} \] を 離散一様分布 という.
連続一様分布
\(a < b\)のとき, 密度関数が \[ \rho(x) = \left\{\begin{array}{cl} \frac{1}{b-a} & (a\leq x \leq b) \\ 0 & (\text{上記以外}) \end{array}\right. \] で表される分布を 連続一様分布 と呼び \(U(a,b)\) と書く. \[ \text{平均}: \frac{a+b}{2}\quad\text{分散}: \frac{(b-a)^2}{12} \]
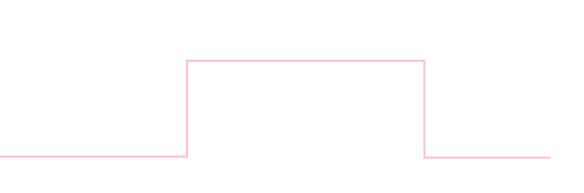
サイコロを1個振ったときの目の値が離散一様分布に従う変数の例です. また, プログラミング言語の標準的な擬似乱数は近似的に離散・連続一様分布に従うものとみなす事ができます.
ベルヌーイ分布
\(0\leq p \leq 1\)として \[ \begin{array}{|c|c|c|c|}\hline X & 1 & 0 \\ \hline P(X=x_i) & p & 1-p \\ \hline \end{array} \] を ベルヌーイ分布 という. \[ \text{平均}: p\quad\text{分散}: p(1-p) \]
結果が2通りしかない試行をベルヌーイ試行と言います. 例えばコイン投げなどです.
二項分布
\(0\leq p \leq 1\)として \[ P(X=k) = \binom nk p^k(1-p)^{n-k}\quad (k=0,1,2,\ldots,n) \] に従う分布を 二項分布 と呼び \(B(n,p)\) と書く. \[ \text{平均}: np\quad\text{分散}: np(1-p) \]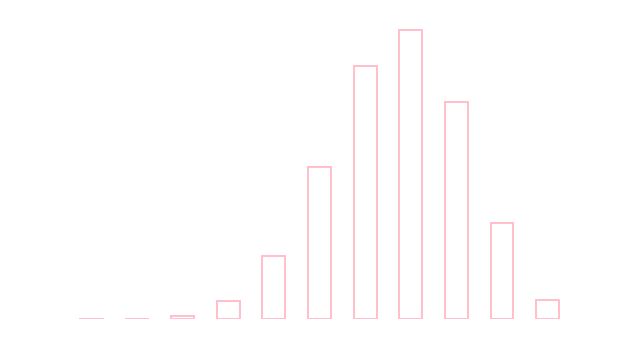
\( B(10, 0.6) \)
二項分布 \(B(n,p)\) は確率 \(p\) で成功するベルヌーイ試行を \(n\) 回行った際の成功回数の分布です.
数式中の
\[ \binom nk = \frac{n!}{k!(n-k)!} \]
は \(n\) 個のものから \(k\) 個のものを選ぶ場合の数です.
\(n\) 回の試行のうちちょうど \(k\) 回成功するのが \(\binom nk\)パターンあり, 個々のパターンの生起確率が \(p^k(1-p)^{n-k}\) であるという事になります.
二項分布の再生性
\(X \sim B(m,p), Y\sim B(n,p)\) ならば \(X+Y\sim B(n+m,p)\).
\(X \sim B(m,p) \)というのは確率変数 \(X\) が確率分布 \(B(m,p)\) に従うという意味です. このように, 確率変数 \(X,Y\) がある分布に従う時に, \(X+Y\) も同じ種類の分布に従う事を 再生性 と言います.
この定理は ベルヌーイ試行を \(m\) 回行った場合の成功回数 \(X\) と \(n\) 回行った場合の成功回数 \(Y\) の和 \(X+Y\) は, 試行を \(m+n\) 回行った場合の成功回数となります. これは明らかですね.
負の二項分布
自然数 \(r\) と実数 \(0\leq p \leq 1\) に対して \[ P(X=k) = \binom{k-1}{r-1}p^r(1-p)^{k-r}\quad (k = r,r+1,r+2,\ldots) \] に従う分布を 負の二項分布 という. \[ \text{平均}: \frac{r}{p}\quad\text{分散}: \frac{r(1-p)}{p^2} \]
負の二項分布での \(P(X=k)\) は確率 \(p\) で成功するベルヌーイ試行が \(r\) 回成功する為に必要な試行の回数が \(k\) 回である確率です.
\(k-1\) 回目までにちょうど \(r-1\) 回成功する確率が \[ \binom{k-1}{r-1} p^{r-1}(1-p)^{(k-r)} \] であり, \(k\) 回目に成功する確率が \(p\) ですから 掛けあわせて \[ \binom{k-1}{r-1} p^r(1-p)^{(k-r)} \] となります.
例えばコイン投げをして10回表が出るためには 平均 \(10\div \frac{1}{2} = 20\) 回投げる必要があります. 標準偏差は約 \(4.5\) となります.
ポアソン分布
\(\lambda > 0\) に対して \[ P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!} \quad (k = 0,1,2,\ldots) \] に従う分布を ポアソン分布 と呼び \(Po(\lambda)\) と書く. \[ \text{平均}: \lambda\quad\text{分散}: \lambda \]
ポアソン分布 \(Po(\lambda)\) は単位時間(単位面積・体積)あたりに平均 \(\lambda\) 回発生する事象が, 単位時間(単位面積・体積)あたりに発生する回数の確率分布です.
例えば, 1日あたり平均 \(30\) 通のメールを受信する場合に1日 \(35\) 通のメールを受け取る確率は \[ P(X=35) = \frac{30^{35} e^{-30}}{35!} \] と計算されます. おおよそ 4.5% となります.
>>> from math import factorial,exp
>>> 30**35 * exp(-30) / factorial(35)
0.04530820008655117
ポアソン過程
時刻 \(t\) までに事象が \(X_t\) 回生起する確率が \[ P(X_t = k) = \frac{(\lambda t)^ke^{-\lambda t}}{k!} \] に従う過程を ポアソン過程 という.
単位時間に \(\lambda\) 回事象が生起するならば, 時刻 \(t\) までには \(\lambda t\) 回事象が生起するはずです.
Webサービスへのアクセス数, 店への来客数など実用上重要な例をポアソン過程とみなす事が出来ます.
ポアソン分布の再生性
\(X \sim Po(\lambda_1), Y\sim Po(\lambda_2)\) ならば \(X+Y\sim Po(\lambda_1+\lambda_2)\)
ポアソンの極限定理
\(\lambda = np\) が定数となるようにしながら \(n\rightarrow\infty\) の極限をとると \[ \lim_{n\rightarrow\infty}\binom nk p^k(1-p)^{n-k} = \frac{\lambda^ke^{-\lambda}}{k!}\] となる.
\(\lambda = np\)が定数ということは, \(n\rightarrow\infty\)のとき \(p\rightarrow 0\)です. つまり, ポアソン分布は成功確率が非常に低いベルヌーイ試行を,多数回行った場合の成功回数の分布と考える事が出来ます.
以下の例は「めったに発生しない事象の生起回数」へのポアソン分布の適用として歴史的に有名です.
ボルトキーヴィッチは著書"Das Gesetz der kleinen Zahlen "(The Law of Small Numbers)において、プロイセン陸軍の14の騎兵連隊の中で、1875年から1894年にかけての20年間で馬に蹴られて死亡する兵士の数について調査しており、1年間当たりに換算した当該事案の発生件数の分布がパラメータ0.61のポアソン分布によく従うことを示している。
Wikipedia:ポアソン分布より引用
【極限定理の証明】
\(\lambda=np\)とおくと
\[ \begin{aligned}
\binom nk p^k(1-p)^{n-k} &= \frac{n(n-1)\cdots(n-k+1)}{k!}\left(\frac{\lambda}{n}\right)^k\left(1-\frac{\lambda}{n}\right)^{n-k} \\
&= \frac{1}{k!}\cdot \left(1-\frac 1n\right)\cdots\left(1-\frac{k-1}{n}\right)(\lambda)^k\left\{\left(1-\frac{\lambda}{n}\right)^{\frac{n}{\lambda}}\right\}^{\lambda\cdot\frac{n-k}{n}} \\
&\overset{n\rightarrow\infty}{\rightarrow} \frac{1}{k!}\cdot \overbrace{1\cdot 1 \cdots 1}^{\text{$k$個}}\cdot \lambda^k (e^{-1})^\lambda\\
&= \frac{\lambda^ke^{-\lambda}}{k!}
\end{aligned} \]
□
超幾何分布
自然数 \(N,K,n\quad (0\leq K \leq N, 0\leq n \leq N)\) に対して \[ P(X=k) = \frac{\binom nk \binom{N-n}{K-k}}{\binom NK} \] に従う確率分布を 超幾何分布 という. \[ \text{平均}: \frac{nK}{N}\quad\text{分散}: \frac{(N-n)n(N-K)K}{(N-1)N^2} \]
超幾何分布は当たりが \(K\) 本入っている \(N\) 本のくじから \(n\) 本引いた時に \(k\) 本当たる確率であると言えます.
\(N\) 本のくじを一列に並べる方法の数は, 当たりくじの場所を \(N\) 箇所から \(K\) 箇所選ぶ方法の数だから \(\binom NK\) 通りです.
左から \(n\) 本の中にあたりくじ \(k\) 本が並ぶような並べ方の総数が \(\binom nk \binom{N-n}{K-k}\) であるので \[ P(X=k) = \frac{\binom nk \binom{N-n}{K-k}}{\binom NK} \] という等式が得られます.
指数分布
実数 \(\lambda > 0\) に対して 確率密度関数が \[ \rho(x) = \left\{\begin{array}{cl} \lambda e^{-\lambda x} & (x \geq 0) \\ 0 & (x < 0) \end{array}\right. \] である分布を 指数分布 という. \[ \text{平均}: \frac 1\lambda\quad\text{分散}: \frac{1}{\lambda^2} \]

ポアソン分布 \(Po(\lambda)\) に従って発生する事象の発生間隔の分布はパラーメータが \(\lambda\) の指数分布に従います.
練習問題
あるWebサービスには1秒当たり平均 5人がアクセスがあります. アクセスがあってから \(0.01\) 秒以内に次のアクセスが来る確率を計算してください.
\[ \int_0^{0.01} 5e^{-5x}\mathrm{d} x = \left[-e^{-5x}\right]_0^{0.01} = -e^{-0.05} + e^0 \approx 0.049 \] つまり約 \(4.9\) %となります.
指数分布の無記憶性
確率変数 \(X\) が指数分布に従う場合, 任意の \(s,t > 0\) に対して \[ P(X > s + t | X > s) = P(X > t) \] が成立する.
\(P(X > t)\) は \(t\) 単位時間以上事象が生起しない確率です.
この定理が言っていることは, \(s\) 単位時間事象が生起しなかったとしても, その後 \(t\) 単位時間待たなければならない確率は変化しないという事です.
正規分布
実数\(\mu,\sigma\quad (\sigma > 0\)に対して 確率密度関数が \[ \rho(x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \] である確率分布を 正規分布 と呼び \(N(\mu,\sigma^2)\) と書く. \[ \text{平均}: \mu\quad\text{分散}: \sigma^2\]
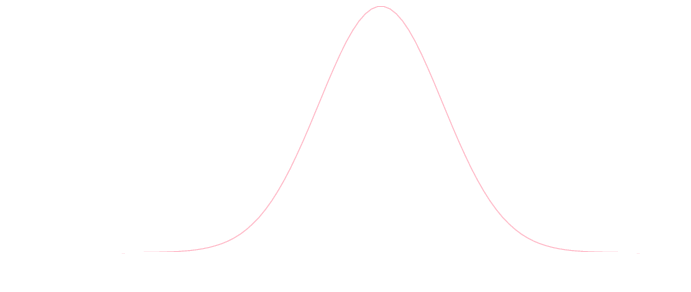
\(N(0,1)\)
ある確率変数の値の平均値からのずれがランダムに発生する場合, それは正規分布に従うと考える事が出来ます. 例えば測定誤差などは正規分布に従うものとしてモデル化されます.
また, 後に説明する 中心極限定理 が成立する事がその重要性を高めています.
正規分布の再生性
\(X \sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)\)ならば \(X+Y\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)\)
多変量分布
複数の確率変数 \(X_1,X_2,\ldots,X_n\) が従う同時確率を与える分布を 多変量分布 と言います.
共分散
確率変数 \(X,Y\) に対して \[ \begin{aligned} \mathrm{Cov}(X,Y) &= E[(X-E[X])(Y-E[Y])]\\ &= E[XY] - E[X]E[Y] \end{aligned} \] を \(X,Y\) の 共分散 という.
相関係数
確率変数 \(X,Y\) に対して \[ \mathrm{Cor}(X,Y) = \frac{\mathrm{Cov}(X,Y)}{\sigma[X]\sigma[Y]} \] を \(X,Y\) の 相関係数 という.
\(\mathrm{Cor}(X,Y) > 0\)のとき, \(X,Y\) には 正の相関 があるといい, \(\mathrm{Cor}(X,Y) < 0\)のときは 負の相関 があるという. \(\mathrm{Cor}(X,Y)=0\)のときは 無相関 であるという.
\[ \mathrm{Cor}(X,Y) > 0\] であるというのは, \[ X-E[X], Y-E[Y]\text{が同符号である傾向がある} \] という事です. 相関係数が大きいほど, 平均値を中心として \(X\) が増加すれば \(Y\) も増加するという傾向がみられます.
共分散についても同様の事が言えます. 相関係数は下のように共分散の値の範囲を正規化したものであるといえます.
独立性と相関
確率変数 \(X,Y\) に対して \[ X,Y\text{が独立}\Rightarrow X,Y\text{は無相関} \] である.
という性質が成り立ちます. 逆は成り立たないことに注意する必要があります. 相関性というのはあくまで分布の平均的な性質です.
共分散・相関係数の多変数版の一般化が分散共分散行列・相関行列です.
分散共分散行列
確率変数ベクトル \(\mathbf{x} = (X_1,X_2,\ldots,X_n)\) に対して, \[ \Sigma = (\mathrm{Cov}(X_i,X_j))_{n,n} \] で定まる行列を,この確率分布の 分散共分散行列 という.
相関行列
確率変数ベクトル \(\mathbf{x} = (X_1,X_2,\ldots,X_n)\) に対して, \[ \Sigma = (\mathrm{Cor}(X_i,X_j))_{n,n} \] で定まる行列を,この確率分布の 相関行列 という.
正規分布に関しては多変数のものも頻繁に必要となります.
多変量正規分布
\(n\)次元ベクトル \(\mathbf{\mu}\) と \(n\) 次正則行列 \(\Sigma\) に対して, 同時確率密度関数 \[ \rho(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^n}\sqrt{\det\Sigma}}\exp\left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^T\Sigma^{-1}(\mathbf{x}-\mathbf{\mu})\right\} \] と表される確率分布を 多変量正規分布 という.\(\mu\) は平均ベクトル, \(\Sigma\) は分散共分散行列である.
簡単な例として, 2変数 \(\mathbf{x}=(x,y)\) で \[ \mathbf{\mu} = (\mu_1,\mu_2)^T, \Sigma = \begin{pmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{pmatrix} \] の場合を直に書き下してみれば, \[ \rho(\mathbf{x}) = \frac{1}{2\pi\sigma_1\sigma_2}\exp\left\{-\frac{(x-\mu_1)^2}{2\sigma_1^2}-\frac{(x-\mu_2)^2}{2\sigma_2^2}\right\} \] となります.
大数の法則・中心極限定理
大数の法則とは, 理論的な確率と統計的な確率が一致するという定理です. 多数回の試行を実際に行うことは難しい場合が多いので大変重要な定理となります.
証明を行う為にはいくつか準備が必要となります. この勉強会では簡単の為, 標本が有限個の場合についてのみを考えることにしますので, 詳しくは専門書を参照してください.
マルコフの不等式
任意の確率変数 \(X\) と \(a > 0\) に対して \[ P(|X|\geq a) \leq \frac{E[X]}{a} \]
【証明】
確率変数 \(Y\) を
\[ Y = \left\{\begin{array}{cl}
1 & (|X|\geq a\text{のとき}) \\
0 & (\text{上記以外})
\end{array}\right. \]
と定義すると, \(P[|X|\geq a] = E[Y]\) である.
ここで
\[ aY \leq |X| \]
である(\(|X|\geq a\)なら \(aY=a\), \(|X| < a\)なら \(aY=0\))ので
\[ aE[Y] \leq E[|X|] \]
である. 従って両辺を \(a\) で割って
\[ P[|X|\geq a] = \frac{E[|X|]}{a} \]
である.
□
チェビシェフの不等式
任意の \(a > 0\) に対して \(\sigma[X] \neq 0\)ならば \[ P(|X-E[X]|\geq a\sigma[X]) \leq \frac{1}{a^2} \] が成立する.
【証明】
\[ P(|X-E[X]|\geq a\sigma[X]) = P((X-E[X])^2 \geq a^2\sigma[X]^2) \]
であるのでマルコフの不等式より
\[ P(|X-E[X]|\geq a\sigma[X]) \leq \frac{E[(X-E[X])^2]}{a^2\sigma[X]^2]} = \frac{\sigma[X]^2}{a^2\sigma[X]^2}=\frac{1}{a^2} \]
である.
大数の法則
\[ P(X=x) = p \] に従う試行を独立に \(n\) 回行った際に \(X=x\) が生起する頻度を確率変数 \(Q_n\) で表すならば, 任意の \(\varepsilon > 0\) に対して, \[ \lim_{n\rightarrow\infty}P(|Q_n-p|>\varepsilon)= 0 \] である.
【証明】
確率変数 \(e_i\quad (i=1,2,\ldots,n)\) を
\[ e_i = \left\{\begin{array}{cl}
1 & \text{$i$ 回目に $X=x$ が生起したとき} \\
0 & \text{上記以外}
\end{array}\right. \]
とすると,
\[ \begin{aligned}
E[e_i] &= 1\cdot P(X=x) + 0\cdot P(X\neq x) = p \\
E[e_i^2] &= 1^2\cdot P(X=x) + 0\cdot P(X\neq x) = p \\
V[e_i] &= E[e_i^2] - (E[e_i])^2 = p - p^2
\end{aligned} \]
である. ここで
\[ Q_n = \frac{e_1+e_2+\cdots + e_n}{n} \]
であるから 期待値・分散の加法性より
\[ \begin{aligned}
E[Q_n] &= \frac{1}{n}(E[e_1] + E[e_2] + \cdots + E[e_n]) = p\\
V[Q_n] &= \frac{1}{n^2}(V[e_1] + V[e_2] + \cdots + V[e_n]) = \frac{p-p^2}{n^2}
\end{aligned} \]
である.
よってチェビシェフの不等式により,任意の\(a > 0\) に対して \[ P(|Q_n - p|> a \frac{\sqrt{p-p^2}}{n}) \leq \frac{1}{a^2} \] が成り立つので任意の \(\varepsilon > 0\) に対して \[ \varepsilon < a\frac{\sqrt{p-p^2}}{n} \] をみたすように \(a\) を取れば \[ P(|Q_n - p| > \varepsilon) \leq \frac{\sqrt{p-p^2}}{\varepsilon^2n^2} \] が成り立つ. したがって \[ \lim_{n\rightarrow\infty}P(|Q_n-p|>\varepsilon)= 0 \] となる. □
中心極限定理とは, 同一の分布に従う試行を繰り返し行なって平均値をとると, 試行回数を増やした時に, 平均値が正規分布に従うという定理です.
この定理の証明は前提としなければならない知識が多いので定理のみ示して具体例を見てみようと思います.
中心極限定理
確率変数 \(X_1,X_2,\ldots,X_n\) が期待値 \(\mu\), 標準偏差 \(\sigma\) の同一の確率分布に従い, 独立であるとする. このとき \(X_i\) の平均 \[ \overline{X} = \frac{1}{n}(X_1+X_2+\cdots +X_n) \] の従う確率分布は \(n\) が大きくなると正規分布 \(N\left(\mu, \frac{\sigma^2}{n}\right)\) に収束(弱収束)する.
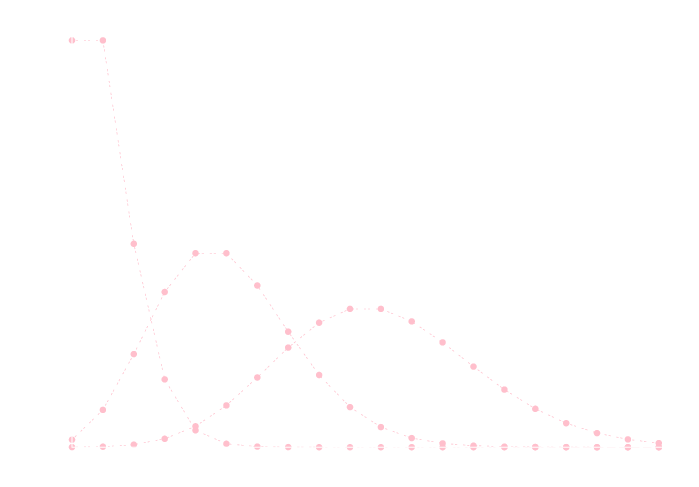
下のグラフは \(\lambda=3\) のポアソン分布に従う乱数 \(N=10,30,50\) 個の平均値をそれぞれ 1000 サンプル計算して 幅\(0.1\) の区間毎にヒストグラム化してプロットしたものです. 平均が \(3\) の正規分布に近づいていく様子が見えると思います.
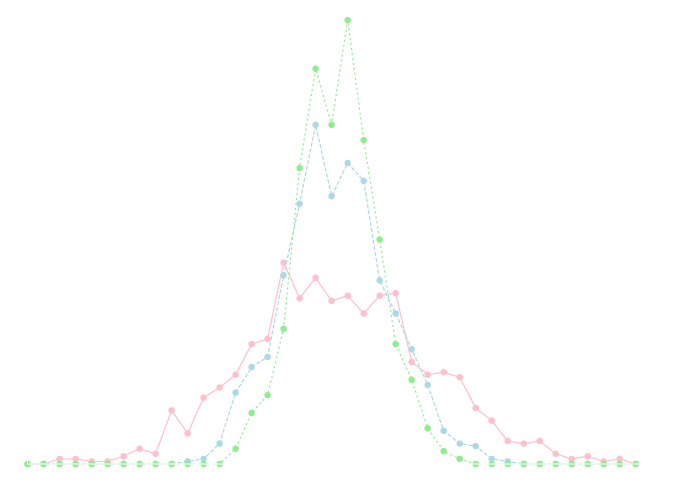
今のデータを生成するのに利用したプログラムです. 他の種類の確率分布についても実験を行ってみてください.
import numpy as np
from collections import Counter
M = 1000
for N in [10,30,50]:
data = [np.average(np.random.poisson(3, N)) for i in range(M)]
hist,key = np.histogram(data, bins=np.arange(1,5,0.1), density=True)
for i in range(len(hist)):
print "{0}\t{1}".format(key[i], hist[i])
print "\n"
今回はここで終わります。
次回は計算機寄りの話題としてまず, 擬似乱数について説明します. その後,統計量の計算機での計算について具体的なデータセットを用意して説明する予定です. 時間があれば,仮説検定などの説明をします.