プログラマの為の
数学勉強会
第12回
(於)ワークスアプリケーションズ中村晃一
2013年11月28日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
確率論入門
今回から確率・統計分野に入ります。
最初に確率の基礎知識を確認しましょう。
単に「確率」と言ってもいくつかの解釈があります。具体的な問題で考えてみましょう。
サイコロを振って\(1\)の目が出る確率が\(\frac{1}{6}\)であるというのはどういう事か?

解釈1
- サイコロの目の出方は6通りであり,それらは同様に確からしい。
- 1の目が出るのはそのうちの1通りの場合である。
- 従って1の目が出る確率は \[ \frac{1}{6} \] である。
組合せ論的確率
全ての起こりうる根元事象が\(n\)通りで同様に確かであるとする。 事象\(A\)を構成する根元事象が\(a\)通りならば,事象\(A\)の起こる確率は \[ P(A) = \frac{a}{n} \] である。
組合せ論的確率では「同様に確からしい」という条件が重要です。
例えば,以下の様な計算はこの意味で妥当ではないと考えられます。
サイコロを振ったら「1が出る」か「1が出ない」の2通りの場合があるから,1の目がでる確率は\( \frac{1}{2} \)である
ところが,そもそも何をもって「同様に確からしい」ということを判断出来るのでしょうか?
これは純粋に数学的に取り扱える様な問題ではなさそうです。 例えばサイコロの例では,サイコロの形状や投げ方と言った物理的な状況を考えなければいけません。
解釈2
- 1の目が出る確率が\(\frac{1}{6}\)であるというのは, サイコロを\(n\)回振ったら,\(\frac{n}{6}\)回程度1の目が出るという事である。
- 振る回数を増やすほど以下の値は\(\frac16\)に近づいていくのである。 \[ \frac{\text{1の目が出た回数}}{\text{振った回数}} \]
統計的確率
\(n\)回試行を行った時に,事象\(A\)が\(a\)回起こったとする。 \(A\)の起こる頻度 \[ \frac{a}{n} \] が\(n\rightarrow\infty\)の時,ある定数に(ほとんど確実に)近づいていくならば,その値が\(A\)の起こる確率\(P(A)\)である。
「組合せ論的確率も統計的確率も結局同じ値になるんじゃないの?」と思った人もいると思います。統計的確率を実際に計算するのは困難なので,もしそうならありがたいです。これは後に大数の法則として説明されます。
また,これらの値は客観的に定まるので客観的確率とも呼ばれます。
こういった個数・頻度を数える事に基づく確率の考え方を頻度主義とも言います。
解釈3
- サイコロの1~6のいずれの目が出やすいのかはわからない。
- よって\(i\)の目が出るということの確信度\(P(i)\)を数値にするならば
\[ P(1) = P(2) = P(3) = P(4) = P(5) = P(6) \]
である。
- よって確信度の総和を\(1\)とするならば
\[ P(1) = \frac{1}{6} \]
である。
主観的確率
事象\(A\)の起こる確率\(P(A)\)とは,事象\(A\)が起こるということの確信度(信念の度合い)を\(0\leq P(A)\leq 1\)で数量化したものである。
主観的確率
事象\(A\)の起こる確率\(P(A)\)とは,事象\(A\)が起こるということの確信度(信念の度合い)を\(0\leq P(A)\leq 1\)で数量化したものである。
確率の主観的な解釈は数学者トーマス・ベイズの名をとってベイズ主義とも呼ばれます。
ベイズ主義では
- 確率を考える主体によってその値が変わり得る
- 新たな情報を得る事でその値が変わり得る
という点に注意しましょう。
先ほどの\(\frac16\)という値は「出目の偏りについて何も情報がない」事から暫定的に求められた値です。実際にサイコロを振ってみて新たな情報を得ると,その値も変化していくでしょう。
サイコロの例だと主観確率という考え方が必要になる理由が分かりにくいと思いますので例を変えましょう。
あるシステム上でユーザー毎に最適な広告を表示する仕組みを作りたいとしましょう。この場合, \(A\)さんが商品\(X\)を購入してくれる確率\(P\)といったものを考える必要が生じます。
この\(P\)を頻度主義的な考え方で数量化するのは難しいでしょう。
また\(A\)さんの新しい行動がある度に\(P\)の値も更新されるべきでしょう。
本勉強会で学ぶ統計学
以上,代表的な確率の解釈を紹介しました。
- 客観確率(頻度主義)
- 組合せ論的
- 統計的
- 主観確率(ベイズ主義)
土台とする確率論が異なれば,統計学の形も異なります。
この勉強会では
- 頻度主義に基づく推計統計学
- ベイズ主義に基づくベイズ統計学
をこの順番に学んでいきます。
公理的確率論
続いて,確率の数学的な取り扱いについて説明します。
これまで説明したいずれの確率解釈も純粋に数学的に取り扱う事の難しい概念を含んでいます。
- 組合せ論的解釈:「同様に確からしい」とは?
- 統計的解釈: 「試行」とは?
- ベイズ的解釈: 「確信度」とは?
こういった哲学的な話題はこの勉強会では扱いません(私もよくわかりません)。
公理的確率論
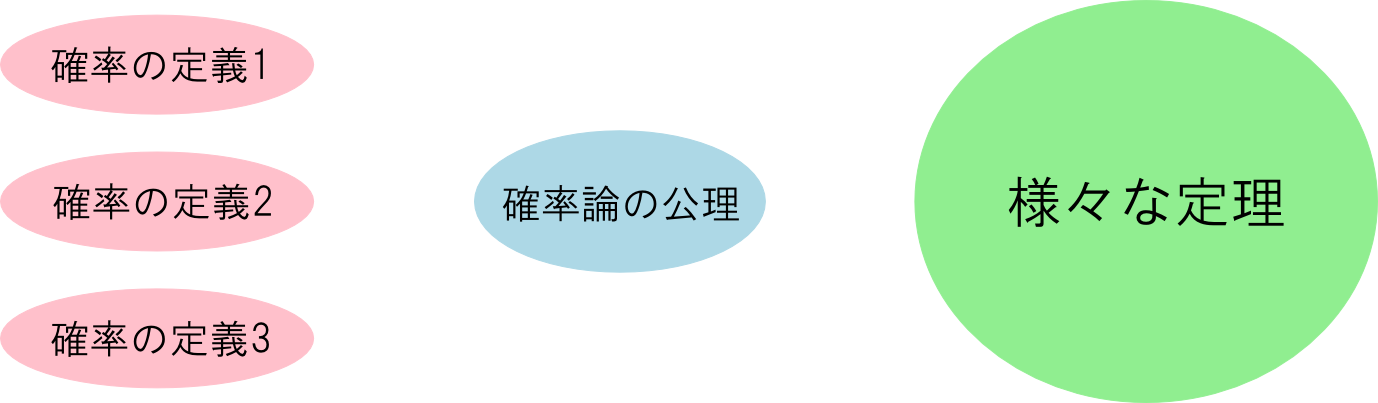
そこで,「公理」という考え方が必要になります。
- 確率などの概念は未定義語とする。
- 「もし\(P(A)\)を\(A\)の確率と呼ぶのならば,\(P\)はどういった性質を満たすべきか?」という事を公理として記述する。
- 公理に基いて確率論の数学体系を構築する。
具体的な確率の定義はいろいろあっても,確率論の公理さえ満たせばその体系で示された全ての定理が使用出来る事になります。
事象
事象は数学的には集合として表現します。
「起こりうる全ての場合(全事象)」を表す集合\(\color{yellow}{\Omega}\)\((\neq\phi)\)を固定した上で, 個々の事象を\(\Omega\)の部分集合であるとして考えます。
例
サイコロを1つ振るという試行は,以下のように集合で表す事ができます。
\[ \begin{aligned} \text{全事象} &:\ \Omega = \{1,2,3,4,5,6\} \\ \text{1の目が出るという事象$A$} &:\ A = \{1\} \\ \text{偶数の目が出るという事象$B$} &:\ B = \{2,4,6\} \end{aligned} \]
【注意】
本来「任意の事象(事象とは?)を集合で表す(表すとは?)事が出来る」か否かといった事は数学的に議論出来る事ではありません。
従って,
\(\Omega\)を全事象を表す集合とする。
みたいな言い方は良くなくて,単に
\(\Omega\)は集合である。
と言うべきです。
本資料の解説文では,理解を助ける為に前者の様な書き方を多用しますので注意してください。
余事象
「\(A\)が起こらない」という事象を\(A\)の余事象と言います。
数学的には,集合\(A\)の\(\Omega\)上での補集合 \[ A^c = \{x\in\Omega\ |\ x\not\in A\} \] を\(A\)の余事象に対応する集合であると考える事ができます。

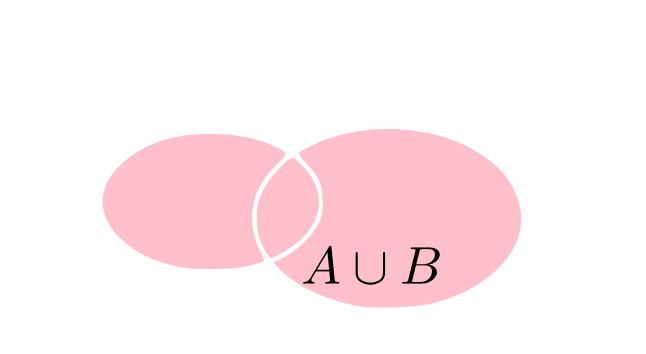
和事象
「\(A,B\)のいずれかが起こる」という事象を\(A,B\)の和事象と言います。
数学的には,集合\(A,B\)の和集合 \[ A\cup B = \{x\in\Omega | x\in A\ \text{または}\ x\in B\} \] を\(A,B\)の和事象に対応する集合であると考える事ができます。
積事象
「\(A,B\)が共に起こる」という事象を\(A,B\)の積事象と言います。
数学的には,集合\(A,B\)の積集合 \[ A\cap B = \{x\in\Omega | x\in A\ \text{かつ}\ x\in B\} \] を\(A,B\)の積事象に対応する集合であると考える事ができます。
同様に,加算個の事象\(A_1,A_2,\cdots\)に対してもその和事象・積事象を考える事が可能であるとすれば, 対応する集合は \[ \begin{aligned} \bigcup_{i=1}^{\infty}A_i &= A_1\cup A_2\cup \cdots \\ \bigcap_{i=1}^{\infty}A_i &= A_1\cap A_2\cap \cdots \end{aligned} \] となります。
有限個の集合の和集合・積集合も \[ \begin{aligned} A_1\cup \cdots \cup A_n &= A_1\cup\cdots \cup A_n\cup\color{yellow}{\phi\cup\phi\cdots} \\ A_1\cap \cdots \cap A_n &= A_1\cap\cdots \cap A_n\cap\color{yellow}{\Omega\cap\Omega\cdots} \\ \end{aligned} \] と表せますので,数学的には加算個の場合だけを考えれば十分です。
ド・モルガンの法則
集合\(A,B\)に対して \[ (A\cup B)^c = A^c \cap B^c,\qquad (A\cap B)^c = A^c \cup B^c \] が成り立つ。加算個の集合に対しては \[ \left(\bigcup_{i=1}^{\infty} A_i\right)^c = \bigcap_{i=1}^{\infty}A_i^c,\qquad \left(\bigcap_{i=1}^{\infty} A_i\right)^c = \bigcup_{i=1}^{\infty}A_i^c \] が成り立つ。
集合を事象と解釈するならば,\((A\cup B)^c = A^c \cap B^c\)という等式は, 「「\(A,B\)のいずれかが起こる」という事が起こらない」という事と 「\(A,B\)は共に起こらない」という事が同じ事象であるという意味になります。他の等式についても考えてみてください。
ド・モルガンの法則より \[ A_1\cap A_2\cap \cdots = (A_1^c\cup A_2^c\cup \cdots)^c \] という形で積集合は補集合・和集合で表せる事がわかります。
積集合の記法は今後も使いますが,原理的には補集合・和集合のみで全ての数学的な議論を進める事ができるという事になります。 これは特に証明を行う場合に便利です。
排反
「\(A,B\)が共に起こることはない」とき,事象\(A,B\)は排反であると言います。
数学的には集合\(A,B\)が互いに素であること,つまり \[ A\cap B = \phi \] である事として表現する事が出来ると考えられます。
さて,集合\(\Omega\)の部分集合のうち「事象」として考えたいものだけを集めた集合を\(\color{yellow}{\mathcal{F}}\)としましょう。
例
サイコロを1つ振るという試行の場合、\(\Omega=\{1,2,3,4,5,6\}\)として \[ \begin{aligned} \mathcal{F} &= 2^{\Omega} \\ &= \{\phi,\{1\},\{2\},\cdots,\{6\},\{1,2\},\{1,3\},\cdots,\{1,2,3,4,5,6\}\} \end{aligned} \] つまり\(\mathcal{F}=(\Omega\text{のべき集合})\)と置けば良いです。
今の例では,\(\Omega\)に対して \[ \mathcal{F} = 2^{\Omega}\quad\text{($\Omega$の部分集合全てからなる集合)} \] とおきましたが,こうでなければならない理由はありません。特に\(\Omega\)が無限集合の場合には\(\mathcal{F}=2^{\Omega}\)だと困る場合があります。
例
\(\mathcal{F}=2^{\Omega}\)でない有限集合での例を無理やり作ってみましょう。
「サイコロを振るけど,偶数か奇数かしか注目しない」というのならば \[ \mathcal{F} = \{\phi, \{1,3,5\},\{2,4,6\},\{1,2,3,4,5,6\}\} \] という集合を「事象の集合」として考える事ができます。
ということで\(\mathcal{F}\)はある程度自由に取れるわけですが,全く自由というわけではありません。
完全加法族
集合\(\mathcal{F}\)は以下の条件を満たすようなものだけを考える事とします。
集合\(\Omega\)のべき集合の部分集合\(\mathcal{F}\subset 2^{\Omega}\)が以下の条件を満たす時, \(\mathcal{F}\)を\(\Omega\)上の完全加法族と言う。
\[ \begin{aligned} 1. &\mathcal{F} \neq \phi \\ 2. &A\in\mathcal{F}\ \text{ならば}\ A^c\in\mathcal{F} \\ 3. &A_1,A_2,\cdots\in\mathcal{F}\ \text{ならば}\ \bigcup_{i=1}^{\infty}A_i \in \mathcal{F} \end{aligned} \]
\(\mathcal{F}\)を「事象の集合」と解釈すれば,条件1,2,3は以下のように解釈できます。
数学的な定義は難しく感じるかもしれませんが,上のようなイメージを持つことが出来れば当たり前に感じられるでしょう。
練習問題
\(\mathcal{F}\)が\(\Omega\)上の完全加法族の時
\[ \begin{aligned} &A_1,A_2,\cdots\in\mathcal{F}\ \text{ならば}\ \bigcap_{i=1}^{\infty}A_i \in\mathcal{F} \\ &\Omega,\phi \in \mathcal{F} \end{aligned} \]である事を証明してください。また,\(\mathcal{F}\)を事象の集合と解釈するならば,それぞれどのような意味でしょうか?
【証明】
1つ目はド・モルガンの法則より。
2つ目について。\(\mathcal{F}\neq\phi\)であることよりある\(A\in\mathcal{F}\)が存在する。よって
\[ \Omega = A\cup A^c \in \mathcal{F},\quad \phi = A\cap A^c \in \mathcal{F} \]
□
よく使われる完全加法族はべき集合\(2^{\Omega}\)と,ボレル集合族です。
ボレル集合族
\(\Omega=\mathbb{R}\)の場合,\((a,b)\)や\((a,\infty)\)や\((-\infty,a)\)など任意の開集合(端を含まない区間)を含む最小の完全加法族をボレル集合族といい
\[ \mathcal{B}(\mathbb{R})\]
などと書く。
\(n\)次ユークリッド空間\(\mathbb{R}^n\)に対しても同様に,その任意の開集合(境界を含まない集合)を含む最小の完全加法族\(\mathcal{B}(\mathbb{R}^n)\)が定義される。
難しく感じますが,数直線\(\mathbb{R}\)上の区間,平面\(\mathbb{R}^2\)内の図形,空間\(\mathbb{R}^3\)内の立体などで通常イメージするものを全て含んでいる集合だと思ってください。
確率空間
\(\Omega\)を集合,\(\mathcal{F}\)を\(\Omega\)上の完全加法族とする。
\(\mathcal{F}\)上の実数値関数\(P: \mathcal{F}\rightarrow\mathbb{R}\)が,
\[ \begin{aligned}
1. & P(A)\geq 0\\
2. & A_1,A_2,\cdots\text{が互いに素の時}\\
& P\left(\bigcup_{i=1}^{\infty}A_i\right) = \sum_{i=1}^{\infty}P(A_i) \qquad\color{yellow}{\text{(完全加法性)}}\\
3. & P(\Omega) = 1\\
\end{aligned} \]
を満たす時,\((\Omega, \mathcal{F}, P)\)の事を確率空間と言う。
\(\Omega\)を標本空間,\(\Omega\)の元を標本,\(\mathcal{F}\)の元を事象,特に\(\Omega\in\mathcal{F}\)を全事象と呼ぶ。\(\mathcal{F}\)の元が互いに素である時,それらは排反であるという。\(P\)を確率測度,\(P(A)\)を事象\(A\)の確率と呼ぶ。
再び,わかりやすく翻訳すれば
となります。
確率測度\(P\)はよく使うので,今後以下のような記号の濫用を行います。
\[ \begin{aligned} P(a) &= P(\{a\})\qquad (a\in\Omega) \\ P(\text{条件}) &= P(\{x\in\Omega\ |\ x\text{は(条件)を満たす}\}) \end{aligned} \]練習問題
確率測度\(P\)に対して \[ P(\phi) = 0 \] である事を示してください。
【証明】
\(\Omega = \Omega\cup\phi\cup\phi\cdots\)であり,\(\Omega,\phi\)は互いに素であるから,完全加法性より
\[ P(\Omega) = P(\Omega) + P(\phi) + P(\phi) + \cdots \]
である。よって
\[ 1 = 1 + P(\phi) + P(\phi) + \cdots \]
であるから
\[ P(\phi) = 0 \]
である。
□
有限加法性
\(P\)を確率測度とする。互いに素な事象\(A_1,\cdots,A_n\)に対して \[ P\left(\bigcup_{i=1}^{n}A_i\right) = \sum_{i=1}^nP(A_i) \] が成立する。
【証明】
\(A_1\cup\cdots \cup A_n = A_1\cup\cdots\cup A_n\cup\phi\cup\phi\cup\cdots\)であるので,完全加法性より
\[ \begin{aligned}
P(A_1\cup\cdots \cup A_n) &= P(A_1)+\cdots +P(A_n) + P(\phi) + P(\phi) + \cdots \\
&= P(A_1)+\cdots +P(A_n)\quad(\because P(\phi)=0)
\end{aligned} \]
□
集合\(X\)と,\(X\)上の完全加法族\(\mathcal{F}\)に対して,\(\mathcal{F}\)上の関数\(\mu:\mathcal{F}\rightarrow [0,\infty]\)が \[ \mu(\phi) = 0 \text{かつ完全加法的である} \] ならば,\(\mu\)を測度と呼びます。
測度は集合の大きさの抽象化と言え,集合の元の数・図形の面積・確率などの概念を包括しています。(ただし,有限加法性でなく完全加法性を考えるので直感の及ばないところまで一般化されます。)
この勉強会では前提としませんが,測度論の基礎的な知識があると確率・統計の理解も深まります。
練習問題
確率測度\(P\)について以下が成り立つ事を証明してください。 \[ \begin{aligned} & P(A^c) = 1-P(A) \\ & A\subset B\ \text{ならば}\ P(A)\leq P(B) \\ & A\subset B\ \text{ならば}\ P(B\setminus A)=P(B)-P(A)\quad(B\setminus A = B\cap A^c) \end{aligned} \]
【証明】
\(\Omega=A\cup A^c\)で\(A,A^c\)は互いに素だから
\[ P(\Omega)=P(A)+P(A^c)\ \Leftrightarrow\ P(A^c)=1-P(A) \]
\(A\subset B\)の時\(B=(B\cap A^c)\cup A\)であり,\(B\cap A^c, A\)は互いに素だから
\[ P(B)=P(B\cap A^c)+P(A)\ \Leftrightarrow\ P(B\setminus A)=P(B)-P(A) \]
また\(P(B\setminus A)\geq 0\)であるから\(P(A)\leq P(B)\)
□
練習問題:確率の加法定理
確率測度\(P\)について以下が成り立つことを証明してください。 \[ \begin{aligned} P(A\cup B) &= P(A)+P(B) - P(A\cap B) \\ P(A\cup B) &= P(A)+P(B)\qquad\text{($A,B$が排反のとき)} \end{aligned} \]
【証明】
\(A\cup B=A\cup (B\cap A^c)\)であり,\(A, B\cap A^c\)は互いに素だから
\[ P(A\cup B) = P(A) + P(B\cap A^c) \]
また\(B\cap A^c = B\setminus (A\cap B)\)であり\(A\cap B\subset B\)であるから
\[ P(B\cap A^c) = P(B)-P(A\cap B) \]
である。従って
\[ P(A\cup B) = P(A) + P(B)-P(A\cap B) \]
である。また\(A,B\)が排反の時は\(A\cap B=\phi\)であるから
\[ P(A\cup B)=P(A)+P(B)-P(\phi)=P(A)+P(B) \]
である。
□
確率測度の例
標本空間を有限集合\(\Omega\),\(\mathcal{F}=2^{\Omega}\)として, \[ P(A) = \frac{\#(A)}{\#(\Omega)} \quad\text{($\#(A)$は$A$の元の数)}\] とすれば,これは確率測度となります。
例
\(\Omega=\{1,2,3,4,5,6\}\)に対して上の確率測度を考えれば,サイコロの数学的なモデルとなります。
確率測度の例
より一般的な設定として,標本空間を有限集合\(\Omega = \{x_1,\cdots,x_n\}\),\(\mathcal{F}=2^{\Omega}\)として, \[ P(x_1) + \cdots + P(x_n)=1 \] となる様に各\(P(x_i)\geq 0\)の値を定めれば確率測度\(P\)が定まります。
例
例えば,いびつなコインを \[ \begin{aligned} &\Omega=\{\text{表},\text{裏}\},\quad\mathcal{F}=2^{\Omega}\\ &P(\text{表})=\frac{51}{100},\ P(\text{裏})=\frac{49}{100} \end{aligned} \] のような確率測度でモデル化する事ができます。
確率測度の例
\(\Omega=\mathbb{R},\ \mathcal{F}=\mathcal{B}(\mathbb{R})\)として, 定数\(a,b\ (a < b)\)を定めて,区間\((a,b)\)に含まれる区間\((x,y)\)に対して \[ P((x,y)) = \frac{y-x}{b-a} \] 区間\((a,b)\)と交わらない集合\(A\)について\(P(A)=0\)と定義すれば確率測度\(P\)が定まります。
例
区間\((0,1)\)からランダムに実数\(x\)を選んだ場合,\(0.3 < x < 0.5\)である確率は \[ P((0.3,0.5)) = \frac{0.5-0.3}{1-0} = 0.2 \] と計算されます。
練習問題
今の確率測度\(P\)に関して, \[ \begin{aligned} P(x) &= 0 \qquad (x\in\mathbb{R})\\ P([x,y]) &= P((x,y)) \\ \end{aligned} \] である事を示してください。
【証明】
\(\mathbb{R} = (-\infty,x)\cup\{x\}\cup(x,\infty)\)より
\[ 1 = P((-\infty,x))+P(x) + P((x,\infty)) \]
である。\(x\in(a,b)\)の時は
\[ P((-\infty,x))=P(a,x)=\frac{x-a}{b-a},\ P((x,\infty))=P(x,b)=\frac{b-x}{b-a} \]
なので\(P((-\infty,x))+P((x,\infty))=1\)となるから\(P(x)=0\)。他の場合も同様。
また, \([a,b]=\{a\}\cup(a,b)\cup\{b\}\)であるから
\[ P([a,b])=P(a)+P((a,b))+P(b)=P((a,b)) \]
□
今の練習問題から \[ \color{yellow}{ P(A) = 0\ \text{は事象$A$が起こらないという事ではない}} \] という事がわかります。同様に \[ \color{yellow}{ P(A)=1\ \text{は事象$A$が絶対起こるという事ではない}} \] という事もわかります。
例えば,\((0,1)\)から実数をランダムに選んだ場合\(0.5\)が選ばれる確率は \[ P(0.5) = 0 \] となりますが,これが\(0.5\)が決して選ばれないという事を意味するとは考えにくいです。
確率変数・確率分布
確率変数
\((\Omega,\mathcal{F},P)\)を確率空間とする。
\(\Omega\)上の実数値関数\(X: \Omega\rightarrow\mathbb{R}\)を確率変数という。
\(X\)が確率変数ならば,任意の実数値関数\(f: \mathbb{R}\rightarrow\mathbb{R}\)について\(f\circ X\)も確率変数となる。これを\(f(X)\)を書く。
例
サイコロを振る試行において \[ X = \left\{\begin{array}{ll} 1 & (\text{$1$が出た時}) \\ 0 & (\text{$1$以外が出た時}) \\ \end{array}\right. \] と置けばこれは確率変数\(X\)となります。
この時,\(\Omega_X=\{0,1\},\ \mathcal{F}_X=2^{\Omega_X}\) \[ P_X(0)=\frac56,\ P_X(1)=\frac16\] と置けば新たな確率空間\((\Omega_X,\mathcal{F}_X,P_X)\)を作る事ができることに注意しましょう。確率変数\(X\)を定めると,\(X\)の値を標本とする確率空間を新たに作ることができます。
確率分布
確率空間\((\mathbb{R},\mathcal{B}(\mathbb{R}),P)\)を確率分布と言う。(より一般に,確率空間\((\mathbb{R}^n,\mathcal{B}(\mathbb{R}^n),P)\)を確率分布と言う。)
確率分布では,確率密度関数で表されるものが重要です。
確率密度関数
ある非負実数値関数\(\rho:\mathbb{R}\rightarrow\mathbb{R}\)が存在して,区間\((a,b)\)に対する確率測度が \[ P((a,b)) = \int_a^b \rho (x)\mathrm{d}x \] と表されるならば,\(\rho\)をこの確率分布の確率密度関数と言う。
(標本空間として\(\mathbb{R}^n\)をとった場合には、重積分で定義されます。)
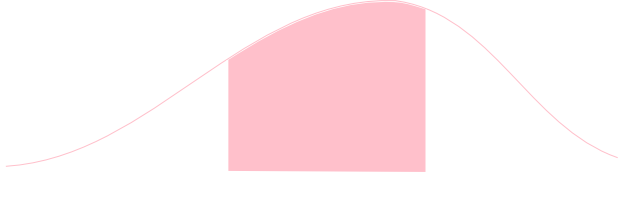
離散的な確率分布
確率分布の定義では標本空間が\(\mathbb{R}\)なので,離散的な値を取る確率分布をどうするのか疑問であると思います。
この場合,例えばサイコロをモデル化するのであれば \[ \begin{aligned} &P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=\frac16\\ &P(A) = 0\quad(\text{$1,2,3,4,5,6\not\in A$のとき}) \end{aligned} \] という確率測度を考えれば良いです。
離散的な確率分布の場合も確率質量関数と呼ばる概念を考える事が出来ますが,
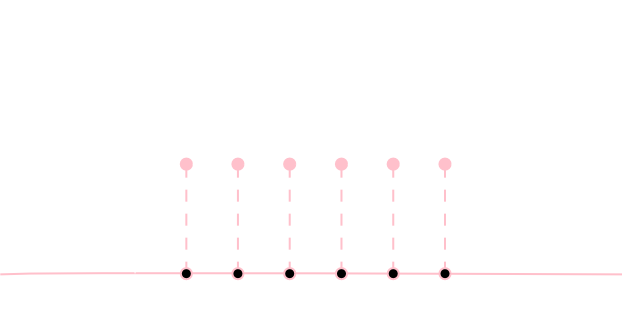
もっとわかりやすく、離散的な確率分布とは \[ \begin{array}{|c|c|c|c|}\hline X & x_1 & x_2 & \cdots \\ \hline P(X=x_i) & p_1 & p_2 & \cdots \\ \hline \end{array} \] という表の事だと考えて下さい。
期待値
離散的な確率分布における期待値
離散的な確率分布
\[ \begin{array}{|c|c|c|c|}\hline
X & x_1 & x_2 & \cdots \\ \hline
P(X=x_i) & p_1 & p_2 & \cdots \\ \hline
\end{array} \]
上の確率変数\(f(X)\)の期待値は
\[ E[f(X)] = \sum_{i=1}^{\infty}f(x_i)p_i \]
である。
(無限和で書いていますが,特別な場合として有限和も含みます。あるところから先を\(p_{n+1}=p_{n+2}=\cdots = 0\)とすれば良いです。)
例
サイコロの出目\(X\)の確率分布 \[ \begin{array}{|c|c|c|c|c|c|c|}\hline X & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline P(X=x_i) & \frac16&\frac16&\frac16&\frac16&\frac16&\frac16\\ \hline \end{array} \] において,\(f(X)=X^2\)の期待値を考えてみましょう。
\[\begin{aligned} E[X^2] &= 1^2\cdot\frac16 + 2^2\cdot\frac16 + 3^2\cdot\frac16 + 4^2\cdot\frac16 + 5^2\cdot\frac16 + 6^2\cdot\frac16\\ &= \frac{91}{6} \end{aligned} \]
連続的な確率分布における期待値
確率分布\((\mathbb{R},\mathcal{B}(\mathbb{R}),P)\)において,確率測度が確率密度関数\(\rho(x)\)を用いて表されるならば,\(f\)の期待値は \[ E[f(X)] = \int_{-\infty}^{\infty}f(x)\rho(x)\mathrm{d} x\] である。
例
確率密度関数が
\[ \rho(x) = \left\{\begin{array}{ll}
2x & (0\leq x \leq 1\text{のとき}) \\
0 & (\text{それ以外のとき})
\end{array}\right. \]
である分布において,\(f(X)=X\)の期待値を考えてみましょう。
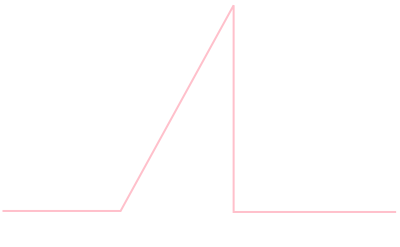
\[ E[X] = \int_{-\infty}^{\infty}x\rho(x)\mathrm{d} x = \int_0^12x^2\mathrm{d}x = \frac{2}{3} \]
平均・分散・標準偏差
期待値\(E[X]\)を,その確率分布の平均という。
平均が\(\mu=E[X]\)である時,期待値\(V[X] = E[(X-\mu)^2]\)を,その分布の分散と言い,分散の平方根\( \sigma[X] = \sqrt{V[X]}\) を標準偏差という。
分散は,確率分布の平均の周りの広がり具合を数量化したものです。
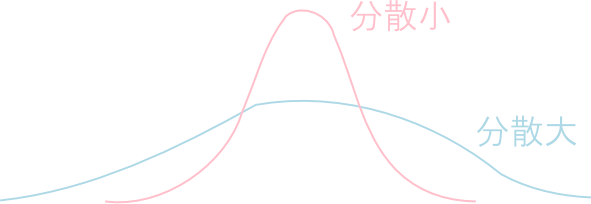
例
サイコロの出目\(X\)の確率分布 \[ \begin{array}{|c|c|c|c|c|c|c|}\hline X & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline P(X=x_i) & \frac16&\frac16&\frac16&\frac16&\frac16&\frac16\\ \hline \end{array} \] の平均・分散・標準偏差を調べましょう。
平均は \[ E[X] = 1\cdot\frac16 + 2\cdot\frac16 + 3\cdot\frac16 + 4\cdot\frac16 + 5\cdot\frac16 + 6\cdot\frac16 = \frac72\] 分散は \[ V[X] = E[(X-7/2)^2] = (1-7/2)^2\cdot\frac16 + \cdots + (6-7/2)^2\cdot\frac16 = \frac{35}{12} \] 標準偏差は \[ \sigma[X] = \sqrt{\frac{35}{12}} \approx 1.7 \]
練習問題
確率密度関数 \[ \rho(x) = \left\{\begin{array}{ll} 1 & \text{($0\leq x \leq 1$のとき)} \\ 0 & \text{(それ以外)} \end{array}\right. \] で定まる確率分布の平均・分散・標準偏差を求めて下さい。
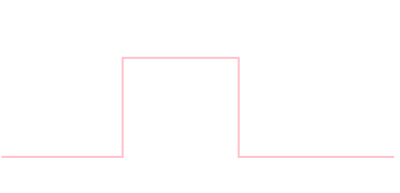
【答え】
平均\(1/2\),分散\(1/12\),標準偏差\(1/2\sqrt{3}\approx 0.29\)
期待値の線型性
有限値を取る確率変数\(X,Y\),定数\(a,b\)について \[ E[aX+bY] = aE[X] + bE[Y] \] が成立する。
これは総和・積分の性質より直ちに言えます。
分散の計算公式
\[ V[X] = E[X^2] - (E[X])^2 \]
【証明】
\(\mu = E[X]\)とおくと
\[ \begin{aligned}
V[X]&= E[(X-\mu)^2] = E[X^2-2\mu X+\mu^2]=E[X^2]-2\mu E[X]+\mu^2E[1] \\
&= E[X^2]-2(E[X])^2+(E[X])^2\times 1 \\
&= E[X^2] - (E[X])^2
\end{aligned} \]
□
同時確率・周辺化
同時確率
事象\(A_1,\cdots,A_n\)に対して \[ P(A_1\cap \cdots \cap A_n) \] を\(A_1,\cdots,A_n\)の同時確率と言い, \[ P(A_1,\cdots,A_n) \] と書く。
同時確率\(P(X\in A,Y\in B)\)が \[ P(X\in A,Y\in B) = \int_B\int_A\rho(x,y)\mathrm{d}x\mathrm{d}y \] と表される時,\(\rho(x,y)\)を同時確率密度関数という。3変数以上でも同様である。
互いに素な集合\(B_1,B_2,\cdots,\)について \[ B_1\cup B_2\cup \cdots = \Omega\] と表されるならば, \[ (A\cap B_1)\cup (A\cap B_2) \cup \cdots = A \] が成立します。この左辺の各集合もやはり互いに素なので \[ P(A\cap B_1) + P(A\cap B_2) + \cdots = P(A) \] が成立します。
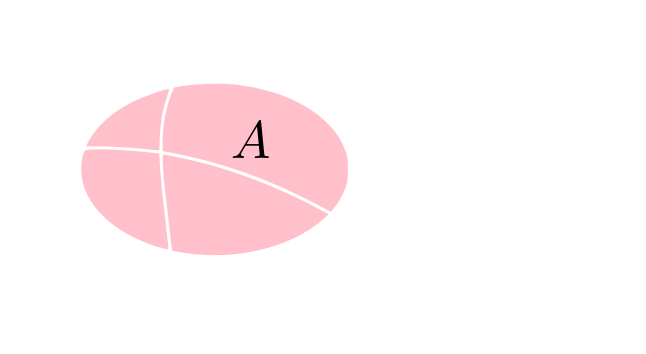
ここでは同時確率\(P(A, B_i)\)を\(B_i\)について全て足し込んで,\(A\)の確率だけ求める(\(B\)を消去する)という事をしています。この作業を同時確率の周辺化と言います。特に,確率変数に関する周辺化が重要です。
同時確率の周辺化
確率変数\(X,Y\)に関する同時確率の,変数\(Y\)の値域全体での和を取る操作を周辺化という。
すなわち,離散的な確率分布における周辺化は \[ P(X=x) = \sum_{i=1}^{\infty}P(X=x, Y=y_i) \] と行い, 同時確率密度関数\(\rho\)で表される分布における周辺化は \[ P(X\in A) = \int_A\int_{-\infty}^{\infty}\rho(x, y)\mathrm{d}y\mathrm{d}x \] と行う。変数が増えても同様である。
練習問題
いびつなコイン\(A,B\)を投げた時の表・裏の出方が,以下の確率分布表に従っていたとします。 \[ \begin{array}{|c|cc|} \hline & \text{$A$:表} & \text{$A$:裏} \\ \hline \text{$B$:表} & 0.18 & 0.42 \\ \text{$B$:裏} & 0.12 & 0.28 \\ \hline \end{array} \] これを周辺化してください。
\[ P(A:\text{表}) = P(A:\text{表}, B:\text{表}) + P(A:\text{表}, B:\text{裏}) = 0.18 + 0.12 = 0.3 \] 従って\(P(A:\text{裏}) = 0.7\) \[ P(B:\text{表}) = P(A:\text{表}, B:\text{表}) + P(A:\text{裏}, B:\text{表}) = 0.18 + 0.42 = 0.6 \] 従って\(P(B:\text{裏})=0.4\)
確率変数\(X_1,X_2,\cdots,X_n\)を持つ分布に関する確率計算は
- 一旦,同時確率\( P(X_1,X_2,\cdots,X_n) \)を求める。
- それを周辺化して知りたい事象の確率を求める。
という手順で行われる事がよくあります。
ここで,周辺化とは非常に計算量の多い作業であるということに注意しましょう。多くの変数についての総和・重積分を計算しなければならない為です。
そこで,後で説明する「事象の独立性」を使って周辺化する変数の数を減らしたり,モンテカルロ法などの高速な近似積分法を使う事が必要となります。
条件付き確率・独立性・ベイズの定理
条件付き確率
\(P(A) > 0\)である時, \[ P(B\ |\ A) = \frac{P(A, B)}{P(A)} \] を\(A\)の下での\(B\)の条件付き確率と言う。
例
サイコロを振って奇数が出た時に,それが\(4\)以上である確率を計算しましょう。
\[ \begin{aligned} P(\text{$4$以上}\ |\ \text{奇数}) &= \frac{P(\text{$4$以上の奇数})}{P(\text{奇数})} \\ &= \frac{\frac{1}{6}}{\frac{3}{6}} = \frac13 \end{aligned} \]
サイコロを振って奇数が出た時に,それが\(4\)以上である確率
とは一体何でしょうか?サイコロを振った時点でそれが\(4\)以上か否かは確定しているはずです。
この確率は主観的確率として解釈する事が可能です。つまり,何も知らない状態では \[ P(\text{$4$以上}) = \frac12 \] であったのが,「奇数が出た」という新たな情報を得ることによって \[ P(\text{$4$以上}\ |\ \text{奇数が出た}) = \frac13 \] に確信度が改訂されたのだと考える事が出来ます。
確率の常法定理
\(P(A) > 0\)のとき \[ P(A,B) = P(A)P(B|A) \] が成立する。
一般に \[ \begin{aligned} P(A_1,\cdots,A_n) = &P(A_1)P(A_2|A_1)P(A_3|A_1,A_2)\\ &\cdots P(A_n|A_1,\cdots,A_{n-1}) \end{aligned} \] が成立する。
独立性
事象\(A,B\)に対して, \[ P(A\cap B) = P(A)P(B) \] が成立する時,これらの事象は独立であるという。そうでない時は従属であるという。
\(P(A) > 0\)であるならば\(A,B\)が独立であるということは \[ P(B) = P(B|A) \] を意味します。これは事象\(A\)が生じたという情報を得ても,事象\(B\)については何もわからないということだと解釈する事が出来ます。
ベイズの定理
ベイズの定理
\(P(A),P(B)>0\)の時 \[ P(B|A) = \frac{P(B)P(A|B)}{P(A)} \] が成立する。
【証明】
確率の常法定理より\(P(A),P(B)>0\)ならば
\[ P(A,B) = P(A)P(B|A) = P(B)P(A|B) \]
が成立するので両辺を\(P(A)\)で割る。
□
ベイズの定理は純粋に数学的に導かれる定理ですが,主観的解釈と共に利用される事が多いです。
つまり,事象\(A\)が生じたという情報を得た事による,事象\(B\)が起きているという事の確信度\(P(B)\)の確信度\(P(B|A)\)への更新は \[ \color{yellow}{ P(B|A) = P(B)\times\frac{P(A|B)}{P(A)} } \] によって行われるべきだという事です。
この意味で\(P(B)\)を事前確率,\(P(B|A)\)を事後確率と言います。
等式 \[ \color{yellow}{ P(B|A) = P(B)\times\frac{P(A|B)}{P(A)} } \] の意味をもっとよく考えてみましょう。
\(B\)であるという条件下で\(A\)が通常より起こり難いならば, \[ P(A|B) < P(A) \] となります。従って,この時は \[ P(B|A) < P(B) \] となります。これは「\(B\)という条件下では起こり難いはずの\(A\)が起こる」と「\(B\)であるという確信度が低下する」という事です。
\(P(A|B) > P(A)\)の場合も同様の解釈を行う事が出来ます。
確率の常法定理を使えば,同時確率の周辺化は \[ P(B)=\sum_{i=1}^{\infty}P(B,A_i) = \sum_{i=1}^{\infty}P(A_i)P(B|A_i) \] と書けます。これを使って,ベイズの定理を書き換えた形もよく利用されます。
ベイズの定理
\(B_1,B_2,\cdots\)が互いに素で,\(\Omega=B_1\cup B_2\cup\cdots\)であるならば \[ P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\displaystyle\sum_{i=1}^{\infty}P(B_i)P(A|B_i)} \] である。
練習問題
ある検査を受けた時に
- ガンだと診断されるという事象を\(A\)
- 実際にガンであるという事象を\(B\)
とします。 \[ P(A|B) = 0.99,\quad P(A|B^c) = 0.005,\quad P(B)=0.001 \] であるとき,ガンだと診断された時に実際にガンである確率を求めて下さい。
【答え】
\[ \begin{aligned}
P(B|A) &= \frac{P(B)P(A|B)}{P(B)P(A|B)+P(B^c)P(A|B^c)} \\
&= \frac{0.001\times 0.99}{0.001\times 0.99 + 0.999\times 0.005} \\
&\approx 16.5\%
\end{aligned} \]
今回はここで終わります。
次回は二項分布・正規分布・ポアソン分布他重要な確率分布,大数の法則,中心極限定理など重要な定理の紹介を行います。