プログラマの為の
数学勉強会
第11回
(於)ワークスアプリケーションズ中村晃一
2013年11月21日
謝辞
この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この資料について
- http://nineties.github.com/math-seminar に置いてあります。
- SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
- 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
- サンプルプログラムはPython及びMaximaで記述しています。
連立一次方程式の反復解法
連立一次方程式 \[ A\mathbf{x} = \mathbf{b} \] の解法として,ガウス消去法やLU分解法などの直接解法は既に紹介しました。 直接解法はメモリの消費が大きいので,直接解法は比較的サイズが小さい連立方程式に向いています。
一方,反復解法はサイズが大きく・係数が疎な(係数に0が多い)連立方程式に向いています。
疎行列
成分がほとんど0の行列を疎行列と言います。現実の問題で現れる行列の多くが疎です。 疎行列は0でない成分の値と場所のみで表現できるので,記憶容量を抑えることができます。
\[ \begin{pmatrix} 0 & 1 & 0 & 0 \\ 3 & 2 & 0 & 0 \\ 0 & 5 & 0 & 1 \\ 0 & 2 & 4 & 0 \end{pmatrix}\ \rightarrow\ \left\{\begin{array}{ll} \text{値}: &[1, 3, 2, 5, 1, 2, 4] \\ \text{行番号}: &[1, 2, 2, 3, 3, 4, 4] \quad\text{(これを更に圧縮)}\\ \text{列番号}: &[2, 1, 2, 2, 4, 2, 3] \end{array}\right. \] 行優先のCSR(Compressed Sparse Row)方式,列優先のCSC(Compressed Sparse Column)方式などいくつかの表現方式があります。
疎行列では,行列演算の計算量を比較的抑える事ができます。特に, \[ A\mathbf{x}\ \text{や}\mathbf{x}^TA \] という形の行列とベクトルの積を高速に計算する事ができます(\(\mathcal{O}(\text{非零要素数})\)のオーダー)。
反復解法
反復解法とは収束する数列 \[ x_0,\ x_1=f(x_0),\ x_2=f(x_1),\ x_3=f(x_2),\ \cdots \] を途中で打ち切る事によって,方程式 \[ \color{yellow}{x = f(x)} \] の近似解を求める手法です。第4回には線形反復法やニュートン法などの反復解法を紹介しました。
連立一次方程式 \[ A\mathbf{x}=\mathbf{b} \] に対しては,適当な行列\(C\)によって \[ \color{yellow}{\mathbf{x}_{i+1} = \mathbf{x}_i - C(A\mathbf{x}_{i}-\mathbf{b}) = (E-CA)\mathbf{x}+C\mathbf{b}} \] という漸化式を作ります。
仮に\(C=A^{-1}\)であれば \[ \mathbf{x}_{i+1} = \mathbf{x}_i - A^{-1}A\mathbf{x}_{i}+A^{-1}\mathbf{b} = A^{-1}\mathbf{b} \] となるので,一回で真の解に収束します。そこで,\(C\)は\(A^{-1}\)に出来るだけ近いものを取れば良いだろうと考えられます。
ヤコビ法
行列\(A\)の対角成分が全て非零であるとする。\(A\)の対角だけ取り出した対角行列を\(D\)として \[ \mathbf{x}_{i+1}=\mathbf{x}_i-D^{-1}(A\mathbf{x}_i-\mathbf{b})=(E-D^{-1}A)\mathbf{x}_i+D^{-1}\mathbf{b} \] により反復する解法をヤコビ法と言う。 初期値は\(\mathbf{x}_0 = \mathbf{0}\)とすれば良い。
例
\[ \begin{pmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} \] をヤコビ法で解いてみましょう。
\[ \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix}^{-1} = \frac{1}{2}\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \] なので \[ \begin{aligned} \begin{pmatrix} x_{i+1} \\ y_{i+1} \\ z_{i+1} \end{pmatrix} &= \begin{pmatrix} x_i \\ y_i \\ z_i \end{pmatrix} - \frac{1}{2} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}^{-1} \left\{ \begin{pmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{pmatrix} \begin{pmatrix} x_i \\ y_i \\ z_i \end{pmatrix} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} \right\} \\ &= \begin{pmatrix} 0 & 1/2 & 0 \\ 1/2 & 0 & 1/2 \\ 0 & 1/2 & 0 \\ \end{pmatrix} \begin{pmatrix} x_i \\ y_i \\ z_i \end{pmatrix} + \begin{pmatrix} -1/2 \\ 0 \\ 3/2 \end{pmatrix} \end{aligned} \] によって反復を行えば良いです。
計算してみると以下のようになります。厳密解は\((x,y,z)=(0,1,2)\)です。
>>> import numpy as np
>>> from numpy import linalg as LA
>>> A = np.array([[2,-1,0],[-1,2,-1],[0,-1,2]])
>>> b = np.array([-1,0,3])
>>>
>>> D = np.diag(np.diag(A)) # 対角だけ取り出す
>>> D
array([[2, 0, 0],
[0, 2, 0],
[0, 0, 2]])
>>> P = np.identity(3) - LA.inv(D).dot(A) # E-D^(-1)A を計算しておく
>>> q = LA.inv(D).dot(b) # D^(-1)b を計算しておく
>>> x = np.array([0,0,0])
>>> for i in range(100): # 反復回数には上限を定める事
... new_x = P.dot(x) + q
... if LA.norm(new_x-x) < LA.norm(new_x) * 1.0e-10: # 相対誤差で収束判定
... break
... x = new_x
...
>>> i
64 # 64回で収束した
>>> x
array([ -2.32830644e-10, 1.00000000e+00, 2.00000000e+00])
上のコードでは簡単の為,終了条件を\( |\mathbf{x}_{i+1}-\mathbf{x}_i|/|\mathbf{x}_{i+1}| < \varepsilon \)としていますが,\(\mathbf{x}_i\)の第\(k\)成分を\(x_k^{(i)}\)として \( \max_k\frac{|x_k^{(i+1)}-x_k^{(i)}|}{|x_k^{(i+1)}|} < \varepsilon \) とする方が一般的だと思います(成分毎の誤差を抑えられる)。
収束性
反復解法はいつでも収束するわけではありません。その収束性は固有値と関係します。
\[ \mathbf{x}_{i+1}=A\mathbf{x}_i+\mathbf{b} \] で反復を行うとします。求める真の解を\(\mathbf{x}\)とすれば \[ \mathbf{x}=A\mathbf{x}+\mathbf{b} \] が成り立つので差を取れば \[ (\mathbf{x}-\mathbf{x}_{i+1})=A(\mathbf{x}-\mathbf{x}_i) \] となります。従って真の解との誤差\(\mathbf{e}_i = \mathbf{x}-\mathbf{x}_i\)は \[ \mathbf{e}_{i+1} = A(\mathbf{e}_i)\ \Rightarrow \color{yellow}{\mathbf{e}_i = A^i\mathbf{e}_0} \] で得られますから \[ \lim_{i\rightarrow\infty}A^i\mathbf{e}_0 = \mathbf{0} \] であれば,収束するということになります。
ここで\(A\)が固有ベクトル\(\mathbf{v}_1,\cdots,\mathbf{v}_n\)からなる基底を持つ場合を考えます。対応する固有値を\(\lambda_1,\cdots,\lambda_n\)とします。
誤差\(\mathbf{e}_i\)の第\(k\)成分を\(e_k^{(i)}\)と表せば前回説明した通り \[ \mathbf{e}_i = A^i\mathbf{e}_0\ \Leftrightarrow\ \color{yellow}{e_k^{(i)} = \lambda_k^i e_k^{(0)}} \] となるので各固有値\(\lambda_k\)について \[ (\lambda_k)^i\ \rightarrow\ 0 \] である事が誤差が0に収束する十分条件となります。その為には\(|\lambda_k|\)の最大値が1未満であれば良いです。
スペクトル半径
行列\(A\)の固有値の絶対値の最大値をスペクトル半径という。スペクトル半径が1未満であれば,任意の\(\mathbf{b}\)に対して \[ \mathbf{x}_{i+1}=A\mathbf{x}_i+\mathbf{b} \] で定まる数列は収束する。
スペクトル半径の計算は面倒である事が多いのですが,ヤコビ法に関しては以下の事実が知られています。
ヤコビ法の収束条件
\(n\)次正方行列\(A\)が,各\(i = 1,\cdots,n\)について \[ |a_{ii}| > \sum_{j\neq i} | a_{ij} | \] を満たす時,\(A\)は優対角であるという。
\(A\)が優対角であれば,方程式 \[ A\mathbf{x} = \mathbf{b} \] に対するヤコビ法は必ず収束する。
ヤコビ法を改良したガウス・ザイデル法では \[ A=L+D+U\qquad\text{($D$は$A$の対角,$L$は対角より下の部分,$U$は上)} \] と分解して\(C = (L+D)^{-1}\)と置きます。すると \[ \begin{aligned} &\mathbf{x}_{i+1}=\mathbf{x}_i - (L+D)^{-1}(A\mathbf{x}_i-\mathbf{b}) \\ \Leftrightarrow & \color{yellow}{\mathbf{x}_{i+1}=D^{-1}(-L\mathbf{x}_{i+1}-U\mathbf{x}_i+\mathbf{b})} \\ \end{aligned} \] という陰的な方程式が得られますが,\(L\)が下三角なので第1行目から順番に解くことができます。
更にガウス・ザイデル法を改良して, \[C = (L+ D/\omega)^{-1}\qquad (0 < \omega < 2) \] とする逐次過大緩和法(SOR)法など様々な手法が存在します。
詳しくは専門書を参照してください。
二次形式
二次形式
変数の2次の項のみで表される多項式 \[ \begin{aligned} f(x_1) &= ax_1^2 \\ f(x_1,x_2) &= ax_1^2 + bx_2^2 + cx_1x_2 \\ f(x_1,x_2,x_3) &= ax_1^2 + bx_2^2 + cx_3^2 + dx_1x_2 + ex_2x_3 + fx_3x_1\\ \vdots \end{aligned} \] を二次形式と呼びます。後の話に必要となる話題だけ説明をします。 また,全ての変数・係数は実数であるとします。
まず,全ての二次形式は \[ \begin{aligned} f(x_1) &= ax_1^2 \\ f(x_1,x_2) &= ax_1^2 + bx_2^2 + \frac{c}{2}x_1x_2 + \frac{c}{2}x_2x_1\\ f(x_1,x_2,x_3) &= ax_1^2 + bx_2^2 + cx_3^2 + \frac{d}{2}x_1x_2 +\frac{d}{2}x_2x_1\\ & + \frac{e}{2}x_2x_3 + \frac{e}{2}x_3x_2 + \frac{f}{2}x_3x_1 + \frac{f}{2}x_1x_3\\ \end{aligned} \] のように,\(x_ix_j\)と\(x_jx_i\)の係数が等しい多項式として書き直す事ができます。よって2次形式は \[ \color{yellow}{ f(\mathbf{x}) = \sum_{i,j} a_{ij}x_ix_j\qquad (a_{ij} = a_{ji})} \] と書くことができます。
さらに,二次形式 \[ f(\mathbf{x}) = \sum_{i,j} a_{ij}x_ix_j\qquad (a_{ij} = a_{ji}) \] に対して \[ A=(a_{ij})\] と置けば \[ \color{yellow}{f(\mathbf{x}) = \mathbf{x}^TA\mathbf{x}} \] と書き表される事がわかります。更に\(a_{ij}=a_{ji}\)より\(A\)は対称行列です。
二次形式
任意の二次形式は,実対称行列(実数成分の対称行列)\(A\)を用いて \[ f(\mathbf{x})= \mathbf{x}^TA\mathbf{x} \] と表す事ができる。
例
\[ f(x,y) = x^2 + 3xy + 2y^2 \] を行列で表してみましょう。\[ f(x,y) = x^2 + \frac{3}{2}xy + \frac{3}{2}yx + 2y^2 \] なので \[ f(x,y) = \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 1 & \frac{3}{2} \\ \frac{3}{2} & 2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \] と表す事ができます。
ここで,実対称行列の性質をいくつか確認しておきましょう。
実対称行列の固有値は全て実数である
【証明】
行列・ベクトルの成分を全て複素数範囲で考える。また複素共役を\(\overline{(\ -\ )}\)で表す。
\[ A\mathbf{v} = \lambda\mathbf{v} \]
ならば
\[ \lambda\mathbf{\overline{v}}^T\mathbf{v} = \mathbf{\overline{v}}^T\lambda\mathbf{v} = \mathbf{\overline{v}}^TA\mathbf{v} = (A\mathbf{\overline{v}})^T\mathbf{v}
= (\overline{A\mathbf{v}})^T\mathbf{v} = (\overline{\lambda\mathbf{v}})^T\mathbf{v} = \overline{\lambda}\mathbf{\overline{v}}^T\mathbf{v} \]
となるので,\(\mathbf{\overline{v}}^T\mathbf{v} = ||\mathbf{v}||^2\neq 0\)であることより
\[ \lambda = \overline{\lambda} \]
である。すなわち\(\lambda\)は実数。
□
実対称行列は直交行列により対角化可能である。
すなわち,\(A\)が実対称行列ならばある直交行列\(P\)が存在して
\[ P^TAP \]
が固有値を対角成分に持つ対角行列となる。
【証明】
\(n\)次実対称行列\(A\)について,数学的帰納法で証明する。
\(n=1\)の時の成立は明らかなので,\(n \geq 2\)の場合を考える。
前頁の定理より,\(A\)の固有値\(\lambda \in\mathbb{R}\)を1つとれる。
\(\lambda\)の固有ベクトルの1つを\(\mathbf{v}_1\)とし,\(\mathbf{v}_1\)を含む正規直交基底
\[ \{\mathbf{v}_1,\cdots,\mathbf{v}_n\} \]
をとる。ここで
\[ Q = (\mathbf{v}_1,\cdots,\mathbf{v}_n) \]
とおけば,これは直交行列であり\(\mathbf{v}_1\)が\(A\)の固有値であることから
\[ Q^TAQ \]
の一列目は\((\lambda,0,\cdots,0)^T\)となる。更に
\[ (Q^TAQ)^T = Q^TA^T(Q^T)^T = Q^TAQ \]
であるから,
\[ Q^TAQ = \begin{pmatrix}
\lambda & \\
& A'
\end{pmatrix} \]
という形である。ここで帰納法の仮定から直交行列\(R\)が存在して
\[ R^TA'R = \Lambda \]
という対角化が可能であるから
\[ P = Q\begin{pmatrix}
1 & \\
& R
\end{pmatrix} \]
とおけば良い。対角化が可能である時,対角成分が固有値である事は前回説明した通り。
□
では、二次形式の話に戻ります。実対称行列\(A\)を \[ A=P^T\Lambda P \] と直交行列で対角化したならば \[ f(\mathbf{x})=\mathbf{x}^TA\mathbf{x} = \mathbf{x}^TP^T\Lambda P\mathbf{x} = (P\mathbf{x})^T\Lambda(P\mathbf{x}) \] となりますから,\(\mathbf{y}=P\mathbf{x}\)と置けば \[ \color{yellow}{ f(\mathbf{x})=\mathbf{y}^T\Lambda\mathbf{y} = \lambda_1y_1^2 + \lambda_2y_2^2 + \cdots + \lambda_ny_n^2} \] と単純化できます。これを二次形式の標準形と言います。
例
\[ f(x,y) = x^2 + y^2 - xy \] を標準形に変換しましょう。対応する行列は \[ \begin{pmatrix} 1 & -1/2 \\ -1/2 & 1 \end{pmatrix} = \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix}^T \begin{pmatrix} 3/2 & 0 \\ 0 & 1/2 \end{pmatrix} \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \] と直交行列で対角化する事ができるので \[ \color{yellow}{ f(x,y) = \frac{3}{2}s^2 + \frac{1}{2}t^2\quad\left( s = \frac{x-y}{\sqrt{2}},\ t = \frac{x+y}{\sqrt{2}}\right)} \] となります。
今の例題の応用ですが,曲線 \[ x^2+y^2-xy=1\cdots (1)\] を作図したい場合には,\((x,y)\longmapsto(s,t)\)の座標変換を行って \[ \frac{3}{2}s^2+\frac{1}{2}t^2 = 1 \] とします。これは\(st\)平面における長半径\(\sqrt{2}\),短半径\(\sqrt{2/3}\)の楕円です。
ところで,直交変換は図形の形状を保つ(基底の直交性と長さを保つから)事がわかるので\(xy\)平面においても(1)の表す曲線は同じ楕円であるということになります。
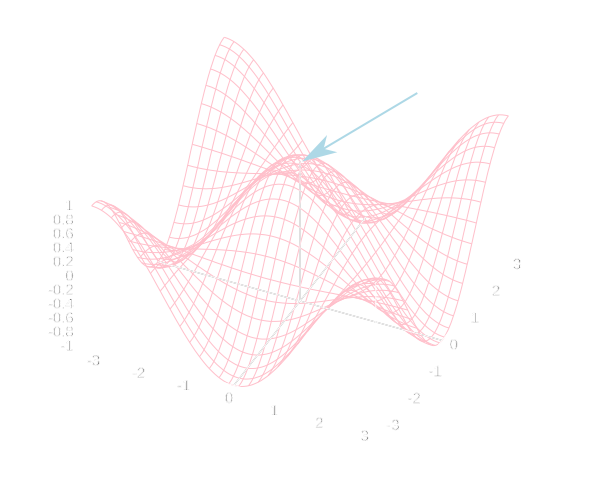
多変数関数の極値
各種最適化問題は,関数の最大値・最小値を求める事に帰着するので,極値の理解が重要となるというのはこれまで説明した通りです。
復習すると,十分滑らかな一変数関数\(y=f(x)\)に関しては \[ \begin{aligned} f'(a)=0,\ f''(a) < 0\ &\Rightarrow\ f(a)\text{は極大値} \\ f'(a)=0,\ f''(a) > 0\ &\Rightarrow\ f(a)\text{は極小値} \\ \end{aligned} \] が成り立つのでした(第3回資料)。
多変数関数において同様の判定を行うことを考えます。二次形式の知識を利用します。
二変数関数で説明します。
十分滑らかな二変数関数\(y = f(x,y)\)について \[ f(a,b)\text{が極値}\ \Rightarrow\ \mathrm{grad} f(a,b) = \left(\frac{\partial f}{\partial x}(a,b),\frac{\partial f}{\partial y}(a,b)\right) = \mathbf{0} \] が成り立つのでした(第4回資料)。
よって,テイラーの定理によって\(f(a,b)\)が極値ならば \[ f(x,y) = f(a,b) + \frac{1}{2}\left((x-a)\frac{\partial}{\partial x} + (y-b)\frac{\partial}{\partial y}\right)^2f(a,b) + \text{(剰余)} \] という形になりますが,関数の連続性から\((x,y)\)と\((a,b)\)が十分近い時には \[ f(x,y) > f(a,b)\ \Leftrightarrow\ \left((x-a)\frac{\partial}{\partial x} + \cdots + (y-b)\frac{\partial}{\partial y}\right)^2f(a,b) > 0 \] という同値関係が成り立ちます。
展開してみれば \[ \begin{aligned} & \left((x-a)\frac{\partial}{\partial x} + (y-b)\frac{\partial}{\partial y}\right)^2f \\ =& \color{yellow}{\frac{\partial^2f}{\partial x^2} (x-a)^2 + \frac{\partial^2f}{\partial y^2}(y-b)^2 + \frac{\partial^2f}{\partial x\partial y}(x-a)(y-b) + \frac{\partial^2f}{\partial y\partial x}(y-b)(x-a) } \end{aligned} \] となります(\(f(a,b)\)の\((a,b)\)を省略)が,これは\(X=x-a,Y=y-b\)を変数とする二次形式になっています。ここで,\(f\)が十分滑らかならば \[ \frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x} \] であった事に注意すれば,行列 \[ H = \begin{pmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} \\ \frac{\partial^2 f}{\partial y\partial x} & \frac{\partial^2 f}{\partial y^2} \end{pmatrix} \] が対称行列となります。
よって,\(H\)の固有値を\(\lambda_1,\lambda_2\)とすれば,適当な変数変換\((x,y)\longmapsto (s,t)\)によって(\((x,y)\)が\((a,b)\)に十分近い範囲で) \[ f(x,y) > f(a,b)\ \Leftrightarrow\ \lambda_1s^2+\lambda_2t^2 > 0 \] と簡略化する事ができます。
(細かい議論がいろいろと必要ですが)右辺の条件は \[ \lambda_1 > 0,\ \lambda_2 > 0 \] ですので\(H\)の固有値によって極値の判定ができるという事になります。
以上は\(n\)変数の場合に一般化する事ができます。
極値の判定
\(f\)を十分滑らかな\(n\)変数関数とする。このとき \[ H(f) = \begin{pmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\partial x_n} \\ \frac{\partial^2 f}{\partial x_2\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n\partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\ \end{pmatrix} \] をヘッセ行列と言い,以下が成り立つ。
\(\mathrm{grad} f(\mathbf{a})=\mathbf{0}\)である点\(\mathbf{a}\)において, \[ \begin{aligned} H(f)\text{の固有値が全て正}\ &\Rightarrow\ \text{$f(\mathbf{a})$は極小値} \\ H(f)\text{の固有値が全て負}\ &\Rightarrow\ \text{$f(\mathbf{a})$は極大値} \\ H(f)\text{が正負の固有値を持つ}\ &\Rightarrow\ \text{$f(\mathbf{a})$は極大でも極小でもない(鞍点という)} \\ \end{aligned} \]
例
\[ f(x,y) = \cos x\cos y \] の値\(f(0,0)=1\)について調べてみましょう。まず \[ \mathrm{grad} f = (-\sin x\cos y, -\cos x\sin y) \] より\(\mathrm{grad}f(0,0) = (0,0)\)です。また点\((0,0)\)でのヘッセ行列の値は \[ H(f)(0,0) = \left.\begin{pmatrix} -\cos x\cos y & \sin x\sin y \\ \sin x\sin y & -\cos x\cos y \end{pmatrix}\right|_{(x,y)=(0,0)} = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \] なので,固有値はどちらも負です。従って\(f(0,0)=1\)は極大値である事がわかりました。
重積分
確率・統計の計算では重積分が頻繁に登場します。しかも,他の分野ではあまり使われない様な非常に高次元の重積分も登場しますので,よく理解する事が必要です。
一変数関数の定積分は \[ \color{yellow}{\int_a^bf(x)\mathrm{d} x = \lim_{n\rightarrow\infty}\sum_{i=1}^nf(t_i)(x_i-x_{i-1})} \] というリーマン和の極限として定義されました(第5回)が,多変数関数においても同様に定積分を定義する事ができます。
二変数の場合を考えます。定積分を行う\(xy\)平面上の領域を\(D\)とします。更に\(x\)軸,\(y\)軸上に分点を \[ x_0 < x_1 < \cdots, y_0 < y_1 < \cdots \] というように取り,\(\Delta S_{ij}=(x_i-x_{i-1})(y_j-y_{j-1})\)とおきます。\(\Delta S_{ij}\)は図の長方形の面積となります。 ここで,図の\(xy\)平面上の長方形の中に点\(s_{ij},t_{ij}\)をとって \[ \sum f(s_{ij},t_{ij})\Delta S_{ij} \] という和を考えます。
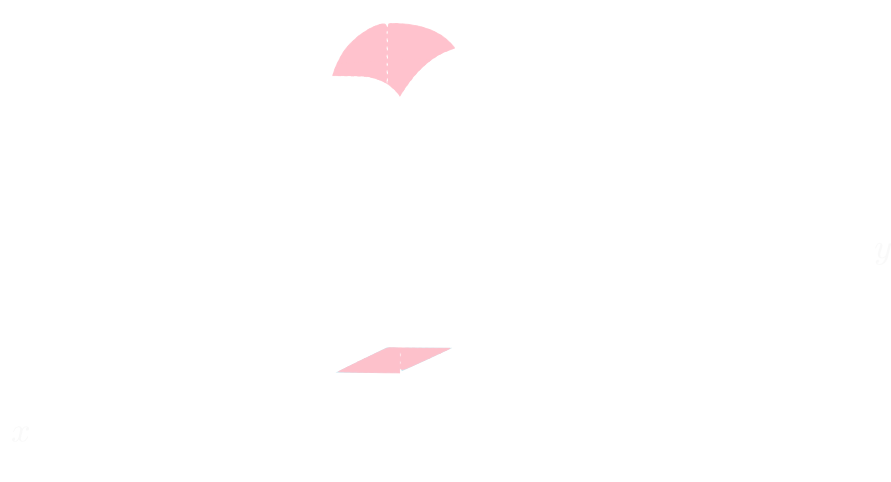
\[ \sum f(s_{ij},t_{ij})\Delta S_{ij} \qquad \cdots(1)\] の和の取り方は
- \(D\)を覆う長方形達について取る
- \(D\)に含まれる長方形達について取る
の2通りを考えます。ここで,\(x_i-x_{i-1},y_j-y_{j-1}\)がいずれも\(0\)に収束するような極限をとった時に, (1)が和の取り方・\((s_{ij},t_{ij})\)の取り方に一切よらずに収束するならば,その値を \(f(x,y)\)の\(D\)上での重積分 と言い \[ \color{yellow}{\int\int_D f(x,y)\mathrm{d}x\mathrm{d}y} \] とか \[ \color{yellow}{\int_D f(x,y)\mathrm{d}x\mathrm{d}y} \] とか \[ \color{yellow}{\int_D f(x,y)\mathrm{d}S} \] などと書きます。
直感的に言えば, \[ \int\int_D f(x,y)\mathrm{d}x\mathrm{d}y \] は下図の様な立体の体積(符号付き体積)となります。
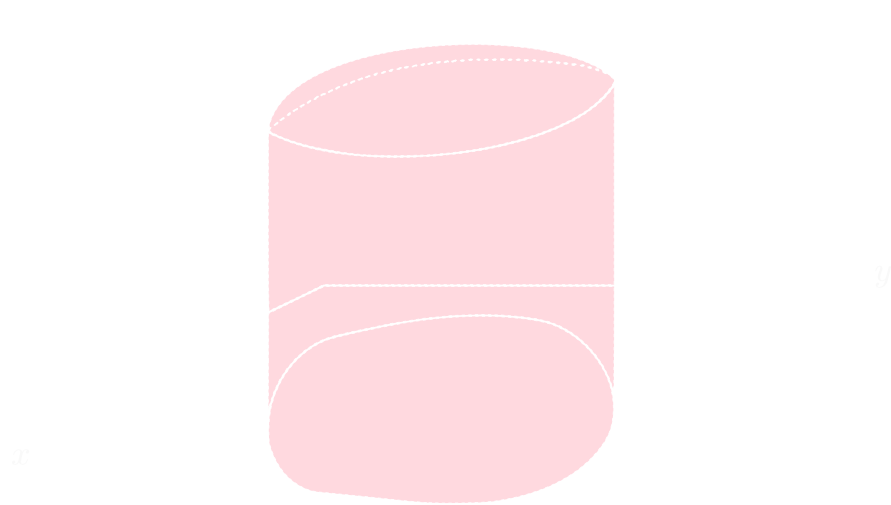
重積分の性質
\(a,b\in \mathbb{R}\)の時 \[ \int_D(af+bg)\mathrm{d}x\mathrm{d}y = a\int_Df\mathrm{d}x\mathrm{d}y + b\int_Dg\mathrm{d}x\mathrm{d}y \]
領域\(D\)が\(D_1,D_2\)に分割できる時 \[\int_Df\mathrm{d}x\mathrm{d} y = \int_{D_1}f\mathrm{d}x\mathrm{d} y + \int_{D_2}f\mathrm{d}x\mathrm{d} y \]
累次積分への変換
重積分を定義通りに計算するのは大変面倒ですので,実際に計算する際には累次積分に変換します。
先ほどのリーマン和は\(\Delta x_i = (x_i-x_{i-1}),\ \Delta y_j = (y_j-y_{j-1})\)として \[ \sum f(s_{ij},t_{ij})\Delta S_{ij} = \sum_i (\sum_j f(s_{ij}, t_{ij})\Delta y_j)\Delta x_i \] と書き直す事ができますので,まず\(y\)に関して積分し,次に\(x\)に関して積分するという事ができると予想できます。
この事の詳しい議論はむずかしいのですが,実用上登場するほとんどの関数では次頁の定理が成り立ちます。
重積分から累次積分への変換
領域\(D\)を \[ a \leq x \leq b,\ g(x)\leq y\leq h(x) \] と表す事ができるならば \[ \int_Df(x,y)\mathrm{d}x\mathrm{d}y = \int_a^b\left\{ \int_{g(x)}^{h(x)}f(x,y)\mathrm{d} y\right\}\mathrm{d} x \] である。
例
\(D\)を以下の領域として
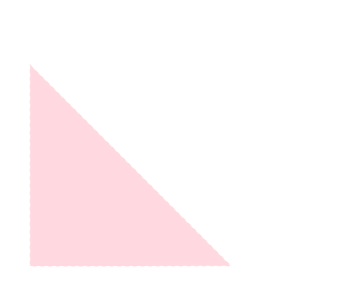
\(x\)を固定すれば図の領域は \[ 0 \leq x \leq 1,\ 0 \leq y\leq 1-x \] となりますので \[ \begin{aligned} \int_D (x^2+y)\mathrm{d}x\mathrm{d}{y} &= \int_0^1\left\{\int_0^{1-x}(x^2+y)\mathrm{d}y\right\}\mathrm{d} x \\ &= \int_0^1 \left[x^2y+\frac{y^2}{2}\right]_0^{1-x}\mathrm{d} x \\ &= \int_0^1 \left(x^2(1-x)+\frac{(1-x)^2}{2}\right)\mathrm{d} x \\ &= \frac{1}{4} \end{aligned} \] となります。
変数の変換
変数\(x,y\)を他の変数\(p,q\)に一対一に置換する事を考えます。この置換えを
\[ x = \phi(p,q),\ y = \psi(p, q) \]
としましょう。
リーマン和は
\[ f(s_{ij},t_{ij})(x_i-x_{i-1})(y_j-y_{j-1}) \]
という形の積の和でしたが,変数を置き換えても\(f\)の値は変化しません。従って置換によって
\[ \color{yellow}{(x_i-x_{i-1})(y_j-y_{j-1})} \]
がどうなるかを考える事となります。
テイラー展開を行ってみると \[ \begin{aligned} \Delta x &= \phi(p+\Delta p, q+\Delta q)-\phi(p, q) \\ &= \phi(p,q)+\frac{\partial \phi}{\partial p}\Delta p + \frac{\partial \phi}{\partial q}\Delta q + \mathcal{O}(\Delta p^2+\Delta q^2) - \phi(p,q)\\ &= \frac{\partial \phi}{\partial p}\Delta p + \frac{\partial \phi}{\partial q}\Delta q + \mathcal{O}(\Delta p^2+\Delta q^2)\\ \end{aligned} \] となります。\(\psi\)についても同様なので \[ \color{yellow}{\begin{pmatrix} \Delta x \\ \Delta y \end{pmatrix} \approx \begin{pmatrix} \frac{\partial\phi}{\partial p} & \frac{\partial\phi}{\partial q} \\ \frac{\partial\psi}{\partial p} & \frac{\partial\psi}{\partial q} \\ \end{pmatrix} \begin{pmatrix} \Delta p \\ \Delta q \end{pmatrix}} \] と書くことが出来て,誤差ベクトルは\(\Delta p^2,\Delta q^2\)で各成分を抑える事ができます。
ここで出てきた行列が表す線形写像は,面積1の正方形を下図の平行四辺形に移します。この平行四辺形の面積は \[ \left| \frac{\partial\phi}{\partial p} \frac{\partial\psi}{\partial q} - \frac{\partial\phi}{\partial q} \frac{\partial\psi}{\partial p} \right| = \left|\det \begin{pmatrix} \frac{\partial\phi}{\partial p} & \frac{\partial\phi}{\partial q} \\ \frac{\partial\psi}{\partial p} & \frac{\partial\psi}{\partial q} \\ \end{pmatrix} \right| \] です。
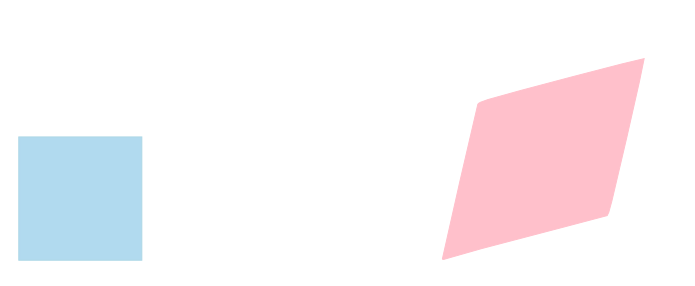
面積\(\Delta p\Delta q\)の長方形についても同様に考えると \[ \Delta x\Delta y \approx \left|\det \begin{pmatrix} \frac{\partial\phi}{\partial p} & \frac{\partial\phi}{\partial q} \\ \frac{\partial\psi}{\partial p} & \frac{\partial\psi}{\partial q} \\ \end{pmatrix} \right| \Delta p\Delta q \] という関係があり,誤差はやはり\(\Delta p^2,\Delta q^2\)で抑える事ができます。
積分変数の変換
変数の変換\( (x,y) \longmapsto (p,q) \)が一対一であり, \[x = \phi(p,q),\ y = \psi(p,q)\] と表されるとする。この時 \[ J = \det \begin{pmatrix} \frac{\partial\phi}{\partial p} & \frac{\partial\phi}{\partial q} \\ \frac{\partial\psi}{\partial p} & \frac{\partial\psi}{\partial q} \\ \end{pmatrix} \] をヤコビアンと言う。この時,変数変換によって領域\(D\)が\(D'\)に移るとすると \[ \int_D f(x,y)\mathrm{d}x\mathrm{d}y = \int_{D'}f(\phi(p,q),\psi(p,q))|J|\mathrm{d}p\mathrm{d}q \] が成立する。
例
\(D\)を単位円の周および内部 \[ x^2 + y^2 \leq 1 \] とした時に \[ \int_D x^2\mathrm{d}x\mathrm{d} y\] を求めてみましょう。
極座標を用いるのが良さそうです。そこで \[ x=r\cos\theta, y=r\sin\theta \] とおきます。すると\(D\)は \[ 0\leq r \leq 1,\ 0 \leq \theta < 2\pi \] という領域に移ります。
また,ヤコビアンは \[ J = \det\begin{pmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{pmatrix} = r \] となるので \[ \begin{aligned} \int_Dx^2\mathrm{d}x\mathrm{d}y &= \int_D'r^2\cos^2\theta\cdot r\mathrm{d} r\mathrm{d} \theta \\ &= \int_0^1\left\{\int_0^{2\pi} r^3\cos^2\theta\mathrm{d}\theta\right\}\mathrm{d}r \\ &= \frac{\pi}{4} \end{aligned} \] が求める答えとなります。
これまでは二変数の場合に限って説明しましたが,\(n\)変数の場合も(直感的な把握は難しいですが)同様にリーマン和の極限として定義され,これまで説明したものと同様の定理が成立します。
例えば三変数の場合に\((x,y,z)\rightarrow (p,q,r)\)と変数変換した場合のヤコビアンは \[ J = \det\begin{pmatrix} \frac{\partial x}{\partial p} & \frac{\partial x}{\partial q} & \frac{\partial x}{\partial r} \\ \frac{\partial y}{\partial p} & \frac{\partial y}{\partial q} & \frac{\partial y}{\partial r} \\ \frac{\partial z}{\partial p} & \frac{\partial z}{\partial q} & \frac{\partial z}{\partial r} \end{pmatrix} \] となり \[ \mathrm{d}x\mathrm{d}y\mathrm{d}z = |J|\mathrm{d}p\mathrm{d}q\mathrm{d}r \] と変換すれば良いです。
重積分は今後何度も登場するのでその都度復習をしていきましょう。
多重積分の数値計算について
重積分は累次積分に直す事が出来るので既に説明して数値積分法を繰り返し使えば計算できます。
しかし,変数1つあたりの積分区間の分割数を\(n\)とすると,\(m\)重積分では\( \mathcal{O}(n^m) \)の計算量が必要になります。
確率・統計の計算ではこの\(m\)が非常に大きくなるためモンテカルロ法という積分法がよく利用されます。モンテカルロ法の理解にはやはり確率の知識が必要となるため,来週以降に説明を行う予定です。
今回はここで終わります。
来週から確率・統計分野に進みます。
初回は確率の基礎事項を確認します。確率論の公理,同時確率,条件付き確率,ベイズの定理,エントロピーなどといった内容になると思います。