プログラマの為の
数学勉強会
第10回

謝辞

この会の企画・会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。

この資料について

• http://nineties.github.com/math-seminar に置いてあります。
• SVGに対応したブラウザで見て下さい。主要なブラウザで古いバージョンでなければ大丈夫だと思います。
• 内容の誤り、プログラムのバグは@9_tiesかkoichi.nakamur AT gmail.comまでご連絡下さい。
• サンプルプログラムはPython及びMaximaで記述しています。

線型変換・固有値・固有ベクトル(続き)

線型変換の中でも重要なのが成分・基底の変換です。

基底変換行列は恒等写像の異なる基底での表示ですので，正則行列\(P\)が必ず存在することがわかります。

特に基底\(\{\mathbf{v'}_i\}\)の各ベクトルの基底\(\{\mathbf{v}_i\}\)での成分 \[ \mathbf{v'}_i = p_{1i}\mathbf{v}_1 + \cdots + p_{ni}\mathbf{v}_n \qquad \cdots (1)\] は，基底変換行列\(P\)を用いて \[ \begin{pmatrix} p_{1i} \\ \vdots \\ p_{ni} \end{pmatrix} = P \mathbf{e}_i \] と表せます((1)の左辺の成分が\(\mathbf{e}_i\)である事に注意)ので， \[ P = P(\mathbf{e}_1,\cdots,\mathbf{e}_n) = (P\mathbf{e}_1,\cdots,P\mathbf{e}_n) = \begin{pmatrix} p_{11} & \cdots & p_{1n} \\ \vdots & \ddots & \vdots \\ p_{n1} & \cdots & p_{nn} \\ \end{pmatrix} \] となります。
また，これと(1)を見比べれば \[ (\mathbf{v'}_1,\cdots,\mathbf{v'}_n) = (\mathbf{v}_1,\cdots,\mathbf{v}_n)P \] が成立しています。これが\(P\)を\(\{\mathbf{v}_i\}\)から\(\{\mathbf{v'}_i\}\)への基底変換行列と呼ぶ理由です。

まず \[ (\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3)P = (\mathbf{v'}_1,\mathbf{v'}_2,\mathbf{v'}_3) \] を\(P\)について解いて，基底変換行列は \[ P = \begin{pmatrix} 2 & 1 & 1 \\ 3 & 3 & 1 \\ -2 & -2 & 0 \end{pmatrix} \] となります。

>>> P = LA.solve(
...     np.array([      # vを列に並べた行列が係数
...             [1, 0, 0],
...             [0, 1, 1],
...             [1, 0, 1]
...     ]), np.array([  # v'を列に並べた行列が定数項
...             [2, 1, 1],
...             [1, 1, 1],
...             [0,-1, 1]
...     ]))
>>> P
array([[ 2.,  1.,  1.],
       [ 3.,  3.,  1.],
       [-2., -2.,  0.]])

すると \[ \begin{aligned} &2\mathbf{v}_1 + 3\mathbf{v}_2 + 4\mathbf{v}_3 = x\mathbf{v'}_1 + y\mathbf{v'}_2 + z\mathbf{v'}_3 \\ \Leftrightarrow&\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} = P\begin{pmatrix} x \\ y \\ z \end{pmatrix} \end{aligned} \] なのでこれを解いて\((x,y,z)=(-5,3,9)\)となります。つまり \[ \color{yellow}{2\mathbf{v}_1 + 3\mathbf{v}_2 + 4\mathbf{v}_3 = -5\mathbf{v'}_1+3\mathbf{v'}_2+9\mathbf{v'}_3} \] が求める答えとなります。

>>> x,y,z = LA.solve(P, [2,3,4])
>>> x,y,z
(-5.0, 3.0000000000000004, 9.0)

続いて基底変換による，線型写像の表現行列の変換を考えます。

以後，ベクトル\(\mathbf{x}\)の基底\(\{\mathbf{v}_i\}\)に関する成分を \[ (x_1,\cdots,x_n) \] 基底\(\{\mathbf{v'}_i\}\)に関する成分を \[ (x'_1,\cdots,x'_n) \] という様に表す事にします。また\(n\)は考えている空間の次元です。

線型変換\(f: V\rightarrow V\)の基底\(\{\mathbf{v}_i\}\)での行列表現を\(A\)とします。つまり \[ \mathbf{y}=f(\mathbf{x})\ \Leftrightarrow\ \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} = A \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \] です。ここで基底\(\{\mathbf{v}_i\}\)から基底\(\{\mathbf{v}'_i\}\)への変換行列を\(P\)とすれば \[ \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} = P\begin{pmatrix} x'_1 \\ \vdots \\ x'_n \end{pmatrix} \] と成分が変換されるのでしたから,上式に代入して \[ P\begin{pmatrix} y'_1 \\ \vdots \\ y'_n \end{pmatrix} = AP\begin{pmatrix} x'_1 \\ \vdots \\ x'_n \end{pmatrix} \Leftrightarrow \begin{pmatrix} y'_1 \\ \vdots \\ y'_n \end{pmatrix} = \color{yellow}{P^{-1}AP}\begin{pmatrix} x'_1 \\ \vdots \\ x'_n \end{pmatrix} \] となります。つまり表現行列は\(A\longmapsto P^{-1}AP\)と変換されます。

このような正則行列\(P\)による \[ A \longmapsto P^{-1}AP \] という変換は行列\(A\)の相似変換と呼ばれます。
相似と呼ぶ理由は,\(A\)と\(P^{-1}AP\)は同じ線型変換を表現するので,変換によって線型写像の性質が保たれる事によります。

基底\(\{1,x,x^2,x^3\}\)での\(f\)の表現行列は \[ A = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{pmatrix} \] です。これを基底変換して求めることにしましょう。

\(\{1,x,x^2,x^3\}\)から\(\{1,\ x,\ 2x^2-1,\ 4x^3-3x\}\)への基底変換行列は \[ P = \begin{pmatrix} 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -3\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 4\\ \end{pmatrix} \] なので \[ P^{-1}AP = \color{yellow}{\begin{pmatrix} 0 & 1 & 0 & 3\\ 0 & 0 & 4 & 0\\ 0 & 0 & 0 & 6\\ 0 & 0 & 0 & 0 \end{pmatrix}} \] が求める行列となります。表現を多項式に戻せば \[ \begin{aligned} &\{a+bx+c(2x^2-1)+d(4x^3-3x)\}'\\ = &(b+3d)+4cx+6d(2x^2-1) \end{aligned} \] であるという事を表しています。

では,固有値・固有ベクトルの話題に進みましょう。

線型変換の固有値は前回やった行列の固有値に帰着します。

【証明】
成分表示に変換する写像を\(\varphi: V\rightarrow K^n\)とする。
\(\varphi\)は同型写像なので,\(\mathbf{x}\in V\)について\(\mathbf{y}=\varphi(\mathbf{x})\)とおくと \[ f(\mathbf{x}) = \lambda\mathbf{x} \Leftrightarrow \varphi(f(\mathbf{x})) = \lambda\varphi(\mathbf{x}) \Leftrightarrow M_f\mathbf{y}=\lambda\mathbf{y} \] である。 □

前回,固有ベクトルを考える事は「良い基底を選ぶ」という事と関係するという話をしました。まずは,以下の簡単な例で見てみましょう。

前回説明した通り, \[ \det (A-\lambda E) = \begin{vmatrix} 2-\lambda & -1 \\ 0 & 3-\lambda\end{vmatrix} = (2-\lambda)(3-\lambda) \] を計算して,固有値\(\lambda = 2, 3\)を得ます。
固有値\(2\)に対応する固有ベクトルは \[ \begin{pmatrix} 2 & -1 \\ 0 & 3 \end{pmatrix}\begin{pmatrix}x \\ y \end{pmatrix} = 2\begin{pmatrix} x \\ y \end{pmatrix}\ \Leftrightarrow\ y=0 \] より\(\mathbf{u}=(1,0)^T\)等となります。 同様にして,固有値\(3\)に対応する固有ベクトルとして\(\mathbf{v}=(1,-1)^T\)等が得られます。

今の例題の結果を図形的に考えてみましょう。

まず\((x,y) \in \mathbb{R}^2\)を\(xy\)平面上の点とみなせば,\(f_A\)は平面上の点を同じ平面上の点に移す変換となります。

例えば \[f_A\begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 & -1 \\ 0 & 3 \end{pmatrix}\begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \] というベクトルの対応を下図のような点の対応と考える事が出来ます。

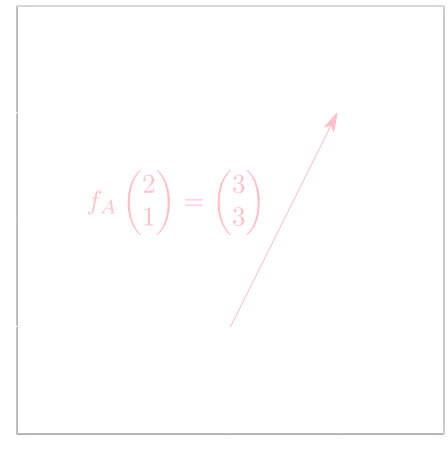
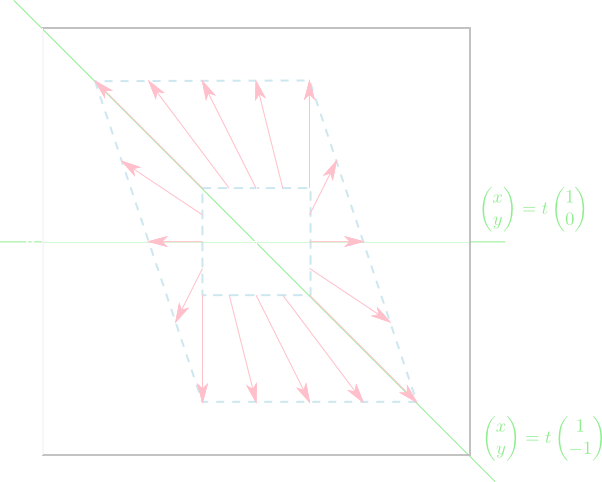
ここで\(x,y\)軸に沿った長方形上の各点の移り方は下のようになります。ねじれるように変換されています。

では,固有ベクトル\(\mathbf{u}=(1,0)^T\)と\(\mathbf{v}=(1,-1)^T\)に平行な直線に沿った平行四辺形はどのような移り方をするでしょうか？

固有ベクトルに沿って描いた平行四辺形は下図のように綺麗に変換されます。 この様に同じ変換でも,軸の取り方(基底の取り方)によってその見え方が大きく変わります。

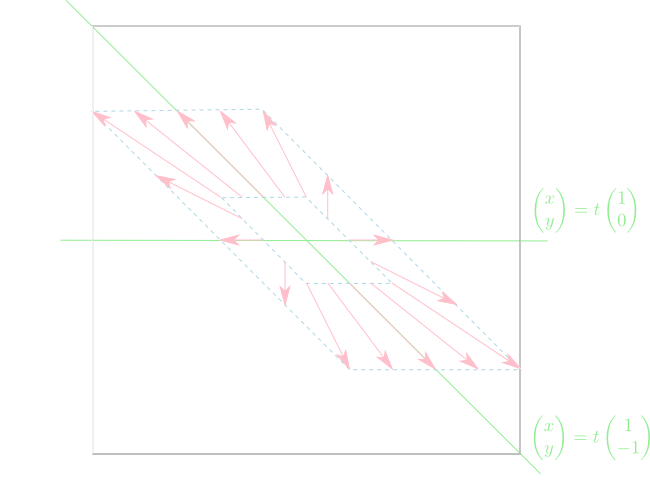
数式を用いて詳しく見て行きましょう。

\(\mathbf{u}=(1,0)^T\)と\(\mathbf{v}=(1,-1)^T\)は\(\mathbb{R}^2\)の基底となるので,任意の\(\mathbf{x}\in\mathbb{R}^2\)は \[ \mathbf{x} = s\mathbf{u} + t\mathbf{v}\qquad(s,t\in\mathbb{R})\] と表示する事が出来ます。すると \[ \begin{aligned} f_A(\mathbf{x}) &= sf_A(\mathbf{u}) + tf_A(\mathbf{v}) \quad\text{(線型性)}\\ &= 2s\mathbf{u} + 3t\mathbf{v} \end{aligned} \] となりますから,\(f_A\)によって成分は \[ (s,t)\longmapsto(2s,3t) \] と変換されます。つまり,変換\(f_A\)は固有ベクトルを基底に選ぶと,対角行列によって表示する事が出来るという事が判りました。 \[ \begin{pmatrix} s \\ t \end{pmatrix} \longmapsto \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} s \\ t \end{pmatrix} \]

【証明】
\(\dim V = n\)とする。\(f\)が基底\(\mathbf{v}_1,\cdots,\mathbf{v}_n\)について対角行列 \[ \Lambda = \begin{pmatrix}\lambda_1 & & \\ & \ddots & \\ & & \lambda_n\end{pmatrix} \] で表示されるならば, \[ \Lambda\mathbf{e}_i = \lambda_i\mathbf{e}_i \] であるから各\(\mathbf{v}_i\)について \[ f(\mathbf{v}_i) = \lambda_i\mathbf{v}_i \] である。従って\(\mathbf{v}_1,\cdots,\mathbf{v}_n\)は固有ベクトルからなる基底である。
逆に\(\mathbf{v}_1,\cdots,\mathbf{v}_n\)が固有ベクトルかつ基底ならば \[ f(\mathbf{v}_i)=\lambda_i\mathbf{v}_i \] の成分を第\(i\)列に取った行列,すなわち対角行列で表示される(第9回資料P48)。 □

以下の定理は対角化可能か判定する上で非常に便利です。

【証明】
\(m=1\)の場合は明らかに成立。そこで\(\mathbf{v}_1,\cdots,\mathbf{v}_m\)が線型独立であると仮定し \[ s_1\mathbf{v}_1+\cdots+s_m\mathbf{v}_m+s_{m+1}\mathbf{v}_{m+1}=\mathbf{0} \cdots (1)\] と置くと,両辺に\(f\)を適用して \[ s_1\lambda_1\mathbf{v}_1+\cdots+s_m\lambda_m\mathbf{v}_m+s_{m+1}\lambda_{m+1}\mathbf{v}_{m+1}=\mathbf{0} \cdots (2) \] となる。但し\(\lambda_i\)は\(\mathbf{v}_i\)の固有値。ここで(1),(2)から\(\mathbf{v}_{m+1}\)を消去すれば \[ s_1(\lambda_{m+1}-\lambda_1)\mathbf{v}_1+\cdots+s_m(\lambda_{m+1}-\lambda_m)\mathbf{v}_m=\mathbf{0} \] となるが,仮定より\(\mathbf{v}_1,\cdots,\mathbf{v}_m\)は線型独立なので \[ s_1(\lambda_{m+1}-\lambda_1)=\cdots=s_m(\lambda_{m+1}-\lambda_m)=0 \] よって,固有値が全て異なるならば \[ s_1 = \cdots = s_m = 0\] となるので,(2)に代入して\(s_{m+1}=0\)。従って \[ \mathbf{v}_1,\cdots,\mathbf{v}_m,\mathbf{v}_{m+1} \] も線型独立となる。 □

今の定理からただちに以下の定理も得られます。

さて,線型写像を対角行列で表示する事によって結局何が行われたのでしょうか？

線形写像\(f: V\rightarrow V\)が対角行列で表現可能であるとします。つまり,\(f\)の固有ベクトルを基底に選んだ時の成分表示を用いれば \[ \begin{aligned} \mathbf{y}=f(\mathbf{x}) &\Leftrightarrow\ \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} = \begin{pmatrix} \lambda_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \\ &\Leftrightarrow\ \color{yellow}{\left\{\begin{array}{c} y_1 = \lambda_1x_1 \\ \vdots \\ y_n = \lambda_nx_n \end{array}\right.} \end{aligned} \] が成立します。(\(\lambda_i\)は\(i\)番目の固有ベクトルの固有値。)

これは\(n\)次元の線型変換を\(n\)個の\(1\)次元の線型変換に分解したのだと説明する事が出来ます。高次元の変換を低次元のより分り易い変換に帰着させるという事が対角化の重要な働きです。

具体的な問題に適用してみましょう。

\(\dim V = m\)とし,\(f\)が対角行列によって表現可能であるとします。この時,固有ベクトル\(\{\mathbf{v}_i\}\)を基底に選ぶ事が出来ます。\(\mathbf{v}_i\)に対応する固有値を\(\lambda_i\)とします。
すると,ベクトル\(\mathbf{x}_n\)の第\(i\)成分を\(x_{i}^{(n)}\)とすれば \[ \mathbf{x}_{n+1}=f(\mathbf{x}_n)\ \Leftrightarrow\ x_{i}^{(n+1)} = \lambda_ix_{i}^{(n)} \quad(i=1,\cdots,m)\] となり,\(x_{i}^{(n)} = (\lambda_i)^nx_{i}^{(0)}\)と解くことが出来ます。従って一般項は \[ \color{yellow}{\mathbf{x}_n = (\lambda_1)^nx_{1}^{(0)}\mathbf{v}_1 + (\lambda_2)^nx_{2}^{(0)}\mathbf{v}_2 + \cdots + (\lambda_m)^nx_{m}^{(0)}\mathbf{v}_m} \] となります。

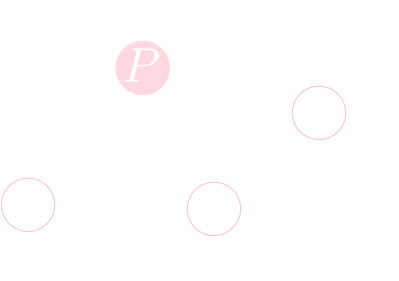
\(\mathbf{x}_n = (p_n,q_n,r_n,s_n)^T\)とおけば,状態遷移図より \[ \mathbf{x}_{n+1} = \begin{pmatrix} 0 & 1/2 & 1/2 & 1 \\ 1/3 & 0 & 1/2 & 0 \\ 1/3 & 1/2 & 0 & 0 \\ 1/3 & 0 & 0 & 0 \end{pmatrix}\mathbf{x}_n\] がなりたちますので,この行列(\(A\)とします)を対角化しましょう。

手計算は面倒なので計算機にやらせると,4つの相異なる固有値 \[1,\ 0.22\cdots,\ -0.72\cdots,\ -\frac12\] と基底変換行列\(P\)が得られました。\(P\)の各列(つまり固有ベクトルの成分)を順番に\(\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3,\mathbf{p}_3\)としましょう。

>>> import numpy as np
>>> import scipy
>>> from scipy import linalg as LA
>>> A = np.array([[0,1.0/2,1.0/2,1],[1.0/3,0,1.0/2,0],[1.0/3,1.0/2,0,0],[1.0/3,0,0,0]],dtype=float)
>>> L,P = LA.eig(A)   # 固有値・固有ベクトルを計算
>>> L
array([ 1.00000000+0.j,  0.22871355+0.j, -0.72871355+0.j, -0.50000000+0.j])

従って,初項\( \mathbf{x}_0 = (1,0,0,0)^T \)の基底\(\{\mathbf{p}_i\}\)に関する成分表示を\((x_1^0,x_2^0,x_3^0,x_4^0)^T\)とすれば, \[ \begin{aligned} \mathbf{x}_n &= 1^nx_1^0\mathbf{p}_1 + (0.22\cdots)^nx_2^0\mathbf{p}_2 + (-0.72\cdots)^nx_3^0\mathbf{p}_3 + (-\frac12)^nx_4^0\mathbf{p}_4 \\ &\xrightarrow{n\rightarrow\infty} \color{yellow}{x_1^0\mathbf{p}_1} \end{aligned} \] となります。これを計算すれば

>>> p1 = P[...,0]       # Pの1列目が1つ目の固有ベクトル
>>> x0 = LA.solve(P, [1,0,0,0])   # 初項を固有ベクトルに関する成分表示に変換
>>> x0[0] * p1
array([ 0.375,  0.25 ,  0.25 ,  0.125])

すなわち, \[ \color{yellow}{(p_n,q_n,r_n,s_n)\xrightarrow{n\rightarrow\infty}(0.375,\ 0.25,\ 0.25,\ 0.125)} \] が求める答えとなります。

2つ目の例として,第1回に紹介した連成ばねの問題を思い出しましょう。

この問題は,質点の質量を\(m\),ばね定数を\(k\),それぞれのばねの変位を\(x_1,x_2\)として微分方程式 \[ \left\{\begin{array}{l} m\frac{\mathrm{d}^2 x_1}{\mathrm{d}t^2}=-2kx_1+kx_2\\ m\frac{\mathrm{d}^2 x_2}{\mathrm{d}t^2}=kx_1-2kx_2\\ \end{array}\right. \Leftrightarrow \color{yellow}{\frac{\mathrm{d}^2}{\mathrm{d}t^2}\begin{pmatrix}x_1 \\ x_2\end{pmatrix} = -\frac{k}{m}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}} \] を解けばよかったのですが,右辺の行列は \[ \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix} = P\begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix} P^{-1} \] と対角化出来るので \[ \begin{aligned} &\frac{\mathrm{d}^2}{\mathrm{d}t^2}\begin{pmatrix}x_1 \\ x_2\end{pmatrix} = -\frac{k}{m}P\begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix}P^{-1}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \\ \Leftrightarrow &\frac{\mathrm{d}^2}{\mathrm{d}t^2}\begin{pmatrix}y_1 \\ y_2\end{pmatrix} = -\frac{k}{m}\begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} \qquad\left(\begin{pmatrix}y_1\\y_2\end{pmatrix} = P^{-1}\begin{pmatrix} x_1\\x_2 \end{pmatrix}\right)\\ \Leftrightarrow& \color{yellow}{\frac{\mathrm{d}^2y_1}{\mathrm{d}t^2}=-3\frac{k}{m}y_1,\ \frac{\mathrm{d}^2y_2}{\mathrm{d}t^2}=-\frac{k}{m}y_2} \end{aligned} \] という2つの微分方程式に変換できます。連成振動は2つの単純な振動の重ねあわせであったという事が判明しました。質点の数がいくつになっても同様です。

さて,固有値を求める為の固有方程式 \[ \det (A-\lambda E) = 0\] は\(A\)が\(n\)次正方のとき,\(n\)次方程式となります。

これまで\(\mathbb{R}\)線型空間ばかりを考えて来ましたが, 実数範囲では\(n\)次方程式が解を持たない場合がある ため取り扱いが面倒になります。

一方\(\mathbb{C}\)線型空間ではこの問題が起きません。

固有多項式は \[ \det (A-\lambda E) = \begin{vmatrix}1-\lambda & -1 \\ 1 & 1-\lambda\end{vmatrix} = \lambda^2-2\lambda+2 \] となりますが, \[ \lambda^2-2\lambda + 2 = 0\] は実数解を持たないため,\(f_A\)は固有値を持ちません。
一方,複素数範囲では \[ \lambda^2-2\lambda + 2 = 0\ \Leftrightarrow\ \lambda = 1\pm i\] と解くことが出来るので,\(f'_A\)は固有値\(1\pm i\)を持ちます。

このように複素数体は非常に良い性質を持っている為,線型代数にかぎらず様々な数学で重宝されます。

さて,行列が対角化出来ない場合に同様の事を考えるとジョルダン標準形という物が出てくるのですが,これを詳しく説明するには直和分解,固有空間,ケーリー・ハミルトンの定理,最小多項式\(\cdots\)など多くの事柄の準備が必要で時間が足りません。定理だけ紹介しますので詳しくは専門書を参照して下さい。

内積空間

線型空間のうち,幾何ベクトル空間ではベクトルの長さやベクトルとベクトルのなす角といった概念を考える事が出来ます。

「内積空間」とは線型空間に幾何ベクトル空間における長さ・角度の様な概念を取り入れた物だと言えます。簡単の為,\(\mathbb{R}\)線型空間だけを考えます。

公理3より任意の\(\mathbf{x}\)に対して\((\mathbf{x},\mathbf{0})=(\mathbf{0},\mathbf{x})=0\)である事に注意して下さい。

内積空間の例:幾何ベクトル空間

幾何ベクトル空間において\(||\mathbf{x}||\)を矢印の長さとし,2つのベクトルの角度を始点を揃えて\(0\leq\theta\leq\pi\)で測ることとします。この時 \[ (\mathbf{x},\ \mathbf{y})=||\mathbf{x}||||\mathbf{y}||\cos\theta \] とおくと,これは内積となります(確認して下さい。)

この時,ベクトルの長さ・なす角・内積の間に \[ ||\mathbf{x}|| = \sqrt{(\mathbf{x},\ \mathbf{x})},\ \cos\theta = \frac{(\mathbf{x},\ \mathbf{y})}{||\mathbf{x}||||\mathbf{y}||},\ \text{特に}\mathbf{x}\perp\mathbf{y}\ \Leftrightarrow\ (\mathbf{x},\ \mathbf{y})=0 \] が成立しています。

ここから,一般の内積空間\(V\)にも長さと直交の概念を取り入れる事が出来ます。

\(-1\leq\cos\theta\leq1\)なので \[-1\leq \frac{(\mathbf{x},\ \mathbf{y})}{||\mathbf{x}||||\mathbf{y}||} \leq 1\] でなければいけませんが,これは次の定理で保証されます。

【証明】
任意の実数\(t\)に対して \[ \begin{aligned} &||t\mathbf{x}-\mathbf{y}||^2 = (t\mathbf{x}-\mathbf{y},\ t\mathbf{x}-\mathbf{y})\geq 0\\ \Leftrightarrow & ||\mathbf{x}||^2 t^2 -2(\mathbf{x},\ \mathbf{y})t + ||\mathbf{y}||^2 \geq 0 \end{aligned} \] が成立するので,左辺\(=0\)の判別式は\(0\)以下である。従って \[ \begin{aligned} &(\mathbf{x},\ \mathbf{y})^2 - ||\mathbf{x}||^2||\mathbf{y}||^2 \leq 0 \\ \Leftrightarrow &-||\mathbf{x}||||\mathbf{y}||\leq(\mathbf{x},\mathbf{y})\leq||\mathbf{x}||||\mathbf{y}|| \end{aligned} \] □

【証明】
コーシー・シュワルツの不等式より \[\{||\mathbf{x}||+||\mathbf{y}||\}^2 - ||\mathbf{x}+\mathbf{y}||^2 = 2(||\mathbf{x}||||\mathbf{y}||-(\mathbf{x},\ \mathbf{y}))\geq 0 \] □

三角不等式より \[ || \mathbf{x}-\mathbf{z} || \leq || \mathbf{x}-\mathbf{y} || + ||\mathbf{y}-\mathbf{z} || \qquad \small{(\because \mathbf{x}-\mathbf{z}=(\mathbf{x}-\mathbf{y})+(\mathbf{y}-\mathbf{z}))}\] が成立します。
内積の公理に加えてこの不等式が成り立つ事から,\( ||\mathbf{x}-\mathbf{y}|| \)が\(\mathbf{x},\mathbf{y}\)の距離と呼ばれるにふさわしいものである事がわかります(詳しくは距離空間という概念の定義を参照してください)。

直感的に説明すると,\(\mathbf{x}\)と\(\mathbf{y}\)の距離が近づき,\(\mathbf{y}\)と\(\mathbf{z}\)の距離が近づくならば,\(\mathbf{x}\)と\(\mathbf{z}\)の距離も近づくという事を言っています。

内積空間は長さ・角度・距離といった概念を備えており,それらは私達が通常イメージするもの(幾何ベクトル空間のもの)と同じような性質を持つという事が言えます。

数ベクトル空間\(\mathbb{R}^n\)に標準内積を入れたものを\(n\)次ユークリッド空間と言い,同じく\(\mathbb{R}^n\)と表します。
座標系を設定すれば幾何ベクトルと実数ベクトルの同型対応 \[ \mathbf{x}\ \longmapsto\ (x_1, x_2)^T \] が得られますが,このとき標準内積で定まる長さ・角度は幾何ベクトルのそれと一致します。

簡単な応用を一つ紹介しましょう。

>>> import numpy as np
>>> from math import sqrt
>>> x = np.array([-0.05,  1.05,  0.95,  0.85, -0.95, -1.35,  0.45, -0.35,  0.65, -1.25])
>>> y = np.array([-0.3 ,  -1  ,  1.1 ,  -0.5,  1.3, -0.3,  0.6, -0.5,  0.7, -1.1])
>>> z = np.array([-0.23,  3.17,  2.67,  2.57, -2.83, -3.83,  1.37, -1.03,  1.77, -3.63])
>>> x_norm = sqrt(x.dot(x)) # ノルムはsqrt((x, x))
>>> y_norm = sqrt(y.dot(y))
>>> z_norm = sqrt(z.dot(z))
>>> x.dot(y)/(x_norm * y_norm)  # x,y のなす角の余弦
0.14344402238399551
>>> x.dot(z)/(x_norm * z_norm)a # x,z のなす角の余弦
0.99945940825616419

より \[ \begin{aligned} &\mathbf{x'},\mathbf{y'}\text{のなす角$\theta$:}\cos\theta = 0.14\ (\text{約}81.8^\circ) \\ &\mathbf{x'},\mathbf{z'}\text{のなす角$\theta$:}\cos\theta = 0.99\ (\text{約}1.9^\circ) \end{aligned} \] となります。　

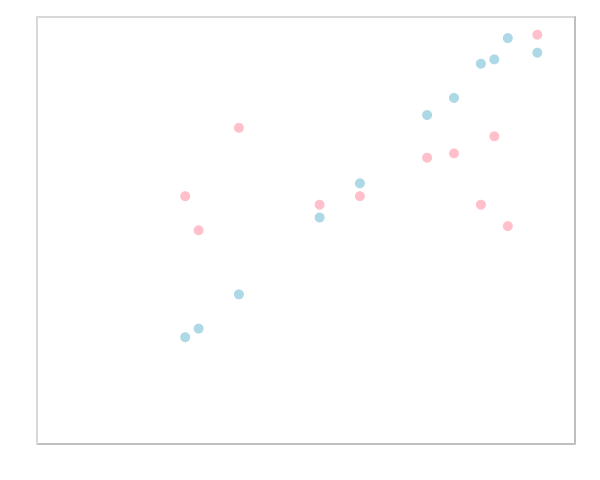
10次元なので「角度」という図形的なイメージは持てませんが,直感的に言えば\(\cos\theta\)をベクトルの向いている方向の近さの度合いだと考える事が出来ます。 実はこれは統計学において「相関係数」と呼ばれる量です。

横軸に\(x_i\)の値,縦軸に\(y_i,z_i\)の値をとって各成分をプロットすると下図のようになっています。

内積空間の例

定数\(a,b\in \mathbb{R},\ a < b \)を固定して,実数係数の\(n\)次以下の多項式からなる線型空間\(P_n\)に演算 \[ (f(x),\ g(x)) = \int_a^b f(x)g(x)\mathrm{d} x\] を入れると\(P_n\)は内積空間となります。

例えば\(a = 0, b = 1\)とすれば \[ \begin{aligned} &||x|| = \sqrt{\int_0^1 x\cdot x\mathrm{d} x} = \frac{1}{\sqrt{3}} \\ &(x,\ x^2)=\int_0^1 x\cdot x^2\mathrm{d} x = \frac{1}{4} \end{aligned} \] などとなります。

ユークリッド空間の標準基底\(\mathbf{e}_1,\cdots,\mathbf{e}_n\)は全て長さが1で互いに直交しています。 この特徴を持つ基底は様々な良い性質を持ちます。

【証明】
\[ \mathbf{x}=x_1\mathbf{v}_1+\cdots + x_n\mathbf{v}_n \] と\(\mathbf{v}_i\)の内積を取れば \[ (\mathbf{x},\ \mathbf{v}_i) = x_1(\mathbf{v}_1,\ \mathbf{v}_i)+\cdots+x_n(\mathbf{v}_n,\ \mathbf{v}_i) \] となりますが,直交性から \[ (\mathbf{x},\ \mathbf{v}_i) = x_i(\mathbf{v}_i,\ \mathbf{v}_i) = x_i||\mathbf{v}_i||^2 \] となります。\(\mathbf{v}_i\neq \mathbf{0}\)なので\(||\mathbf{v}_i||\neq 0\)だから \[ x_i = \frac{(\mathbf{x},\ \mathbf{v}_i)}{||\mathbf{v}_i||^2} \] □

【証明】 \( \mathbf{v}_1,\cdots,\mathbf{v}_n\)を直交系として \[ s_1\mathbf{v}_1+\cdots+\mathbf{v}_n = \mathbf{0} \] とすれば,各\(i\)について \[ s_i = \frac{(\mathbf{0},\ \mathbf{v}_i)}{||\mathbf{v}_i||^2} = 0 \] である。 □

【証明】
\[ \begin{aligned} (\mathbf{x},\ \mathbf{y}) &= (x_1\mathbf{v}_1 + \cdots + x_n\mathbf{v}_n,\ y_1\mathbf{v}_1 + \cdots + y_n\mathbf{v}_n \\ &= x_1y_1(\mathbf{v}_1,\mathbf{v}_1) + x_1y_2(\mathbf{v}_1,\mathbf{v}_2)+\cdots + x_ny_n(\mathbf{v}_n,\mathbf{v}_n) \\ &= x_1y_1 + \cdots + x_ny_n \end{aligned} \] □

今の定理により(有限次元の\(\mathbb{R}\)線型空間を前提とすれば) \[ \color{yellow}{\text{「あらゆる内積は上手く基底を取れば成分の標準内積と一致する」}} \] という事が言えそうです。
「全ての線型写像は行列で表示出来る」と同様の事が言えることになります。

問題は \[ \color{yellow}{\text{「任意の有限次元$\mathbb{R}$内積空間に正規直交基底が存在するか？」}}\] という事になります。

【証明】

基底\(\mathbf{u}_1,\cdots,\mathbf{u}_n\)を適当にとる。
まず\(\mathbf{v}_1 = \frac{\mathbf{u}_1}{||\mathbf{u}_1||}\)とおく。\(\mathbf{v}_1\)はそれ1つで正規直交系をなす。
ここで正規直交系\(\mathbf{v}_1,\cdots,\mathbf{v}_k\ (k < n)\)が作れたと仮定し \[ \color{yellow}{\mathbf{w}_{k+1} = \mathbf{u}_{k+1} - (\mathbf{u}_{k+1},\ \mathbf{v}_1)\mathbf{v}_1- (\mathbf{u}_{k+1},\ \mathbf{v}_2)\mathbf{v}_2\cdots- (\mathbf{u}_{k+1},\ \mathbf{v}_k)\mathbf{v}_k} \] と置くと\(\mathbf{w}_{k+1}\)は\(\mathbf{v}_1,\cdots,\mathbf{v}_k\)の全てと直交する。 また\(\mathbf{w}_{k+1}=\mathbf{0}\)ならば\(\mathbf{u}_1,\cdots,\mathbf{u}_{k},\mathbf{u}_{k+1}\)が線型独立である事と矛盾するので,\(\mathbf{w}_{k+1}\neq\mathbf{0}\)。 そこで\(\mathbf{w}_{k+1}\)を正規化して \[ \mathbf{v}_{k+1} = \frac{\mathbf{w}_{k+1}}{||\mathbf{w}_{k+1}||} \] とすれば正規直交系\(\mathbf{v}_1,\cdots,\mathbf{v}_{k+1}\)を作る事が出来る。これを\(n\)個そろうまで続ければ良い。 □

答えは \[ \small{\left\{ \left(\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}}\right)^T,\ \left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)^T,\ \left(-\frac{1}{\sqrt{6}},\sqrt{\frac{2}{3}},\frac{1}{\sqrt{6}}\right)^T \right\}} \] となります。それぞれ長さが1で,直交している事を確認してください。
手計算は面倒なので数式処理システムであるMaximaで計算しました。

(%i1) u1: [1,0,1];   /* 元とする基底 */
(%o1)                              [1, 0, 1]
(%i2) u2: [2,1,0];
(%o2)                              [2, 1, 0]
(%i3) u3: [0,1,1];
(%o3)                              [0, 1, 1]
(%i4) norm(v) := sqrt(v.v);       /* vのノルム。 '.'は内積 */
(%o4)                       norm(v) := sqrt(v . v)
(%i5) v1: u1/norm(u1);            /* 基底1つめ。長さを1にするだけ。 */
                                 1           1
(%o5)                        [-------, 0, -------]
                              sqrt(2)     sqrt(2)
(%i6) w2: u2 - (u2.v1)*v1;        /* u2からv1方向を抜いて */
(%o6)                             [1, 1, - 1]
(%i7) v2: w2/norm(w2);            /* 長さを1にする。 */
                             1        1          1
(%o7)                    [-------, -------, - -------]
                          sqrt(3)  sqrt(3)    sqrt(3)
(%i8) w3: u3 - (u3.v1)*v1 - (u3.v2)*v2;   /* u3からv1,v2方向を抜いて */
                                     1     1
(%o8)                             [- -, 1, -]
                                     2     2
(%i9) v3: w3/norm(w3);            /* 長さを1にする。 */
                           1         sqrt(2)         1
(%o9)            [- ---------------, -------, ---------------]
                    sqrt(2) sqrt(3)  sqrt(3)  sqrt(2) sqrt(3)

(%i1) dot(f, g) := integrate(f*g, x, -1, 1);  /* 内積を定義 */
(%o1)               dot(f, g) := integrate(f g, x, - 1, 1)
(%i2) norm(f) := sqrt(dot(f, f));   /* ノルムを定義 */
(%o2)                     norm(f) := sqrt(dot(f, f))
(%i3) u1: 1;            /* 元にする基底達 */
(%o3)                                  1
(%i4) u2: x;
(%o4)                                  x
(%i5) u3: x^2;
                                       2
(%o5)                                 x
(%i6) u4: x^3;
                                       3
(%o6)                                 x
(%i7) v1: u1/norm(u1);          /* 1つ目は長さを1にするだけ */
                                       1
(%o7)                               -------
                                    sqrt(2)
(%i8) w2: u2 - dot(u2,v1)*v1;   /* 2つ目からv1方向を抜いて, */
(%o8)                                  x
(%i9) v2: w2/norm(w2);          /* 長さを1にする */
                                   sqrt(3) x
(%o9)                              ---------
                                    sqrt(2)
(%i10) w3: u3 - dot(u3,v1)*v1 - dot(u3,v2)*v2;  /* 3つ目からv1,v2方向を抜いて, */
                                     2   1
(%o10)                              x  - -
                                         3

(%i11) v3: w3/norm(w3);         /* 長さを1にする */
                                          2   1
                              3 sqrt(5) (x  - -)
                                              3
(%o11)                        ------------------
                                      3/2
                                     2
(%i12) w4: u4 - dot(u4,v1)*v1 - dot(u4,v2)*v2 - dot(u4,v3)*v3;  /* 4つ目からv1,v2,v3方向を抜いて, */
                                    3   3 x
(%o12)                             x  - ---
                                         5
(%i13) v4: w4/norm(w4);         /* 長さを1にする */
                                         3   3 x
                             5 sqrt(7) (x  - ---)
                                              5
(%o13)                       --------------------
                                      3/2
                                     2
(%i14) [v1, v2, v3, v4];    /* 以下が求められた正規直交基底 */
                                         2   1               3   3 x
                             3 sqrt(5) (x  - -)  5 sqrt(7) (x  - ---)
            1     sqrt(3) x                  3                    5
(%o14)  [-------, ---------, ------------------, --------------------]
         sqrt(2)   sqrt(2)           3/2                  3/2
                                    2                    2

以上より\(P_3\)の正規直交基底として \[ \left\{\frac{1}{\sqrt{2}},\ \sqrt{\frac{3}{2}} x,\ \sqrt{\frac{5}{2}}\cdot\frac{1}{2}(3x^2-1),\ \sqrt{\frac{7}{2}}\cdot\frac{1}{2}(5x^3-3x)\right\} \] が得られました。

これは第6回にやりましたルジャンドル多項式を正規化した物となっています。第6回の内容を読み返すと新しい発見があると思います。

正規直交基底であると言う事は,任意の\(n\)次以下多項式\(f(x)\)をルジャンドル多項式\(\ell_0(x),\cdots,\ell_n(x)\)の線型和 \[ f(x)=a_0\ell_0(x) + a_1\ell_1(x) + \cdots + a_n\ell_n(x) \] に変換する為には単純に内積をとって \[ a_i = (f,\ \ell_i)=\int_{-1}^1f(x)\ell_i(x)\mathrm{d}x \] という計算をすれば良いことになります。

【練習問題】
\[ 1+2x+3x^2+4x^3 \] をルジャンドル多項式の線型和に直して下さい。

今の練習問題の結果から,任意の \[ f(x) \in V \] の \[ f(x) = \frac{c}{\sqrt{2}} + a_1\cos x + \cdots + a_n\cos nx + b_1\sin x + \cdots + b_n\sin nx \] という表現は,各基底との内積を取って \[ \begin{aligned} &c = \left(f(x),\ \frac{1}{\sqrt{2}}\right) = \frac{1}{\pi\sqrt{2}}\int_{-\pi}^{\pi}f(x)\mathrm{d} x \\ &a_i = (f(x),\ \cos ix) = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\cos ix\mathrm{d} x \\ &b_i = (f(x),\ \sin ix) = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\sin ix\mathrm{d} x \\ \end{aligned} \] によって得られる事がわかります。

ここで,強引ですが\(f(x)\in V\)という仮定を外して, \[ \begin{aligned} &c = \left(f(x),\ \frac{1}{\sqrt{2}}\right) = \frac{1}{\pi\sqrt{2}}\int_{-\pi}^{\pi}f(x)\mathrm{d} x \\ &a_i = (f(x),\ \cos ix) = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\cos ix\mathrm{d} x \\ &b_i = (f(x),\ \sin ix) = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\sin ix\mathrm{d} x \\ \end{aligned} \] によって定まる \[ \widetilde{f}_n(x) = \frac{c}{\sqrt{2}} + a_1\cos x + \cdots + a_n\cos nx + b_1\sin x + \cdots + b_n\sin nx \] という関数を考えてみましょう。

例えば\(f(x)=x\)という関数に対して,\(\widetilde{f}_n(x)\)を求めてみると \[ \widetilde{f}(x)=2\sin x - \frac{2}{2}\sin 2x + \frac{2}{3}\sin 3x + \cdots + (-1)^{n-1}\frac{2}{n}\sin nx \] となります。これをグラフにしてみれば以下のようになります。

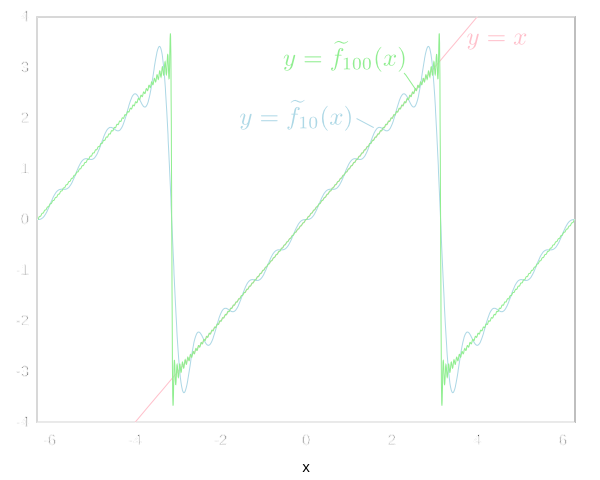
\(f(x)\)と\(\widetilde{f}_n(x)\)は\(-\pi < x < \pi\)の範囲では良く一致しているように見えます。\(n\)が大きい方がより一致しているような気もします。\(f(x)\)を様々に取り替えても同様の現象が見られます。

すると「\(n\rightarrow \infty\)としたらどうなるのか？」という興味が湧くと思います。こういった問題を取り扱うのがフーリエ解析という理論になります。無限次元の内積空間,無限級数の積分など「無限」が絡むので非常に難しい数学となりますが,興味のある方は勉強してみてください。

最後に正規直交基底に関する定理を１つだけ紹介します。

【証明の概要】
\(A^TA\)の第\((i,j)\)成分は\(A^T\)の第\(i\)行,つまり\(A\)の第\(i\)列と\(A\)の第\(j\)列の標準内積である事から明らかです。

今回はここで終わります。

線型代数の入門的な題材は一通り解説しました。一次方程式の反復解法が残っていますが来週にまわします。

来週は反復法に加え,微積分範囲でやり残している多変数関数の極値,重積分をやる予定です。