圏論勉強会
第9回

@ワークスアプリケーションズ

謝辞

この勉強会の企画，会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。

この会について

• 圏論(category theory)を題材にいろんなことを学びます。
• 分かり易さを重視して初歩的な例を多用します。
• 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
• 中高生も数人見ているらしいのでプログラミングと関係が浅い内容も取り上げます。
• この資料はhttp://nineties.github.com/category-seminarに置いてあります。

第9回

領域理論・不動点意味論

第9回の内容

今回は「領域理論」及び「不動点意味論」というプログラム意味論の重要な分野について紹介します。

本日の内容はとても2時間で扱いきれる様な物ではありませんので,初歩的な(しかし重要な)事柄のみを扱います。web上で得られる詳しい資料としては

• プログラム意味論については
  勝股審也:プログラミング言語の意味論
• (来週やる)始代数・終余代数については
  Jiri Adamek他"Initial algebras and terminal coalgebras: a survey"

などがあります。

プログラム意味論とは

プログラム意味論とは

プログラミング言語の意味を数学的に探求する理論計算機科学の分野を意味論(semantics)と言います。

表示的意味論とは

表示的意味論(denotational semantics)では,データ・プログラムを集合や関数などの数学的対象(表示(denotation))に対応させる事によって意味を表現する手法を用います。

例

問:以下で定義された$\mathrm{fact}$の意味は？(引数は自然数とする)

表示的意味論では(例えば)関数 $$ \mathrm{fact}(n) = n! \qquad (n\in\mathbb{N})$$ によって$\mathrm{fact}$の意味を表現します。

操作的意味論とは

操作的意味論(operational semantics)では,状態遷移系(数学的に形式化されたインタプリタ)を定義し, プログラムの1ステップの実行を状態遷移系への作用として記述する手法を用います。

例

問:以下で定義された$\mathrm{fact}$の意味は？(引数は自然数とする)

例えば,項書換え系という状態遷移系を用いると$\mathrm{fact}(5)$の評価は $$ \begin{aligned} \mathrm{fact}(5) &\rightarrow \mathrm{if}\ 5 = 0\ \mathrm{then}\ 1\ \mathrm{else}\ 5*\mathrm{fact}(5-1) \\ &\rightarrow 5*\mathrm{fact}(4) \\ &\rightarrow 5*(\mathrm{if}\ 4 = 0\ \mathrm{then}\ 1\ \mathrm{else}\ 4*\mathrm{fact}(4-1))\\ &\rightarrow \cdots \end{aligned} $$ の様に進みます。このような意味の与え方が操作的意味論の手法です。

公理的意味論とは

公理的意味論(axiomatic semantics)では,公理と推論規則を定義する事によってプログラムの意味を記述する手法を用います。

例

問:以下で定義された$\mathrm{fact}$の意味は？(引数は自然数とする)

手続き型言語の公理・推論規則の体系であるホーア論理(Hoare Logic)が有名です。

このようにプログラムへの意味の与え方には様々な方法があります。 今回紹介する「領域理論」「不動点意味論」は表示的意味論分野の理論となります。

領域理論

表示的意味論の土台が領域理論(domain theory)です。

表示的意味論は何らかの数学的対象の上に構築されますが,集合と(全域的)関数ではプログラムの意味を上手く表示出来ない事が判り デイナ・スコット(Dana Scott)などによって領域の研究が始められました。

領域理論の要点

領域理論では以下の事が主張されます。

• 計算の領域は最小値を持つ完備半順序集合である。
• 計算を表示する関数は連続関数である。

どのような意味か気になると思いますが,まずはいくつか定義と定理の確認を行います。

cpo

計算が行われる「領域」の定義です。

先ほどの圏論的な定義を翻訳すると以下のようになります。

連続関数

これも翻訳すると以下のようになります。

これから判るように、ここで単に「連続関数」と呼んでいるものは「単調な連続関数」の事です。

最小不動点定理

完備半順序集合と連続関数を用いる事の恩恵として以下の定理が得られます。

一般に関数$f$に対して$x = f(x)$を満たす$x$を$f$の不動点(fixed point)と言います。

【証明:不動点であること】
$D$をcpo,$F:D\rightarrow D$を連続関数とする。
$0$は始対象であるから $$ 0 \leqq F(0) $$ が成り立つ。さらに$F$は単調であるからこの不等式より $$ F(0) \leqq F^2(0) $$ が得られる。これを繰り返して$\omega$-chain $$ 0 \leqq F(0) \leqq F^2(0) \leqq F^3(0) \leqq \cdots \quad\cdots (1) $$ を得る。すると$D$はcpoなので $$ \lim_{\rightarrow} F^i(0) $$ が存在する。従って$F$は連続であるから $$ F(\lim_{\rightarrow}F^i(0)) = \lim_{\rightarrow}F(F^i(0)) = \lim_{\rightarrow}F^{i+1}(0) = \lim_{\rightarrow}F^i(0) $$ となる。(最後の変形は,$\omega$-chain $\{F^{i+1}(0)\}$の先頭に$0\leqq F(0)$を繋げたものは$(1)$と一致する為。)
従って$\displaystyle\lim_{\rightarrow}F^i(0)$は$F$の不動点である。 □

【証明続き:最小の不動点であること】
$F$の不動点$x = F(x)$が他に存在したと仮定すると,$0$は始対象であるから $$ 0 \leqq x $$ が成り立ち,さらに$F$は単調であるから $$ F(0) \leqq F(x) = x$$ が成り立つ。これを繰り返して任意の$i\in\omega$に対して $$ F^i(0) \leqq x$$ が得られる。すると余極限$\displaystyle\lim_{\rightarrow}F^i(0)$の性質より $$ \lim_{\rightarrow}F^i(0) \leqq x $$ となる。従って$\displaystyle\lim_{\rightarrow}F^i(0)$は$F$の最小の不動点である。 □

最小不動点定理の重要性

不動点は再帰と密接に関わります。最小不動点定理が重要であるのは,最小不動点の存在だけでなく,その具体的な構成方法を与えるからです。

何故cpoを考えるのか？

まず,$n$は自然数であるとして以下のコードの表示を考えてみて下さい。

$n \geqq 10$の時,$f(n)$を評価しても値は得られないので $$ f(n) = \left\{\begin{array}{cc} 0 & \text{($n<10$のとき)} \\ \text{値なし} & \text{($n\geqq 10$のとき)} \end{array}\right. $$ の様になります。このように定義域の一部でしか定義されない関数を部分関数(partial function)と言います。プログラムの意味論では部分関数を適切に表現する必要があります。

ボトム

部分関数を表現する為に,ボトム(bottom)と呼ばれる「値なし」の状況を表現する為の値をデータ領域に追加します。 これは記号$\color{red}{\bot}$で表されます。

集合$A = \{a,b,c,\cdots\}$に$\bot$を追加した集合を

と表す事にします。

例えば,先ほどの関数$f$は$f: \mathbb{N}_{\bot} \rightarrow \mathbb{N}_{\bot}$というドメイン・コドメインを持つ関数として表す事が出来ます。

部分オブジェクト

次に,cpo $A$と$B$の直積 $$ A\times B = \{(a,b) | a\in A, b\in B\} $$ を考えると,一部だけが定義された状態のデータが生じます。

例えば領域$\mathbb{N}_{\bot} \times\mathbb{N}_{\bot}$には $$ (\bot, \bot),\ (1, \bot),\ (\bot, 0),\ (1, 2),\cdots $$ などのデータが含まれる事になります。

この意味で領域の値を部分オブジェクト(partial object)などとも呼びます。

部分オブジェクトという概念が登場しましたが,これにcpoの構造を自然に入れる事が出来ます。

部分オブジェクトの順序

まず$ A_{\bot} = \{\bot,a,b,c,\cdots \}$の各要素には

によって順序を入れます。この形の領域を平坦なcpo(flat cpo)とも呼ばれます。

例えば$\mathbb{N}_{\bot}$の様子は下図の様になります。

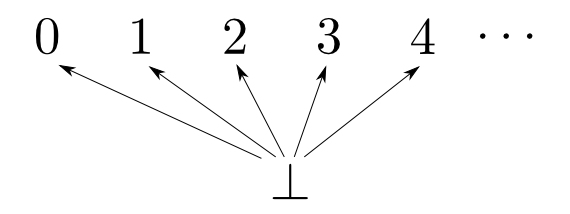
部分オブジェクトの順序

対$(a,b)$には

によって順序を入れます。

例えば$\mathbb{N}_{\bot}\times\mathbb{N}_{\bot}$の様子は下図の様になります。

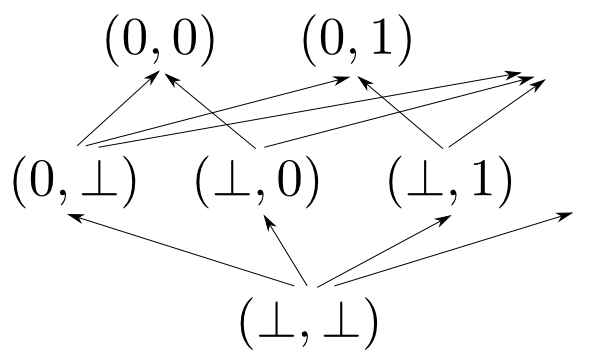
部分オブジェクトの順序

さらに関数自体もデータの一種ですが,これにも半順序構造が入ります。 関数$f, g: A\rightarrow B$間の順序は

によって順序を入れます。

例えば$f,g:\mathbb{N}_{\bot}\rightarrow\mathbb{N}_{\bot}$を $$ \begin{align} f(n) & = 0 \\ g(n) & = \mathrm{if}\ n < 10\ \mathrm{then}\ 0\ \mathrm{else}\ g(n+1) \end{align} $$ と定義した場合$g\leqq f$となります。

cpoに関する定理

cpoの構成に関しては以下のような定理が成り立ちます。

時間の関係上証明は省略しますが $$\begin{aligned} & \bot_{A\times B} = (\bot_{A},\bot_{B}),\ \lim_{\rightarrow}(a_i,b_i) = (\lim_{\rightarrow}a_i,\lim_{\rightarrow}b_i) \\ & \bot_{[A\rightarrow B]} = \text{(常に$\bot_{B}$を返す関数)},\ (\lim_{\rightarrow}f_i)(x) = \lim_{\rightarrow}f_i(x) \end{aligned}$$ とすれば良いです。但しcpo $D$の最小値を$\bot_{D}$と表しています。

順序関係の直感的な解釈

部分オブジェクト$a$,$b$が $$ a \leqq b$$ の関係であるという状況は

• $b$は$a$より良く定義されている。
• $b$は$a$より詳しい情報を持っている。

などと解釈する事が出来ます。

cpoの直感的な解釈

今の考え方に基づくと,計算の領域としてcpoを用いる事が自然だと思えるのではないでしょうか。

• 最小値$\bot$は「何も情報がない状態」を表している。
• $\omega$-chain $$ x_0\leqq x_1\leqq x_2\leqq \cdots $$ は情報量が向上していく($\bot$の部分が減っていく)ようなデータの列に対応する。
• $\omega$余完備であるということは,この列の全ての情報を含む,最小のデータが存在する事を表す。

単調関数の直感的な解釈

続いて関数$f: A\rightarrow B$が単調であるとは

が成り立つ事でした。

この条件は「入力の情報量を増やしたら,出力の情報量も増える」という事だと解釈出来ます。

再帰関数の不動点意味論

つまり,

と置くと $$ \mathrm{fact} = F(\mathrm{fact}) $$ と表されるので,

と述べる事が出来ます。

再帰関数と不動点

このようにある再帰関数の表示$f$は適当な関数$F$を用いて

という形で表現する事が出来ます。

最小不動点=ノイズが最小の不動点

$F$の不動点は複数存在し得ますが,最小不動点$f$は $$ g = F(g) $$ を満たすような$g$の中で情報量が最小の関数であると直感的に説明する事が出来ます。

例

という関数を考えます。先ほどと同様にするとこれは

の不動点という事になります。

例

ここで$c\in\mathbb{N}_{\bot}$を任意の定数として $$ f(n) = \mathrm{if}\ n=0\ \mathrm{then}\ 1\ \mathrm{else}\ c$$ という関数を考えると $$ f = F(f) $$ が成り立つ(練習問題)ので不動点となりますが,例えば$c = 100$にした

には元のプログラムに無い情報が含まれてしまっています。これでは適切な表示だと言えないでしょう。

不動点意味論

そこで再帰プログラムの表示$f$を

という形式で与える事にします。このような意味論を不動点意味論(fixed point semantics)と言います。

例

$$ F(f) = \lambda n. \mathrm{if}\ n = 0\ \mathrm{then}\ 1\ \mathrm{else}\ n*f(n-1)$$ の最小不動点$\displaystyle f = \lim_{\rightarrow}F^i(\bot)$を調べます。

まず $$F(\bot) = \lambda n.\mathrm{if}\ n=0\ \mathrm{then}\ 1\ \mathrm{else}\ \bot$$ となります。(乗算は$n*\bot = \bot$のように評価されます。)

すると $$\begin{aligned} F^2(\bot) &= \lambda n. \mathrm{if}\ n = 0\ \mathrm{then}\ 1\ \mathrm{else}\ n*F(\bot)(n-1)\\ &= \lambda n. \mathrm{if}\ n = 0\ \mathrm{then}\ 1\ \mathrm{else}\ n*(\mathrm{if}\ n-1=0\ \mathrm{then}\ 1\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n = 0\ \mathrm{then}\ 1\ \mathrm{else}\ n*(\mathrm{if}\ n=1\ \mathrm{then}\ 1\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n = 0\ \mathrm{then}\ 1\ \mathrm{else}\ (\mathrm{if}\ n=1\ \mathrm{then}\ 1*1\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n < 2\ \mathrm{then}\ n!\ \mathrm{else}\ \bot\\ \end{aligned} $$ となります。

例(続き)

以下同様にすると $$ F^i(\bot) = \lambda n. \mathrm{if}\ n < i\ \mathrm{then}\ n!\ \mathrm{else}\ \bot$$ が得られます。つまり$ F^i(\bot) $は$i$未満の自然数$n$については$n!$を返す関数です。

すると任意の$i$について $$ F^i(\bot) \leqq f $$ を満たすような$f$は $$ f = \lambda n. n! $$ しか無いのでこれが最小不動点となります。

例2

今の例では,最小不動点を用いるありがたみが解りにくいと思いますので,有名な例をもう一つ紹介します。

この$f$が一体どのような部分関数によって表示されるのか,パッと見ではよく分かりません。 しかし,以下の$F$の最小不動点を計算するだけで自動的に求めてしまうことが出来ます。 $$ F(f) = \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ f(f(n+11))$$

例2(続き)

順番に計算してみると $$\begin{aligned} F(\bot) &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ \bot \\ F^2(\bot) &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ F(\bot)(F(\bot)(n+11)) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ F(\bot)(\mathrm{if}\ n+11 > 100\ \mathrm{then}\ n+11-10\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ F(\bot)(\mathrm{if}\ n > 89\ \mathrm{then}\ n+1\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ n > 89\ \mathrm{then}\ F(\bot)(n+1)\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ n > 89\ \mathrm{then}\ (\mathrm{if}\ n>99\ \mathrm{then}\ n-9\ \mathrm{else}\ \bot)\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ n > 89\ \mathrm{then}\ (\mathrm{if}\ n>99\ \mathrm{then}\ n-9\ \mathrm{else}\ \bot)\ \mathrm{else}\ \bot) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ n =100 \ \mathrm{then}\ 91 \ \mathrm{else}\ \bot) \end{aligned} $$ となります。$n-9$に辿り着くのは$n=100$の時のみである事に注意して下さい。

例2(続き)

同様に計算を進めると $$ F^i(\bot) = \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ 100\leqq n < 99+i\ \mathrm{then}\ 91\ \mathrm{else}\ \bot)$$ が得られます。

従ってこの極限が最小不動点ですので,マッカーシーの91関数は

という関数である事が判りました。

Haskellを使った説明

import Data.Function

-- 実際に動くコードで最小不動点のアイデアを理解しましょう。
-- fact(n) = n!の例を使います。

-- 以下のfactFの最小不動点がfactです。
factF :: (Integer -> Integer) -> (Integer -> Integer)
factF f = \n -> if n == 0 then 1 else n*f(n-1)

-- すると以下のような関数の列が出来ます。
-- factNはN未満の自然数nについては正しくn!を返し,N以上の自然数についてはundefinedを返します。
fact0 = undefined
fact1 = factF undefined
fact2 = factF (factF undefined)
fact3 = factF (factF (factF undefined))
fact4 = factF (factF (factF (factF undefined)))
fact5 = factF (factF (factF (factF (factF undefined))))

-- 求める関数factはこの列の極限です。
-- Haskellの標準ライブラリには最小不動点を求める為の関数fixが用意されており
-- 以下の様にfactを得る事が出来ます。
fact = fix factF

不動点帰納法

数列 $$ \bot,F(\bot),F^2(\bot),F^3(\bot),\cdots,F^i(\bot),\cdots $$ の極限として最小不動点 $$ \lim_{\rightarrow}F^i(\bot) $$ が与えられるわけですが,この構造に基づいて帰納的に最小不動点の性質について証明を行う事が出来ます。

不動点帰納法で利用できる命題

cpo $D$の値を引数にとる命題$P(x)$が以下の条件を満たすとします。

このような$P(x)$を許容的(admissible)などと呼びます。

不動点帰納法

このような不動点の構成に基づく帰納法を不動点帰納法と言います。

先ほどのマッカーシーの91関数に関する簡単な命題を証明してみます。

$f\leqq g$が真であるということは($\mathbb{N}_{\bot}$が平坦なcpoなので) $$ f(n) \neq \bot \ \text{ならば} f(n) = g(n) $$ という事を意味します。

【証明】
$\bot \leqq g$である事は明らか。
$h:\mathbb{N}_{\bot}\rightarrow\mathbb{N}_{\bot}$が$h\leqq g$を満たすと仮定すると $$ \begin{aligned} F(h) &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ h(h(n+11))\\ &\leqq \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ g(g(n+11))\\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ g(\mathrm{if}\ n>89\ \mathrm{then}\ n+1\ \mathrm{else}\ 91) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ (\mathrm{if}\ n>89\ \mathrm{then}\ g(n+1)\ \mathrm{else}\ 91) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\\ &\qquad (\mathrm{if}\ n>89\ \mathrm{then}\ (\mathrm{if}\ n>99\ \mathrm{then}\ n-9\ \mathrm{else}\ 91)\ \mathrm{else}\ 91) \\ &= \lambda n. \mathrm{if}\ n > 100\ \mathrm{then}\ n-10\ \mathrm{else}\ 91 \\ &= g \end{aligned} $$ より$F(h)\leqq g$である。従って不動点帰納法により $$ \lim_{\rightarrow}F^i(\bot) \leqq g$$ である。□

第9回はここで終わります

お疲れ様でした。
領域理論、不動点意味論に思いの外時間がかかってしまったので,始代数・終余代数と不動点の関係,プログラム運算の続きは来週に回します。