圏論勉強会
第5回
@ワークスアプリケーションズ
中村晃一2013年6月13日
謝辞
この勉強会の企画,会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この会について
- 圏論(category theory)を題材にいろんなことを学びます。
- 分かり易さを重視して初歩的な例を多用します。
- 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
- 中高生も数人見ているらしいのでプログラミングと関係が浅い内容も取り上げます。
- この資料はhttp://nineties.github.com/category-seminarに置いてあります。
第5回: 様々な射
第5回の内容
前回は射によって考える事の重要性を話しましたが,今回は射の持つ様々な性質について説明していきます。射は関数概念の一般化とも考えられるので,集合・関数に関係する話も紹介します。
同型射
同型の定義
f:A→Bに対して,g:B→Aが存在し,
が成り立つならばfを同型射(isomorphism)と呼ぶ。
また,圏CにおいてAとBの間に同型射が存在するならば,CにおいてAはBと同型(isomorphic)であると言い,
A≅B
と表す。
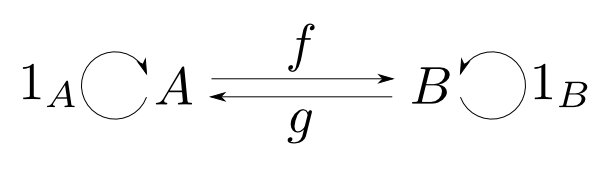
逆射
f:A→Bが同型射ならば
となるgは一意に定まる。このようなgを逆射(inverse)と言いf−1と表す。
 【一意性の証明】
【一意性の証明】
g,h:B→Aがfの逆射であるとすると右図が可換となるから,
g=h
となる。つまり逆射は一意に定まる。
□
同型射とは
同型射f:A→Bの存在,つまり A≅B である事はその圏に於いてAとBが本質的に同じものである事を表していると解釈出来ます。
これまで何となく≅を使いましたが,ちゃんと見ていく事にします。
函手は同型性を保つ
函手は合成射と恒等射を保つので下図の上の図式が可換ならば下の図式も可換となります。
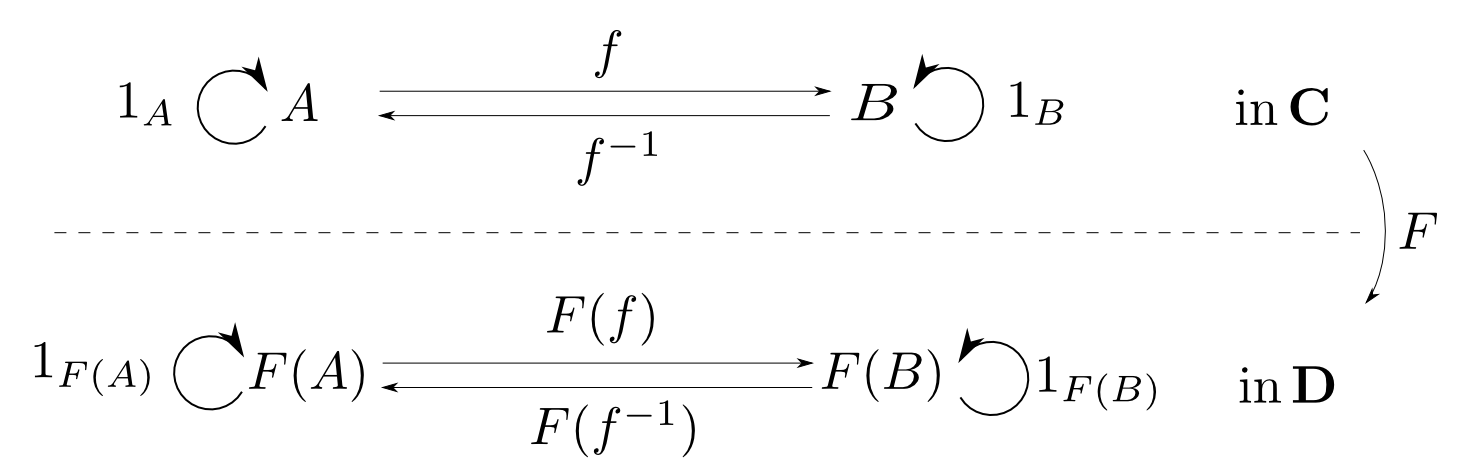
函手は同型性を保つ
つまり,以下の様な事が言えます。
函手F:C→Dについて fが同型射 ⇒ F(f)も同型射fが同型射 ⇒ F(f−1)=F(f)−1A≅B⇒F(A)≅F(B)
Cで同型⇔Copで同型
定義の対称性から明らかですが,Cでの同型射は双対圏Copにおける同型射に移ります。
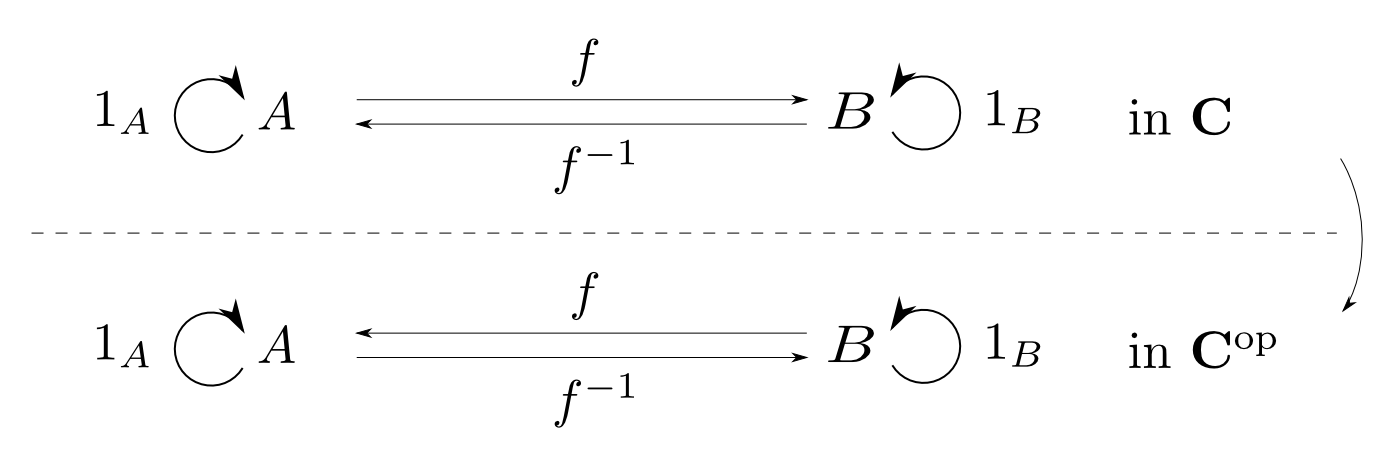
よって反変函手F:Cop→Dも同型性を保ちます。 A≅B⇒F(A)≅F(B)
特にHomC(X,−)は共変函手,HomC(−,X)は反変函手だったので,
A≅Bならば,任意のCの対象Xについて Hom(X,A)≅Hom(X,B)Hom(A,X)≅Hom(B,X)
となります。つまり同型な対象の周りの射一対一に対応しています。

同型射f:A⇆B:f−1が存在する場合には,「fを左から合成する事」が同型射 Hom(X,A)→Hom(X,B) を与え,「f−1を右から合成する事」が同型射 Hom(A,Y)→Hom(B,Y) を与えます。
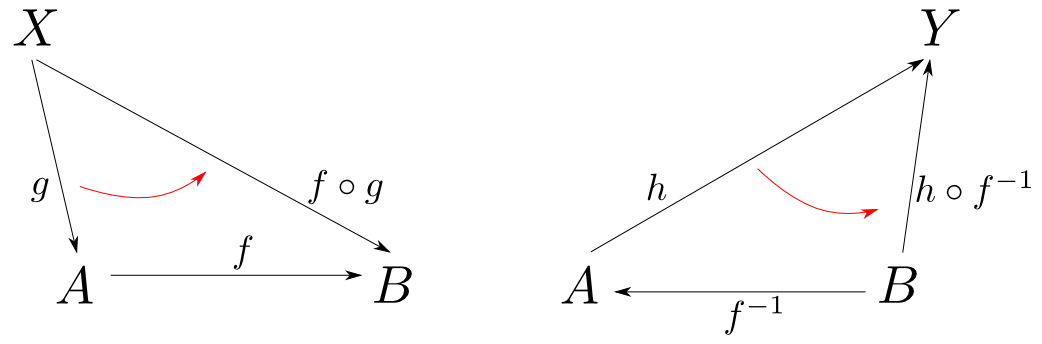
するとA≅Bの時,Aの周りの射をBの周りに移しても図式の可換性がそのまま保たれます。
A,Bの周りの射はただ一対一に対応するだけでなく,それらに成り立つ等式(可換図式)も一対一に対応している事になります。
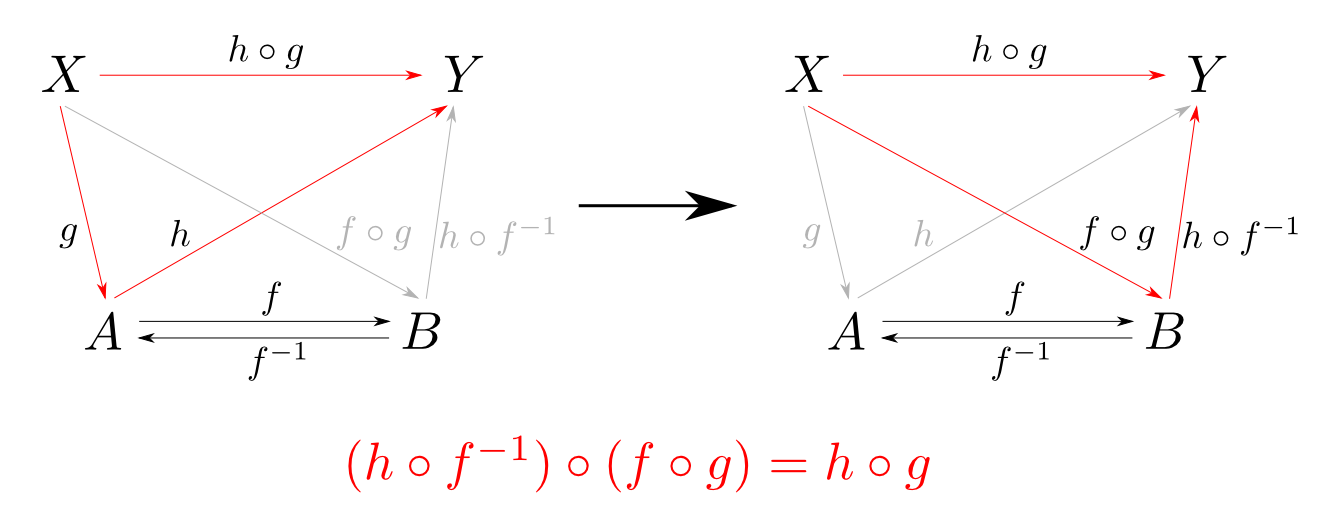
同型ならば区別出来ない
直感的に言うと,圏論の言葉のみを用いた場合
「A≅BのときAに関して成り立つ事はBに関しても成り立つ。逆も然り。」
という事になります。
逆に言うと同型である対象AとBをそれらが満たす性質のみによって区別する事は出来ないという事になります。
「同型ならば区別出来ない」の例
R>0を正の実数の集合とすると同型写像 f(x)=ax, f−1(x)=loga(x)(a>0,a≠1) によって (R,+)≅(R>0,×)in Mon が得られます。
すると(R,+)と(R>0,×)で異なる性質は対象や射の中身を覗かない限りMon内部では観測出来ないという事になります。
同値関係
集合A上の二項関係∼が
- 反射律: 任意のx∈Aについてx∼x
- 対称律: 任意のx,y∈Aについてx∼y ⇒ y∼x
- 推移律: 任意のx,y,z∈Aについてx∼y かつ y∼z ⇒ x∼z
を満たす時∼をA上の同値関係(equivalence relation)という。
厳密な定義とは異なりますが、「二項関係」とは「x=y」,「x≦y」, 「xがyの倍数」などの二引数の述語(真か偽を返す関数)の事だと思って良いです。
同型は同値関係
圏Cにおける同型≅はCの対象の集合上の同値関係になっています。つまり
が成り立ちます。
証明は練習問題としますが,ついでに以下の公式を得ます。
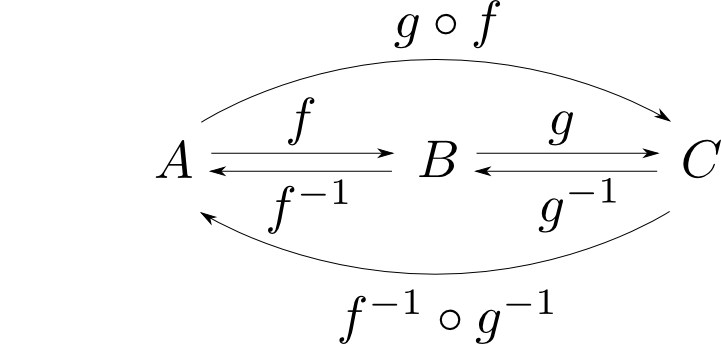
f:A→B, g:B→Cが同型射ならば (g∘f)−1=f−1∘g−1
【証明の概略】
反射律は任意のAについて1Aが同型射である事,対称律はfが同型射ならば逆射f−1も同型射である事,推移律はf,gが下図のような同型射ならばf−1∘g−1が逆射となる事を示せば良いです。そして逆射の一意性より上の公式が示されます。
モノイドにおける同型
モノイド(M,⋅)を圏とみなした時の同型射はeを単位元として x⋅y=y⋅x=e を満たすx,y∈M,つまり可逆元(invertivle element)の事です。
例えば(R,×)の同型射は0以外の全ての実数です。
「関数」や「準同型」以外の同型射の例となります。
半順序集合における同型
半順序集合(A,≦)においては x≦y, y≦x ⇒ x=y だったので,(A,≦)を圏とみなした場合,任意の対象xについてそれと同型なのはx自身のみとなります。
証明の圏における同型
P,Qを論理式とした時P≅Qであるとは P ⇒ QQ ⇒ P の証明が共に存在する事となります。つまり証明の圏における同型とは同値(equivalence)の事です。
Setsにおける同型
まず準備として単射・全射の定義の確認をします。
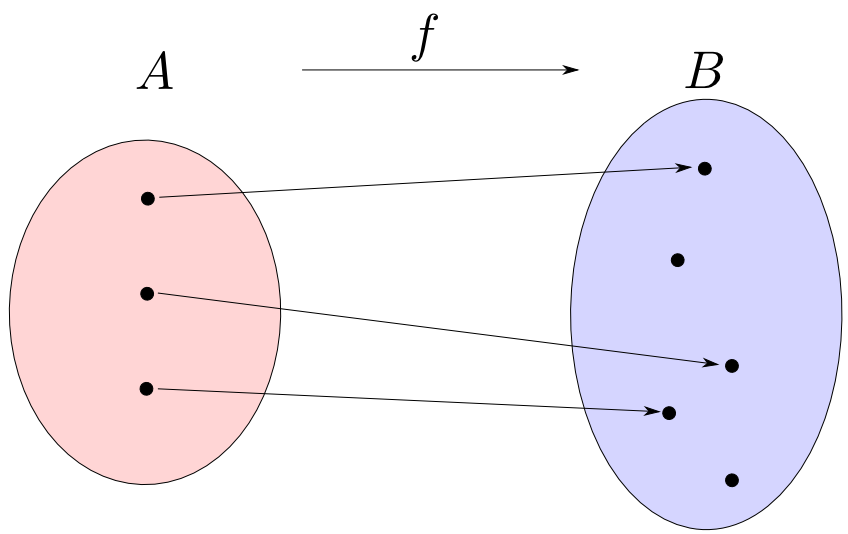
関数f:A→Bが単射(injection)であるとは,任意のx1,x2∈Aに対して
f(x1)=f(x2) ⇒ x1=x2
が成り立つ事である。
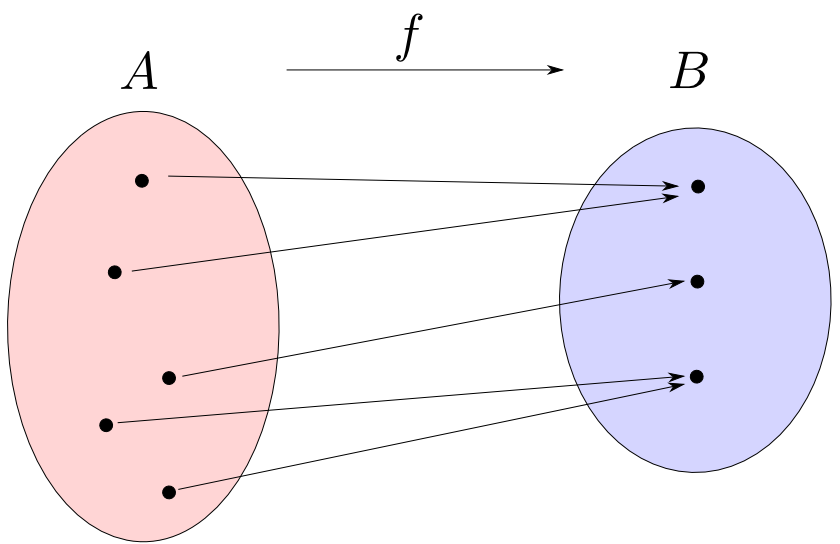
一方全射(surjection)であるとは,任意のy∈Bに対してf(x)=yを満たすx∈Aが存在する事である。
単射であり全射である関数を全単射(bijection)と呼ぶ。
単射
単射は異なるAの要素を異なるBの要素に移します。
全射
全射はその行き先(値域)がB全体を網羅します。
全単射
全単射は要素の一対一対応を与えます。
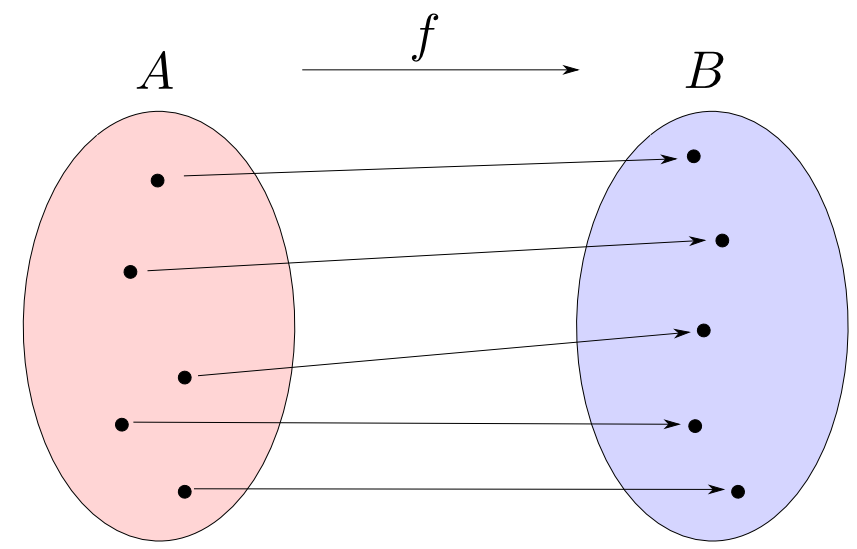
Setsにおける同型射とは全単射の事です。
【同型射ならば全単射である事の証明】
f,f−1が同型射とその逆射f:A⇆B:f−1であるとすると
f(x1)=f(x2)⇒f−1∘f(x1)=f−1∘f(x2)⇒1A(x1)=1A(x2)⇒x1=x2
なのでfは単射。また任意のy∈Bに対してx=f−1(y)∈Aが存在し,
f(x)=f∘f−1(y)=1B(y)=y
を満たすのでfは全射。従ってfは全単射である。
【全単射ならば同型射である事の証明】
f:A→Bが全単射であるとすると,任意のy∈Bについてf(x)=yを満たすxが存在する。ここでf(x1)=y,f(x2)=yであるとするとf(x1)=f(x2)であるからfの単射性よりx1=x2となる。すなわち任意のy∈Bについてf(x)=yを満たすxが唯一つ存在するので,この対応g:y=f(x)↦xは関数である。このとき任意のx∈Aについてg(f(x))=xとなるからg∘f=1A。また任意のy=f(x)∈Bについてf(g(y))=f(x)=yとなるからf∘g=1B。従ってfは同型射である。 □
集合のサイズを測る
有限集合A,Bの要素数が等しい事を「全単射f:A→Bが存在する事」として定義するのは自然です。

集合の濃度
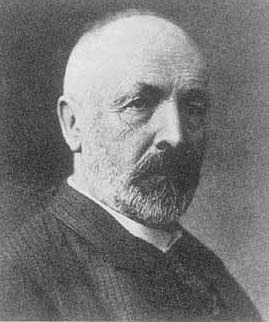
ゲオルグ・カントール(1845-1918)はこの考え方を無限集合にも一般化して「射で集合のサイズを測る」方法を確立しました。
集合Aのサイズを表す濃度(cardinal number)|A|というものを
を満たす様に定義する事が出来ます。
例えばf(x)=2xが自然数から0以上の偶数への全単射となるので |自然数の集合|=|0以上の偶数の集合| となります。
カントールの定理
任意の集合AについてAからその冪集合P(A)への全射は存在しない。従って全単射も存在しない。
Aが無限集合の場合にはP(A)も無限集合となりますが,AとP(A)の濃度が異なるという事をこの定理は言っています。今回濃度の大小の話はしていませんが,カントールは無限集合にもサイズの大小があるという事を発見したわけです。
カントールの対角線論法
【証明】
全射f:A→P(A)が存在したと仮定して
X={x∈A|x∉f(x)}
とする。ここでXの要素は全てAの要素要素だからXはAの部分集合の一つであるから,fの全射性より
X=f(x)
を満たすx∈Aが存在する。するとx∈X=f(x)ならばx∉X,x∉X=f(x)ならばx∈Xであるからx∈X⇔x∉Xとなり矛盾。従ってこのような全射fは存在しない。□
単純に面白いということもありますが,「集合論」は数学の土台ですのでこういった基本的な事実は知っておきましょう。
また,対角線論法は計算機科学の重要な定理の証明にも使用されます。 圏論による一般化と併せて後の回に扱う予定です。
レトラクト
g∘f=1A, f∘g=1B が「共に」成り立つ事が同型の定義でした。この条件を弱めるとセクション・レトラクションが定義されます。
レトラクト
射s:A→B,r:B→Aについて r∘s=1A が成り立つ時sをrのセクション(section),rをsのレトラクション(retraction)と言う。またAをBのレトラクト(retract)と言う。
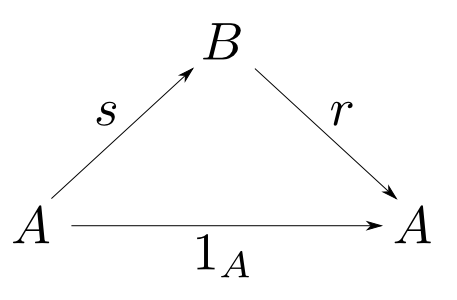
レトラクトとは
直感的に説明するとAがBのレトラクトであるということはBがAを取り出せる形で含んでいるという事を表しています。これによって様々な状況が説明されます。

函手はレトラクトを保つ
レトラクトは等式(可換図式)によって定義される事に注意しましょう。従って任意の函手F:C→Dはレトラクトを保ちます。
Setsにおけるレトラクト
Setsにおいて,r∘s=1Aであるならばsは単射,rは全射となります。この事実は後で一般化された形で見ます。
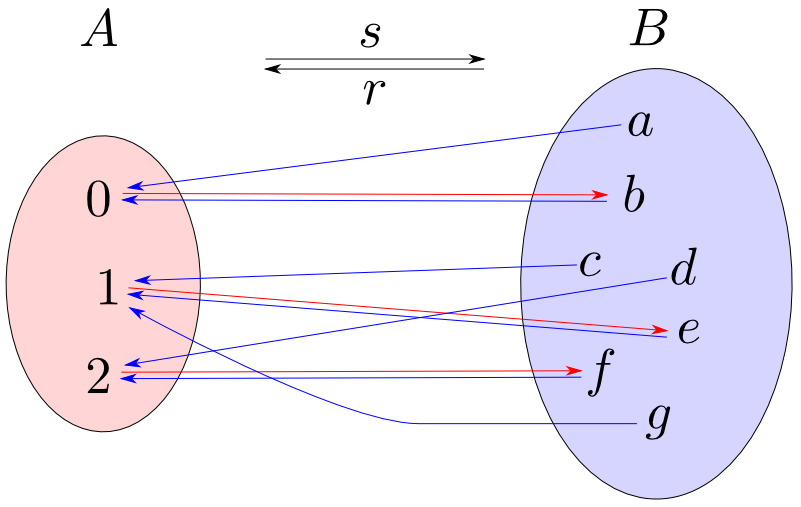
全射r:B→AによってBの要素は(Aの要素と同じ数だけの)空でない互いに素な集合に類別(classify)されます。
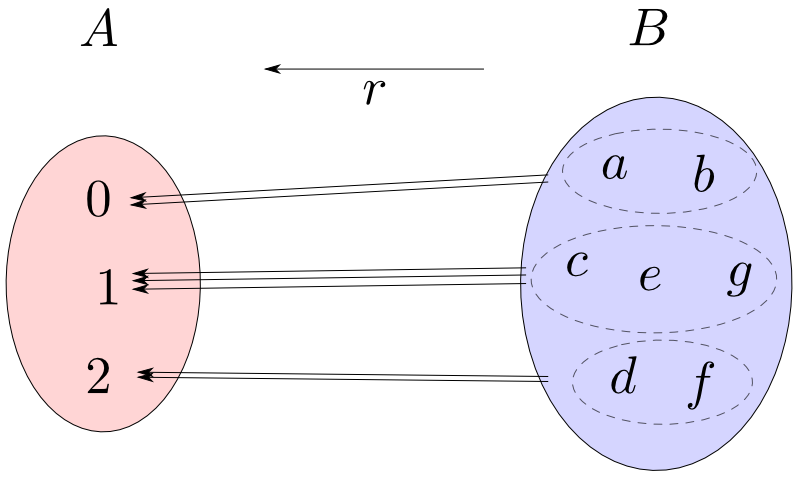
全射rのセクションがsが存在するならば,sはrによって類別された各集合から一つずつ元を選択する事に相当します。
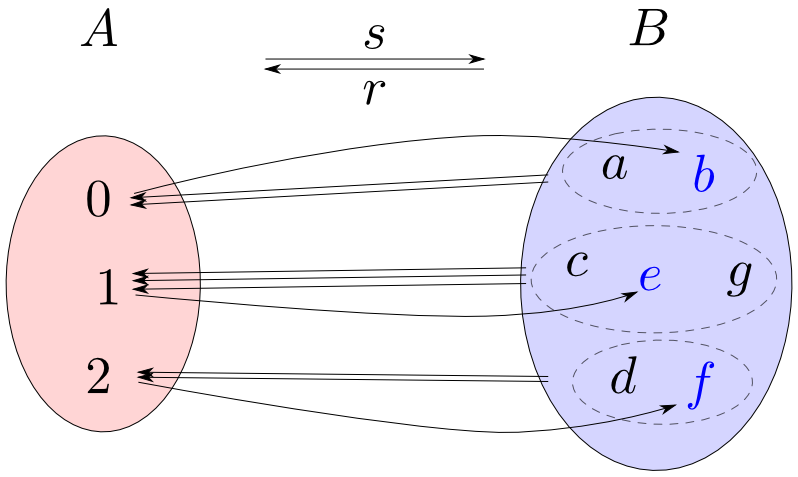
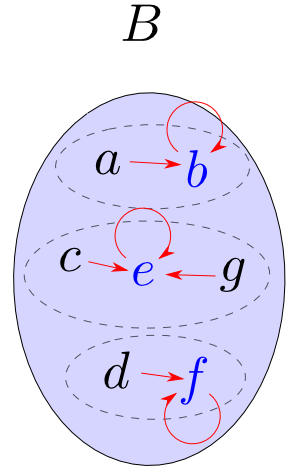
ここでe=s∘r:B→Bとおくとeはrによって類別された各集合の元を,sによって選択された元に移す関数となります。
この操作は一度やれば何度やっても変わりませんから e∘e=e が成り立ちます。この性質については後で説明します。
射r:B→Aのセクションが存在する事は以下と同値。
任意の対象Xと射f:X→Aについて下図が可換となるような射g:X→Bが存在する。
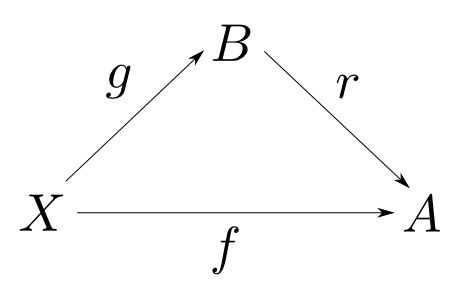
【前者⇒後者の証明】
r:B→Aのセクションs:A→Bが存在するならばg=s∘fとおくと
r∘g=r∘s∘f=1A∘f=f
が成り立つ。
【後者⇒前者の証明】
X=A,f=1Aの場合を考えるとgがrのセクションである。
同様に射s:A→Bのレトラクションが存在する事は以下と同値。
任意の対象Xと射f:A→Xについて下図が可換となるような射g:B→Xが存在する。
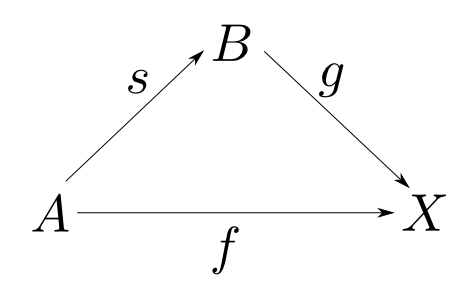
証明は練習問題とします。
モノ射・エピ射
AがBのレトラクトであるということはBがAを取り出せる形で含んでいる事を表していると説明しました。
しかし,次に説明するように取り出せないけどBがAを含んでいるという状況があります。
位相空間と連続写像からなる圏を考えます。D2を円板,S1をその縁とすると確かにD2はS1を含んでいます。
しかしD2に穴を開けずにS1に変形する事は出来ないので,S1はD2のレトラクトになっていません。
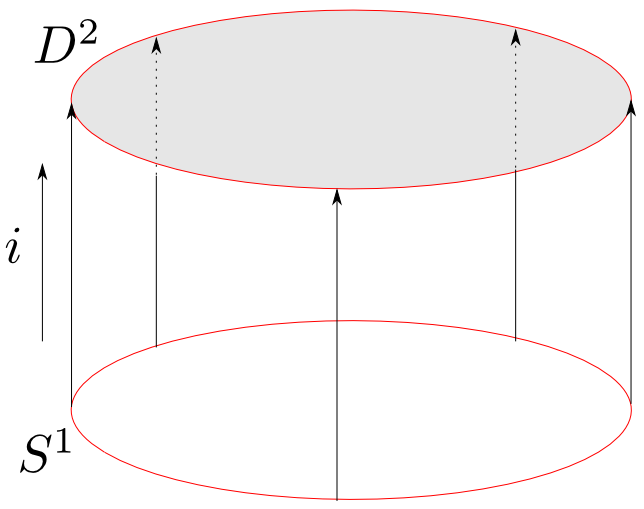
(直感的な意味での)「AがBの一部であるという事」ををレトラクトによって定義するのは条件が強すぎるという事が判ります。
セクション・レトラクションの条件を緩めて,単射・全射の圏論による一般化を考えます。
f:A→Bがレトラクションr:B→Aを持つという事は r∘f=1A が成り立つ事でした。この事はfを左から消す事が出来る事を表しています。セクションについても同様です。
A→Bへのモノ射・エピ射とはセクション・レトラクションと同様の性質をB→Aの向きの射の存在に依らずに定義したものと言えます。
モノ射
射m:A→Bがモノ射(monomorphism)であるとは,任意の対象Xと射f,g:X→Aについて
m∘f=m∘g ⇒ f=g
が成り立つ事である。
mがモノ射である事をモニックであるとも言い,記号ではm:A↣Bと表す。
Setsにおけるモノ射とは単射の事です。
【モノ射ならば単射である事の証明】
f:A→Bがモノ射であるとする。x1,x2∈Aがx1≠x2であるとする。x1,x2に対応する定数関数¯x1,¯x2:1→Aを考えると,¯x1≠¯x2となりfがモノ射であるからf∘¯x1≠f∘¯x2となる。すなわち,これに1の元を代入すればf(x1)≠f(x2)となる。
対偶を取れば任意のx1,x2∈Aについて
f(x1)=f(x2) ⇒ x1=x2
となるのでfは単射である。
【単射ならばモノ射である事の証明】
f:A→Bが単射であるとする。関数g,h:X→Aがg≠hならばあるx∈Xが存在してg(x)≠h(x)となる。するとfが単射であることよりf(g(x))≠f(h(x))であるからf∘g≠f∘hとなる。対偶を取れば
f∘g=f∘h ⇒ g=h
となるのでfはモノ射である。□
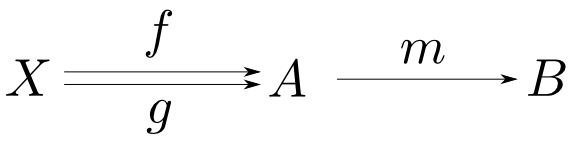
エピ射
射e:A→Bがエピ射(epimorphism)であるとは,任意の対象Xと射f,g:B→Xについて
f∘e=g∘e ⇒ f=g
が成り立つ事である。
eがエピ射である事をエピックであるとも言い,e:A↠Bと表す。
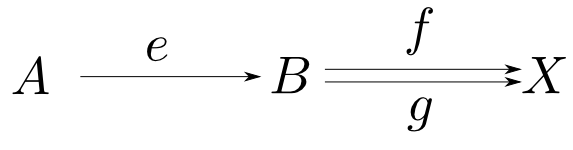
Setsにおけるエピ射とは全射の事です。
【エピ射なら全射である事の証明】
f:A→Bがエピ射でありかつ全射でないとすると,あるb∈Bについてb=f(x)を満たすx∈Aが存在しない。ここで関数g,h:B→{0,1}をg(x)=0
h(x)={0(x≠b)1(x=b)
によって定義すると,g≠hであるのにg∘f=h∘fとなる。これはfがエピ射である事に矛盾するので,fは全射である。
【全射ならばエピ射である事の証明】
f:A→Bが全射であるとする。関数g,h:B→Xがg≠hであるとするとあるy∈Bが存在しg(y)≠h(y)である。ここでfは全射であるからy=f(x)を満たすxが存在しg(f(x))≠h(f(x))となる。従ってg∘f≠h∘fであるから対偶をとって
g∘f=h∘f ⇒ g=h
すなわちfはエピ射である。□
同型射・セクション・レトラクションとの関係
以下の事実が言えます。証明は簡単なので練習問題とします。
- 同型射はモニックかつエピック
- fがレトラクションを持つならばfはモニック
- fがセクションを持つならばfはエピック
モニックかつエピック ⇏ 同型射
今見たようにモノ射は単射の一般化,エピ射は全射の一般化と言えます。
しかし,射fがモニックかつエピックであっても同型射であるとは限りません。
モニックかつエピックだが同型射でない例
Monにおける準同型 f:(N,+)→(Z,+) をf(x)=xによって定義します。これは明らかに同型射ではありませんが,モニックかつエピックです。g:(Z,+)→(M,⋅)があったとすると,g(−n)は必ずg(n)の逆源に移ります。従ってZのn≧0の部分のみによってg全体が定まるという事になります。
証明はAwodeyのテキストのExample 2.5にあります。時間があれば,当日説明します。
モノ射とエピ射は双対
fがCにおけるモノ射ならば,Copにおいてはエピ射となります。逆も然りです。すると一方の性質から他方の性質を自動的に得る事が出来ます。
例えばf:A↣B, g:B↣Cならばg∘f:A↣Cとなる事が示せます(練習問題)。
すると双対性によりf:A↠B, g:B↠Cならばg∘f:A↠C事も自動的に言えます。
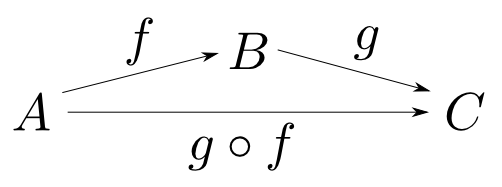
冪等射
冪等射
射e:A→Aが冪等射(idempotent)であるとは, e∘e=e が成り立つ事である。
分裂冪等射
先ほど述べた様にセクションとレトラクションs:A→B:r, r∘s=1Aを用いて e=s∘r と定義すると e∘e=s∘r∘s∘r=s∘1A∘r=s∘r=e なのでeは冪等射となります。
このようにセクションとレトラクションで表される冪等射を分裂冪等射(split idempotent)と言います。
プログラミングの文脈での冪等性
列と連結からなるモノイドにおいて[e]が冪等射であるとします。すると, [a,b,⋯,x,e,e,e,e,e,y,⋯]=[a,b,⋯,x,e,y,⋯] です。これをプログラムの命令の列だと思うと,eは連続して実行しても一回だけ実行しても同じ命令を表します。
例えば「ボタンを連打しても一回押しても同じ処理」、「同じ変数への同じ値の書き込み」などです。
この様にある種の冗長性(redundancy)を扱う場面で冪等性が登場する事があります。
第5回はここで終わります
お疲れ様でした。
関数によって類別や選択,包含関係などの2つの集合の関係が表現される事を見ました。
圏論では全てを射で考えるので,このような射の解釈に親しむ事がとても大切です。
次回は積・余積などを始めとする普遍的な対象について,その構成方法について説明をします。