圏論勉強会
第2回
@ワークスアプリケーションズ
中村晃一2013年5月23日 $$ \newcommand\append{{+\hspace{-.7em}+}} $$
謝辞
この勉強会の企画,会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。
この会について
- 圏論(category theory)を題材にいろんなことを学びます。
- 分かり易さを重視して初歩的な例を多用します。
- 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
- この資料はhttp://nineties.github.com/category-seminarに置いてあります。
第2回:モノイド・群
第2回の内容

モノイド勉強会
@ワークスアプリケーションズ
中村晃一2013年5月23日
第2回の内容
本日は予定を変更して一旦圏論を離れ,モノイド・群という概念について紹介します。 モノイド・群は「対象が$1$つの圏」でもありますので,本格的に圏論を学習する前に是非抑えておきたい内容です。
用語・記法について
- 自然数$\mathbb{N}$とは$0$以上の整数の事とします。
- 2項演算子$\star$の第1引数,第2引数を定数に固定した関数を便宜的に以下の様に表す事にします。 $$ \color{red}{(a\ \star)} : x \mapsto a \star x $$ $$ \color{red}{(\star\ a)} : x \mapsto x \star a $$ 例えば $$ (2\ +)(3) = 2 + 3 \qquad (+\ 2)(3) = 3 + 2$$ という感じです。
モノイド
モノイド
モノイド(monoid)とは集合$M$,$M$上の二項演算$\cdot$の組$(M, \cdot)$で,以下の条件を満たすものである。
- 結合律: 任意の$x,y,z \in M$について $$ (x\cdot y)\cdot z = x\cdot (y \cdot z)$$
- 単位元の存在: $e \in M$が存在し,任意の$x \in M$について $$ e\cdot x = x\cdot e = x $$
$M$をこのモノイドの台集合(underlying set)と言う。誤解の恐れがない場合にはモノイドと台集合に同じ記号を用いる。
モノイド:自然数と加法
$\mathbb{N}$を自然数の集合,$+$を整数の足し算としたとき, $$ (\mathbb{N}, +) $$ はモノイドとなります。単位元は$0$です。
モノイドの条件を全て満たす事を確認しましょう。
- $x,y \in \mathbb{N}$ならば$x + y\in\mathbb{N}$
- $(x + y) + z = x + (y + z)$
- $0 + x = x + 0 = x$
モノイド:自然数と乗法
$\mathbb{N}$を自然数の集合,$\cdot $を整数の掛け算としたとき, $$ (\mathbb{N}, \cdot) $$ はモノイドです。単位元は$1$です。
- $x,y \in \mathbb{N}$ならば$x \cdot y\in\mathbb{N}$
- $(x \cdot y) \cdot z = x \cdot (y \cdot z)$
- $1 \cdot x = x \cdot 1 = x$
加法・乗法によるモノイド
加法については
- 整数$\mathbb{Z}$,有理数$\mathbb{Q}$,実数$\mathbb{R}$,複素数$\mathbb{C}$,$\cdots$
- $2$の倍数,$3$の倍数,$\cdots$
- $\{a+b\sqrt{2} | a,b\in \mathbb{Q}\}$
など。乗法については
- 整数$\mathbb{Z}$,有理数$\mathbb{Q}$,実数$\mathbb{R}$,複素数$\mathbb{C}$,$\cdots$
- 正の自然数$\mathbb{N}^{+}$
- $\{1,2,4,8,16,32,\cdots\}$
など、様々な集合がモノイドの条件を満たします。
モノイド:列と連結
$[A]$を集合$A$を要素の有限列 $$ [a_0, a_1,\cdots,a_n] \qquad (a_i \in A) $$ とし,$\append$を列の結合 $$ [a_0,\cdots,a_m]\append[b_0,\cdots,b_n] = [a_0,\cdots,a_m,b_0,\cdots,b_n] $$ としたとき,$ ([A], \append) $はモノイドです。単位元は空列$[\,]$です。
- $x,y \in [A]$ならば$x \append y\in [A]$
- $(x \append y) \append z = x \append (y \append z)$
- $[\,] \append x = x \append [\,] = x$
モノイド:文字列と連結
「列」の一例として,文字列も連結に関してモノイドとなります。単位元は空文字列$\text{""}$です。
$$ \text{"Hello"} \append \text{" "} \append \text{"World!"} = \text{"Hello World!"} $$モノイド:論理積・論理和
$(\{\mathrm{true},\mathrm{false}\}, \mathrm{and})$ 単位元は$\mathrm{true}$。
$(\{\mathrm{true},\mathrm{false}\}, \mathrm{or})$ 単位元は$\mathrm{false}$。
モノイド:集合の$\mathrm{join}$,$\mathrm{meet}$
$(\mathcal{P}(A), \cup)$ 単位元は$\emptyset$。
$(\mathcal{P}(A), \cap)$ 単位元は$A$。
$\mathcal{P}(A)$は$A$の部分集合全てからなる集合($A$のべき集合(power set))です。例えば $$ \mathcal{P}(\{1,2,3\}) = \{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}\}$$ のような集合です。
モノイド:最大値・最小値
$A$を最小値$m$を持つ数値の集合とすると,$(A, \max)$は$m$を単位元とするモノイドです。
$A$を最大値$M$を持つ数値の集合とすると,$(A, \min)$は$M$を単位元とするモノイドです。
今の3つの例は「有界半束はモノイドである」という事実の具体例です。 「束」は積・余積と関係するので後の回に説明します。本日は分からなくても大丈夫です。
プログラミングにおけるモノイド
集約演算
データ列に対する集約・集積演算はモノイドと関係します。
- 値の和・積を求める。
- 条件を満たす要素を集める。
- 最大値・最小値を計算する。
- 全て~であるか?~を満たす物があるか?
関数型言語では畳み込み(folding)と呼ぶ事が多いです。
格納データを直列化出来るコンテナに対して,モノイドによる畳込みを定義する事が出来ます。
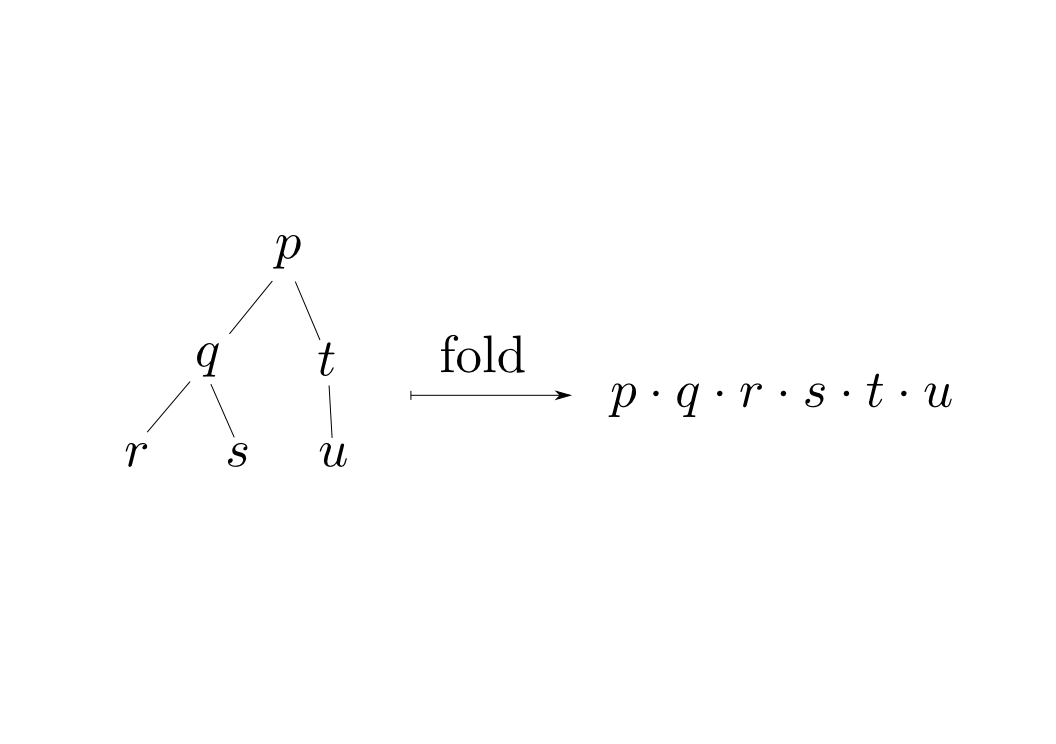
モノイドの結合性は任意の部分列から畳み込む事を正当化しますので,効率のよいアルゴリズムを考える際に重要です。
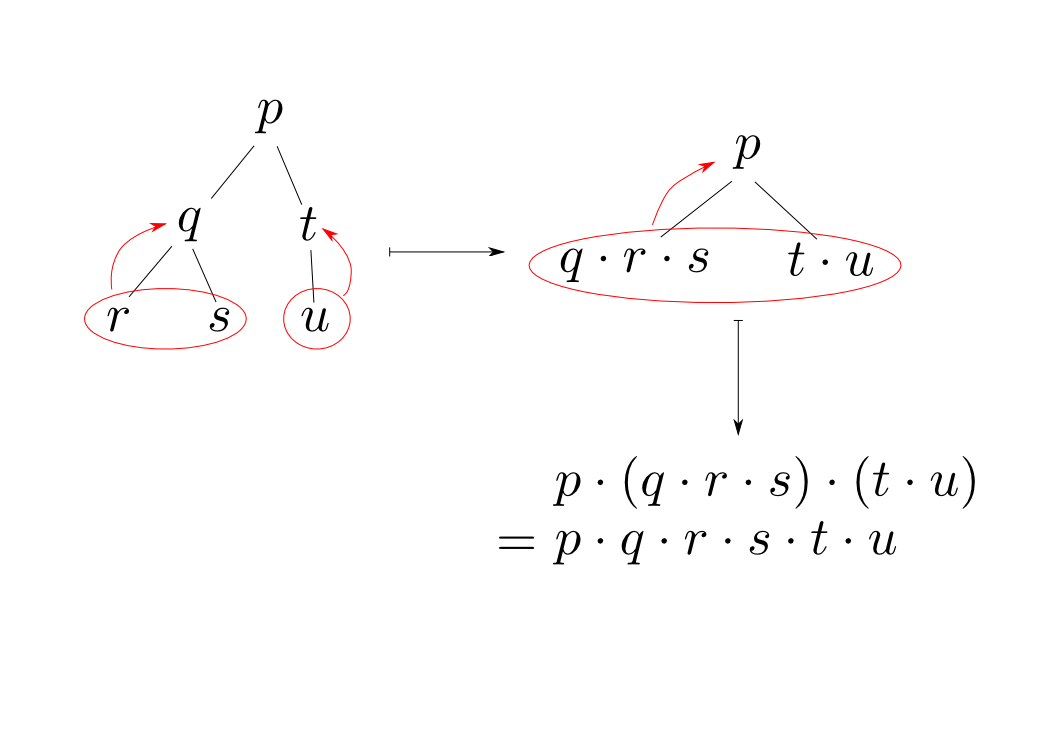
都合良くモノイドな値を格納している事は少ないので,個々の値を適当なモノイドにマッピングする操作とセットで考えましょう。
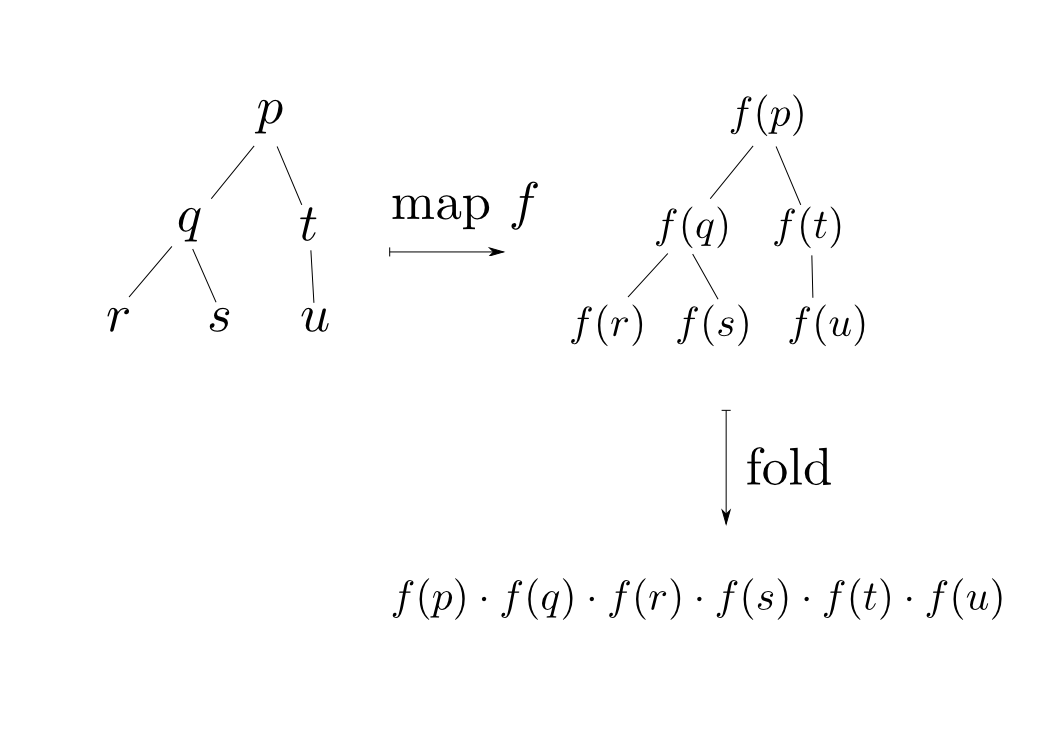
つまり,$\mathrm{map}$と$\mathrm{fold}$を合成した関数によって様々な畳み込みを行うことがはずです。

Haskellでの例
GHCiをお持ちの方は..... > となっている部分のコードを動かしてみて下さい。
-- モノイド,畳込み,木のライブラリを読み込みます
Prelude> :m +Data.Monoid Data.Foldable Data.Tree
Prelude Data.Monoid Data.Foldable Data.Tree> :set prompt "> "
-- 木を作ってみます
> let tree = unfoldTree (\x -> (x, [1..x-1])) 4
> let showTree t = putStr . drawTree . fmap show $ t
> showTree tree
4
|
+- 1
|
+- 2
| |
| `- 1
|
`- 3
|
+- 1
|
`- 2
|
`- 1
-- Monoidというライブラリには様々なモノイドが定義されています。
> :info Monoid
class Monoid a where
mempty :: a
mappend :: a -> a -> a
mconcat :: [a] -> a
-- Defined in `Data.Monoid'
instance Monoid [a] -- Defined in `Data.Monoid'
instance Num a => Monoid (Sum a) -- Defined in `Data.Monoid'
instance Num a => Monoid (Product a) -- Defined in `Data.Monoid'
instance Monoid Ordering -- Defined in `Data.Monoid'
instance Monoid a => Monoid (Maybe a) -- Defined in `Data.Monoid'
instance Monoid (Last a) -- Defined in `Data.Monoid'
instance Monoid (First a) -- Defined in `Data.Monoid'
instance Monoid (Endo a) -- Defined in `Data.Monoid'
instance Monoid a => Monoid (Dual a) -- Defined in `Data.Monoid'
instance Monoid Any -- Defined in `Data.Monoid'
instance Monoid All -- Defined in `Data.Monoid'
instance Monoid b => Monoid (a -> b) -- Defined in `Data.Monoid'
instance (Monoid a, Monoid b, Monoid c, Monoid d, Monoid e) =>
Monoid (a, b, c, d, e)
-- Defined in `Data.Monoid'
instance (Monoid a, Monoid b, Monoid c, Monoid d) =>
Monoid (a, b, c, d)
-- Defined in `Data.Monoid'
instance (Monoid a, Monoid b, Monoid c) => Monoid (a, b, c)
-- Defined in `Data.Monoid'
instance (Monoid a, Monoid b) => Monoid (a, b)
-- Defined in `Data.Monoid'
instance Monoid () -- Defined in `Data.Monoid'
-- fmapという関数は木の各ノードに関数を適用してくれます。
-- 下の例では,各整数を足し算によるモノイドの値にマッピングしています。
> showTree (fmap Sum tree)
Sum {getSum = 4}
|
+- Sum {getSum = 1}
|
+- Sum {getSum = 2}
| |
| `- Sum {getSum = 1}
|
`- Sum {getSum = 3}
|
+- Sum {getSum = 1}
|
`- Sum {getSum = 2}
|
`- Sum {getSum = 1}
-- 要素がモノイドの値である木に対し,foldを適用すると畳込みが行われます。
> fold (fmap Sum tree)
Sum {getSum = 15}
-- fmapとfoldを続けて行なってくれる(もちろん,内部的にはより効率のよい実装になっている)関数が
-- foldMapです。
> foldMap Sum tree
Sum {getSum = 15}
-- foldMapの計算結果はモノイドの要素としての値です。getXXXXなどの関数で中身を取り出す事が出来ます。
> getSum (foldMap Sum tree)
15
-- 積
> foldMap Product tree
Product {getProduct = 48}
-- 列(Haskellでは \x -> f(x)という記法で引数がxの関数を表します。)
> foldMap (\x -> [x]) tree
[4,1,2,1,3,1,2,1]
-- 文字列
> foldMap show tree
"41213121"
-- 集合のjoin
> foldMap (\x -> Data.Set.singleton x) tree
fromList [1,2,3,4]
-- 組(タプル)を使うと複数の畳み込みを同時に行えます。
> foldMap (\x -> (Sum x, Product x)) tree
(Sum {getSum = 15},Product {getProduct = 48})
-- 木のノード数の計算
> foldMap (\x -> Sum 1) tree
Sum {getSum = 8}
-- evenという関数は整数が偶数か否かを判定します。
> showTree (fmap even tree)
True
|
+- False
|
+- True
| |
| `- False
|
`- False
|
+- False
|
`- True
|
`- False
-- evenにAllを合成してみます。
> showTree (fmap (All . even) tree)
All {getAll = True}
|
+- All {getAll = False}
|
+- All {getAll = True}
| |
| `- All {getAll = False}
|
`- All {getAll = False}
|
+- All {getAll = False}
|
`- All {getAll = True}
|
`- All {getAll = False}
-- Allは論理積によるモノイドを表します。全てが偶数であるか => No
> foldMap (All . even) tree
All {getAll = False}
-- Anyは論理和です。
> foldMap (Any . even) tree
Any {getAny = True}
-- 条件分岐と組み合わせてみます。条件を満たさないものを単位元に移せば,
-- 条件を満たす値だけでの畳込みとなります。
> foldMap (\x -> if even x then Sum x else Sum 0) tree
Sum {getSum = 8}
とても便利ですね~
冷静に考えるとまだよく分からない。
- 足すとか掛けるとか,一種類の計算しか出来ないのか?
- 何が出来て何が出来ないのか?
例えば絵を描くという作業

- 円を描いて
- 線を引いて
- 色を塗って
- ・・・
絵とは一連の作業の集積では?
例えばロボットの操作
- 右を向け
- 前へ進め
- 止まれ
- ・・・
ロボットの動きとは一連の命令の集積では?
モノイド: endomorphismと合成
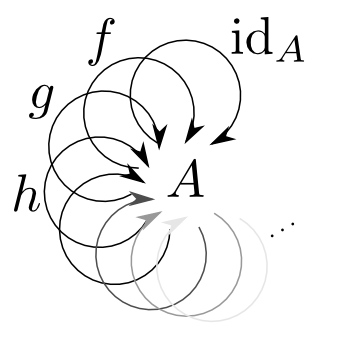
ドメインとコドメインが同じ集合である関数を,自己準同型写像(endomorphism)と言います。
集合$A$上の自己準同型全ての集合は関数合成に関して,恒等関数$\mathrm{id}_A$を単位元とするモノイドです。 このモノイドを$\color{red}{\mathrm{End}(A)}$と表すことにします。
Haskellでの例
-- Endomorphismの使用例です。
-- 以下は1を足すという関数。整数から整数へのendomorphismです。
> (+ 1) 2
3
-- 3を掛けるという関数。これも整数上のendomorphismです。
> (3 *) 3
9
-- このようなendomorphismをEndoというモノイドにして畳み込む事が出来ます。
-- foldMap (\x -> if even x then Endo (x *) else Endo (+ x)) tree
-- 正しこの畳込みの結果得られるのは
-- Endo { appEndo = 関数(表示出来ない) }
-- というモノイドとしての値ですので,appEndoで関数を取り出して何か数値を代入する必要があります。
-- 偶数なら掛けて,奇数なら足すという畳込みです。複数種類の演算を混ぜる事が出来ました。
> appEndo( foldMap (\x -> if even x then Endo (x *) else Endo (+ x)) tree ) 0
60
-- 検算をしてみます。
-- 要素の順番は以下のようになっています。
> foldMap (\x -> [x]) tree
[4,1,2,1,3,1,2,1]
-- これが
-- (4 *) . (+ 1) . (2 *) . (+ 1) . (+ 3) . (+ 1) . (2 *) . (+ 1)
-- というendomorphismの合成に移ります。
> ((4 *) . (+ 1) . (2 *) . (+ 1) . (+ 3) . (+ 1) . (2 *) . (+ 1)) 0
60
モノイドの表現
もしかして,任意のモノイドは自己準同型のなすモノイドとして表せるのでは?
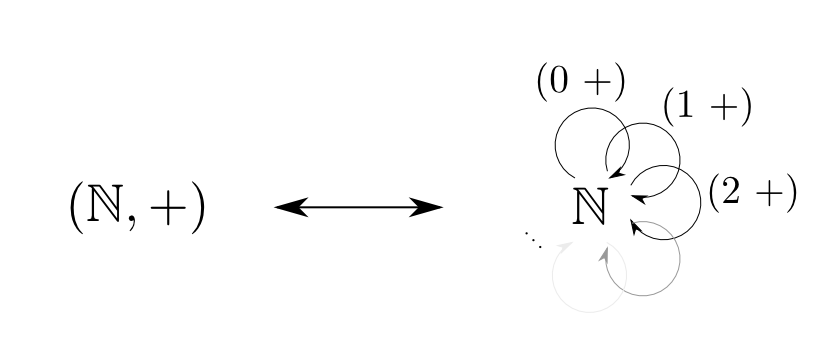
いくつか言葉を準備して,この現象について考えてみます。
準備: モノイド準同型
モノイドからモノイドへの構造を保ったマッピングを(モノイドの)準同型写像(homomorphism)と言います。「写像」を省略して準同型と呼びます。ところでモノイドの構造とは結合的な2項演算と単位元の事でした。
モノイド$(M,\star)$から$(N,\diamond)$への準同型$F: (M,\star) \rightarrow (N,\diamond)$とは,$M$から$N$への関数であり以下の条件を満たすもの。
- $ F(x\star y) = F(x)\diamond F(y)$
- $ F(e_{\star}) = e_{\diamond}\quad(\text{$e_{\star}$,$e_{\diamond}$は各モノイドの単位元}) $
準同型の例: $\mathrm{length}$
有限列の長さを得る関数$\mathrm{length}$は準同型
$$ \mathrm{length} : ([A],\append) \rightarrow (\mathbb{N},+) $$
と見なせます。
準備: モノイドの同型
同型とは「本質的に同じ」という事です。
モノイド$M$から$N$への準同型$f: M\rightarrow N$に対して準同型$g: N\rightarrow M$が存在し, $$ g\circ f= \mathrm{id}_M \qquad f\circ g = \mathrm{id}_N $$ である時,$f$を$M$から$N$への同型写像(isomorphism)と言う。モノイド$M$と$N$の間に同型写像が存在する時,$M$と$N$は同型(isomorphic)であると言い $$ M \cong N $$ と表す。
同型の例: $x \mapsto a^x$
例えば$f(x) = 2^x$という関数は準同型 $$ f: (\mathbb{N},+) \rightarrow (\{1,2,4,8,16,\cdots\},\cdot) $$ と見なせます。
同様に$g(x) = \log_2 x$が逆方向の準同型を与え, $$ \log_2 2^x = x \qquad 2^{\log_2 x} = x $$ なので$f$が同型写像である事が判ります。 $$ (\mathbb{N},+) \cong (\{1,2,4,8,16,\cdots\},\cdot) $$
準備: 部分モノイド
同じ演算からなるモノイド$(A, \cdot)$と$(B,\cdot)$について,$A \subseteq B$であるならば$A$は$B$の部分モノイドであると言い $$ (A,\cdot) \subseteq (B,\cdot) $$ と表す。
例えば,下のような例があります。 $$(\{0,2,4,6,8,\cdots\},+) \subseteq (\mathbb{N}, +) \subseteq (\mathbb{Z}, +) $$
定理
任意のモノイドは適当な集合$A$について$\mathrm{End}{A}$の部分モノイドと同型。
この定理は「表現定理」と呼ばれる一連の定理の一つです。
「モノイド」というよく分からない抽象概念に「集合と関数」からなる具体的な表現を与える事によって,
その正体が掴みやすくなるのです。今後の授業でも度々登場する重要なテーマです。
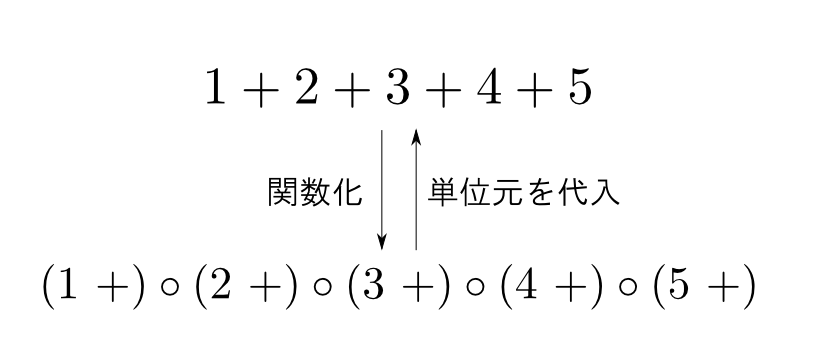
モノイド$M=(\{a,b,\cdots\},\cdot)$に対して,$\overline{M} = \{(a\ \ \cdot),(b\ \ \cdot),\cdots\}$とする。$e\in M$を単位元とする。すると,任意の$a,b\in M$に対して
- 任意の$x\in M$について$((a\cdot b)\ \ \cdot)(x) = (a\ \ \cdot)\circ(b\ \ \cdot)(x) = a\cdot b\cdot x$ なので $$ ((a\cdot b)\ \ \cdot) = (a\ \ \cdot)\circ(b\ \ \cdot) $$
- 任意の$x\in M$について$(e\ \ \cdot)(x) = e\cdot x = x$なので $$ (e\ \ \cdot) = \mathrm{id}_{M} $$
すなわち$\phi: a\mapsto (a\ \ \cdot)$は$M$から$\overline{M}\subseteq\mathrm{End}(M)$への準同型を定める。
ここで$\overline{M}$から$M$への写像$\psi: f\mapsto f(e)$を考えると,
- 任意の$x \in M$について $$ \psi\circ \phi(x) = \psi((x\ \ \cdot)) = (x\ \ \cdot)(e) = x\cdot e = x$$
- 任意の$(x\ \ \cdot) \in \overline{M}$について $$ \phi\circ\psi((x\ \ \cdot)) = \phi((x\ \ \cdot)(e)) = \phi(x) = (x\ \ \cdot)$$
すなわち $$ \psi\circ\phi = \mathrm{id}_{M}\qquad\phi\circ\psi = \mathrm{id}_{\overline{M}}$$ となる。
従って$(M, \cdot) \cong (\overline{M}, \circ)$ □
同様に$a\mapsto (\cdot\ \ a)$という同型写像を考える事も出来ます。ただし,畳み込みの順番を保つ為には関数合成の順番を逆にしたモノイド($\mathrm{End}(A)$の反モノイドと言います。)への写像を考える必要があります。
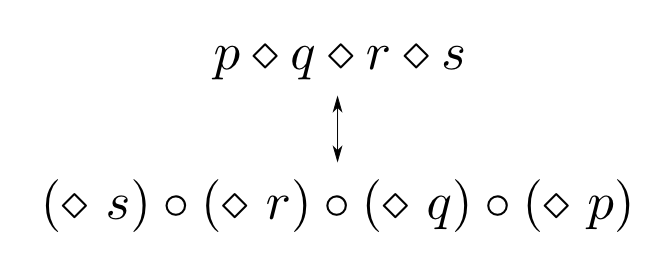
$\mathrm{foldr}と\mathrm{foldl}$
関数型言語を勉強するとそのうち$\color{red}{\mathrm{foldr}}$,$\color{red}{\mathrm{foldl}}$という謎の関数に出くわします。この授業でも今後よく登場すると思います。
さて,名前から分かる様にこれも畳み込みを行う関数ですのでモノイドと関係があるはずです。 今回はそのような視点からこれらを眺めてみます。
$\mathrm{foldr},\,\mathrm{foldl}$とは
$\mathrm{foldr}$は二項演算$\star : A\times B\rightarrow B$,$x \in B$を受け取り,$A$の要素の列を以下のように$B$の値に畳み込みます。
同様に$\mathrm{foldl}$は二項演算$\diamond : B\times A\rightarrow B$,$x \in B$を受け取り,以下のように畳み込みます。
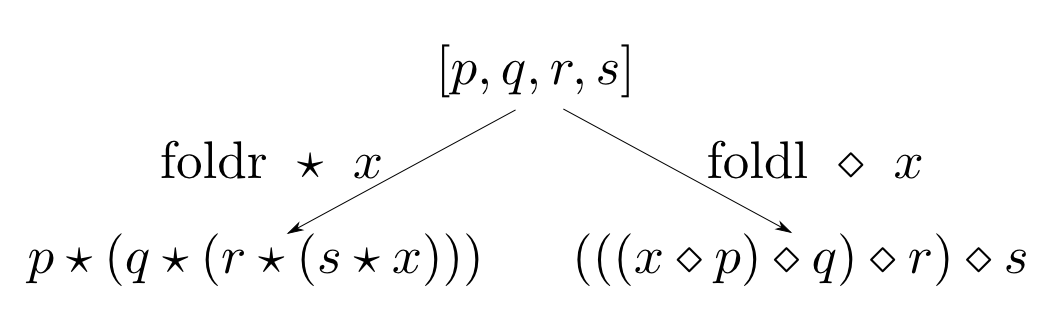
書きなおすと・・・
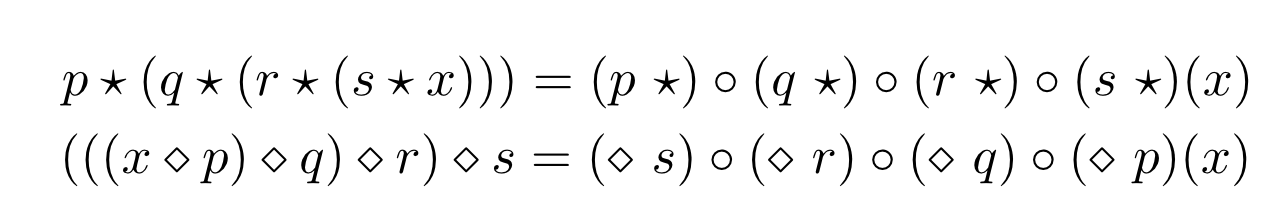
つまり$\mathrm{foldr},\,\mathrm{foldl}$は、自己準同型へのマッピングと値の代入を一挙に行なってくれる関数という見方が出来ます。数学的には作用素モノイドという概念と関係します。
$\star$,$\diamond$はモノイドの演算でなくても良いので非常に汎用的な関数であると言えます。
Haskellでの例
-- (x :)という関数はリストの先頭にxを追加するリストからリストへのendomorphismです。
> (1 :) [0,1,2]
[1,0,1,2]
-- [1,2,3,4,5]をこのendomorphismにして[2,3]に右から順番に適用してみます。
-- 5,4,3,2,1の順番に追加が行われた事が判ります。
> Data.Foldable.foldr (\x -> (x :)) [2,3] [1,2,3,4,5]
[1,2,3,4,5,2,3]
-- 今度は左から順番に適用してみます。foldrとfoldlは渡す関数の引数の順番が逆なので
-- flipという関数を挟む必要があります。
-- 1,2,3,4,5の順番に追加が行われた事が判ります。
> Data.Foldable.foldl (flip (\x -> (x :))) [2,3] [1,2,3,4,5]
[5,4,3,2,1,2,3]
-- foldr,foldlには任意のendomorphismを食わす事が出来ますから、様々な複雑な処理を行えます。
-- 例えばconst []という関数は引数を捨てて空リストを返す関数です。リストを引数に取れば
-- リストからリストへのendomorphismとなります。
> (const []) [2,3]
[]
-- リストを順番に見ていって,3に出くわしたら入力を捨てて空にしてしまうという例です。
> Data.Foldable.foldr (\x -> if x == 3 then const [] else (x :)) [2,3] [1,2,3,4,5]
[1,2]
-- foldrには任意のendomorphismを食わす事ができますが,有用なパターンは独立したモノイドとして
-- 取り出す事が出来ます。先ほどの掛けたり足したりの例から取り出してみます。
-- まず掛けたり,足したりする関数を合成すると全てf(x) = ax+bという形になります。
-- f(x) = ax+bとg(x) = cx+dを合成してみると
-- f(g(x)) = a(cx+d)+b = acx + ad+b
-- となります。係数だけ取り出してみれば
-- (a, b) と (c, d)の積が(ac, ad+b)になるという事です。こうして新しいモノイドを取り出す事が出来ました。
-- AddMulというモノイドを定義してみます
-- AddMulは2つのIntegerからなります。deriving (Show)というのはデータを表示出来るようにする為の指示です。
> data AddMul = AddMul Integer Integer deriving (Show)
-- モノイドである事を宣言します。
-- 単位元(mempty)は恒等関数f(x) = x = 1x + 0に対応するAddMul 1 0です。
-- 二項演算(mappend)は上で述べた通りです。
> instance Monoid AddMul where mempty = AddMul 1 0; AddMul a b `mappend` AddMul c d = AddMul (a*c) (a*d + b)
-- 先ほどの例をAddMulを使って計算してみます。
> appEndo( foldMap (\x -> if even x then Endo (x *) else Endo (+ x)) tree ) 0
60
-- (a *)という関数はa x + 0なのでAddMul a 0
-- (+ b)という関数は1 x + bなのでAddMul 1 bです。
> foldMap (\x -> if even x then AddMul x 0 else AddMul 1 x) tree
AddMul 16 60
-- 畳み込まれた結果は実はf(x) = 16x + 60という関数だという事が判りました。
-- 確認してみると確かに16x + 60となっている事が判ります。
> appEndo( foldMap (\x -> if even x then Endo (x *) else Endo (+ x)) tree ) 1
76
> appEndo( foldMap (\x -> if even x then Endo (x *) else Endo (+ x)) tree ) 2
92
自由モノイド
$\mathrm{foldMap}\ f$という関数は列の各要素を$f$でマッピングしてから畳み込む関数でした。
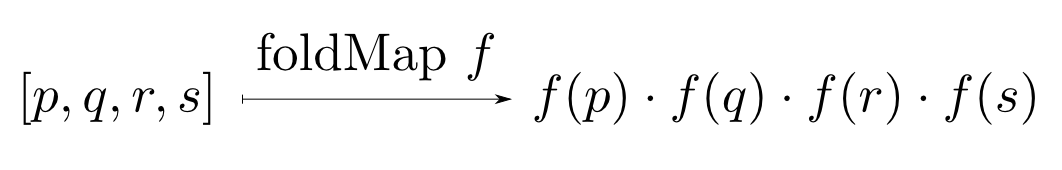
ところで連結演算によて列自体もモノイドとなります。すると$\mathrm{foldMap}\ f$はモノイド準同型と見なせます。
自由モノイド
「畳込み」を「列に縮約演算を入れる事」だと思えば,全ての畳み込みが「列と連結」からのモノイド準同型として作れる事になります。つまり,「列と連結」は特別なモノイドです。
この事を$([A], \append)$は$A$上の自由モノイド(free monoid)であると言います。
抽象的な自由モノイドの定義が欲しい!
「列と連結」という自由モノイドの定義は非常に具体的です。
「もの」と「矢印」と「矢印の連結」よって定義を与える事が出来れば,後に圏論に進んだ際にモノイド以外の概念に応用できるはずです。
自由モノイドの本質とは
任意の空でない列は下図のように長さ$1$の列に分解出来ます。一切の縮約演算が行われていないから,このような分解が出来るわけです。
すると,任意長の列からの準同型は「長さ$1$の列のマッピング」のみによって完全に決定されます。
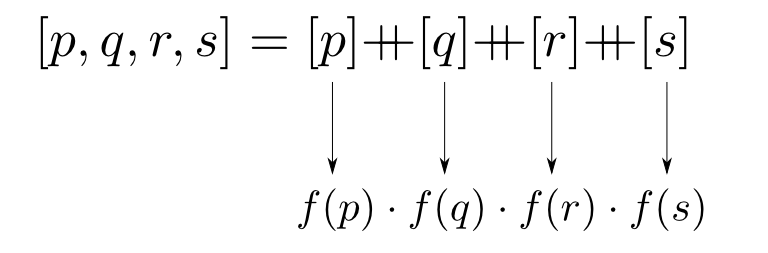
これがまさに$\mathrm{foldMap}$という関数が行なっている事です。
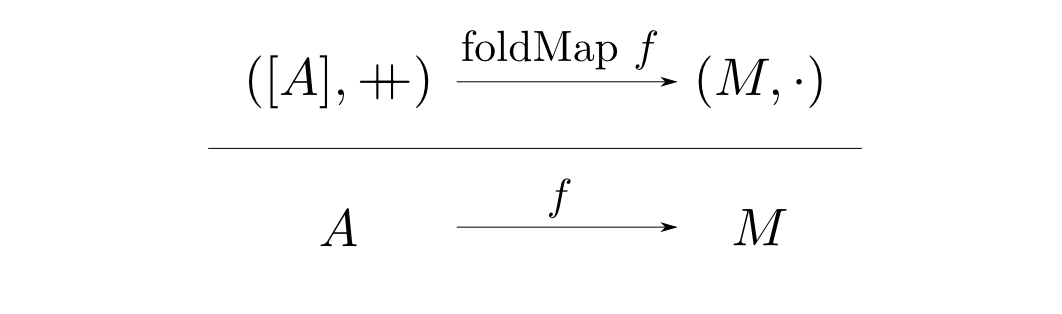
集合$A$の要素を長さ$1$の列にする関数を$i$とすると,下の図式が可換である事は
$$ \mathrm{foldMap}\ f\ [a] = f(a) $$
が任意の$a\in A$について成り立つという事です。
今説明したように,この可換図式が$\mathrm{foldMap}\ f$の機能を完全に決定します。(証明は後の回にやります。)
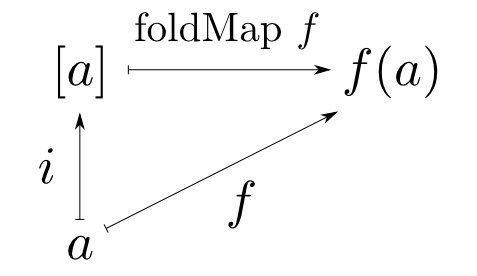
自由モノイドの定義
モノイド$F(A)$が集合$A$上の自由モノイドであるとはそれがある関数$i: A\rightarrow F(A)$を備えており,任意の関数$f: A\rightarrow M$に対して下側の図式が可換となるようなモノイド準同型$\overline{f}: F(A)\rightarrow M$が唯一つ存在することである。

自由モノイドは同型を除いて一意なので自由モノイドとは「列・連結」と同一視出来るものです。時間がないので証明は省略します。(Awodey本のProposition 1.10参照)
定理の内容を理解するのにはなかなか時間が掛かると思いますが,今後の為に是非復習を行なって下さい。
最後に
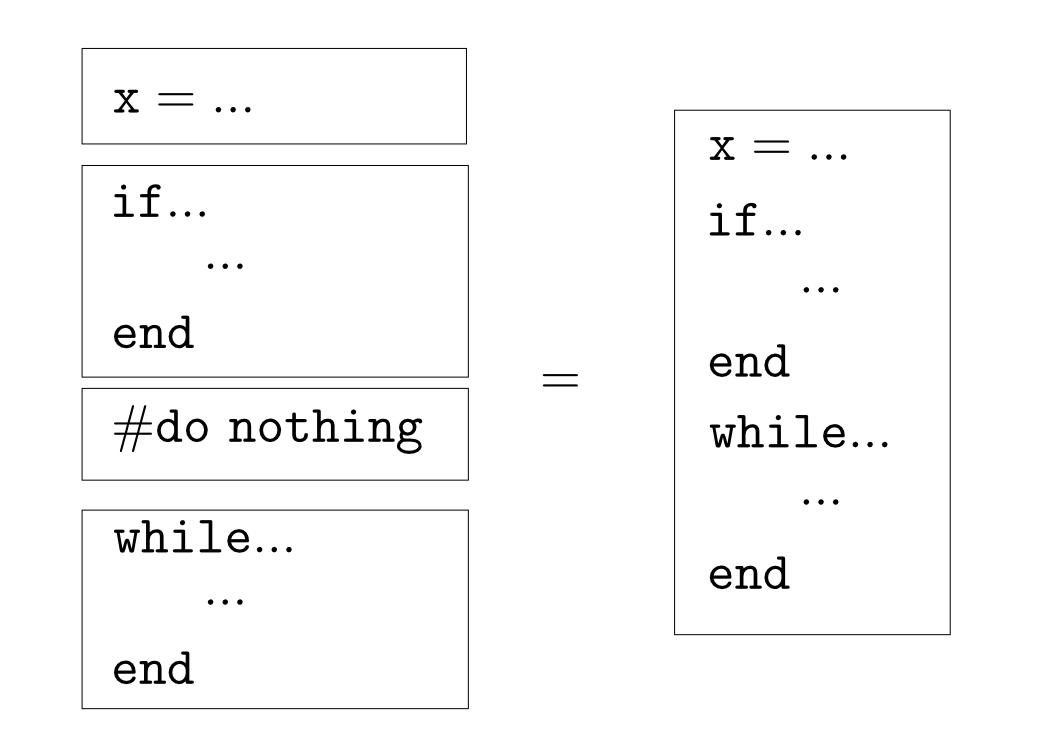
モノイド: プログラム
プログラムを「文(statement)の列」と思うと,「何もしない文」を単位元とし「文を並べる事」を演算とするモノイドと見なせます。
群
群
群(group)とはモノイド$(M,\cdot)$であり,
任意の$x\in M$に対して
$$ x \cdot y = y \cdot x = e \qquad \text{($e$は単位元)} $$
となる$y$が存在するものである。
$y$を$x$の逆元(inverse)と言い,
$$ y = x^{-1} $$
と表す。
群の例
- $(\mathbb{Z}, +)$,$(\mathbb{Q}, +)$,$(\mathbb{R},+)$,$(\mathbb{C},+)$
- $(\mathbb{Q}^{*}, \cdot)$, $(\mathbb{R}^{*}, \cdot)$($A^{*}$は$A$から$0$を除いた集合)
- $(\{\cdots,-4,-2,0,2,4,\cdots\}, +)$
- $(\{\cdots,\frac{1}{4},\frac{1}{2},1,2,4,\cdots\},\cdot)$
一方,以下のようなモノイドは群ではありません。
automorphism

ドメインとコドメインが同じ全単射の関数を,自己同型写像(automorphism)と言います。
集合$A$上の自己同型全ての集合は関数合成に関して,恒等関数$\mathrm{id}_A$を単位元とする群となります。 この群を$\color{red}{\mathrm{Aut}(A)}$と表すことにします。
正二面体群
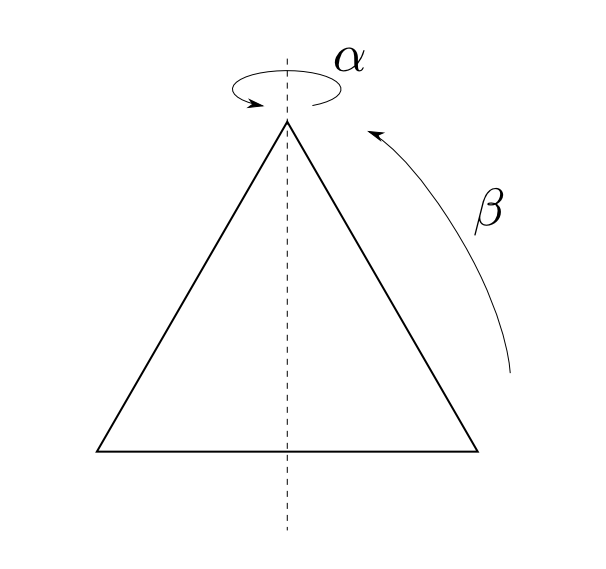
正$n$角形を正二面体と言います。下図は正三角形です。
正三角形の位置・形を変えない変換は「何もしない変換」「点線に関する対称移動($\alpha$)」「反時計回りに$120^\circ$回転($\beta$)」とこれらを組み合わせて出来る変換に限られます。そのような変換全体は群となります。
このように群は何らかの対称性を記述する為に使えます。
暗号
誤解を恐れずに言うと$\mathrm{Aut}(\text{文章の集合})$の中にありとあらゆる暗号化方法が入っています。その中で逆元の計算が困難な部分群を探すと強力な暗号化が出来ます。
実際にはそんなに単純な話ではありませんが,暗号理論と群論が密接に関わっているという事はわかると思います。

定理
任意の群は適当な集合$A$について$\mathrm{Aut}(A)$の部分群と同型。
モノイドの場合と同じ形の表現定理が存在します。証明は省略します。
ところで(圏$\mathbf{Sets}$における)$\mathrm{Aut}(A)$には非常に有用な見方があります。
対称群・置換群
集合上の自己同型写像は置換(permutation)と同一視出来ます。集合$A$上の置換全体のなす群を対称群(symmetric group)と呼び$\mathrm{Sym}(A)$と表します。対称群の部分群を置換群と呼ぶことにします。
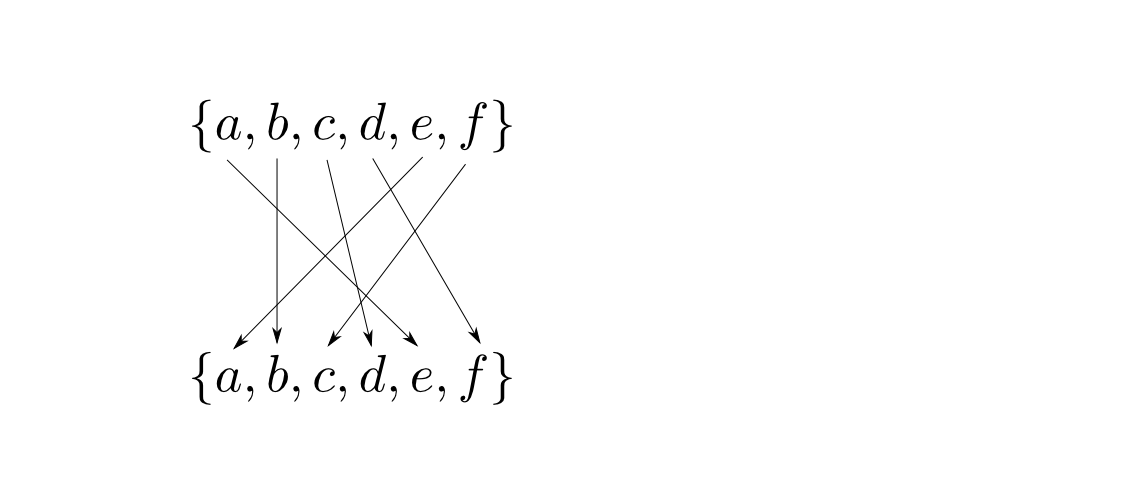
対称群・置換群
集合上の自己同型写像は置換(permutation)と同一視出来ます。集合$A$上の置換全体のなす群を対称群(symmetric group)と呼び$\mathrm{Sym}(A)$と表します。対称群の部分群を置換群と呼ぶことにします。
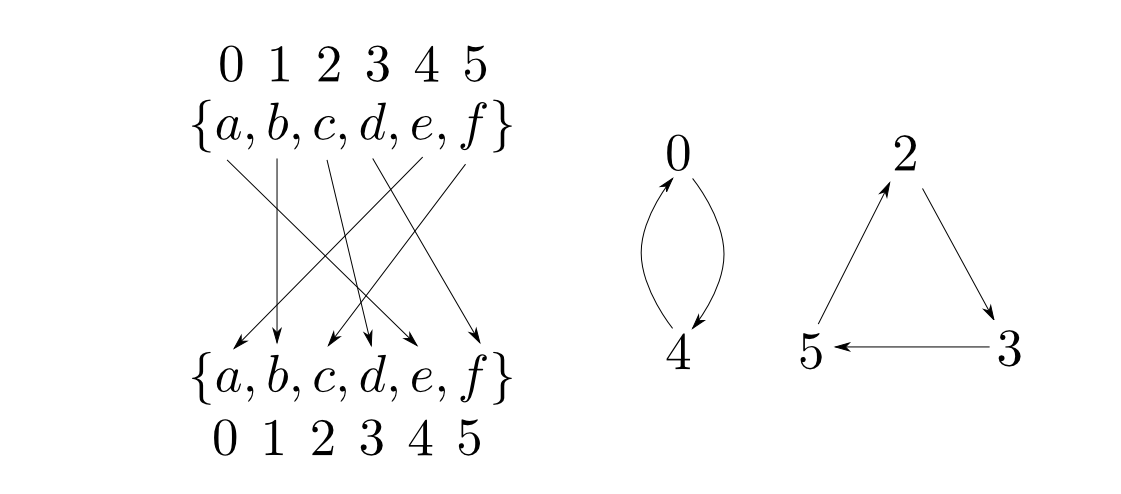
ケイリー(Cayley)の定理
任意の群は適当な置換群と同型。
先ほどの定理とほぼ同じ内容ですが「写像」と「置換」では大分印象が違います。 (要素の数が有限個の群の場合には)置換群による表現は計算機で扱う上で大変都合の良い形式であると言えます。
自由群
省略
第2回はここで終わります
お疲れ様でした。
圏論勉強会なのに圏論をやらずにすみませんでした。しかし,本日やったモノイド・群の表現,自由モノイドの概念は圏論によってさらに一般化する事が出来ます。本日の内容を理解しておくと,今後の学習がしやすくなると思いますので頑張って復習をして下さい。