圏論勉強会
第12回

@ワークスアプリケーションズ

謝辞

この勉強会の企画，会場設備の提供をして頂きました
㈱ ワークスアプリケーションズ様
にこの場をお借りして御礼申し上げます。

この会について

• 圏論(category theory)を題材にいろんなことを学びます。
• 分かり易さを重視して初歩的な例を多用します。
• 関数型言語の経験がある方がより楽しめると思います。資料中では主にHaskellを使います。
• 中高生も数人見ているらしいのでプログラミングと関係が浅い内容も取り上げます。
• この資料はhttp://nineties.github.com/category-seminarに置いてあります。

第12回

自然性・米田の補題

第12回の内容

圏論はもともと自然性というものを記述する為に生まれました。今回は自然性と圏論の重要な定理である米田の補題の紹介をします。 また、来週の内容を先取りして随伴を少しだけやります。

自然変換・自然同型

自然変換

函手$F, G: \mathbf{C}\rightarrow\mathbf{D}$間の自然変換(natural transformation) $$ \vartheta: F \rightarrow G$$ とは,$\mathbf{D}$の射$\vartheta_X: F(X) \rightarrow G(X)$の集合であり,任意の$\mathbf{C}$の射$f: X\rightarrow B$に対して下図が可換であるもの。 $\vartheta_X$を$\vartheta$の$X$成分(component)と言う。

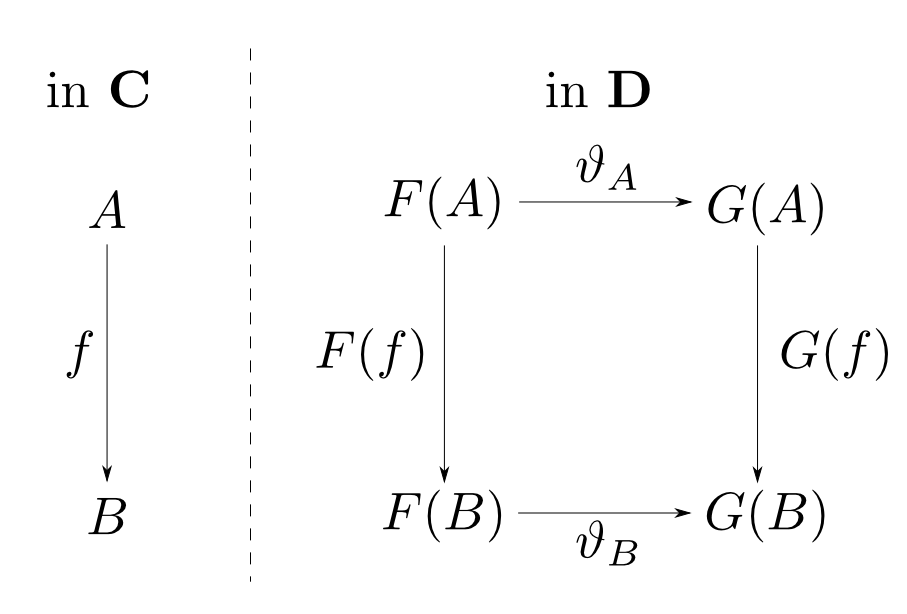
自然性とは

圏論において主に興味の対象となるのは、個々の対象や射ではなく様々な構成(construction)です。

構成は函手として扱われる事が多いですが、自然性とは構成と構成の関係の整合性を表します。

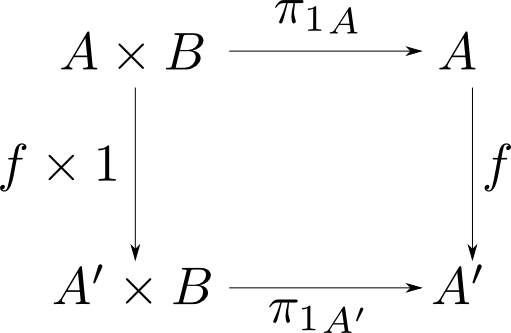
自然性の例

構成$ F(X) = X\times B$と$G(X) = X$に対して$A\times B$の第一成分を取り出す射影を${\pi_1}_{X}$ を$X$-成分とする自然変換 $$ \pi_1 : F\rightarrow G $$ が存在します。$ {\pi_1}_{A'}\circ (f\times 1) = f\circ{\pi_1}_{A} $が成立する事を確認して下さい。

自然同型

自然同型の例

「$A,B,C$のいずれに関しても」というのは

• 函手$-\times(B\times C)$と$(-\times B)\times C$
• 函手$A\times(-\times C)$と$(A\times -)\times C$
• 函手$A\times(B\times -)$と$(A\times B)\times -$

のいずれもが自然同型である事を言います。

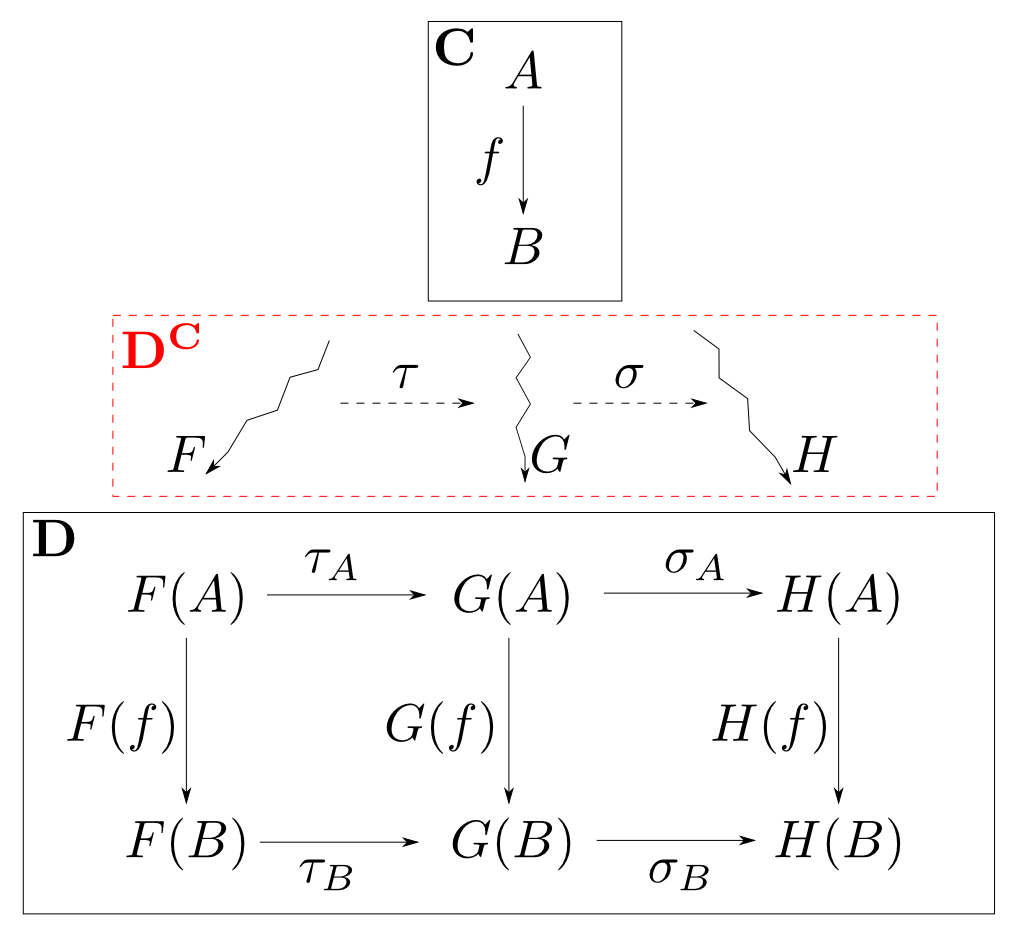
函手圏

圏$\mathbf{C}$と圏$\mathbf{D}$を固定します。

• 対象: $\mathbf{C}$から$\mathbf{D}$への函手
• 射: 自然変換

からなる圏を函手圏(functor category)と言い$\mathbf{D}^\mathbf{C}$と表します(第3回の復習)。

自然同型は函手圏における同型に他なりません。

函手圏=指数対象

圏が対象、函手が射である圏を$\mathbf{Cat}$と言いましたが、函手圏$\mathbf{D}^\mathbf{C}$は$\mathbf{Cat}$における指数対象となります。

$\mathbf{Cat}$には終対象$\mathbf{1}$と積圏$\mathbf{C}\times\mathbf{D}$が存在するので、$\mathbf{Cat}$はデカルト閉圏であるという事になります。

証明はAwodey本の7.6節を参照して下さい。

函手圏の$\mathrm{Hom}$集合

函手圏$\mathbf{D}^\mathbf{C}$における$\mathrm{Hom}(F,G)$は、自然変換 $$\vartheta: F\rightarrow G$$ の集合となります。分り易さの為に $$ \mathrm{Nat}(F, G) = \mathrm{Hom}_{\mathbf{D}^\mathbf{C}}(F, G) $$ と略記します。

米田の補題

集合値函手

コドメインが$\mathbf{Sets}$である函手 $$ F: \mathbf{C}\rightarrow\mathbf{Sets}$$ を集合値函手(Set-valued functor)と言います。

何故このようなものが重要になるかですが、函手圏$\mathbf{D}^\mathbf{C}$には$\mathbf{D}$の構造が反映される(第4回)という話を思い出しましょう。集合値函手のなす圏 $$ \mathbf{Sets}^{\mathbf{C}} $$ には$\mathbf{Sets}$の性質が遺伝するので、それを使って間接的に$\mathbf{C}$に関して調べる事が出来るようになります。

米田の補題

$F$に関して自然というのは任意の自然変換$\vartheta:F\rightarrow G$に対して、以下の図式が可換となる事を言います。

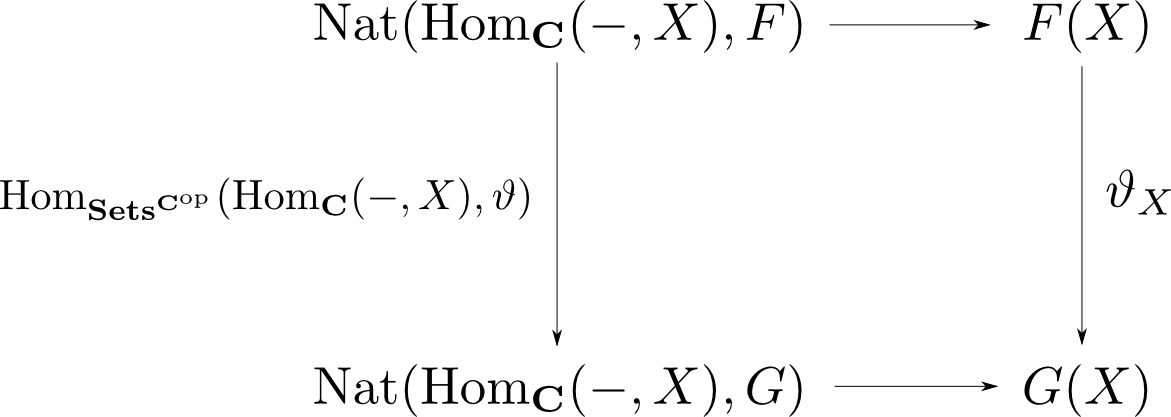
$X$に関して自然というのは任意の$\mathbf{C}$の射$f:X\rightarrow Y$に対して、以下の図式が可換となる事を言います。

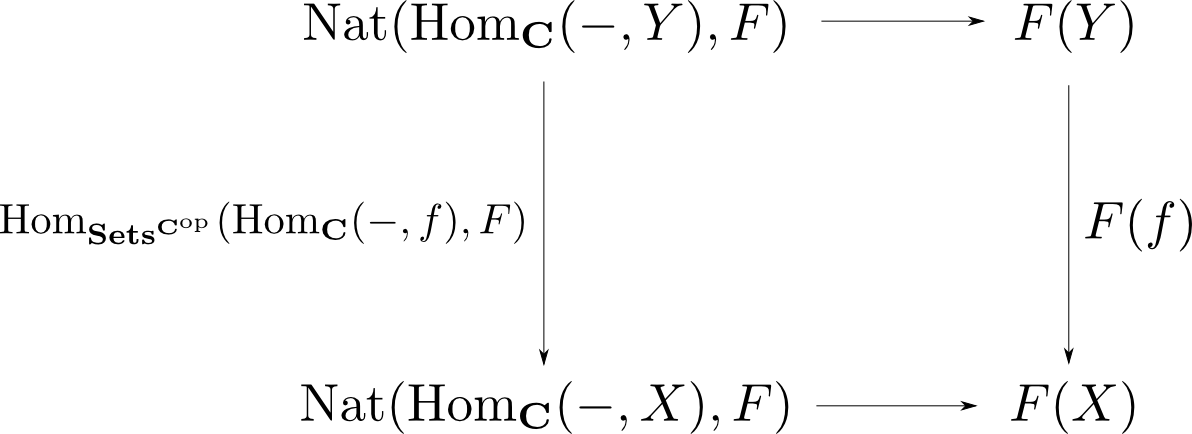
具体例:その1

具体例:その2

$ X = B^A$, $F(X) = \mathrm{Hom}(X\times A, B)$とおいてみると $$ \begin{aligned} &\mathrm{Nat}(\mathrm{Hom}(-,B^A),\mathrm{Hom}(-\times A,B)) \\ \cong & \mathrm{Hom}(B^A\times A, B) \\ \end{aligned} $$ が成り立ちます。

米田の補題の証明の概略

【証明:$\psi=\phi^{-1}$である事]
任意の$f: B\rightarrow A$に対して $$ \begin{aligned} \psi(\phi(\vartheta))_B(f) = \psi(\vartheta_A(1_A))_B(f) \\ = F(f)(\vartheta_A(1_A)) \\ = (\vartheta_B\circ \mathrm{Hom}(f,X))(1_A) \\ = \vartheta_B(1_A\circ f) \\ = \vartheta_B(f) \\ \end{aligned} $$ であるので$\psi\circ\phi = 1$である。 また任意の$x \in F(X)$に対して $$ \begin{aligned} \phi(\psi(x)) &= \psi(x)(1_X) \\ &= F(1_X)(x) \\ &= 1_{F(X)}(x) \\ &= x \end{aligned} $$ であるので$\phi\circ\psi = 1$である。以上より $$ \psi^{-1} = \phi$$ である。□

米田の補題の双対

$\mathbf{C}^\mathrm{op}$を$\mathbf{C}$に取り替えると以下の双対な定理も成立します。

Haskellのコードに翻訳してみる

米田の補題の応用

米田の補題より任意の$A,B$に対して $$ \mathrm{Hom}_{\mathbf{Sets}^{\mathbf{C}^{\mathrm{op}}}}(\mathrm{Hom}(-,A),\mathrm{Hom}(-,B)) \cong \mathrm{Hom}_{\mathbf{C}}(A,B) $$ が成立する事が導かれます。

米田の原理

今の等式より、以下の定理が得られます。これを米田の原理(Yoneda principle)などと呼ぶ事もあります。

米田の原理の使用例

前回複雑な証明を行った同型 $$ (A^B)^C \cong A^{(B\times C)} $$ は、任意の$X$に対して $$ \begin{aligned} \mathrm{Hom}(X, (A^B)^C) & \cong \mathrm{Hom}(X\times C, A^B) \\ & \cong \mathrm{Hom}((X\times C)\times B, A) \\ & \cong \mathrm{Hom}(X\times (B\times C), A) \\ & \cong \mathrm{Hom}(X, A^{(B\times C)}) \\ \end{aligned} $$ が成り立つ事と、curry化・積の結合則が自然同型である事から示されます。

米田埋め込み

米田の原理では対象$A$と函手$\mathrm{Hom}(-, A)$の対応が重要な役割を果たしました。この対応は函手 $$ y(A) = \mathrm{Hom}(-, A): \mathbf{C}\rightarrow\mathbf{Sets}^{\mathbf{C}^\mathrm{op}} $$ となりますが、これを米田埋め込み(Yoneda embedding)と呼びます。

圏$\mathbf{C}$をより良い性質を持った$\mathbf{Sets}^{\mathbf{C}^\mathrm{op}}$に一旦埋め込む事によって、先ほどのように見通しの良い議論を行う事が可能になります。圏論における重要な道具の一つです。

随伴

随伴は来週もやりますが、少しだけ先取りします。

随伴とは

圏論の創始者の１人であるS.MacLaneは

というスローガンを掲げました。この勉強会でこれまで説明した事の殆ど全てを、随伴によって説明する事が出来ます。

随伴

圏$\mathbf{C},\mathbf{D}$と函手$F: C\leftrightarrows D: G$について, 任意の$X,Y$に関して自然な同型 $$ \phi: \mathrm{Hom}_{\mathbf{D}}(F(X), Y) \cong \mathrm{Hom}_{\mathbf{C}}(X, G(Y)) $$ が存在するならば$(F,G,\phi)$を随伴(adjunction)と言う。また$F$を$G$の左随伴(left adjoint),$G$を$F$の右随伴(right adjoint)と言い $$ F\dashv G$$ と表す。

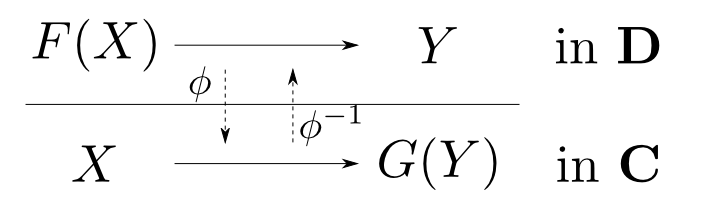
単位元と余単位元

随伴$(F,G,\phi)$に対して $$ \eta_X = \phi(1_{F(X)})\qquad \epsilon_Y = \phi^{-1}(1_{G(Y)}) $$ により定まる自然変換$\eta: 1_{\mathbf{C}}\rightarrow G\circ F$及び,$\epsilon: F\circ G\rightarrow 1_{\mathbf{D}}$を随伴の単位元(unit)、余単位元(counit)という。

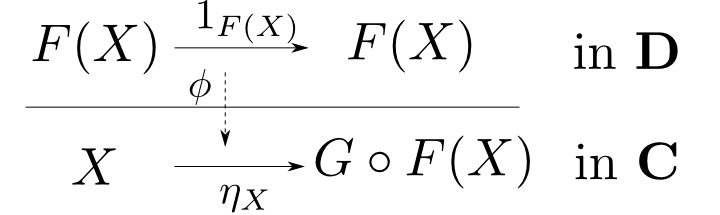
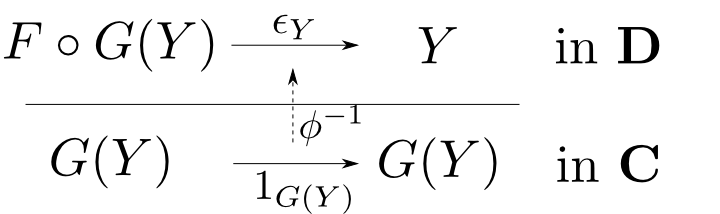
随伴の例:その1

圏$\mathbf{C}$が任意の二対象の積をもつ場合 $$ \Delta(X) = (X, X)$$ で定義される函手(対角函手)$\Delta: \mathbf{C}\rightarrow\mathbf{C}\times\mathbf{C}$の右随伴が函手 $$ \times (A,B) = A\times B $$ となります。すなわち $$ \Delta \dashv \times $$ です。

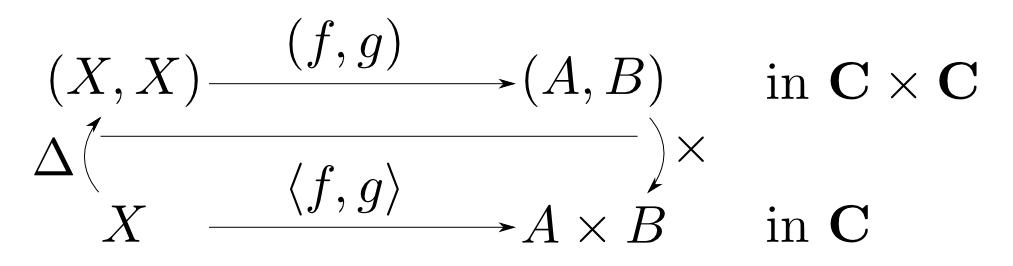
$\Delta\dashv\times$の余単位元

また $$ \langle \pi_1, \pi_2 \rangle = 1_{A\times B} $$ である事から $$ \epsilon_{A\times B} = \phi^{-1}(1_{A\times B}) = (\pi_1, \pi_2) $$ となります。

随伴の例:その2

全く同様になりますが、対角函手 $$ \Delta(X) = (X, X) $$ の左随伴が函手 $$ +(A,B) = A + B$$ となります。すなわち $$ + \dashv \Delta \dashv \times $$ という関係があります。

随伴の例:その3

前回やったカリー化

は $$ (-)\times A \dashv (-)^A $$ という随伴に対応しています。そして、この随伴の余単位元が評価射(evaluation map)となります。

第12回はここで終わります

お疲れ様でした。
今回紹介した他にも随伴の例が沢山ありますので、最終回はそれらの紹介と随伴に関する重要定理の紹介をした後、モナドをやります。